Second Contact Shell Mutation Diminishes Streptavidin-Biotin Binding Affinity Through Transmitted Effects on Equilibrium Dynamics

Abstract

We report a point mutation in the second contact shell of the high-affinity streptavidin-biotin complex that appears to reduce binding affinity through transmitted effects on equilibrium dynamics. The Y54F streptavidin mutation causes a 75-fold loss of binding affinity with 73-fold faster dissociation, a large loss of binding enthalpy (ΔΔH, 3.4 kcal/mol at 37 °C) and a small gain in binding entropy (TΔΔS, 0.7 kcal/mol). The removed Y54 hydroxyl is replaced by a water molecule in the bound structure, but there are no observable changes in structure in the first contact shell and no additional changes surrounding the mutation. Molecular dynamics simulations reveal a large increase in atomic fluctuations for W79, a key biotin contact residue, compared to the wild type complex. The increased W79 fluctuations are caused by loss of water-mediated hydrogen bonds between the Y54 hydroxyl group and peptide backbone atoms in and near W79. We propose that the increased fluctuations diminish the integrity of the W79-biotin interaction and represent a loosening of the “tryptophan collar” which is critical to the slow dissociation and high affinity of streptavidin-biotin binding. These results illustrate how changes in protein dynamics distal to the ligand binding pocket can have a profound impact on ligand binding, even when equilibrium structure is unperturbed.

Protein structural fluctuations (fluctuations about the mean conformation) are thought to play a major role in ligand binding and catalysis, but measuring and predicting the impact of these fluctuations on binding affinity and catalytic efficiency remains an extraordinary challenge. Point mutations and binding events that are distal from protein active sites can dramatically affect binding and catalysis through transmitted effects on protein dynamics rather than conformation, as seen in well-characterized enzymes such as dihydrofolate reductase,^1-4 in thermophilic enzymes compared to their mesophilic homologs,^5-7 and in “dynamically-driven allostery” in cAMP-CAP⁸ and ligand-PDZ domain binding.⁹ Loss of conformational entropy and side chain mobility during protein-ligand binding is well-documented,^10,11 and in some cases compensated for by a gain in conformational fluctuations away from the binding site.^12,13 However, there are few examples where the effects of a point mutation on protein-ligand binding energetics have been directly related to an observed change in fluctuations, with no equilibrium structural changes in the binding pocket.

In previous crystallographic and molecular dynamics simulation studies of wild type streptavidin, we observed that biotin binding caused notable decreases in protein dynamics – reduced temperature factors in refined crystal structures and diminished atomic fluctuations in MD simulations – at sites far removed from the biotin binding pocket. We hypothesized that it might be possible to impact biotin binding by introducing conservative point mutations at sites outside the first contact shell that would preserve equilibrium structure but alter local protein dynamics. To test this hypothesis, we designed a set of eight streptavidin mutants, each with a single point mutation of a second contact shell residue, in an attempt to increase local protein structural fluctuations by disrupting a hydrogen bonding network and/or displacing an adjacent bound water molecule. We screened the mutants based on biotin dissociation rate changes, and selected two mutants, Y54F and F130L, with k_off(mutant) / k_off(wild type) > 50 for further analysis. We refined x-ray structures for both mutants to confirm that the mutations had no significant effect on biotin-contacting side chain positions in the bound structure. We performed molecular dynamics simulations to first confirm the conservation of equilibrium structure in the simulations and then to compare the structural fluctuations of these mutants with wild type streptavidin. In parallel, we characterized the biotin binding thermodynamics.

We have reported preliminary results for the F130L mutation previously.¹⁴ Here we present a crystallographic, computational and biophysical study for Y54F, a streptavidin mutation that causes a 75-fold loss of binding affinity, with no observable changes in equilibrium binding pocket structure, but a large increase in fluctuations of a key biotin-binding residue, W79. The removal of the Y54 hydroxyl group disrupts a water-mediated hydrogen bond network involving protein backbone atoms of N49, W79, and R84, which leads to significantly increased motion for loop L5,6, and much larger side chain fluctuations for W79, a key biotin aromatic contact. The large loss of binding enthalpy and small gain of binding entropy relative to wild type are consistent with a mutation that loosens the “tryptophan collar” that traps biotin during binding.^15-17 These observations directly relate changes in ligand binding thermodynamics with altered protein dynamics at a distal site, and demonstrate the importance of including dynamic effects originating outside the binding pocket in structure-based drug and enzyme design.

EXPERIMENTAL PROCEDURES

Protein expression and purification

The Y54F mutation was created in the synthetic core streptavidin gene in pET21a (Novagen, San Diego, CA) using the QuikChange protocol (Stratagene, La Jolla, CA) as described previously,¹⁸ and confirmed by sequencing. Protein was expressed using the T7 expression system in BL21(DE3) E. coli and purified as described previously.¹⁷ The expected mass and purity of the mutant were confirmed using electrospray mass spectrometry.

Kinetic measurements

The rates of biotin dissociation from streptavidin variants were measured using a cold-chase radiometric method described previously.¹⁹ Briefly, 10 nM ³H-biotin and 30 μM Y54F or WT streptavidin in 50 mM sodium phosphate buffer, pH 7.0, 100 mM NaCl, were equilibrated at the experimental temperature for 2 h, then a large excess of unlabeled biotin (50 μM final concentration) was added and mixed rapidly. Aliquots of 200 μL were removed periodically and immediately ultrafiltered using chilled, 30k Microcon filters (Millipore, Billerica, MA). The filtrate was counted to quantify the amount of ³H-biotin released as a function of time.

Dissociation rate constants for protein-ligand complexes at each temperature were determined by fitting each data set by a one-term exponential decay. These k_off values were used to calculate initial estimates of ΔH^± and ΔS^± in a global fit of all data, with ΔH^± and ΔS^± as the only adjustable parameters, using the equation

$$I_t=I_0\left\{1-\text{exp}\left[-\frac{k_{B}T}{h}\text{exp}\left(\frac{T\Delta S^{\ne }-\Delta H^{\ne }}{RT}\right)\cdot t\right]\right\}$$ (1)

where I_t is the measured ³H count at time t, I_o is the initial ³H count, k_B is Boltzmann's constant, h is Planck's constant, and R is the gas constant. Dissociation experiments at each temperature were performed on two separate days.

Equilibrium measurements

Equilibrium binding enthalpies were measured at 12, 25 and 37 °C using a VP-ITC isothermal titration calorimeter (Microcal, Northampton, MA). Streptavidin at 30 μM in 50 mM sodium phosphate, pH 7.0, 100 mM NaCl, was titrated with 25 5-μL injections of 500 μM biotin. Heat flow was integrated and data were fit using Origin software. Two titrations were performed at each temperature.

Equilibrium binding affinity relative to WT streptavidin was determined using a radiometric competitive binding method described previously.¹⁹ Y54F and WT streptavidin at a range of concentrations competed with 50 nM WT streptavidin with a polyhistidine tag for 20 nM ³H-biotin, in 50 mM sodium phosphate, pH 7.0, 100 mM NaCl, for 24 h at 37 °C. The partitioning of ³H-biotin between proteins was measured by precipitating the his-tagged WT protein using nickel-nitrilotriacetic acid agarose resin (Qiagen, Valencia, CA) and counting ³H-biotin remaining in solution. These counts, corrected for unbound ³H-biotin, were fit as the root of the competitive binding equation

$$\frac{K_C}{K_P}\cdot {[C\cdot L]}^2+\left(L_T+C_T+\frac{K_C}{K_P}(P_T-L_T)\right)\cdot [C\cdot L]-L_T{C}_T=0$$ (2)

where K_C and K_P are the equilibrium dissociation constants for the competitor and WT, respectively, and [C·L], L_T, C_T and P_T are the concentrations of competitor-bound ligand, total ligand, total competitor, and total WT protein, respectively. The ΔK_d value in Table IV is the average value from two experiments on separate days.

Table 4.

Thermodynamic parameters for biotin binding: Y54F versus wild type at 37 °C

Parameter	Y54F
Δ K d	75 ± 10
ΔΔG° (kcal/mol)	2.7 ± 0.1
ΔΔH° (kcal/mol)	3.4 ± 0.2
TΔΔS° (kcal/mol)	0.7 ± 0.2
Δ k off	73 ± 4
ΔΔG≠ (kcal/mol)	2.6 ± 0.3
ΔΔH≠ (kcal/mol)	5.8 ± 0.2
TΔΔS≠ (kcal/mol)	3.2 ± 0.4

Crystallization

The Y54F mutant of “core” streptavidin²⁰ was co-crystallized with biotin using hanging drop vapor diffusion techniques. Crystals were obtained by mixing protein (12.5 mg/mL in water) with a two-fold molar excess of biotin. The reservoir solution for Y54F was 60% saturated ammonium sulfate, 5% isopropanol. Drops of protein and ligand solution were mixed with an equal volume of reservoir solution before equilibration. Crystals were transferred to a crystallization solution containing 30% glycerol as a cryoprotectant before freezing at 100 K in a nitrogen stream for diffraction data collection.

Crystals of uncomplexed Y54F were obtained using similar techniques, but with a reservoir solution containing 2.5 M sodium chloride, 0.1 M sodium / potassium phosphate, pH 6.2. The cryoprotectant for these crystals was 30% ethylene glycol.

Diffraction data collection

Diffraction data for the Y54F-biotin complex were collected at Stanford Synchrotron Radiation Lightsource (SSRL) beamline 9-2 (λ = 0.97946 Å) at 100 K using a Mar 325 CCD detector and were processed using HKL2000.²¹ The space group for the Y54F crystals is I222 with two subunits in the asymmetric unit. Data for the uncomplexed protein were collected at SSRL beamline 12-2 (λ = 1.0 Å) at 100 K using a Pilatus detector and were processed using XDS.²² The space group is I4₁22 with one subunit in the asymmetric unit. Data set statistics are shown in Table 1a.

Table 1a.

Data collection
Mutant	Y54F(biotin complex)	Y54F(uncomplexed)
Unit cell dimensions (a,b,c,)	46.61, 94.11, 104.60 Å	57.273, 57.273, 171.715 Å
(α, β, γ)	90., 90., 90. °	90., 90., 90. °
Space group	I222	I4122
Resolution	50.0-1.22 Å (1.26-1.22)	36.6-1.15 Å (1.21-1.15)
Unique reflections	68448	51198
Completeness (last shell)	99.8% (98.4%)	99.1% (93.6%)
Redundancy (last shell)	13.4 (10.0)	14.7 (9.6)
I/sigma (last shell)	23.1 (3.0)	21.8 (2.3)
Rmerge (last shell)	0.121 (0.613)	0.057 (0.967)

Structure solution and refinement

The initial structural model for Y54F was obtained from an isomorphous structure – the biotin complex of wild type streptavidin (PDB ident 1MK5). The structural model was refined using REFMAC-5²³ in the CCP4 suite.²⁴ R_free²⁵ was calculated using 5% of the data in the test sets. All atoms were refined with anisotropic temperature factors. Riding hydrogen atoms were added to the models, and Babinet scaling was used to account for bulk solvent effects.

Sigma A weighted |Fo|-|Fc| and 2|Fo|-|Fc| electron density maps²⁶ were viewed with XtalView²⁷ and COOT²⁸ for graphical evaluation of the model and electron density maps. XtalView, MOLSCRIPT²⁹, and Raster3d³⁰ were used to produce the structural figures for this paper.

In the biotin complex, a small peak about 1.4 Å from the biotin sulfur was seen in difference electron density maps indicating that a small portion of the biotin bound to the protein was oxidized. Reasonable atomic displacement parameters were obtained for an oxygen atom with 0.2 occupancy at this position. Comparison of the wild type biotin complex indicates that this minor oxidized component can be accommodated with no noticeable distortion of the equilibrium structure.

The final structural model for Y54F consists of two streptavidin subunits (chain A: residues 14-134, B: 15-136), two biotin molecules, three sulfate ions, 215 fully-occupied water molecules, 33 partially occupied waters, and four glycerol molecules. MolProbity³¹ was used for model validation.

The structure of Y54F in the absence of biotin was determined and processed in similar ways. The initial model was obtained using the BALBES molecular replacement pipeline³² and PDB entry 1MM9. The final model consists of one streptavidin subunit (residues 16-135), one chloride ion, 89 fully-occupied water molecules, 30 partially occupied waters, and one ethylene glycol molecule.

Table 1b contains refinement statistics for both structures. Coordinates and structure factors for the biotin complex of the Y54F mutant have been deposited in the Protein Data Bank with identifier 3T6F. The uncomplexed structure has PDB identifier 3T6L.

Table 1b.

Refinement
Mutant	Y54F(biotin complex)	Y54F(uncomplexed)
Resolution	70.0-1.22 Å (1.25-1.22 Å)	36.6-1.30 Å (1.33-1.30 Å)
R factor (overall)	0.129	0.137
R factor (working set)	0.129 (0.192)	0.135 (0.129)
Rfree (test set=5% of the overall)	0.151 (0.211)	0.160 (0.194)
# unique reflections	64975	33868
Average B value (protein)	12.8 Å2	16.5 Å2
Average B values (biotin)	9.6 Å2	---
Average B values (glycerols/ethylene glycols)	33.3 Å2	24.7 Å2
Average B values (water molecules)	29.8 Å2	25.7 Å2
Average B values (sulfate/chloride ions)	23.3 Å2	19.7 Å2
Ramachandran quality
% of residues in favored regions	97.9%	100%
in allowed regions	100%	100%
rms deviation - bond lengths	0.011 Å	0.017 Å
- bond angles	1.54 °	1.83 °

Molecular dynamics simulations

Starting coordinates for the Y54F-biotin complex simulations were taken from the current x-ray structure. The eight histidine residues in the tetramer were singly protonated to model the ionization state expected for a neutral solution. Hydrogen atoms were added to all protein heavy atoms using the Leap module in AMBER 9.³³ The full complex was solvated in a truncated octahedral box containing 19,584 water molecules, and eight sodium counterions were added to maintain charge neutrality for the system.

The simulation methods and protocol are comparable to that reported previously for solution phase simulations of WT streptavidin.³⁴ Briefly, all calculations were performed using the AMBER ff99 force field^35,36 with modifications by Simmerling and co-workers,³⁷ the SPC/E water model³⁸ and a sodium cation model from Åqvist.³⁹ Biotin parameters were taken from previous work by Israilev and co-workers.⁴⁰ Force calculations were performed with periodic boundary conditions, a 9.0 Å cutoff on real space interactions, a homogeneity assumption to approximate the contributions of long-range Lennard-Jones forces to the virial tensor, and smooth particle-mesh Ewald for long-range electrostatics.⁴¹ The SHAKE algorithm⁴² was used to constrain the lengths of all bonds to hydrogen atoms and the SETTLE algorithm⁴³ was used to constrain the internal geometry of all rigid SPC/E water molecules. A Langevin thermostat⁴⁴ with collision frequency 3 ps^-1 was used to maintain the system temperature. All energy minimizations and dynamics were performed with the PMEMD module of AMBER 9.³¹ To avoid artifacts arising from reuse of particular sequences of random numbers,⁴⁵ the random number generator seed was incremented with every restart of the dynamics.

To prepare the system for equilibrium MD simulations, hydrogen atoms, water molecules and sodium atoms were first relaxed by 2000 steps of steepest-descent energy minimization while crystallographically resolved protein atoms were held in place by 1000 kcal/mol-Ų position restraints. The protein heavy atoms were then energy minimized while solvent particles were tightly restrained to their new positions, and finally all components of the system were energy-minimized with no restraints. Restrained dynamics of the system were conducted for a total of 450 ps, beginning with a 0.5 fs time step in the constant volume, constant temperature ensemble and 16.0 kcal/mol-Ų restraints on all crystallographically observed protein atoms. The restraints were gradually reduced to 1.0 kcal/mol-Ų over the first 150 ps before switching to the constant pressure ensemble, increasing the time step to 1.5 fs, and reducing the restraints to 0.0625 kcal/mol-Ų over the next 300 ps. Production dynamics were propagated in the constant pressure ensemble with a 1.5 fs time step for 500 ns with no position restraints.

All MM-GBSA and MM-PBSA calculations were performed using the SANDER module of AMBER 9. In the Generalized Born calculations, the electrostatic solvation energy was calculated using a model developed by Onufriev et al.⁴⁸ with a protein dielectric constant of 1.0 and solvent dielectric constant of 80. The nonpolar solvation contribution was computed using the LCPO method.⁴⁹ For the Poisson-Boltzmann calculations, a finite-difference algorithm implemented in Sander was used, with a 0.5Å grid spacing, a 1.4Å solvent probe radius, a protein dielectric constant of 1.0 and solvent dielectric constant of 80. The nonpolar solvation contribution was computed as described above for the Generalized Born calculations. We did not calculate explicit entropy contributions for the binding free energies, since we know from our experimental measurements that the ΔΔS contribution is small (TΔΔS ~ 0.7 kcal/mol). For each method, we employed the “single trajectory approach”, I.e., we extracted configurations for the complex, the unbound protein, and the free ligand from our equilibrium trajectories of the complexes, rather than running separate MD simulations for free streptavidin and free ligand to generate configurations for the unliganded protein and free ligand independently. Since the available crystal structures all show that biotin-bound and unliganded streptavidin structures are nearly identical, and since the biotin molecule has only limited conformational flexibility (in the valeric acid side chain) and is bound in essentially identical conformations in both WT and Y54F mutant complexes, we believe that the single trajectory approach is quite reasonable.

RESULTS

Screen of second contact shell mutations

Eight streptavidin mutations in the second contact shell were screened based on the change in biotin dissociation rate, Δk_off = k_off(mutant) / k_off(wild type) (Table II). Two mutations with Δk_off > 50 were selected for crystallography and further analysis: F130L and Y54F. F130L had by far the largest effect on dissociation rate; this mutation and its effects on biotin binding, which were not attributed to changes in dynamics, have been described previously.¹⁴ Y54F caused 73-fold faster biotin dissociation at 37 °C and is the focus of this report.

Table 2.

Impact of second contact shell mutations on dissociation rate

Mutation	koff (mutant) / koff (wild type)
F130L	7,600*
Y54F	73
T106V	11
Q24A	5.0
R84A	3.6
W75F	3.2
H127W	1.6
K121A	1.2

^*12 °C; all others at 37 °C. Biotin dissociation for F130L was too fast to measure above 12 °C.

Effects of Y54F on equilibrium complex structure

The Y54F mutation has minimal effect on the equilibrium structure of the streptavidin-biotin complex (Figure 1). Minor structural changes are observed in the vicinity of the mutation site (Figure 2, A), but no significant changes occur in the positions of side chains contacting biotin. Table III lists observed streptavidin-biotin hydrogen bond distances in wild type and Y54F streptavidin.

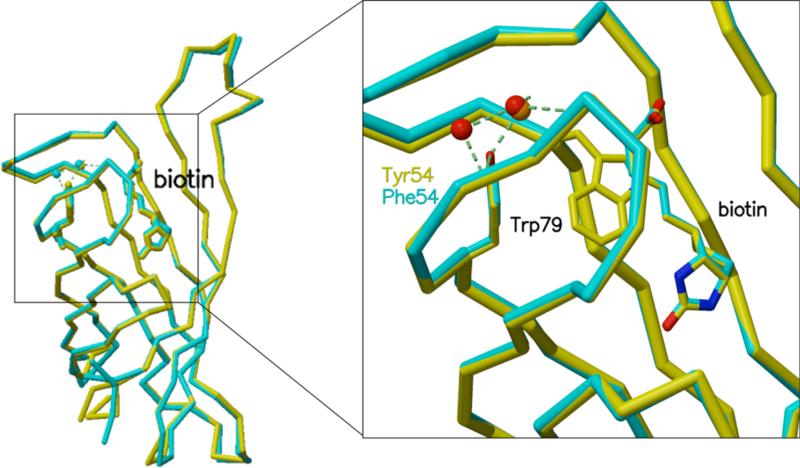
Figure 1.

Overlay of wild type (yellow) and Y54F (blue) streptavidin structures. The Y54F mutation has no significant effect on the overall protein backbone structure (left) or on the structure surrounding biotin and the mutation site (right).

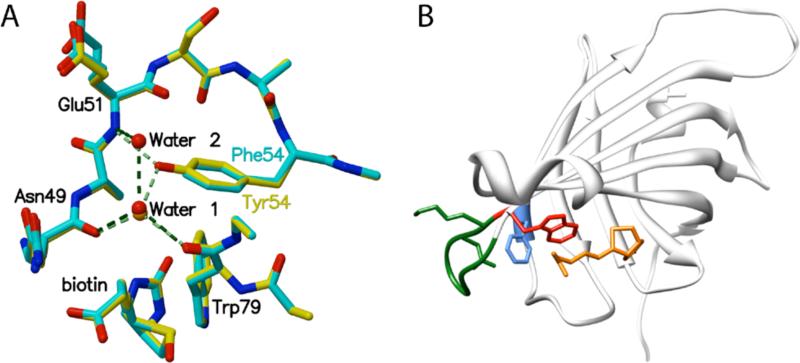
Figure 2.

(A) Superposition of details from biotin bound Y54F (blue) and wild type streptavidin (yellow) structures. Removal of the Y54 hydroxyl group disrupts a hydrogen bonding network involving Trp79, Glu51, Asn49, and a bound water molecule (Water 1). The mutation results in a small cavity filled by a new bound water molecule (Water 2) in one of two subunits in the bound crystal structure. (B) Disruption of the hydrogen bond network involving Y54 (F54 is shown in blue) results in larger atomic fluctuations for loop L5,6 (green) and W79 (red), a key aromatic biotin contact. (Biotin is shown in orange.)

Table 3.

Streptavidin-biotin hydrogen bond distances in wild type and Y54F

Atom names		Structure	WT (1MK5)		Y54F
Biotin	Protein	Subunit	A	B	A	B
O11	N Asn 49		2.84	2.88	3.01*	2.94
O12	OG A Ser 88		2.79	2.90	2.84*
O12	OG B Ser 88					2.90*
N1	OD2 Asp 128		2.79	2.82	2.79	2.81
O3	ND2 Asn 23		2.99		3.02	2.94
O3	OD1 Asn 23			2.88
O3	OG A Ser 27		2.64	2.62	2.69	2.69
O3	OG B Ser 27		2.37
N2	OH Tyr 43		2.71	2.69	2.69	2.68
N2	OG A Ser 45		2.99	2.97	2.96	2.98
N2	OG B Ser 45		2.84

The removal of the Y54 hydroxyl group disrupts hydrogen bonds to neighboring main-chain atoms and to a bound water molecule (Water 1 in Figure 2, A) and creates a small cavity in the protein which is filled by an additional water (Water 2) in one of the two subunits in the liganded Y54F structure. The molecules in the deposited PDB entry in the Water 1 site are numbers 6248 (A chain) and 6139 (B chain). The Water 2 site is occupied by number 6140 (B chain).

Effect of Y54F on binding energetics

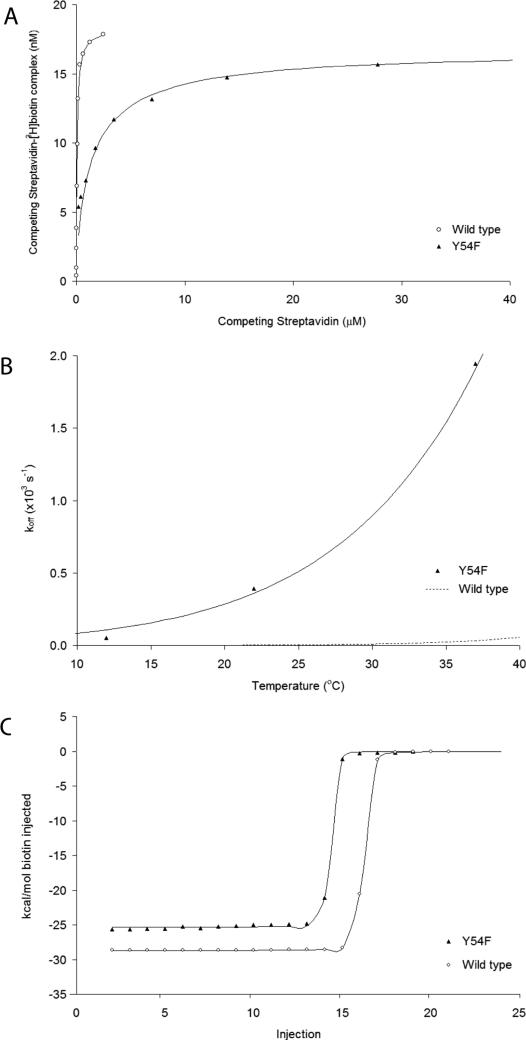
The Y54F mutation causes a loss of binding affinity of 75 ± 10 relative to WT streptavidin at 37 °C, measured using a competitive binding assay for ³H-biotin, corresponding to a decrease in binding free energy of 2.7 ± 0.1 kcal/mol (Table IV; Figure 3 shows competitive binding, calorimetric and kinetic data). The loss of binding energy is due to a large loss of binding enthalpy (ΔΔH°, 3.4 kcal/mol), partially compensated by a more favorable entropy of binding (TΔΔS°, 0.7 kcal/mol, calculated from ΔΔG° = ΔΔH° - TΔΔS°). Activation thermodynamic parameters for Y54F were calculated by fitting all kinetic data to an Eyring model using ΔH^≠ and ΔS^≠ as the only adjustable parameters; activation parameters for WT were based on previously published values.¹⁸

Figure 3.

Effects of the Y54F mutation on biotin binding affinity (A), dissociation kinetics (B), and binding enthalpy (C). (A) Competitive binding of Y54F and WT versus His-tagged WT (50 nM) for ³H-biotin (20 nM) at 37 °C. Y54F causes a 75-fold loss in binding affinity. (B) The temperature-dependence of biotin dissociation from Y54F and WT was used to determine thermodynamic activation parameters, ΔH^≠ and ΔS^≠, by fitting data to an Eyring model. Biotin dissociation is 73-fold faster for Y54F than WT streptavidin at 37 °C. (C) Calorimetric titration curves for Y54F and WT streptavidin titrated with biotin at 37 °C, showing a large loss of binding enthalpy for Y54F (ΔΔH°, 3.4 kcal/mol).

Effects of Y54F on equilibrium dynamics

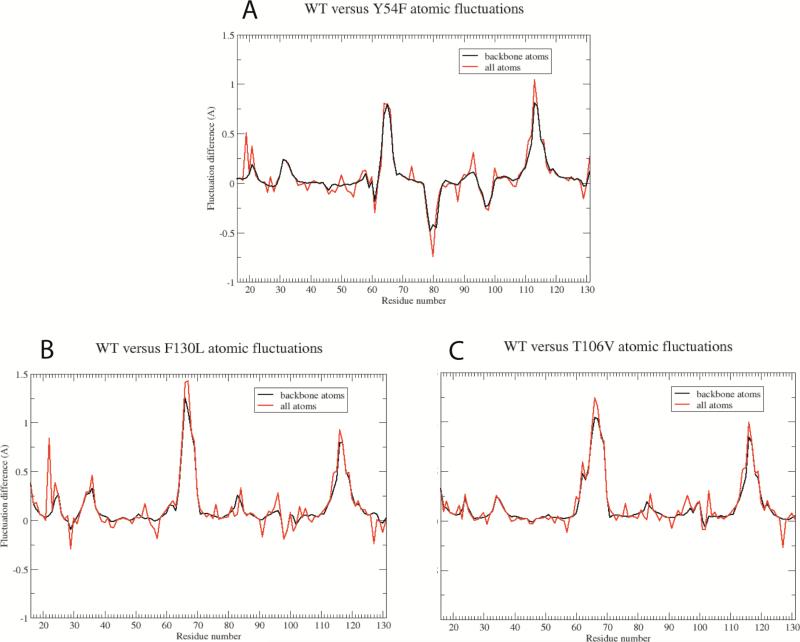
We generated a 500 ns trajectory of the liganded Y54F mutant for analysis and comparison to a corresponding wild type complex trajectory³⁴ and to trajectories for two other mutants we are studying, F130L¹⁴ and T106V. The structural fluctuations for Y54F appear to stabilize after ~ 75 ns, as assessed by RMSD values for trajectory snapshots from the starting x-ray coordinates. The RMSD value for core atoms – all atoms excluding loop residues and the amino and carboxy termini – stabilizes at ~ 0.7 Å, and the RMSD for all atoms plateaus at ~ 1.6 Å. We therefore performed all subsequent analyses using the final 425 ns of the MD trajectory.

The time-averaged structures for both Y54F and the wild type complex are quite similar, indicating that the Y54F mutation has negligible impact on equilibrium structure, consistent with the high-resolution crystallographic results. The simulations reveal a significant increase in structural fluctuations for loop L5,6, located at the edge of the β-barrel core, in liganded Y54F relative to wild type and all other mutants (Figure 4). This small loop is formed by residues K80, N81, N82, Y83 and R84, and its increased mobility is due to the loss of a water-mediated hydrogen bond network between the Y54 hydroxyl group and protein backbone atoms in residues W79 and N49. There are also transient hydrogen bonding interactions between Y54 and backbone atoms from residues N81 and R84 over the course of the wild type MD trajectory. In wild type streptavidin and all other mutants we have studied, this water-mediated hydrogen bond network restricts the range of motion for loop L5,6 in all four streptavidin subunits. However, in the Y54 mutant, loss of the hydroxyl group disrupts the hydrogen bond network (Figure 2, A) and removes restraints that limit motion of the loop residues.

Figure 4.

Differences in atomic fluctuations averaged over all atoms in each residue for WT versus mutant streptavidin complexes: (A) Y54F, (B) F130L, and (C) T106V. Positive values indicate greater mobility in the WT complex versus the mutant. The large negative peak observed for residues 78-82 in panel A indicates that these residues exhibit significantly increased motion in the Y54F mutant complex. In contrast, we observe no increased motion for these residues in the other mutant simulations (B, C). The large positive peaks present in all three panels for residues 64-69 (loop L4,5) and residues 113-118 (loop L7,8) indicate larger ranges of motions for these large, flexible loops in the WT simulation. Much larger absolute fluctuations are observed for these loop residues than other residues in the protein, and as the simulations are propagated for longer time periods, the atomic fluctuation differences in these loop regions decrease asymptotically to baseline.

In an attempt to assess whether the increased structural fluctuation for loop L5,6 in the mutant is simply an artifact of limited configurational sampling, we compared fluctuations for wild type versus F130L and T106V complexes, each computed from independent 500 ns trajectories (Figure 4, B and C). As seen in these plots, only the Y54F mutant exhibits increased fluctuations in loop L5,6. These trends, coupled with the clear structural basis for the increased fluctuations, suggest that the increased loop mobility observed in Y54F is real and not a simulation artifact.

The increased mobility for loop L5,6 appears to impact biotin binding thermodynamics even though these loop residues are well removed from the ligand binding pocket. The dramatically increased backbone mobility observed for residues K80-N82 contributes to the increased range of motion observed for W79 via direct mechanical coupling through the backbone atoms. In addition, increased mobility of loop residues, particularly N81, reduces packing constraints for side chains that contact W79, thus reducing packing constraints for W79 itself, allowing increased side chain mobility. In the MD simulation, all other streptavidin-biotin contacts besides W79 are perfectly maintained, keeping biotin firmly “locked” in position; i.e., biotin is immobilized and cannot move together with the W79 side chain to maintain consistent interactions. As a result, W79-biotin interactions are disrupted frequently over the course of the MD trajectory.

We have shown previously that in wild type streptavidin, W79 forms a crucial contact with biotin.¹⁷ Mutation of this residue to smaller side chains reduces biotin binding affinity significantly (W79F: ΔΔG = 1.0 kcal/mol; W79A: ΔΔG = 7.9 kcal/mol at 37 °C). Our simulation results suggest that we have reduced biotin binding affinity by degrading the strength of the W79-biotin interaction through increased fluctuations that diminish the contact time of this side chain with biotin. The magnitude of the effect for the Y54F mutation (ΔΔG = 2.7 kcal/mol) is reasonable relative to earlier mutagenesis studies for W79.^16-17 In W79F mutant, the F79 side chain maintained good contact with biotin,¹⁶ and this mutation had a modest impact on binding affinity.¹⁷ In the W79A mutant, the alanine side chain was too small to maintain contact with biotin, and the impact on binding affinity was dramatic.¹⁷ The Y54F mutant has an intermediate effect: the increased W79 side chain fluctuations significantly diminish but do not eliminate the biotin interaction as a function of time over the trajectory, and the impact on binding affinity is greater than that for W79F but less dramatic than W79A.

The increased atomic fluctuations observed for the W79 side chain and adjacent L5,6 loop suggest that Y54F should display an enhanced biotin dissociation rate, and we observe this experimentally (Δk_off = 73). W79 is one of four tryptophan residues that form the so-called “tryptophan collar” which locks biotin into position once it enters the binding pocket.^15,16 Increased W79 side chain fluctuations would make the tryptophan collar “looser” and less effective at preventing dissociation. The increased mobility of the L5,6 loop also means the binding site entrance opens wider and more frequently, favoring an enhanced biotin dissociation rate.

In an attempt to provide more quantitative support for our hypothesis, we have used the equilibrium MD trajectories to estimate the relative binding free energy for biotin to WT versus Y54F streptavidins. Previously, we calculated the absolute binding free energy for biotin to WT streptavidin by using a free energy perturbation technique to implement an effective potential of mean force calculation along a biotin dissociation reaction coordinate.⁴⁶ We computed a binding free energy of -17.0 ± 3.0 kcal/mol, in excellent agreement with the experimental value of -18.3 ± 1.0 kcal/mol.¹⁵ While this approach produced quantitatively accurate results, the procedure is extremely computationally expensive, and the expected statistical uncertainty (± 3.0 kcal/mol) is comparable to the relative binding free energy difference we wish to calculate in this current study. For these reasons, we chose instead to use the mixed molecular mechanics/continuum model methods MM-GBSA and MM-PBSA to extract binding free energy estimates for our WT and Y54F complexes from the equilibrium trajectories.⁴⁷

We first utilized the MM-GBSA method to estimate biotin binding free energies, since the Generalized Born continuum model is much less expensive computationally than Poisson-Boltzmann methods. As in all other trajectory analyses, we omitted the first 75 ns of each equilibrium trajectory. We calculated the absolute binding free energy for each subunit independently, and also calculated results for fragments, or sub-blocks, of the full trajectories to check for variations in computed binding free energy as a function of total number of configurations included in the calculations. The MM-GBSA analysis yielded absolute binding free energies that do not agree well with the experimental measurements or earlier free energy perturbation calculations, and the standard deviations in the computed results are quite large. For the WT complex, the calculated binding free energy is -64.5 kcal/mol ± ~30.0 kcal/mol, while the result for the Y54F mutant is -84.6 ± ~25.0 kcal/mol. The computed binding free energies were generally consistent for the full trajectories versus trajectory fragments, although the standard deviations are smaller when trajectory fragments containing only 10,000 – 15,000 configurations are used in the calculations. These results suggest that biotin should bind more tightly to the Y54F mutant by ~20 kcal/mol, although the standard deviations are so large that no firm conclusions can be drawn from these results.

We next utilized the MM-PBSA method to estimate the binding free energies for each complex. This method is considerably more expensive than the MM-GBSA technique (E.g., calculation of the absolute binding free energy for one subunit requires ~fifteen days of CPU time for each trajectory on a 24-processor Intel cluster), so we have computed PBSA results for only two of four subunits in each complex thus far. Given that the MM-GBSA results were comparable for each subunit, we expect the same will be true for the MM-PBSA calculations. Unlike the Generalized Born calculations, the MM-PBSA method yields results that appear much more physically reasonable, and the standard deviations are smaller as well. For the WT complex, the computed binding free energy is -22.3 kcal/mol ± 11.0 kcal/mol, while for the Y54F mutant the result is -22.6 kcal/mol ± 7.3 kcal/mol. As was the case with the MM-GBSA analysis, the computed binding free energies are consistent whether the full trajectories or only fragments consisting of 10,000 – 15,000 configurations are used. However, unlike the MM-PGSA calculations, using fewer configurations does not reduce the standard deviations for the MM-PBSA method. These results suggest that biotin binds essentially equally well to both WT streptavidin and Y54F mutant, although again the standard deviations are too large to draw any meaningful conclusions.

While it is somewhat disappointing that neither continuum method provided any compelling evidence for biotin binding preference, some interesting data did emerge from these calculations nonetheless. The molecular mechanics component of these calculations (the “gas-phase” contribution) shows consistently for all subunits that the WT complex is preferred by ~ 6-7 kcal/mol, suggesting that the intrinsic biotin-streptavidin interactions are better in the WT complex. This result agrees reasonably well with the experimental relative binding enthalpy difference, ΔΔH = 3.4 kcal/mol, also favoring the WT complex.

DISCUSSION

Our biophysical experiments show that the Y54F mutation reduces biotin binding free energy significantly (ΔΔG = 2.7 kcal/mol at 37 °C) and leads to a dramatically increased biotin dissociation rate (Δk_off = 73). The crystal structure reveals no differences relative to the wild type streptavidin-biotin complex in the first contact shell: there are no changes in hydrogen bonding distances or side chain conformations for residues immediately surrounding biotin (Table III), and no perturbation of protein structure surrounding the mutation (Figure 1). However, the loss of the Y54 hydroxyl group disrupts a hydrogen bonding network involving protein backbone atoms of N49, W79, and R84 (Figure 2, A). Our MD simulations for the wild type complex suggest that this water-mediated hydrogen bond network stabilizes the backbone structure for the L5,6 loop. When immobilized, this loop provides packing constraints that maintain the W79 side chain in close juxtaposition to biotin, thus supporting or “stabilizing” the important W79-biotin interaction. In the Y54F mutant, the stabilizing hydrogen bond network is disrupted and the loop residues exhibit dramatically increased mobility. This increased loop mobility in turn leads to an increase in W79 side chain fluctuations which diminish the W79-biotin interaction as a function of time over the duration of the MD trajectory. The time-averaged or equilibrium structure from the MD trajectory is consistent with the Y54F crystal structure, and suggests no meaningful change in the W79-biotin interaction. Hence, the diminished W79-biotin interaction we observe is a dynamic effect, and we propose that the modified dynamics are responsible for the reduced biotin binding free energy observed experimentally.

The MM-GBSA and MM-PBSA results did not provide any additional compelling support for our hypothesis to explain why biotin binds more favorably to WT streptavidin, in part because the standard deviations in our calculations are much larger than the ΔΔG value we were attempting to calculate. The MM-GBSA calculations yielded absolute binding free energy estimates that were physically unreasonable. By contrast, the MM-PBSA results were only ~20-30% too large, when compared to experimental measurements. The superior performance of the MM-PBSA method for absolute free energy estimates is not surprising, and is consistent with previous studies.^50,51 We suspect that neither continuum method can represent adequately the detailed hydration structure present in the binding site for the unliganded WT and Y54F streptavidins. We know from our numerous streptavidin crystal structures that there are typically four to six water molecules that form specific hydrogen bonds in the binding pocket when biotin is absent. We also know from our previous MD simulations that this hydrogen bonding network is dynamic and in exchange with bulk water, even though the individual water positions exhibit occupancy values close to one in the crystal structures and in the simulations. We believe that our previous explicit solvent calculation of absolute binding free energy for biotin to WT streptavidin performed well in part because those simulations modeled the binding site “rehydration” accurately upon biotin dissociation, based on comparisons to the resolved water molecules in the corresponding crystal structures. It is possible to perform mixed explicit/implicit solvent calculations, including selected water molecules explicitly in the calculations while treating the remainder of the solvent with a GBSA or PBSA method, and that approach may be necessary to get more reliable results for the complexes studied here. Mixed explicit/implicit solvent model calculations have been shown to provide improved results in some cases, although they can be quite sensitive to exact number and placement of explicit water molecules.⁵² These calculations would be exceptionally tedious to perform for the biotin-streptavidin complexes, since explicit water molecules would have to be selected carefully from each snapshot of an equilibrium MD trajectory for unliganded streptavidin to create the ensemble of configurations for unliganded protein to use in the subsequent MM-PBSA calculations.

The continuum model calculations did provide some support for our hypothesis. As noted above, all calculations consistently showed that gas-phase WT complex is favored over the Y54F mutant complex by 6-7 kcal/mol, in respectable agreement with the experimental ΔΔH measurement that favors WT complex by 3.4 kcal/mol. Since we know from our crystal structures that the hydration of WT and Y54F complexes is quite similar, for both the biotin-bound and the unliganded protein, we expect that solvation/desolvation free energies may be comparable for each complex. We also know from the crystal structures that biotin adopts the same conformation in both WT and mutant complexes, so there should be little or no difference in ligand conformational strain energy for the two complexes. Therefore, it is perhaps not too surprising that the gas-phase molecular mechanics contribution from the MM-PBSA/MM-GBSA calculations, when combined with the experimental ΔΔS result, exhibits reasonable agreement with the experimental binding free energy difference.

The magnitude of the impact of the Y54F mutation on biotin binding seems reasonable in the context of previous mutagenesis involving residue W79.^16,17 The increased local dynamics we observe with this point mutant has a more significant impact than the conservative binding site mutation, W79F, but a less significant impact than the W79A mutation, which effectively eliminates the biotin interaction.

The MD simulations provide a reasonable explanation for the enhanced biotin dissociation rate measured for the Y54F mutant. The increased W79 side chain fluctuations should make the tryptophan collar looser or weaker and facilitate biotin dissociation, since in wild type streptavidin this tryptophan collar represents the primary barrier for biotin dissociation.^{17, 46} The increased mobility observed for the L5,6 loop also favors an increased dissociation rate since the binding pocket entrance is open wider and more frequently in Y54F than in the wild type complex.

The large loss of equilibrium binding enthalpy (3.4 kcal/mol at 37 °C) and small gain in binding entropy (0.7 kcal/mol) for Y54F are consistent with a mutation that causes a weakened interaction with biotin and a small gain in configurational entropy in the bound state. Increased fluctuations of residue W79 would reduce contact time for this side chain with biotin, reducing van der Waals interactions and binding enthalpy. A proportionate increase in binding entropy might also have been expected, but only a small increase was observed. However, other factors are likely to be significant. For example, Y54F gains two more bound water molecules during biotin binding in the area immediately surrounding the mutation (Waters 1 and 2 in Figure 2, A), while wild type streptavidin gains none. (These waters are present in liganded Y54F, but absent in unliganded Y54F (not shown), while in the wild type structure, Water 1 is present and Water 2 is absent regardless of the binding state.) Binding additional waters is unfavorable entropically for Y54F and may oppose any gain in configurational entropy; however, a much more detailed biophysical and computational study would be required to estimate the contributions of bound waters to the binding energetics.

In summary, we have used a combination of biophysical measurements, x-ray crystallography, and MD simulation to characterize a streptavidin point mutation distal from the biotin binding pocket, Y54F. This mutation reduces biotin binding free energy significantly but has no observable effect on equilibrium structure, either in the binding pocket or at the mutation site. Our combined experimental and computational analysis suggests that the reduced biotin binding affinity is a result of increased structural fluctuations of the W79 side chain, an important contact residue for biotin. The increased W79 side chain fluctuations are coupled to increased mobility in the adjacent L5,6 loop residues K80-N82, which in turn is caused by disruption of a hydrogen bonding network involving the Y54 hydroxyl group. These results suggest that dynamical effects can impact ligand binding thermodynamics and dissociation kinetics even in the absence of observable equilibrium structural changes in the first contact shell. These results also demonstrate how distal point mutations can serve as the origin of dynamical changes that are relayed mechanically to effect changes remotely – in this example, altered protein-ligand binding.

Abbreviations

MD

molecular dynamics

WT

wild type

Y54F

tyrosine to phenylalanine mutation at amino acid position 54

RMSD

root mean square deviation

MM-GBSA

molecular mechanics-generalized Born surface area

MM-PBSA

molecular mechanics-Poisson-Boltzmann surface area