FLUCTUATING SYNAPTIC CONDUCTANCES RECREATE IN VIVO-LIKE ACTIVITY IN NEOCORTICAL NEURONS

Abstract

To investigate the basis of the fluctuating activity present in neocortical neurons in vivo, we have combined computational models with whole-cell recordings using the dynamic-clamp technique. A simplified ‘point-conductance’ model was used to represent the currents generated by thousands of stochastically releasing synapses. Synaptic activity was represented by two independent fast glutamatergic and GABAergic conductances described by stochastic random-walk processes. An advantage of this approach is that all the model parameters can be determined from voltage-clamp experiments. We show that the point-conductance model captures the amplitude and spectral characteristics of the synaptic conductances during background activity. To determine if it can recreate in vivo-like activity, we injected this point-conductance model into a single-compartment model, or in rat prefrontal cortical neurons in vitro using dynamic clamp. This procedure successfully recreated several properties of neurons intracellularly recorded in vivo, such as a depolarized membrane potential, the presence of high-amplitude membrane potential fluctuations, a low-input resistance and irregular spontaneous firing activity. In addition, the point-conductance model could simulate the enhancement of responsiveness due to background activity.

We conclude that many of the characteristics of cortical neurons in vivo can be explained by fast glutamatergic and GABAergic conductances varying stochastically.

Synaptic background activity is invariably present in intracellular recordings of neocortical neurons in vivo, and modeling studies have suggested that it may have important consequences on the integrative properties of these neurons (Barrett, 1975; Holmes and Woody, 1989; Bernander et al., 1991; Destexhe and Paré, 1999). Background activity is maximal during the active states of the brain, when cortical neurons fire spontaneously at relatively high rates (5–20 Hz in awake animals; see Hubel, 1959; Evarts, 1964; Steriade, 1978; Matsumura et al., 1988; Steriade et al., 2001). This highly fluctuating activity was simulated in vitro by injecting noisy current waveforms (Mainen and Sejnowski, 1995; Stevens and Zador, 1998; Fellous et al., 2001). This approach, however, does not take into account the conductance due to background activity.

Given that the neocortex is characterized by a very dense synaptic connectivity (5000–60 000 excitatory synapses per neuron; Cragg, 1967; DeFelipe and Fariñas, 1992), these cells could potentially experience considerable amounts of synaptic conductances during periods of intense network activity. A recent estimation of the electrophysiological parameters of background activity in cat parietal cortex in vivo (Paré et al., 1998) provided evidence for a ‘high-conductance’ state (see also Borg-Graham et al., 1998). By combining intracellular recordings in vivo with computational models of camera lucida-reconstructed pyramidal neurons, it was estimated that synaptic background activity accounts for up to 80% of the total conductance of the cell (Destexhe and Paré, 1999). This high-conductance state of cortical neurons could be reproduced by assuming that glutamatergic and GABAergic synapses release at relatively high rates (about 1 Hz and 5 Hz, respectively; see Destexhe and Paré, 1999).

This type of detailed biophysical model reproduces membrane properties typical of cortical neurons in vivo, such as a lowered input resistance, a depolarized membrane potential (V_m) around −65 mV and persistent V_m fluctuations. However, such models require relatively large computational resources to simulate the amount of synaptic inputs and their location in dendrites, and cannot be used for applications in real time, such as recreating in vivo-like membrane activity in cortical neurons in vitro. To address this problem, we introduce here a new model of background activity. We used a paradigm which could in principle be applied experimentally, and which consists in representing background activity by a stochastic point-conductance model that can be fit to voltage-clamp data. We show how to obtain the optimal parameters of this point-conductance model, and use it to recreate in vivo-like activity in a single-compartment model of cortical neurons and in dynamic clamp in vitro. Parts of these results have appeared in two conference abstracts (Destexhe and Rudolph, 2000; Fellous et al., 2000).

EXPERIMENTAL PROCEDURES

Detailed biophysical models

Computational models were based on morphologically reconstructed neocortical pyramidal cells from cat parietal cortex (one from layer II–III, two from layer V and one from layer VI), which were obtained from two previous studies (Douglas et al., 1991; Contreras et al., 1997). The cell primarily used here is depicted in Fig. 1 (top). The passive properties were adjusted by matching the model to intracellular recordings obtained in the absence of synaptic activity (Destexhe and Paré, 1999). Voltage-dependent conductances were inserted in the soma, dendrites and axon and were described by Hodgkin and Huxley (1952) type models. Low densities of Na⁺ currents were used in the soma and dendrites (30–120 pS/μm²), and densities were 10 times higher in the axon (Destexhe and Paré, 1999).

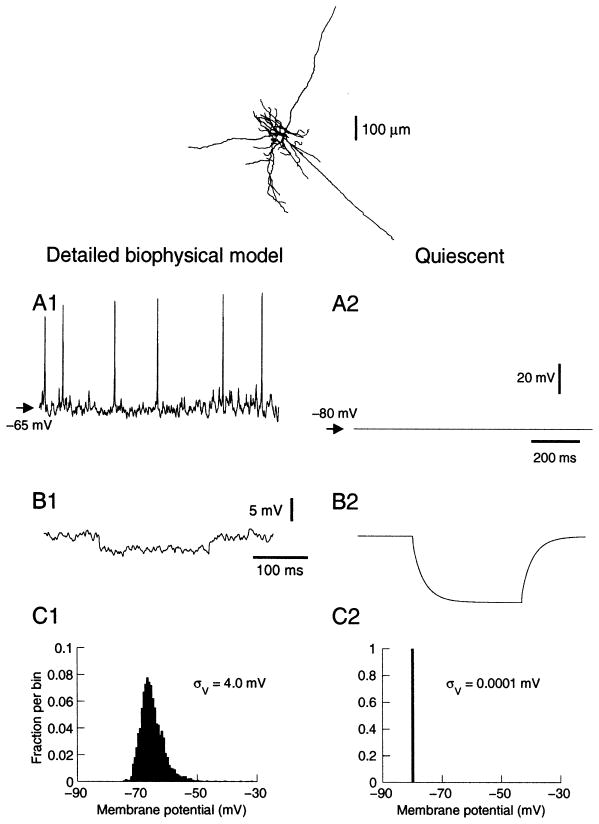
Fig. 1.

Properties of neocortical neurons in the presence of background activity simulated using a detailed biophysical model. (Top) A layer VI pyramidal neuron reconstructed and incorporated in simulations. (A) Membrane potential in the presence of background activity (A1) and at rest (A2). Background activity was simulated by random release events described by weakly correlated Poisson processes of average releasing frequency of 1 Hz and 5 Hz for excitatory and inhibitory synapses, respectively (Destexhe and Paré, 1999). (B) Effect on input resistance. A hyperpolarizing pulse of −0.1 nA was injected at −65 mV in both cases (average of 100 pulses in B1). The presence of background activity (B1) was responsible for about five-fold decrease in input resistance compared to rest (B2). (C) Membrane potential distribution in the presence (C1) and in the absence (C2) of background activity.

To simulate synaptic inputs, pyramidal cells were divided into different regions (soma, perisomatic dendrites, main dendrites, axon initial segment) and the density of glutamatergic α-amino-3-hydroxy-5-methyl-4-isoxazole propionate (AMPA) and GABAergic (GABA_A) synapses in each region was estimated from morphological studies (see White, 1989; DeFelipe and Fariñas, 1992). The number of synapses per 100 μm² of membrane were: 10–20 (GABA_A, soma and perisomatic dendrites), 40–80 (GABA_A, axon initial segment), 8–12 (GABA_A, dendrites) and 55–65 (AMPA, dendrites), leading to a total of 16 563 glutamatergic and 3376 GABAergic synapses for the layer VI cell shown in Fig. 1.

Synaptic currents were simulated by kinetic models of glutamatergic (AMPA) and GABAergic (GABA_A) receptor types (Destexhe et al., 1998). Quantal conductances were estimated from matching the model to recordings of miniature synaptic events in cat parietal cortex (Paré et al., 1997), and were 1200 pS for AMPA and 600 pS for GABA_A (Destexhe and Paré, 1999). Metabotropic and N-methyl-D-aspartate (NMDA) receptors were not included.

The release conditions corresponding to synaptic background activity were estimated based on intracellular recordings performed in cat parietal cortex during active states. The same cells were recorded before and after total suppression of network activity by microperfusion of tetrodotoxin (TTX) (Paré et al., 1998). Based on the model of miniature events, the release frequency at synapses was increased to match the recordings during active states, assuming that synaptic conductances and release properties are uniform and described by Poisson processes. This led to estimates of the average release frequency during active states, which was about 1 Hz and 5.5 Hz for glutamatergic and GABAergic synapses, respectively (Destexhe and Paré, 1999). In addition, the model had to include a weak correlation between release events to match the amplitude of V_m fluctuations observed experimentally.

Point-conductance model

A point-conductance model was generated to approximate synaptic background activity. The total synaptic current, I_syn, was decomposed into a sum of two independent conductances:

$$I_{\text{syn}}=g_{\text{e}}(t)(V-E_{\text{e}})+g_{\text{i}}(t)(V-E_{\text{i}})$$ (1)

where g_e(t) and g_i(t) are time-dependent excitatory and inhibitory conductances, respectively; E_e = 0 mV and E_i = −75 mV are their respective reversal potentials and were identical to that of the detailed biophysical model.

The conductances g_e(t) and g_i(t) were described by a one-variable stochastic process similar to the Ornstein–Uhlenbeck process (Uhlenbeck and Ornstein, 1930):

$$\frac{{\text{d}g}_{\text{e}}(t)}{\text{d}t}=-\frac{1}{{\tau }_{\text{e}}}[g_{\text{e}}(t)-g_{\text{e}0}]+\sqrt{D_{\text{e}}}{\chi }_1(t)$$ (2a)

$$\frac{{\text{d}g}_{\text{i}}(t)}{\text{d}t}=-\frac{1}{{\tau }_{\text{i}}}[g_{\text{i}}(t)-g_{\text{i}0}]+\sqrt{D_{\text{i}}}{\chi }_2(t)$$ (2b)

where g_e0 and g_i0 are average conductances, τ_e and τ_i are time constants, D_e and D_i are noise ‘diffusion’ coefficients, χ₁(t) and χ₂(t) are Gaussian white noise of zero mean and unit standard deviation (see Results for values).

The numerical scheme for integration of these stochastic differential equations takes advantage of the fact that these stochastic processes are Gaussian, which leads to an exact update rule (Gillespie, 1996):

$$g_{\text{e}}(t+h)=g_{\text{e}0}+[g_{\text{e}}(t)-g_{\text{e}0}]exp(-h/{\tau }_{\text{e}})+A_{\text{e}}{N}_1(0,1)$$ (3a)

$$g_{\text{i}}(t+h)=g_{\text{i}0}+[g_{\text{i}}(t)-g_{\text{i}0}]exp(-h/{\tau }_{\text{i}})+A_{\text{i}}{N}_2(0,1)$$ (3b)

where N₁(0,1) and N₂(0,1) are normal random numbers (zero mean, unit standard deviation) and A_e, A_i are amplitude coefficients given by:

$$\begin{array}{l}{A}_{\text{e}}=\sqrt{\frac{D_{\text{e}}{\tau }_{\text{e}}}{2}\left[1-exp\left(\frac{-2h}{{\tau }_{\text{e}}}\right)\right]}\\ A_{\text{i}}=\sqrt{\frac{D_{\text{i}}{\tau }_{\text{i}}}{2}\left[1-exp\left(\frac{-2h}{{\tau }_{\text{i}}}\right)\right]}\end{array}$$

This update rule provides a stable integration procedure for Gaussian stochastic models, which guarantees that the statistical properties of the variables g_e(t) and g_i(t) are not dependent on the integration step h.

Single-compartment models

The point-conductance model was inserted in a single compartment that included voltage-dependent conductances described by Hodgkin and Huxley (1952) type models:

$$\begin{array}{l}{C}_{\text{m}}\frac{\text{d}V}{\text{d}t}=-g_{\text{L}}(V-E_{\text{L}})=I_{\text{Na}}-I_{\text{Kd}}-I_{\text{M}}-\frac{1}{a}{I}_{\text{syn}}\\ I_{\text{Na}}={\overline{g}}_{\text{Na}}{m}^{3}h(V-E_{\text{Na}})\\ I_{\text{Kd}}={\overline{g}}_{\text{Kd}}{n}^4(V-E_{\text{K}})\\ I_{\text{M}}={\overline{g}}_{\text{M}}p(V-E_{\text{K}})\end{array}$$ (4)

where C_m = 1 μF/cm² is the specific membrane capacitance, g_L = 0.045 mS/cm² is the leak conductance density, and E_L = −80 mV is the leak reversal potential. I_Na is the voltage-dependent Na⁺ current and I_Kd is the ‘delayed-rectifier’ K⁺ current responsible for action potentials. I_M is a non-inactivating K⁺ current responsible for spike frequency adaptation. These currents and their parameters were the same as in the biophysical model (see Destexhe and Paré, 1999). a is the total membrane area, which was 34 636 μm² for the layer VI cell described in Fig. 1.

All simulations and analyses were performed in the NEURON simulation environment (Hines and Carnevale, 1997) and were run on DELL workstations (Dell Computer Corporation, Round Rock, TX, USA) under the LINUX operating system.

In vitro experiments

Coronal slices of rat pre-limbic and infra-limbic areas of pre-frontal cortex were obtained from 2–4-week-old Sprague–Dawley rats. Rats (Harlan, Indianapolis, IL, USA) were anesthetized with Metofane (methoxyflurane, Mallinckrodt, Mundelien, IL, USA) and decapitated. Their brains were removed and cut into 350-μm-thick slices using standard techniques. Slices were then placed in a submerged chamber containing artificial cerebrospinal fluid (ACSF, mM: NaCl, 125; NaH₂CO₃, 25; D-glucose, 10; KCl, 2.5; CaCl₂, 2; MgCl₂, 1.3; NaH₂PO₄, 1.25) saturated with 95 % O₂/5% CO₂, at room temperature. Whole-cell patch-clamp recordings were achieved using glass electrodes (4–10 MΩ) containing (mM: KMeSO₄, 140; HEPES, 10; NaCl, 4; EGTA, 0.1; Mg-ATP, 4; Mg-GTP, 0.3; phosphocreatine 14). Patch clamp was performed under visual control at room temperature. The voltage was corrected for a 10-mV junction potential. In some experiments, synaptic transmission was blocked by D-2-amino-5-phosphonovaleric acid (50 μM), 6,7-dinitroquinoxaline-2,3-dione (10 μM), and bicuculline methiodide (20 μM). All drugs were obtained from RBI-Sigma (Natick, MA, USA), freshly prepared in ACSF and bath-applied. Data were acquired in current-clamp mode using an Axoclamp 2A amplifier (Axon Instruments, Foster City, CA, USA). We used regularly spiking layer V pyramidal cells. A total of nine visually identified pyramidal cells were used in this study.

Data were acquired using a dual computer setup. The first computer was used for standard data acquisition and current injection. Programs were written using Labview 6.1 (National Instrument, Austin, TX, USA), and data were acquired with a PCI-16-E1 data acquisition board (National Instrument). Data acquisition rate was either 10 or 20 kHz. The second computer was dedicated to dynamic clamp. Programs were written using either a Labview RT 5.1 or a Dapview (Microstar Laboratory, Bellevue, WA, USA) front-end and a language C back-end. Dynamic clamp (Sharp et al., 1993) was implemented using a PCI-7030 board (National Instrument) at a rate of 1 kHz, or a DAP-5216a board (Microstar Laboratory) at a rate of 10 kHz. Dynamic clamp was achieved by implementing a rapid (1 ms or 0.1 ms) acquisition/injection loop in current-clamp mode. Data were analyzed offline using MATLAB (The Mathworks, Natick, MA, USA).

All experiments were carried in accordance with animal protocols approved by the NIH.

RESULTS

We first analyze the properties of background activity in a detailed biophysical model of a neocortical pyramidal cell and decompose this activity into excitatory and inhibitory conductances. We then design a simple model that captures the spectral and amplitude characteristics of these conductances. This model is tested using a single-compartment representation and in real cortical neurons maintained in vitro. In both cases, we show to what extent this point-conductance representation captures the properties of neurons in vivo.

Detailed biophysical model of synaptic background activity

We first illustrate a detailed biophysical model of in vivo-like activity (Destexhe and Paré, 1999), which was built based on intracellular recordings in cat parietal cortex in vivo (Paré et al., 1998). This model incorporated the dendritic morphology of reconstructed neocortical pyramidal neurons from cat cortex, it contained voltage-dependent currents in the soma, dendrites and axon, and synaptic activity was simulated by Poisson-distributed random release events at excitatory and inhibitory synapses. The model was matched to intracellular recordings obtained during total suppression of network activity using TTX. By comparing electrophysiological parameters (average V_m, input resistance, V_m distribution) before and after TTX, in control conditions and by reversing inhibitory postsynaptic potentials using chloride-filled pipettes, one could estimate the release conditions at glutamatergic and GABAergic synapses corresponding to background activity. Excitatory and inhibitory synapses had to release according to weakly correlated Poisson processes (Destexhe and Paré, 1999).

Figure 1 shows an example of such activity simulated in a layer VI cell. The membrane fluctuated around −65 mV and spontaneously generated action potentials at an average firing rate of about 10 Hz (Fig. 1A1), which is within the range of experimental measurements in cortical neurons of awake animals (Hubel, 1959; Evarts, 1964; Steriade, 1978; Matsumura et al., 1988; Steriade et al., 2001). Without background activity, the cell was resting at −80 mV (Fig. 1A2), similar to experimental measurements after microperfusion of TTX (Paré et al., 1998). The model reproduced the ~80% decrease of input resistance (Fig. 1B), as well as the distribution of membrane potential (Fig. 1C) typical of in vivo activity (see Paré et al., 1998; Destexhe and Paré, 1999).

Statistical and spectral properties of synaptic background activity

A model of synaptic background activity must include the large conductance due to synaptic activity and also its large V_m fluctuations, as both aspects are important and determine cellular responsiveness (Hô and Destexhe, 2000). To build such a model, we first need to characterize these fluctuations. To this end, we recorded the total synaptic current resulting from synaptic background activity using an ‘ideal’ voltage clamp (series resistance of 0.001 MΩ) in the soma. This current (I_syn in Eq. 1) was decomposed into a sum of two currents, associated respectively with an excitatory (g_e) and an inhibitory (g_i) conductance. The latter were calculated by running the model twice at two different clamped voltages (−65 and −55 mV), leading to two equations similar to Eq. 1. The time course of the conductances was obtained by solving these equations for g_e and g_i, at each time step.

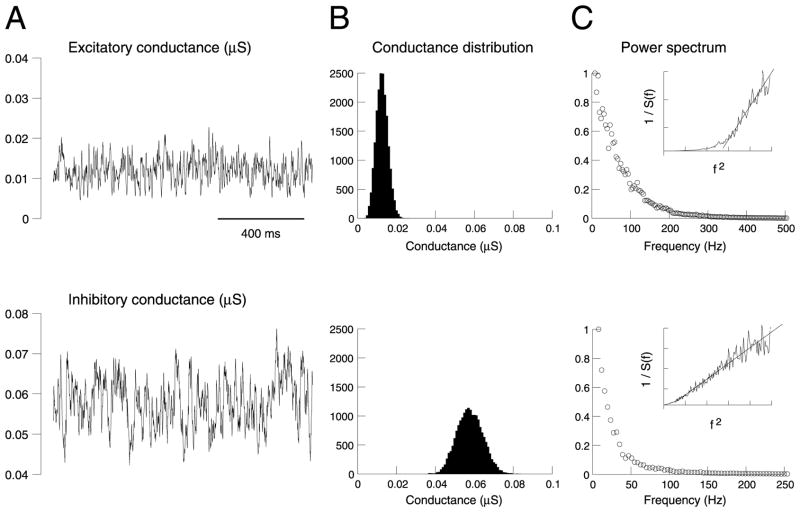
The time course of g_e and g_i during synaptic background activity is illustrated in Fig. 2A. As expected from the stochastic nature of the release processes, these conductances were highly fluctuating and had a broad, approximately symmetric distribution (Fig. 2B). It is also apparent that the inhibitory conductance g_i accounts for most of the conductance seen in the soma, similar to voltage-clamp measurements in cat visual cortex in vivo (Borg-Graham et al., 1998). This is not surprising here, because the release frequency of GABAergic synapses is five times larger than that of glutamatergic synapses, their decay time constant is slower, and the perisomatic region contains exclusively GABAergic synapses (DeFelipe and Fariñas, 1992). The average values and standard deviations were respectively 0.012 and 0.0030 μS for g_e, and 0.057 and 0.0066 μS for g_i.

Fig. 2.

Statistical properties of the conductances underlying background activity in the detailed biophysical model. (A) Time course of the total excitatory (top) and inhibitory (bottom) conductances during synaptic background activity. (B) Distribution of values for each conductance, calculated from A. (C) Power spectral density of each conductance. The insets show the inverse of the power spectral density (1/S(f)) represented against squared frequency (f² ; same scale used).

The power spectral density of g_e and g_i (Fig. 2C) shows a broad spectral structure, as expected from their apparent stochastic behavior, but also there was a clear decay at larger frequencies, showing that these processes are analogous to ‘colored noise’. Interestingly, the power spectrum clearly seems to decay in 1/f² for inhibitory synapses, as shown by representing the inverse of the power spectrum as a function of f² (Fig. 2C, insets). However, for excitatory synapses, the 1/f² decay was only true for high frequencies.

Point-conductance model of synaptic background activity

Next, we searched for stochastic representations that would capture the amplitude of the conductances, their standard deviation and their spectral structure. We considered the Ornstein–Uhlenbeck process, which was originally introduced to describe Brownian motion (Uhlenbeck and Ornstein, 1930):

$$\frac{\text{d}x}{\text{d}t}=-\frac{x}{\tau }+\sqrt{D}\chi (t)$$ (5)

where x is the random variable, D is the amplitude of the stochastic component, χ(t) is a normally distributed (zero-mean) noise source, and τ is the time constant (τ = 0 gives white noise, τ >0 gives ‘colored’ noise).

The advantage of using this type of stochastic model is that the distribution of variable x and its spectral characteristics are known analytically (see details in Gillespie, 1996). x is Gaussian and its variance is given by:

$${\sigma }^2=D\tau /2$$ (6)

and its power spectral density is:

$$S(f)=\frac{2D{\tau }^2}{1+{(2\pi f\tau )}^2}$$ (7)

where f is the frequency.

The Gaussian nature of the Ornstein–Uhlenbeck process and its spectrum in 1/f² qualitatively match the behavior of the conductances underlying background activity in the detailed biophysical model. Moreover, the variance and the spectral structure of this model can be manipulated by only two variables (D and τ), which is very convenient to fit this model to experimental data (using Eqs. 6 and 7).

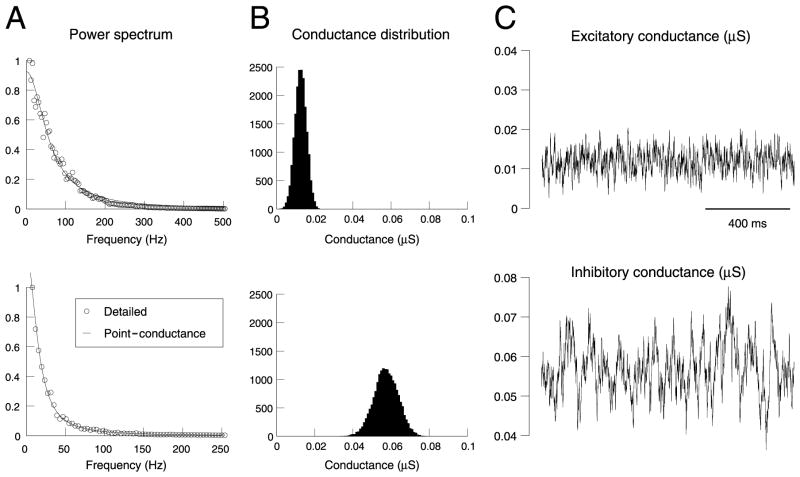
We applied this procedure to obtain a simple point-conductance representation of synaptic background activity. The model described by Eq. 2a, b was fit to the detailed biophysical simulations shown in Fig. 2. The results of this fitting procedure are shown in Fig. 3. Eq. 7 provided excellent fits to the power spectral density (Fig. 3A), for both excitatory and inhibitory conductances. By using average values and standard deviations estimated from the distribution of conductances in Fig. 2B, the parameters of the model could be estimated (values listed in Table 1 and Experimental procedures). The resulting stochastic model had a distribution (Fig. 3B) and temporal behavior (Fig. 3C) consistent with the conductances estimated from the detailed model (compare with Fig. 2). Moreover, the point-conductance model was more than two orders of magnitude faster to simulate.

Fig. 3.

Fit of a point-conductance model of background synaptic activity. (A) Power spectral density of the conductances from the biophysical model (top = excitatory, bottom = inhibitory). The continuous lines show the best fits obtained with the stochastic point-conductance model. (B) Distribution of conductance values for the point-conductance model. (C) Time course of the excitatory and inhibitory conductances of the best stochastic model. The same data lengths as in Fig. 2 were used for all analyses.

Table 1.

Effect of cellular morphology

Cell	Layer VI	Layer III	Layer Va	Layer Vb
Area (μm2)	34 636	20 321	55 017	93 265
Rin (MΩ)	58.9	94.2	38.9	23.1
ge0 (μS)	0.012	0.006	0.018	0.029
σe (μS)	0.0030	0.0019	0.0035	0.0042
τe (ms)	2.7	7.8	2.6	2.8
gi0 (μS)	0.057	0.044	0.098	0.16
σi (μS)	0.0066	0.0069	0.0092	0.01
τi (ms)	10.5	8.8	8.0	8.5

Synaptic background activity was simulated in four reconstructed neurons from cat cerebral cortex, using several thousand glutamatergic and GABAergic inputs distributed in the soma and dendrites (see Experimental procedures; Destexhe and Paré, 1999). The same respective densities of synapses were used in all four cells. The table shows the parameters of the best fit of the point-conductance model using the same procedure. These parameters generally depended on the morphology, but their ratios were approximately constant (g_e0/g_i0 and σ_e/σ_i).

Meaning of the different parameters

To characterize the effect of the different parameters and understand their biophysical significance, we compared the best fits of the point-conductance model obtained for different variations of the biophysical model. Table 1 shows the optimal parameters of the point-conductance models obtained from biophysical models with the same densities of all conductances, but different cellular morphologies. The average conductances (g_e0, g_i0) clearly depend on cellular morphology, which is expected because larger cells have larger numbers of synapses. Consequently, g_e0 and g_i0 vary approximately as the inverse of the the input resistance of the cell (Table 1).

Interestingly, although the absolute values of g_e0 and g_i0 clearly depended on the particular cell morphology, their ratio was approximately constant (g_i0≃5 g_e0 ; see Table 1). As discussed above, inhibitory conductances are larger because inhibitory synapses release on average five times more than excitatory synapses. Also, the decay time constant of GABA_A-mediated currents is slower than that of AMPA-mediated currents, resulting in larger integrated conductances. However, the quantal conductance is twice smaller for GABA_A (600 pS) compared to AMPA (1200 pS). These factors combine so that the net inhibitory conductance is approximately five times larger than excitatory conductances.

Table 1 also shows that the time constants τ_e and τ_i seem approximately independent of cellular morphology, with the exception of the layer III pyramidal cell. The latter effect is presumably due to the fact that these cells are electrotonically more compact and have fewer excitatory synapses than large cells from deep layers. However, τ_e and τ_i were greatly affected by changing the decay time constant of the synaptic currents in the detailed biophysical model (not shown).

The standard deviations (σ_e, σ_i) were only weakly affected by the above parameters. However, changing the correlation in the background activity had a marked effect on σ_e and σ_i, as shown in Table 2. In these simulations, the only parameter that changed was the correlation, while the same cellular morphology and biophysical parameters were used. This effect may be understood by noting that, when changing the correlation, the release statistics are unaffected at individual synapses, and therefore the total conductance remains the same. However, the correlation affects the respective timing of release events at different pairs of synapses, which translates into a change of σ_e and σ_i in the point-conductance model.

Table 2.

Effect of input correlation

Correlation	0.000056	0.00042	0.0012
ge0 (μS)	0.012	0.012	0.012
σe (μS)	0.0014	0.0030	0.0050
τe (ms)	2.4	2.7	2.96
gi0 (μS)	0.058	0.057	0.058
σi (μS)	0.0029	0.0066	0.011
τi (ms)	11.2	10.5	9.6

Three simulations of the layer VI pyramidal neuron (Fig. 1A) were run with identical parameters, except for the correlation which is indicated. The table shows the values of the best fit of the point-conductance model for each case.

Single-compartment models of in vivo-like activity

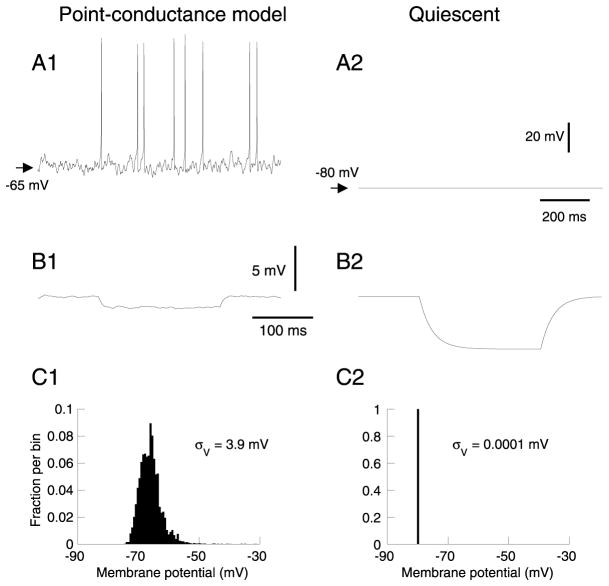
We next used the point-conductance approach to build a single-compartment model of synaptic background activity in neocortical neurons. We first investigated the basic membrane properties of the model, including the effect of background activity on the average V_m and input resistance, as well as the statistical properties of subthreshold voltage fluctuations (Fig. 4). In the absence of background activity, the cell was resting at a V_m of around −80 mV (Fig. 4A2), similar to measurements in vivo in the presence of TTX (Paré et al., 1998). In the presence of synaptic background activity, intracellular recordings indicate that the V_m of cortical neurons fluctuates around −65 mV, a feature that was reproduced by the point-conductance model (Fig. 4A1; compare with the biophysical model in Fig. 1A1). The point-conductance model also captured the effect of background activity on input resistance (Fig. 4B; compare with Fig. 1B), as well as on the amplitude of voltage fluctuations (Fig. 4C; compare with Fig. 1C). The standard deviation calculated from the V_m distributions (see Fig. 4B) was about σ_V = 4 mV for both models.

Fig. 4.

Membrane potential and input resistance of the point-conductance model. (A) Membrane potential in the presence (A1) and in the absence (A2) of synaptic background activity represented by two fluctuating conductances. The point-conductance model was inserted in a single compartment with only a leak current (same conductance density as the detailed model). (B) Effect on input resistance (same description and hyperpolarizing pulse as in Fig. 1B). (C) V_m distribution in the presence (C1) and in the absence (C2) of the fluctuating conductances.

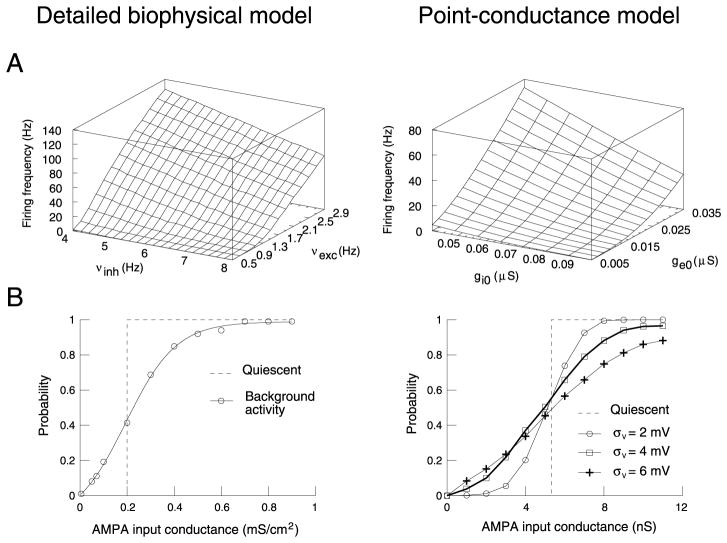
We next compared the firing behavior of the two types of model. The presence of background activity gave rise to V_m fluctuations and irregular firing in both models (see Figs. 1A1 and 4A1). The variation of the average firing rate as a function of the conductance parameters is remarkably similar in both models (Fig. 5A). Although the absolute firing rates were different, the shape of the 3-D plot was correctly captured by the point-conductance model. A rescaling of the absolute value can be obtained by changing the excitability of the cell by manipulating Na⁺/K⁺ channel densities (not shown).

Fig. 5.

Comparison of point-conductance and detailed biophysical models. (A) Firing rate as a function of the strength of excitation and inhibition. The biophysical model was identical to Fig. 1, while the point-conductance model was inserted in a single-compartment containing the same voltage-dependent currents as the biophysical model. The strength of excitation/inhibition was changed in the detailed model by using different release frequencies for glutamatergic (ν_exc) and GABAergic (ν_inh) synapses, while it was changed in the point-conductance model by varying the average excitatory (g_e0) and inhibitory (g_i0) conductances. g_e0 and g_i0 were varied within the same range of values (relative to the optimal value), compared to ν_exc and ν_inh in the detailed model. (B) Enhanced responsiveness to glutamatergic (AMPA) inputs. Left panel (modified from Hô and Destexhe, 2000): an AMPA-mediated input was simulated in the detailed model, and the cumulated probability of spikes specifically evoked by this input was computed for 1000 trials. The curves show the probabilities obtained when this procedure was repeated for various values of AMPA conductance. Right panel: same paradigm in the point-conductance model. Four conditions are compared, with different values of standard deviation of the V_m (σ_V). In both models, there was a non-null response for subthreshold inputs in the presence of background activity.

The point-conductance model also captured the modulation of cellular responsiveness by background activity shown previously in detailed biophysical models (Hô and Destexhe, 2000). The protocol used was to simulate a uniformly distributed AMPA-mediated synaptic conductance of progressively larger strength. The probability of spikes specifically evoked by this stimulus was then computed from the post-stimulus time histograms and is represented as a function of stimulus strength. This response curve was shown to be shifted by in vivo-like synaptic background activity compared to quiescent conditions (Fig. 5B, left panel; Hô and Destexhe, 2000). Without background activity (dashed line) the probability was all-or-none, reflecting the threshold for action potentials. With background activity (continuous line), the response curve was graded and there was a non-null response for subthreshold inputs (<0.2 mS/cm²).

This enhancement of responsiveness was also present in a single-compartment model where synaptic background activity was simulated by a point-conductance representation (Fig. 5B, right panel). In this case, the probability of response was computed following activation of a single AMPA-mediated synapse. Using different values of σ_e and σ_i, yielding different σ_V, gave rise to different responsiveness (Fig. 5B, symbols in right panel), with no effect on the average V_m. This effect of fluctuations was qualitatively similar to that observed in the detailed model (Hô and Destexhe, 2000).

Recreation of in vivo-like activity by dynamic clamp

We next used the point-conductance model to recreate in vivo type activity in real neurons. To this end, we injected the current computed from the point-conductance model in rat prefrontal cortical pyramidal cells in vitro. We took advantage of the relation between the parameter values and the input resistance of the cell (Table 1) to estimate heuristically these parameters using the following criteria. The parameters g_e0 and g_i0 were estimated such as to provide a ~15-mV depolarizing drive and four to five times reduction of input resistance, as found experimentally (Paré et al., 1998; Destexhe and Paré, 1999). The parameters σ_e and σ_i (or D_e and D_i) were then adjusted to yield voltage fluctuations with a standard deviation around σ_V = 4 mV. These conditions are illustrated in Fig. 6A for the voltage effect and Fig. 6B for the input resistance. The V_m distributions are depicted in Fig. 6C. Similar results were obtained for all the neurons tested (n = 9; the absolute values of the parameters g_e0, g_i0, σ_e and σ_i depended on the cell, but their ratio was kept constant: g_e0/g_i0 = 0.2, σ_e/σ_i = 0.4). Thus, the point-conductance representation recreates intracellular conditions similar to in vivo recordings.

Fig. 6.

Point-conductance clamp of neurons from rat prefrontal cortex in vitro. (A) Intracellular recording of a prefrontal cortex layer V pyramidal cell in control condition (A2), and injected with the point-conductance model (A1; g_e0 = 0.014 μS, g_i0 = 0.05 μS, σ_e = 0.0058 μS, σ_i = 0.0145 μS, τ_e = 2.7 ms, τ_i = 10.7 ms). The current computed by the point-conductance model, and injected in real time, is depicted in A1, lower trace. The point-conductance clamp depolarized the cell by about 15 mV, and introduced membrane potential fluctuations. (B) Average response of a different cell to a 200-pA hyperpolarizing pulse in control (B2) and in point-conductance clamp (B1) conditions (10 trials; g_e0 = 0.02 μS, g_i0 = 0.1 μS, σ_e = 0.005 μS, σ_i = 0.012 μS, τ_e = 2.7 ms, τ_i = 10.7 ms). The input resistance was decreased by 4.3-fold. (C) Distribution of membrane potential before (C2) and after (C1) the activation of the point-conductance clamp (same cell as in A). The standard deviation of the membrane fluctuations (σ_V) was increased to about 4 mV.

Finally, to test whether the timing of fluctuations – and therefore the spike discharges – are also similar to in vivo, we analyzed the statistics of the spontaneous discharge recreated by the point-conductance model. The spontaneous discharge of cortical neurons in awake animals is highly variable (Softky and Koch, 1993; Shadlen and Newsome, 1998). This variability is quantified by the coefficient of variation (CV), which is defined as:

$$\text{CV}=\frac{{\sigma }_{\text{ISI}}}{\langle \text{ISI}\rangle }$$ (8)

where 〈ISI〉 and σ_ISI are, respectively, the average value and the standard deviation of interspike intervals.

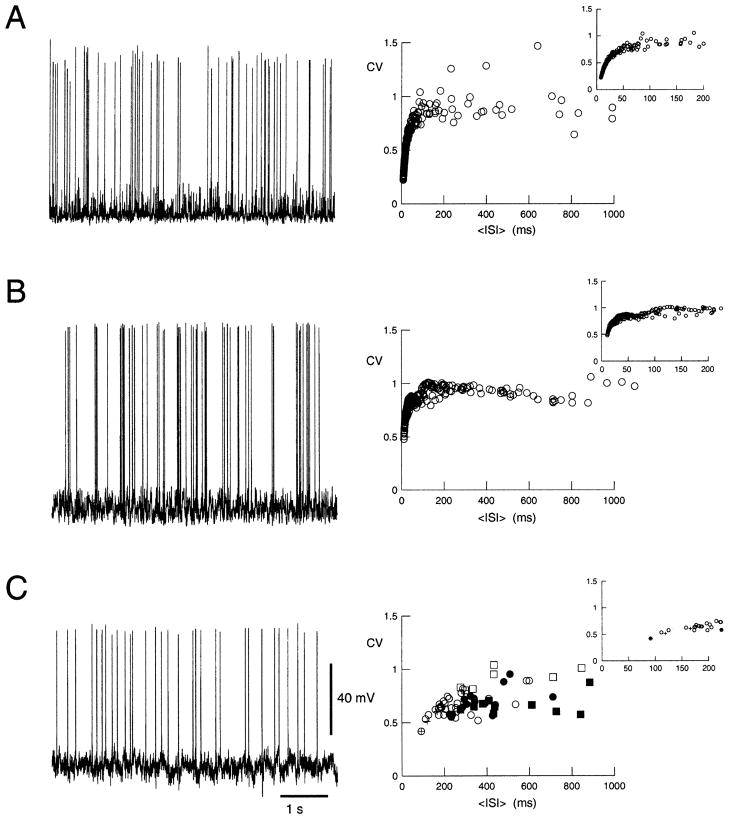
This quantity was computed in the models and in the dynamic-clamp experiments. The CV converged towards a constant value for periods of about 20 s of spontaneous activity (not shown). High CV values were observed in the detailed biophysical model (Fig. 7A), in the point-conductance single-compartment representation (Fig. 7B) and in the point-conductance clamp in vitro (Fig. 7C). In the latter case, however, the CV-ISI curve seemed to be shifted towards higher ISI values compared to the models. In all cases, the CV values obtained for large ISI ( >200 ms) were comparable (CV = 0.93 ± 0.21, 0.94 ± 0.14 and 0.72 ± 0.13 for Fig. 7A, B and C, respectively). These values are consistent with the averaged CV values measured in awake monkeys (Softky and Koch, 1993; Shadlen and Newsome, 1998).

Fig. 7.

High variability of spontaneous discharges. The left panels show a 6-s trace of spontaneous activity to illustrate the variability of discharges; the right panels show the CV calculated for periods of >33 s of activity in different conditions and represented against the mean ISI. (A) Detailed biophysical model (same parameter settings as in Fig. 1). The different CV values on the left were obtained by varying excitatory and inhibitory release frequencies (range of 0.5–2.9 Hz and of 4.0–8.0 Hz, respectively). (B) Point-conductance model (identical parameters as in Fig. 5; g_e0 and g_i0 were varied within the range of 0.003–0.035 μS and 0.017–0.145 μS, respectively). (C) Point-conductance clamp in vitro (same parameters as in Fig. 6). The different symbols in the right panel indicate different cells; the different points correspond to variations of the parameters (g_e0 = 0.005–0.0375 μS; g_i0 = 0.025–0.05 μS; σ_e = 0.00025–0.009 μS; σ_i = 0.00025–0.033 μS). All three models gave high CV values.

DISCUSSION

We have shown here that it is possible to draw a relatively simple point-conductance representation of synaptic background activity with only two variables and that this model is sufficient to account for several typical properties of neocortical neurons in vivo. We discuss here possible applications and further developments of this model, as well as how it could be tuned using experimental data.

Point-conductance models of in vivo activity

In the past, several ways have been considered for introducing noise in neurons. First, the addition of noise as a membrane current, which was realized both theoretically (Stein, 1967; Ricciardi and Sacerdote, 1979; Smith, 1992) and experimentally (Mainen and Sejnowski, 1995; Stevens and Zador, 1998; Fellous et al., 2001). A related approach consisted in introducing noise through stochastic variations of the spike threshold (Gerstner, 1995). These approaches, however, neglected an important component of background activity: the conductance, which is predominant in cortical neurons in vivo (Paré et al., 1998). Here we have proposed a method that explicitly incorporates this component by introducing two stochastic ‘point’ conductances varying according to the Ornstein–Uhlenbeck process. This approach captures several basic membrane properties of cortical neurons recorded in vivo, such as the lowered input resistance, a depolarized V_m, persistent voltage fluctuations and high variability of discharges.

One of the advantages of this approach is that various parameters of background activity translate into different parameters of the simplified model. The average release frequency of excitatory and inhibitory synapses affects the average conductances (g_e0 and g_i0), whereas the correlations among the synaptic inputs mostly affect the standard deviation of synaptic conductances (σ_e and σ_i in Table 2). The latter observation extends previous approaches which have demonstrated a profound impact of input correlations on the standard deviation of the membrane potential (Destexhe and Paré, 1999; Feng and Brown, 2000; Harsch and Robinson, 2000; Salinas and Sejnowski, 2000; Svirskis and Rinzel, 2000). We suggest here that background activity can be represented by two stochastically varying conductances, whose average value is related to the average release frequency, and standard deviation reflects input correlations.

The point-conductance approach can also be applied to build a single-compartment model to capture the membrane properties (Fig. 4) and responsiveness (Fig. 5B) of more detailed biophysical models. This confirms the previous suggestion that responsiveness is dependent on both the conductance and the membrane potential fluctuations present in background activity (Hô and Destexhe, 2000). It also confirms that variations in the morphology of dendrites – including their suppression – only lead to qualitative changes of responsiveness. These questions could be investigated further by combining point-conductance clamp with controlled synaptic stimulation in vitro.

Future developments of this model should address the presence of glutamate NMDA receptors, which were not included here but may play a role in the pattern of firing and the variability of discharges (Harsch and Robinson, 2000). The principal difficulty here is that NMDA receptors are voltage-dependent, which would result in the inclusion of voltage-dependent parameters in Eq. 2a, b. However, assuming that AMPA and NMDA receptors are colocalized, NMDA receptors would have the same presynaptic signal as AMPA receptors and both receptor types could possibly be merged into a single equation. This should allow the inclusion of NMDA receptors in a model of roughly the same complexity as the present one.

Recreating in vivo-like activity in vitro

We have shown here that point-conductance models can be injected into real cells in vitro by the dynamic-clamp technique, leading to in vivo-like membrane activity. The conductance injected represents the total synaptic current that converges to the soma, and therefore probably recreates conditions close to the somatic recording during intense network activity in vivo. However, one has to bear in mind that the dendrites are probably not correctly affected by a somatic point-conductance injection because of their remote electrotonic location. Consequently, point-conductance models should be used in neurons that are as small as possible to limit electrotonic artifacts of this type. Another possibility is to augment electrotonic compactness by using recordings in the presence of cesium in the electrode, or in the presence of neuromodulators.

If electrotonic artifacts can be minimized, the point-conductance injection could be used in conjunction with synaptic stimulation to investigate how the membrane potential fluctuations affect cellular responsiveness. It should also be possible to use this model to determine if neocortical pyramidal cells display phenomena like stochastic resonance, which is an enhancement of responsiveness in the presence of noise (Wiesenfeld and Moss, 1995). In this case, the point-conductance model would provide a more realistic source of ‘noise’ to investigate such phenomena.

The high variability of spontaneous discharges observed in neocortex in vivo (Softky and Koch, 1993; Shadlen and Newsome, 1998) can be reproduced by the models and by the point-conductance clamp (Fig. 7). However, the CV-ISI curves obtained here were significantly shifted compared to in vivo curves (compare right panels of Fig. 7 with Fig. 2 of Softky and Koch, 1993). The main reason for this difference was that the latter study investigated visual responses, with average firing rates well above 100 Hz, while we focused here on spontaneous activity, which involves much lower firing rates (around 10 Hz). The CV-ISI curve was also more shifted in the point-conductance clamp compared to the models. Possible reasons for this difference may be more prominent K⁺ currents underlying spike after-hyperpolarization and spike-frequency adaptation, or the high input resistance (and slow membrane time constant) inherent in whole-cell recordings. This predicts that affecting the input resistance and K⁺ currents using neuromodulators (McCormick, 1992; McCormick et al., 1993) should affect the CV-ISI relations. Future models and more refined experiments will be needed to characterize the influence of these different factors and identify the determinants of irregular firing activity in vivo.

Applications to in vivo experiments

Another useful property of the point-conductance model is that the distribution and the power spectral density of the stochastic variables can be tracked analytically (see Eqs. 6 and 7). Consequently, the parameters of this model can be completely determined from experiments. This could be applied to characterize the fluctuating synaptic activity in vivo by using voltage-clamp recordings. Voltage-clamp experiments in vivo are feasible (Borg-Graham et al., 1998) and it should be possible to use this technique to record long periods of spontaneous activity at different clamped voltages, calculate the distributions and spectra of excitatory and inhibitory conductances, and fit the model as described in Figs. 2 and 3. This possibility is presently under investigation.

Another possible application derives from the observation that the average conductances, g_e0 and g_i0, are mostly influenced by the intensity of background activity and cellular geometry, whereas their standard deviations, σ_e and σ_i, mostly reflect the correlation between synaptic events (Tables 1 and 2). Fitting the point-conductance model to voltage-clamp recordings in vivo may therefore provide an independent estimate of these parameters, and therefore a possible method to probe and compare different states of network activity recorded during the same intracellular experiment.

Abbreviations

ACSF

artificial cerebrospinal fluid

AMPA

α-amino-3-hydroxy-5-methyl-4-isoxazole propionate

CV

coefficient of variation

EGTA

ethylene glycol-bis(2-aminoethyl-ether)-N,N,N′,N′-tetraacetic acid

HEPES

N-(2-hydroxyethyl)-piperazine-N′-(2-ethanesulfonic acid)

ISI

interspike interval

NMDA

N-methyl-D-aspartate

TTX

tetrodotoxin

V_m

membrane potential