Performance and scaling effects in a multilayer microfluidic extracorporeal lung oxygenation device

Abstract

Microfluidic fabrication technologies are emerging as viable platforms for extracorporeal lung assist devices and oxygenators for cardiac surgical support and critical care medicine, based in part on their ability to more closely mimic the architecture of the human vasculature than existing technologies. In comparison with current hollow fiber oxygenator technologies, microfluidic systems have more physiologically-representative blood flow paths, smaller cross section blood conduits and thinner gas transfer membranes. These features can enable smaller device sizes and a reduced blood volume in the oxygenator, enhanced gas transfer efficiencies, and may also reduce the tendency for clotting in the system. Several critical issues need to be addressed in order to advance this technology from its current state and implement it in an organ-scale device for clinical use. Here we report on the design, fabrication and characterization of multilayer microfluidic oxygenators, investigating scaling effects associated with fluid mechanical resistance, oxygen transfer efficiencies, and other parameters in multilayer devices. Important parameters such as the fluidic resistance of interconnects are shown to become more predominant as devices are scaled towards many layers, while other effects such as membrane distensibility become less significant. The present study also probes the relationship between blood channel depth and membrane thickness on oxygen transfer, as well as the rate of oxygen transfer on the number of layers in the device. These results contribute to our understanding of the complexity involved in designing three-dimensional microfluidic oxygenators for clinical applications.

Introduction

Extracorporeal oxygenators are used for short term respiratory support in coronary artery bypass graft (CABG) surgeries and as a rescue therapy for acute respiratory distress syndrome (ARDS) patients¹. These oxygenators have extended and increased patient survival but are only rated for short-term use. In addition, blood priming volumes, defined as the total volume of blood in the oxygenator, are large, and the heavy reliance on high levels of anticoagulants in patients undergoing membrane oxygenation leads to significant safety problems and high rates of complications². More efficient oxygenators with smaller blood priming volumes and less reliance on anticoagulants might significantly expand the use of membrane oxygenation in acute care in both the pediatric and adult population. Safer and longer-term oxygenation technologies are also needed for patients with chronic lung disease such as chronic obstructive pulmonary disease (COPD). Chronic lung disease patients require long-term respiratory support as a bridge to lung transplant or potentially as a destination therapy in light of the severe shortage of donor organs and the drawbacks of immunosuppressive therapy. Development of a longer lasting and potentially wearable oxygenation system will enable safer and more efficacious application of the technology for acute and chronic lung disease conditions and will improve and extend the lives of large numbers of patients for whom a current therapeutic solution does not exist.

Currently, acute pulmonary failure is most often treated by mechanical ventilation in an ICU setting, which is limited due to reliance on the patient’s damaged lungs for blood oxygenation. Chronic lung disease patients receive a combination of portable oxygen therapy, which also relies on damaged lungs, and a variety of drug therapies which have limited efficacy. For cardiopulmonary support during bypass surgery and in certain cases of cardiopulmonary failure, support is provided by membrane oxygenators, which are typically composed of bundles of porous membrane hollow fibers^3–5. Due to limitations inherent in hollow fiber technology, current membrane oxygenators require large priming volumes, with adult units requiring 220 to 560 mL⁶ of blood, and neonatal machines requiring as much as 130 mL⁷.

Microfluidic technologies have emerged for a range of lab-on-a-chip applications and are now being explored for medical devices for support of the liver, kidney and lung, as well as other target applications. An in vitro model for applications in drug discovery for lung diseases based on microfluidics technology has recently been developed⁸ and several groups have reported progress in the development of prototype systems for microfluidic lung oxygenators. Early pioneering efforts explored the use of microfluidic techniques to fabricate microchannel networks for blood flow and oxygenation^9–11. More recently, several groups have reported the development of prototype devices for clinical applications including cardiopulmonary support for acute lung failure in the ICU and portable oxygenators for wearable pulmonary support for COPD patients^12–14.

The primary advantage of a microfluidic approach lies in its ability to better mimic the physiology of vascular flow and oxygen transfer in the human lung. In comparison with existing hollow fiber cartridge systems, microfluidic technologies can provide smoother blood flow pathways and transitions at branching points, thinner gas transfer membranes with dimensions that are closer to the actual alveolar membrane thickness, and shallow channels that improve oxygen transfer by reducing the distance between the oxygen source and the blood. Most efforts to date have explored the performance of 2D planar structures comprised of a single blood flow network layer and a gas source layer sandwiching a gas transfer membrane^13,14. Clinical devices will likely require expanding this geometry into a third dimension to provide sufficient oxygen transfer at physiologically acceptable levels of fluid mechanical resistance for clinical scale blood flows. Here we present the first report of a biomimetic vascular design for oxygenator applications scaled into multiple layers. We probe scaling effects including the fluid mechanical resistance at interconnects and oxygen transfer in devices comprising up to 10 layers of transfer modules. We also investigate the influence of blood flow rate, membrane thickness and blood channel depth on the efficiency of oxygen transfer, concluding with a discussion on challenges facing development of a clinically useful device for acute and chronic lung disease.

Materials and methods

Device design

The device consists of individual bilayer units (henceforth referred to as transfer modules) of microvascular networks and gas transfer compartments sandwiching a transfer membrane. The transfer modules are stacked and fluidically coupled to operate as one larger oxygenator to efficiently transfer O₂ and CO₂ while maintaining physiological blood flow streamlines. Each individual transfer module is made of polydimethylsiloxane (PDMS), and consists of a vascular channel layer and an oxygen channel layer, separated by a thin, non-porous but gas-permeable membrane, as has been previously described¹². Each transfer module is connected to the overall stack by vertical channels, creating a 10-transfer module device with a single inlet and a single outlet for blood in two opposite corners and companion inlet/outlets in the other diagonal corners to connect the gas compartments within each transfer module. With an arrangement of alternating vascular and oxygen channels, the overall device utilizes the high surface area to volume ratio of each vascular layer in a larger overall network, enabling efficient transfer of oxygen to blood.

The microvascular networks within each transfer module were designed to eliminate areas of disturbed blood flow by implementing a series of bifurcating microchannels of varying widths and lengths that mimic the scaling laws seen in physiologic vasculature^15,16. By creating a fluid path that incorporates smooth bifurcations and uniform fluid distribution, the wall shear stress along the channel is controlled within physiological limits¹⁷.

The specific dimensions of the multiple-width bifurcating channel network were selected to follow design rules for mimicking natural vasculature and to ensure smooth transitions at branching points¹⁸. Murray’s Law was used to determine the proper diameter proportions between a parent and daughter vessels at a bifurcation based on energy minimization considerations^19–22. Physiological considerations including the nature of the velocity profile, smoothness of blood flow, and reduction of clotting and inflammatory responses, as well as processing limitations and fabrication considerations are all reflected in the design of the bifurcations and channel dimensions¹⁹.

Extension of these considerations for blood flow into three dimensions through the vertical interconnects remains a challenge for the microfluidic technology described herein. While disturbed flow and sudden transitions are avoided in the horizontally arranged vascular networks in each transfer module, these detrimental features will be present in the transition regions from the vertical channels into each horizontal module; future efforts are aimed at developing biomimetic distribution networks for flow between the stacked transfer modules in multilayer scaled oxygenator devices.

Device fabrication

Channel layer fabrication

Photolithographic masks that featured the vascular and oxygen channel designs were designed in Tanner L-Edit (Monrovia, CA) and used to make channel molds on silicon wafers with SU-8 negative photoresist. The patterned channel molds were built using microfabrication techniques, as previously described^12,16,23. The height of the SU-8 features for the vascular network layer was targeted to either 50 or 100 μm for all channels in the network. For the gas transfer layer channels, the height was fixed at 100 μm for all experiments. The patterned wafers were passivated with C₄F₈ using an STS ICP system (SPTS, Allentown, PA) for ease of PDMS release. The individual vascular and oxygen channel layers that form each transfer module were made from PDMS elastomer and curing agent (Sylgard 184, Dow Corning, Midland, MI). PDMS prepolymer and curing agent, mixed in a 10:1 ratio by weight, was poured onto the silicon wafer molds, degassed in vacuum for 30 minutes, and placed in a 65°C oven to cure for a minimum of 3 hours. All PDMS channel layers were 1 mm thick, except for the layers that were used as the top and bottom of the overall device stack, which were 2.5 mm in thickness to accommodate tubing connections. After the PDMS was cured, each piece was cut to size. Inlet and outlet ports were punctured in the thick top and bottom channel pieces with a 1.5 mm biopsy punch.

Membrane fabrication and attachment

The thin, non-porous membrane in the middle of each transfer module was also made from PDMS, and was fabricated by spin-coating PDMS onto an unpatterned, passivated silicon wafer using a CEE 100 spin coater (Brewer Science, Rolla, MO). The thickness of the membrane was controlled by the spin speed and cycle length. The membranes for the test devices were made of PDMS spun at 2000 and 550 RPM with ramp-up rates of 1000 RPM/sec and 500 RPM/sec respectively, and all coatings were spun for 60 seconds at the target speed. After spin-coating, the PDMS-coated wafers were placed in a 65°C oven to cure for a minimum of 45 minutes. Post-fabrication membrane measurements showed that the average thickness was 30 μm for the membranes spun at 2000 RPM, and 117 μm for the membranes spun at 500 RPM. Other membrane thicknesses, including 11 um, 22 um, 50 um and 77 um, were likewise obtained by adjusting spin speed accordingly.

Membranes were attached to the oxygen channel pieces with an oxygen plasma bonding process using a March250X asher (March Plasma Systems, San Francisco, CA). The membrane, which was still attached to the unpatterned, passivated silicon wafer, and the oxygen channel layers were plasma treated at 250 mTorr pressure and 100 Watts power, for a total of 10 seconds. This treatment time was previously optimized to provide minimum plasma exposure while still forming a strong bond between the PDMS layers. The plasma-treated surfaces of the oxygen channel layers and the membrane were mated together, and the stack was placed into the 65°C oven under a load of ~2 pounds. After approximately 10 minutes, the membrane was cut around the edge of the oxygen channel piece with a sharp blade. The bonded assembly was then gently separated from the silicon wafer.

To attach the vascular channel piece, the same plasma parameters were used to treat the opposite side of the membrane and the patterned side of the vascular PDMS piece, as illustrated in Figure 1a. After plasma treatment, the two layers were bonded using alignment marks on the face of each piece. The complete transfer module was then placed in a 65°C oven under 1–3 pounds of weight for about 10 minutes. Using a 2 mm biopsy punch, each central transfer module was punctured with 4 through-holes in the designated inlet and outlet areas marked by the pattern, as shown in Figure 1b, allowing both the oxygen and the vascular channels to connect with the next layer of their respective type.

Figure 1.

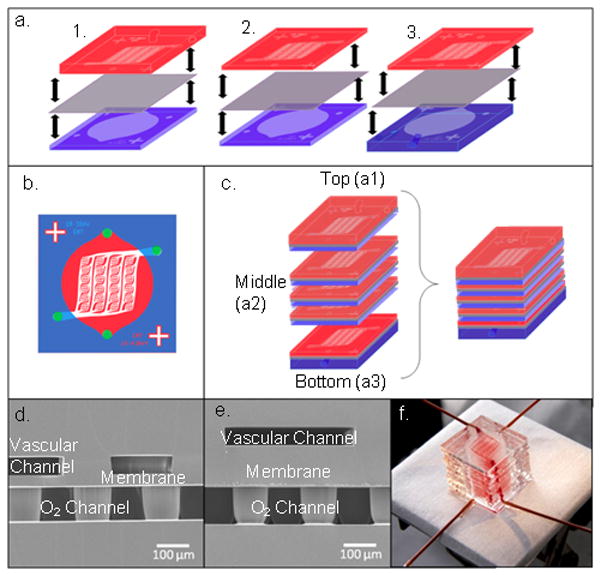
a) A schematic of the transfer module assembly alignment. In each case, the oxygen channel piece (blue) is bonded to the membrane (purple) first, and then aligned to the vascular channel piece (pink). This process is done for the top transfer module (1.), each middle transfer module, comprised of thin oxygen and vascular channel pieces (2.), and the bottom transfer module (3.). b) A schematic of a middle post-alignment transfer module shows hole-punching sites marked by purple dots. c) The entire device is built by assembling each individual transfer module first, then bonding all of the layers together in an alternating manner. d) An SEM image of a cross section of a transfer module comprising a 50 μm deep vascular channel network on the top, a 30 μm thick membrane, and a 100 μm deep oxygen channel on the bottom, where support posts can be seen throughout the channel. e) An SEM image of a cross section of a transfer module comprising a 50 μm deep vascular channel network on the top, a 117 μm thick membrane, and a 100 μm deep oxygen channel on the bottom. f) A 10-transfer module (10-TM) oxygenation device shown filled with blood in the vascular channel.

Device assembly

After the individual transfer modules were fabricated, they were attached to one another using the same oxygen plasma treatment parameters as previously described and shown in Figure 1c. A combination of polyetheretherketone (PEEK) tubing (Upchurch Scientific, Oak Harbor, WA) and Silastic tubing (Dow Corning, Midland, MI) was connected to the device inlets and outlets. The PEEK tubing was used to minimize error from oxygen transfer with the environment in our final measurements, and the Silastic tubing was used for connection to blunt-tipped syringe needles (Small Parts, Seattle WA). Dow Corning 1044 Silicone Rubber RTV coating (Dow Corning, Midland, MI) was used to seal device-tubing interfaces. Cross-sectional SEM images of transfer modules with 50 μm vascular channels and 30 and 117 μm membranes are shown in Figures 1d and 1e, respectively. A complete device comprising ten transfer modules with whole bovine blood flowing through the vascular networks is shown in Figure 1f.

Three device configurations were fabricated. A 10-TM consisted of a stack of 10 transfer module units. A 1-TM consisted of a single oxygen layer and single vascular layer with a thin PDMS membrane sandwiched in between. A 2-TM consisted of two 1-TM devices attached in an inverted fashion to one another as described previously¹². Measurements of oxygen transfer into the blood were taken in both the 2-TM devices and in 10-TM devices to assess scaling phenomena related to oxygenation. The 1-TM configuration was used to assess scaling phenomena related to the fluid mechanical resistance of individual bilayers by comparing to a 10-TM.

Resistance modeling

For clinical applications, a number of fluid dynamic parameters must be considered to enable safe and efficacious performance of the device. In addition to the aforementioned wall shear stress, parameters such as blood flow rates, pressure drops and fluid mechanical resistive losses must be managed. As the microfluidic device is scaled up, the parallel nature of the device construction causes the fluid resistance to decrease accordingly. We explored the behaviour of fluid resistance as a function of channel dimensions and stacking of the oxygenator into three dimensions. Important factors in this analysis include the tubing and tubing interconnects, as well as distensibility of the thin PDMS membrane.

The resistance of the microfluidic vascular network was determined by modeling a single layer using the SimHydraulics fluid simulation software package (MathWorks, Natick, MA). The model was simplified by separating the network into 3 levels: the single capillary bed, a “column” of 6 capillary beds and the channels which feed into and out of them, and finally the entire network, representing the microvascular network layout shown in Figure 1b. The capillary bed was modeled as non-circular pipes with rigid walls using laminar friction constants extrapolated from the literature²⁴ connected at nodes. A pressure drop over the bed was introduced and the resulting flow was used to calculate the resistance. The resistance was consistent over a wide range of flow rates, only increasing as the flow transitioned from laminar to turbulent at flow rates approximately 60 times the normal operating flow rates. Using these values, dimensions for a pipe with equivalent resistance and turbulence transition properties were determined, and an equivalent resistance pipe was used in place of each of the 6 capillary beds in the 6 bed “column” substructure model. The above process was repeated for the column substructure in the model of the full single layer network model, and the fluid elements were adjusted to the appropriate dimensions for each case analyzed.

Resistance testing

For initial resistance testing, pressure across the vascular network was measured by flowing DI water through the vascular channel. As described in the fabrication section, two 1-TM devices were tested and compared with a 10-TM device. Pressure was measured with a flow-through pressure transducer (Honeywell, Morristown, NJ) and read with an Omega digital multimeter (Omega, Stamford CT). Each pressure measurement was tested three times and the average value reported. Pressure-flow curves were obtained for two 1-TM devices at each of two channel depths (50 microns and 100 microns), and one 10-TM device; all devices tested for flow resistance had a membrane thickness of 50 μm.

A Harvard syringe pump with a 5 mL syringe was used to perfuse water through the pressure transducer and the vascular network channel. The vascular outlet was left open to the atmosphere. This test was performed at flow rates ranging from 0.1 to 9 mL/min, with each flow rate being tested at least three times. The measured pressure drop across the network was then used to calculate the network resistance. Similar measurements were taken as a function of flow rate for the interconnect regions and the tubing. These measurements were used to infer the actual resistance of the microvascular networks and the added resistances of interconnects and tubing as a function of scaling of the device.

Oxygen transfer modeling

The most critical performance parameter in lung oxygenators is gas transfer, both of oxygen into the blood and carbon dioxide out of the blood. Computational modeling (COMSOL Inc., Burlington, MA) of a simplified bilayer cross-section of a single channel was carried out in order to simulate the oxygen transfer from a source channel through a layer of PDMS into a flowing blood channel (Figure 2).

Figure 2.

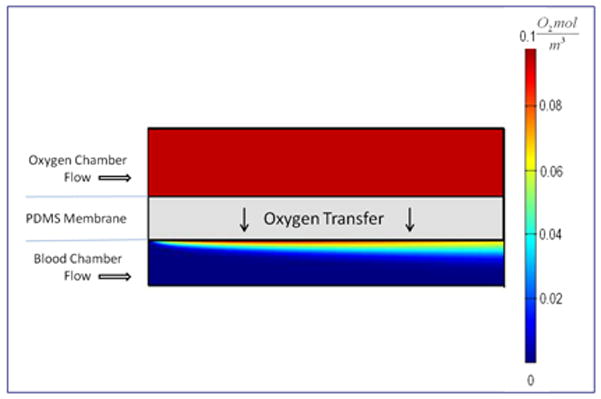
Oxygen distribution within a small section of the computational domain. The model was run with oxygen and blood flowing in the same direction at different flow rates. The color map indicates the oxygen concentration within both the blood and oxygen chambers; oxygen concentration in the membrane is not shown (Not drawn to scale).

Parameters such as the depths of the oxygen and blood channels and thickness of the membrane were taken directly from the device design. The oxygen diffusion and permeation rates in the various domains were taken from available values in the literature^25,26. A representative channel of the bifurcated network was used as the model domain for simulations that in turn served as an efficient trade-off between model accuracy and computing time. A mid-sized channel in the network with a width of 310 microns and a length of 3 mm was chosen using which the blood flow rate through the channel was derived by simple analysis of the distribution of flow through the entire network; equations used by the computational study are shown in Table 1.

Table 1.

Equations employed for performing the computational study. Note that I∈{o,b}, where ‘o’ denotes the oxygen chamber and ‘b’ denotes the blood chamber, and ‘p’ denotes the PDMS layer.

Number	Name	Equation	Applicable domain(s)
(1)	Continuity equation	$${\rho }^{\mathbf{i}}(\nabla ·{\mathbf{u}}^{\mathbf{i}})=0$$	Oxygen and blood chambers
(2)	Momentum equation	$${\rho }^{\mathbf{i}}({\mathbf{u}}^{\mathbf{i}}·\nabla ){\mathbf{u}}^{\mathbf{i}}=-\nabla {\text{P}}^{\mathbf{i}}+\nabla ·\left({\mu }^{\mathbf{i}}\nabla {\mathbf{u}}^{\mathbf{i}}\right)$$	Oxygen and blood chambers
(3)	Carreau model	$${\mu }^{\mathbf{b}}={\mu }_{\infty }^{\mathbf{b}}+\left({\mu }_0^{\mathbf{b}}-{\mu }_{\infty }^{\mathbf{b}}\right){\left[1+{(\lambda {\stackrel{.}{\gamma }}^{\mathbf{b}})}^2\right]}^{\frac{(\text{n}-1)}{2}}$$	Blood chamber
(4)	Convection-Diffusion equation	$${\mathbf{u}}^{\mathbf{i}}·\nabla {\text{C}}^{\mathbf{i}}={\text{D}}^{\mathbf{i}}{\nabla }^2{\text{C}}^{\mathbf{i}}$$	Oxygen and blood chambers
(5)	Diffusion equation	$${\text{D}}^{\mathbf{P}}{\nabla }^2{\text{C}}^{\mathbf{p}}=0$$	PDMS layer

The continuity and momentum equations were solved within the oxygen and blood chambers (Eqns. 1–2 in Table 1), where uⁱ, ρⁱ, Pⁱ, and μⁱ are the velocity, density, pressure and the viscosity, respectively. In order to capture boundary layer effects of the fluid within the blood chamber, a Carreau model was employed for all the simulations to account for shear thinning behavior of blood at low shear rates (Eqn. 3)²⁷. Here, μⁱ is the effective blood viscosity, ${\mu }_{\infty }^{\text{i}}=0.0035\text{kg}/(\text{m}.\text{s})$. and ${\mu }_0^{\text{i}}=2.5\text{kg}/(\text{m}.\text{s})$ are the blood viscosities at infinite and zero shear rates, respectively, γ̇ⁱ is the shear rate, λ = 25 s is a time constant, and n = 0.25 is a power law index^28–30. Within the oxygen and the blood chambers, oxygen transport follows a convection-diffusion process (Eqn. 4), where C_i, i ∈ {o,b} denotes concentration within both the domains. However, within the PDMS layer, oxygen transport follows a simple diffusion process (Eqn. 5). Diffusivity values for the model were assumed as D^o = 2e⁻⁹ m²/s, D^b = 1.97e⁻⁹ m²/s, and D^p = 1.6e⁻⁹ m²/s, for the oxygen chamber, PDMS layer, and the blood chamber, respectively^25,26.

Testing oxygen transfer into blood

Oxygenation through the thin membranes into flowing blood was assessed experimentally as a function of several critical operational parameters for the device, including blood flow rate, membrane thickness, and the depth of the blood flow network channels. Oxygen transfer was characterized for multiple devices for each configuration. These tests were performed with heparinized bovine blood (Lampire Biological Laboratories, Pipersville, PA) which was initially heated to 37°C and brought to venous conditions for pH and O₂ and CO₂ concentrations. Prior to testing, the devices were primed with deoxygenated PBS, and checked for the absence of bubbles in the device, and leaks and tears in the membranes.

A clinical blood gas analyzer (BGA) (Instrumentation Laboratory, Bedford, MA) was used to measure the dissolved oxygen in the blood, and a hemoximeter (ITC, Edison, NJ) was used to measure oxygen bound to hemoglobin directly, by detecting the oxyhemoglobin content (percent of hemoglobin bound to oxygen) before and after each experiment. A syringe containing venous conditioned blood was attached to the vascular inlet tubing of a primed device, and flow was driven by a syringe pump (Harvard Apparatus, Holliston, MA). The device was purged with 1 mL of blood; flowing oxygen was then introduced to the oxygen channel inlet at 0.15 psig. After the flow reached steady state, and all visual inspections confirmed the absence of bubbles or leaks within the device, a 2 mL sample of blood was drawn at the outlet of the vascular tubing with a second syringe pump set to the infuse rate of the first pump. After the sample was collected, flow into the device was stopped and the sample was tested with the BGA and hemoximeter.

The oxygen transfer rate was derived from measurements of the difference in total oxygen concentration between the blood entering the device and blood exiting the device. Using the oxygen binding capacity of hemoglobin (1.35 mL O₂ per gram of haemoglobin), we calculated oxygen bound to hemoglobin in each sample. The BGA provided the partial pressure of the dissolved oxygen in the blood in mmHg; using the solubility of oxygen in blood at 37°C (0.03 mL O₂/liter of blood/mmHg partial pressure), we determined the dissolved oxygen in blood. The oxygen transfer rate was calculated by adding the concentration values of dissolved and bound oxygen and multiplying by the blood flow rate.

Results

Network Resistance

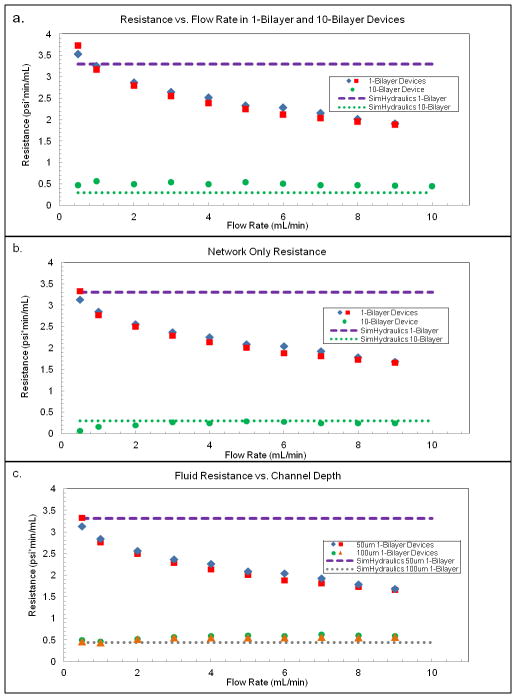
In Figure 3a, the hydraulic resistances of two single-transfer-module (1-TM-a and 1-TM-b) and one 10-transfer module (10-TM) vascular networks are plotted as a function of flow rate. These tested devices had 50 micron deep channels throughout the network. The resistance of the 1-TM devices is much higher than that of a 10-TM device, but resistance does not scale by the expected factor of 10. Device-to-device variability in resistance values between the two 1-TM devices is relatively small, and each data point represents the average of three measurements on a given device at each flow rate. Predicted fluid resistances of the 1-TM and 10-TM devices from the SimHydraulics analysis are also shown for comparison. We hypothesized that the discrepancies between the model and the data were due to interconnect resistances from the length of tubing from the pump to the device and the curved length of channel connecting the external tubing to the vertical pipe connecting the layers. Tubing and interconnect resistances remain fixed (independent of the number of transfer modules) and become proportionally larger for low-resistance stacked devices with many parallel layers. When these resistances are subtracted from the measured resistances (Figure 3b), the 10-TM device shows a resistance of about 0.3 psi*min/mL, which is approximately 1/10^th the resistance of a 1-TM device (3.2 psi*min/mL) at low flow rates. At these flow rates the SimHydraulics model of the microvascular networks in the planar layers is in agreement with test data for both the single and 10 layer devices.

Figure 3.

a) The measured resistance with respect to flow rate is shown for two 1-TM (1-bilayer) device as well as one 10-TM (10 bilayer) device. Resistance tests were performed using DI water through each device at various flow rates. b) Resistance for tubing and the inlet and outlet was tested at all flow rates for each device, and the combined tubing/interconnect resistance was subtracted from the total device resistance to provide the resistance measurement of the vascular network alone. c) The calculated resistance with respect to flow rate is shown for single vascular networks with two different channel depths, 50 and 100 μm. Two devices of each type were tested at each flow rate three times to obtain an average resistance as a function of flow rate through the vascular network; only the average resistance is shown for clarity. SimHydraulics simulations of the vascular network channels with rigid walls at a depth of 50 and 100 μm were run to predict the channel resistance, and are shown in the plot as dashed lines.

A second trend revealed by the fluid resistance measurements shown in Figure 3b is the reduction in resistance as a function of flow rate in the 1-TM devices. We hypothesized that distensibility of the channels, particularly of the gas transfer membrane wall, is the driving force behind this effect. The 10-TM device exhibits no such significant drop in resistance, presumably because the same overall flow rate is distributed over several layers, resulting in a lower transmembrane pressure per layer. A second possible factor in the stable resistance values for the larger device may be that the mechanical stability of the larger device constrains each layer, adding structural rigidity and preventing expansion of the channels. The outside walls of devices are also distensible, which will be more evident in the pressure-flow behavior of smaller devices where the surface-to-volume ratio is larger.

We also investigated the influence of the channel depth on resistance. In Figure 3c, the fluid resistances of two 1-TM devices with different channel depths are shown as a function of flow rate. The dashed lines indicate the predicted hydraulic resistance for each of these cases, based on the SimHydraulics model. Again, we hypothesize that the distensibility at higher flow rates is a major factor in the device with 50 μm deep channels, but is not observable in the device with 100 μm deep channels. The absence of apparent distensibility in the device with deeper channels illustrates the reduction in transmembrane pressure for a given flow rate passed through a larger cross-section, lower resistance network.

Oxygen transfer into blood

Oxygen transfer drives the design and scaling of membrane oxygenators, and determines clinically important parameters such as the blood priming volume and membrane surface area required to provide sufficient oxygenation of the blood³¹. We characterized the effect of membrane thickness, channel depth, and blood flow rate on oxygen transfer. In each experiment, the flow rate is the dominant factor controlling overall oxygen transfer, as higher flow rates lead to higher oxygen transfer in all cases tested. However, from a clinical standpoint, increases in flow rate ultimately provide diminishing returns, as the efficiency of oxygen transfer begins to drop at high blood flow rates. This can be seen by plotting the ratio of the oxygen transfer rate to blood flow rate (Figure 4). Although oxygen transfer increases with blood flow, the rate of increase drops sharply as the flow rate is increased beyond a certain point. In the high flow regime, the residence time of the blood is insufficient to permit oxygen from the source to reach the entire volume of the passing blood, reducing the efficiency of oxygenation even though the oxygen concentration in the blood continues to increase slightly. The effects of device geometry and blood flow rate on oxygen transfer lead to a critical trade-off between transfer efficiency and blood priming volume, necessitating optimization studies that minimize priming volume while maintaining sufficient oxygen concentrations in the patient’s bloodstream during therapy.

Figure 4.

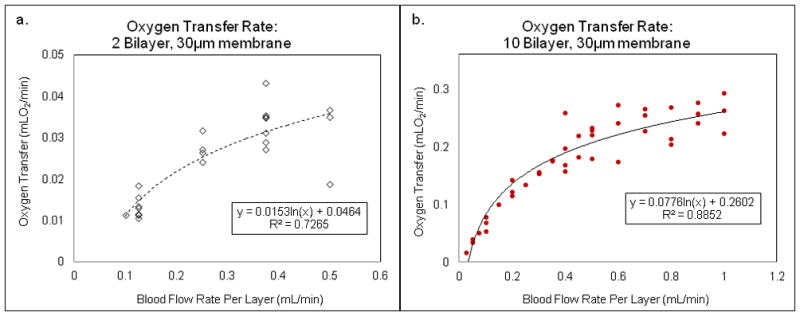
Blood flow rate effects on the oxygen transfer in three 2-layer devices (a) and three 10-layer devices (b).

Most of the oxygen transfer measurements were conducted with 10-TM devices. Initially, we investigated the use of the 2-TM device¹³ comprising two inversely oriented single transfer modules. Oxygen transfer rate measurements in 2-TM and 10-TM devices are shown in Figures 4a and 4b, respectively, with best-fit logarithmic curves and R-squared values shown for each set of data. In Figure 4a, six different devices were tested, while in Figure 4b, four different devices were tested. Not each device was tested at each flow rate, and the different devices are not distinguished in the graphs, but all data taken is included. In each case, the oxygen transfer rate rises with flow rate, eventually beginning to level off at high flow rates. Data from repeat testing of 10-TM devices was more reproducible than for 2-TM devices, likely due to the smoothing effects on aberrations in flow and oxygen transfer being averaged over a larger number of transfer modules. Therefore, all of our remaining experiments were conducted using 10-TM devices.

Figure 5 compares the oxygen transfer rates for two sets of 10-TM devices with 30 μm membranes, constructed with 50 and 100 μm deep vascular channels. In Figure 5a, the oxygen transfer rate is plotted against the blood flow rate, while in Figure 5b, the effective oxygen concentration of the blood is plotted against the flow rate. Data for four different 50 micron channel devices and two different 100 micron channel devices are shown in the figure. As mentioned earlier, the more clinically relevant indicator is shown in Figure 5b, as oxygenators need to provide sufficient transfer to maintain a patient’s blood at oxygen concentrations of at least 4% of the total blood volume². As seen in Figure 5, the 50 μm channel provides slightly more oxygen transfer than a 100 μm channel at a given blood flow rate. Though the priming volume of a 50 μm deep vascular channel device is half that of a 100 μm deep vascular channel device, similar levels of oxygen transfer are achieved, suggesting that microfluidics-based devices are capable of providing highly efficient oxygen transfer in small blood volumes by reducing the maximum distance through which gas must travel in order to fully oxygenate the blood.

Figure 5.

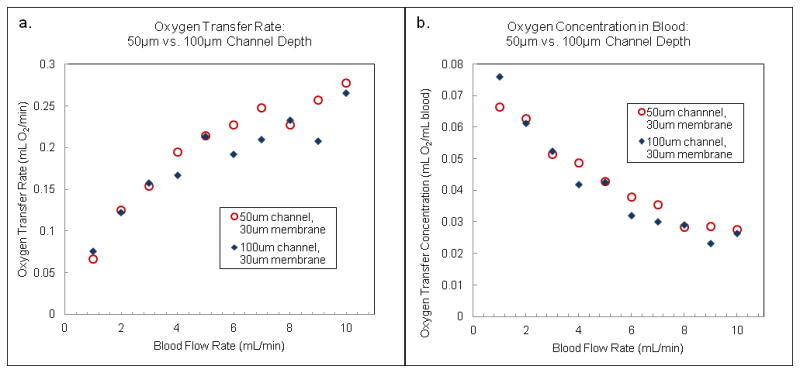
(a) Oxygen transfer rate (mL O₂/min) for a 10-TM device with 50 micron deep channels (circles) compared with a 10-TM device with 100 micron deep channels (diamonds) as a function of flow rate. (b) Oxygen concentration (mL O₂/mL blood) for the same two devices as a function of flow rate. The gas transfer membranes in these devices were 30 microns thick.

A critical design parameter for a membrane oxygenator is the membrane thickness. Thinner membranes will transfer oxygen more readily, due to the increase in oxygen permeance¹². Figure 6a shows the oxygen transfer values for four devices each with 30 and 117 μm membranes, in 10-TM devices constructed with 50 μm deep vascular channels; again the average values are shown in the chart and error bars omitted for the reasons mentioned earlier. The thinner membrane does provide more oxygen transfer across a range of flow rates, but not by a large factor. The oxygen permeance of the thinner membrane is roughly 4 times higher than that of the thick membrane; therefore oxygen transfer might be expected to be significantly enhanced. However, the measurements indicate modest improvements in oxygen transfer for significantly thinner membranes, suggesting that oxygen transport across the membrane is not the limiting factor governing transfer.

Figure 6.

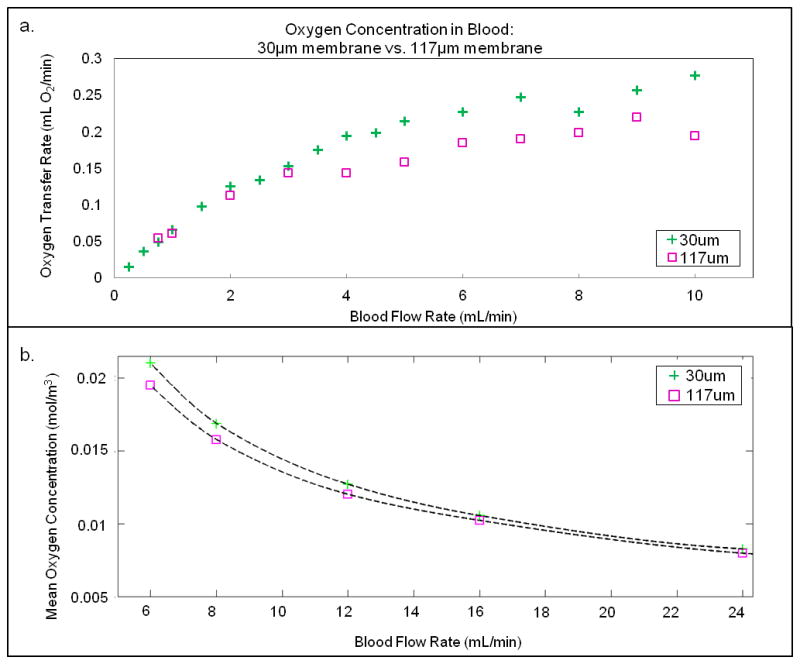
(a) Measurements of oxygen concentration in the blood for 10-TM devices constructed using 30 micron thick membranes (crosses) versus 117 micron thick membranes (squares) as a function of flow rate. (b) Computational model simulating the effect of gas transfer membrane thickness in a single representative channel, as described in the text.

A modeling-based calculation of oxygen transfer for these two cases is shown in Figure 6b; again we see that the thinner membrane (30 μm) provides superior oxygen transfer than the thicker membrane, but not by a large factor. The simulation was a 2D simplification of a cross section of a single 50 micron deep channel, separated by a PDMS membrane from a 75 μm deep oxygen channel. The simulation was run for 30 and 117 μm membrane thicknesses, and the mean oxygen concentration in the vascular channel was calculated against the vascular inlet flow rate. For all flow rates considered, the 30 μm thick membrane resulted in a higher oxygen concentration in the vascular channel. However, as the inlet flow rates increased, the difference between the two membranes diminishes.

In order to assess the scaling of oxygen transfer as the number of layers is increased, we have compared the experimental rate of oxygen transfer in 2-TM devices with that obtained for 10-TM devices. Total oxygen transfer data for each of these sets of devices is shown in Figure 7a, along with a best-fit polynomial curve to the data, across a range of blood flow rates. Averages for five different 2-Bilayer and four 10-Bilayer devices are plotted in Figure 7a. The flow rates shown in the graph are per layer for direct device comparison. The curve fit is necessary in order to compare data at the same blood flow rate because each device was tested at a different set of blood flow rates. In Figure 7b, the ratio of oxygen transfer rates is plotted by comparing the curve fitting data across a range of overlapping flow rates. From Figure 7b, it is evident that the expected scaling of 5x is approached across a range of comparable blood flow rates. It is not clear why 5x scaling is seen at the lowest and highest flow rates tested, while a scaling closer to 4.25x is seen in the mid-range of blood flow rates. The range of comparison is bounded by limitations in the maximum rate of blood flow in the smaller device before membrane distension, or damage to the membranes occurs. This scaling behavior suggests that as devices are scaled to larger numbers of layers for clinical applications, oxygen transfer has the potential to scale accordingly. For tissue engineering applications, it is useful to consider oxygen transfer on a volume density basis, as high efficiency oxygenation in small total device volumes becomes critical³².

Figure 7.

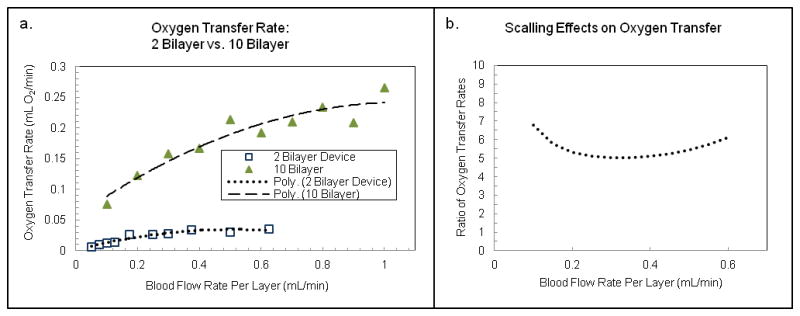
Scaling of oxygen transfer rate between devices with 2 versus 10 transfer modules (bilayers). (a) Oxygen transfer rate (mL O2/min) plotted for a 2-bilayer device (circles) and a 10-bilayer device (diamonds) as a function of blood flow rate per layer. In each case, the data has been fit with a polynomial curve in order to make direct comparisons between oxygen transfer rates at a given flow rate per layer. (b) Ratio of oxygen transfer rates for the 10-bilayer versus 2-bilayer devices as a function of blood flow per layer taken from the best-fit curves in (a), showing that the oxygen transfer rate scales by 4 – 6x when the number of transfer modules (bilayers) is increased by a factor of 5.

Discussion

We have assessed the performance of the prototype microfluidic oxygenator, its oxygen transfer characteristics and fluid mechanical resistance as a function of multi-layer. Resistance associated with tubing and interconnects becomes dominant for devices with larger numbers of layers, while distention of the gas transfer membrane diminishes as transmembrane pressure is reduced and the number of layers increases. Oxygen transfer rates appear to scale directly with the number of transfer modules contained within the device.

As a single transfer module device is scaled up into a multi-layer stack, the fluid mechanical resistance drops in proportion to the number of layers. Resistances in the tubing and at interconnect points become more significant as the device is scaled up; the resistance of the multilayer network is reduced as the layers are connected in parallel, while the resistances of the tubing and connections remain fixed. In order to reduce undesirable resistances and pressure drops, it is therefore critical to develop and utilize low-resistance tubing and interconnect geometries for scaling of microfluidic devices. Ultimately, the design of a clinical device will require careful consideration of scaling effects related to fluid resistance, channel geometry, structural rigidity, gas transfer, and the relationships between these various elements of the device design.

The oxygen transfer capabilities of the lung assist device are governed by membrane thickness, channel depth, network design, and blood flow rate. Target values of critical features of a clinical scale device, including overall size, blood prime volume, and total blood-membrane contact surface area, must be balanced against the required oxygen transfer rate. One of the primary goals in the design of a clinically useful device is to minimize blood priming volume and membrane surface contact area while maximizing the efficiency of gas transfer. The test data reported here demonstrate that blood flow rate is the chief factor that controls oxygen transfer into blood. Though the oxygen transfer rate rises as blood flow rate is increased, the rate of the oxygen transfer increase diminishes, ultimately resulting in an overall decrease in oxygen concentration of the blood. Since final oxygen concentration is a major design parameter in a blood oxygenating device, there is a trade-off between the blood flow rate and the oxygen saturation. If a minimum transfer rate per volume of blood is targeted, then the device can be set to operate just below that critical flow rate, in order to minimize device size and blood priming volume.

Thinner membranes are intuitively more efficient at transferring oxygen and CO₂, and all of our oxygen testing data shows that 30 μm membranes transfer more gas than 117 μm membranes, as expected. However, the advantage is not proportional to permeability, because at the operating conditions of our devices, the membrane becomes saturated with oxygen while the uptake of oxygen by blood occurs at a much slower rate. Due to this phenomenon, the difference in oxygen transfer between the two membrane thicknesses is very modest across all flow rates. Further analysis of the data and computational simulations will be necessary to establish a global optimum for membrane thickness as a function of gas transfer and other parameters such as device robustness, yield and distensibility. Ultimately, carbon dioxide gas transfer effects must also be probed as a function of device parameters as well; recent studies indicate that optimal CO2 transfer rates may be obtained using a porous polycarbonate membrane integrated into a microfluidic device³³.

We found that a network with 50 μm deep channels showed a small but clear benefit in oxygen transfer over a 100 μm deep vascular network. A shallower network has a lower priming volume and is thus more clinically desirable. When scaling up a device however, other factors must be considered. Other groups¹⁵ have cited that the influence of channel depth on oxygen transfer is also dependent on channel length. For short channels, shallow depths show more efficient oxygen transfer, while for longer channels, deeper channels maximize oxygen transfer. These effects must be balanced to optimize device performance.

Conclusion

We have investigated the influence of device scaling on several important performance-related parameters for membrane oxygenators. Requirements for next-generation membrane oxygenators include high levels of oxygen transfer, low blood prime volumes, and improved blood flow. Device scaling has significant effects on fluid mechanical resistance, requiring attention towards reducing interconnect-related resistance losses and pressure drops as the device is scaled by increasing the number of layers. In terms of oxygen transfer, thinner gas transfer membranes result in improved transfer, but improvements are limited by membrane saturation. Reduced blood channel depth increases the gas transfer rates slightly, but has the more important benefit of proportionately reducing the blood prime volume of the device. These effects have been simulated using a finite element model for blood flow and gas transfer, which will be further used to define the projected device performance as it is scaled towards clinical use.