Volumetric Navigators (vNavs) for Prospective Motion Correction and Selective Reacquisition in Neuroanatomical MRI

Abstract

We introduce a novel method of prospectively compensating for subject motion in neuroanatomical imaging. Short 3D EPI volumetric navigators (vNavs) are embedded in a long 3D sequence, and the resulting image volumes registered to provide an estimate of the subject’s location in the scanner at a cost of less than 500 ms, ~ 1% change in contrast, and ~ 3% change in intensity. This time fits well into the existing gaps in sequences routinely used for neuroimaging, thus giving a motion-corrected sequence with no extra time required. We also demonstrate motion-driven selective reacquisition of k-space to further compensate for subject motion. We perform multiple validation experiments to evaluate accuracy, navigator impact on tissue intensity/contrast, and the improvement in final output. The complete system operates without adding additional hardware to the scanner and requires no external calibration, making it suitable for high-throughput environments.

1 Introduction

High-resolution neuroanatomical MR imaging requires scans with durations measured in minutes. However, subject motion during a 3D-encoded acquisition can result in the entire scan being corrupted to the extent that it is unusable. The common solution to this problem is to discard and reacquire the entire scan, but this implies a substantial cost in time. 2D-encoded scans offer greater resistance to subject motion, but at the cost of SNR. Alternatively, sedation is used with certain populations (e.g., pediatric clinical subjects) but imposes a risk and is not normally considered ethical for research purposes. A 3D acquisition method that is insensitive to subject motion is preferable in both research and clinical settings.

Motion-correction systems in MRI can be grouped into two general methods: prospective and retrospective. Retrospective methods use information about the subject’s motion to estimate what k-space data would have been measured if the subject had not moved during scanning [1–4]. Prospective methods use motion-tracking data acquired during the scan to follow the subject with the gradient axes of the sequence, measuring the desired k-space data directly [5–14]. Additionally, it is possible to combine the two methods so that retrospective processing corrects residual errors in the prospective system [15]. A retrospective system can access all of the k-space data while performing reconstruction; a prospective system must necessarily rely only on previous measurements to estimate the current position of the patient. However, a prospective system avoids the need to estimate missing k-space data, allowing for direct reconstruction while avoiding possible sources of estimation error in the k-space data.

We also differentiate two types of motion correction problems that arise in MRI: between-scan and within-scan. In fMRI, a series of EPI or spiral volumes are acquired in rapid succession and then the time-course of each voxel’s intensity is analyzed. In this case, the problem of between-scan motion arises since it is essential that voxels represent the same anatomical region across volumes in order for time-courses to be valid. Several retrospective motion correction methods are available for this problem, registering either slice-by-slice or volume-by-volume to estimate the data that would have been acquired in each volume if the subject had not moved [16–18]. Prospective motion correction can also be employed for this problem, for example the orbital navigator system [6] that inserts 3-plane circular k-space navigators, or the PACE system [5] that registers each completed EPI volume back to the first time-point and so requires no navigators.

In high-resolution anatomical scanning, the issue arises that subject motion during the scan can make the k-space data inconsistent, resulting in ghosting, blurring, and similar well-known artifacts. Several systems are available to estimate motion-free k-space data retrospectively using information captured during the scan; PROPELLER [2] and SNAILS [4] use redundant sampling of the center of k-space during each TR to record the required information. It is also possible to track subjects using cameras and optical landmarks [19], or with gradient-sensing probes [9], although these systems require the optical targets or probes be affixed rigidly to the subject and additional hardware added to the scanner system. Additionally, calibration is required to ensure correct coordinate mapping between scanner and camera coordinates.

More directly related to our proposed method, a variety of prospective systems based on navigator scans have been previously presented. Fourier Transform identities predict that translations in the spatial domain will result in phase shifts in the Fourier domain and rotations in the spatial domain will result in rotations in the Fourier domain. Thus, under the assumption that rigid head motion produces identical rigid transformation of both magnitude and phase components of the image data, it is possible to acquire only a small region of k-space as a navigator and use this subsampled data to estimate rigid motions; orbital [6], spherical [7, 13], and cloverleaf [8] navigators exemplify this approach. Alternatively, the PROMO method uses repeated acquisitions of three orthogonal 2D magnitude images as its navigator, registering them in image coordinates, and then smoothing the estimate across the repeated acquisitions via an extended Kalman filter [10–12].

In this work we demonstrate the use of volumetric EPI navigators combined with selective data reacquisition to produce 3D multiecho MPRAGE (MEMPRAGE) [20], 3D T2SPACE, and 3D T2SPACE FLAIR sequences with the same T1 and T2 contrast properties as their commercial counterparts, but with substantially reduced sensitivity to motion. We have selected these sequences because they are routinely used at our imaging center to acquire high-quality brain morphometry data. We demonstrate the reduced motion sensitivity of our sequences and compare them to their non-navigated counterparts on the 1.5 T Avanto and 3 T TIM Trio scanners (Siemens Healthcare, Erlangen, Germany). Our method is similar to PROMO in that we use a navigator to collect full magnitude image data and register our information in the spatial domain; in Discussion we will highlight the various design choices that make our proposed method substantially different.

We additionally present a series of experiments designed to quantify the performance of our system. We measure the jitter in our motion tracks using a static phantom. We then evaluate the effect of inserting a navigator on the contrast of the parent scan using human subjects who were asked to remain stationary. Finally, we perform a series of directed-motion experiments to quantify the improvement produced by each part of our motion correction system when used for brain morphometry.

2 Methods

2.1 EPI vNavs and prospective motion correction

Our volumetric navigators are 3D-encoded EPIs with 8 mm resolution and 256 mm FOV in all three directions, giving 32³ voxels in the volume. The TE is 5.0 ms, the TR is 11 ms, and the bandwidth is 4596 Hz/px. We acquire our volume with 25 shots: the first excitation is used to collect a navigator for N/2 ghost reduction and the remaining 24 are acquired to fill 3/4 of k-space, with zero-padding accounting for the remaining k-space data. This gives us a total acquisition time of 275 ms. We use a flip angle of 2 degrees to minimize the effect on the anatomical sequences’ contrast. Additionally, since our navigator and anatomical sequences all use non-selective pulses, there is no localized spin history interaction between the components. To address wrap issues from the non-selective pulse the EPI navigator is acquired with the readout direction aligned head-foot so that the 2× readout oversampling employed in the navigator can ensure a wrap-free FOV. An example slice is shown in Fig. 1.

Figure 1.

Example of 32 sagittal slices acquired by the EPI navigator during an MEMPRAGE at 3 T with a 32-channel head coil.

The choice of specific navigator sequence is highly customizable inside our framework. We have found that for general adult neuroimaging the protocol specified above works well with little interaction on the part of the scanner operator. However, our sequence has been programmed so that a large variety of 2D and 3D EPI sequences can be used instead, just by setting up the desired protocol on the scanner and executing one “test shot” of the navigator (described in section 2.3). This flexibility has proven valuable, for example, in pediatric settings where no fixed navigator FOV is appropriate for the heads of all subjects who arrive at the MR in a given day; the operator can quickly size the navigator to each subject.

We insert one navigator into each TR of the anatomical sequence (we call the anatomical sequence the parent sequence). After playing out several dummy TRs to reach steady state, we use the navigator volume acquired during the first TR as our baseline for the imaging coordinates. As subsequent navigators are acquired in later TRs, we register each navigator back to the baseline navigator volume and realign the imaging coordinates of the parent and navigator as necessary. Registration of the navigators is performed using the optimized PACE algorithm which has been established as an efficient system for registering whole-head EPI [5]. We find that, depending on the specific Siemens image reconstruction system attached to a given scanner, 80–200 ms is sufficient time for registration and communication between the software systems required to realign the imaging coordinates. Thus, we have produced a navigate-and-correct sequence sub-block that consumes 355–475 ms for its complete acquisition, registration, and communication when inserted into a parent sequence. In its traditional fMRI application, PACE has a lag of two TRs because while the data from TR i is being registered, the subsequent TR (i + 1) is being measured, so the correction from TR i is only available at the beginning of TR (i + 2) [5]. In the setup described above there is no such lag; the navigator is acquired and the correction is applied to the imaging coordinates immediately before the parent sequence’s readout train.

2.2 Selective reacquisition

Our once-per-TR correction of the imaging coordinates allows us to compensate for subjects changing position across TRs. However, our system cannot directly compensate for motion that occurs during a single TR. To address this issue, we compute a “motion score” for each TR, using the difference between the navigators on opposite sides of the parent sequence’s readout train to estimate how much motion occurred during each TR. This difference requires no additional time to compute since the second navigator is always imaged in the estimated coordinates of the first navigator. Thus, the motion estimate derived from the second navigator is also our estimate of the difference between the navigators. We compute the motion score by first determining the magnitude of the angle of rotation via

$$|\theta |=\left|\text{arccos}\right\{\frac{1}{2}[-1+\text{cos}({\theta }_x)\text{cos}({\theta }_y)+\text{cos}({\theta }_x)\text{cos}({\theta }_z)+\text{cos}({\theta }_y)\text{cos}({\theta }_z)+\text{sin}({\theta }_x)\text{sin}({\theta }_y)\text{sin}({\theta }_z)]\left\}\right|,$$ (1)

where θ_x, θ_y, and θ_z are the respective Euler angles of the estimated rotation, expressed so that rotation is applied first around the x-axis, then the y-axis, and finally the z-axis. Many other expressions of this quantity are possible, depending on how the 3D rotation is represented (e.g., via quaternions). From this we define

$$\mathrm{\Delta }R=64{\{{[1-\text{cos}(|\theta |)]}^2+{[\text{sin}(|\theta |)]}^2\}}^{1/2}$$ (2)

which is the largest displacement experienced by any point on a sphere with 64 mm radius, rotated by |θ|. We can then combine this with the estimated translations to give our final motion score

$$\text{score}=\mathrm{\Delta }R+{({\mathrm{\Delta }}_x^2+{\mathrm{\Delta }}_y^2+{\mathrm{\Delta }}_z^2)}^{1/2},$$ (3)

where Δ_x, Δ_y, and Δ_z are the estimated translations in x, y, and z respectively. The score for a given motion estimate is then the maximum, over all points on a sphere with 64 mm radius, of the estimated displacement. This radius is chosen to roughly represent that of a human brain, but in general simply provides a weighting between the rotation and translation components of the motion score.

TRs are ordered in a priority queue based on their motion scores. Once all the TRs have been executed in their normal order, the sequence begins reacquiring TRs based on their order in the priority queue. Each reacquired TR’s motion score is compared with the previous acquisition of that TR and the least-motion-damaged acquisition of each TR is retained while more-damaged acquisitions are discarded. When initiating a scan, the operator at the scanner console is given an option for how many TRs should be reacquired, essentially allowing them to select how much extra “insurance” scan time should be expended on reacquisition to correct for motion during the scan.

While this reacquisition system does entail a time penalty for scans that employ it, we note that this still represents a substantial efficiency improvement over acquiring two scans and keeping the best, or even acquiring two scans and merging the best k-space segments from each. Our reacquisitions are selectively driven by the motion estimates generated from our navigators, allowing us to ensure that reacquisition time is not wasted reacquiring regions of k-space that are already motion-free.

2.3 Integration into anatomical sequences

We have previously stated that our navigator sub-blocks require roughly 355 ms to execute. This time fits easily into the gaps that are designed into the MEMPRAGE, T2SPACE, and T2SPACE FLAIR sequences. All of our sequences were implemented using the Siemens IDEA environment with all reconstruction occurring using the ICE system. Our sequences run like their non-navigated counterparts, and all image reconstruction occurs on the scanner with images appearing on the console as in their commercial counterparts. From a workflow perspective, the principal difference is that our sequences require the user to run a single “test shot” of the vNav before the parent sequence is run. From the operator’s perspective, this appears in the workflow as a standard 3D-encoded EPI sequence, and it is run like the other sequences in the workflow. Measurement and reconstruction of the “test shot” takes less than 1 second, but allows the user to confirm the FOV dimensions and location in addition to any other EPI parameters that need to be changed for the experiment; the resulting EPI protocol is saved to disk and used as the basis for the vNavs embedded in the rest of the study. When a sequence with embedded vNavs is run, two image series are produced: one containing the vNav volumes (useful for rapid inspection of subject motion during the scan) and a second containing the parent scan volume.

MEMPRAGE and T2SPACE FLAIR

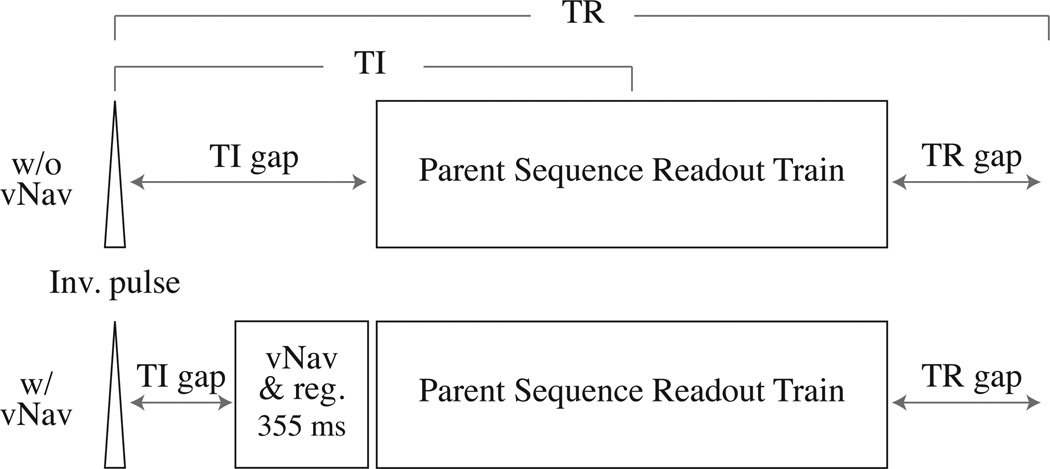
Both the MEMPRAGE and T2SPACE FLAIR sequences have an inversion pulse at the beginning of every TR, followed by a TI gap, then their readout train, and then finally a TR gap before the start of the next TR. With this layout, we opt to put our navigator block inside the TI gap, immediately before the readout train, as shown in Fig. 2. This location allows us to ensure that we have corrected for the subject’s location as near as possible to the moment when the readout train commences, limiting the chances the subject will move between navigator and readout.

Figure 2.

Sequence diagrams for MEMPRAGE/T2SPACE FLAIR before and after insertion of our vNav and registration block. For most acquisitions we find that there is enough time in the existing TI gap to insert our entire block.

In order for our reacquisition system to estimate the total motion during a TR in one of these sequences, we must compare the navigator obtained before the readout train with the navigator acquired in the subsequent TR. This means that the final TR of reacquisition cannot be used, as we will not be able to estimate a motion score for it. We address this by putting a “dummy” TR on the end of the reacquisition TRs — the very last TR of the complete sequence — and use the dummy TR’s navigator to estimate motion in the second-to-last TR while discarding the dummy readout train.

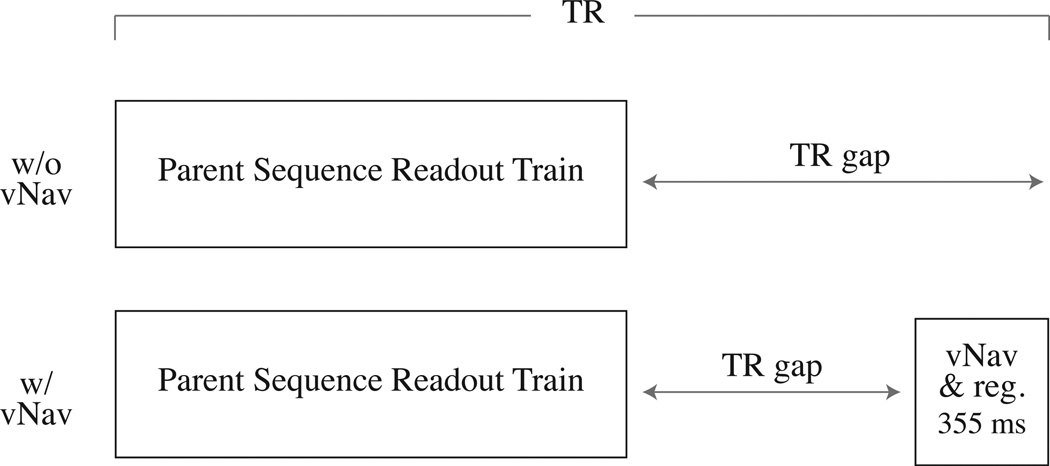
T2SPACE

The T2SPACE sequence does not have an inversion pulse and instead simply contains a long TR gap to produce proper contrast. As such, we must insert our vNav at the end of each TR in order to ensure that our motion estimate is as close as possible to the parent’s readout train, as shown in Fig. 3. Since the vNav now occurs at the end of the first TR, when we choose to do reacquisition we do not have a motion estimate for the first TR, and so we opt to repeat it at the end of the scan, before we begin the reacquisitions, so we have an instance of the first TR’s measurement that is bracketed by vNavs. However, unlike with MEMPRAGE and T2SPACE FLAIR, we do not have to insert a dummy TR at the end of the sequence, so there is only one dummy TR (the first) in this scan as well.

Figure 3.

Sequence diagrams for T2SPACE before and after insertion of our vNav and registration block. In this case we insert the navigator at the end of the TR, immediately before the parent readout train in the subsequent TR. This ensures the TR of the parent sequence is not altered and so image contrast is unaffected.

2.4 Validation

Static phantom studies

Even when the subject is stationary, we expect some variance in our position estimates due to a combination of interpolation error in the PACE algorithm and noise in the navigator scan. To determine the amount of variability, and the effect of field strength and coil changes on the algorithm, we performed a series of studies with a stationary phantom. A pineapple, strapped to a stationary platform, was used as a phantom to measure the variance of our motion estimates with a known stationary object. The pineapple was imaged with a 5-minute MEMPRAGE scan having 105 TRs. The vNav was setup with the protocol described above. We were not interested in the MEMPRAGE image output, but instead in the estimated motion tracks of the pineapple. In the first scan the pineapple was not moved at all. In the second scan the pineapple was rotated approximately 5 degrees after the imaging had started to measure how a motion that invalidates the initial shim might impact the EPI’s reliability as a volume navigator. Measurements were made using Siemens 1.5 T Avanto and 3 T TIM Trio scanners, with the 12- and 32-channel head coils.

Intensity and contrast studies

Given that our system locates the navigator during the TR of the parent sequence, it is important for us to validate that there is no detrimental effect on the final image intensities or contrast. We hypothesized that the 25 low-flip-angle pulses employed by the navigator immediately before the readouts would reduce the magnetization available to the subsequent parent sequence readout, but that the effect would be uniform spatially and across tissue types.

To study this, we asked three subjects to remain still while they were scanned with the MEM-PRAGE, T2 SPACE, and T2SPACE FLAIR sequences (one subject each). All measurements were made using a 3 T TIM Trio scanner and the 32-channel head coil. The MEMPRAGE subject was scanned three times without vNavs, twice with vNavs where the motion estimates were ignored, and twice with vNavs where motion estimates were applied as corrections and 20 TRs of reacquisition were measured. The volumes acquired with reacquisition were reconstructed both with and without the reacquired TRs, giving a total of 9 volumes per subject over four conditions (3 no vNav, 2 vNav without motion correction, 2 vNav with motion correction, 2 vNav with motion correction and reacquisition). All volumes had TR 2530 ms, TI 1340 ms, FOV 256 mm × 256 mm × 176 mm, 1 mm isotropic resolution, bandwidth 651 Hz/px, 3× GRAPPA acceleration in the outer-most phase encode loop, and four echoes (TEs 1.74, 3.6, 5.46, and 7.32 ms) that were combined in image-space by taking the root mean square for the four measurements at each voxel to produce the final volumes for analysis.

We performed similar studies to evaluate the intensity change in T2 SPACE and T2 SPACE FLAIR sequences. First, we scanned subjects with a single non-navigated MEMPRAGE with the same parameters as above. Second, we scanned them three times with the T2 SPACE or T2SPACE FLAIR without vNavs, twice with vNavs enabled but ignoring motion estimates, and finally twice with vNavs and motion correction and 20 TRs of reacquisition. As in the MEMPRAGE experiment, we reconstructed the with-reacquisition data excluding the reacquisitions to give a total of ten volumes: 1 MEMPRAGE plus the 9 T2 SPACE (FLAIR) volumes. T2 SPACE volumes were acquired with TR 3200 ms, TE 425 ms, FOV 256 mm × 256 mm × 256 mm, 1 mm isotropic resolution, bandwidth 651 Hz/px, and 2× GRAPPA acceleration in the inner phase-encode loop. T2 SPACE FLAIR volumes were acquired with TR 5000 ms, TI 1800 ms, TE 354 ms, FOV 256 mm × 256 mm × 160 mm, 1 mm isotropic resolution, bandwidth 651 Hz/px, and 2× GRAPPA acceleration in the inner phase-encode loop.

For the MEMPRAGE subject, the nine volumes were analyzed using parts of the FreeSurfer longitudinal analysis stream: our analysis consisted of skull-stripping each volume, followed by an unbiased co-registration of the brain volumes [21, 22], then the construction of a within-subject “average volume” (taking the voxel-wise median), upon which segmentation is finally run [23–33]. This gives us a single segmentation that we can apply to all nine volumes to select voxels that should represent identical underlying anatomy. Additionally, we can divide any two volumes to get their “ratio volumes”, as they should be in near-perfect alignment.

For the T2 SPACE (FLAIR) subjects, FreeSurfer was used on the single MEMPRAGE to produce a surface model of the brain and additionally a segmentation. The T2 SPACE or T2 SPACE FLAIR volumes for a subject were then brought into alignment with the computed surface model via bbregister [34], bringing the segmentation into alignment with the T2 SPACE (FLAIR) volumes and allowing us to select equivalent voxels within a given subject’s volumes and similarly produce “ratio volumes”.

In all three subjects, we chose two large regions for analysis: the complete grey matter ribbon and the merged white matter regions as identified by FreeSurfer. To avoid partial-volume effects we eroded these labels by two pixels for white matter and one pixel for grey matter. This produced two voxel label sets, each containing many disconnected islands. However, because the same label set is used on all volumes, the disconnectedness is not important for voxel-wise comparisons. We anticipated that our navigators would have a small scaling effect on the voxel intensities, as some of the magnetization will have already been rotated into the transverse plane by the navigator and thus not be available for the parent sequence. To evaluate this we plotted the joint density of the voxel intensities in the experimental conditions with the mean intensity of each voxel in the three no-vNav volumes.

Directed-motion studies

We performed directed-motion experiments with four volunteers to evaluate the improvement produced by our system when imaging subjects who both continuously “wiggle” and occasionally make “impulse” movements that change their head position. Each subject was imaged four times with matched MEMPRAGE scans all having TR 2530 ms, TI 1300 ms, FOV 256 mm × 256 mm × 176 mm, 1 mm isotropic resolution, bandwidth of 651 Hz/px, 3× GRAPPA acceleration, and four echoes (TEs 1.74, 3.6, 5.46, and 7.32 ms) that were combined in image-space via RMS to produce the final volumes for analysis (the echoes are the inner-most loop of the sequence, employed to reduce distortions without sacrificing SNR [20]). All measurements were made using a 3 T TIM Trio scanner and the 32-channel head coil. The four imaging conditions were:

1. subject asked to remain still; no navigators;

2. subject asked to remain still; navigators enabled and motion correction enabled;

3. subject asked to reposition themselves 1/4 of the way into the scan, move continuously for central 30 seconds of scan, and reposition themselves again 3/4 of the way through the scan; navigators enabled to measure motion track, but motion correction was disabled;

4. subjects asked to move as above; navigators enabled, motion correction enabled, and 15 TRs of reacquisition enabled.

We additionally reconstructed the fourth scan excluding the reacquisition to generate the volume that would have been produced if no reacquisition time was used. Thus, for each subject we had five MEMPRAGE volumes. These five volumes were brought into alignment by skull-stripping them with FreeSurfer, applying FreeSurfer’s unbiased robust registration tool [21, 22] to the resulting brains, and then applying the computed rigid transform to the original DICOM files to give the aligned volumes.

We were interested in how closely the with-motion conditions resembled the no-motion condition. The first method of evaluation was a visual qualitative inspection of the images. However, we were also interested in quantifying the quality improvements. One of the common effects of motion in 3D scans is ghosting in the direction of the outer-most phase-encoding loop. Thus, for each subject we selected a VOI outside the head in this direction and measured the change in mean intensity in the VOI. While ghosting outside the head is not actually detrimental to image quality, we take this as an estimate of the quantity of ghosting inside the head, since the effect should not be particularly spatially specific.

As the majority of MEMPRAGE scans at our center are analyzed with FreeSurfer, we were also interested in the overlap of the resulting segmentations. For each subject, we ran the full FreeSurfer automatic pipeline independently on the DICOM files that had been brought into alignment as described above. In this way, we produced five segmentations for each subject, all of which were in common coordinates because the DICOM files had been previously registered. For our study we computed two overlap scores: the average Dice coefficients of nine subcortical segmentations (hippocampus, caudate, putamen, pallidum, amygdala, thalamus proper, and the lateral, third, fourth, and inferior lateral ventricles) and the average Dice coefficients of the segmented cortical ribbon. Given two regions, A and B, and using |A| and |B| to represent the number of voxels in region A and B respectively, the Dice coefficient is [35]

$$\text{Dice}(A,B)=\frac{2|A\cup B|}{|A|+|B|}.$$ (4)

3 Results

Static phantom studies

The median absolute value of each of the six estimated motion components is given in Table 1 along with the median absolute value of the motion score generated via equation (3). The motion score that we compute is the motion of the most-displaced point on a sphere with 64 mm radius centered in the image. When we compute this for our stationary pineapple, we get a measure of the worst-case error that might occur in a normal human brain due to errors in our motion estimation system.

Table 1.

Median absolute value of the motion estimates produced from a stationary pineapple that was shimmed before imaging (marked “good-shim”) and a stationary pineapple after it has been rotated roughly 5 degrees to invalidate the previous shim (marked “bad-shim”). The first three rows are the translation estimates (in µm), the subsequent three rows are the estimated Euler angles (in 10⁻⁵ deg), and the last row is the motion score we compute. Each condition contains columns showing the 12- and 32-channel coil results. Rotated cases exclude the estimates from before the rotation was applied, as well as several subsequent TRs to prevent confounds between real motion and noise in the motion estimate; a total of 15 TRs was dropped in each condition.

	good-shim 1.5 T		bad-shim 1.5 T		good-shim 3 T		bad-shim 3 T
	12-ch	32-ch	12-ch	32-ch	12-ch	32-ch	12-ch	32-ch
Δx (µm)	27.1	33.1	55.5	38.5	62.6	34.6	41.0	24.7
Δy (µm)	50.5	140.5	44.2	175.7	14.0	59.5	28.0	102.8
Δz (µm)	115.4	163.1	71.7	228.2	20.6	48.0	17.4	23.7
θx (10−5 deg)	3.29	2.30	2.19	2.69	0.63	1.19	0.90	1.84
θy (10−5 deg)	3.18	3.73	2.24	5.98	0.88	1.11	1.63	0.64
θz (10−5 deg)	1.50	2.61	1.76	2.31	0.32	2.17	2.13	3.37
score (µm)	321.7	430.5	246.1	540.2	118.2	200.5	170.2	257.4

Intensity and contrast studies

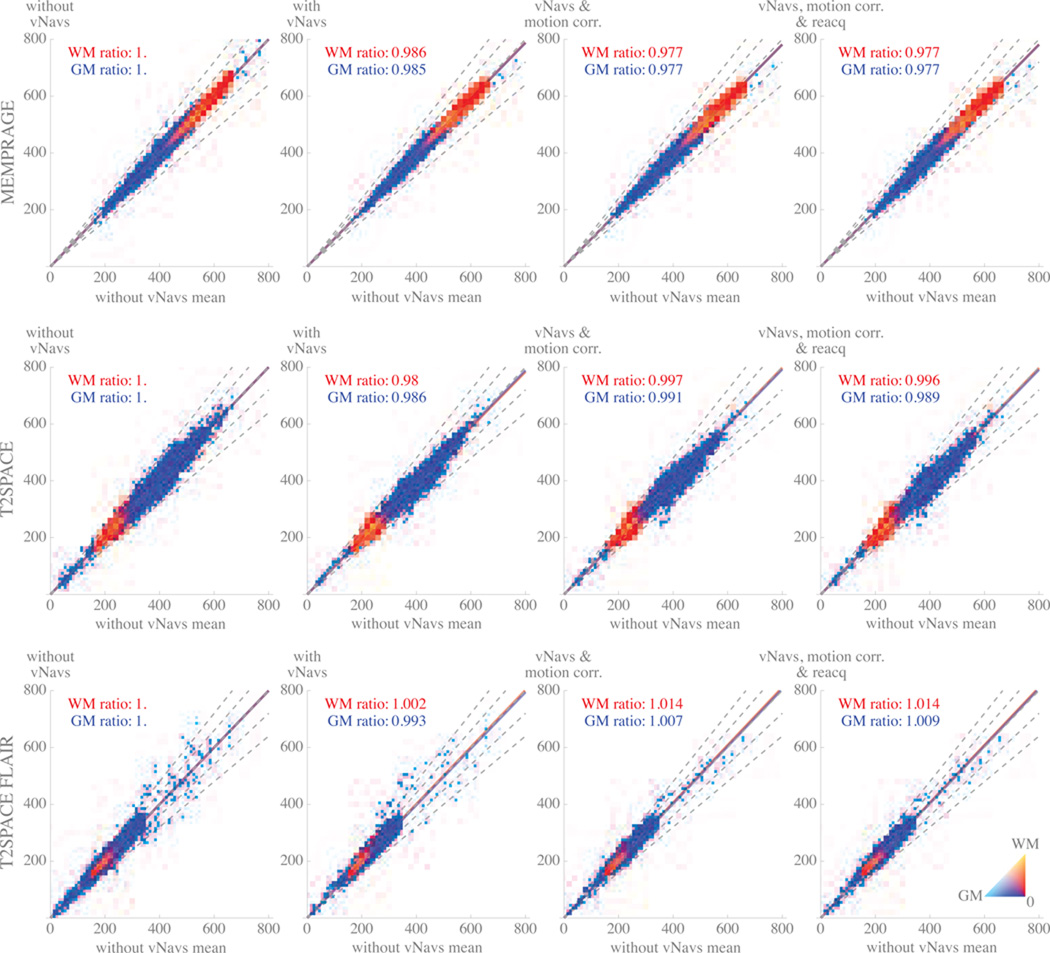
To evaluate whether the navigators, motion correction, or reacquisition affect image intensity or contrast, in Figure 4 we visualize the voxel intensity in the experimental conditions relative to when there is no navigator inserted for each of the MEMPRAGE, T2SPACE, and T2SPACE FLAIR. Our control condition intensity for each voxel was produced by averaging each of the three no-vNav volumes together voxel-wise, giving one control intensity value at each voxel. Since all the volumes were registered across conditions, we can then pair the control intensity of each voxel with an intensity in one of the experimental volumes, giving a population of intensity pairs that we visualized as 2D histograms.

Figure 4.

Density plots showing change between co-registered control and experimental scans of stationary volunteer at 3T using MEMPRAGE (top row), T2SPACE (middle row), or T2SPACE FLAIR (bottom row). For each plot, volumes acquired in an experimental condition (one of: no vNavs; with vNavs; with vNavs and motion correction; with vNavs, motion correction, and reacquisition) were co-registered with a control volume produced by averaging three navigator-free acquisitions. Pairing each experimental volume with the control volume gave a set of voxel intensity-pairs describing change between control and experimental sequences; masking each volume for grey and white matter selected the voxels of interest that are plotted. The x-axis in all plots represents mean intensity in the control (without navigators) volume. The y-axis in each plot represents intensity in the experimental condition of interest. Color shows the relative number of WM and GM voxels at a given location in 2D space (color scale shown in bottom right); white regions had no voxels. Dashed grey lines represent 1.0 (i.e., no change in voxel intensity), +10%, +20%, −10%, −20%. Solid red line shows the mean ratio between white matter voxel intensities in the experimental and control conditions. Solid blue line shows the same for grey matter. The slope of these two lines are written in each plot.

The first column of 4 is the plot of the paired no-vNav volumes with the control volume. The slope of the best-fit ratio between the experimental and control data in the first column of plots is identically 1, as the control data is the average of the experimental data in this condition. However, the dispersion of the data shows us the “natural” variation of the grey and white matter in each sequence, providing a reference point for subsequent comparison.

In the subsequent three columns of 4 we plot the effect of gradually introducing the three components of our system: navigators, real-time motion correction, and reacquisition. In each of these sub-plots, the intensity of the experimental condition (on the y-axis) is the average intensity of the two acquisitions in the specified experimental condition.

Directed-motion studies

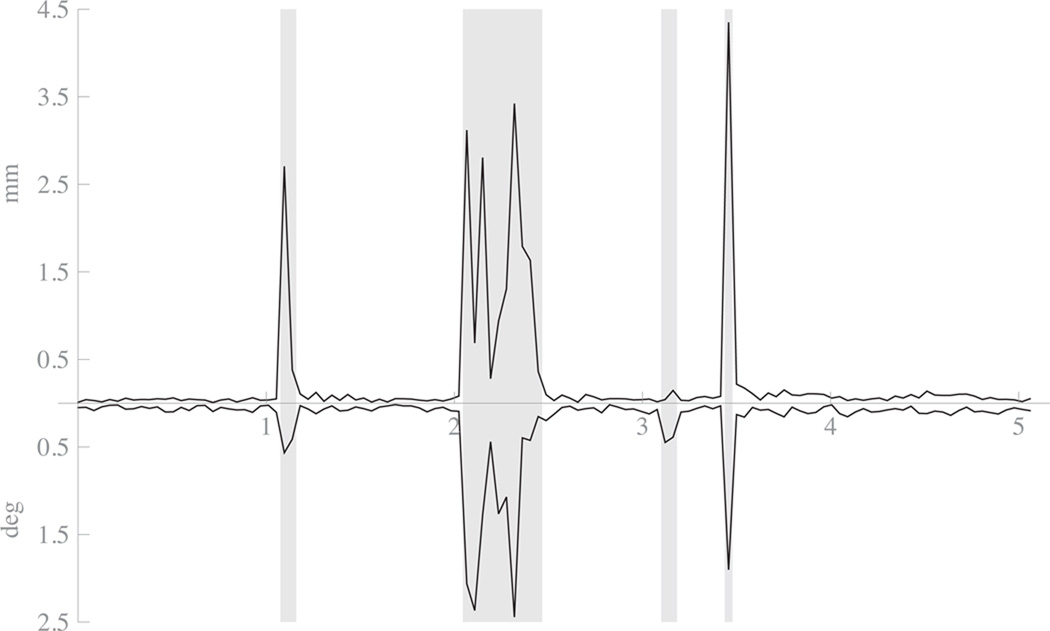
A representative slice from one subject’s MEMPRAGE volumes is shown in Figure 5 for a qualitative visual comparison. The between-TR motion differences for this subject, as estimated from the navigators, is shown in Figure 6. Note that, since it was difficult to exactly describe “how much” motion was required from our subjects when providing instruction, we found that our subjects did not all actually move the same amount; subjects 1 and 4 show substantially more movement than subjects 2 and 3, with subject 3 having moved the least. However, this irregularity allows us to show the scale of the effects achieved by our system for different ranges of subject motion.

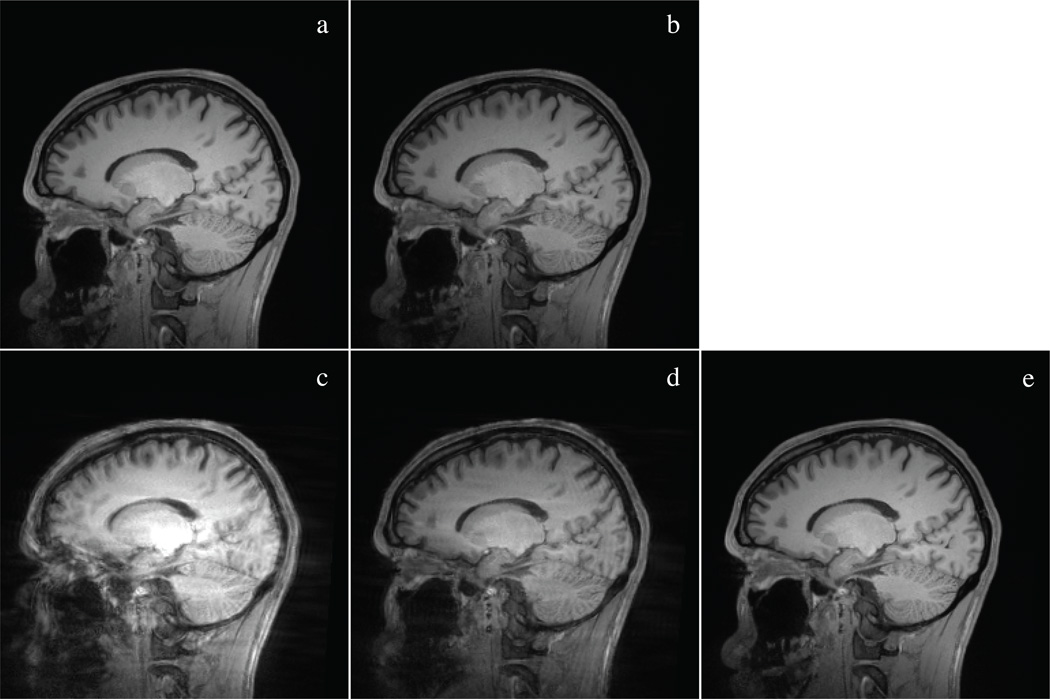
Figure 5.

Representative slice from all five 3 T MEMPRAGE volumes of motion study subject 4. The five conditions displayed are a) no motion, no navigator; b) no motion, motion correction on; c) motion with navigator but no motion correction; d) motion with motion correction but no reacquisition; e) motion with motion correction and reacquisition. a) and b) show the subtle change in contrast induced by including the navigators, c) is so motion degraded as to be of questionable value, d) is substantially improved but shows residual contrast degradation and ringing, and e) is relatively close to the no-motion conditions.

Figure 6.

Plot of motion as estimated from navigators from subject 4 with-motion-and-motion-correction condition. The top path shows absolute displacement in mm from previous TR’s estimated position. The bottom path shows the absolute rotation around the volume center in degrees from the previous TR’s estimated position. The x-axis is in units of minutes. Areas shaded with grey background were the periods automatically selected for reacquisition by the system.

We further analyzed the mean intensity of a volume immediately behind the head, selected to be in the direction of the outer-most phase encoding loop and so to maximize sensitivity to motion artifacts. The mean values for each subject in each condition are shown in Table 2.

Table 2.

Mean intensity of selected VOI just behind the subjects’ heads (all volumes were 3 T MEMPRAGE). Values are the ratio of mean intensity in the listed experimental condition to the mean intensity with no motion and no navigators

	subject 1	subject 2	subject 3	subject 4
no motion, w/ moco	1.06	1.00	1.01	1.09
motion, w/o moco or reacq	3.11	3.00	1.22	2.93
motion, w/ moco, w/o reacq	3.89	4.11	1.12	2.97
motion, w/ moco and reacq	1.39	1.28	1.07	1.49

The Dice coefficient between the FreeSurfer segmentations produced in the four with-navigator conditions and the single no-motion-no-navigator condition was computed for each subject and is shown in Table 3.

Table 3.

Dice overlap ratios for the four with-navigator conditions compared to the one no-motion-no-navigator condition. For each subject and condition, we computed ratios for the average of nine subcortical areas (labelled “sub”) and for the grey matter ribbon (labelled “cort”) segmented using FreeSurfer from 3 T MEMPRAGE volumes.

	subject 1		subject 2		subject 3		subject 4
	sub	cort	sub	cort	sub	cort	sub	cort
no motion, w/ moco	91.4	93.3	92.3	94.5	92.1	95.14	90.3	95.0
motion, w/o moco or reacq	67.5	49.1	82.5	81.6	87.4	86.2	69.2	52.7
motion, w/ moco, w/o reacq	79.4	82.5	85.6	86.3	91.6	94.0	81.3	84.3
motion, w/ moco and reacq	89.0	90.6	89.3	91.9	91.0	94.3	84.3	89.5

4 Discussion

The system we have presented and evaluated shares many design decisions with the previously published PROMO method [10, 11]: we use an image-based navigator, update the imaging coordinates during dead-time in the parent sequences, and can reacquire motion-damaged TRs at the end of the scan. These similarities make it important to also outline some of the substantial differences between our system and PROMO, which we will briefly do in this section.

The PROMO system requires 100 ms per navigate-and-register block, but must repeat this block multiple times per TR in order to achieve its high-quality motion estimate. In the published description of PROMO’s integration with neuroanatomical sequences, the block was repeated five times, giving a total navigate-and-register time of 500 ms. By comparison, we acquire and register a single vNav per TR, requiring 355 ms on current Siemens hardware. This difference can be seen as two choices along a trade-off. While the PROMO system acquires a less-informative navigator, it does so quickly and has the flexibility to acquire fewer of them if necessary. By using vNavs, we decide to spend somewhat less overall time acquiring a more-informative navigator in one block and then use all the information to register it at the end. However, our method comes at the expense of flexibility should a shorter navigator be required.

We have opted to insert our navigate-and-update block directly before the readout train in each of the three sequences described here while the PROMO system applies its navigate-and-update block following the readout train in each TR. This can be seen as a trade-off selecting the lag between the motion estimate and the parent sequence readout train, and the interactions between the navigator and the parent sequence. Note that because our navigator excites the whole imaging volume with each pulse, we do not induce a “slice shadow” in our parent volumes from placing our navigator before the parent sequence readout train. However, our placement does impose a minimum TI gap that occasionally conflicts with very high-resolution MEMPRAGE sequences as their readout trains become quite long. Conversely, placing the navigator after readout, as in PROMO, constrains the minimum TR or maximum TI.

Our selective-reacquisition system is also similar to PROMO, in that we use the estimated motion from the navigators bracketing each TR to produce a motion score. The principle differences are that, while PROMO scans have a variable time and stop when a selected maximum motion score is reached, our system fixes the total scan time and then uses the whole time to keep improving the k-space measurements. Additionally, where PROMO uses the 1-norm of the estimated rotation and translations, we produce a motion score by calculating the worst-case displacement of a point on a sphere with 64 mm radius, centered in the imaging volume.

As the system is in many concrete ways different from PROMO, we have attempted to evaluate our design decisions with a series of experiments evaluating both the accuracy of the system and its impact on the signal measured by the parent sequence.

Considering Table 1, our system produces substantially more accurate estimates at 3 T over 1.5 T, which we expect is due to the higher SNR. Additionally, we find that the 32-channel coil produces less accurate estimates than the 12-channel coil; although we are continuing to explore why this is the case, we note that in all field and coil configurations, the measured error is small enough to be useful for our morphometry protocols. The median absolute value of the motion score gives an indication of the most-displaced point inside a subject brain due to jitter; referring to Table 1 we can see that this value is on the order of 0.5 mm or less, making it generally acceptable for the resolutions used in neuroanatomical imaging.

In Figure 4 we plot the effects the navigators, motion correction, and reacquisition each have on the parent sequences’ white and grey matter intensities. The first column of the plot shows the natural variation in voxel intensities over three runs when no navigators are present. The subsequent three columns allow us to study artifacts that a navigator-based motion-correction system might introduce:

1. Local intensity changes would appear as off-diagonal islands of voxels. We used a spatially non-selective pulse in our navigator, and so we expected that any intensity changes in the image would be spatially uniform. Note that even very small islands, those that might not be apparent in mean or variance measurements, should stand out on our plots. The lack of off-diagonal islands in 4 indicates that our system has not introduced local intensity changes.

2. Local changes in variability would appear as a broadening of the grey or white matter ridge around the main diagonal at a specific point. Again, if the effect were small or local enough, it might not be particularly apparent in summary statistics, but should be clear in the density plots. Since we do not see local broadening in any of the experimental conditions, our system has not introduced any local changes in variability.

3. Global changes in grey/white contrast would appear as a separation of the lines of best fit for white and grey matter. Across all conditions, the largest observed contrast change was in T2SPACE FLAIR with a 1.1% effect, while MEMPRAGE showed at most a 0.1% contrast effect and T2SPACE showed at most 0.7%. For comparison, our repeated scanning without any navigators also shows a contrast variation of 0.1% for MEMPRAGE, 0.3% for T2SPACE, and 0.4% for T2SPACE FLAIR, indicating that there may be a < 1% global contrast effect attributable to our system in T2SPACE-type sequences.

4. Global changes in intensity appear as the lines of best fit for white and grey matter moving away from the 1.0 ratio dashed line. In the MEMPRAGE and T2SPACE sequences, we see the slightly decreased intensity we expected due to the introduction of the navigator pulses; an effect of approximately 3%. Unexpectedly, we see a very small increase in the T2SPACE FLAIR intensity, although this effect is so small that we cannot make any significant claims about it.

In general, the scale of the observed effects and the fact that they seem to be global both spatially and across tissue types, gives us confidence that the introduction of vNavs and our motion correction system is unlikely to induce changes in tissue intensity or relative contrast that would be detrimental to either a human reader using the images diagnostically or a machine system performing automatic processing on the volumes.

In our directed motion studies, a visual inspection of the five conditions for each subject revealed that, as expected, the images reconstructed with prospective motion correction and reacquisition are more similar to the no-motion images than the volumes produced with prospective correction but no reacquisition, and these are in turn better than the scans without prospective motion correction (see Figure 5).

The results in Table 2 show that for all subjects the navigators induce a very small amount of jitter-based ghosting outside the head even when the subject does not move. Interestingly, this data shows that ghosting is worse in the case of motion-correction-without-reacquisition condition than when the subject moved without any motion correction applied. We note that this may be because, during the central portion of scanning (i.e., the portion containing the most scan energy) the subject freely moved continuously and thus the motion estimates may not have been fully in line with the subject’s position, perhaps even making the misalignment worse than when the subject’s motion was simply “averaged out” in the motion-without-motion-correction condition. This also agrees with the result we see in the last row of the table, where the mean ghost intensity is greatly reduced by the inclusion of the reacquired measurements of these TRs.

The Dice coefficients in Table 3 indicate that, for all subjects, there is a degradation of the FreeSurfer segmentation with subject motion. We also see that the segmentation improves with the use of motion correction, and improves almost back to the initial no-motion results when reacquisition is employed.

5 Conclusions

We have described a novel EPI-based navigator for motion correction in anatomical MRI sequences and demonstrated its application in three morphometric sequences. Our proposed method shares many high-level features with the previously published PROMO system [10–12], and so we have explained both the similarities and differences between the two approaches and explored the trade-offs between them.

We have demonstrated a variety of experiments that allow us to validate both the correctness of our motion-tracking system and the impact that the navigators have on the parent sequence. We have used a stable phantom to estimate the jitter present in our motion estimates both when well-shimmed and when motion has invalidated the shim. The results of these experiments indicate that our motion tracking is accurate well below the resolutions at which we are imaging. Our choice of navigator and placement lead us to expect a small change in tissue intensity compared to the same scan without navigators. Our experiments show that there is, indeed, a small impact on the intensity of the parent sequence, but it does not seem to affect contrast. Critically, we have demonstrated that there are not spatially varying changes in intensity or contrast, and thus our navigator is not inducing local artifacts. Finally, we performed directed-motion studies to demonstrate the effectiveness of EPI-based volumetric navigators combined with PACE as a registration engine for providing prospective motion correction in anatomical imaging sequences.

Combining these results, we conclude that the use of our motion tracking system can provide measurable improvement when imaging moving subjects. Our motion-corrected MEMPRAGE, T2 SPACE, and T2 SPACE FLAIR sequences are viable candidates for use wherever the stock versions of these sequences are currently employed, providing a reduction in scans lost due to motion. This conclusion is in line with our previous experience using a similar system in single-voxel spectroscopy [14].