Tackling the combined effects of reverberation and masking noise using ideal channel selection

Abstract

Purpose

A new signal processing algorithm is proposed and evaluated in this study for the suppression of the combined effects of reverberation and noise.

Method

The proposed algorithm decomposes, on a short-term basis (every 20 ms), the reverberant stimuli into a number of channels and retains only a subset of the channels satisfying a signal-to-reverberant ratio (SRR) criterion. The construction of this criterion assumes access to a priori knowledge of the target (anechoic) signal and the aim of the present study is to assess the full potential of the proposed channel-selection algorithm assuming that this criterion can be estimated accurately. Listening tests were conducted with normal-hearing listeners to assess the performance of the proposed algorithm in highly reverberant conditions (T₆₀ = 1.0 s) which included additive noise at 0 and 5 dB SNR.

Results

A substantial gain in intelligibility was obtained in both reverberant and combined reverberant and noise conditions. The mean intelligibility scores improved by 44 and 33 percentage points at 0 and 5 dB SNR reverberant+noise conditions. Feature analysis of the consonant confusion matrices revealed that the transmission of voicing information was most negatively affected, followed by manner and place of articulation.

Conclusions

The proposed algorithm was found to produce substantial gains in intelligibility, and this benefit was attributed to the ability of the proposed SRR criterion to accurately detect voiced/unvoiced boundaries. Detection of those boundaries is postulated to be critical for better perception of voicing information and manner of articulation.

Introduction

Reverberation is present in most daily listening situations. Reverberation can cause significant changes in speech quality and can also have a very negative impact on speech intelligibility as it blurs, for instance, temporal and spectral cues and flattens formant transitions (Nabelek et al., 1989). Although moderate amounts of reverberation do not affect speech recognition performance by normal-hearing listeners, it has a detrimental effect on speech intelligibility by hearing impaired and elderly listeners (Nabelek, 1993; Assmann and Summerfield, 2004), as well as by automatic speech recognition (ASR) systems (Palomäki et al., 2004). The negative effects of reverberation on intelligibility vary across age (Neuman et al., 2010; Neuman and Hochberg, 1983) and between native and non-native listeners (Nabelek and Donahue, 1984).

Nabelek and Letowski (1985) studied the effects of reverberation on vowel recognition by ten elderly adults with binaural sensorineural hearing loss and found that the mean vowel recognition score obtained in a reverberation time (T₆₀) of 1.2 s was approximately 12 percentage points lower than the mean score obtained in the non-reverberant (anechoic) conditions. Compared to vowels, consonants are generally affected more by reverberation. The stop consonants, for instance, are more susceptible to reverberation distortion than other consonants, particularly in syllable-final position. This is because reverberation “fills in” the gaps present during stop closures. When noise is added to reverberation, different consonant confusions are made by listeners from those made in reverberation or in noise (Nabelek et al., 1989). That is, noise generally masks speech differently than reverberation. The combined effects of reverberation and noise are quite detrimental to intelligibility (Nabelek and Mason, 1981; Nabelek and Pickett, 1974a). In a recent study with normal-hearing children and adults, Neuman et al. (2010) assessed speech intelligibility in reverberation+noise conditions in terms of speech reception threshold (SRT). When comparing to SRT norms obtained by adults in anechoic conditions, Neuman et al. (2010) reported an SNR loss¹ of 1.5–3 dB for adults and 7.5–9.5 dB for young children (6 yrs) when reverberation (T₆₀ = 0.3–0.8 s) was added. The SNR loss decreased as a function of age.

Addressing the degradation in speech intelligibility and/or quality due to reverberation has given rise to several dereverberation algorithms (e.g., see Benesty et al., 2007; Naylor and Gaubitch, 2010; Kollmeier and Koch, 1994; Jin and Wang, 2009). Dereverberation by means of inverse filtering or passing a reverberant signal through a finite impulse response (FIR) filter that inverts the reverberation process remains one of the most commonly-used methods today (Miyoshi and Kaneda, 1988). However, the main drawback of inverse filtering methods is that the acoustic impulse response must be known in advance or alternatively needs to be ‘blindly’ estimated. Such algorithms, however, have severe limitations as room impulse responses (RIRs), particularly in highly-reverberant rooms, have thousands of filter taps making their inversion a computationally expensive task. Furthermore, some RIRs exhibit non-minimum phase characteristics. Techniques that do not rely on inversion of the room impulse response are thus more attractive and more practical.

An alternative technique based on channel selection is explored in the present paper. Such a technique is attractive as it does not rely on the inversion of the RIR. The proposed method is based on decomposing, in short-time segments (every 20 ms), the reverberant signal into a number of channels (via an FFT) and retaining only a subset of channels at each segment. The proposed criterion for selecting the appropriate channels is based on instantaneous measurements of the signal-to-reverberant ratio (SRR). Envelopes (computed using the FFT magnitude spectrum of each 20-ms segment) corresponding to channels with SRR larger than a pre-set threshold are selected while envelopes corresponding to channels with SRR smaller than the threshold are zeroed out. The SRR reflects the ratio of the energies of the signal originating from the early (and direct) reflections and the signal originating from the late reflections. Note that the resulting reverberant signal is composed of the superposition of these two aforementioned signals. Hence, the underlying motivation in using the proposed SRR criterion is to retain the signal components arising from the early reflections while discarding the signal components generated from the late reflections. Early reflections are known to be beneficial to speech intelligibility in binaural hearing (e.g., see Litovsky et al., 1999) for normal-hearing listeners, whereas late reflections are known to be detrimental to speech intelligibility as they are responsible predominantly for the smearing of the temporal envelopes and filling of the gaps (e.g., closures) in unvoiced segments (e.g., stops) of the utterance.

The above SRR criterion for channel selection has been used and evaluated in our prior study (Kokkinakis et al., 2011) with cochlear implant listeners. That study, however, only evaluated the effects of reverberation, i.e., with no additive noise present. In the present study, we evaluate the proposed channel-selection criterion using normal-hearing listeners in conditions wherein additive noise is present in addition to reverberation. Nonsense syllables are used for testing to avoid ceiling effects. The aim of the present study is twofold: (a) to determine the effectiveness of the proposed channel-selection criterion in suppressing or minimizing the combined effects of reverberation and noise, and (b) to determine which consonant feature (voicing, manner of articulation or place of articulation) is affected the most in reverberation+noise conditions.

Method

Listeners

A total of 8 normal-hearing, with pure-tone thresholds less than 25 dB HL (at frequencies of 250 Hz up to 8 kHz), all native speakers of American English were recruited for the intelligibility tests. Their age ranged from 18 to 26 years and all subjects were paid for their participation. The majority of the subjects were undergraduate students from the University of Texas at Dallas.

Stimuli

Telephone band-limited (300–3400 Hz) syllables in /aCa/ context were used for testing. The consonant set included 16 consonants recorded in /aCa/ context, where C= /p, t, k, b, d, g, m, n, dh, l, f, v, s, z, sh, jh/. All consonants were produced by an American male speaker and were recorded in a soundproof booth using Tucker Davis Technologies recording equipment. The consonants were originally sampled at 25 kHz and downsampled to 8 kHz. To simulate the receiving frequency characteristics of telephone handsets, all clean and corrupted signals were filtered by the modified intermediate reference system (IRS) filters (ITU-T Recommendation P. 48, 1996). Telephone band-limited consonants were used to avoid ceiling effects.

The reverberant signals were generated by convolving the clean signals with real room impulse responses, recorded by Van den Bogaert et al. (2009), with average reverberation time equal to T₆₀ = 1.0 s and direct-to-reverberant (DRR) ratio of −0.49 dB for a 5.50 m × 4.50 m × 3.10 m (length × width × height) room. The distance between the single-source signal and the microphone was 1 m. Speech-shaped noise was added to the reverberant signals at 0 dB and 5 dB SNRs, i.e., the reverberant speech signal served as the target signal in the SNR computation.

Proposed algorithm based on channel selection

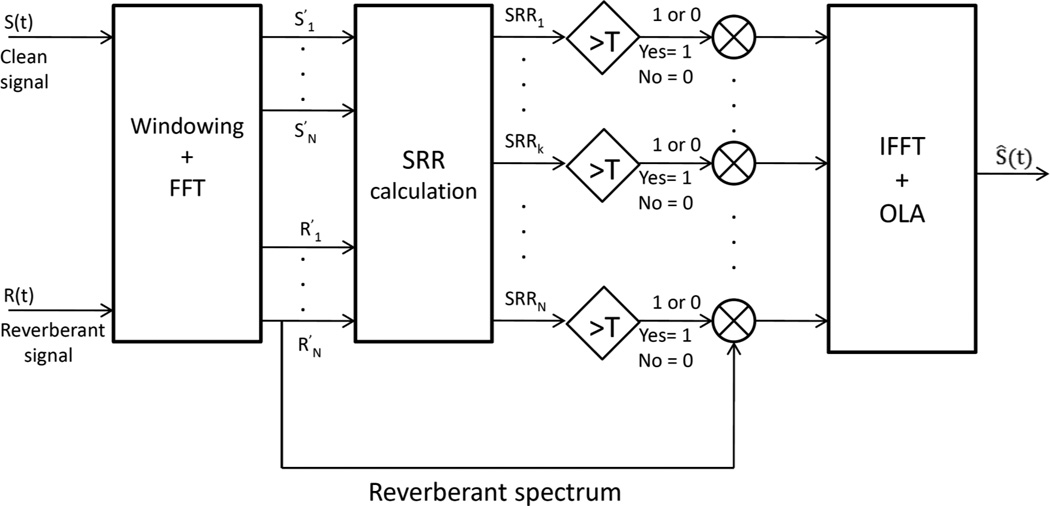
The proposed algorithm, henceforth called ideal channel-selection (ICS) algorithm, is depicted in Figure 1. It is termed ideal to indicate that a priori information about the target signal is used. First, the clean and corrupted signals are segmented into 20-ms frames (with 50% overlap between frames) using a Hanning window, and a discrete Fourier transform (DFT) is computed. Note that in the frequency domain, the DFT decomposes the signal into N frequency bins or channels (an M-channel filterbank could alternatively be used in place of the DFT), where N is the duration of the frame in samples. Of the N/2 available channels (due to the DFT symmetry), a subset is selected based on the signal-to-reverberant ratio (SRR) criterion², which is computed as follows:

$$SRR(f,t)=10{\text{log}}_{10}\frac{{|S(f,t)|}^2}{{|R(f,t)|}^2},$$ (1)

where t indicates the frame index, f the channel or frequency bin index, and S(f,t) and R(f,t) denote the complex DFT spectra of the clean (anechoic) and corrupted (reverberant or reverberant+noise) signals respectively. Envelopes (computed using the FFT magnitude spectrum of each 20-ms segment) corresponding to channels with SRR > T are selected, while envelopes corresponding to channels with SRR ≤ T are discarded, where T denotes a pre-set threshold value. Mathematically, this can be expressed by applying a gating or binary gain (BG) function to the spectrum of the reverberant signal as follows:

$$\widehat{S}(f,t)=R(f,t).BG(f,t).$$ (2)

Where

$$BG(f,t)=\{\begin{array}{cc}\hfill 1,& \mathit{\text{if}}SRR(f,t)>T\hfill \\ 0,\hfill & \hfill \mathit{\text{ \hspace{1em}\hspace{1em}\hspace{1em}otherwise}}\end{array}$$ (3)

where T represents the threshold value expressed in dB. To reconstruct the enhanced (dereverberated) signal in the time-domain, the inverse DFT of Ŝ(f, t) is computed and the signal is finally synthesized using the overlap-add (OLA) method (MATLAB implementation of the above ICS algorithm is available from our website³). It is important to stress that the above binary time-frequency gain function (Eq. 3) is applied to the reverberant spectrum and does not explicitly “clean out” reverberation, but rather selects the reverberant channels satisfying the SRR criterion (Eq. 3).

Figure 1.

Block diagram of the proposed ideal channel-selection algorithm.

The above operation of (ideal) binary gating is also known in the literature as the ideal binary mask or ideal time-frequency mask, and has been used extensively in computational models of auditory scene analysis (see review in Wang and Brown, 2006). The ideal binary mask uses as a channel-selection criterion the instantaneous SNR computed at each time- frequency unit and has been used in applications where the objective is to segregate a target speaker from a mixture (see Brungart et al., 2006; Li and Loizou, 2008a). The SNR criterion is clearly not appropriate for the reverberation-alone conditions since there are no additive maskers present. Given these differences, we will be referring to our algorithm as ideal channel-selection algorithm rather than as ideal binary mask algorithm. Both algorithms select in each frame a subset of channels, but the selection is made using different criteria.

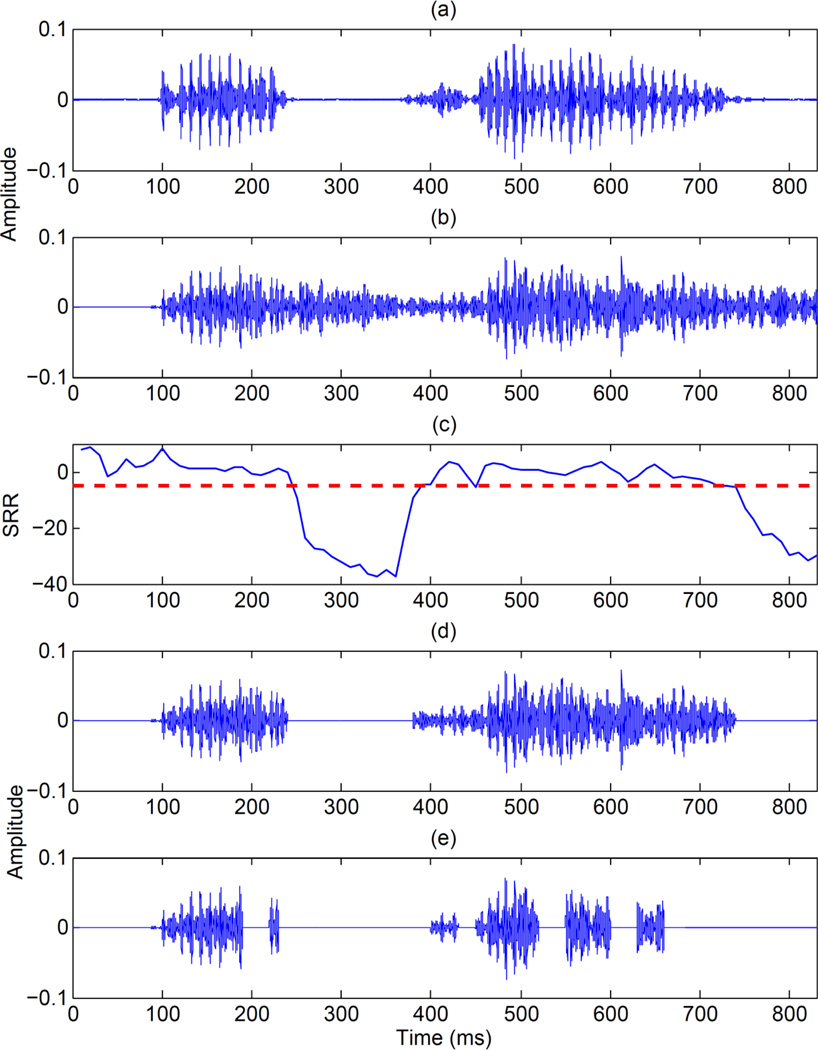
The choice of the threshold T in Eq. 3 is important in the construction and application of the proposed channel-selection criterion. To illustrate this, we show in Figure 2 example synthesized waveforms of the syllable /a p a/, with the threshold set to T = −8 dB (panel d) and T = 0 dB (panel e). As shown, the latter threshold (0 dB) is aggressive, since apart from discarding the corrupted unvoiced segments and associated gaps, it also eliminates speech in the voiced frames, which in turn leads to distortion of the processed signal. In contrast, the use of T = −8 dB seems to eliminate the overlap-masking effects caused by the overlapping of succeeding segments of speech (in our case, the stop /p/) by the preceding phonetic segments (vowel /a/ in this example). As shown in Figure 2, by appropriately thresholding the SRR function (shown in panel c), we can reliably identify the vowel/consonant boundaries even in highly reverberant settings (T₆₀ = 1.0 s).

Figure 2.

Band-pass filtered waveforms (f = 1 kHz, bandwidth = 138 Hz) of “apa” for: (a) clean, (b) reverberant (T₆₀ = 1.0 s), (d) reverberant signal processed by ICS with T = −8 dB and (e) reverberant signal processed by ICS with T = 0 dB. Panel (c) shows the instantaneous SRR values (horizontal line indicates the fixed threshold set at −8dB).

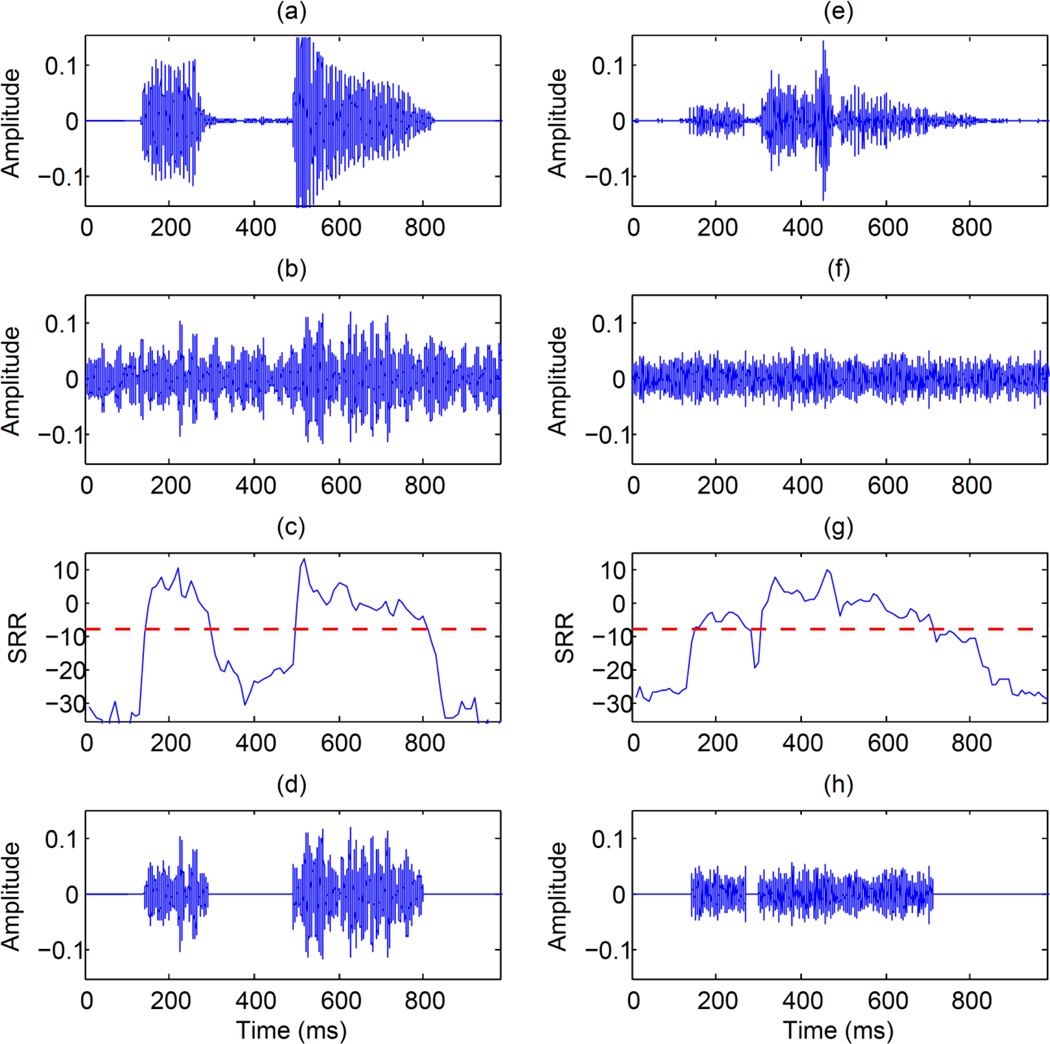
Figure 3 shows example synthesized waveforms of the syllable /a s a/ corrupted by reverberation and additive noise at +5 dB SNR. Waveforms from a low-frequency channel (f = 500 Hz) are shown in the left column and waveforms from a high-frequency channel (f = 3060 Hz) are shown in the right column. As can be seen in panels (d) and (h) the retained (by the channel-selection process) waveforms are still corrupted by noise, however, the vowel/consonant boundaries are preserved. The gap in the /s/ spectrum, for instance, at t = 300–500 ms is maintained in the retained waveform (compare panels (a) and (d)).

Figure 3.

Panels in the left column show band-pass filtered waveforms of “asa” in a low-frequency channel (f = 500 Hz, bandwidth = 81 Hz) and panels in the right column show band-pass filtered waveforms in a high-frequency channel (f = 3060 Hz, bandwidth = 418 Hz). Panels (a) and (e) show the clean waveforms, panels (b) and (f) show the reverberant+noise (1.0 s, 5dB) waveforms, panels (d) and (h) show the reverberant+noise (1.0 s, 5dB) waveforms processed by ICS with T = −8 dB. Panels (c) and (g) show the instantaneous SRR values (horizontal line indicates the fixed threshold set at −8dB).

The motivation for choosing the SRR criterion to guide the channel-selection process is as follows. To a first order approximation and to some extent, the SRR provides a simple measure of the ratio of the signal energy produced by the early reflections (and direct path) to the signal energy produced by the late reflections. It seems reasonable then to select a given channel only when the signal energy produced by early reflections dominates the energy produced by late reflections originating from the preceding signal. This is demonstrated in Figures 2 and 3. In Figure 2, for instance, during the /p/ closure (t = 245–362 ms) the reverberant signal contains a significant amount of energy caused by leakage from the preceding vowel (overlap-masking). This energy is introduced primarily by the late reflections. The SRR takes extremely low values (−10 to −40 dB) during that period of the /p/ closure, wherein the contributions from the late reflections dominate. Consequently, by discarding a channel when the SRR is extremely low, we are reducing (and to some extent, minimizing) the overlap-masking effects. In contrast, a large SRR value suggests dominance of the energy from the direct signal (and early reflections), as is often the case during the voiced segments (e.g., vowels) of the utterance (overlap-masking may occur during voiced segments due to the energy originating from the preceding consonant, however, its effect is minimal). Consequently, channels containing energy from early reflections are retained (see for instance the vowel segment from t = 450 ms to t = 738 ms).

In reality, the denominator in the SRR contains energy from both the early and late reflections, but nonetheless we make the assumption that the contribution of the early reflections is small. This assumption holds for the most part during unvoiced phonetic segments containing spectral gaps (e.g., stop closures), particularly in the low frequencies where the vowel formants reside and overlap-masking effects dominate. Ideally, it would be desirable to decouple the contributions of the early and late reflections, but that is not straightforward or easy to do particularly when the reverberation time (T₆₀) is long. For that reason, the entire reverberant signal is used in the denominator of the SRR for practical purposes. Similarly, we assume that the energy produced from the early reflections is close to that produced by the direct path. The proposed experiments will test whether the above approximations and assumptions hold.

It should be pointed out that a number of alternative criteria to the SRR criterion have been proposed and evaluated by Mandel et al. (2010). However, these criteria were evaluated in the context of improving the performance of automatic speech recognition systems rather than as means for improving speech intelligibility. In addition, most of the criteria proposed by Mandel et al. (2010) required access to the RIR. Hence, estimating such criteria poses great challenges. In contrast, the construction of the SRR criterion does not require access to the RIR.

As mentioned earlier, we denote the proposed algorithm as the ideal channel-selection (ICS) algorithm where the term ideal is used to indicate that a priori knowledge is used to construct the SRR. In practice, the SRR needs to be estimated from the reverberant signal alone. The aim of the proposed experiments is to assess the full potential of the SRR criterion in terms of intelligibility benefit. If a large benefit is observed, that would suggest that significant efforts need to be devoted to developing techniques for estimating accurately the SRR. The resulting data from the proposed experiments will provide the upper bound in performance that can be obtained when the SRR criterion is estimated accurately.

Procedure

The listeners participated in a total of 14 conditions which included: (1) clean anechoic stimuli, (2) reverberant stimuli, (3) stimuli corrupted by noise alone (at 2 SNRs) and (4) reverberant+noise (at 2 SNRs) stimuli. Six additional conditions involved ICS-processed stimuli (reverberant and reverberant+noise) using two different threshold values (T = −8 dB and 0 dB). We denote the reverberant stimuli as R, the stimuli corrupted by noise alone as N, and the reverberant+noise stimuli as R+N. Three other conditions were included for comparative purposes based on a commonly-used spectral subtractive (Wu and Wang, 2006) algorithm for suppressing reverberation. This algorithm was applied to the reverberant and reverberant+noise (R+N) stimuli. The spectral subtraction algorithm has been found to be beneficial in removing the impact of late reverberation (Wu and Wang, 2006), and is used in the present study as an additional control condition⁴.

The consonants were presented to the listeners in random order. Six repetitions per condition were used. The presentation order of the various conditions was randomized across subjects. A practice session, in which the clean (anechoic) consonants were presented to the listeners, preceded the actual test. To collect responses, a graphical user interface (GUI) was used that allowed the subjects to identify the consonants they heard by clicking on the corresponding button on the GUI. All listening experiments were performed in a sound-proof room (Acoustic Systems, Inc) using a PC connected to a Tucker-Davis system 3. Stimuli were presented to the listeners monaurally through Sennheiser HD 250 Linear II circumaural headphones at a comfortable listening level. The test session lasted for approximately 2 hours. A short break was given to the subjects every 30 minutes to minimize listener fatigue.

Results and discussion

Consonant Identification in Reverberation and Noise

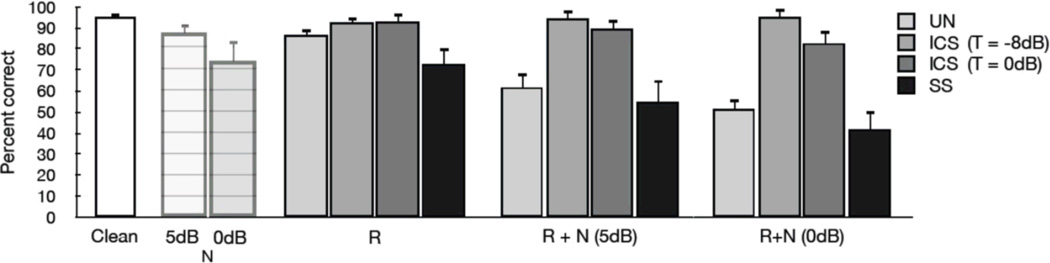
The results, expressed in terms of the mean percentage of consonants identified correctly, are shown in Figure 4. The bar labeled as “clean” represents the mean score obtained in anechoic conditions. Two-way ANOVA (repeated measures)⁵ indicated significant effect of SNR [F(2,14) = 63.2, p < 0.0005], significant effect of ICS threshold [F(2,14) = 257.1, p < 0.0005], and significant interaction [F(4,28) = 44.8, p < 0.0005]. As shown in Figure 4, the ICS algorithm improved speech intelligibility in all conditions, including the reverberation-alone (i.e., with no additive noise) condition. The choice of ICS threshold affected performance in the two noisy conditions, but had little effect in quiet due to ceiling effects. For that reason, an interaction was observed between the SNR and ICS threshold.

Figure 4.

Mean intelligibility scores obtained in the various conditions involving reverberation (R), noise (N) and combined reverberation and noise (R+N). The leftmost bar shows performance obtained in (clean) anechoic conditions. Scores obtained with unprocessed stimuli are labeled as UN and scores obtained with stimuli processed via the spectral-subtractive algorithm are labeled as SS.

ICS improved intelligibility in all conditions tested. Post-hoc tests, according to Tukey’s HSD, were conducted to assess the differences in scores between conditions. The intelligibility scores obtained in the reverberation-alone condition improved by more than seven percentage points when the ICS algorithm was used. This difference was found to be statistically significant (p = 0.003). Larger improvements with the ICS algorithm were noted in the reverberation+noise conditions. Recognition scores improved from 61.7% correct to 94.5% correct at 5 dB SNR, and from 51.4% to 95.2% at 0 dB SNR. In all cases, the intelligibility improvement (relative to that with unprocessed stimuli) by the proposed ICS algorithm were found to be statistically significant (p < 0.005) when implemented with either threshold value (T = −8 or 0 dB). In the 0-dB R+N condition, the score obtained with the ICS threshold set to T = −8 dB was found to be significantly (p <0.0005) higher than the score obtained with the ICS threshold set to T = 0 dB. In the 5-dB R+N condition, the score obtained with the ICS threshold set to T = −8 dB was not found to be significantly (p > 0.05) higher than the score obtained with the ICS threshold set to T = 0 dB. High performance was consistently obtained across all conditions tested when the ICS threshold was set to T = −8 dB. It is worth noting that in all conditions tested, performance with the ICS was near that obtained by listeners in anechoic conditions, i.e., near 96% correct.

Figure 4 also shows performance obtained in the condition wherein the stimuli were corrupted only by noise (no reverberation). The intelligibility scores were 86.59% and 73.05% at SNRs of 5 and 0 dB respectively. These scores decreased to 62% and 51% respectively after adding reverberation. In both noise conditions (0 and 5 dB SNR), scores were reduced by 30% after reverberation was added. Noise and reverberation degrade intelligibility in a complementary fashion. That is, regions in the spectrum that were not originally corrupted by reverberation are affected/masked by noise, leading to a severe degradation in intelligibility (30% reduction in our study). As reported by others, the combined effects of noise and reverberation are greater than the sum of both effects taken separately (Nabelek and Mason, 1981; Nabelek and Pickett, 1974b). This was also confirmed with the data in our study. Table 1 shows the effects of reverberation, noise and combined effects of reverberation and noise for individual subjects. These effects were computed by assessing the decrement in performance relative to the performance obtained in anechoic conditions. The combined effect was computed, for instance, as the difference between the scores obtained in the R+N condition and the scores in the anechoic condition. For nearly all subjects (except S6) and for both SNRs tested, the combined effects were greater than the sum of the reverberation and noise effects.

Table I.

Effects of reverberation, noise, and the combination of reverberation and noise on consonant-identification (%) for individual subjects. Low scores reflect small effects relative to the scores obtained in the anechoic condition.

Subjects	Reverberation	Noise (5dB)	Combined (R+N 5dB)	Noise (0dB)	Combined (R+N 0dB)
1	4.2	12.5	43.8	15.6	47.9
2	2.1	5.2	32.3	14.6	41.7
3	7.3	0.0	32.3	17.7	42.7
4	15.6	8.3	40.6	31.3	54.2
5	7.3	10.4	33.3	27.1	43.8
6	9.4	12.5	31.3	34.4	36.5
7	10.4	11.5	31.3	27.1	39.6
8	14.6	9.4	24.0	10.4	44.8

As can be seen from Figure 4, the performance of the spectral-subtractive dereverberation algorithm (Wu and Wang, 2006) was not satisfactory. The scores obtained using the spectral-subtraction algorithm in the reverberant-alone condition were significantly (p < 0.005) lower than the scores obtained using the unprocessed reverberant stimuli. This is partly due to the fact that applying spectral subtraction may introduce signal distortion and therefore produce a drop in the consonant identification scores. Secondly, the reverberant conditions examined in this study were quite challenging (this algorithm was originally tested in shorter reverberation times (T₆₀ = 0.2–0.4 s) by Wu and Wang (2006)). Performance in R+N conditions was even worse. We believe that it was because the SS algorithm was not originally developed to cope with low SNR conditions, as it had been originally tested at high SNRs (20 dB).

In brief, the proposed ICS algorithm was found to produce substantial gains in intelligibility in both reverberation-alone conditions and conditions involving additive noise (see Figure 4). This outcome was consistent with the benefit observed by cochlear implant listeners in our prior study (Kokkinakis et al., 2011). We attribute the intelligibility benefit to the ability of the SRR criterion to accurately detect voiced/unvoiced boundaries (see Figure 2). In continuous speech, reliable access to these vowel/consonant boundaries has been found to be critical for lexical segmentation and word retrieval (Stevens, 2002; Li and Loizou, 2008b).

Analysis of Consonant Errors

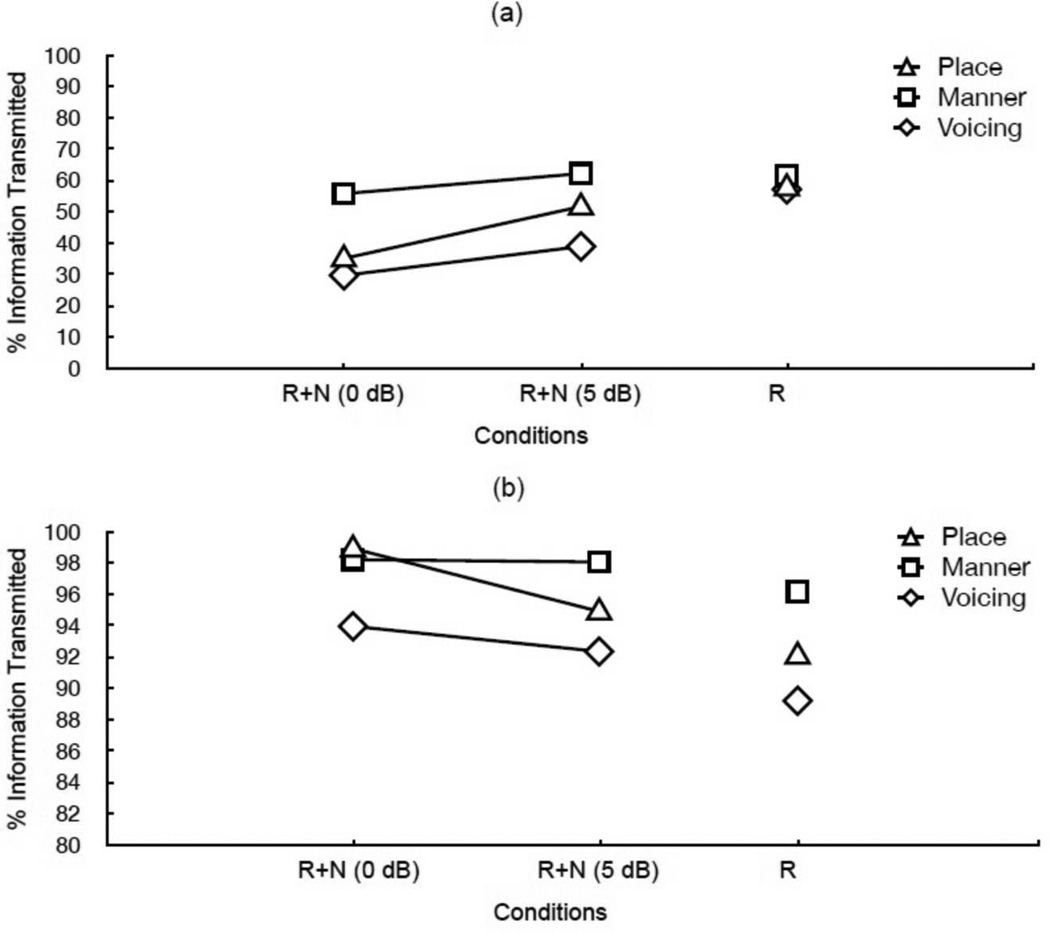
The consonant confusion matrices were analyzed in terms of percentage of transmitted information as per Miller and Nicely (1955) and the mean feature scores for place of articulation, manner of articulation, and voicing features are presented in Figure 5. Two-way ANOVA (repeated measures) indicated significant effect of SNR [F(1,7) = 8.6, p = 0.022], significant effect of feature error [F(2,14) = 13.3, p = 0.001], and non-significant interaction [F(2,14) = 0.649, p = 0.538]. As can be seen from Figure 5, all three features, especially the voicing feature, were significantly [F(2,14) = 13.3, p = 0.001] affected in the reverberation+noise conditions. In the presence of reverberation, the place of articulation scores were generally higher than the manner and voicing scores.

Figure 5.

Relative information transmitted for (a) unprocessed stimuli in reverberant (R) and combined reverberant+noise conditions (R+N) and (b) stimuli processed via the ICS algorithm in different conditions (for better clarity, the y-axis range is limited within 80 and 100%).

Overall, based on Figure 5, we can conclude that the transmission of voicing information is most affected in the reverberation+noise conditions. We attribute this to overlap-masking effects, which are largely responsible for filling up the gaps (e.g. stop closures) present in some consonants (e.g., stops) making it difficult to distinguish between, for instance, the unvoiced stops (e.g., /t/) from the voiced stops (e.g., /d/). The filled gaps (by reverberation and noise) clearly affect the perception of voice onset time, and it is well known that in intervocalic stops, the duration of voice onset time as well as the duration of aspiration are effective cues signaling voicing contrast (Borden et al., 1994). These cues are severely corrupted by the combined effects of reverberation and noise.

All feature errors in place, manner and voicing were compensated by the use of ICS algorithm. An average improvement of about 8 percentage points in amount of transmitted information was achieved in the reverberation-alone condition. A larger improvement was noted at 0 dB and 5 dB SNR respectively and that amounted to approximately 64 and 43 percentage points for place, 43 and 36 points for manner, and 65 and 54 points for voicing in reverberation+noise conditions (on average, only 4%, 2%, and 6% below the scores obtained for place, manner, and voicing features respectively in the anechoic quiet conditions).

Predicting the intelligibility of reverberant+noise speech

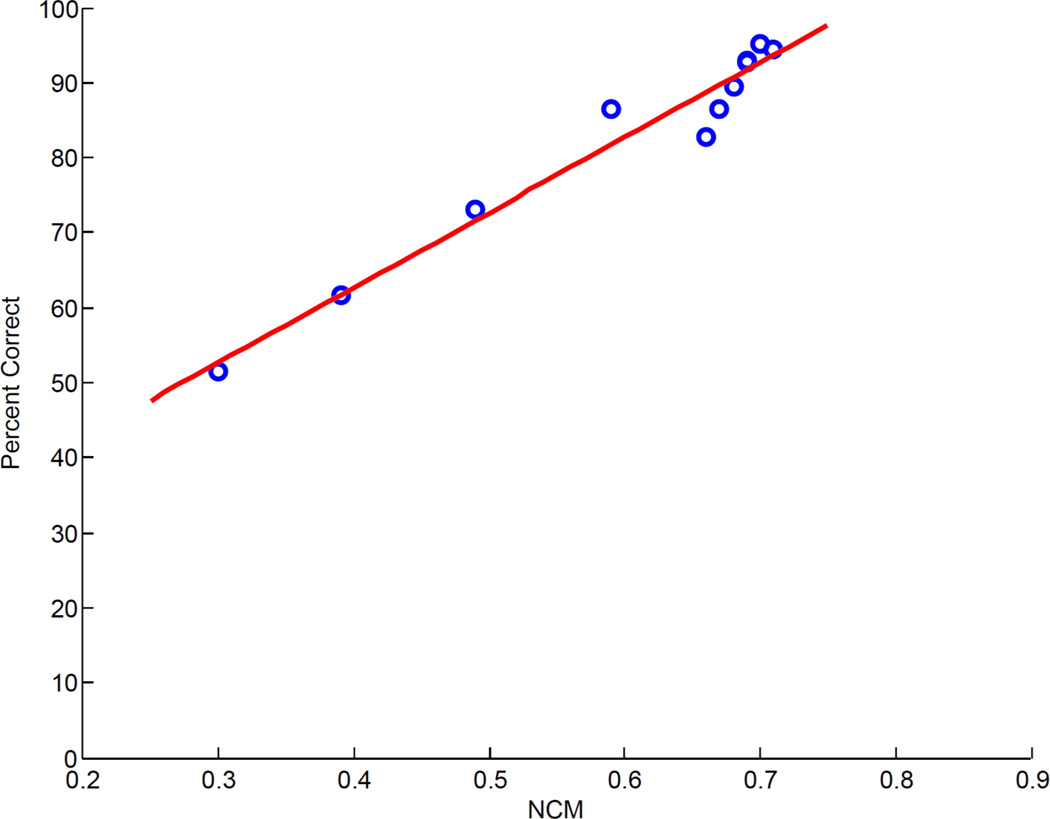
The speech-transmission index (STI) has been shown in a number of studies to predict reliably the intelligibility of speech in reverberation and/or in noise (Houtgast and Steeneken, 1985). Aside from the STI measure, not many intelligibility measures exist that can predict the combined effects of reverberation and noise. In the present study, we evaluate the performance of a speech-based STI measure which has been found previously to correlate highly with the intelligibility of noise-masked and noise-suppressed speech (Ma et al., 2009; Chen and Loizou, 2010). More precisely, we selected the normalized covariance measure (NCM) which is similar to the speech-transmission index in that it computes the STI as a weighted sum of transmission index values determined from the envelopes of the probe and response signals in each frequency band (Goldsworthy and Greenberg 2004). Unlike the traditional STI measure, however, which quantifies the change in modulation depth between the probe and response envelopes using the modulation transfer function, the NCM measure is based on the covariance between the probe (input) and response (output) envelope signals. The NCM measure has not been evaluated previously in situations where noise is present along with reverberation. Figure 6 shows the scatter plot of the mean consonant intelligibility scores obtained in all conditions (except the control conditions) against the corresponding mean NCM values. A linear fit is shown, but alternatively a sigmoidal-shaped function could be used to fit the data (computed correlation coefficient was found to be the same with either fitting function). The resulting Pearson’s correlation coefficient was found to be quite high, r = 0.98. These data clearly show that the NCM measure is an effective measure for predicting not only speech intelligibility in noise (Ma et al., 2009) but also intelligibility of speech which has been corrupted by both reverberation and noise.

Figure 6.

Scatter plot of the mean consonant recognition scores obtained in this study in the various conditions against the corresponding NCM index values.

Conclusions

The combined effects of reverberation and noise have been found in the present study to be quite detrimental to consonant recognition, an outcome consistent with prior studies (Nabelek and Mason, 1981; Nabelek and Pickett, 1974b). A signal processing algorithm was proposed for the suppression of combined reverberation and noise. This algorithm is based on the decomposition of the reverberant stimuli into a number of frequency channels, and the selection of channels with signal-to-reverberant ratio (SRR) exceeding a preset threshold (−8 dB). Channels with signal-to-reverberant ratio values falling below the threshold were discarded. Hence, in the proposed algorithm, neither reverberation nor noise was explicitly suppressed or attenuated in any way since the channel-selection process was applied directly to the reverberant+noise stimuli. When presented to normal-hearing listeners, the synthesized stimuli have been found to yield substantial gains in consonant identification. This outcome suggests that the combined effects of reverberation and noise do not completely mask important speech information. The channel-selection process, as guided by the SRR criterion, is a powerful process that can uncover quite effectively important speech information from the corrupted (by reverberation and noise) stimuli. Analysis of the consonant confusion errors indicated that the proposed algorithm significantly improved the trans- mission of voicing information, along with manner and place of articulation. Much of the intelligibility benefit was attributed to the ability of the SRR channel-selection criterion to accurately detect and preserve voiced/unvoiced boundaries, often smeared in the presence of reverberation.