Detection of Spatial Correlations in Protein Structures and Molecular Complexes

Summary

Protein structures are frequently related by spectacular and often surprising similarities. Structural correlations among protein chains are routinely detected by various structure-matching techniques, but the comparison of oligomers and molecular complexes is largely uncharted territory. Here we solve the structure-matching problem for oligomers and large molecular aggregates, including the largest molecular complexes known today. We provide several challenging examples that cannot be handled by conventional structure-matching techniques and we report on a number of remarkable correlations. The examples cover the cell-puncturing device of bacteriophage T4, the secretion system of P. aeruginosa, members of the dehydrogenase family, DNA clamps, ferredoxin iron-storage cages, and virus capsids.

Highlights

► Structure-matching techniques reveal striking similarities among protein complexes ► Large-scale structural transitions in the evolution of the dehydrogenase family ► Similar molecular shapes built from distinct molecular components ► Exceptional structural correlations among virus capsids

Introduction

The three-dimensional structures revealed by X-ray analysis and other molecular imaging techniques provide a vast amount of information on the structural, functional, and evolutionary relationships among proteins. Discovery and comprehension of the often delicate and intricate relationships are greatly assisted by appropriate structure-matching techniques. To capture the whole extent of structural correlations, it is frequently necessary to compare oligomers and molecular complexes rather than individual chains. There is a steady supply of new and updated methods for the pairwise comparison of polypeptide chains (for reviews, see, e.g., Tramontano, 2009; Hasegawa and Holm, 2009; Valas et al., 2009; Sippl, 2009), but only a few methods are known that accept multiple-chain proteins as input (e.g., Krissinel and Henrick, 2004; Mukherjee and Zhang, 2009; Nguyen and Madhusudhan, 2011).

The detection of structural matches among protein complexes is hampered by a number of problems and intricacies. The correlations generally extend over many protein chains, where individual chains may contribute only partially to structurally similar regions. Structure-matching techniques have to cope with the flexibility of protein chains, domain movements, subunit rearrangements, and structural models derived from poorly resolved electron densities. Proteins frequently contain symmetries and repetitions that result in independent multiple matches that cannot be superimposed simultaneously. To capture all these relationships, it is necessary to report and comprehend the whole spectrum of structural matches (Sippl and Wiederstein, 2008). Beyond this, the largest molecular complexes known today, like virus capsids (Zhang et al., 2010; Sangita et al., 2004), ribosomes (Wimberly et al., 2000; Ban et al., 2000), RNA-polymerase (Cramer et al., 2001), chloride channel (Dutzler et al., 2002), cell-puncturing devices (Kanamaru et al., 2002), or clathrin-coated vesicles (Fotin et al., 2004) may contain well over 10,000 amino acid residues. The mere size of these structures poses a considerable computational challenge.

The structure-matching technique presented here, called TopMatch, works across the whole bandwidth of protein architectures and molecular dimensions, ranging from peptide chains to large molecular complexes. TopMatch integrates established structure-matching techniques (Sippl, 1982, 2008, 2009; Sippl and Stegbuchner, 1991; Feng and Sippl, 1996; Sippl et al., 2001, 2008; Sippl and Wiederstein, 2008; Suhrer et al., 2009) with appropriate techniques for the processing of large molecular complexes. The remarkable aspects introduced here are the construction of composite alignments from precise local alignments and the definition of an alignment score that combines alignment length with the spatial deviation of superimposed structures. The score is used as a measure of significance of structural correlations and provides a convenient numeric criterion for the ranking of alignments. The construction of composite alignments is a strategy that successfully copes with many of the problems and intricacies encountered in the comparative analysis of large molecular complexes.

Detailed quantitative accounts of structural correlations among large molecular complexes are rare. Hence, a particular focus of this communication is to provide a collection of various types of relationships that are biologically relevant. The cases are chosen to highlight many of the peculiarities encountered in the comparison of complex structures. The problems discussed below are all challenging in the sense that they involve distant relationships among large protein chains, oligomers, and molecular aggregates. Conventional structure-matching techniques are generally unable to tackle these problems successfully, since multiple chains are involved. These examples, as well as any other structure-matching problem, can be solved interactively using the TopMatch web service.

The presentation is organized in two parts. The first is a description of the properties of structural matches and alignments. This information is required for the subsequent discussion of structural correlations. In the second part, we investigate a number of structural correlations in some detail.

Results

Basic and Composite Alignments

The primary result obtained from a pairwise comparison of a query structure, Q, and a target structure, T, is a set of precise basic alignments. The construction of basic alignments has been described (Sippl, 1982; Feng and Sippl, 1996; Sippl et al., 2001; Sippl and Wiederstein, 2008) and benchmarked (e.g., Sippl et al., 2001) previously. This set of basic alignments captures the whole spectrum of structural similarities among Q and T. In the case of large proteins and protein complexes, there are generally several basic alignments that are independent in the sense that they do not overlap with respect to the amino acid sequence of Q and T. Frequently, such alignments can be combined to form a single composite alignment, provided larger spatial deviations are tolerated than in the construction of basic alignments.

The construction of composite alignments involves a combinatorial problem, since proper subsets have to be found among the set of basic alignments. The associated problem of combinatorial explosion can be largely circumvented when the basic alignments are ranked by a proper measure of significance. Below we review the basic properties of alignments, define and discuss a measure of significance for alignment ranking, and describe the construction of composite alignments from basic building blocks.

Properties of Structure Alignments

In the following, the structures of proteins are represented by C^α atoms. This level of approximation is sufficiently precise for most applications. The residues within a protein are numbered consecutively from the N to the C terminus. Multiple chains are joined to a single chain where the order is immaterial. Hence, in terms of the inner workings of TopMatch there is no difference between single- and multiple-chain proteins.

An alignment, A, consists of a collection of n blocks, $A=\left\{B_1,B_2,\dots ,B_n\right\}$. A block, B_p, corresponds to a gapless alignment of a fragment in Q and a second fragment of the same length in T. To be precise, each block B_p is defined by three numbers, a_p, the start of the block in Q, b_p, the start of the block in T, and s_p, the length of the block. Hence, B_p contains the residue pairs $\left(a_p+i,b_p+i\right)$, for $0\le i<s_p$, aligning fragment $\left(a_p,\dots ,a_p+s_p-1\right)$ of Q to fragment $\left(b_p,\dots ,b_p+s_p-1\right)$ of T. The n blocks of an alignment, A, are disjoint, i.e., they do not have any residues in common.

A particular structure alignment, A, relates two molecules in a certain way. The relationship is rather complex and we need several parameters to describe it. In particular, the length of an alignment, the corresponding spatial deviation of C^α atoms, the similarity of the aligned sequences, and the number of permutations are essential aspects of structure alignments.

The length, L, of A is obtained as

$$L=\sum _{p=1}^n{s}_p,$$

where n is the number of blocks in A and S_p is the length of block B_P. Relating L to the number of residues, Q_L, of Q, we obtain the query cover,

$$Q_c=100\times \frac{L}{Q_L},$$

and, similarly, the target cover,

$$T_c=100\times \frac{L}{T_L},$$

where T_L is the size of the target. These numbers measure the extent of similarity in terms of the number of structurally equivalent residue pairs (Sippl, 2008).

The spatial deviation of two sets of coordinates Q and T is commonly reported in terms of the residual root-mean-square error E_r calculated from the optimal superposition of Q and T,

$$E_r=\sqrt{\frac{1}{L}\sum r_i^2},$$

where

$$r_i^2={\left({\mathbf{x}}_i-{\mathbf{y}}_i\right)}^2,$$

is the squared distance between the equivalent atoms x_i (query) and y_i (target). Here, L is the alignment length and $i=1,\dots ,L$ labels the pairs of equivalent C^α atoms as defined by the respective alignment. The procedure to compute the optimal superposition is described in the Computational Methods section.

It is clear that the similarity between Q and T increases with increasing alignment length, L, and decreases with increasing residual error, E_r. Both aspects are conveniently combined by Gaussian functions,

$$S=\sum _i^L{e}^{-r_i^2/{\sigma }^2},$$

where the r_i are computed from the optimal superposition of Q and T as defined above. We call S = S(A) the similarity of Q and T with respect to alignment A. For a perfect match, the r_i are zero and the sum S evaluates to the alignment length, L. Generally, $0\le S\le L$, where the actual value is controlled by the scaling factor σ. Dividing S by L yields the similarity on a per-residue basis,

$$s=\frac{S}{L}=\frac{1}{L}\sum _{i=1}^L{e}^{-r_i^2/{\sigma }^2}.$$

The typical distance error is then obtained from s as

$$S_r=\sigma \sqrt{-\text{ln}s}.$$

From the construction of S_r, it follows that there is a strong correlation between S_r and E_r (e.g., Table 1).

Table 1.

Parameters of Structure Alignments

Figure	Query	Target	T	L	QC	TC	S	Sr	Er	Is	P
1A	3izx,A	3iyl,W	b	216	17	20	180	2.97	3.09	14	0
1B	3izx,A	3iyl,W	b	139	11	13	118	2.84	2.94	14	0
1C	3izx,A	3iyl,W	c	634	49	60	380	5.01	5.59	12	0
2A	1hxm,AB	3qcv,HL	b	223	51	51	203	2.12	2.21	25	0
2B	1hxm,AB	3qcv,HL	b	179	41	41	158	2.47	2.56	25	0
3AB	2i9p,ABCD	3fwn,AB	c	641	55	69	497	3.53	3.83	19	1
3AC	2i9p,ABCD	3i83,AB	c	406	35	68	294	3.97	4.28	12	1
3BC	3fwn,AB	3i83,AB	c	260	28	44	178	4.31	4.87	13	2
4C	1k28@1	1y12@1	b	339	12	35	289	2.79	2.92	8	0
5A	1k28@1	1dab,A	c	321	12	60	243	3.69	3.95	10	0
6A	2pol@1	1plq@1	c	645	83	88	549	2.81	2.94	10	0
6C	1plq,A(1:127)	1plq,A(128:258)	b	114	87	90	103	2.21	2.30	14	0
6D	1plq,A(1:127)	2gia,A(72:217)	b	97	72	76	85	2.60	2.70	11	5
7A	3bkn,A	2za6,A	b	152	89	94	136	2.33	2.42	16	0
7B	3bkn@1	2za6@1	c	3649	89	94	3202	2.53	2.61	17	0
8A	2buk,A	1vb4,A	c	115	59	63	94	3.13	3.27	4	0
8B	2buk@1,Aaxyz	1vb4@1,Aaxyz	c	354	36	38	252	4.09	4.37	7	0

Figure, the respective figure and panel; Query, name of the query structure consisting of the PDB code and chain identifier(s) with optional residue numbers in parentheses (from N to C terminus), where the @ sign and the associated number refer to the biological unit as defined in the respective PDB file; Target, name of the target structure (same encoding rules as for the query); T, alignment type (basic, b, or composite, c); L, alignment length; Q_c, query cover; T_c, target cover; S, similarity; Sr, average distance error; E_r, root-mean-square error; I_s, fraction of pairs of identical residues; P, number of permutations. The numeric parameters are defined in the main text.

In the computation of the similarity S, the scale parameter σ determines the rate of reduction of alignment length L as a function of increasing distance error, S_r (and hence E_r). Therefore, an appropriate value for σ can be found from

$$\sigma =\frac{S_r}{\sqrt{-\text{ln}s}}.$$

For example, if we require that an average distance error of S_r = 3.0 Å corresponds to a relative similarity of s = 80%, then the appropriate value of σ is,

$$\sigma =\frac{3.0}{\sqrt{-\text{log}\left(0.8\right)}}=6.35\text{Å}.$$

All alignments described here are ranked using σ = 7 Å. Although this definition of σ involves the average quantity s, it is clear that in the computation of the similarity S the distances r_i are weighted individually by the exponential $\text{exp}\left(-r_i^2/{\sigma }^2\right)$. A distance r_i = 0 always has weight 1 (independent of σ). For σ = 7, a distance error of r_i = 3 scales to 0.83, whereas r_i = 6 scales to 0.48; i.e., with increasing error the weight drops in a nonlinear fashion, as determined by the Gaussian function.

Clearly an alignment A also establishes a relationship among the sequences of Q and T. The similarity among the sequences is expressed as the percentage of pairs of identical residues,

$$I_s=100\times \frac{I_p}{L},$$

with I_p the absolute number of such pairs and L the alignment length.

By default, TopMatch generates alignments that may contain permutations of the sequence of T relative to Q. To detect permutations, the blocks of A are sorted in ascending order relative to the sequence of Q, i.e., $a_p<a_{p+1}$. In a linear alignment, we always have $b_p<b_{p+1}$ for sequence T. Hence, a discontinuity, $b_p>b_{p+1}$, corresponds to a permutation of sequence T relative to Q. The number of permutations, P, is the total number of such discontinuities found among the blocks of A. Within a single chain, permutations may point to substantial rearrangements in the respective genes or they may reveal distinct topologies of a particular protein fold. However, in the alignment of multiple chains, the relative order of monomers is arbitrary, and permutations of blocks that involve distinct chains of T are not counted as permutations. In the construction of alignments by TopMatch, permutations can be suppressed but then the alignments of multichain complexes may be incomplete.

Construction of Composite Alignments

As already noted, in a pairwise comparison of two structures, Q and T, TopMatch generally yields several basic alignments (Sippl and Wiederstein, 2008). For example, the comparison of the viral capsid proteins 3izx-A and 3iyl-W (Figure 1) produces 23 distinct basic alignments, and for large proteins and complexes the number may rise to several hundred. In terms of the residual error, these alignments are quite precise, with Er values generally below 3.5 Å. In larger proteins and protein complexes, individual alignments may cover distinct regions of the molecules. They can be combined to larger composite alignments provided the respective basic alignments are compatible in sequence and in structure.

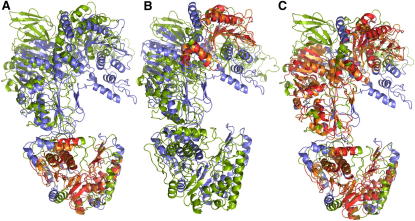
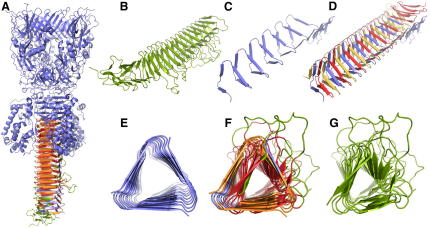
Figure 1.

Precise Local Alignments Are Joined to a Single Composite Alignment

The capsid proteins found in the shells of the cytoplasmatic polyhedrosis virus (Bombyx mori cyprovirus, 3izx, resolution 3.1 Å) and the subvirion particle of aquareovirus (grass carp reovirus, 3iyl, resolution 3.3 Å) contain a number of local structural correlations that can be combined to cover a large fraction of both molecules.

(A) Basic alignment of residues 16A–356A of 3izx and residues 24W–377W of 3iyl.

(B) Basic alignment of residues 554A–696A of 3izx and residues 512W–661W of 3iyl.

(C) Composite alignment assembled from the complete set of basic alignments obtained for 3izx chain A and 3iyl chain W.

To ensure the compatibility of the sequences of two alignments, A₁ and A₂, we remove all blocks of A₂ that collide with blocks in A₁. Simply, a block in A₂ collides with a block in A₁ whenever the blocks share residues with respect to Q or T. On the other hand the structures of A₁ and A₂ are compatible when the superposition of Q and T according to alignment A₁ also superimposes those parts of the structure that are covered by alignment A₂, at least approximately. Therefore, we superimpose Q and T according to A₁ but evaluate the spatial deviation with respect to A₂ only. Then the respective similarity, S, and distance errors, S_r and E_r, are proper estimates for the compatibility of A₁ and A₂. In particular we may control structural compatibility of A₁ and A₂ by a proper bound on the distance error. The particular bound used here is $S_r<6\text{Å}$.

With the combination of two alignments defined in this way we are ready to construct composite alignments. First, the basic alignments are sorted by similarity, S, so that $S\left(A_i\right)>S\left(A_{i+1}\right)$. Then A₁ is the alignment of maximum similarity S. To construct composite alignment, C₁ is set as C₁ = A₁. Then, for each A_i ≠ A₁, remove colliding blocks and evaluate S_r(A_i) with respect to the transformation obtained from C₁. If S_r(A_i) is acceptable, set C₁ = C₁ +A_i and continue with A_i+1. Once all the A_i are consumed, C₁ corresponds to a composite alignment or is equal to A₁. Finally the parameters L, S, and so on are computed for the complete alignment C₁. The procedure is repeated with C₁ = A₂, and so on until the basic alignments are exhausted. Finally the C_i are sorted by S. The TopMatch web service reports the top five alignments with the parameters defined above together with the alignment type (b for basic and c for composite alignments) and the query and target structures are superimposed and displayed in a graphical window, as described in the Computational Methods section.

In general, the extent of similarity among two structures Q and T cannot be captured by a single optimal alignment even if basic alignments are combined to composite alignments. There are several reasons for this. Proteins, in particular assemblies of protein chains, frequently have internal symmetries that translate into multiple structural matches. The corresponding alignments are usually indistinguishable in terms of alignment length, but they match distinct regions of the molecules. In fact, the number of alignments that are connected by symmetry operations is directly related to the symmetries within and between two molecules. In a similar way, repetitions in protein structures result in a multitude of alignments, although in these cases the alignments are generally not related by symmetry operations.

Proteins exhibit various types of structural variation. A particular molecule may have distinct arrangements of chains and structural domains in different crystal structures depending on the specific molecular environment. Similarly, in the evolution of proteins, mutations may cause large-scale movements of one structure relative to another. In all such cases, a rigid body superposition can only match parts of the molecule, and hence, several alignments are required to capture the whole extent of similarity. The structural relationships discussed in the following sections exemplify several of these relationships and the concepts introduced here. They are chosen to illustrate specific issues and subtleties encountered in the comparison of structures, but they also highlight several intricate and perhaps astonishing connections among protein molecules. The respective figures highlight the structural correlations, whereas the associated alignment parameters are assembled in Table 1.

Distortions and Domain Movements in Polypeptide Chains and Protein Complexes

The size and flexibility of large protein complexes combined with the limited resolution of the molecular models obtained provide particular challenges for structure-matching techniques. For example, the capsid proteins found in the shells of the cytoplasmatic polyhedrosis virus (Bombyx mori cyprovirus, 3izx, resolution 3.1 Å [Yu et al., 2011]) and the subvirion particle of aquareovirus (grass carp reovirus, 3iyl, resolution 3.3 Å [Zhang et al., 2010]) were both determined by cryo-electron microscopy. The structures of chain A of 3izx (1,057 amino acid residues) and chain W of 3iyl (1,284 amino acid residues) share a number of similarities revealed by a series of structural matches with corresponding alignment lengths around 200 residues or less (Figures 1A and 1B; Table 1). These basic alignments can be combined to composite alignments covering large regions of the molecules with L = 634 residues and E_r = 5.6 Å (Figure 1C). The strong correlations among the structures of these capsid proteins point to a common origin, although the percentage of identical residues, which is below 15% in all the alignments obtained, indicates that there is no correlation on the sequence level.

Regarding the construction and interpretation of structural alignments, this example is instructive in several ways. The many dislocations and contortions frequently observed among the structures of large molecules and at low resolution promote mix-ups of strands of β-sheets, helix bundles, and other repetitive structures that are close in space, resulting in alignments that are contaminated by mismatched structural elements. Forcing the construction of alignments to proceed from precise basic alignments to composite alignments completely avoids these pitfalls. Whereas composite alignments reveal the global extent of similarity, basic alignments put the focus on those regions where two molecules match quite precisely. Such regions frequently correspond to functional sites, or they may point to structural regions that are important for folding and stability of molecular structures.

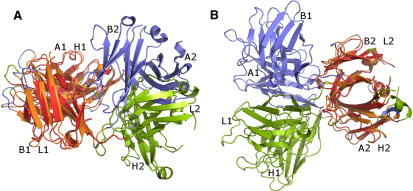
The effect of large-scale movements in related oligomeric proteins is illustrated using the structures of the human γδ T cell antigen receptor (1hxm, chains A and B, [Allison et al., 2001)]) and the Fab fragment of a humanized monoclonal antibody (3qcv, chains H and L, [Fleming et al., 2011 ]). Each chain of these homodimers consists of two immunoglobulin domains. Since all domains (four in each dimer) have similar folds, there are a multitude of structural matches between the two dimers, resulting in more than 100 basic alignments. The most significant of these alignments (L = 223, E_r = 2.2 Å; Figure 2A; Table 1) matches the N-terminal domains of 1hxm (residues 1–126 of chains A and B) with the N-terminal domains of 3qcv (residues 1–109 of chains H and L). The result immediately reveals that the mode of dimerization of these N-terminal domains is the same in both molecules. At the same time, the orientation of the C-terminal domains relative to the N-terminal domains is quite different. However, a second alignment matches 179 residue pairs of the C-terminal domains (Figure 2B; Table 1). Again, due to their conserved mode of dimerization, the two domains of each dimer superimpose with a small residual error of E_r = 2.6 Å, and taken together, the similarity among the N- and C-terminal domains covers the complete dimers. However, the respective basic alignments are not joined to a composite alignment, since the spatial deviation obtained from their simultaneous superposition exceeds 6 Å.

Figure 2.

Multiple Correlations in Protein Structures

The structures of the human γδ T cell antigen receptor (1hxm, chains A and B, blue) and the Fab fragment of a humanized monoclonal antibody (3qcv, chains H and L, green) have multiple correlations. The structural matches are colored orange (1hxm) and red (3qcv).

(A) Structural match between the N-terminal domains A1 and B1 of 1hxm and the N-terminal domains H1 and L1 of 3qcv (A1 matched with H1 and B1 with L1, respectively).

(B) Structural match between the C-terminal domains A2 and B2 of 1hxm and the C-terminal domains H2 and L2 of 3qcv (A2 matched with H2 and B2 with L2, respectively).

Structural Correlations among Dehydrogenases

The dehydrogenase family is a widespread group of enzymes participating in many essential metabolic pathways. Many of these enzymes contain domains (Rossman-fold), which are used for the binding of the cofactors NAD and NADH. The molecules frequently assemble to homodimers and higher-order oligomers. The comparative analysis of these molecules reveals a number of surprising large-scale structural transitions that must have occurred in the evolution of these enzymes (Figure 3; Table 1). The biologically active unit of human hydroxyisobutyrate dehydrogenase (2i9p [Kavanagh et al., 2006]) seems to be a homotetramer consisting of 1,175 amino acid residues. The resulting protein complex has several symmetry elements, reflecting the construction of the molecule from four identical chains (Figure 3A). The structure of the tetramer segregates into five domains. The large central-helical domain is formed by the C-terminal parts of the four chains, which are heavily entangled, whereas the four NAD-binding domains, each corresponding to the N-terminal part of an individual chain, stick out from the complex.

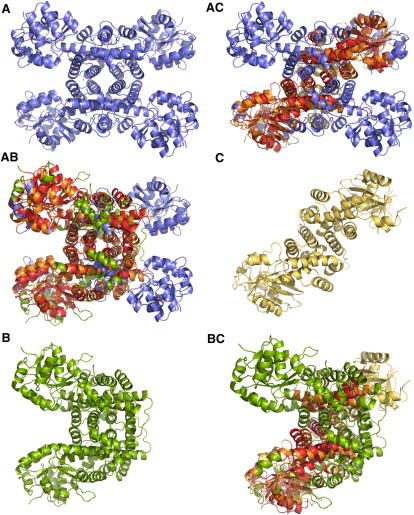
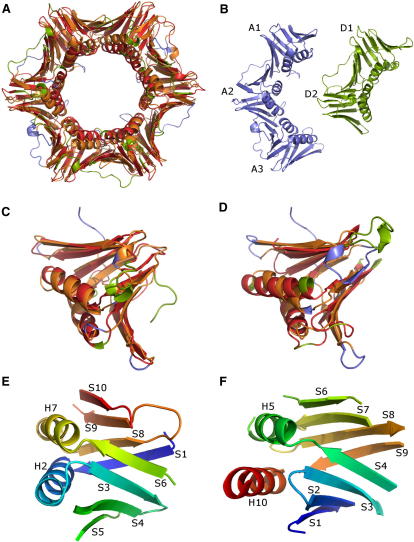
Figure 3.

Structural Correlations among Members of the Dehydrogenase Family Involve the Whole Molecular Complexes

(A) Homo-tetramer of human hydroxyisobutyrate dehydrogenase (2i9p, chains A, B, C, and D, blue).

(B) Homo-dimer of 6-phosphogluconate dehydrogenase from E.coli (3fwn, chains A and B, green).

(C) Homo-dimer of 2-dehydropantoate 2-reductase from the proteobacterium Methylococcus capsulatus (3i83, chains A and B, yellow).

(AB) Superposition of (A) and (B), with aligned regions in orange (2i9p) and red (3fwn).

(AC) Superposition of (A) and (C), with aligned regions in orange (2i9p) and red (3i38).

(BC) Superposition of (B) and (C), with aligned regions in orange (3fwn) and red (3i38).

The enzyme 6-phosphogluconate dehydrogenase from E. coli (3fwn [Chen et al., 2010]), forms a homodimer composed of 934 amino acid residues (Figure 3B). The NAD binding domains of 2i9p and 3fwn are quite similar, but beyond that, the structures of the individual chains appear rather different (not shown). However, the superposition of the complete oligomers reveals that the 3fwn dimer is completely covered by the 2i9p tetramer (Figure 3AB). In particular, the position and orientation of the two NAD-binding domains match quite precisely. From the symmetry of 2i9p, it is clear that there is a second equivalent match with 3fwn involving the two NAD-binding domains on the opposite side of the molecule (blue domains in Figure 3AB).

Another dehydrogenase-related enzyme is 2-dehydropantoate 2-reductase from the proteobacterium Methylococcus capsulatus (3i83 [Bonanno et al., 2009]). The active molecule (Figure 3C) is a homodimer of 587 amino acid residues. Again the structure of the 3i83 dimer is largely covered by the 2i9p tetramer, but in a rather different way compared to 3fwn, since the 3i83 dimer crosses the 2i9p tetramer diagonally (Figure 3AC). Again the two matching NAD-binding domains are in a very similar relative position and orientation in spite of the large distance between them. And again due to the symmetry of 2i9p, there is a second equivalent superposition along the second diagonal of 2i9p (not shown). Given the similarity of 2i9p to 3fwn and 3i83, it follows that there must be a match between the latter two molecules. This is indeed the case (Figure 3BC), but the match covers only one NAD-binding domain and parts of the central-helical domain. The pairwise mutual sequence similarity among all three molecules is below 20%, but their common structural features are quite extensive.

Given the strong structural correlations among these molecules, the question arises how these structures have evolved. Each of the three complexes is built from the information contained in a single gene. Therefore, the structural transitions that lead from one complex to another should be reflected by recombination events on the gene level. In fact, it seems rather obvious that 3fwn is the result of a partial internal duplication of a gene of the 2i9p-type. The mutation quite precisely duplicates the C-terminal part of the 2i9p chain that is used for the assembly of the central domain. However, whereas in 2i9p four chains congregate, in 3fwn, the central domain can only accommodate two of the elongated chains. Hence, the partial duplication of the 2i9p gene yields an elongated gene of the 3fwn type, but in terms of structure, the mutation effectively splits off two NAD-binding domains from the complex. Structures of the 2i9p and 3fwn type are common in eukaryotes and eubacteria, suggesting that the internal duplication leading from 2i9p to 3fwn occurred before the divergence of these kingdoms several billion years ago. Besides these examples, the dehydrogenase family contains many correlations that point to intriguing structural transitions in the evolution of these enzymes (e.g., Sippl, 2009). It is clear that such relationships are comprehensible only if the biologically active oligomers are taken into account.

Pores and Needles

Bacteriophage T4 uses an efficient cell-puncturing device (1k28 [Kanamaru et al., 2002; Leiman et al., 2009]) for infecting cells. The device, consisting of a baseplate, a tail-tube with integrated lysozymes, and a membrane-puncturing needle, has a three-fold symmetry axis. A complex molecule like this is expected to have many structural matches with other proteins of variable size and function. Here, we explore two quite distant relationships.

A clear match is obtained between the baseplate ring of 1k28 and the protein secretion apparatus (1y12 [Mougous et al., 2006]) from Pseudomonas aeruginosa (Figure 4). The similarity is restricted to the inner wall of the ring structure. The six-fold symmetry axis of 1y12, which superimposes quite well with the three-fold symmetry of the cell-puncturing device, results in six equivalent rigid-body superpositions. The accuracy of these matches is quite amazing. In each case, 339 pairs of equivalent residues can be superimposed to a residual error of E_r = 2.9 Å where the fraction of identical residue pairs is as low as 8%. The various views of the superimposed structures reveal that the architecture and dimensions of the inner rings, including the inclination of the β strands is the same in both molecules (Figure 4). Another intriguing detail is the precise match of the three helices at the periphery of the baseplate ring of 1k28 with three of the six helices of the secretion apparatus, 1y12 (Figure 4C).

Figure 4.

Large β-Strand Rings Can Be Formed by Trimers and Hexamers

(A) Trimeric bacteriophage T4 cell puncturing device (1k28, blue).

(B) Hexameric protein secretion apparatus from Pseudomonas aeruginosa (1y12, green).

(C) Superposition of 1k28 and 1y12. The matching parts are in orange (1k28) and red (1y12). See also Figure 2 in Leiman et al. (2009).

A quite exceptional match is obtained between the needle of the cell-puncturing device (1k28) and the structure of pertactin (1dab [Emsley et al., 1996]), a Bordetella pertussis virulence factor (Figure 5). The match is rather unexpected since the 1k28 needle is a homotrimer, whereas the pertactin needle is built from a single chain that folds into a β helix. The triangular cross-section (Figure 5) shows that the 1k28 trimer has a perfect three-fold symmetry, whereas the 1dab monomer is rather distorted, with many loops protruding predominantly from one of the three sides of the molecule. Given the distinct genetic architectures of these molecules it seems quite impossible that they could have evolved from a common ancestor. Since the overall shape of the molecules is astonishingly similar (321 equivalent residues, E_r = 3.9 Å, I_s = 10%), and since both structures perform quite similar functions (adhesion, docking, penetration), this is an example where a particular molecular device is realized by grossly distinct architectures.

Figure 5.

Structurally Equivalent but Topologically Distinct β Helices Can Be Formed by Monomers and Entangled Trimers

(A) Bacteriophage T4 cell puncturing device (1k28, blue) and Bordetella pertussis virulence factor pertactin (1dab, green) superimposed with the matching β helix parts in orange and red, respectively.

(B) The monomeric chain of 1 dab (green).

(C) Single chain of the 1k28 trimer (blue).

(D) The three chains of the 1k28 trimer colored blue, red, and yellow, respectively.

(E) Cross-section of the 1k28 trimer.

(F) Cross-section of the superimposed 1k28 trimer (blue) and 1 dab monomer (green), with the matching parts in orange and red, respectively.

(G) Cross-section of the 1 dab monomer (green).

DNA Clamps

DNA sliding clamps are ring-shaped proteins of approximate hexagonal symmetry. Their ring structures are highly conserved throughout all kingdoms of life. In particular, the trimeric rings of eukaryotes and archaea are entirely equivalent to the dimeric clamps found in bacteria (Figure 6). For example, the structures of 2pol (Kong et al., 1992), the dimeric β-subunit of the E. coli polymerase III, and 1plq (Krishna et al., 1994), the trimeric S. cerevisiae DNA polymerase processivity factor PCNA, match precisely (Figure 6A; Table 1). The monomers of DNA clamps (Figure 6B) contain two (eukaryotes and archaea) and three domains (bacteria). From the approximate hexagonal symmetry, it is clear that the individual domains within the monomers have similar structures. For example, domains D1 and D2 of 1plq are equivalent (Figure 6C; Table 1), although their sequences are uncorrelated (I_s = 14%).

Figure 6.

The Hexagonal Rings of DNA Sliding Clamps Contain Six Domains of Similar Structure

(A) Superposition of the β-subunit of E. coli polymerase III (2pol, blue) and the S. cerevisiae DNA polymerase processivity factor PCNA (1plq, green), with the matching parts in orange and red, respectively.

(B) Domain composition of DNA clamps in bacteria and eukaryotes. The bacterial monomer (2pol, chain A, blue) and the eukaryotic monomer (1plq, chain A, green). The individual domains are labeled from N to C terminus.

(C) Superposition of domains D1 (residues A1–A127, blue and orange) and D2 (residues A128–A258, green and red) of 1plq.

(D) Superposition of domain D1 of 1plq (blue and orange) and the MRP1 chain of the guide-RNA binding complex 2gia (residues A72–A217, green and red).

(E) Topology of 1plq-D1 with the helices and strands numbered from N to C terminus. The spectrum of colors progresses from blue (N terminus) to red (C terminus).

(F) Topology of 2gia with number and color schemes as in (E).

At present, proteins corresponding to a single DNA clamp domain are unknown, but there is a striking similarity to the monomeric chains of 2gia (Schumacher et al., 2006), a mitochondrial RNA-binding complex (Figure 6D; Table 1). In terms of the spatial arrangement of structural elements, the two folds are entirely equivalent. However, the alignment contains five permutations, and hence, the topologies of the DNA clamp domain and the RNA-binding proteins are grossly distinct (Figures 6E and 6F). Also, the DNA- and RNA-binding sites of these molecules are in different locations. Sliding clamps interact with DNA through helices H2 and H7 (Figure 6E), whereas in the RNA-binding complex, the interaction is mediated by strands S6–S9 on the opposite side of the fold (Figure 6F). Hence, the structural similarity between these proteins is a curiosity demonstrating that the formation of a particular protein fold can be achieved in entirely different ways.

Large Complexes

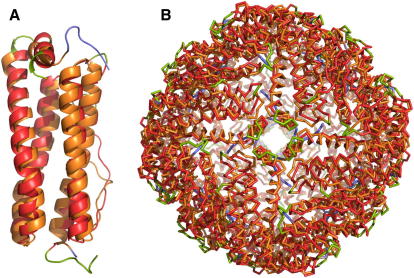
Ferritins are iron-storage proteins that form spherical particles consisting of 24 identical amino acid chains. Despite their low sequence similarity (I_s = 17%), the structures of the individual chains of bacterioferritin from Mycobacterium smegmatis (3bkn, resolution 2.72 Å, 161 amino acids [Janowski et al., 2008]) and horse apoferritin (2za6, resolution 1.75 Å, 171 amino acids [Yoshizawa et al., 2007]) superimpose rather precisely with an alignment length of L = 152 residue pairs and a corresponding residual error of E_r = 2.4 Å (Figure 7A). The superposition of the spherical particles (3,864 and 4,104 amino acids, respectively) matches 3,649 residue pairs (E_r = 2.6 Å; Figure 7B) and hence, the structure of this complex is strongly conserved over large evolutionary distances. Due to the symmetry of the molecules, there are 24 equivalent alignments of identical length and residual error, but the individual alignments link distinct chains. This result implies that all 24 chains are in indistinguishable structural and chemical environments. The degree of structural conservation among these complexes is quite amazing, since the geometry of the interfaces between subunits, as well as the conformations of the subunits themselves, has remained largely invariant in spite of the extensive divergence of their sequences, which resulted in the replacement of more than 80% of amino acid types. Conversely, it is equally surprising that the geometric constraints imposed by the architecture of these molecules can be satisfied by grossly distinct sequences.

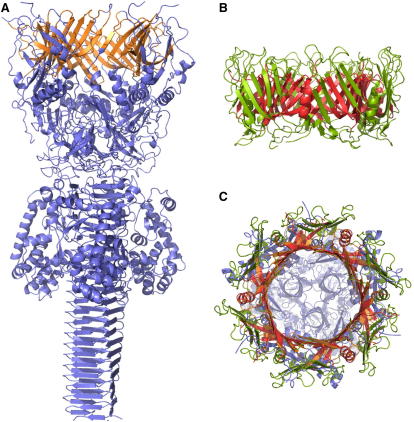
Figure 7.

Eukaryotic and Bacterial Ferritin Iron Cages Have Strongly Conserved Structures but Highly Divergent Sequences

(A) Single chain of bacterioferritin from Mycobacterium smegmatis (3bkn, chain A, blue) and horse apoferritin (2za6, chain A, green), with the matching parts in orange and red, respectively.

(B) Superposition of the complete ferritin cages of 3bkn and 2za6. The color scheme is the same as in (A).

Among the largest structures known today are the shells of several viruses. For example, satellite tobacco necrosis virus, a single-stranded RNA virus, forms a capsid containing a total of 11,040 amino acid residues (2buk, resolution 2.45 Å [Jones and Liljas, 1984]). The capsid of Sesbania mosaic virus, another single stranded plant RNA virus, has been studied in various modified forms. The CP-NΔ36 deletion mutant (1vb4 [Sangita et al., 2004]) generates a capsid containing 11,760 amino acid residues. The capsids of 2buk and 1vb4 are both constructed from 60 identical subunits that assemble to the T = 1 variant of the virus particles (Caspar and Klug, 1962; Erickson et al., 1985). The subunits are single polypeptide chains whose folds contain a central β-sandwich. Roughly two thirds of the monomeric chains can be superimposed (L = 115, E_r = 3.3 Å [Figure 8A]). The structures of proteins containing β-sheets always match to a certain extent, even if there is no phylogenetic relationship among them. Hence, the match does not necessarily imply a common origin of these viruses, and the sequences are in fact unrelated (I_s = 4%).

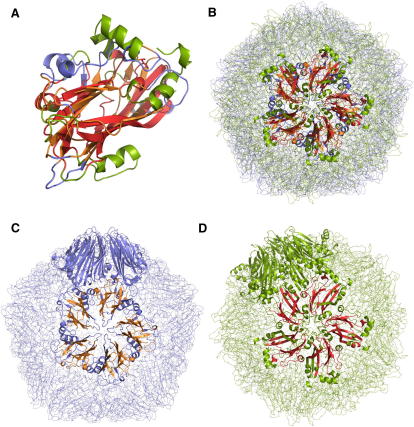
Figure 8.

Capsids of Satellite Tobacco Necrosis Virus (2buk) and Sesbania Mosaic Virus (1vb4) Have Structural Correlations on the Monomer and Pentamer Level

(A) Superposition of the monomers of 2buk (chain A, blue) and 1vb4 (chain A, green), with the matching parts in orange and red, respectively.

(B) Superposition of 2buk and 1vb4 pentamers (coloring as in (A)). The superimposed pentamers are shown as cartoons and the remaining 55 chains as ribbons.

(C) The virus capsid of 2buk as in (B), with an additional adjacent pentamer shown as cartoons.

(D) The virus capsid of 1vb4 as in (B) with an additional adjacent pentamer shown as a cartoon.

On the other hand, both capsids are envelopes of single-stranded plant RNA viruses, both contain 60 identical subunits, and both have icosahedral symmetry. In both cases, the individual chains form pentamers corresponding to the 12 faces of the icosahedral capsids. These coincidences evoke a possible phylogenetic relation that might exist between these structures. In fact, the pentamers of 2buk and 1vb4 can be superimposed as a whole where the β-sandwiches in the pentamers attain similar location and orientation (Figure 8B). However, the mode of association between two adjacent pentamers differs considerably among the two capsids, so that pairs of pentamers cannot be superimposed simultaneously (Figures 8C and 8D).

The observed structural correlations are perhaps not strong enough to verify the hypothesis of a common phylogenetic origin of these plant viruses. Rather, the important point here is that the capsids do have remarkable correlations that can be detected, exposed, and immediately visualized by structure matching techniques, despite the size and complexity of these molecular aggregates.

Discussion

The examples discussed in the previous sections cover a wide range of protein architectures, and they include some of the largest protein complexes known today. One obvious goal in choosing these examples is to provide an overview of the broad range of structure-matching problems that can be successfully solved with appropriate computational tools.

It is clear however, that, although structure-matching tools provide the means for discovery, the important part is the analysis and comprehension of the detected correlations (e.g., Taylor, 2000; Andreeva and Murzin, 2010). In the case of the dehydrogenase structures (Figure 3), the connection between the 2i9p and 3fwn oligomers can be traced to a duplication event on the gene level. However, the relationship of these structures to 3i83 is obscure. To understand the evolution of these enzymes, it is necessary to study the family as a whole. At present, this is a rather demanding exercise (e.g., Sippl. 2009), where the outcome largely depends on the available structures. But in any case, given the relationships among these molecules (Figure 3), it is clear that the comparative analysis of protein structures requires that the complete active molecules are taken into account. Important correlations are often not detectable on the level of individual chains.

The number of known structures will soon exceed 100,000, and beyond that, the determination of structures is likely to continue with ever increasing speed. The structures represent an enormous body of information that is exponentiated by pairwise relationships among them. A necessary step in digesting and organizing this information is the identification of mutual similarities among the structures. Hence, structure-matching tools should be routinely accessible to a broad community of structural and molecular biologists. This in turn requires that the tools are efficient, reliable, and easy to use. These goals have been in focus throughout the development of TopMatch and the associated web-based service (see Experimental Procedures). The computations leading to the structural matches discussed here, as well as any other structure-matching experiment, can be executed and visualized using this service. The response is immediate, except for very large structures, where the response time is in the order of seconds.

Experimental Procedures

Superposition, Similarity, and Deviation

The optimal superposition of two structures joined by an alignment, as defined in the main text, is obtained by minimizing the root-mean-square error of two coordinate sets x_i of the query, Q, and y_i of the target, T, where $i=1,\dots ,L$, and L is the length of the alignment. The following recipe computes this transformation most efficiently (Arun et al., 1987; Sippl and Stegbuchner, 1991). We choose to keep the query Q fixed in space. Then the transformation that needs to be applied to the target coordinates, y_i, for the optimal fit with the coordinates of x_i of Q is

$${\mathbf{z}}_i=\mathbf{R}\left({\mathbf{y}}_i-\mathbf{y}\right)+\mathbf{x},$$

where $\mathbf{x}=L^{-1}\sum {\mathbf{x}}_i$ and $\mathbf{y}=L^{-1}\sum {\mathbf{y}}_i$ are the centroids of Q and T, respectively, and R is a rotation matrix. The latter is obtained from the singular value decomposition of the matrix T,

$$\mathbf{V}\mathbf{S}{\mathbf{W}}^T=\mathbf{T}=\sum _i^L\left({\mathbf{x}}_i-\mathbf{x}\right){\left({\mathbf{y}}_i-\mathbf{y}\right)}^T,$$

i.e., T is a sum over the outer products of vectors. Then R = WV^T is the desired rotation provided the determinant of R is +1. If the determinant is -1—a rather frequent result, particularly for short alignments—then R involves a reflection. In this case, to obtain a proper rotation, it is necessary to multiply the column of V associated with the smallest singular value, i.e., with the smallest element of the diagonal matrix S, by -1. This subtlety is easily missed, since reversing the sign of any column of V yields a proper rotation, but the result may be suboptimal. Then the distances r_i between equivalent pairs of C^α atoms are obtained from r_i = x_i - z_i, from which the root-mean-square error, E_r, the similarity, S, and the associated average deviation of distances, S_r, are computed as defined above.

Visualization

In the application of structure-matching techniques, the appropriate and efficient visualization of aligned structures in 3-D, as well as their projection in 2-D, is a most critical step. Given a specific alignment, the TopMatch implementation generates a file in PDB format (Berman et al., 2000) containing the complete query and the transformed target structure, which are then immediately channeled into the molecular graphics programs PyMOl (DeLano, 2002) or Rasmol (Sayle and Milner-White, 1995), or, using the web-service (see below), into Jmol (Hanson, 2010). The standardized coloring scheme for pairwise alignments is blue for the query, Q, and green for the target, T. The aligned regions, i.e., the ungapped blocks of an alignment, are shown in orange (Q) and red (T). For the simultaneous display of more than two structures, the color scheme may be extended (e.g., Figure 3). Highlighting the blocks of an alignment in this way puts the focus on the aligned regions. The figures shown here are all prepared using the PyMOl program.

Program Access

The Center of Applied Molecular Engineering (CAME) has maintained a web service for structure comparison for several years. The remarkable implementation described here (TopMatch 7.3) replaces previous versions and can be accessed via the previous link (http://topmatch.services.came.sbg.ac.at). The web service provides instructions for program usage, including visualization of aligned structures in 3-D (Jmol) and facilities to upload structures. However, since all structures in PDB are accessible through the server it is generally not necessary to upload any files. A stand-alone version of the TopMatch program can be downloaded from the CAME web site (http://www.came.sbg.ac.at).

Published: April 3, 2012