Online monitoring and error detection of real-time tumor displacement prediction accuracy using control limits on respiratory surrogate statistics

Abstract

Purpose: To evaluate Hotelling’s T² statistic and the input variable squared prediction error (Q^(X)) for detecting large respiratory surrogate-based tumor displacement prediction errors without directly measuring the tumor’s position.

Methods: Tumor and external marker positions from a database of 188 Cyberknife Synchrony™ lung, liver, and pancreas treatment fractions were analyzed. The first ten measurements of tumor position in each fraction were used to create fraction-specific models of tumor displacement using external surrogates as input; the models were used to predict tumor position from subsequent external marker measurements. A partial least squares (PLS) model with four scores was developed for each fraction to determine T² and Q^(X) confidence limits based on the first ten measurements in a fraction. The T² and Q^(X) statistics were then calculated for every set of external marker measurements. Correlations between model error and both T² and Q^(X) were determined. Receiver operating characteristic analysis was applied to evaluate sensitivities and specificities of T², Q^(X), and T²∪Q^(X) for predicting real-time tumor localization errors >3 mm over a range of T² and Q^(X) confidence limits.

Results: Sensitivity and specificity of detecting errors >3 mm varied with confidence limit selection. At 95% sensitivity, T²∪Q^(X) specificity was 15%, 2% higher than either T² or Q^(X) alone. The mean time to alarm for T²∪Q^(X) at 95% sensitivity was 5.3 min but varied with a standard deviation of 8.2 min. Results did not differ significantly by tumor site.

Conclusions: The results of this study establish the feasibility of respiratory surrogate-based online monitoring of real-time respiration-induced tumor motion model accuracy for lung, liver, and pancreas tumors. The T² and Q^(X) statistics were able to indicate whether inferential model errors exceeded 3 mm with high sensitivity. Modest improvements in specificity were achieved by combining T² and Q^(X) results.

INTRODUCTION

Radiation beam gating and tumor tracking technologies are designed to manage tumor motion in real-time during radiotherapy. The performance of these devices rests heavily on their ability to rapidly and accurately localize the tumor.^{1, 2, 3, 4} Direct tumor tracking systems are limited to electromagnetic tracking⁵ and continuous x-ray imaging systems.⁶ Electromagnetic tracking systems are approved for use in the prostate exclusively at the time of this writing, and x-ray imaging systems continuously impart ionizing radiation over the duration of the treatment. Thus, many systems correcting for respiration-induced tumor motion instead infer the position of the tumor from surrogates of respiration.^{1, 2}

Methods for estimating tumor position from respiratory surrogates range from simple respiratory surrogate signal scaling to mathematically complex, multi-input models. Regardless of its form, the model only remains valid while there is a constant relationship between the tumor position and the respiratory surrogate signal(s).⁷ However, the tumor-surrogate relationship can change during the treatment fraction,^{7, 8, 9, 10, 11} causing the surrogate-based model to degrade over time.^{11, 12, 13}

Berbeco et al. observed that tumor motion inferred from an external marker block during gated radiation treatments varies beam-to-beam and day-to-day with no apparent external warning.²To our knowledge, no prospective method for detecting inferential model breakdown from surrogate signals has been developed. Instead, systems must frequently interrupt treatment to validate a model through additional ground-truth measurements of tumor position. The Cyberknife Synchrony™ system, for instance, validates its model at a user-selected rate of about once per minute by localizing tumor-implanted fiducials with stereoscopic radiographs.¹³ This technique of prescheduled intermittent data collection for model validation has at least three shortcomings:

• (1)If changes to the tumor-surrogate relationship occur shortly after one tumor localization, then the model can have large localization errors until the changes are detected at the next tumor localization minutes later;
• (2)Added and unnecessary tumor localizations not leading to model updates result in unnecessary exposure to ionizing radiation; and
• (3)Pausing for image-based tumor localization extends the duration of the treatment fraction.

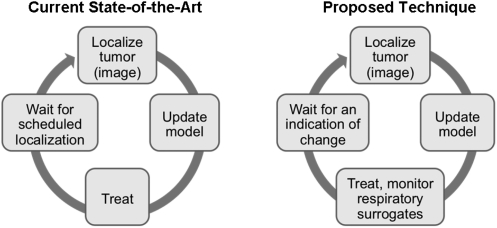
In this study, we propose a novel method for continuously monitoring a respiratory surrogate model of tumor motion through exclusive analysis of respiratory surrogate measurements (Fig. 1). The purpose of this study was to describe and evaluate Hotelling’s T² statistic and the input variable squared prediction error, Q^(X), for predicting the accuracy of tumor localization models in lung, liver and pancreas cases. The impact of this monitoring method on clinical workflow was also evaluated.

Figure 1.

Schematic of proposed improvement to respiratory surrogate-based model monitoring.

METHODS

Data

A database of Cyberknife Synchrony™ system log files consisting of 130 fractions from 63 lung cancer patients, 10 fractions from 5 liver cancer patients, and 48 fractions from 23 pancreas cancer patients was analyzed. The Cyberknife Synchrony™ log files included independently measured but concurrent 3D tumor and external marker localizations captured once every three beams (or an average of 63 s apart). Tumors were localized as the centroid of a set of implanted fiducial markers measured in stereoscopic radiographs. Three LED surrogate markers affixed to the torso were localized optically by a camera system. The position of the tumor was aligned in time with those of the external markers according to the timestamps in the system log files. Each treatment fraction dataset consisted of at least 40 (ranging from 40 to 112, median of 61) concurrent tumor and external sensor localizations. The data were truncated to include only the longest period of uninterrupted treatment in each fraction and to exclude both pretreatment image acquisitions and unplanned radiographs acquired during treatment for the purpose of repositioning the patient.

Partial least squares (PLS) regression for predicting tumor positions

A PLS model for inferring tumor position from the surrogate marker displacements was developed for each treatment fraction. The accuracy of PLS for determining tumor position from surrogate marker displacements has been reported previously.^{11, 12, 14} PLS is one of a class of methods for modeling relationships between an input matrix, X, and an output matrix, Y, by means of scores, which may also be called latent variables. The input matrix is composed of m respiratory surrogate signals, x_i for i = 1 to m, such that X = [x₁x₂ … x_m]. The input matrix can also be represented as n rows, each consisting of a set of respiratory surrogate measurements, z_i for i = 1 to n, captured at one point in time such that X = [z₁z₂ … z_n]^T. The n × 3 output, Y, consists of three tumor displacement dimensions and n samples. Each column of the input and output matrices was mean-centered and scaled to unit-variance.

In this study, the iterative SIMPLS¹⁵ algorithm was used to decompose X and Y into $X=T·W^T$ and $Y=U·Q^T$, for n × m matrix T of input scores, n × m matrix U of output scores, m × m matrix W of input weights, and p × m matrix Q of output weights. The first column of T, t₁, was given by $t_1=X·X^T·Y/\mathit{norm}(X·X^T·Y)$. The elements of the first column of W, w₁, and the first X basis, v₁, were each equal to one. The following iterative regression process was then repeated for i = 1 to m. First, the Y loadings and scores were calculated as $q_i=Y^T·t_i$ and $u_i=Y^T·q_i$, respectively. Next, the X basis was updated with each iteration as $v_i=v_{i-1}-V_{i-1}·(V_{i-1}^T·{(t_i^T·X)}^T)$, where V_i − 1 = [v₁, v₂, …, v_i − 1]. Finally, subsequent X weights and scores were calculated as $w_i=(S_{i-1}-v_i·(v_i^T·S_{i-1}))·q_i$ and $t_i=X·w_i$.

Because the PLS algorithm determines scores in order of decreasing contribution to the PLS model, utilizing only the first A of m factors serves to select the input information most relevant to the outputs. Thus, the score and loading matrices were compressed as $X=\hat{T}·\hat{W}+E$ and $Y=\hat{U}·\hat{Q}+F$, where $\hat{T}$ was the n × A matrix $\hat{T}=[t_1,\hspace{1em}{t}_2,...,t_A]$, $\hat{W}$ was the m × A matrix $\hat{W}=[w_1,\hspace{1em}{w}_2,...,w_A]$, $\hat{U}$ was the n × A matrix $\hat{U}=[u_1,\hspace{1em}{u}_2,...,u_A]$, and $\hat{Q}$ was the p × A matrix $\hat{Q}=[q_1,\hspace{1em}{q}_2,...,q_A]$. The residual matrices were E and F. Cross-validation was used to select the appropriate number of factors, A, for each training dataset. The regression coefficient matrix, B, was given by $\hat{B}=\hat{R}·{\hat{Q}}^T$, where $\hat{R}=[r_1,\hspace{1em}{r}_2,...,r_A]$ and $\hat{Q}=[q_1,\hspace{1em}{q}_2,...,q_A]$.

Tumor position was predicted as $\hat{Y}=X·\hat{B}$ or, from a single new set of measurements, z_new, as ${\hat{y}}_{\mathit{new}}=z_{\mathit{new}}·\hat{B}$. The inferential model error, e, was calculated as $e=\sqrt{\sum {({\hat{y}}_{\mathit{new}}-y_{\mathit{new}})}^2}$, the Euclidean distance between PLS-predicted tumor positions (${\hat{y}}_{\mathit{new}}$) and radiographically measured tumor predictions ($y_{\mathit{new}}$).

Tumor motion models and model monitoring

Two PLS models were created for each training dataset: one for prediction and a second for monitoring. In our previous work,¹² we have shown that the input projection process leads to models that can more accurately predict tumor displacement from surrogate marker motion. However, we found that projecting the inputs degrades the ability to monitor the model for tumor-surrogate relationship changes. The PLS models for prediction and for monitoring differed in their input matrix, X.

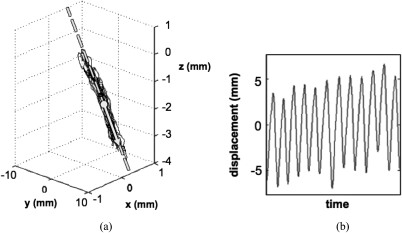
In either case, the first 10 samples (n = 10) of concurrent surrogate marker and tumor localizations in the treatment fraction dataset were used as training data for the model. For the monitoring model, X was a 10 × 9 matrix describing the 3D positions of three surrogate markers at ten samples. For the tumor displacement prediction model, X was a 10 × 3 matrix in which each column was a one-dimensional (1D) representation of the three-dimensional (3D) motion of one of the surrogate markers. These 1D surrogate signals were created by orthogonally projecting the surrogate marker displacements captured during the training data acquisition period onto a line. This line was defined by the displacements’ 3D mean, M, and first principal component vector (Fig. 2). The 1D representation for each sample was defined as the distance between the projected point and M.

Figure 2.

The surrogate marker projection process. (a) Example of 3D surrogate marker motion data, including its mean and first principal component vector (dot and arrow, respectively) and its projection line (dashed). (b) The 1D representation of the 3D data in (a).

Respiratory surrogate-based monitoring metrics

Respiratory surrogate data captured during the initial model development period were compared to respiratory surrogate data captured over the course of a treatment fraction. Using this technique, whether the real-time tumor displacement prediction is occurring under conditions described by the model could be determined. Thus, the quality of the model can be monitored without stopping treatment to explicitly measure the tumor position.

For each 1 × 3 vector of inputs, z_i, an associated score vector, ${\hat{t}}_i$, was calculated as ${\hat{t}}_i^T=z_i·\hat{W}$, where $\hat{W}$ was the compressed weight vector calculated as part of the PLS regression process. The scores were then used to calculate the associated Hotelling statistic, T², and input variable squared prediction error, Q^(X), for each surrogate marker displacement dataset. The T² and Q^(X) statistics rely on measurements of the surrogate markers exclusively and do not utilize gold-standard tumor position measurements.

Hotelling’s T² statistic characterizes the amount of variation in the inputs to the model. Aberrant T² values indicate that the relationship between inputs has changed and that the model must be extrapolated to fit the new input data. T² was calculated as $T^2=t_{\mathit{new}}^T·S^{-1}·t_{\mathit{new}}$ from the estimated training data score covariance matrix, $S=\frac{{\hat{T}}^T·\hat{T}}{n-1}$.¹⁶

The input variable squared prediction error, Q^(X), measures the data in a row of the residual matrix, E, in the compression step $X=\hat{T}·\hat{W}+E$ described above. This metric describes the amount of variance not captured by the scores, $\hat{T}$, used to predict the tumor position. An increase in Q^(X) over time indicates that less of the information in the respiratory surrogate inputs is being used by the model. Q^(X) was given by $Q^{(X)}={\sum }_{i=A+1}^m{({\hat{z}}_i-z_i)}^2$ for sample i, where ${\hat{z}}_i=t_i·\hat{W}$ and represents the surrogate marker measurement vector, $z_i$, compressed to 1 score (A = 1).¹⁷

Performance of respiratory surrogate-based monitoring

Large error detection

Treatment fraction-specific limits on T² and Q^(X) were calculated and tested for $(1-\alpha )$ percentile confidence limits for $0<\alpha <1$. The confidence limits were used as control limits for T² and Q^(X). For T², confidence limits were determined from $T_{\alpha }^2=\frac{(n^2-1)A}{n(n-A)}{F}_{\alpha }(A,n-A)$, where n = 10 was the quantity of training samples used to generate the model, one score was used in the PLS model created to monitor the tumor localization model (A = 1), and $F_{\alpha }(A,n-A)$ was the upper $(100\%)·(\alpha )$ critical point of the F distribution with (A, n – A) degrees of freedom. Confidence limits on Q^(X) were calculated through the Jackson-Mudholkar¹⁸ formula,

$$Q_{\alpha }={\theta }_1{[1-\frac{{\theta }_2{h}_0(1-h_0)}{{\theta }_1^2}+\frac{z_{\alpha }\sqrt{2{\theta }_2{h}_0^2}}{{\theta }_1}]}^{1/h_0},$$

in which $z_{\alpha }$ is the upper $(100\%)·(\alpha )$ critical point of the normal distribution, ${\theta }_j={\sum }_{i=A+1}^m{\lambda }_i^j$, n = 10, $h_0=1-\frac{2{\theta }_1{\theta }_3}{3{\theta }_2^2}$, and λ_i is the ith eigenvalue of ${({\hat{z}}_{\mathit{new},i}-z_{\mathit{new},i})}^T({\hat{z}}_{\mathit{new},i}-z_{\mathit{new},i})$.

The ability of T² and Q^(X) to predict whether a tumor displacement prediction is accurate to within 3 mm was evaluated for each α. Prediction of large (>3 mm) errors was based on whether T² or Q^(X) exceeded the treatment fraction-specific confidence limits and was validated against radiographic measurements. To evaluate the performance of the method, sensitivity and specificity were explored under various conditions. Sensitivity measured the proportion of errors >3 mm that was detected. Specificity represents the proportion of errors <3 mm that was identified as likely to be <3 mm. Sensitivity and specificity were determined for: (1) T² confidence limit; (2) Q^(X) confidence limit; and (3) the union of results from T² confidence limit and Q^(X) confidence limit, in which the method predicts large error if either T² or Q^(X) exceeds its respective confidence limit threshold. Receiver operating characteristic (ROC) analysis was performed to evaluate sensitivity versus specificity at any confidence limit between 0% and 100%.

In addition to the surrogate marker measurements concurrent with the tumor displacement, the utility of past surrogate marker measurements was evaluated for data up to 10 s prior to the surrogate marker-based tumor localization. For this multiple measurement method, the proportion of T², Q^(X), or T²∪Q^(X) values in the testing period that exceeded the confidence limit(s) was calculated. A threshold value for predicting large inferential model errors (for example, at least 10% of the measurements during the 5 s prior to the tumor localization) was selected to maximize specificity at the target sensitivity.

Time to error and time to alarm

For each treatment fraction and monitoring method, the times from the end of the training dataset to the first large error (time to error) and to the first confidence limit-based indication of large error (time to alarm) were determined. Results were compared to the timing of images captured by the Cyberknife Synchrony™ system to validate its own model during the treatment.

Effect of tumor site

Results were stratified by tumor site for lung (130 fractions) and pancreas (48 fractions) cases, using 2 s of surrogate marker data preceding the tumor localization.

RESULTS

Large error detection

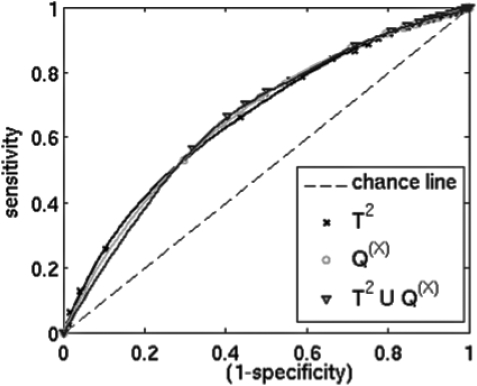
The T² and Q^(X) statistics were able to indicate such phenomena as large errors associated with gradual decreases in inferential model accuracy and transient surrogate marker tracking errors. All three confidence limit tests, T², Q^(X), and T²∪Q^(X), were predictive of large errors. Sensitivity and specificity varied with confidence limit selection, with increasing sensitivity associated with decreased specificity (Fig. 3). T²∪Q^(X) was associated with specificity 1%–2% higher than either T² or Q^(X) alone at 90%–95% sensitivity (Table TABLE I.).

Figure 3.

ROC curves showing ability to predict localization errors exceeding 3 mm for various confidence levels.

TABLE I.

Summary of monitoring performance for all tumor sites at 90% and 95% sensitivity.

			Time to alarm
Method	Sensitivity (%)	Specificity (%)	Mean (min)	st. dev. (min)
T2	90	23	6.0	8.8
Q(X)	90	24	7.6	9.9
T2∪Q(X)	90	24	7.2	9.8
T2	95	13	4.0	8.1
Q(X)	95	14	4.6	8.1
T2∪Q(X)	95	15	5.3	8.2

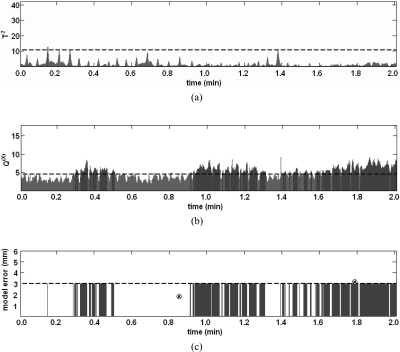
Neither T² nor Q^(X) increased monotonically, and T² in particular varied cyclically with phase of respiration (Fig. 4). Incorporating past measurements of surrogate marker displacements improved model monitoring performance for Q^(X) and T²∪Q^(X). For 95% sensitivity, the best specificity for T²∪Q^(X) was achieved by requiring that 5% of T²∪Q^(X) values acquired over the past 3 s exceed the confidence limit threshold.

Figure 4.

Example of (a) T², (b) Q^(X), and (c) tumor localization error versus time elapsed since the training data. In (a) and (b), horizontal dashed lines represent control limits, and times in which the control limit is exceeded are shaded. In (c), the horizontal dashed line represents a 3 mm error limit, and radiographic tumor localizations errors are indicated at t = 0.8 min and t = 1.8 min by circled x’s (⊗). It is likely that localization errors exceed 3 mm from 0.3 to 0.5 min and after 0.9 min, but radiographic validation is only possible at two moments over this 2 min period.

Time to error and time to alarm

For the inferential modeling method used in this study, the mean (± standard deviation) time from the last tumor localization to an error >3 mm was 12 ± 12 min for those fractions in which errors >3 mm occurred. This mean time excludes the 6% of fractions in which no tumor position prediction error was >3 mm.

For this dataset, the mean time to alarm for the Cyberknife Synchrony system was 1.1 min. For T² and Q^(X) values giving the highest specificity at 90% sensitivity (Table TABLE I.), the mean times from training data to indication of large errors (mean time to alarm) for T², Q^(X), and T²∪Q^(X) were 6.0, 7.6, and 7.2 min, respectively. In 5% of fractions, the error never exceeded 3 mm. However, there were no fractions for which neither T² nor Q^(X) did not exceed the confidence limit threshold for at least one set of surrogate marker measurements.

Effect of tumor site

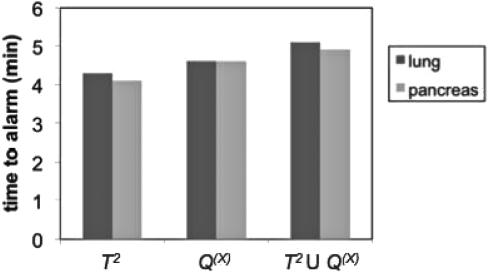
There was no significant difference between lung and pancreas cases in time to alarm (Fig. 5). The specificities for each site were equal to the specificities for the pooled lung, liver, and pancreas results at 90%–95% sensitivity given in Table TABLE I..

Figure 5.

Comparison of mean time to alarm for lung and pancreas results using 2 s of data.

DISCUSSION

The results of this study establish the feasibility of using confidence limits on T² and Q^(X) statistics of respiratory surrogate measurements in online monitoring of the accuracy of real-time respiration-induced tumor motion models. The T² and Q^(X) statistics were able to indicate whether inferential model errors exceeded 3 mm with high sensitivity. For 95% error prediction sensitivity, specificity was 15%, and the mean time to alarm was 5.3 min. Modest improvements in specificity were achieved by combining T² and Q^(X) results and by expanding the input to include the previous 3 s of respiratory surrogate data.

Real-time motion management systems rely on rapid, accurate tumor localization. For respiratory surrogate-based systems, current clinical practice is to establish a model before beginning treatment and then either to assume that the model will remain valid or to periodically validate the model according to some pre-established schedule. If the gold-standard radiographic tumor localizations are too sparse, large targeting errors may occur in the interim. Conversely, radiographic images captured while the model remains accurate result in exposure to unnecessary ionizing radiation and extend the duration of the treatment fraction. Seppenwoolde et al. found that the timing of gold-standard image-based tumor localizations determines the accuracy of the model but that the patient-specific benefit of increasing the imaging frequency varies widely.¹³ The method described by this study is a novel, knowledge-based technique for timing image acquisitions used to update respiratory surrogate tumor motion models by relying exclusively on surrogate measurements.

Applying a confidence limit-based threshold made it possible to detect errors >3 mm with a high degree of sensitivity (>90%). As shown in the ROC curves of Fig. 4, varying α led to a tradeoff between sensitivity and specificity. In the context of this application, sensitivity refers to the probability that a large error will be detected by the confidence limit method. Thus, in this manuscript, we have focused on parameters leading to high (90%–95%) sensitivity and decreased (13%–24%) specificity. Low specificity indicates an increased rate of false positives. In this application, false positives correspond to unnecessary image acquisitions. To investigate the impact of this relatively low specificity on clinical workflow, we have described the time to alarm for 90%–95% sensitivity.

The mean time to alarm for 90%–95% sensitivity was 4–8 min, representing a four- to eight-fold decrease in image acquisition frequency over the Cyberknife Synchrony™ method. Because there was considerable variability in the time to errors >3 mm, acquiring images at a preselected regular interval often would result in missing large errors. For this dataset, the Cyberknife Synchrony™ system localized the tumor via radiographs every third beam delivered, with a mean interval of 63 s between image acquisitions. The current version of the Cyberknife SYNCHRONY™ software allows the operator to select a constant time interval of up to 2.5 min between radiographic image acquisitions. This maximum time interval for the Cyberknife Synchrony™ system is more than double the average frequency of the proposed T²∪Q^(X) method.

This study determined the performance of respiratory surrogate monitoring for predicting PLS-based tumor localization errors.¹² This method can be extended to other tumor displacement inferential approaches to minimize the imaging frequency of existing systems, thereby decreasing treatment interruptions and overall patient in-room time. Through monitoring, this method also has the potential to increase the targeting accuracy of any real-time motion compensation device, including radiation gating systems. Berbeco et al. has concluded that gating margins based on a single simulation session at the beginning of the treatment may not be enough to evaluate residual motion of a gated treatment.² Respiratory surrogate monitoring through T² and Q^(X) can detect increases in residual motion during the treatment, allowing the clinicians to pause treatment to collect images when necessary to ensure that tumor motion is in accordance with the internal margin for the plan.

In many cases, the Hotelling statistic (T²) and the input variable squared prediction error (Q^(X)) both exceeded confidence limit thresholds together, a result commonly seen in process control monitoring through these metrics.¹⁶ However, the statistics did not always indicate alarm concurrently. In some cases T² indicated large error first, but in other cases Q^(X) indicated large error first. As a result, combining the metrics resulted in a slight increase in performance of the method. Mathematically, T² and Q^(X) are independent. Their concurrent increase is indicative of a common cause: some change in the tumor-surrogate relationship. Transient and long-term changes in the tumor-surrogate relationship have been described by Ozhasoglu et al., Seppenwoolde et al., Hoisak et al., and Ionsascu et al. and are manifested as shifts in the phase offset between tumor and surrogate motion, baseline drifts in tumor position or surrogate signal, or other complex behavior leading to lapses in correlation.^{7, 10, 19, 20} Our previous work has shown that the tumor-surrogate relationship changes during most treatment fractions.¹¹

The method described in this study resembles statistical process control (SPC) monitoring utilized in chemical process control applications.^{16, 18, 21} However, in classical SPC, metrics are derived directly from the model that is being monitored. By contrast, in this method separate models for monitoring and for tumor displacement prediction were created. For optimal tumor localization accuracy, it was necessary to project surrogate marker data from 3D to 1D.¹² This reduction in input dimensionality from m = 9 to m = 3 reduced the number of scores available for calculating T², which uses scores 1 to A, and Q^(X), which uses scores A + 1 to m. As a result, reducing input dimensionality from 9 to 3 would have decreased the specificity, and consequently the time to alarm, for a given sensitivity. For instance, by utilizing the 3D (9 input) marker data for monitoring, at 95% sensitivity the mean time to alarm increased from 2–4 min to 4–8 min.

Neither T² nor Q^(X) increased monotonically over time. The T² statistic was cyclic in nature, increasing during certain phases of respiration, and both T² and Q^(X) were associated with some degree of noise. In the future, it may be possible to reduce this periodicity by carefully selecting training data encompassing a wide range of respiratory phases. It was possible to improve specificity for Q^(X) and T²∪Q^(X) by considering time trends in T² and Q^(X) values. We speculate that utilizing multiple surrogate marker data samples (1–3 s of data from 26 Hz measurements) helped to overcome the effects of both noise and training data selection.

CONCLUSIONS

In this work, we present a novel approach to determining tumor position prediction errors in real-time and from measurements of external marker respiratory surrogates exclusively. In a large cohort of lung, liver, and pancreas cases, the T² and Q^(X) statistics can predict whether tumor localization error exceeds 3 mm with 95% sensitivity and 15% specificity and a mean time to alarm of 5.3 min. The mean time to alarm for 90%–95% sensitivity was 4–8 min, representing a four- to eight-fold decrease in image acquisition frequency over the Cyberknife Synchrony™ method. Thus, this approach has the potential to reduce imaging frequency and, consequently, imaging dose during respiratory surrogate-guided treatments. Results did not differ by tumor site.