Using Confirmatory Factor Analysis to Measure Contemporaneous Activation of Defined Neuronal Networks in Functional Magnetic Resonance Imaging

Abstract

Functional neuroimaging often generates large amounts of data on regions of interest. Such data can be addressed effectively with a widely-used statistical technique based on measurement theory that has not yet been applied to neuroimaging. Confirmatory factor analysis is a convenient hypothesis-driven modeling environment that can be used to conduct formal statistical tests comparing alternative hypotheses regarding the elements of putative neuronal networks. In such models, measures of each activated region of interest are treated as indicators of an underlying latent construct that represents the contemporaneous activation of the elements in the network. As such, confirmatory factor analysis focuses analyses on the activation of hypothesized networks as a whole, improves statistical power by modeling measurement error, and provides a theory-based approach to data reduction with a robust statistical basis. This approach is illustrated using data on seven regions of interest in a hypothesized mesocorticostriatal reward system in a sample of 262 adult volunteers assessed during a card-guessing reward task. A latent construct reflecting contemporaneous activation of the reward system was found to be significantly associated with a latent construct measuring impulsivity, particularly in males.

Introduction

Confirmatory factor analysis (CFA) is a hypothesis-driven variant of exploratory factor analysis that is based on measurement theory and represents a special case of structural equation modeling (SEM) (Bollen, 1989). Measurement theory is the branch of applied mathematics and statistics concerned with the measurement of phenomena in science and applied settings. The measurement model underlying CFA treats each specific observed measure, or indicator, as one of multiple fallible manifest indicators of an underlying latent (unmeasured) construct. In measurement theory, each observed measure reflects both the underlying “true” score on the latent construct plus measurement error. CFA allows statistical tests of measurement models (hypotheses regarding loadings of multiple manifest indicators on the underlying latent construct). Because CFA models allow for measurement error in the manifest variables, inferences about the latent constructs can be interpreted as if the latent constructs been measured without error.

CFA-based measurement models are readily embedded in broader SEMs to test hypotheses regarding associations among latent constructs and other important variables, taking advantage of the reduced measurement error in the latent construct. Similarly, the latent construct can be formally tested for associations and interactions with other variables such as sex or diagnostic status in CFA/SEM to address systematic heterogeneity (Bollen, 1989; Brown, 2006).

Mathematically, the SEM for the association between two latent constructs defined by CFA measurement models (defined, for example, by 7 and 3 manifest indicators, respectively) can be expressed as follows. Let X_j be the jth of 7 manifest indicators of a latent construct ξ, j = 1, …, 7, and let Y_k be the kth of 3 manifest indicators for a second latent construct ŋ, k = 1, 2, 3. The model consists of two CFA measurement models

$$\begin{array}{c}{Y}_k={\nu }_k+{\lambda }_{\mathit{\text{yk}}}\eta +{\epsilon }_{\mathit{\text{yk}}}\hfill \\ X_j={\alpha }_j+{\lambda }_{\mathit{\text{xj }}}\xi +{\epsilon }_{\mathit{\text{xj}}},\hfill \end{array}$$

and a structural regression model relating the two latent constructs

$$ŋ=\gamma \xi +\zeta ,$$

where ξ is normally distributed with mean zero. In these models, ε_y1, …, ε_y3, ε_x1, …, ε_x7, and ζ are all mutually independent of one another, and are normally-distributed with mean zero as well. γ is the regression coefficient relating η to ξ, and the residual ζ represents the variability in η not explained by ξ. The residuals ε_yk and ε_xj represent measurement error in Y_k and X_j relative to the true constructs η and ξ, and ν_k and α_j are the means of Y_k and X_j. The model estimation procedure makes a working assumption of multivariate normality of the data (Y₁, …, Y₃, X₁, … X₇). This assumption is used to derive the resulting parameter estimates. However, the estimates themselves are robust to the normality assumption, and the standard errors and resulting hypothesis tests for model comparison and testing are estimated in this work via a procedure that is also valid even if the normality assumption is violated (Bollen, 1989; Brown, 2006).

When fully standardized, the factor loadings of each manifest indicator on the latent factor and regression coefficients can be interpreted as marginal correlations and provide an easily interpreted metric for determining the centrality of each manifest variable to the latent construct. Thus, the square of the loading indicates the proportion of variance in the manifest indicator accounted for by the latent construct (Bollen, 1989; Brown, 2006).

Although CFA is a mainstay of research on behavioral constructs with multiple indicators, including neuropsychological tests (Genderson et al., 2007; Wang et al., 2010), it has not been applied to data arising from fMRI stimulation protocols. This is unfortunate, as the application of this strategy to fMRI is straightforward and potentially quite beneficial. An important instance of manifest variables in fMRI is the blood oxygen level dependent (BOLD) response in each of several pre-specified brain regions of interest (ROI). CFA would treat these BOLD responses in the ROIs as fallible manifest indicators of a construct reflecting contemporaneous activation of the elements of a hypothesized neuronal network.

Advantages of CFA Relative to Exploratory Multivariate Methods

CFA shares many of the advantages of traditional multivariate methods such principal components analysis (PCA) (Butler et al., 2007) and partial least squares (PLS) (Krishnan et al., 2011; McIntosh et al., 1996). Each method derives latent constructs that reflect correlated concurrent activations of multiple ROIs. Indeed, simply extracting the first eigenvariate from a single “network ROI” defined by multiple ROIs would similarly yield a single unit-free latent measure of activation of the entire network (essentially a principal component) that would be very similar to a latent construct derived from the same ROIs in a CFA measurement model. Each of these approaches has the advantages of focusing analyses on the network as a whole and providing a theory-based method of data reduction. This reduction addresses the vexing problem of multiple statistical comparisons in neuroimaging research (and attendant adjustments of alpha levels for significance tests). As a result, all multivariate methods can maximize the statistical power of given sample sizes when validly specified. Nonetheless, there are a number of advantages to the use of CFA over other multivariate methods in neuroimaging research:

1. First and foremost, PCA, PLS, and related methods are inherently exploratory and are not designed for formal statistical tests of alternative hypotheses. In contrast, CFA and SEM are confirmatory methods that allow formal statistical tests of multiple aspects of hypothesized models of neuronal networks. Not all topics in neuroimaging research areas are currently mature enough to propose testable hypotheses, but increasing numbers of topics are ready and CFA provides a highly useful formal statistical method for exposing testable hypotheses to risk of refutation.

   Consider five such highly informative statistical tests that can be conveniently implemented in CFA/SEM. First, there is not a widely accepted method for determining the number of components to extract in PCA-based methods. In CFA/SEM, however, nested alternative models can be directly compared using likelihood ratio chi-square statistics. A model is nested in another model when it is based on the same elements, but uses a subset of the free parameters of the parent model (Bollen, 1989; Brown, 2006). Second, if the best fitting model in CFA involves more than one latent neuronal factor, the test of the significance of the correlations among those factors would provide an index of their connectivity. Third, CFA provides statistical tests of the significance of the loading of each ROI on the latent construct. Fourth, formal statistical tests of the association of latent neuronal constructs with behavior and other external criteria can be easily implemented in SEM. Fifth, one can readily test for the significance of interactions between model paths and key variables such as age or sex. This facility for statistical testing provides a basis for well-found advances in understanding neuronal networks and their correlates.

2. Furthermore, when the statistical fit of a hypothesized model is found to be inadequate, CFA provides detailed information regarding the degree and source of misfit within the model. This provides a strong empirical basis for modifying the model. When empirical misfit information is considered in the light of theoretical understanding of the hypothesized network, informed model modifications can be estimated and statistically evaluated. Modification indices (MIs) identify specific areas of ill fit in a model and quantify the extent to which the model χ2 would be reduced by specific changes to the measurement model (Brown, 2006). MIs are generated by most application software implementing CFA. When MIs are used to refine a model, the analysis is no longer testing a fully a priori hypothesis, however. Because changes to CFA models based on MIs can capitalize on chance associations, their use adds an exploratory element that is appropriate during early stages of research on a topic, but the modified model must be independently verified in independent samples. In the case of neuroimaging research, care also must be taken only to make changes to measurement models for neuronal networks that are consistent with neurobiological evidence.

3. CFA models error variance separately from unexplained variance in the underlying constructs (Bollen, 1989; Brown, 2006). As a result, the latent construct of activation of a neuronal network provided by CFA is measured with less error than each of the ROIs that define the network. Other things equal, this will yield greater statistical power for hypothesis testing, relative to piecemeal ROI-specific analyses. Thus, CFA/SEM removes bias due to measurement error in the estimation of relations among latent constructs. In contrast, because PCA-based strategies do not distinguish common and error variance, error is included in the extracted components, which can reduce the reliability of component scores (Brown, 2006).

4. Another advantage of CFA’s statistical model is that limitations of the data in terms of uncertainty and the ability to compare competing models are automatically integrated into the analysis. For example, only models that are sufficiently parsimonious can be fitted to the data; these models are referred to as “identified.” Overly-flexible models may have more degrees of freedom than the data or study design can support. Such models are “unidentified” because the data contain no information about the model. A model that is “just identified” will fit the data perfectly, indicated by goodness-of-fit statistics being equal to zero (Bollen, 1989).

5. CFA and SEM can be used to evaluate both substantive and methodologic issues in imaging research. By providing a framework for testing differences in measurement models across groups, it allows formal statistical tests of whether data can be combined across samples, scanners, and groups (e.g., sexes or ethnic groups) without misrepresenting relationships. This can be done in multiple-group analyses that compare model parameters in different groups or by testing interactions with covariates. We illustrate both approaches in the present study to determine if data from two different subject groups, obtained in different scanners using the same probe paradigm, can be combined.

Illustration of the Application of CFA

We provide an illustration of the use of CFA/SEM in an empirical study that incorporates both multiple manifest indicators of a hypothesized mesocorticostriatal (MCS) reward system and multiple manifest indicators of the behavioral trait of impulsivity. There is substantial evidence that reward functions related to impulsivity in humans are mediated by a MCS neuronal network consisting of at least the ventral striatum (VS) and the anterior cingulate cortex (ACC) (Buckholtz et al., 2010; Dreher et al., 2009; Kirsch et al., 2003; Stoeckel et al., 2008; Tzschentke, 2000). In addition, the regulation of impulsive behavior has been linked to the functioning of these same regions as well as the ventrolateral prefrontal cortex (PFC) and parietal cortices (Casey and Durston, 2006). Both to illustrate the use of CFA in testing hypotheses regarding the ROIs participating in the hypothesized MCS reward network and to test the hypothesis that activation of the MCS network is significantly related to the trait of impulsivity, we assess neuronal responses to reward cues using an adaptation (Forbes et al., 2009b) of a well-validated card-guessing task involving monetary reward (Delgado et al., 2000) and related activation in the MCS reward system to a widely used measure of impulsivity.

Impulsivity is an important trait because it is correlated with maladaptive antisocial behavior, substance use disorders, personality disorders, and bipolar disorder (Moeller et al., 2001). In one theoretical model, higher levels of impulsivity are thought to reflect, at least in part, higher sensitivity to rewards and lower inhibition of prepotent responses (Forbes et al., 2009a; Hahn et al., 2009). Consistent with this view, there is evidence of greater activation of the VS to cues indicating rewards in individuals with higher scores on the trait of impulsivity (Forbes et al., 2009a; Hahn et al., 2009). Using CFA/SEM, we test the hypothesis that variations in contemporaneous activation of ROIs in the hypothesized MCS reward system during reward trials of the card-guessing task will be associated with variations in the latent trait of impulsivity.

To illustrate the correspondence between the latent MCS construct derived in CFA and the corresponding principal component, we took the first eigenvariate of a single “network ROI” defined by all of the ROIs hypothesized to constitute the network. We then illustrated the advantages of CFA in providing the loading of each of these ROI on the latent construct and testing its significance.

To provide illustrative tests of the robustness of CFA to variations in preprocessing steps and to two kinds of model misspecification (i.e., excluding an ROI that is central to the network and including an ROI that is weakly related to the network) in the present data, we conducted three sets of sensitivity analyses. First, all analyses were repeated iteratively while eliminating each of the hypothesized ROIs one at a time. Second, all analyses were repeated while adding one ROI at a time that had not been hypothesized to be part of the MCS reward system. For these analyses, we selected both extra-network ROIs that are not thought to play roles in reward processing and one ROI from an additional area commonly activated during the processing of visual reward cues (Buckholtz et al., 2010; Gaffan et al., 1988; Krawczyk et al., 2007). That is, the latter ROI could have been hypothesized to be part of a more extended reward network. Third, we varied the extraction of ROI data by relaxing the thresholds (on p-values and required number of activated voxels) defining the ROIs and repeated the integrated CFA/SEM modeling on these data.

Method

Participants

The use of CFA in fMRI research is illustrated using a heterogeneous sample composed of 262 adult volunteers recruited and scanned at the University of Pittsburgh and Duke University.

Duke sample

A total of 173 18–22 year old participants (102 women; mean age 19.76 ± 1.28 years) were included from an ongoing parent protocol, the Duke Neurogenetics Study (DNS), which assesses a wide range of behavioral and biological traits among nonpatient, young adult student volunteers. All participants provided informed consent in accord with Duke University guidelines and were in good general health. The participants were free of: (1) medical diagnoses of cancer, stroke, diabetes requiring insulin treatment, chronic kidney or liver disease, or lifetime history of psychotic symptoms; (2) use of psychotropic, glucocorticoid, or hypolipidemic medication; and (3) conditions affecting cerebral blood flow and metabolism (e.g., hypertension). Diagnosis of any current DSM-IV Axis I mental disorder, as determined by clinical interview using the electronic MINI (Sheehan et al., 1998), was not an exclusion as the DNS seeks to establish broad variability in multiple behavioral phenotypes related to psychopathology (e.g., trait anxiety, impulsivity).

Pittsburgh sample

A total of 89 31–54 year old participants (51 women; mean age 44.24 ± 6.80 years) were included from the Adult Health and Behavior (AHAB) project, which assessed a wide range of behavioral and biological traits among nonpatient, middle-aged community volunteers. All participants provided informed consent in accord with University of Pittsburgh guidelines, and were in good general health. The participants were free of: (1) medical diagnoses of cancer, stroke, diabetes requiring insulin treatment, chronic kidney or liver disease, and lifetime history of psychotic symptoms; (2) use of psychotropic, glucocorticoid, or hypolipidemic medication; and (3) conditions affecting cerebral blood flow and metabolism (e.g., hypertension). One study showing greater activation of the VS by reward cues in individuals with higher impulsivity has been published from the AHAB sample (Forbes et al., 2009a), other elements of the MCS reward system were not addressed. Unlike the DNS sample, the AHAB sample was free of any current DSM-IV Axis I disorder (but not lifetime history of diagnoses) as determined by clinical interview using the Structured Clinical Interview for DSM-IV Axis I Disorders (SCID) (First et al., 1996)).

Measures and procedures

Impulsivity

The trait of impulsivity was measured using the three subscales of the reliable and valid Barratt Impulsiveness Scale (BIS), motoric impulsiveness (BIS_M), nonplanning (BIS_N), and cognitive impulsiveness (BIS_C), which was completed by the participants (Patton et al., 1995). The BIS principally measures a lack of constraint or effortful control of thoughts and action tendencies and high scores on this measure have been associated with reward sensitivity—a tendency to respond quickly in ways that maximize immediate rewards at the expense of achieving long-term goals (de Wit et al., 2007; Hariri et al., 2006). Minimal sex differences have been reported for this measure of impulsiveness (Cross et al., 2011).

MCS reactivity paradigm

An identical challenge paradigm designed to engage the reward system was administered during fMRI to both the Duke and Pittsburgh samples. As described previously (Forbes et al., 2009a; Gianaros et al., 2011; Hariri et al., 2006; Hariri et al., 2009) our blocked-design paradigm consisted of pseudorandom presentation of trials wherein participants played a card guessing game and received positive or negative feedback (i.e., correct or incorrect guess) for each trial. During each trial, participants had 3 seconds to guess, via button press, whether the value of a visually presented card would be higher or lower than 5 (index and middle finger, respectively). The numerical value of the card was then presented for 500 milliseconds and followed by appropriate feedback (green upward-facing arrow for positive feedback; red downward-facing arrow for negative feedback) for an additional 500 milliseconds. A crosshair was then presented for 3 seconds, for a total trial length of 7 seconds. Each block was comprised of 5 trials, and the paradigm consisted of 3 blocks of predominantly positive feedback (80% correct) and 3 blocks of predominantly negative feedback (20% correct) interleaved with 3 control blocks. During control blocks, participants were instructed to simply make button presses during the presentation of an “x” (3 seconds), which was followed by an asterisk (500 milliseconds) and a yellow circle (500 milliseconds). Each block was preceded by an instruction of “Guess Number” (positive or negative feedback blocks) or “Press Button” (control blocks) for 2 seconds resulting in a total block length of 38 seconds and a total task length of 342 seconds.

Participants were told that their performance on the card game would determine a monetary reward to be received at the end of the game. Participants were unaware of the fixed outcome probabilities associated with each block and were led to believe that their performance would determine a net monetary gain at the end of the scanning session. We included one incongruent trial within each task block (e.g., 1 of 5 trials during positive feedback blocks was incorrect, resulting in negative feedback) to prevent participants from anticipating the feedback for each trial and to maintain participants’ engagement and motivation to perform well.

BOLD fMRI data acquisition

Duke sample

Each participant was scanned using a research-dedicated GE MR750 3T scanner (General Electric, Milwaukee, WI, USA) at the Duke-UNC Brain Imaging and Analysis Center. This scanner is equipped with high-power high-duty-cycle 50-mT/m gradients at 200 T/m/s slew rate, and an eight-channel receive-only SENSE head coil for parallel imaging at high bandwidth up to 1 MHz. A semi-automated high-order shimming program was used to maximize global field homogeneity. A series of 34 interleaved axial functional slices aligned with the anterior commissure-posterior commissure (AC-PC) plane were acquired for full-brain coverage using an inverse-spiral (spiral in) pulse sequence to reduce susceptibility artifact (TR/TE/flip angle = 2000 ms/30 ms/60°; FOV = 240 mm; 3.75 × 3.75 ×4 mm voxels; interslice skip = 0). Four initial RF excitations were performed (and discarded) to achieve steady-state equilibrium.

Pittsburgh sample

Each participant was scanned using a Siemens 3T Allegra scanner (Siemens AG, Medical Solutions, Erlangen, Germany) equipped with 40-mT/m gradients at 400 T/m/s slew rate and a 12-channel standard radiofrequency birdcage coil. This scanner is developed specifically for advanced brain imaging applications and characterized by increased T2* sensitivity and fast gradients that minimize echo spacing, thereby reducing echo-planar imaging geometric distortions and improving image quality. An autoshimming procedure was conducted to minimize field inhomogeneities. A series of 34 interleaved axial slices aligned with the AC-PC plane were acquired with a gradient-echo echo planar Cartesian imaging sequence (TR/TE/flip angle = 2000 ms/25 ms/70°; FOV = 200 mm, 3.125 × 3.125 × 3 mm voxels; interslice skip = 0). Two initial RF excitations were performed (and discarded) to achieve steady-state equilibrium. However, the first two acquired volumes were discarded during preprocessing to further ensure steady-state equilibrium.

BOLD fMRI data analysis

Whole-brain image analysis of all fMRI data was conducted at the Laboratory of NeuroGenetics at Duke University using the general linear model (GLM) of SPM8 (www.fil.ion.ucl.ac.uk/spm/doc/manual.pdf; please consult SPM8 documentation for detailed information about image processing and statistical analyses). Images for each subject were realigned to the first volume in the time series to correct for head motion, spatially normalized into a standard stereotactic space (Montreal Neurological Institute template) using a 12-parameter affine model (final resolution of functional images = 2 mm isotropic voxels), and smoothed to minimize noise and residual difference in gyral anatomy with a Gaussian filter, set at 6 mm full-width at half-maximum. Voxel-wise signal intensities were ratio normalized to the whole-brain global mean.

Variability in single-subject whole-brain functional volumes was determined using the Artifact Recognition Toolbox (http://www.nitrc.org/projects/artifact_detect). Individual whole-brain BOLD fMRI volumes meeting at least one of the following two criteria were entered as regressors of no interest during the determination of task-specific effects: 1) significant mean-volume signal intensity variation (i.e., within volume mean signal greater or less than 4 standard deviations of mean signal of all volumes in time series), and 2) individual volumes where scan-to-scan movement exceeded 2 mm translation or 2° rotation in any direction. Only 1.5% of all volumes were identified as artifacts and accounted for in this manner, thus we believe this approach enhanced our capacity to determine task-specific effects by excluding effects due to volumes with substantial variability without compromising our power to detect task-specific effects by excluding a large number of volumes.

Following preprocessing, first-level condition-specific effects of feedback (i.e., reward) were estimated for each individual using linear contrasts (Positive Feedback > Negative Feedback), i.e., weighted sum of the beta images derived with the canonical hemodynamic response function. Individual contrast images were then used in second-level random effects models accounting for scan-to-scan and participant-to-participant variability to determine group mean condition-specific regional responses using one-sample t-tests. Thresholds used were p < 0.05, FWE corrected and ≥10 contiguous voxels for VS analyses and p < 0.001 (uncorrected) and ≥10 contiguous voxels for whole-brain analyses, from which parameter estimates were derived for the additional ROIs.

VS masks of interest were constructed in MNI space using the Talairach Daemon option of the WFU PickAtlas Tool, version 1.04 (Wake Forest University School of Medicine, Winston-Salem, North Carolina). Two spheres of 10 mm radius were created around MNI coordinates x = ±12, y = 12 & z = −8 (mm) to encompass the VS in the right and left hemisphere, respectively. Because of the relatively extensive raw fMRI signal loss and noise typically observed in the VS and adjacent regions, single-subject BOLD fMRI data were included in subsequent analyses, including CFA, only if there was a minimum of 90% signal coverage (i.e., presence of clear fMRI signal) in the VS masks bilaterally. For the Duke sample, this criterion resulted in 173 single-subject data sets (102 women; mean age 19.76 ± 1.28 years) with adequate coverage, and for the Pittsburgh sample in 89 data sets (51 women; mean age 44.24 ± 6.80 years). Six additional cortical regions of interest for extraction from the whole-brain analyses (i.e., ACC, ventrolateral PFC and parietal cortex; details in Table 1) were selected based on prior work on MCS reward and corticostriatal behavioral control networks (Casey and Durston, 2006; Hariri et al., 2006; McClure et al., 2004).

Table 1.

Coordinates and t-values for the maximally responsive voxel within regions of interest in the contrast of positive information on reward > negative information on reward.

Regions of Interest		Anatomical Coordinates	t
Ventral striatum	Bilateral	0, 10, −10	7.27
Parietal cortex	R	42, −42, 44	5.33
	L	−42, −46, 38	4.94
Ventrolateral PFC	R	42, 48, −6	3.64
	L	−38, 48, 2	3.82
Dorsal ACC	L	−2, 18, 46	3.97
Perigenual ACC	L	−4, 42, 4	3.63

Note: L = left; R = right. For the cortical regions of interest, the peak voxel represents the center of the 5mm sphere from which parameter estimates were extracted; t values are from whole-brain tests of activation by the reward task. Statistical thresholds used were p < 0.05, FWE corrected and ≥10 contiguous voxels for VS analyses and p < 0.001 (uncorrected) and ≥10 contiguous voxels for whole-brain analyses.

BOLD parameter estimates for CFA

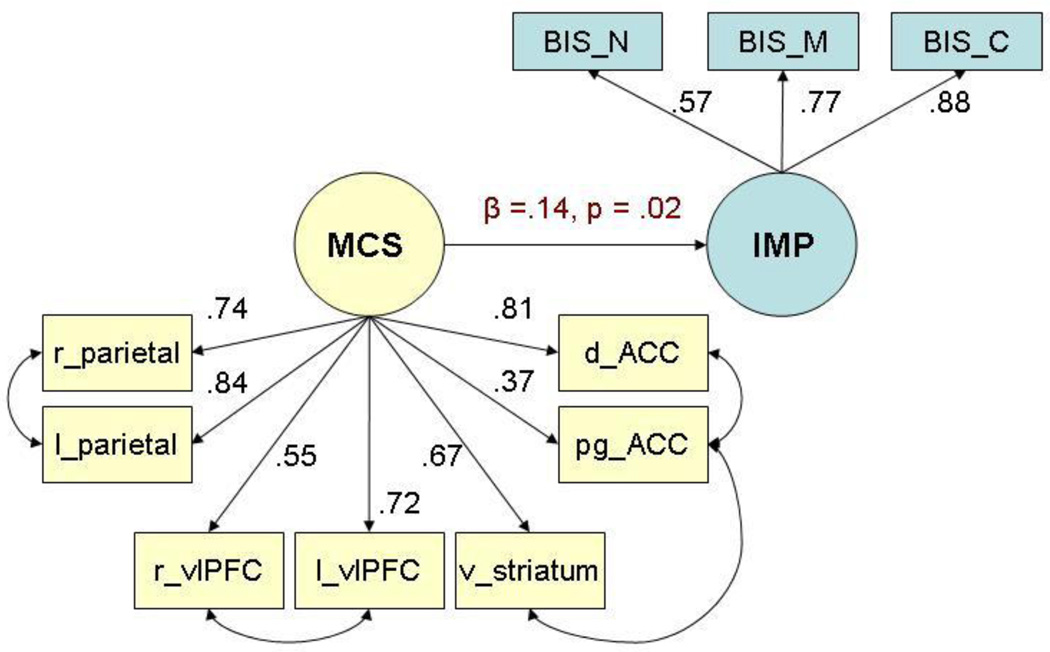
To facilitate CFA, BOLD parameter estimates from VS and cortical clusters exhibiting a main effect of task (i.e., differential effects of positive versus negative feedback as described below) were extracted using the VOI eigenvariates tool in SPM8 (www.fil.ion.ucl.ac.uk/spm/doc/manual.pdf), effectively yielding a weighted mean of contrast estimates over each region, where atypical voxels are downweighted. For the VS, these BOLD parameter estimates were extracted from the entire functional clusters within the left and right hemisphere VS ROI masks, respectively. Because of the size and contiguity of functional cortical clusters in the whole-brain analyses, parameter estimates were extracted from a 5 mm radius sphere centered on the maximally responsive voxel within each ROI (see Fig. 1 and Table 2).

Figure 1.

Task-evoked group-level activations for selected ROIs. Bilateral VS can be seen in (a), bilateral parietal cortex in (b), left vlPFC in (c), right vlPFC in (d), and dorsal and perigenual ACC in (e) (all p<0.001 uncorrected, 10 voxel extent threshold). VS activation at the p<0.05 FWE corrected, 10 voxel extent threshold used in VS analyses is shown in (f).

Table 2.

Means (standard deviations) for BOLD response eigenvariates for contrasts in condition-specific unit-less effect parameter estimates in each region of interest of the hypothesized mesocorticostriatal reward system.

	Combined Sample
Regions of Interest	Full	Males	Females	Pittsburgh	Duke
Bilateral ventral striatum	0.08 (0.22)	0.11 (0.24)	0.06 (0.22)	0.09 (0.22)	0.08 (0.22)
Right parietal cortex	0.08 (0.26)	0.12 (0.30)	0.06 (0.24)	0.11 (0.22)	0.07 (0.28)
Left parietal cortex	0.08 (0.26)	0.10 (0.28)	0.06 (0.26)	0.10 (0.22)	0.07 (0.28)
Right ventrolateral PFC	0.09 (0.39)	0.13 (0.33)	0.06 (0.42)	0.06 (0.28)	0.10 (0.44)
Left ventrolateral PFC	0.09 (0.37)	0.14 (0.37)	0.05 (0.37)	0.07 (0.26)	0.10 (0.42)
Dorsal ACC	0.09 (0.40)	0.15 (0.45)	0.06 (0.36)	0.10 (0.28)	0.09 (0.45)
Perigenual ACC	0.09 (0.42)	0.16 (0.51)	0.04 (0.35)	0.01 (0.32)	0.13 (0.47)

In addition to producing the necessary values for the identification of latent factors through CFA, extracting parameter estimates from functional clusters activated by our fMRI paradigm rather than clusters specifically correlated with our independent variables of interest, precludes the possibility of any correlation coefficient inflation that may result from capitalizing on the same data twice (Viviani, 2010). We have successfully used this more conservative and rigorous analytic strategy in recent studies (Carre et al., in press; Hyde et al., 2011).

Statistical analyses

Sex, age, and site were included as simultaneous predictors in all analyses to account for differences between the two samples. Two CFAs were first fit using Mplus 5.1 (Muthén and Muthén, 2008) to test the two hypothesized measurement models for (a) the three BIS impulsivity scores, and (b) BOLD responses during the card-guessing task in eight preselected ROIs: bilateral VS, ventrolateral PFC, parietal cortices, and the perigenual and dorsal ACC (see Table 1 for anatomical coordinates). Maximum-likelihood estimation with robust standard errors computed with a sandwich estimator (Kauermann and Carroll, 2001) was used to reduce the impact of any non-normality.

Because BOLD response in the right and left VS were correlated at r = .90, a single bilateral VS ROI (20 mm sphere centered at x = 0, y = 10, z = −10 mm) was used in these analyses to simplify the measurement model, resulting in the seven ROIs listed in Table 1. When the right and left VS were entered separately to check this decision, the results of the SEM were unchanged regarding the association between the latent MCS and impulsivity constructs, but the very high correlation between right and left VS resulted in a non-positive definite residual covariance matrix and robust standard errors could not be computed.

The association between the latent impulsivity and latent reward system constructs derived from the two separate measurement models was tested in a single SEM in the same software using robust maximum likelihood estimation. For illustrative purposes, two different tests of interactions were conducted to determine if there were statistically significant differences between the sexes and the sites (and their samples and scanners) in the association between the latent constructs that would argue that data should not be combined across sites or sexes. First, these interactions were added to the final model and tested using trapezoidal numerical integration (Chawla et al., 1996) with 15 integration points per dimension in Mplus. Second, because sex and site are binary variables, these interactions also were tested in multigroup analyses in Mplus, by constraining the factor loadings and item means to be the same across groups. The multi-group specification allows the latent model to vary between groups; a constraint can then be imposed to test whether the coefficient of latent reward in the regression of latent impulsivity can be held constant across groups.

Results

Means and standard deviations of BOLD responses in each ROI in the hypothesized MCS reward system are presented in Table 2 for the combined full sample, by sex in the full sample, and by site. Pearson partial correlations controlling sex, age, and site between the seven ROIs and the three subscales of the BIS are presented in Table 3. Although the total score of the BIS was not used in the CFAs, it is presented in Table 3 for reference.

Table 3.

Partial Pearson correlations controlling sex, age, and site between BOLD responses in each of seven regions of interest hypothesized to be part of a mesocorticostriatal reward system measured using a card-guessing reward paradigm in functional magnetic resonance imaging and three subtests of the Barrett Impulsiveness Scale, separately for 109 males and 153 females.

	Subscales and Total Score of Barratt Impulsiveness Scale
Regions of Interest	Nonplanning		Motoric		Cognitive		Total Score
	M	F	M	F	M	F	M	F
Bilateral ventral striatum	.19+	.06	.18+	.05	.29**	.01	.25*	.05
Right parietal cortex	.18+	.00	.12	.05	.13	−.09	.17+	.00
Left parietal cortex	.16	.05	.19*	.08	.19*	.00	.21*	.06
Right ventrolateral PFC	.01	.07	.05	.07	.09	−.07	.05	.04
Left ventrolateral PFC	.16+	.14+	.12	.09	.18+	.04	.17+	.12
Dorsal ACC	.17+	.07	.21*	.03	.18+	.01	.22*	.05
Perigenual ACC	.09	.06	.08	.02	.07	−.04	.10	.03

Nominal significance levels:

⁺p < .10;

^*p < .05;

^**p < .01.

Note: M = males; F = females; PFC = prefrontal cortex; ACC = anterior cingulate cortex.

Measurement model for the MCS reward system

Differential BOLD responses for the seven ROIs hypothesized to participate centrally in the MCS reward system were first subjected to CFA to construct the measurement model for the latent neuronal system. One latent neuronal network factor was hypothesized. All loadings were significant at p < 0.0001, which exceeds the adjusted alpha correcting for testing multiple factor loadings (.05 / 7 = .007).

Two widely used fit indices were used to quantify and evaluate the fit of the hypothesized measurement model for the seven ROIs to the data (Browne and Cudeck, 1993): Root mean square error of approximation (RMSEA) and standardized root mean square residual (SRMR). In the initial model, these fit indices did not indicate an acceptable fit to the data for this model: RMSEA = 0.15; SRMR = 0.07; which were both outside the conventional limits of acceptable model-to-data fit (RMSEA <0.10 and SRMR <0.05) (Browne and Cudeck, 1993). However, the modification indices for this CFA of the MCS reward system ROIs indicated that several pairs of ROIs were correlated to a greater extent than was fully explained by their contributions to the latent MCS reward system construct: right with left ventrolateral PFC, right with left parietal cortices, bilateral VS with perigenual ACC, and perigenual ACC with dorsal ACC. Because these correlations identified by the modification indices are consistent with both structural and functional data on neural reward processing, these ROIs were allowed to correlate freely in a revised CFA model. When these changes were made to the neuronal measurement model shown in Fig. 2, the fit indices were both in the traditional “close” fit ranges (Browne and Cudeck, 1993): RMSEA: 0.04 (90% CI = 0.02 – 0.06); SRMR = 0.04.

Figure 2.

Fully standardized path coefficients for best-fitting model, controlling for age, sex, and site for the full sample of females and males (N = 262). Fully standardized path coefficients can be interpreted as marginal correlations between the two variables on either side of the arrow.

To illustrate the formal method of testing alternative models defined by different numbers of latent neuronal factors in CFA, we compared this 1-factor model to a 2-factor model in which the highly correlated bilateral VS, perigenual ACC, and dorsal ACC comprised a second factor. The fit of the 2-factor model was significantly worse than the 1-factor model, χ² = 22.80, DF = 1, p < .001.

Measurement model for impulsivity

CFA of the three subtests of the impulsivity scale was conducted. All three subtests loaded significantly on the latent impulsivity construct at p < .0001, which were significant after correcting for multiple testing. A model with three manifest indicators is “just identified” with zero degrees of freedom (Reichardt, 2002) in the sense that a single latent construct is sufficient to explain all pairwise correlations among the three manifest indicators.

Association between the MCS reward system and impulsivity

As illustrated in Fig. 2, the two CFA measurement models were embedded in a single SEM to test the association between the latent MCS reward system and latent impulsivity constructs. Robust maximum-likelihood estimation of the full SEM model achieved a “close” fit of the model to the data according to both fit indices: RMSEA = .043 (95% confidence interval 0.022 – 0.062); SRMR = 0.044. The path between the latent neuronal construct and the latent construct for impulsivity revealed a significant positive association, fully standardized β = 0.145, p = 0 .021.

Comparison of CFA/SEM to univariate tests and other methods of combining ROIs

To illustrate the advantages of using such CFA/SEM models over individual tests of associations, seven individual tests of associations were conducted between BOLD responses in each of the ROIs and in the hypothesized MCS reward system and impulsivity. To make these “univariate” tests parallel to the full CFA/SEM shown in Figure 1, they were conducted in SEM using the same latent impulsivity construct defined by three subtests of the Barrett Impulsiveness Scale, controlling sex, age, and site. As reported in Table 4, two of the univariate associations were nominally significant at .05, but none was significant after Bonferroni correction for multiple testing (α = .05/7 = .007) or the less conservative Holm step-down method. This contrasts with the significant association between the latent MCS and latent impulsivity constructs shown in Figure 1, which does not require Bonferroni correction because only one test of the association between the MCL and impulsivity latent constructs was conducted.

Table 4.

Fully standardized associations between BOLD responses in each of the seven regions of interest in the hypothesized mesocorticostriatal reward system and a latent impulsivity construct defined by three subtests of the Barrett Impulsiveness Scale, tested individually in separate structural equation models, adjusting for sex, age, and site.

Regions of Interest	β	Nominal p =
Bilateral ventral striatum	0.14	0.02
Right parietal cortex	0.05	0.39
Left parietal cortex	0.11	0.06
Right ventrolateral PFC	0.02	0.72
Left ventrolateral PFC	0.07	0.12
Dorsal ACC	0.57	0.03
Perigenual ACC	0.04	0.49

Note: PFC = prefrontal cortex; ACC = anterior cingulate cortex; N = 109 males and 153 females; none of the seven tests of associations were significant after correcting for multiple testing at p = .05/7 = .007.

We also compared the results of the CFA/SEM to two common ways of capturing the variance in all 7 ROIs at the same time to demonstrate that they yield similar results: taking the simple mean of the 7 measured ROIs and taking the first eigenvariate of all 7 regions treated as a single ROI. The latent construct for impulsivity was regressed on each of these in separate SEMs with the usual covariates. The mean of the 7 mean ROIs just failed to exhibit a significant association with latent impulsivity, β = 0.11, p = 0.054. This is likely because this does not generate a latent component score. The first eigenvariate of the combined ROIs, which is a type of principal component, was associated with latent impulsivity to the same extent as the latent neural construct from the CFA measurement model, β = 0.14, p = 0.02.

Moderation of associations in CFA/SEM

To illustrate two methods of testing of moderators of the observed brain-behavior relations in this modeling approach, additional models were fit to test for moderation by data collection sites, and separately, by the sex of the participant. When the interaction was directly tested, there was not a significant interaction with site (unstandardized β = −0.72, p = 0.69). Similarly, the multiple-groups test of this interaction was not significant, χ² = 0.02, p = 0.89, indicating lack of evidence that data from the two sites should not be combined.

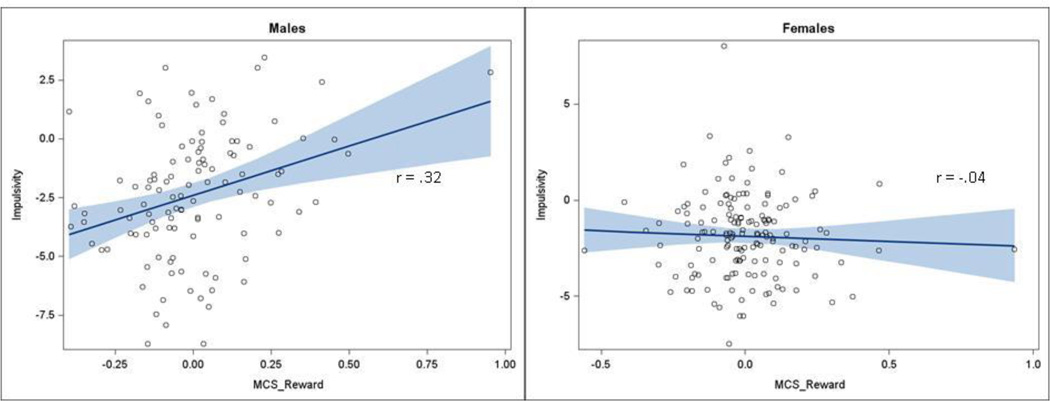
In contrast, the direct test of the interaction with sex was significant (unstandardized β = −3.01, p < 0.05). Similarly, the multiple-groups test of this interaction achieved borderline significance, χ² = 3.65, p = 0.056, suggesting that there may be stronger association between the latent construct reflecting contemporaneous activation of the ROIs in the MCS reward network and impulsivity in males than females. When the SEM was specified separately for the 109 males (RMSEA = 0.05; 90% CI: 0.00 – 0.08; SRMR = 0.05), the MCS reward network was positively associated with impulsivity (fully standardized β = 0.26, p < .005). In contrast, among the 153 females (RMSEA = 0.05; 90% CI: 0.02 – 0.08; SRMR = 0.06), the association was slightly negative and not statistically significant (fully standardized β = −0.01, p = 0.86). As shown in Fig. 3, these associations between the latent MSC reward network and impulsivity constructs correspond to Pearson correlations of r (109) = 0.32, p < 0.001 for males and r (153) = −0.04, p = 0.60 for females.

Figure 3.

Scatter plots and best-fit linear regression lines with 95% confidence intervals for the association between the estimated latent MCS reward network and impulsivity constructs among males (n = 109) and females (n = 153).

Robustness of CFA model to variations in preprocessing and model misspecifications

Three series of analyses were conducted to provide illustrative tests of the robustness of the CFA measurement model in the present SEM.

Variations in preprocessing

Table 5 presents the results of a comparison of the results of the primary CFA/SEM analysis shown in Figure 1 to those of analyses based on ROI values derived with more lenient thresholds and larger spheres. Across three variations in preprocessing, the loadings of the ROIs on the latent MCS reward factor changed very little and the results of the SEM regression analysis relating the latent MCS reward factor to the latent impulsivity factors were essentially unchanged.

Table 5.

Comparison of the results of the primary CFA/SEM analysis to those of sensitivity analyses based on values derived with more lenient thresholds and larger spheres.

	Primary Analyses			Sensitivity Analyses
	20 mm bilateral VS 849 voxels; 5 mm others			30 mm bilateral VS 858 voxels; 10 mm others			30 mm bilateral VS 1651 voxels; 10 mm others			30 mm bilateral VS/ 4438 voxels; 10 mm others
Loadings on Latent MCS Reward Factor
Dorsal ACC	0.809			0.856			0.864			0.877
Perigenual ACC	0.369			0.475			0.482			0.499
Bilateral VS	0.668			0.713			0.746			0.785
Left ventrolateral PFC	0.724			0.751			0.747			0.738
Right ventrolateral PFC	0.546			0.629			0.627			0.622
Left parietal	0.836			0.883			0.877			0.869
Right parietal	0.738			0.815			0.809			0.797
Regression of Latent Impulsivity on Latent MCS Reward
	Regression Coefficient	S.E.	p =	Regression Coefficient	S.E.	p =	Regression Coefficient	S.E.	p =	Regression Coefficient	S.E.	p =
	0.145	0.063	0.021	0.132	0.060	0.029	0.130	0.060	0.031	0.123	0.060	0.040

Note: Primary analyses are those reported in Figure 1; values for the three sensitivity analyses were based on a threshold of p < 0.05, uncorrected (0 voxel extent threshold) and a 10 mm sphere for the cortical ROIs; for the bilateral VS ROI, we varied the thresholds from p < 0.05 FWE corrected (10 voxel extent) to p<0.001 uncorrected (0 voxel extent) to p<0.05 uncorrected (0 voxel extent) and a 30 mm sphere to obtain the indicated cluster sizes of 858, 1651 and 4438 voxels respectively; there were no variations in the loadings of the three impulsivity subscales on the latent impulsivity factor in the sensitivity analyses.

Omission of ROIs central to the latent construct

Series A in Table 6 presents the results of analyses that test the robustness of the CFA model in the present data when omitting one ROI central to the construct at a time. Because the latent construct is defined by the contributions of multiple ROIs, it is not surprising that the results do not change appreciably at the level of both factor loadings and SEM regression coefficients when one ROI is omitted.

Table 6.

Results of two series of analyses to test the robustness of CFA when (a) each of the hypothesized ROIs is omitted one at a time, and (b) when ROIs not hypothesized to be centrally related to the MCS reward system are included in the models.

A. Series Omitting One ROI Hypothesized to be Related to the MCS Reward System at a Time
Loadings on Latent MCS Reward Factor
Dorsal ACC	-	0.813	0.778	0.836	0.808	0.845	0.799
Perigenual ACC	0.329	-	0.335	0.370	0.365	0.432	0.352
Bilateral VS	0.628	0.669	-	0.683	0.668	0.666	0.681
Left ventrolateral PFC	0.739	0.730	0.732	-	0.724	0.695	0.720
Right ventrolateral PFC	0.545	0.554	0.553	0.541	-	0.554	0.526
Left parietal	0.865	0.824	0.850	0.800	0.839	-	0.839
Right parietal	0.734	0.742	0.779	0.722	0.733	0.736	-
Regression of Latent Impulsivity on Latent MCS Reward
	Regression Coefficient (S.E.)	Regression Coefficient (S.E.)	Regression Coefficient (S.E.)	Regression Coefficient (S.E.)	Regression Coefficient (S.E.)	Regression Coefficient (S.E.)	Regression Coefficient (S.E.)
	0.136 (0.066)	0.142 (0.064)	0.127 (0.065)	0.141 (0.062)	0.149 (0.062)	0.142 (0.063)	0.156 (0.064)

B. Series Adding Three ROIs (5mm Spheres, p < 1 uncorrected) Not Hypothesized to be Related to the MCS Reward System ROI One at a Time
	Occipital cortex	Retrosplenial cortex	Angular gyrus	Posterior Inferior Temporal Gyrus
	−8 −86 18	−6 −56 18	−48 −64 20	48, −62, −6
Loadings on Latent MCS Reward Factor
Dorsal ACC	0.812	0.821	0.808	0.809
Perigenual ACC	0.393	0.411	0.396	0.421
Bilateral VS	0.686	0.703	0.683	0.695
Left ventrolateral PFC	0.724	0.717	0.726	0.706
Right ventrolateral PFC	0.539	0.538	0.541	0.535
Left parietal	0.830	0.816	0.834	0.831
Right parietal	0.725	0.710	0.731	0.752
Extra-network ROI	[0.394]	[0.411]	[0.436]	[0.733]
Regression of Latent Impulsivity on Latent MCS Reward
	Regression Coefficient (S.E.)	Regression Coefficient (S.E.)	Regression Coefficient (S.E.)
	0.141 (0.063)	0.141 (0.063)	0.139 (0.063)

Note: All loadings and regression coefficients are fully standardized; In series A, all regression coefficients for latent impulsivity on latent MCS reward were significant at p = 0.014 –0.050; in series B, all regression coefficients were significant at p = 0.025 – 0.027; in series B, the loadings for the ROIs not hypothesized to be related to the MCS reward system are in brackets.

Inclusion of ROIs not central to the latent construct

The first three columns in Series B in Table 6 show the results for the CFA measurement model for the neuronal reward network and the SEM regression of the latent reward construct on the latent impulsivity construct when three ROIs not hypothesized to participate in the MCS reward network were added one at a time to CFA neuronal measurement model. The loadings for these additional ROIs were each significant in this large sample at p < .0001. Nonetheless, the loadings were modest, with the latent MCS reward construct explaining only 15.5–19.0% of the variance in each added ROI. Because each manifest variable only contributes to a latent construct in CFA only to the extent of its factor loading, the addition of these extra-network ROIs had minimal effects on factor loadings of the other ROIs and no appreciable effect on the association between the two latent constructs. Adding ROIs with near zero factor loadings would have had essentially no effect.

It is essential to note that the significant loadings of the extra-network ROIs are not an artifact of CFA. Rather, they reflect the fact that the raw Pearson correlations of these ROIs with the 7 ROIs hypothesized to comprise the MCS reward network were themselves all small but significant: angular gyrus (range = 0.17 – 0.44; median = 0.34; all p < .005), occipital lobe (range = 0. 12 – 0.44; median = 0.31; all p < .05), and retrosplenial cortex (range = 0.13 – 0.57, median = 0.28).

In addition, an ROI in the ventral stream of the visual system (posterior inferior temporal gyrus) was added to the model (last column of Series B in Table 6) that was not hypothesized to be part of the MCS reward network, but is known to be activated by visual reward cues (Buckholtz et al., 2010; Gaffan et al., 1988; Krawczyk et al., 2007). The loading of this ROI on the latent MCS reward construct was considerable. Because of its high correlation with the hypothesized ROIs, however, its addition did not appreciably change the factor loadings for the hypothesized ROIs or the association between the latent MCS reward system and latent impulsivity factors. Thus, had a more distributed reward system network including the posterior inferior temporal gyrus been hypothesized, the results of the model would not have changed appreciably. As long as the central ROIs are included in the CFA, adding additional ROIs that do or do not participate in the hypothesized network will have little effect, with the degree of their participation in the network clearly indicated by their factor loadings.

Discussion

We described the use of CFA measurement models in SEM to conduct formal statistical tests of hypotheses regarding the contemporaneous activation of pre-selected ROIs measured in fMRI stimulation paradigms when those ROIs are believed to be part of coherent neuronal networks engaged by the stimulation task. In this strategy, the contemporaneous activation of each ROI is conceived as a fallible manifest indicator of the latent neuronal network.

The use of CFA in hypothesis-driven fMRI research on neuronal networks offers numerous advantages. CFA is a fully developed and evaluated statistical approach that can readily be used to evaluate the extent to each pre-selected ROIs participates in a hypothesized neuronal network. CFA models error variance separately and yields a quantification of the activation of the network as a whole that is measured with less error than each of the ROIs that define the network, providing improved statistical power. Furthermore, using CFA in neuroimaging provides a hypothesis-driven method for data reduction. As with exploratory multivariate methods based on PCA, measurements of multiple ROIs can be reduced to a small number of constructs with clear empirical and statistical meaning, thus improving power by reducing the number of statistical comparisons. CFA differs from other multivariate methods that are also useful in data reduction, however, both in the way in which error is modeled and because CFA can easily be used to conduct formal tests of a priori hypotheses.

Future studies should evaluate the power advantages inherent in data reduction using CFA versus analyses of individual ROIs and should directly compare the results of PCA-based methods and CFA using simulated data sets. In addition, simulations could be used to evaluate the effects of variations in pre-processing methods and the inclusion of incorrectly specified ROIs.

Illustration of CFA

We provided a substantive illustration of the use of CFA with multiple manifest indicators of a hypothesized MCS reward system assessed in fMRI during a reward-based stimulation task and multiple manifest indicators of the behavioral trait of impulsivity. In the first step of the analyses, we evaluated a measurement model for the hypothesized MCS reward system. Initially, the fit was fair but not in the range generally regarded as acceptable. The modification indices for this CFA indicated that several biologically plausible changes to the measurement model would improve the fit of the MCS measurement model to the data. These indices indicated that several pairs of ROIs should be allowed to correlate independent of their correlations through the latent construct. These changes resulted in fit indices in the “close” fit range. Although these modifications of the model were reasonable and justified, the use of modification indices means that the results of the analyses generate a hypothesis that can be tested in future studies, but do not constitute a test of a fully a priori hypothesis. Because adjustments to the measurement model for the MCS do not bias the test of association with the latent reward construct, however, these results yield a hypothesis that is plausible and consistent with the present data.

As shown in Fig. 2, every ROI loaded significantly on the latent MCS reward circuit construct, although there were highly informative variations in the magnitudes of these loadings. Note that the loading of the perigenual ACC on the latent MCS reward system construct was markedly lower than for the other ROIs. In this case, the latent MCS construct accounted for only .369² = 13.6% of the variance in BOLD response of the perigenual ACC. In contrast, the latent MCS construct accounted for 29.8–66.9% of the variance in the other ROIs. Although activation of the perigenual ACC in this task was significantly correlated with activation of the other ROIs, the modest amount of explained variance suggests that the perigenual ACC does not centrally participate in this network. Rather its modest factor loading may reflect either widespread nonspecific brain activation in response to reward cues or participation in another network modestly related to reward processing.

It is important to note, however, that inclusion of the perigenual ACC in the latent MCS reward construct as hypothesized has little impact on either the measurement model or the association between the latent reward system and impulsivity constructs. This is because data from the perigenual ACC play a role in the CFA/SEM only to the extent of the loading of this ROI on the neuronal construct (i.e., its covariance with the other ROIs). This issue is addressed again below when the robustness of the CFA model is addressed.

The CFA measurement model for the MCS reward system and the CFA measurement model for impulsivity were combined in a single SEM to test the association between the latent MCS reward system and latent impulsivity constructs. As hypothesized, variations in the latent MCS neuronal reward system construct were found to be positively correlated with variations in the impulsivity construct, and tests of the interaction with sex indicated that the association of the MCS reward system with impulsivity may be significantly stronger in males. As shown in Fig. 2, variation in the latent MCS construct scores accounted for an estimated 10.2% of the variance in latent impulsivity in males.

Tests of robustness of the CFA model

We conducted three series of illustrative tests of the robustness of the CFA measurement model in these data to procedural variations in preprocessing and two kinds of model misspecification (i.e., excluding an ROI that is central to the network or including an ROI that is not strongly related to the network). When the results of these analyses reported in Tables 5 and 6 are considered together, it is clear that the specified CFA/SEM was robust to each of these variations. When the most important ROIs that define a neuronal latent construct are included, the omission of a small proportion of the ROIs often will not change the latent construct enough to influence findings. Similarly, because of the way in which it is constructed, CFA is highly robust to the inclusion of additional indicators regardless of the magnitudes of their factor loadings. Additional ROIs that are highly correlated with the hypothesized manifest indicators will not change the model because, due to their high correlations, they provide an additional information on the construct. Conversely, the addition of manifest indicators with low correlations with other manifest indicators will contribute little to the latent construct. This is reflected in their modest factor loadings. As long many of the ROIs that centrally participate in the neuronal network are in the model, CFA is highly robust to such misspecifications.

Interpretation of CFA in terms of neuronal networks

When multivariate methods such as PCA yield a latent component on which all ROIs substantially load, and when CFA yields a latent factor on which the loadings of all ROIs are statistically significant, it is tempting to interpret such findings as evidence that all ROIs participate in the same contemporaneously activated neuronal circuit. In this context, the findings reported in the first three columns of Series B of Table 6 have importance. As the functional neuroimaging field moves away from studies of single ROIs in small samples to the measurement of multiple ROIs in large samples, it will become necessary to confront the meaning of small but statistically significant correlations between extra-network ROIs and ROIs hypothesized to participate centrally in these networks. It will be important to determine if these modest correlations reflect only correlated measurement and processing artifacts, or if they reveal something approaching “whole-brain” responses to stimulation paradigms that involve many distributed nodes to varying degrees. Indeed, robust correlations between a set of ROIs may reflect individual differences in BOLD responses throughout the brain that give the impression that the specified ROIs are correlated when, in a broad sense, all ROIs would be correlated in this scenario. It will only be possible to determine the relative association of each ROI network to the hypothesized network by comparing their loadings to other ROIs thought not to be part of the network. Although statistical methods have been developed for studying some key properties of the brain as a whole (Rubinov and Sporns, 2011), variations in factor loadings in CFA provide a convenient way of addressing this phenomenon when relatively small numbers of ROIs are studied by focusing on relative magnitudes of factor loadings of ROIs.