Dynamic Margins of Stability During Human Walking in Destabilizing Environments

Abstract

Understanding how humans maintain stability when walking, particularly when exposed to perturbations, is key to preventing falls. Here, we quantified how imposing continuous, pseudorandom anterior-posterior (AP) and mediolateral (ML) oscillations affected the control of dynamic walking stability. Twelve subjects completed five 3-minute walking trials in the Computer Assisted Rehabilitation ENvironment (CAREN) system under each of 5 conditions: no perturbation (NOP), AP platform (APP) or visual (APV) or ML platform (MLP) or visual (MLV) oscillations. We computed AP and ML margins of stability (MOS) for each trial. Mean MOS_ml were consistently slightly larger than NOP during all perturbation conditions (p ≤ 0.038). Mean MOS_ap for the APP, MLP and MLV oscillations were significantly smaller than during NOP (p < 0.0005). Variability of both MOS_ap and MOS_ml was significantly greater during the MLP and MLV oscillations than during NOP (p < 0.0005). We also directly quantified how the MOS on any given step affected the MOS on the following step using first-return plots. There were significant changes in step-to-step MOS_ml dynamics between experimental conditions (p < 0.0005). These changes suggested that subjects may have been trying to control foot placement, and consequently stability, during the perturbation conditions. Quantifying step-to-step changes in margins of dynamic stability may be more useful than mean MOS in assessing how individuals control walking stability.

INTRODUCTION

Understanding how humans maintain and control stability when walking, particularly when being exposed to perturbations or irregular terrain, is key to preventing falls and predicting likelihood of falling. Quantifying walking stability in a computationally and physiologically correct manner and effectively identifying individuals with “unstable” gait has proven to be major challenge for the field. This is further complicated by the inherent risks of actually making people fall, particularly individuals who are already physically limited.

Standing stability is generally defined in static terms, based on the relationship between a person’s center of mass (COM) and their base of support (BOS). As long as the projection of the COM remains within the horizontal bounds of the BOS, one remains stable. This definition cannot, however, be properly applied to walking, or even standing, as it does not take into account the horizontal velocity of the COM (Pai and Patton, 1997). To address this limitation, Hof et al. (2005) proposed a new measure referred to as the ‘margin of stability’ (MOS) which can more appropriately be applied to dynamic tasks like walking. The margin of stability (MOS) is defined as the distance between a velocity adjusted or ‘extrapolated’ position of the COM (XcoM) and the edge of an individual’s BOS at any given instant in time. The MOS is directly related to the impulse (I) required to cause instability (Hof et al., 2005).

This definition of stability suggests that foot placement could be used to control MOS magnitude during walking (Hof, 2008). Thus, one potential goal of walking may be to maintain some minimum MOS. Rosenblatt and Grabiner (2010) showed that average lateral MOS did not change significantly between overground and treadmill walking in healthy subjects, although step width did. This supports the idea that foot placement during walking could be chosen to achieve a constant lateral MOS. Similarly, MacLellan and Patla (2006a; 2006b) found no difference in average MOS in the mediolateral (ML) direction on rigid versus compliant surfaces. However, they did find a difference in the average anterior-posterior (AP) MOS. Maintenance of average lateral MOS was also observed in amputees walking on irregular surfaces (Curtze et al., 2010). These results suggest that individuals may use foot placement to control lateral stability during walking and that this control is independent of walking surface. However, these studies quantified only average MOS. Mean MOS cannot indicate how an individual recovered from any single step because it only quantifies an individual’s overall, average stability over an entire series of steps. Quantifying step-to-step fluctuations likely could reveal more about the step-to-step control of stability (Hausdorff et al., 1995; Gates et al., 2007; Dingwell and Cusumano, 2010; Dingwell et al., 2010) than means or standard deviations alone.

By applying continuous, small magnitude perturbations, we examined how humans control stability when walking while constantly experiencing perturbations. Similar perturbations were applied physically using oscillating platforms (Brady et al., 2009; McAndrew et al., 2010; McAndrew et al., 2011) and/or visually using scene changes in virtual environments (Warren et al., 1996; O’Connor and Kuo, 2009; McAndrew et al., 2010; McAndrew et al., 2011). Except for McAndrew et al. (2011), who examined nonlinear measures of dynamic stability, these studies primarily quantified how these externally imposed oscillations affected movement variability and/or changes in stepping characteristics. How COM movements during walking are maintained and controlled when people are subjected to continuous physical or visual perturbations has yet to be determined. Perturbations that constantly challenge an individual’s stability at every point in the gait cycle may be more relevant to dynamic, real world settings than typical un-perturbed gait analyses.

This study determined how COM margins of stability (MOS) were affected when humans were exposed to continuous, pseudorandom perturbations. We quantified means and standard deviations of MOS, but also quantified step-to-step MOS dynamics. We hypothesized that during perturbations, participants would exhibit decreased MOS in the direction of the perturbation being applied and greater MOS variability while undergoing perturbations than during unperturbed walking. We also hypothesized that step-to-step changes in MOS would reflect on-going control adaptations that cannot be quantified by calculating means or standard deviations.

METHODS

A complete description of the experimental setup is given in McAndrew et al. (2010). All participants provided written informed consent and the study was approved by the Institutional Review Board at Brooke Army Medical Center (Ft. Sam Houston, TX).

Briefly, we collected data on 12 healthy, young adult participants walking in a Computer Assisted Rehabilitation ENvironment (CAREN) system (Motek, Amsterdam, The Netherlands). The CAREN system consists of a 7-m diameter dome with a virtual scene projected to 300° field of view and, in the bottom of the dome, a platform with a treadmill embedded in it. The platform can move with six-degrees of freedom, though only horizontal oscillations were used in the present study. The virtual scene was of a dirt path with trees and mountains in the background. White poles lined the path to enhance visual parallax (Bardy et al., 1996; McAndrew et al., 2010).

Each participant completed 5 3-minute walking trials in the CAREN system for each of the following perturbation conditions: no perturbation (NOP), anterior-posterior platform (APP) or visual (APV) oscillations or mediolateral platform (MLP) or visual (MLV) oscillations. Oscillations were applied as a pseudo-random sum of sines with 4 incommensurate frequencies (0.16, 0.21, 0.24 and 0.49 Hz) using the following equation:

$$D(t)=A·[1.0·sin(0.16·2\pi t)+0.8·sin(0.21·2\pi t)+\dots +1.4·sin(0.24·2\pi t)+0.5·sin(0.49·2\pi t)]$$ (1)

where D(t) was the translation distance [m], A was a scaling factor and t was time [sec]. The visual and platform oscillations were scaled with A = 0.05 and A = 0.50, respectively. During platform oscillations, the platform oscillated horizontally in the AP or ML directions (APP and MLP, respectively). During the AP visual oscillations, the visual scene appeared to move forward and backwards with net progression down the virtual path. During the ML visual oscillations, the visual scene moved left-to-right around a vertical axis centered on the horizon at the end of the virtual path. Net progression through the virtual environment was matched to the speed of the treadmill during all perturbation conditions. Subjects were given ~2 minutes to “adapt” to each condition before data collection began. However, because these oscillations were pseudo-random, subjects never completely “adapted” to these unpredictable signals, which was the desired effect.

Kinematic data were collected using a 24-camera Vicon motion capture system (Oxford Metrics, Oxford, UK) at 60 Hz. Participants wore 22 reflective markers. Four markers each were placed on the head, pelvis and on each foot. Markers were also placed over the acromium processes, C7 and T8 vertebrae, sternum and xyphoid process. Not all markers were used for the present analyses. Gaps in motion data were filled using a linear interpolation of data from a marker on the same rigid body segment.

Center of mass (COM) position was estimated as the average position of the 4 pelvis markers (right and left anterior and posterior superior iliac spine), similar to Whittle (1997). COM velocity was found by computing the first derivative of the COM position.

Dynamic margins of stability were adapted from Hof et al. (2005). Extrapolated center of mass (XcoM) was calculated as:

$$\mathit{XcoM}=x+\frac{\stackrel{.}{x}}{{\omega }_0}$$ (2)

where x was the COM position, ẋ was the COM velocity and

$${\omega }_0=\sqrt{\frac{g}{l}}$$ (3)

where g = 9.81 m/s² was the gravitational constant and l was the equivalent pendulum length, which in this study was taken as the mean distance from the lateral heel marker to the COM at heelstrike. The dynamic margin of stability (MOS) was then defined as:

$$\mathit{MOS}=\mathit{XcoM}-\mathit{BOS}$$ (4)

where BOS was the boundary of the base of support. Anterior-posterior margins of stability (MOS_ap) were calculated as the AP distance between the XcoM and the toe marker of the leading foot (i.e. the most anterior edge of the BOS; Fig. 1A). Mediolateral margins of stability (MOS_ml) were calculated as the lateral distance between the XcoM and the lateral heel marker of the leading foot (i.e., the foot undergoing loading response; Fig. 1A). MOS was calculated at heelstrike for every step for each trial (~350 steps per 3-minute trial). Heel strike was identified as the local minima of the vertical component of the C7 marker position (Dingwell and Marin, 2006; Dingwell et al., 2007). MOS variability was calculated as the standard deviation of all MOS for a given trial. All processing and analysis was performed using Matlab R2009b (The Mathworks, Inc).

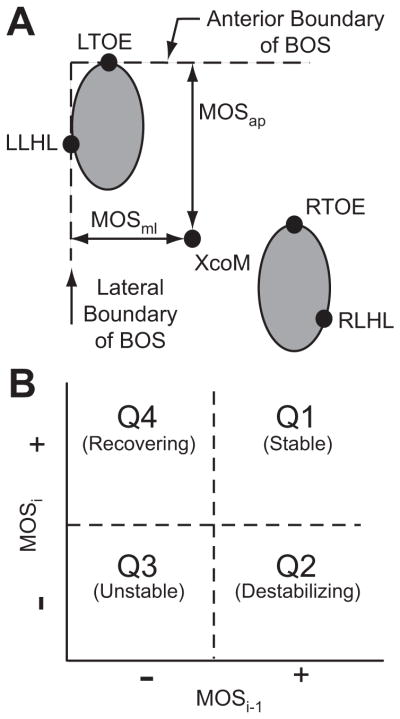
Figure 1.

A) MOS_ap was defined as the distance between the anterior boundary of the BOS, defined by the leading toe marker (either LTOE or RTOE for the left and right foot, respectively) and the XcoM. MOS_ml was defined as the distance between the lateral boundary of the BOS and the XcoM. The lateral boundary of the BOS was defined by the lateral heel marker (LLHL and RLHL for the left and right foot, respectively) of the lead foot. Here, the left foot is shown leading. B) Quadrants of the MOS_i vs. MOS_i-1 plane (i.e., first-return map) were defined to compare step-to-step changes in MOS. Points in Q1 indicate stable steps followed by stable steps. Points in Q2 indicate stable steps followed by unstable steps. Points in Q3 indicate unstable steps followed by unstable steps. Points in Q4 indicate unstable steps followed by stable steps.

To examine step-to-step adaptations, we plotted the distribution of points on first-return plots (Strogatz, 1994; Seyfarth et al., 2002; Geyer et al., 2005) of MOS (i.e. MOS_i versus MOS_i-1; Fig. 1B). Initial steps (MOS_i-1) with positive MOS (i.e., “stable”) followed by steps (MOS_i) with positive MOS were plotted in quadrant Q1. Stable steps (positive MOS_i-1) followed by “unstable” steps with negative MOS_i were plotted in quadrant Q2. Unstable steps (negative MOS_i-1) followed by unstable steps (negative MOS_i) were plotted in quadrant Q3. Most importantly, unstable steps (negative MOS_i-1) that were immediately followed by stable steps (positive MOS_i) were plotted in quadrant Q4. These quadrant Q4 data points indicated control and/or recovery from a potentially unstable step.

Two-factor analyses of variance (ANOVAs) (Condition × Subject) were used to assess statistical significance of differences in mean MOS and MOS variability relative to NOP. Three-factor ANOVAs (Condition × Subject × Foot) were used to assess differences between MOS on the right and left sides of the body. Two-factor ANOVAs were used to assess differences between quadrants (Condition × Quadrant) of the first-return maps (Fig. 1B). All statistical analyses were conducted using PASW Statistics 18 (SPSS, Inc., Chicago, IL) or Minitab 15 (Minitab, Inc., State College, PA).

RESULTS

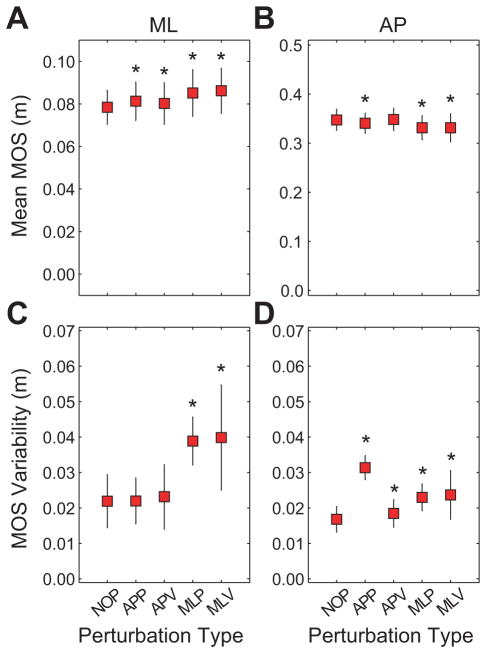
Mean MOS_ml was significantly larger than NOP during all perturbation conditions (p ≤ 0.038; Fig. 2A). However, mean MOS_ap for the APP, MLP and MLV conditions were significantly smaller than NOP (p < 0.0005; Fig. 2B). MOS_ml variability was greater during the MLP and MLV conditions (p < 0.0005; Fig. 2C). MOS_ap variability was greater during all experimental conditions (p ≤ 0.012; Fig. 2D). There were significant Condition × Subject interactions for both MOS_ap and MOS_ml and for both MOS_ml and MOS_ap variability (p < 0.0005).

Figure 2.

A) Mean MOS in the mediolateral (ML) direction. B) Mean MOS in the anterior-posterior (AP) direction. C) Variability of ML MOS. D) Variability of AP MOS. Error bars indicate between-subject standard deviations. * indicate significant (p < 0.05) differences from NOP.

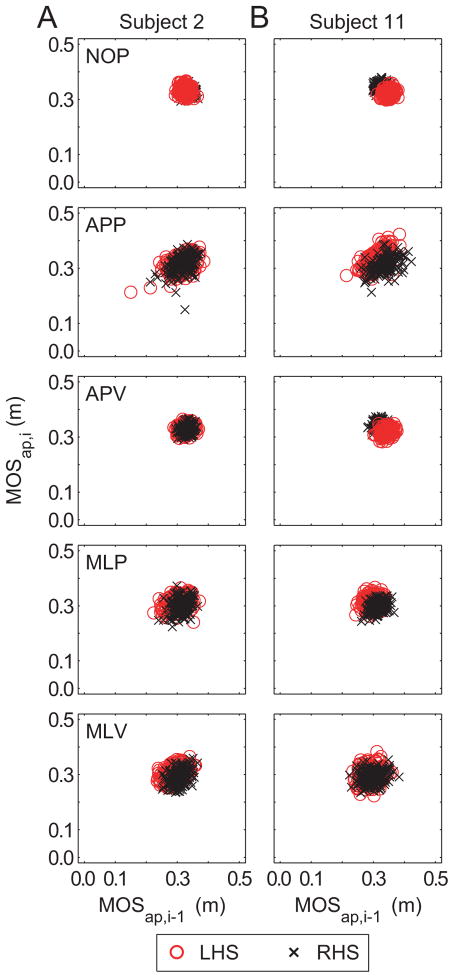
In the MOS_ap first-return plots, nearly 100% of the data points appeared in Q1 (Table 1; Fig. 3). Increased MOS_ap variability (Fig. 2D) was reflected in less tightly clustered data points for the experimental conditions, particularly MLV (Table 1; Fig. 3). The MLV condition caused a slight increase in MOS_ap Q4 population. There were no significant Condition × Quadrant effects for MOS_ap (p = 0.187).

Table 1.

Summary of percentage of data points in each quadrant of the MOS_i vs. MOS_i-1 plots (see Fig. 1B) for all subjects.

Quadrant	Condition	NOP	APP	APV	MLP	MLV
MOSap	Q1	100±0.0	100±0.0	100±0.0	100±0.0	99.99±0.08
	Q2	0.0±0.0	0.0±0.0	0.0±0.0	0.0±0.0	0.005±0.038
	Q3	0.0±0.0	0.0±0.0	0.0±0.0	0.0±0.0	0.0±0.0
	Q4	0.0±0.0	0.0±0.0	0.0±0.0	0.0±0.0	0.005±0.038
MOSml	Q1	100±0.0	99.99±0.08	98.45±11.97	97.34±2.97	96.06±6.98
	Q2	0.0±0.0	0.005±0.040	0.770±5.968	1.34±1.49	1.964±3.463
	Q3	0.0±0.0	0.0±0.0	0.0±0.0	0.005±0.036	0.016±0.071
	Q4	0.0±0.0	0.005±0.040	0.775±6.006	1.322±1.468	1.963±3.478

Figure 3.

First-return plots for AP MOS showing MOS_ap,i for step i versus MOS_{ap,i- 1} for the previous step, i-1. Columns (A) and (B) show data from 2 representative subjects. Red ‘o’ indicate MOS_ap,i-1 was at left heelstrike (LHS). Black ‘x’ indicate MOS_ap,i-1 was at right heelstrike (RHS).

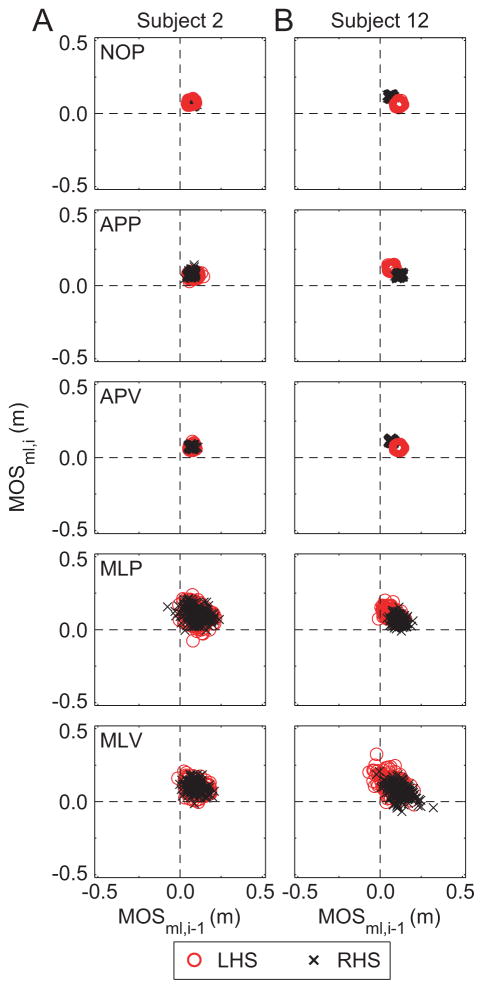
Similarly, the MOS_ml first-return plots had 96 – 100% of the data points in Q1 (Table 1; Fig. 4). Again, cluster tightness decreased for the MLP and MLV conditions, and resulted in Q2 and Q4 population increases, more so than the APP or APV conditions (Table 1; Fig. 4). There were significant Condition × Quadrant effects for MOS_ml (p < 0.0005).

Figure 4.

First-return plots for ML MOS showing MOS_ml,i for step i versus MOS_ml,i-1 for the previous step, i-1. Columns (A) and (B) show data from 2 representative subjects who exhibited different stepping responses to the perturbations. Red ‘o’ indicate MOS_ml,i-1 was at left heelstrike (LHS). Black ‘x’ indicate MOS_ml,i-1 was at right heelstrike (RHS). Note that Subject 12 (B) is more asymmetrical than Subject 2 (A), but is not more unstable.

There were significant differences between right and left feet (Table 2 and Fig. 5A) for MOS_ml (p < 0.001). Subjects exhibited larger MOS_ml values at right heelstrike than at left heelstrike for all conditions. The Condition × Foot interaction was not significant (p = 0.204). Subjects also tended to exhibit slightly larger MOS_ap values at right heelstrike than at left heelstrike for all conditions (Table 2 and Fig. 5B). However this difference did not reach statistical significance (p = 0.162) and the Condition × Foot interaction was also not significant (p = 0.828).

Table 2.

Summary of right and left MOSap and MOSml [mm] for all subjects.

Foot	Condition	NOP	APP	APV	MLP	MLV
MOSap	L	343.4±28.4	337.4±37.4	344.4±29.7	326.9±34.2	325.7±39.3
	R	350.6±25.0	342.8±37.0	351.1±28.0	334.7±32.0	333.9±37.2
MOSml	L	59.6±14.1	63.5±15.0	60.3±17.3	67.0±35.8	67.4±40.7
	R	97.1±16.6	99.2±18.2	100.3±17.4	103.7±37.3	105.2±39.8

Figure 5.

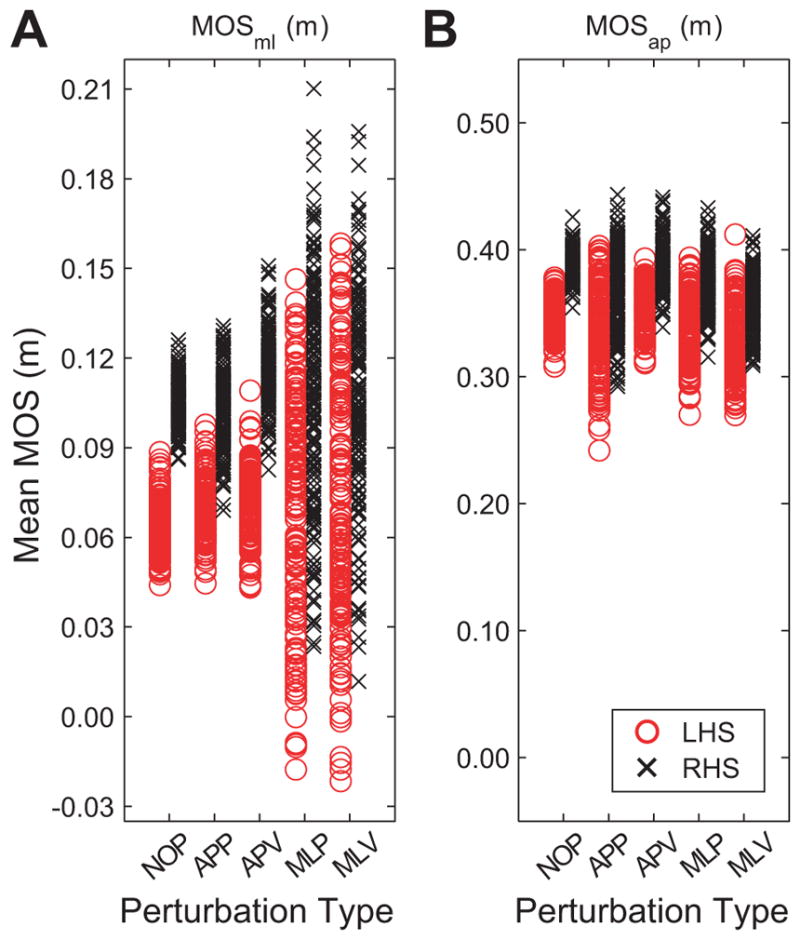
A) MOS_ml by right and left foot for all test conditions for a typical subject (Subject 6). B) MOS_ap by right and left foot for all test conditions for the same subject as in (A). LHS indicates MOS at left heelstrike. RHS indicates MOS at right heelstrike. This subject clearly shows the strong medilateral right-left asymmetry, where right steps were associated with greater lateral stability (A). A less pronounced (but still apparent) asymmetry, also in favor of the right leg, was seen in the anterior-posterior MOS (B).

DISCUSSION

Preventing falls and predicting fall risk requires understanding how humans control their dynamic stability while walking. Exposing people to moderate perturbations like irregular terrain can directly challenge this ability. Here, we quantified how continuous, pseudorandom oscillations of the support surface and visual field altered instantaneous COM-based margins of stability during walking. We quantified not only average responses (means and standard deviations; Fig. 2), but also first-return plots (Figs. 3–4) that more directly revealed step-to-step control. AP perturbations induced increased mean MOS_ml (Fig. 2A) and MOS variability (Figs. 2C–D), but only effected APP mean MOS_ap (Fig. 2B). Meanwhile, ML perturbations induced increased mean MOS_ml (Fig. 2A) and mean MOS_ap (Fig. 2B) and increased both MOS_ml and MOS_ap variability (Figs. 2C–D).

Mean MOS_ap did not increase during both AP perturbations (Fig. 2B), as expected. Conversely, we previously showed that these same AP perturbations both altered AP orbital stability and both short- and long-term local stability (McAndrew et al., 2011). Part of this difference lies in the very different definitions of “stability” used. Our previous study examined the sensitivity to small fluctuations in AP trunk velocity trajectories, whereas MOS_ap accounts for the relationship between the BOS boundaries and COM motion (Fig. 1A).

Mean MOS_ml increased slightly when either visual or walking surface perturbations were applied in either the AP or ML directions (Fig. 2A). Others have suggested that lateral foot placement might be controlled to maintain stable walking (Hof, 2008). MOS_ml remained approximately constant for overground vs. treadmill walking (Rosenblatt and Grabiner, 2010) and when walking overground versus over foam (MacLellan and Patla, 2006), supporting this idea. Here, subjects’ foot placements resulted in small, but consistent increases in mean MOS_ml during continuous visual and support surface perturbations. This most likely resulted from these subjects taking slightly wider steps, as previously reported (McAndrew et al., 2010). Interestingly, patients with trans-femoral amputation (who have a high risk of falling) also exhibited larger mean MOS_ml and wider step widths than healthy controls (Hof et al., 2007). If a larger MOS implies a more stable system (Hof et al., 2005), then our findings seem highly counter-intuitive: that subjects would be more stable when specifically exposed to de-stabilizing perturbations.

Conversely, MOS variability increased substantially during the ML perturbations (Figs. 2C–D). This resulted in more steps with either smaller or negative MOS_ml (Figs. 3B & 4B), indicating an increased challenge to stability not captured by mean MOS measures (Fig. 2). Infrequent, short and medial adjustments in foot placement can adversely affect balance when walking on a cluttered surface (Moraes et al., 2007). The increased MOS variability observed here may in part reflect an increased frequency of such short, medial adjustments of foot placement. During the ML perturbations, our participants also demonstrated decreased lateral short-term local and orbital stability (McAndrew et al., 2011) and increased SL variability (McAndrew et al., 2010), the latter of which may predict increased fall risk in the elderly (Maki, 1997). Thus, measures of mean MOS that do not capture changes in MOS variability appear to be poor indicators of instability.

While measures of mean MOS (Fig. 2A–B) fail to capture the step-to-step variability in MOS, measures of MOS variability (Fig. 2C–D) likewise assume all step-to-step fluctuations are random and uncorrelated and thus fail to capture how that variability evolves dynamically from each step to the next (Dingwell and Cusumano, 2010; Dingwell et al., 2010). The first-return map analyses (Strogatz, 1994) (Figs. 3–4) more directly indicated that subjects did indeed control their stability from step-to-step, particularly for MOS_ml (Fig. 4). The populations of quadrants Q2 and Q4 increased in parallel in the perturbation conditions. Thus, nearly every time a stable step was followed by an unstable step (Q2), that unstable step was then followed immediately by a stable step (Q4). Stable steps may not all be purely corrective steps because every step was perturbed in this study. However, the patterns of changes in Q2 and Q4 populations still indicate a strong relationship between the stability of consecutive steps. Such subtleties are lost in statistical calculations of means and variance. The “outlying” step patterns are likely far more important for understanding stability control and fall risk. Our results argue strongly for applying analyses that adequately capture step-to-step dynamics (Dingwell and Cusumano, 2010; Dingwell et al., 2010).

We also found consistent MOS_ml asymmetries between right and left heel strikes (Table 2; Figs. 4 and 5A). Rosenblatt and Grabiner (2010) observed similar asymmetries and suggested they might be functional. Several studies support the idea that lower limb asymmetries reflect a functional separation of the tasks of support and propulsion (Hirokawa, 1989; Sadeghi et al., 1997; Sadeghi et al., 2000). On average, our subjects exhibited greater lateral stability (i.e. larger MOS_ml) on their right legs across all perturbation conditions (Table 2; Fig. 5). This might possibly reflect differences in the stability requirements of each leg to be able to provide support versus propulsion. However, since examining left-right asymmetries was not a goal of this study, we can only speculate here. The present findings suggest that more detailed studies of the origins and relevance of these asymmetries are warranted.

In this study, we estimated COM motion using the four pelvis markers. Whittle (1997) showed that the center of the pelvis estimated the motion of the center of gravity (COG) well in the ML and vertical directions, with small differences in timing and displacement in the AP direction. Similarly, the sacral marker (essentially the average of the 2 PSIS markers used here) provided a reasonable approximation of vertical COM motion at freely selected walking speeds (Gard et al., 2004). Here, a more rigorous whole-body model may have provided slightly different numerical estimates of COM motion. However, we expect any such differences would have affected the MOS calculations similarly across all experimental conditions. Thus, using any different choice of COM definition would likely have yielded qualitatively similar outcomes for our MOS measures.

The present findings may have implications for conducting balance rehabilitation in individuals with asymmetric lower limb impairments. For example, patients with trans-femoral amputation exhibited greater mean MOS on their prosthetic side during preferred walking (Hof et al., 2007). However, both here in this study (Fig. 5) and in Rosenblatt and Grabiner (2010), even healthy individuals with two intact limbs also adopted asymmetric MOS patterns. These conflicting findings may call into question the goal of restoring symmetrical gait in patients with primarily unilateral impairments.

These results also have important implications for fall risk assessment. In particular, they suggest the importance of identifying individuals who exhibit small or unstable stability margins (i.e., negative MOS_ml) and/or ineffective corrective responses. A single step with a negative MOS_ml does not necessarily mean that person will immediately fall, only that corrective action is needed to avoid a fall. Individuals who exhibit more unstable steps need to exert more corrective actions, which requires greater control and greater effort. Decreased muscle strength is a risk factor for falling in the elderly (Pavol et al., 2002; Pijnappels et al., 2008; Pijnappels et al., 2008). Having to make more corrective motions with diminished muscle strength would likely increase fall risk. The present results strongly suggest that quantifying means and/or variability of MOS_ap and/or MOS_ml is not likely to be especially informative. However, quantifying the percent of unstable steps (particularly of negative MOS_ml) and/or the percentage of consecutive unstable steps, is likely to be far more relevant. The occurrence of individually unstable steps, and the subsequent responses to those steps are the critical markers of stability control. Only approaches that appropriately capture step-to-step dynamics (Dingwell et al., 2010) can identify these.