Systems genetics of the nuclear factor-κ B signal transduction network. I. Detection of several quantitative trait loci potentially relevant to aging

1. Introduction

A promising theory of the aging process holds that senescence is brought about by dysregulation of transcription factors governing central physiological processes, including energy metabolism, and immunological homeostasis (Vellanoweth et al. 1994; Supakar et al., 1995; Roy et al. 1996, 2002; Roy 1997; Chung et al. 2000, 2001, 2002, 2006, 2009; Lavrovsky et al. 2000; Giardina and Hubbard, 2002; Gosselin and Abbadie, 2003; Herbein et al. 2006; Yu & Chung, 2006; Salminen et al. 2008a&b). One such transcription factor that has come to the forefront is nuclear factor kappa B (NF-κB) and its associated signal transduction network (STN), thus giving rise to the concept of NF-κB-dependent senescence. The NF-κB STN has also been implicated in the pathophysiology of complex diseases associated with aging, including cancer (Dolcet et al. 2005; Karin 2006; Inoue et al. 2007; Maeda and Omata 2008), neurological disorders (Kaltschmidt et al. 2005; Mattson 2006; Mattson and Meffert 2006; Memet 2006), and the metabolic syndrome, including type 2 diabetes (T2D), obesity, and cardiovascular disease (CVD) (Sonnenberg et al. 2004; de Winther et al. 2005; Xanthoulea et al. 2005; Bastard et al. 2006; Schwartz and Reaven, 2006; Gil et al. 2007). Thus, studies on the genetic regulation of the NF-κB STN may contribute toward understanding the physiology of senescence and the pathophysiology of age-associated complex diseases.

In a current approach variously known as system- or systems-genetics it has been argued that the incorporation of a systems biology perspective can greatly aid efforts to delineate the genetic architecture underlying transcriptional regulatory networks (Galitski, 2004; Schadt et al. 2005; Drake et al. 2006; Kadarmideen et al. 2006; Sieberts and Schadt 2007; Werner 2007; Ayroles et al. 2009; Mackay et al. 2009). Here we employ these methods to study the genetic regulation of the NF-κB STN.

We first derive a network of gene expression variables intrinsic to the NF-κB STN using Ingenuity Pathway Analysis (IPA, http://www.ingenuity.com) methods. We then perform principal components factor analysis (PCFA) to identify sets of highly correlated gene expression variables within the network, where we take the factors identified to be multivariate proxies of functional modules at the molecular level. This is similar to methods that exploit the inherent correlation structure in a transcriptional profiling array to detect modules within a system (Han et al. 2004; Ihmels et al. 2004; Xia et al. 2006; Xue et al. 2007; Zhan 2007; Han 2008; Kutalik et al. 2008; Wang et al. 2008). Lastly, using statistical genetic variance component methods (Blangero et al., 2001; Almasy and Blangero, 2008, 2010), we seek to identify and localize quantitative trait loci (QTLs).

2. Materials and Methods

2.1. Study Population

Our analyses were performed on data from the San Antonio Family Heart Study (SAFHS), which is a study of the genetic determinants of cardiovascular disease (CVD) in Mexican American families of San Antonio, Texas. The SAFHS population is comprised of large Mexican American extended families randomly ascertained with respect to CVD (MacCluer et al. 1999). The SAFHS protocols were approved by the Institutional Review Board at the University of Texas Health Science Center at San Antonio and all study participants provided written informed consent.

We note that the crude prevalence of CVD in our sample is 19 %, and so the extent to which our findings are applicable to “normal aging” is somewhat debatable. However, it is widely held that aging and age-associated complex diseases such as CVD have common underlying causes such as inflammation and oxidative stress (Chung et al. 2000, 2001, 2002, 2006, 2009; Brüünsgaard et al., 2001, 2003; Yu & Chung, 2006; Salminen et al. 2008a&b). Moreover, as detailed in more theoretical work by our group (Blangero et al., 2000, 2001; Almasy and Blangero, 2008), our statistical genetic approach is optimal for the detection of causal genes for complex diseases.

2.2. Genotype Data

Fasting blood samples were obtained from study participants at a clinic exam and transported daily to the Southwest Foundation for Biomedical Research (SFBR), San Antonio, Texas. Plasma and serum were isolated by low-speed centrifugation and the buffy coat was harvested for DNA extraction. DNA extracted from lymphocytes was used in polymerase chain reactions (PCRs) for the amplification of individual DNA (N = 1339) at 432 dinucleotide repeat microsatellite loci (STRs), spaced approximately 10 centiMorgan (cM) intervals apart across the 22 autosomes, with fluorescently-labeled primers from the MapPairs Human Screening set, versions 6 and 8 (Research Genetics, Hunstsville, AL). PCRs were performed separately according to manufacturer specifications in Applied Biosystems 9700 thermocyclers (Applied Biosystems, Foster City, CA). The products of separate PCRs, for each individual, were pooled using the Robbins Hydra-96 Microdispenser, and a labeled size standard was added to each pool. The pooled PCR products were loaded into an ABI PRISM 377 or 3100 Genetic Analyzer for laser-based automated genotyping. The STRs and standards were detected and quantified, and genotypes were scored using the Genotyper software package (Applied Biosystems).

Mistyping analyses were performed on the preliminary genotype marker data using SimWalk2, following the recommendations of the program developers for accounting for mistyping error (Sobel and Lange 1996; Sobel et al. 2002). Our overall rate of blanking mistyped markers was 1.37%. These mistyping analyses allow investigators to account for Mendelian errors and spurious double recombinants, both of which can severely reduce the power of a linkage analysis if not accounted for (Sobel et al. 2002). On addressing mistyping error, these genotype data were then used to compute maximum likelihood estimates of allele frequencies in SOLAR (Almasy and Blangero 1998). Empirical estimates of identity-by-descent (IBD) allele sharing at points throughout the genome for every relative pair were computed using the Loki package (Heath 1997). The multipoint IBD estimates are required under our variance components modeling approach. The Simwalk II and Loki programs both require chromosomal maps. We used the set of high-resolution chromosomal maps provided by the research group at deCODE genetics, Reykjavik, Iceland, which are available online as a supplemental table to the primary article (Kong et al. 2002).

2.3. Microarray Gene Expression Data

2.3.1. Expression profiling

The expression profiling methodology is described, in detail, in Göring et al. (2007). In brief, frozen lymphocyte samples were available from 1,280 individuals, collected during their first clinic visit between 1991 and 1995, after an overnight fast, in EDTA tubes. Lymphocytes were isolated from a 10ml sample using Histopaque (Sigma Chemical Co., St. Louis, MO), following the suggested protocol of the manufacturer, washed, and stored in a freeze media in liquid nitrogen.

Total RNA was isolated using a modified procedure of the QIAGEN RNeasy^® 96 protocol for isolation of total RNA from animal cells using spin technology (QIAGEN Inc., Valencia, CA), and a total of 500ng total RNA dried down and stored at −20°C. Anti-sense RNA (aRNA) was synthesized, amplified and purified using the Ambion MessageAmp II Amplification Kit (Ambion, Austin, TX) following the Illumina Sentrix Array Matrix 96-well expression protocol (Illumina Inc., San Diego, CA). Synthesized cDNA samples were purified using QIAGEN’s QIAquick 96 PCR purification supplementary protocol for spin technology (QIAGEN document QQ01.doc, October 2001). Biotin-16-UTP (Roche, Germany) labeled aRNA was synthesized using Ambion’s proprietary MEGAscript^® in vitro transcription (IVT) technology and T7 RNA Polymerase. Purification of aRNA samples was performed using QIAGEN’s RNeasy^® 96 protocol for RNA cleanup using spin technology, and a total of 1.5μg aRNA was dried and stored at −20°C prior to sample hybridization.

Hybridization of aRNA to Illumina^® Sentrix^® Human Whole Genome (WG-6) Series I BeadChips and subsequent washing, blocking and detecting were performed using Illumina’s BeadChip 6×2 protocol. Samples were scanned on the Illumina^® BeadArray^™ 500GX Reader using Illumina^® BeadScan image data acquisition software (version 2.3.0.13). Illumina^® BeadStudio software (version 1.5.0.34) was used for preliminary data analysis, with a standard background normalization, to generate an output file for statistical analysis. In total we interrogated 47,289 unique transcripts: 22,151 probes (47%) are targeted at Reference Sequence (RefSeq) transcripts, and the remaining 25,128 probes (53%) correspond to other, generally less well characterized transcripts (including predicted genes).

2.3.2. Identification and standardization of expressed transcripts

In order to identify transcripts that exhibited sufficient quantitative expression in lymphocytes, the distribution of expression values for a given transcript was compared to the distribution of the expression values of the controls that are imbedded in each chip. For each transcript, we performed a χ² “tail” test of whether there was a significant excess of samples with values above the 95th percentile of the control null distribution. This test was used because it allows detection of even those transcripts that are clearly present above baseline levels in only a subset of individuals, while not being detectable above baseline levels in most individuals. Using a false discovery rate of 0.05, we identified 20,413 transcripts that exhibited significant expression by this criterion.

To minimize effects due to RNA quantity and quality we performed within and across sample normalization. This conservative procedure results in normalized expression phenotypes that are comparable between individuals and across transcripts.

2.4. Network Analysis Methods

We used Ingenuity Pathways Analysis (Ingenuity® Systems, www.ingenuity.com) to identify published gene/gene product interactions between NF-κB and the genes detected in our transcriptional profiling. Our genes of interest were overlaid onto a global molecular network developed from the literature on reported connectivity recorded in the Ingenuity Pathways Knowledge Base. This allows the generation of gene networks, and graphical representation of the molecular relationships between genes/gene products.

2.5. Principal Component Factor Analysis (PCFA)

To aid in the discovery of QTLs controlling gene expression networks, we use the approach of PCFA, which has been widely used in genetic studies of the metabolic syndrome (Arya et al. 2002; Liu et al. 2003; North et al. 2003, 2005; Cai et al. 2004; Lin et al. 2005; Edwards et al. 2008). We note also that PC analysis (PCA), which is the first step of PCFA, is widely used in gene expression analyses, usually in combination with other statistical approaches (Selaru et al. 2004; Wang and Gehan 2005; Roden et al. 2006; Wang et al. 2007; Ringnér 2008). Moreover, PCA has been used to identify functional modules of gene expression variables that manifest at the molecular level (Alter et al. 2000; Selaru et al. 2004; Janes and Yaffe 2006; Roden et al. 2006; Alter 2007). Generally, PCFA is a data-reduction technique that produces representative subsets in multivariate space—termed factors—of the original set of variables that explain a disproportionately higher portion of the total variance in the data. PCFA first uses PCA to find “raw” factors, and then uses a factor rotation procedure, such as varimax rotation, to produce factors that may be easier to interpret (Dunteman 1989; Kachigan 1991; Manly 1994; Jolliffe 2002). Factors with eigenvalues >1 were retained for subsequent analysis, and, to aid in factor interpretation, variables with factor loadings >|0.4| were taken to be the defining variables of the factor (Edwards et al. 1994; Arya et al. 2002; Stevens 2002; Cai et al. 2004; Lin et al. 2005).

2.6. Variance Components (VC) Models

Consider a data vector of N individuals, y_N×1, which we assume follows the multivariate normal distribution, and is well-described by the following linear model:

$${\mathbf{y}}_{N\times 1}={\mathbf{X}}_{N\times k}{\mathbf{\beta }}_{k\times 1}+{\mathbf{g}}_{N\times 1}+{\mathbf{e}}_{N\times 1},$$ Eq. 1

where X_N×k is a matrix of individual fixed effects (including a column of “1s” followed by the covariate effects), β_k×1 is a vector of the grand mean and (k−1) beta-coefficients, and g_N×1 and e_N×1 are unobservable vectors of random genetic and environmental effects. The model for the multivariate mean is given by:

$$E[\mathbf{y}]=\mathbf{\mu }=\mathbf{X}\mathbf{\beta },$$ Eq. 2

Eq. 2 where we have dropped the dimension subscripts for simplicity. Let the residuals vector between the data and the mean vector be given as: Δ = y − Xβ. Assuming independent genetic and environmental effects, the covariance matrix of the data vector, denoted by Σ (of dimensions N × N), is modeled as:

$$E[\mathbf{\Delta }{\mathbf{\Delta }}^{\prime }]=\mathbf{\sum }=2\mathbf{\Phi }{\sigma }_g^2+\mathbf{I}{\sigma }_e^2,$$ Eq. 3

where the kinship matrix, Φ, and the identity matrix, I, partition the total variance into shared genetic and random environmental variance components, respectively. We note that y, φ_xz, and δ_xz are the scalar versions of y, Φ, and I. From this equation, we get the polygenic heritability, given as $h^2=\frac{{\sigma }_g^2}{{\sigma }_g^2+{\sigma }_e^2}$.

To model a QTL effect, we add it to the linear model in Equation 1 as an unobservable random effect, and its variance component to the model for the covariance matrix in Equation 3 as follows:

$$\mathbf{\sum }=2\mathbf{\Phi }{\sigma }_g^2+\mathbf{I}{\sigma }_e^2+\widehat{\mathbf{\Phi }}{\sigma }_q^2,$$ Eq. 4

where ${\sigma }_q^2$ is the QTL variance, and Φ̂ is the matrix of pair-wise estimates of identity-by-descent at a given point or locus in the genome based on flanking marker information.

2.7. Inferential Procedures: Likelihood ratio and LOD score

Our inferences are either directly formed from the results of the likelihood ratio test (LRT) or indirectly in that, under the VC approach, the LOD score is derived as the ratio of the LRT statistic, denoted by Λ, to twice ln(10). Let the parameters under the full polygenic model (Equations 1–3) be collected in a column vector: $\mathbf{\theta }={\left[\begin{array}{ccc}\mathbf{\beta }& {\sigma }_g^2& {\sigma }_e^2\end{array}\right]}^{\prime }$. Under this model, the likelihood function of the parameter vector conditional on the data is then given by:

$$lnL(\mathbf{\theta }\mid \mathbf{y},\mathbf{X})=-\frac{1}{2}\left[Nln(2\pi )+ln\mid \mathbf{\sum }\mid +{\mathbf{\Delta }}^{\prime }{\mathbf{\sum }}^{-1}\mathbf{\Delta }\right].$$ Eq. 5

Using this equation, maximum likelihood estimates are computed in SOLAR (Almasy and Blangero, 1996), and Λ is given as minus twice the difference of likelihoods between the null and alternative hypotheses:

$$\mathrm{\Lambda }=-2\left[lnL\left({\mathbf{\theta }}_{H_0}\right)-lnL\left({\mathbf{\theta }}_{H_A}\right)\right]=-2lnL\left(\frac{{\mathbf{\theta }}_{H_0}}{{\mathbf{\theta }}_{H_A}}\right),$$ Eq. 6

where θ_H0 and θ_HA represent the parameter vectors under the null (H₀) and alternative (H_A) hypotheses, respectively. In general, Λ is distributed as a chi-square random variable with degrees of freedom (d.f.) given by the difference in the number of estimated parameters under the null and alternative hypotheses. For variances and/or standard deviations, however, the null hypothesis is on a boundary of the parameter space, in which case Λ has been shown to be distributed as a 50:50 mixture of point-mass at 0 and a chi-square variate with 1 d.f (Self and Liang 1987).

Inferences for multipoint genome-wide linkage scans are traditionally made on the basis of LOD scores. To provide a conservative corrective for the number of tests under a typical genome-wide linkage scan, a LOD score greater than or equal to 3.0 is taken to indicate significance of linkage (MacCluer et al. 1999; Ott 1999).

3. Results

3.1. Network Analysis

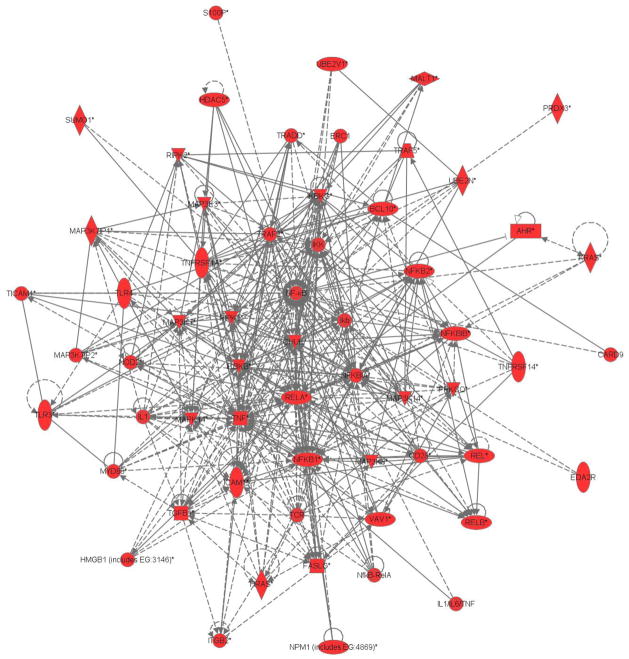
We used IPA to construct a network based solely on evidence of a first degree relationship (no intermediary gene/product) between each of the 20,413 transcripts that had detectable expression levels and NF-κB. We identified 60 genes with published first-degree gene/gene product interactions with NF-κB in our dataset, as shown in Figure 1.

Figure 1.

Gene expression network of the heritable transcripts in the nuclear factor kappa B signaling pathway.

3.2. Pathway Analysis

The core of the NF-κB STN is made up five proteins of the Rel family, RelA (p65), RelB, c-Rel, NF-κB1 (p50/p105), and NF-κB2 (p52/p100), which form homodimers or heterodimers that are present in bound form in the cytoplasm, but upon activation may translocate to the nucleus to stimulate transcription (Ghosh and Karin 2002; Li and Verma 2002; Hayden et al. 2006; Xiao et al. 2006; Hoffmann and Baltimore 2006; Vallabhapurapu and Karin 2009). In the cytoplasm, the NF-κB core proteins are bound by inhibitors of NF-κB (IκB), and are activated by phosphorylation of IκB by IκB kinases (IKK) (Ghosh and Karin 2002; Liou 2002; Hoffmann and Baltimore 2006; Xiao et al. 2006; Perkins 2007; Vallabhapurapu and Karin 2009). Once activated by IKK mediated phosphorylation of the NF-κB/IκB complex, NF-κB can take either of two main pathways, the canonical or classical pathway and the noncanonical or alternative pathway (Bonizzi and Karin 2003; Hayden et al. 2006; Xiao et al. 2006; Vallabhapurapu and Karin 2009).

Using information available in the literature, we limited further analyses to a subset of the NF-κB STN to 19 transcripts. First of all, we selected a core component comprised of the transcripts central to the NF-κB STN, which included four of the five core proteins, namely Rel, RelA, RelB, and NF-κB1, one inhibitor, namely IκBα, and two members of the activator kinases, namely IKKβ and IKKγ. We also included tumor necrosis factor α (TNFα) because of its ubiquitous involvement in upregulating inflammatory pathways, mainly through the NF-κB STN, in relation to senescence (Brüünsgaard et al. 2001; Brüünsgaard and Pedersen 2003; Krabbe et al. 2004; Sonnenberg et al. 2004; Tedgui and Mallat 2006). An additional 12 transcripts were selected because they were either a cell-surface receptor protein or an important adaptor protein that interacts with a receptor protein. These include toll-like receptors 3 and 4 (TLR3 and TLR4), three members of the TNF receptor superfamily (TNFRSF), namely TNFRSF1A, TNFRSF6, TNFRSF14, two TNF receptor associated factors (TRAF), namely TRAF2 and TRAF5, two transcripts of TNF receptor 1 associated death domain protein (TRADD), the adaptor protein myeloid differentiation factor-88 (MyD88), and two transcripts of toll/interleukin-1 receptor (TIR) domain-containing adaptor inducing interferon-β (TRIF).

3.2. Principal Components Factor Analysis (PCFA)

Currently, TLR signaling pathways are classified as being either MyD88-dependent or MyD88-independent/TRIF-dependent (Akira et al. 2001; Heine and Lien 2003; Akira and Takeda 2004; West et al. 2006; Atkinson 2008). Therefore, we decided to perform PCFA on the 19 transcripts named above, but also on two subsets, one excluding just the MyD88 transcript, and the other excluding the two TRIF transcripts. We call the set of 19 transcripts the “All-Transcripts” (AT) set, the subset excluding MyD88 the “TRIF-dependent” (TD) set, and the subset excluding the TRIF transcripts the “MyD88-dependent” (MD) set. The latter two variable sets were considered in order to take advantage of the fact that PCFA finds factors that are made up of variables that are correlated within-factor but are orthogonal across factors, which would potentially accentuate effects that are truly independent of either MyD88 or TRIF, respectively. Conversely, the AT set was considered because of the potential for synergistic effects involving both MyD88 and TRIF.

For the AT set, eigenvalues and percent variance explained for all factors with an eigenvalue greater than 1 are presented in Table 1. The factor loadings after varimax rotation for the AT set are presented in Table 2. Similarly, for the TD and MD sets, the eigenvalues and percent variance explained for all factors with an eigenvalue greater than 1 and the factor loadings are respectively presented in Tables 3–6.

Table 1.

Factors, Eigenvalues, and Variance Explained: All Transcription Variables

	Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6	Factor 7
Eigenvalue	3.879	2.172	2.016	1.591	1.267	1.131	1.034
% Variance Explained	20.983	11.751	10.905	8.607	6.855	6.120	5.596
Cumulative Variance	20.983	32.734	43.639	52.246	59.101	65.221	70.817

Table 2.

Factor Loadings: All Transcription Variables

	Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6	Factor 7
IKBKB	0.046	−0.098	0.390	0.047	−0.318	0.210	0.100
IKBKG	0.135	−0.428	0.726	0.087	0.155	0.058	0.008
NFKB1	0.172	0.003	0.017	−0.005	0.212	−0.044	0.093
IKBA	−0.831	0.106	−0.192	0.071	−0.055	−0.170	−0.223
RELB	−0.025	0.232	0.273	−0.059	0.011	−0.506	−0.616
REL	−0.196	0.358	0.130	−0.050	0.699	0.112	−0.305
TLR3	−0.004	−0.104	−0.061	0.058	−0.111	0.007	−0.026
TLR4	−0.205	0.295	−0.206	0.728	0.180	0.151	−0.086
TNFRSF14	0.099	−0.076	0.786	0.004	−0.059	−0.055	−0.035
TNFRSF1A	0.355	−0.336	0.042	0.654	−0.352	0.111	−0.161
TNFSF6	0.203	0.085	0.043	−0.022	0.082	0.864	0.021
TNF	−0.921	0.030	−0.007	0.067	0.019	−0.093	−0.138
TRADDa	0.161	−0.818	0.162	−0.082	0.059	−0.111	0.201
TRADDb	0.141	−0.162	−0.022	0.146	0.772	0.058	0.066
TRAF2	−0.175	−0.629	0.300	−0.216	−0.369	0.140	−0.257
TRAF5	0.136	−0.376	0.193	−0.418	0.063	−0.017	0.592
TRIFa	−0.115	0.144	−0.024	0.015	0.047	0.040	−0.194
TRIFb	−0.333	−0.111	−0.016	0.079	0.107	0.023	−0.813
MYD88	−0.140	0.085	0.329	0.746	0.138	−0.257	0.009

Table 3.

Factors, Eigenvalues, and Variance Explained: TRIF-Dependent

	Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6
Eigenvalue	3.835	2.161	1.801	1.488	1.263	1.053
% Variance Explained	21.918	12.351	10.293	8.504	7.218	6.017
Cumulative Variance	21.918	34.269	44.563	53.066	60.284	66.301

Table 6.

Factor Loadings: MyD88-Dependent

	Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6
IKBKB	0.099	−0.104	−0.069	0.094	−0.220	0.066
IKBKG	0.110	−0.168	−0.907	0.121	0.035	0.014
NFKB1	0.142	0.065	0.031	−0.023	−0.942	0.030
IKBA	−0.867	0.018	0.101	−0.064	0.146	−0.142
RELB	−0.128	−0.004	−0.017	−0.020	0.004	−0.127
REL	−0.100	0.100	−0.058	−0.162	−0.015	0.042
TLR3	−0.018	−0.024	−0.022	0.046	0.078	−0.009
TLR4	−0.123	0.133	0.073	0.134	−0.016	0.020
TNFRSF14	0.091	−0.124	−0.203	0.034	−0.125	−0.024
TNFRSF1A	0.150	−0.063	−0.114	0.930	0.022	0.047
TNFSF6	0.140	0.004	−0.010	0.040	−0.028	0.974
TNF	−0.939	−0.084	0.037	−0.111	0.051	−0.065
TRADDa	0.132	−0.216	−0.205	0.098	−0.041	−0.052
TRADDb	0.074	0.121	−0.048	−0.045	−0.112	0.068
TRAF2	−0.073	−0.917	−0.163	0.065	0.070	−0.005
TRAF5	0.180	−0.045	−0.133	−0.111	−0.128	−0.002
MYD88	−0.099	0.072	−0.090	0.132	−0.028	−0.068

3.3. Heritability and Linkage

In the ensuing, factors will have AT, TD, or MD as a suffix to indicate which set they were derived from. The heritability for each factor across the three variable sets are reported in Table 7. All of the factors were significantly heritable. The heritabilities ranged from a low of 19% to a high of 52%.

Table 7.

Heritabilities for all factors

Variable set or subset	Heritability, and standard error for:
	Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6	Factor 7
All Transcripts	0.51 (0.05)	0.34 (0.05)	0.21 (0.06)	0.49 (0.05)	0.27 (0.06)	0.41 (0.06)	0.44 (0.05)
TRIF-Dependent	0.48 (0.05)	0.34 (0.05)	0.30 (0.05)	0.48 (0.05)	0.29 (0.06)	0.48 (0.05)	NA
MyD88-Dependent	0.52 (0.05)	0.24 (0.05)	0.19 (0.05)	0.40 (0.05)	0.23 (0.05)	0.30 (0.06)	NA

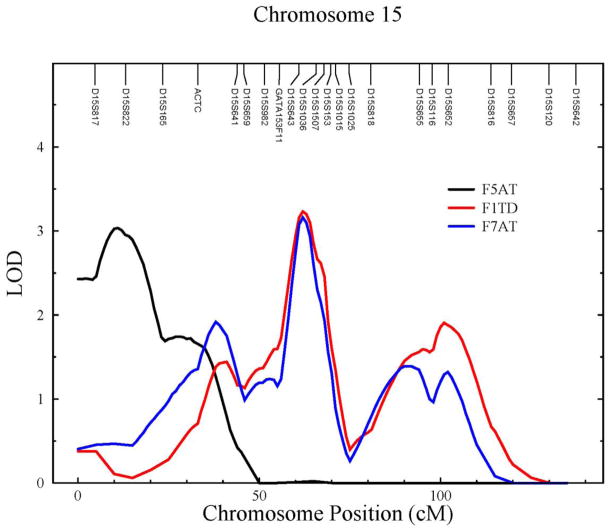
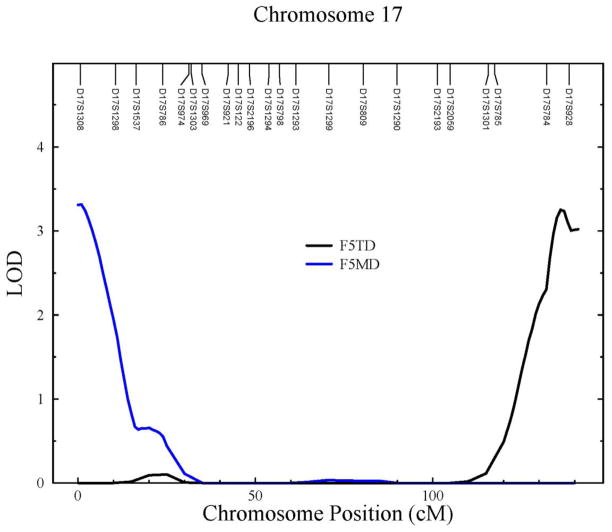
The genome-wide maximum LOD scores for all factors are reported in Table 8. Each variable set gave rise to at least one factor with a LOD score greater than 3, two on chromosome 15 at 15q12 and 15q22.2, and another two on chromosome 17 at 17p13.3, and 17q25.3 (Table 8; Figs. 2&3). We also found several suggestive signals (2 < LOD score < 3) at 1q32.1, 1q41, 2q34, 3q23, and 7p15.3 (Table 8). We do not believe that the three suggestive signals on chromosomes 15 and 17 are distinct from the nearby locations reported just above at 15q12, 15q22.2, and 17p13.3.

Table 8.

Standard linkage results: genome-wide maximum LOD scores for all factors

Variable set or subset	LOD score, cytogenetic location:
	Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6	Factor 7
All Transcripts	1.96 1q32.3	2.22 7p15.3	1.96 7q36.2	2.08 2q34	3.03 15q12	1.73 5p13.3	3.16 15q22.2
TRIF-Dependent	3.23 15q22.2	2.04 1q32.1	1.87 9p24.1-p23	2.48 15q14	3.25 17q25.3	2.12 17p12	NA
MyD88-Dependent	2.64 1q41	1.50 4q34.3	1.97 18p11.21	2.61 15q22.3	3.31 17p13.3	2.10 3q23	NA

Figure 2.

LOD plots on chromosome 15 for F5AT (black), F1TD (red), and F7AT (blue).

Figure 3.

LOD plots on chromosome 17 for F5TD (black), and F5MD (blue).

4. Discussion

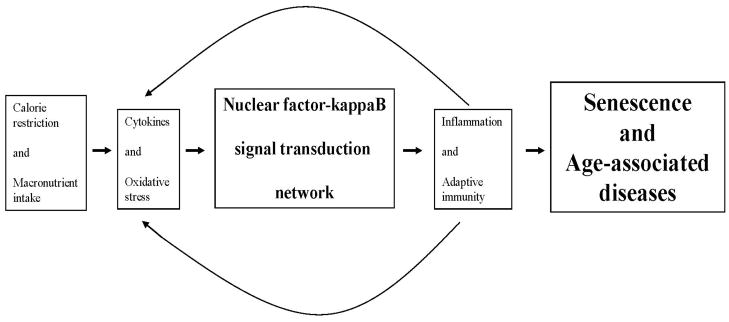
It has long been thought that NF-κB and its associated STN plays a major role in aging (Vellanoweth et al. 1994; Supakar et al., 1995; Roy et al. 1996, 2002; Roy 1997; Chung et al. 2000, 2001, 2002, 2006, 2009; Lavrovsky et al. 2000; Giardina and Hubbard, 2002; Gosselin and Abbadie, 2003; Herbein et al. 2006; Yu & Chung, 2006; Salminen et al. 2008a&b). We have dubbed this work the theory of NF-κB-dependent senescence. An attractive characteristic of the theory of NF-κB-dependent senescence is the elegance of mechanistically unifying it with at least four other prominent theories of aging, namely the oxidative stress, calorie restriction, inflammation, and immunological theories, and with a related theory on the etiology of the metabolic syndrome, namely the macronutrient intake theory of Dandona and colleagues (Dandona et al. 2004a,b,c, 2005).

The canonical and alternative signaling pathways of the NF-κB STN are set in train by extracellular signals and stimuli, such as proinflammatory cytokines and oxidative stress (Xiao 2004; Perkins 2007). Acting independently and/or in concert, the two pathways regulate the innate and adaptive arms of the immune response, including inflammation and cell-mediated pathways, respectively (Li and Verma 2002; Liou 2002; Bonizzi and Karin 2003; Liang et al. 2004; Hayden et al. 2006; Xiao et al. 2006; Vallabhapurapu and Karin 2009). In related work, it has been shown that by directly modulating oxidative stress, calorie restriction indirectly regulates NF-kappa B expression (Kim et al. 2002a&b, 2008; Jung et al. 2009). This is consistent with demonstrations that macronutrient intake promotes oxidative stress, which in turn upregulates the NF-κB STN (Dandona et al. 2004a,b,c, 2005). Thus, the NF-κB STN constitutes a critical nexus for linking calorie restriction, macronutrient intake, and oxidative stress to inflammatory and adaptive immunity pathways in relation to senescence (Figure 4).

Figure 4.

Schematic diagram of the nuclear factor kappa B signal transduction network in relation to other physiological processes important in senescence and age-associated disease.

To better understand the genetic regulation of the NF-κB STN, and, by extension the genetic architecture underlying NF-κB-dependent senescence, we used a comprehensive systems genetics approach. First, we constructed a gene expression network representative of the NF-κB STN. Then, with the goal of concentrating our efforts on the most important sources of variation, we used a PCFA approach on a subset of the NF-κB STN. Finally, we analyzed the factors so derived using a statistical genetic VC approach. We found that these factors are all significantly heritable, and, further, we found strong evidence of four QTLS at chromosomes 15q12, 15q22.2, 17p13.3, and 17q25.3, and suggestive evidence of potential QTLs on chromosomes 1, 2, 3, and 7.

To facilitate discussion of these QTLs in relation to the PCFA results, we abbreviate the factors by “F” followed by the factor number, and then by the AT, TD, or MD abbreviations as appropriate. For example, factor 5 under the AT set is abbreviated as F5AT. We also restrict our discussion to our strongest results (i.e. QTLs with a LOD score > 3). We found that five PCFA factors gave rise to the 4 main linkage signals on chromosomes 15 and 17. The composite variables F7AT and F1TD have the same three NF-κB STN variables loading onto the factor, namely RELB, TRAF5, and TRIF, and as expected they give rise to what appears to be the same linkage signals. Similarly, F5AT and F5TD also have the same NF-κB STN variables loading onto the factor, namely REL and TRADD, and their linkage signals on chromosomes 15 and 17 are similar. The maximum LOD scores for F5AT and F5TD are 3.03 at chromosome 15q12 and 3.25 at chromosome 17q25.3, respectively, and suggestive LODS scores for the same traits are 2.21 at chromosome 17q25.3 and 2.74 at chromosome 15q12, respectively. Given that MyD88 is the main difference between the AT and TD sets, it may be that the putative QTL on chromosome 15q12 is relatively more important in the MD TLR signaling pathway and that the putative QTL on chromosome 17q25.3 is relatively more important in the TD TLR signaling pathway. F5MD had only one NF-κB STN variable loading onto the factor, namely NFKB1. We note that none of the cytogenetic locations of the putative QTLs coincide with the cytogenetic locations of the constituent genes in the relevant factors. Thus, we have identified what appear to be trans-QTLs influencing three of the five main core proteins of the NF-κB STN, namely Rel, RelB and NFKB1, and three other important signaling proteins, namely TRADD, TRIF, and TRAF5.

As reported in Schadt et al. (2005) and discussed in Sieberts and Schadt (2007), trans-QTLs can play prominent roles as drivers of complex disease causation if they are centrally located in a network known to be important in complex disease. Their group was able to identify and functionally validate three candidate genes as causal for obesity, and these genes were first identified as trans-QTLs centrally located in a gene expression network known to be important in obesity. Regarding our situation, the work of Schadt and colleagues is encouraging because our trans-QTLs are centrally located within the NF-κB STN.

The work reported herein is part of an ongoing investigation of the genetic regulation of the NF-κB STN by way of a systems genetics approach. While our findings regarding the heritable factors of the NF-κB STN and their associated trans-QTLs are important, we emphasize that together they constitute what is only a first step in the process of gene discovery. We are currently pursuing more fine-detail genetic analyses by examining the transcripts and single nucleotide polymorphisms within the 1-LOD intervals of the QTLs identified here.

Table 4.

Factor Loadings: TRIF-Dependent

	Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6
IKBKB	0.169	−0.093	0.613	0.165	−0.249	−0.030
IKBKG	−0.028	−0.392	−0.184	0.122	0.229	−0.120
NFKB1	0.028	−0.002	0.904	−0.059	0.201	−0.179
IKBA	−0.175	0.131	−0.167	−0.053	−0.078	0.844
RELB	−0.792	0.097	0.023	−0.122	−0.086	0.015
REL	−0.387	0.335	−0.060	−0.350	0.541	0.182
TLR3	−0.003	−0.066	−0.100	0.064	−0.148	0.016
TLR4	0.006	0.579	0.053	0.508	0.302	0.319
TNFRSF14	−0.069	−0.084	0.255	0.001	−0.022	−0.103
TNFRSF1A	−0.027	−0.101	−0.004	0.882	−0.095	−0.202
TNFSF6	0.102	0.042	0.048	0.020	0.054	−0.202
TNF	−0.119	0.036	−0.057	−0.118	−0.015	0.913
TRADDa	0.179	−0.812	0.081	0.115	0.164	−0.159
TRADDb	0.069	−0.004	0.122	0.004	0.849	−0.100
TRAF2	−0.143	−0.714	−0.042	0.111	−0.328	0.202
TRAF5	0.518	−0.482	0.201	−0.353	0.041	−0.236
TRIFa	−0.187	0.149	−0.045	−0.046	0.073	0.118
TRIFb	−0.728	−0.101	−0.114	0.139	0.091	0.421

Table 5.

Factors, Eigenvalues, and Variance Explained: MyD88-Dependent

	Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6
Eigenvalue	3.496	2.055	1.933	1.576	1.245	1.016
% Variance Explained	21.163	12.443	11.699	9.538	7.539	6.153
Cumulative Variance	21.163	33.606	45.305	54.843	62.382	68.535

Highlights.

• Gene expression network of the nuclear factor kappa B (NF-κB) signaling network.

• Principal components factor analysis used to derive composite traits.

• Identified and localized quantitative trait loci (QTL) underlying the NF-κB signaling network.