Measures for characterizing directionality specific volume changes in TBM of brain growth

Abstract

Tensor based morphology (TBM) is a powerful approach to analyze local structural changes in brain anatomy. However, conventional scalar TBM methods are unable to present direction-specific analysis of volume changes required to model complex changes such as those during brain growth. In this paper, we describe novel TBM descriptors for studying direction-specific changes in a subject population which can be used in conjunction with scalar TBM to analyze local patterns in directionality of volume change during brain development. We illustrate the use of these methods by studying brain developmental patterns in fetuses. Results show that this approach detects early changes local growth that are related to the early stages of sulcal and gyral formation.

1 Introduction

Tensor based morphology (TBM) is now widely used as a method to detect structural brain differences across a population or across time. TBM studies involve statistical analysis of deformation fields computed from non-rigid registration of different anatomies. Scalar TBM, in its original form [1], is still being used to analyze structural changes caused by neurodegenerative conditions in adult brains [2]. But more recently, TBM is also being increasingly used for modeling of growth in developing brains [3] [4] [5]. However, a key weakness of scalar TBM is that it explicitly ignores directionality of volume changes. The multivariate, strain tensor metric proposed by Lepore et al. [6], captures anisotropic volume changes completely. However, this metric also ignores volume independent, local orientation changes within the brain, and is unable to specify the directionality of shape change for intuitive anatomical understanding [7]. Studying the complex shape changes during brain development is a key motivation for the extension of TBM to look at patterns of direction specific volume change. For example, development of the sylvian fissure in the fetal brain is related to superior-inferior expansions in the frontal and temporal lobes along with left-right contractions in the inferior aspect of the frontal cortex and superior aspect of the temporal cortex [8].

In this paper, we propose a method that allows us to study both volumetric and directional changes associated with growth modeling. Specifically we use polar decomposition to extract local orientation information from the deformation tensors. This orientation information is represented in the form of a measure of common directionality of growth, which is then analyzed to detect regions in which the rate of growth in a direction significantly changes. In this paper we (i) propose a descriptor to quantify population-wide direction change patterns; (ii) combine these with conventional scalar TBM so as to study population-wide changes in both volume and direction; and (iii) present a test to extract the primary growth direction at each tissue location. We evaluate the proposed methods by applying them to a study of fetal brain growth.

2 Methods

For a cross-sectional population of N subjects, we compute a transformation T_i i = 1, 2, …N for each subject, which maps the anatomical changes required to spatially normalize that particular subject to the average space. At each voxel p, the local changes can be derived from the deformation tensor which is defined as the gradient of the transformation ( $T_i^p[x,y,z]$) at that voxel and is given by $(J_i^p)=\left[\frac{{\delta }^3{T}_i^p[x,y,z]}{\delta x\delta y\delta z}\right]$ By computing J at each voxel, we form a map of local changes across the subject population. In this paper, we use the tensor decomposition properties of the Jacobian matrices to identify deformation direction.

2.1 Deformation Direction vector (DDV)

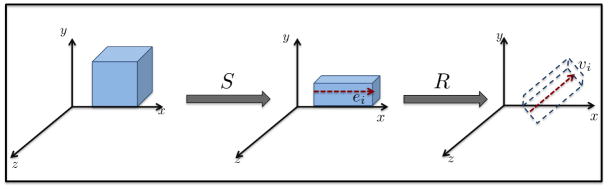
The principal deformation direction can be obtained from the principal component of the Jacobian matrix at each voxel. In order to avoid stability issues associated with eigen analysis of any Jacobian matrix, we leverage the polar decomposition property of J [9] to compute the primary deformation direction indirectly. At each voxel, the Jacobian matrix, being a second order tensor, can be separated into a rotational and a strain component.

$$J=RS$$ (1)

where S is the symmetric, positive definite strain tensor ( $S={(J^{T}J)}^{\frac{1}{2}}$). R = S⁻¹ J is the orthogonal, rotation matrix such that R⁻¹ = R^T and det R = +1. As illustrated Figure 1, this decomposition is analogous to first stretching the voxel by S and then rotating it by R to realize the deformation. Therefore, the direction of deformation, is computed by extracting the principal eigenvector of strain (e) from S, and rotation this by R yields the DDV. Here, we would like to emphasize that e only specifies the principal direction of strain and not the direction of the complete deformation. For each subject, we compute a DDV map (DDV at each voxel) which is used to analyze local changes in directionality.

Fig. 1.

Computation of deformation direction vector (DDV) from polar decomposition of Jacobian matrix

Statistical Analysis DDV

The DDV map can then be used in the TBM framework to detect population wide changes. In Equation 2, the basis vectors correspond to the three primary, orthogonal directions in reference anatomy: inferior-superior, left-right and anterior-posterior. The scalar multiplicative factors (x, y, z) from the DDV are separated to form three directional component maps (DCM). The DCM can be considered statistically independent within the single deformation tensor, as knowledge of the scalar component along one direction gives no information about the other two values in the DDV.

$$\mathit{DDV}(x_i,y_i,z_i)=x_i(1,0,0)+y_i(0,1,0)+z_i(0,0,1)$$ (2)

Regression

In order to minimize local variations in direction, the DCMs are individually smoothed by a Gaussian kernel. In this work, we chose the kernel size (σ= 2mm) experimentally so as to obtain the best final quality of the fitting. Using regression, we examine if there is a relationship between the basis vectors and variables of interest related to each subject (such as age or clinical criteria) using the multivariate general linear model at each voxel [10]. Growth models of DDV with respect to age can be performed using multivariate, multiple regression as shown in Equation 2.1. Here A corresponds to the vector of DCM values at each voxel, V₁, …, V_m are the independent variables (age, gender, clinical condition, etc.) and ε are the errors. (The matrix dimensions of each of the variables are indicated below each variables in Equation 2.1). Linear least square methods are used to solve for β₁, …, β_m at each voxel.

$$\begin{array}{ccc}A=& V_1{\beta }_1& +\dots +V_m{\beta }_m+\epsilon \\ (n\times 3)& (n\times 1)(1\times 3)& (n\times 1)\end{array}$$

Hypothesis Testing

Resulting regression coefficient (β₁, …, β_m) maps are tested for significance using a standard t-test. Statistical significance was computed and these were corrected multiple comparisons using permutation tests [11]. The corrected p-value maps of the three directional components can then be analyzed individually or can be combined using Fisher’s meta-analysis method [12] for independent tests. Let $h_o^1,h_o^2\dots h_o^k$ be the k independent null hypotheses being tested. Fisher’s meta-analysis tests the null hypothesis that all the individual null hypotheses are true. The alternate hypothesis of the meta-analysis is that at least one of the individual null hypothesis is false. The p-values from the individual tests are combined using the formula $\kappa =-2{\sum }_{i=1}^k{log}_e(p_i)$ where p_i is the p-value of the i^th individual hypothesis test. The meta-analysis statistic κ has a chi-squared distribution under the null hypothesis with 2k degrees of freedom.

The β₁, …, β_m values are estimates of increase or decrease in volume along a particular direction and the hypothesis tests estimate statistical significance of these changes. Multivariate hypothesis tests are not well suited for this metric as a meaningful covariance between directions cannot be established.

2.2 Principal Growth Direction (PGD)

In scalar TBM, the definition of volume change is well understood i.e. undeformed voxels have a Jacobian determinant of 1 and any deviation from this value is considered as change. For directional properties such a distinct baseline does not exist. Therefore, here we propose to start by first computing the most common growth direction at each tissue location across the population being studied and then analyze how directional growth is varying with respect to this direction at each location. For this we make use of the DDV map for each subject which provides orientation information specific to each subject at any given location. As described in Equation 3, PGD at a voxel is defined as the DDV (of a single subject) which has the least circular distance [13] from DDVs of all the other (N −1) subjects.

$$\mathit{PGD}=\underset{{\mathit{DDV}}_i}{argmin}\left(\sum _{j=1}^N\frac{1}{2}\left(1-\frac{{\mathit{DDV}}_i·{\mathit{DDV}}_j}{\mid {\mathit{DDV}}_i\left|\right|{\mathit{DDV}}_j\mid }\right)\right);\forall i\ne j;i=1,2,\dots N$$ (3)

The PGD map gives us a baseline which can be used along with the results from the directional TBM in Section 2.1 to study how these directionality of growth changes with age and development ⁴.

3 Application – Early fetal brain growth

The following experiments were performed using clinical MR scans of 40 fetal subjects at gestational ages ranging from 20.57 to 27.86 weeks. The mothers were referred for fetal MRI due to questionable abnormalities on prenatal ultrasound or a prior abnormal pregnancy. All women had normal fetal MRI and all newborns have had normal postnatal neurodevelopment. Fetal imaging was performed in our institution on a 1.5T scanner (GE Healthcare, Mulwaukee, WI) without sedation of the mother or the fetus. For each subject multiple stacks of single-shot fast spin-echo (SSFSE) T2-weighted slice images (pixel size 1 mm × 1 mm, slice thickness ≈ 3 mm) re acquired in the approximately axial, sagittal and coronal planes with respect to the fetal brain. The MR sequence parameters (TR = 4500 ms, TE = 91 ms) were originally designed for clinical scans and cannot be adjusted for image analysis purposes. High resolution 3D volumes were reconstructed from 2D slice MR images using the slice intersection motion correction (SIMC) technique [14]. The reconstructed volumes were automatically segmented into individual tissue types (developing grey matter, developing white matter, the germinal matrix) using an atlas-based approach with probabilistic atlases generated from a spatiotemporal model of the fetal brain [15]. Smoothed tissue segmentation atlases were then used with a template free elastic registration method [16] to spatially normalize the subjects. For each subject, the Jacobian matrix maps were computed, from the resulting deformation fields, to quantify the pattern of deformation required to spatially normalize individual anatomies. For each subject, we computed the DDV maps and performed multivariate, multiple linear regression on the population with age as the independent variable and the directional coefficients as the dependent variables. The regression coefficients were tested for statistical significance. We also computed, using the DDV maps, a PGD map for the subject population.

3.1 Results and Discussion

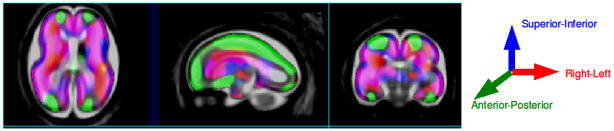
Figure 2 shows the principal growth direction for the given age range overlaid on the spatially normalized average MRI, and displayed using the Rview software⁵. Overall growth shows a distinct spatial pattern. The intermediate zone (developing white matter (WM)), along the most dorsal and ventral areas, is growing primarily in the anterior-posterior (A-P) direction during this period. Along the cortical plate, PGD alternates between superior-inferior (S-I) and right-left (R-L) growth direction corresponding to the formation of sulci and gyri respectively. At the sylvian fissure we see that the growth is primarily along the R-L direction corresponding to the deepening of the fissure. The ventricles do not show a clear direction of growth as during this period in fetal brain development, the ventricles do not change significantly in absolute size as the brain grows.

Fig. 2.

Principal growth direction (PGD) vectors for the group of fetal anatomies studied. Each reference anatomical direction is indicated by one color: red = left-right (R-L); green = anterior-posterior (A-P); blue = superior-inferior (S-I). The panels from left to right indicate axial, sagittal and coronal views of the brain.

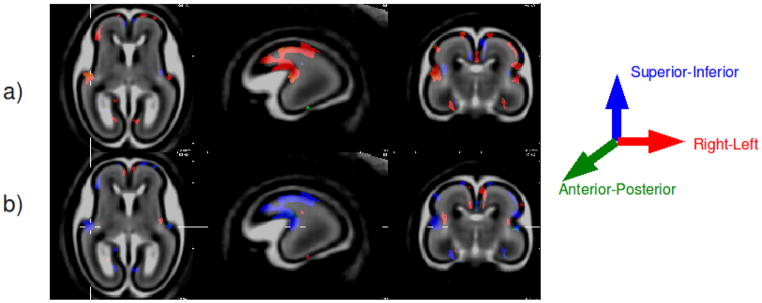
Figure 3 shows the regions where directional growth has changed significantly with age. The regions showing significant changes correspond to regions of major cortical folding. The largest cluster of significant voxels occur at the sylvian fissure where the significant acceleration of growth in the R-L direction and deceleration along the S-I direction indicate deepening of the fissure. As indicated by the cross-hairs, we see that the in addition to growth acceleration in the R-L direction, there is also a A-P growth component indicating “flattening” of the superior aspect of the temporal lobe at the sylvian fissure. To accommodate these changes in the cortical regions, we see that the intermediate zone underlying the fissure is being “stretched” in the S-I direction its growth in the R-L direction is restricted by neighboring structures.

Fig. 3.

Growth rate maps showing regions exhibiting significant change in growth direction with age. Row (a): Regions showing accelerated growth the associated anatomical direction. Row (b): Regions showing decelerated growth and the associated anatomical direction. Each reference anatomical direction is indicated by one color: red = left-right (R-L); green = anterior-posterior (A-P); blue = superior-inferior (S-I). The panels from left to right indicate axial, sagittal and coronal views of the brain.

Considering both Figures 2 and 3 together, we see that brain growth is characterized by spatially varying, directional growth. In some regions this directionality does not change significantly as the fetus matures. For example, the intermediate zone which showed a very strong A-P growth direction in Figure 2 does not exhibit significant accelerations and decelerations in any direction in the period of growth considered for this study. Major shape changes in the cortex occur due to significant changes in directional growth at sites of sulci and gyri. The effect of these changes in direction on underlying tissue is determined by the rate of those changes in the given time-period. For example, the rate of directional change associated with the formation of the calcrine sulcus is not large enough to significantly change directions in the underlying WM. In comparison, the formation of the sylvian fissure occurs at a more rapid rate and thereby significantly changes growth directionality both in the cortex and the underlying WM.

4 Conclusion

In this paper, we have introduced two novel descriptors that quantify directionality of change. This is the first time that local rotational information obtained from the deformation vector is being included in TBM analysis. The two descriptors are complementary in that the PGD describes the similarities in growth directions among the subject population and DDV regression allows us to detect changes in growth direction. The DDV can be incorporated into standard TBM framework and can be used along with other descriptors of volumetric changes. The clinical value of this method increases since we are able to specify a single direction of growth for the sake of intuitive understanding. The inclusion of directional growth information with standard TBM, allows us to detect additional changes in tissue structure. Directional information is particularly helpful in the study of brain development. Here, the combination of volume and direction change patterns are able to better explain the mechanism of brain growth than the study of volumes changes alone. That being said, the use of these descriptors need not be restricted to only brain development studies. Any TBM application where brain structural differences (within or between groups) arise from directional variations in tissue gain/loss can be studied using the proposed descriptors.

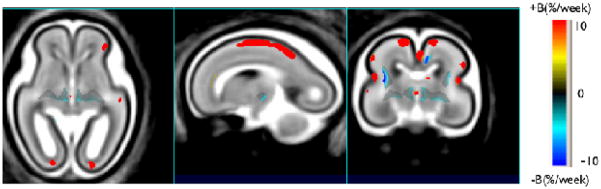
Fig. 4.

For comparison we have included growth rate (specified by regression coefficients, B) maps computed using scalar TBM. B value maps are overlaid on average MR image. Yellow and red regions correspond to accelerated growth and shaded blue regions correspond to decelerated growth when compared to supratentorial brain growth.