Implications of quantum metabolism and natural selection for the origin of cancer cells and tumor progression

Abstract

Empirical studies give increased support for the hypothesis that the sporadic form of cancer is an age-related metabolic disease characterized by: (a) metabolic dysregulation with random abnormalities in mitochondrial DNA, and (b) metabolic alteration – the compensatory upregulation of glycolysis to offset mitochondrial impairments. This paper appeals to the theory of Quantum Metabolism and the principles of natural selection to formulate a conceptual framework for a quantitative analysis of the origin and proliferation of the disease. Quantum Metabolism, an analytical theory of energy transduction in cells inspired by the methodology of the quantum theory of solids, elucidates the molecular basis for differences in metabolic rate between normal cells, utilizing predominantly oxidative phosphorylation, and cancer cells utilizing predominantly glycolysis. The principles of natural selection account for the outcome of competition between the two classes of cells. Quantum Metabolism and the principles of natural selection give an ontogenic and evolutionary rationale for cancer proliferation and furnish a framework for effective therapeutic strategies to impede the spread of the disease.

INTRODUCTION

Cancer is a group of some 200 diseases that involve a variety of changes in cell structure, morphology, and physiology. In an important review, Hanahan and Weinberg¹ enumerated several alterations in cellular dynamics and physiology that underlie the cancer phenotype. In our view, the three most critical features of cancer cells are

• 1.Self-sufficiency in growth signals and insensitivity to inhibitory signals,
• 2.Evasion of programmed cell death,
• 3.Limitless replicative potential with a potential for the invasion of other organs.

In addition to these demographic and physiological changes, most cancer cells utilize aerobic glycolysis irrespective of their tissue of origin. The alteration from oxidative phosphorylation to glycolysis – called the Warburg effect – is quasi-universal and has now become a diagnostic tool for cancer detection.

The upregulation of glycolysis in cancer cells has damaging effects on the mitochondrial genome, which in turn can lead to metabolic dysregulation and alterations in cellular dynamics. The problem, which now emerges can be stated as follows. Is the upregulation of glycolysis, the primary cause of cancer, as Warburg contended, or as is currently debated,^{2, 3} is cancer the result of specific nuclear gene mutation or chromosomal abnormality?

A resolution of this problem would have important implications regarding therapeutic strategies for the disease. Genomic and chromosomal abnormalities as the primary causes would entail radiation and chemotherapy as the dominant means of managing the disease. However, metabolic dysregulation as the primary cause^{4, 5, 6} would imply both diagnostic and therapeutic strategies based primarily on metabolic intervention, such as monitoring and normalizing glycolytic and oxidative phosphorylation activity in cancer and in normal cells.

The genomic perspective has dominated both research and management strategies of cancer. This dominance prevails in spite of the fact that the genomic paradigm does not readily accommodate certain critical observations concerning the incidence of the disease. The three most pertinent observations, which are inconsistent with the genomic model, can be classified under the following rubrics:

• 1.Ontogenetic: Cancer incidence is tissue specific; epithelial cells are more cancer prone than mesenchymal cells, and incidence and severity varies markedly from one organ to another.⁷
• 2.Epidemiological: Cancer incidence increases exponentially with age and abates with age at advanced ages.⁸
• 3.Phylogenetic: Cancer is widespread among multicellular organisms, but cancer incidence is species dependent. The number of genetic events necessary to induce malignant transformation is fewer in mice than in humans. Spontaneous regression of tumors is common in mice but rare in humans.⁹

Genomic instability, i.e. mutations in the nuclear genes, as the primary cause of cancer can also be questioned by appealing to mutagenetic data. Most cancer cells express many and different types of nuclear gene mutations. However, the large number and variety of pathogenic mutations are not consistent with the low mutation rate of most nuclear genes. Epidemiological studies indicate that cancer causing gene mutations are rare and the vast majority of cases are sporadic in origin.⁶

The difficulties in reconciling these classes of observations with the genomic model have stimulated a renewed interest in the metabolic hypothesis proposed originally by Warburg.^{10, 11} A new variety of studies now furnish strong evidence to indicate defective energy metabolism due to mitochondrial dysfunction¹² as characterizing nearly all sporadic cancers irrespective of cellular or tissue origin. The alteration in metabolic activity, from oxidative phosphorylation to glycolysis to accommodate this dysfunction, is the basis for a new class of analytic models of the origin of cancer cells.⁵ These models invoke metabolic instability as the primary cause of cancer. While a shift to glycolytic metabolism in terms of the energy production may only be on the order of 20% of less, in view of the vastly lower efficiency of the glycolytic pathway (almost an order of magnitude lower than oxidative phosphorylation), the consumption of glucose is actually predominantly directed towards glycolysis, which leads to an increased demand on nutritional resources with tumor progression.

In view of these considerations, the origin and proliferation of cancer can now be seen to be driven by the following sequence of events:

• 1.Metabolic instability: Impairment of mitochondrial function with a resulting damage to the respiratory mechanism.
• 2.Metabolic alteration: The upregulation of glycolysis – an essential compensatory mechanism of energy production that functions to ensure cell viability by stabilizing the amount of ATP produced.
• 3.Natural Selection: The competition between normal cells utilizing predominantly oxidative phosphorylation, and tumor cells utilizing predominantly glycolysis.

  These three events constitute the driving force which, we believe, ultimately leads to what was originally considered the primary cause, namely

• 4.Genomic instability: The increased vulnerability of tumor suppressor genes due to mitochondrial impairments.

This sequence of events underscores metabolic instability as the principal cause of cancer and genomic instability as a consequence. The genomic abnormalities observed can now considered to be the result of mitochondrial dysregulation that increases the production of reactive oxygen species and accelerates aberrant cell-cell signaling.

In this model, the metabolic instability which induces respiratory damage is due to abnormalities in mitochondrial DNA, the electron transport chain, or in the structure of the phospholipids that form the inner mitochondrial membrane. Cancer is thus seen as primarily an age-related, multi-stage¹³ metabolic disease¹⁴ whose origin lies in the cumulative effects of molecular instabilities in the mitochondria and the cytosol.^{5, 6}

The phylogenetic, ontogenetic and epidemiological features, we have noted are consistent with this metabolic perspective. The species-dependence of cancer incidence can be illustrated by contrasting the ecological and evolutionary history of humans and mice;¹⁵ humans and mice have experienced different ecological constraints throughout their evolutionary history. Mice are opportunistic species characterized by large fluctuations in resource abundance. Humans are an equilibrium species whose vital resources are limited and showing small variation in abundance. The evolutionary models¹⁶ predict that opportunistic species evolve to states defined by weak demographic stability, with population numbers highly sensitive to random perturbations in their individual birth and death rates. Equilibrium species evolve to states of strong demographic stability with population numbers relatively insensitive to random perturbations in the individual birth and death rates. The positive correlation between demographic stability and metabolism entails that opportunistic species such as mice will have metabolic networks which are highly vulnerable to the effects of abnormalities in mitochondrial DNA, whereas equilibrium species such as humans, will have metabolic networks which are robust and resilient against such perturbations. The comparative studies of the rate of mitochondrial mutagenesis in mice and humans¹⁷ are consistent with these predictions. The higher metabolic stability of human cells in comparison with murine cells entails that the number of genetic events necessary to induce malignant tumors will be greater in humans than in mice. This concurs with the power law dependence, which is close to a sixth power of age for most types of cancers,⁷ of the incidence of cancer as a function of age based on epidemiological data for mice and humans,¹ respectively.

The tissue dependence of cancer prevalence is demonstrated by differences in the metabolic stability of mesenchymal cells and epithelial cells and the tendency of laboratory mice to develop cancer in cells of mesenchymal tissues such as lymphomas and sarcomas, rather than in cells of epithelial origin leading to carcinomas. The exponential increase in cancer incidence with age and the stabilization of this incidence at advanced ages is consistent with predictions based on the evolutionary dynamics and metabolic theory of aging. This theory predicts that the mortality rate of equilibrium species such as humans will increase exponentially with age and abate at advance ages, generating what is now called the mortality plateau.

The claims we have just described regarding the metabolic instability hypothesis for the origin of cancer are primarily phenomenological. However, there exists analytic support for the claim that the sporadic form of cancer is an age-related metabolic disease. This support derives from formal and analytic ontogenic and evolutionary models of cells and organisms.

Ontogenetic processes have been analyzed in a class of models called Quantum Metabolism – an analytic model of energy transduction in cells.^{18, 19} This formalism exploits the methodology of the quantum theory of solids to derive analytic expressions for the cellular metabolic rate in terms of cell size. These expressions show that metabolic rate is highly dependent on the mode of coupling between the electron transport chain and ADP phosphorylation, and predicts different parameter values for cells utilizing oxidative phosphorylation and cells utilizing glycolysis. Quantum Metabolism thus provides an analytic framework for distinguishing between metabolic rate in normal cells and cancer cells. The theory represents a cornerstone for the analysis of the origin of cancer cells.⁵

The proliferation of cancer cells has been analyzed in terms of a class of models called directionality theory – an analytic study of genotype and phenotype changes in cellular populations under the forces of mutation and natural selection.²⁰ The main concept in directionality theory is evolutionary entropy, a measure of the diversity of the pathways of energy flow within individual cells in a replicating population. The demographic parameter evolutionary entropy predicts the outcome of competition between incumbent populations and the variant that arises due to mutations. It is the basis for an entropic selection principle which specifies the conditions under which one cell type will replace another due to natural selection. The concept thus plays a central role in the analysis of conditions which evolve the proliferation of cancer cells which are in competition with normal cells for the existing space and nutritional resources.

The main objective of this article is to delineate various diagnostic, preventive and therapeutic strategies for cancer, which emerge from the proposition that sporadic cancer is intrinsically a metabolic disease. These strategies are intimately linked to analytical arguments based on Quantum Metabolism and directionality theory. In view of this, we will give a brief account of the analytic basis, which underlies these theories, and then discuss the cancer therapeutic strategies, which derive from the applications of these theories to the study of cancer.

This article is organized as follows: Section 2 gives a brief overview of Quantum Metabolism. Section 3 describes the entropic selection principle. In Section 4 we show how the integration of these two models suggests several classes of metabolic interventions, which could play a critical role in cancer therapy. The nature of these interventions is intimately linked to the Quantum Metabolism theory. This theory gives explicit expression for the metabolic rate of normal and cancer cells. These expressions suggest how the metabolic rate can be modified in order to alter the selective advantage of normal cells in comparison to cancer cells, thereby arresting the transition towards malignancy. Section 5 discusses therapeutic strategies.

QUANTUM METABOLISM

Energy transfer in material solids is driven primarily by differences in intensive thermodynamic quantities such as pressure and temperature. Empirical studies show that temperature and the specific heat of solids satisfy certain empirical relations – as embodied for example in the Dulong and Petit law. The quantum theory of solids, as developed by Einstein and later by Debye, was proposed to explain these empirical relations. The crucial observation in these models was the consideration of the heat capacity as associated with the vibrations of atoms in a crystalline solid.²¹

However, living organisms are essentially isothermal. There is very little difference in temperature between different parts of a cell. On the other hand, energy flow in living organisms is mediated by differences in the turnover time of various metabolic processes in the cell, which occur in cyclical fashion. Empirical studies that go back to Kleiber in 1961²² have shown that the cycle time of these metabolic processes is related to the metabolic rate, that is the rate at which the organism transforms the free energy of nutrients into metabolic work, maintenance of constant temperature and structural and functional organization of the cells. Quantum Metabolism^{18, 19} exploits the methodology of the quantum theory of solids to provide a molecular level explanation of these empirical relations. This molecular explanation drives the derivation of the new rules relating metabolic rate and body size.

Energy transduction in material solids: Material oscillation

Einstein and Debye (see for example Ashcroft and Mermin²¹) both considered the heat capacity as associated with the harmonic vibrations of atoms in a crystalline solid. The vibrations were treated according to quantum theory and satisfied the following tenet:

Quantization principle for material oscillation: The energy stored by an oscillator with frequency ω can only be an integral multiple of a fundamental energy quantum hω:

$$E_n=nh\omega ,n=1,2,3,...$$ (1)

Here, h is Planck's constant. Einstein's model was based on the assumption that the vibrational motions of the various atoms are decoupled from one another and all atoms in the crystal vibrate with the same frequency. The model proposed by Debye, which proved to be more consistent with empirical observations, assumed that the atoms in the solid execute coupled vibrations about the fixed lattice site leading to the propagation of waves (phonons) in the solid and the frequencies of these vibrations span a range of values from zero to a maximum (Debye) frequency.

Energy transduction in cells: Enzymatic oscillators

The production of ATP, the energy currency of living organisms is mediated by the coupling of two molecular chains:²³

• 1.The redox chain, which describes the transfer of electrons between redox centers within the electron-transport chain.
• 2.The ATP-ase motor, which is involved in the phosphorylation of ADP to ATP.

There are two distinct mechanisms by which these two events are coupled: oxidative phosphorylation, which involves an electrical process, and substrate phosphorylation, which implicates a purely chemical process. The transfer of electrons between redox centers is described by a cyclic scalar process, which induces a vectorial process characterized by a net movement of protons from one molecular center to another. The transit time of this cyclic process determines the total metabolic flux, that is, the number of proton charges released by the redox reactions. This transit time, which we call the metabolic cycle time, denoted τ, will play a fundamental role here. In oxidative phosphorylation, which occurs in the mitochondria, the electron transport between redox centers is coupled to the outward pumping of protons across the mitochondrial membrane thus generating an electrochemical gradient, called the proton motive force, Δp. Substrate phosphorylation, which is localized within the cytosol is driven by a set of enzymes which couple ADP phosphorylation to the electron transport chain.

The molecular dynamics model proposed to investigate this coupling by electrical and chemical means assumes that the energy generated by the redox reactions can be stored in terms of coherent vibrational modes of enzymatic oscillators embedded in the cellular organelles.

Quantum Metabolism rests on the notion that the enzymatic oscillations in cellular organelles and the material oscillators in crystalline solids can be analyzed in terms of the same mathematical formalism used by Einstein and Debye in the quantum theory of solids. This realization is deduced from a formal correspondence between the thermodynamic variables in physical systems, and the metabolic quantities in biological processes. The principal variables in the quantum theory of solids are the specific heat, the Gibbs-Boltzmann entropy and the absolute temperature T. The fundamental unit of energy is given by E = k_BT, the typical thermal energy per molecule.

The critical variables in the theory of quantum metabolism are the metabolic rate, the entropy production rate and the mean cycle time, τ. This quantity describes the mean turnover time of the redox reactions within the cellular organelles. The fundamental unit of energy is now given by E(τ) = gτ. Here, the value assumed by g will depend on the mechanism, electrical or chemical, by which the electron transport chain is coupled to ADP phosphorylation. The correspondence between the thermodynamic variables and bioenergetic quantities is given in Table 1.

Table 1.

The correspondence between thermodynamic variables and bioenergetic quantities.

Thermodynamic variables	Bioenergetic quantities
Temperature (K)	Metabolic cycle time (s)
Specific heat (J kg-1 K-1)	Metabolic rate (J kg-1 s-1)
Gibbs-Boltzmann entropy (J K-1)	Entropy production rate (J K-1 s-1)

Note that since physical systems are described here at thermodynamic equilibrium, their parameters involve thermodynamic variables. Biological systems operate far from thermodynamic equilibrium (albeit close to steady states), hence their bioenergetic quantities involve fluxes, i.e. rates of change of energetic values.

The analytical basis for this correspondence is the following tenet: The rate of energy production in chemical reactions in cells satisfies a variational principle which is formally analogous to the minimization of the free energy in equilibrium statistical physics.

The above tenet and the formal correspondence in Table 1 derive from a general variational principle in the ergodic theory of dynamical systems; see Demetrius²⁴ and Arnold et al..²⁵

Quantum metabolism appeals to the following analogue of Planck's quantization principle:

Quantization principle for enzymatic oscillators: The metabolic energy stored by an enzymatic oscillator with frequency ω is quantized according to the following rule:

$$E_n=n\kappa \omega$$ (2)

Here, κ is an analogue of Planck's constant and we will refer to it as the biological Planck's constant. Quantization is due to integer ATP numbers being produced in the cell's mitochondria and their relatively low energy content comparable to physical quantum processes.²⁶ This is discussed in detail in a later section. In exploiting this quantization principle, the model appeals to two critical assumptions analogous to those made by Debye in the study of material oscillators forming a lattice of crystalline solids.

Enzymatic oscillators and cycle time

We introduced the term enzymatic oscillator since enzymes undergo electrochemical oscillations about their fixed positions. These oscillations are generated by the metabolic energy associated with the transfer of electrons between donor and acceptor pairs in the electron transfer chain in mitochondria. A number of recent papers provided a description of cells^{27, 28} and mitochondria as individual oscillators whose dynamics may obey collective, network properties in terms of high-amplitude, self-sustained and synchronous oscillations of bioenergetic parameters under both physiological and patho-physiological conditions.²⁹ Since their power spectrum exhibits an exponent vastly different from that for random behavior, a description of the metabolic activity involving mitochondrial proteins involves coupled quantum oscillators of the Debye type.

Based on typical data for ion pumps in biological membranes, the range of values expected for the cycle time τ is found to be between 10^-6 s and 10^-3 s.^{30, 31, 32, 33} The energy generated per cycle, gτ, is on the order of 10^-20 J which corresponds to the value of energy for the almost universal energy currency in biological systems which is due to the hydrolysis of the ATP (or less frequently GTP) molecule. ATP synthesis in a mitochondrion or a chloroplast requires approximately 60 kJ/mol of energy delivered through electron transport reactions or absorption of photons, respectively. ATP hydrolysis releases approximately 30 kJ/mol of free energy (dependent on the concentration and pH values), which can be viewed as a biological energy unit or quantum. The human body requires the production of its weight in ATP every day in order to function,³⁴ which translates into 10²¹ ATP molecules per second. Since there are on the order of 3.5 × 10¹³ cells in the human body and each cell has on the order of 10³ mitochondria, there are approximately 3 × 10⁴ ATP production events per mitochondrion per second. This involves a complex set of biochemical reactions called oxidative phosphorylation whose net effect is a conversion of 1 molecule of glucose into 38 molecules ATP. Consequently, the frequency of the oxidative phosphorylation reaction is approximately 1,000 Hz for each complex or the characteristic time scale is 10^-3 s as stated above.

Using the energy quantization identity E₀ = κf and substituting the energy value for ATP production with its characteristic frequency, we readily estimate the value of the biological equivalent of Planck's constant to be κ = 10^-24 J/s which, when compared to the physical Planck's constant h = 6.6 × 10⁻³⁴ J/s, gives a ratio of κ/h = 1.8 × 10¹¹. This is a very large number but it may have a simple explanation. While the physical Planck's constant corresponds to a single atom and a single quantum of energy taking it to a higher energy state, the biological constant corresponds to a single energy-producing organelle, namely a mitochondrion. There are approximately 1.9 × 10¹⁴ atoms per cell and approximately 1000 mitochondria per cell, which gives 1.9 × 10¹¹ atoms per mitochondrial “sphere of influence” within the cell. This means that an energy unit produced in a mitochondrion may be imparted to any of these atoms in its vicinity. This number (1.9 × 10¹¹) is reasonably close to the value of κ/h=1.8 × 10¹¹. The so–defined biological Planck constant does not necessarily refer to quantum mechanical nature of the process (such as, e.g., the particle-wave duality) but to a discrete form of biochemical energy and a formal analogy at the level of mathematical description of metabolism as will be discussed below.

It is also worth briefly pointing out another physical aspect of cellular metabolism, namely its collective character resulting in synchronized oscillations that propagate through biological matter. Assuming that metabolic processes propagate in a wave-like fashion, and using the standard relationship between the wavelength λ, propagation velocity v, and frequency f, λ = v/f, with v on the order of 1 μm/s and f = 1000 Hz, as stated above, we find that λ is on the order of 1 nm. This is consistent with the value of proton displacement in electric fields of mitochondrial membranes.^{30, 31}

Metabolic rate and body size

The fundamental variables in the theory of quantum metabolism are the metabolic rate, P, the rate at which the cell transforms resource energy into cellular work, and the cycle time τ, the mean turnover time of the metabolic processes in the cellular organelle. These two quantities, as shown by Demetrius and Tuszynski,¹⁹ are analytically related by means of an expression formally analogous to the relation between specific heat and temperature in the quantum theory of solids. We have P ∼ τ^d.

The meaning of the dimensionless parameter d, 0 < d < 3, is explained below. The total metabolic flux generated by the enzymatic reactions depends on the geometric configuration of the enzymes localized within the cellular matrix. The metabolic flux is related to N(r), the total number of metabolites crossing a cell boundary of radius r per unit time, t. For systems where the enzymes are localized in a plane within the cellular matrix, we have N(r) ∼ r². In systems where the enzymes are distributed uniformly within the cell, we have N(r) ∼ r³. In general, we introduce a simple scaling relation between N and r:

$$N\left(r\right)=a{r}^d$$ (3)

where d, the effective dimensionality of the network, can be viewed as the number of degrees of freedom of the enzymes embedded in the cellular matrix. In view of Eq. 3, we define the dimensionality of the oscillator network, d, as

$$d=\underset{r\to \infty }{lim}\left(\frac{\log N\left(r\right)}{\log r}\right).$$ (4)

Clearly, the parameter d depends on the internal organization of the oscillator network. The above arguments entail the following characterization of the dimensionality parameter. In the case of mitochondria, d in most cases is expected to correspond to the Euclidean dimension D of the embedding physical space (D = 1, 2, 3), since energy transfer across the membrane is by mass transport.

The above relation between P and τ underpins the allometric rules relating metabolic rate and body size for both unicellular and multicellular organisms. The derivation rests on the total metabolic energy, U, generated by the metabolic processes and the following characterization in terms of metabolic rate P = U/τ, and body size U = aW.

These considerations yield the allometric rule:

$$P=\alpha W^{d/d+1}$$ (5)

The proportionality constant α in Eq. 5 is given by α = cg where c is a numerical constant. The characterization of g, as noted earlier, is conditional on the mode of coupling between the electron transport chain and ADP phosphorylation.

Electrical coupling. When the mode of coupling is electrical, a situation which occurs when energy production is largely by oxidative phosphorylation, the parameter g is determined by proton transduction within and across the bio-membrane. The bioenergetic parameter, C, stands for proton conductance and Δp for the proton motive force are the critical variables. We have

$$C=C_{o}exp(-\Delta E/RT).$$ (6)

Here, ΔE is the activation energy and R is the gas constant. The proton gradient Δp is given bythe well-know formula in biophysics, namely

$$\Delta p=\Delta \psi -(2.3RT/F)\Delta \mathrm{pH}.$$ (7)

where ΔΨ is the membrane potential, and F denotes Faraday's constant.

Chemical coupling. When the mode of coupling is chemical, as in the case of substrate phosphorylation, the parameter g is determined by the reaction rates of the glycolytic enzymes and we have

$$g^{\prime }=g_0\exp (-\Delta G/RT).$$ (8)

where ΔG is the activation free energy.

In both cases g has an Arrhenius form being proportional to exp(−βΔE) where β =(RT)^-1 as has been determined empirically for a number of species.³⁵

The relations Eq. 7 and Eq. 8 indicate that the metabolic rate of cells using oxidative phosphorylation will be dependent on the bioenergetic parameters that characterize the mitochondrial membrane; in cells utilizing glycolysis, the metabolic rate will be dependent on the activity of the glycolytic enzymes. These differences between the two major mechanisms of metabolic energy production will play an important role in our study of competition between the two classes of cells.

THE ENTROPIC PRINCIPLES OF SELECTION

Most normal cells utilize predominantly oxidative phosphorylation as a mechanism to generate ATP. Most cancer cells utilize predominantly glycolysis. This altered metabolism, the upregulation of glycolysis, is the strategy cells with impaired mitochondrial function (and/or driven by hypoxia) adopted in order to obtain adequate ATP for their metabolic needs. The cells with up-regulated glycolysis exhibit several of the recognized hallmarks of cancer cells. The proliferation of cancer cells is therefore contingent on the outcome of competition between the cells with predominant oxidative phosphorylation activity and the cells with up-regulated glycolysis.

Evolutionary entropy, as defined for a population of replicating cells, is given by

$$S=-\sum _{j=1}^d{p}_j\log p_j.$$ (9)

Here d is the number of different states of the cell cycle. The quantity p_j describes the probability that the “mother” of a random “daughter” cell is in the stage j of the cell cycle.

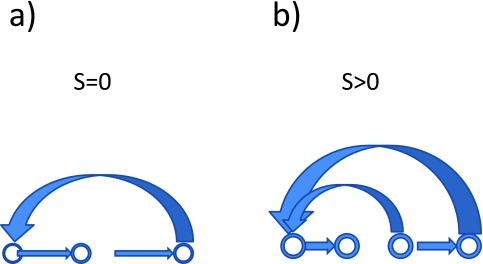
The quantity S describes the diversity of energy flow within the population and characterizes the variability in the rate at which the cells pass through the various stages of the cell cycle. A population in which all cell pass through the stages of the cell cycle at the same rate and with the same phase – a synchronous population – has entropy zero. A population in which each cell passes through the different phases of the cell cycle at different rates has positive entropy – an asynchronous population. See Figure 1.

Figure 1.

A diagram of energy flows within populations of cells. (a) Synchronous population: In this model there is a unique pathway of energy flow, hence S = 0. (b) Asynchronous population: In this model there are multiple pathways of energy flow hence S > 0.

The entropic principle of selection is a set of rules that predicts the outcome of selection between cells with different phenotypes. The principle asserts that the outcome of natural selection is a stochastic process, which is contingent on the resource constraints – its abundance and its diversity, and predicted by evolutionary entropy.

Evolutionary entropy as a measure of selective advantage

The dynamics of selection involving a resident population of size M, say a rare variant, is dependent on the population size and the resource abundance, R. When resource abundance and population size are both infinite, the outcome of selection is predicted by the population growth rate. However, when resources are finite in abundance, and population size is finite, it was shown¹⁶ that the outcome of selection is contingent on the resource abundance and its diversity and predicted by the demographic parameter evolutionary entropy, a measure of diversity of energy flow in the population.

The selective advantage, denoted s, in this class of models can be quantified by introducing the function

$$s=-(\Phi -\gamma /M)\Delta S.$$ (10)

Here, ΔS = S* − S, where S and S* denote the evolutionary entropy of the incumbent (e.g. normal cells) and variant (e.g. cancer cells) populations, respectively. The quantity Φ, the reproductive potential, and γ, the demographic index, are statistical parameters, which depend on the age or stage specific mortality and replication rates of the individual cells in the population. Here, Φ and γ have units of inverse time. These parameters characterize certain measures of the resource constraints and have been precisely defined and discussed elsewhere.^{20, 36} Briefly, the following two situations may arise leading to the same outcome, where the variant population increases in frequency: (a) Φ <0, γ >0, ΔS >0, and (b) Φ >0, γ <0, ΔS <0. If we let M tend to infinity, then the selective advantage becomes: s = −Φ ΔS, and we have the corresponding conditions for the variant population increasing in infrequency: (a) Φ <0, ΔS >0, and (b) Φ >0, ΔS <0.

The parameters Φ and γ are demographic but they characterize certain properties of the environment, namely its abundance and diversity as follows: (i) Φ <0, resources constant and limited, (ii) Φ >0, resources vary in abundance, (iii) γ <0 resource with homogenous composition; a singular resource, and (iv) γ >0 resource with heterogenous composition, diverse resource. The mathematical basis of Φ and γ is described elsewhere.^{20, 36}

The term selective advantage describes the restrictions on the parameters Φ, γ and the demographic variable S, which determines the sign of s and hence the outcome of competition between the two types. When s > 0, the variant type X^* will increase in frequency and displace the resident; when s < 0, the variant type, initially rare, will become extinct with a certain probability dependent on the population size of the resident.

The expression for s given by Eq. 10 furnishes a set of conditions on resource abundance described by Φ, and diversity characterized by γ, which determines the success or failure of the variant type X^* in the competition for resources. This set of criteria is called the entropic principle of selection. These criteria are qualitatively depicted as follows:

• (Ia)When resources are diverse in composition, and abundance is constant and limited, variants with increased entropy will almost always increase in frequency.
• (Ib)When resources are singular in composition, and undergo large variations in abundance, variants with decreased entropy will almost always increase in frequency.

We can furthermore infer from the measure of selective advantage given by Eq. 10, that when M tends to infinity, the measure of selective advantage is now given by s = −Φ ΔS. Implications of Eq. 10 can be summarized as follows. If (Φ − γ/M) <0, ΔS > 0, which implies also Φ <0, γ >0, the variant population increases in frequency. If (Φ − γ/M) >0, ΔS <0, which implies Φ >0, γ <0, the variant increases in frequency as well.

This measure indicates that for infinite size, the selective outcome is now determined uniquely by resource abundance. We now have the following criteria:

• (IIa)When resource supply is constant and limited, the variants with increased entropy will prevail.
• (IIb)When resources are subject to large variation in abundance, the variants with decreased entropy will prevail.

The metabolic principle of natural selection

The entropic principle of natural selection describes selective criteria in terms of evolutionary entropy.³⁷ It is a measure of demographic stability, that is, the rate at which the population returns to the steady state condition after a random perturbation in the cellular replication and survivorship rate.

As shown recently by Demetrius, Legendre and Harremoes³⁸ evolutionary entropy is analytically related to the metabolic rate. This is given by

$$S=a+\log P,$$ (11)

where a is a taxon-specific constant.

Now cells utilizing oxidative phosphorylation and cells utilizing glycolysis differ in terms of their metabolic rate. We now appeal to the selection principle to derive a criterion for selective outcome involving a population of cells utilizing oxidative phosphorylation, and a variant population, utilizing glycolysis. Here, we assume that population size is sufficiently large that the effects of resource diversity on selection can be neglected.

In view if Eq. 11, ΔP ΔS >0, and the measure of selective advantage can be expressed in terms of the metabolic rate S= -Φ ΔP, hence both (i) Φ<0, ΔP>0 and (ii) Φ>0, ΔP<0, lead to the variant population increases. We state it as follows when adapted to the context of cancer cells.

• (IIIa)When resources are constant and limited, cells utilizing oxidative phosphorylation will increase in frequency.
• (IIIb)When resources are subject to large variation in abundance, cells utilizing glycolysis will increase in frequency.

The principles (IIIa) and (IIIb) constitute the basis for the evolutionary rationale of the Warburg effect, that is the increased glycolytic flux observed in cancer cells. The metabolism of glucose to lactate by glycolysis generates only 2 ATP molecules per molecule of glucose, whereas oxidative phosphorylation generates up to 36 molecules of ATP upon complete oxidation of one glucose molecule. The question which this raises concerns the selective advantage of a less efficient metabolism, glycolysis. The metabolic selective principle asserts that the selective advantage is conditioned by the cellular microenvironment – the diversity and the magnitude and variation in abundance of the resource. Large variations ion oxygen and glucose characterize the microenvironment of cancer cells. This condition confers a selective advantage to a fermentative metabolism and explains the growth advantage, which the Warburg effect confers on cancer cells.

THE ORIGIN OF CANCER

A central tenet of modern molecular biology is the primacy of the genetic program in monitoring the transition in an organism from conception to reproductive maturity. All cells in the reproductively mature organism are genetically identical; the physiological and phenotypic differences in cell types in the reproductively mature organism are derived from differences in gene expression.

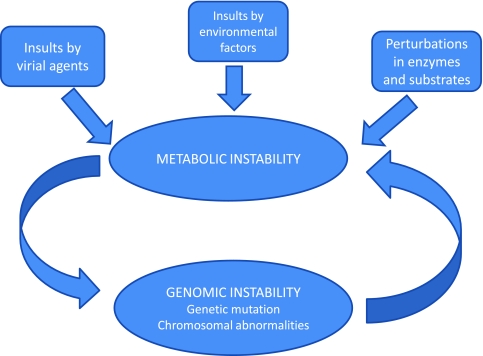
Aging can be described as the continuous decline in the production of metabolic energy and the increased spreading of the energy over the various storage modes in the macromolecules that are involved in energy transduction within the cell. This spatial spreading of energy increases the vulnerability of the cell to injury from external forces and concomitantly the susceptibility of the organism to age-related diseases.³⁹ The process can be described by the following sequence of events (see Figure 2):

• 1.Molecular instability. This process refers to the reduction in the energy states of the molecules that determine the cellular metabolic network. These bioenergetic changes are the result of random losses in molecular fidelity and a concomitant increase in thermodynamic entropy. Accordingly, aging is not the result of a genetic program but a consequence of a stochastic process. The cumulative loss of molecular fidelity will ultimately overwhelm the processes of damage repair and thereby increase the vulnerability of the cell to injury by external agents.
• 2.Metabolic instability. This notion pertains to impairment in the energy producing organelles and hence a damage in the capacity of these organelles to maintain stable concentrations of ATP. The vulnerability of the metabolic networks to pathology will depend on the level of molecular instability induced by the aging process. The magnitude of molecular instability increases with age and abates with age at advanced age. Thus, cancer is an age-related disease whose incidence will increase with age and stabilize at advanced ages.
• 3.Metabolic alteration. This refers to the upregulation of glycolysis to compensate for the decline in ATP production by oxidative phosphorylation. The cellular microenvironment confers a selective advantage to cells adopting the glycolytic mode of energy transduction. This leads to the proliferation of the cancer phenotype.
• 4.Genomic instability. Aerobic glycolysis has a disruptive effect on the oncogenes and tumor suppressor genes. This leads to increase mutability of the nuclear genome – an event we describe by the term genomic instability. The loss of the genomic caretakers involved in sensing and repairing DNA damage will in turn dysregulate energy processing in the mitochondria and thereby induce metabolic instability. The cyclic process involving genomic and metabolic instability will enable pre-malignant cells to attain the various hallmarks of cancer.

Figure 2.

A schematic illustration of the transition to malignancy.

The program of cancer initiation we described here can be triggered by a large family of unspecific conditions, namely: viruses, carcinogens, inflammation and ionizing radiation.⁶ These unspecific conditions do not necessarily directly cause cancer: they simply accelerate the transition to metabolic instability. The theory we have described indicates that the transition towards the cancer phenotype is determined by the selective advantage of the cells utilizing the glycolytic mode of energy production. The selective advantage depends on two main factors: (a) the abundance and the diversity of the resources the cells utilize, and (b) the relative metabolic rate of the normal and tumor cells.

THERAPEUTIC STRATEGIES

Our model for the origin of cancer contends that sporadic cancer is an age-related metabolic disease. From this perspective, normal cells are characterized by the oxidative phosphorylation mode of metabolic regulation, and cancer cells are described by the glycolytic mode of energy processing.

Our analysis of metabolic dysregulation as the primary cause of the disease suggests that therapeutic strategies, which are based on impeding the transition from an oxidative mode of regulation to a glycolytic mode, may be an effective approach in controlling the disease.

Quantum metabolism and the entropic principle of selection are two theoretical frameworks for developing effective therapeutic strategies. According to Quantum Metabolism, cellular metabolic rate depends on the mechanism of energy processing, oxidative phosphorylation or glycolysis. The scaling coefficient, α, in cells using oxidative phosphorylation is determined by the bioenergetic parameters, proton conductance, C, and the proton-motive force, Δp. Here, we have α ∼ C Δp where Δp = ΔΨ − a ΔpH, with ΔΨ denoting the membrane potential and ΔpH representing the change in pH across the membrane.

The scaling coefficient for cells utilizing glycolysis depends on the mean reaction rate K of the glycolytic enzymes, hence α ∼ K.

According to the entropy selection principle, the outcome of competition between normal cells utilizing predominantly oxidative phosphorylation and the cancer cells utilizing predominantly glycolysis is conditional on the diversity and the variation in resource abundance of the microenvironment. We have the following:

• 1.A diverse resource, which is constant and limited, will favor cells with oxidative phosphorylation activity – the normal cells.
• 2.A singular resource, which is subject to large variations in abundance will favor cells with glycolytic activity – the cancer cells.

These two classes of observations furnish a theoretical basis for the following types of therapeutic strategies:

• (I)Modifying the metabolic rate of cancer cells.

  The allometric scaling laws for metabolic rate which Quantum Metabolism describes suggest the following class of metabolic interventions: (a) The use of drugs which target the glycolytic and pentose phosphate pathway enzymes, (b) Imposing limitations on substrate abundance and increasing the diversity of possible substrates, and (c) Lifestyle modifications – diet and exercise.

• (II)Modifying the metabolic rate of normal cells.

  The analysis indicates that in the case of cells using oxidative phosphorylation, the metabolic rate is dependent on bioenergetic parameters. These quantities are the proton conductance and the proton-motive force. The latter is determined by the membrane potential and the difference in pH across the membrane. Consequently, the membrane composition will play a critical role in regulating the metabolic rate.

  We elaborate on these observations with some specific examples. Cancer cells upregulates the glycolytic enzymes:²⁶ hexokinase, phosphofructokinase, lactate dehydrogenase, etc., which can be inhibited by pharmacological agents with potential therapeutic effects which could deprive cancer cells of their selective advantage. Metabolic rates can be controlled by variations in temperature and pH as well as the use of anti-oxidizing agents such as vitamins and nutraceuticals.⁴⁰ One of the well-known characteristics of cancer cells is their difference in pH (acidity) compared to normal cells. Interestingly, cancer cells appear to exhibit greater heat sensitivity than normal cells, which may also lead to therapeutic applications. Recent biochemical and clinical studies have revealed a profound and selective toxic effect of elevated temperatures on tumor cells. The metabolic rate of normal cells is primarily determined by the phospholipid composition of the mitochondrial membrane. This composition can be modified by exercise and diet.⁴¹

• (III)Modifying the cycle time

  Metabolic rate P is related to the cycle time τ by P ∼ aτ^d where a is a proportionality constant and d the dimensionality parameter. Cavalier et al.⁴² and Kadenbach⁴³ have documented various types of inhibitors and modifying agents, which may impinge on mitochondrial activity and thereby affect cycle time. The most significant of these inhibitors are agents in: (a) the Krebs cycle – which block one or more of the TCA cycle enzymes, (b) the respiratory chain – which block respiration in the presence of either ADP or uncoupling agents, and (c) phosphorylation chain – which abolish the burst of oxygen consumption.

These inhibitors will modify the cycle thereby regulating the metabolic rate and thus affecting the selective advantage of the cancer cells.

The understanding of the metabolic basis of carcinogenesis, which this evolutionary study generates, suggests new methods for regulating cellular metabolic rate and thereby impeding the transition from a benign tumor to a malignant state. Further details of the strategy based on metabolic interventions can be found elsewhere.⁵

CONCLUSIONS

Sporadic forms of cancer are age-related metabolic diseases, which have their origin in the mitochondria and cytosol of cells. Molecular infidelity and its concomitant metabolic instability are an inherent and integral part of the aging process. This is characterized by dysregulation of the metabolic system and a compensatory shift from oxidative phosphorylation to substrate-level phosphorylation. The analytic study of cancer progression and cancer therapy requires an elucidation of (a) the molecular basis of the process of metabolic regulation and (b) the selective event which defines competition between these two metabolic mechanisms, oxidative phosphorylation and glycolysis. Quantum Metabolism, an analytic theory of energy transduction in cells and an entropic selection principle, a general rule of cellular competition for energy sources, furnish the analytical framework for elucidating these issues of cancer progression and involving this to forge new methods of cancer therapy based on metabolic intervention. Finally, while this is still in an early stage of discovery, stem cells are likely to be utilizing competitive advantage in terms of their metabolism and signaling as has recently been indicated by linking their metabolism to differentiation.⁴⁴