Dynamic density functional theory of solid tumor growth: Preliminary models

Abstract

Cancer is a disease that can be seen as a complex system whose dynamics and growth result from nonlinear processes coupled across wide ranges of spatio-temporal scales. The current mathematical modeling literature addresses issues at various scales but the development of theoretical methodologies capable of bridging gaps across scales needs further study. We present a new theoretical framework based on Dynamic Density Functional Theory (DDFT) extended, for the first time, to the dynamics of living tissues by accounting for cell density correlations, different cell types, phenotypes and cell birth/death processes, in order to provide a biophysically consistent description of processes across the scales. We present an application of this approach to tumor growth.

INTRODUCTION AND MOTIVATION

In oncology and tumor biology, a wealth of genomic, proteomic and pathology-based cell phenotypic and microenvironmental data are collected at the microscale (i.e., cell scale and below). Treatment strategies, on the other hand, are determined by tumor response at the tissue-scale in space over long scales in time. Thus, a fundamental gap that is currently hampering progress in individualized cancer care is the extrapolation of patient-specific microscale quantitative information into formulations of therapeutic and intervention strategies at clinically relevant scales (e.g., organ scales). What is urgently needed is the development of biophysically sound mechanistic connections among the multi-modal, multi-dimensional and multiscale phenomena and variables involved in tumor progression. Such multiscale models would enable the integration of abundant microscale phenotype data (cell architecture, mitotic rates, etc) into a comprehensive picture of individual tumor behavior and response to treatment at clinically relevant scales that emerge from the underlying microscopic processes.

We recognize that oncologists and tumor biologists focus almost exclusively on processes at the sub-cellular and cellular domains (e.g., signaling pathways), and largely overlook physical phenomena associated with transport of cells and chemicals (e.g., oxygen diffusion) and momentum (e.g., mechanical forces among cells and other stromal components), which occur at the mesoscopic scale that spans the distance over which transport gradients are established (i.e., 100 − 200 μm of tissue for the establishment of oxygen gradients). These mesoscopic phenomena are the missing link to bridge the current gap between the scales.

To help bridge this gap, we propose a mathematical approach based on Dynamic Density Functional Theory¹ (DDFT), which provides a mesoscale continuum framework directly derived from a stochastic, discrete model. Unlike standard mean-field models, the DDFT approach accounts for correlations.^{1, 2} We extend the approach to model the spatio-temporal dynamics of multicellular systems by including cell type, phenotype and birth/death processes, which are major features of biological tissues.

The DDFT, and its stochastic, discrete counterpart, can be used to develop a hybrid continuum-discrete multiscale model that satisfies the following properties we deem essential for a multiscale model: 1) different representations to describe the same quantity of interest at different scales as needed (e.g., discrete representations are used in regions where the continuum model is not valid due, for example, to fluctuations); 2) direct calibration/validation of the cell-scale parameters and equations from individual microscale measurements; and finally 3) upscaling techniques to formulate (and close) the continuum equations at the larger scales. In contrast to current approaches, such a multiscale model would provide an accurate description of the feedback and interactions among processes across different scales and enable the model components at the meso- and tissue scales to be precisely determined from cell scale modeling, and underlying biological measurements, without “fitting” them directly.

CURRENT APPROACHES: “MULTIPLE-SCALE” MODELS

Due to the intrinsic multiscale nature of cancer, a deeper understanding requires the development of models that integrate and combine the phenomena spanning the multiple scales involved. Hybrid continuum-discrete implementations,³ which typically seek to combine the best of the tissue (continuum) and cellular (discrete) scale approaches while minimizing their limitations, are a very promising modeling approach. Many published methods claim to be multiscale because they are based on a hybrid description of the tumor components, typically by using a discrete representation of the various cell populations and continuum fields to describe cell substrates (e.g., nutrients, oxygen and diffusible factors). These models incorporate processes at multiple scales but have difficulties in capturing the non-trivial interactions among scales that are responsible for the growth of malignant tissue and do not satisfy the definition of multiscale model introduced above. Here, we concisely review two promising recent approaches to the development of functional multiscale models for solid tumor growth. A more complete review may be found in Refs. ^{4, 5, 6}.

Decoupled multiple-scale approach

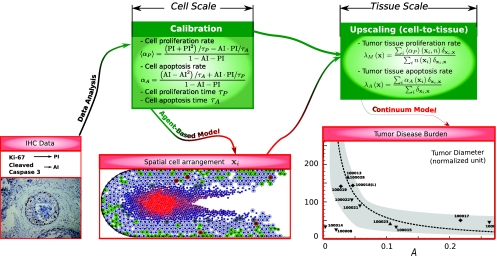
A mechanistic agent-based model (ABM) of tumor growth was recently introduced^{7, 8} and applied to simulating the progression of ductal carcinoma in situ (DCIS) of the breast (Fig. 1). Cell motion is determined from an overdamped balance of adhesive, repulsive, and motile forces exerted among the cells and by the extracellular matrix (ECM). Cells (which may have different sizes) are associated to individual phenotypic states, e.g., proliferative, motile. Transition rates between the states are governed by exponentially distributed random variables. As illustrated in Fig. 1, a “bottom-up” approach was used for ABM parameter calibration from experimental data at the cell-scale (immunohistochemistry of pathology specimens). In particular, experimentally measured indexes of proliferation and apoptosis were used to obtain average rates of individual cell proliferation and apoptosis rates in the ABM. Note that such a calibration has also been successfully performed in the context of liver regeneration.⁹ However, in Refs. ^{7, 8}, an upscaling calibration protocol based on volume-averaging was additionally used with the ABM to calculate the coarse-grained proliferation and apoptotic volume rate parameters at the tissue scale, which provided input to a continuum model¹⁰ thus avoiding fitting. A “top-down” approach was used to compare the model results to tumor volumes measured in patients. This led to the first accurate, patient-specific assessment of DCIS tumor volumes – a key translational issue in current surgical planning.¹¹

Figure 1.

Flow of information across the formulations at the cellular and tissue scales in a decoupled multiple-scale approach for DCIS.⁷, ¹¹ Bottom images: (left) Bottom-up calibration: immunohistochemistry measurements from patient tissue used for parameter calibration⁷ (proliferation and apoptotic indices PI and AI); (center) ABM simulation of DCIS;⁷ (right) Top-down validation: comparison of model-predicted tumor volume (dashed curve) to the corresponding volume measured from histology of the excised tumors from patients (symbols). Reprinted with permission from Ref. 8. Copyright 2010, Cambridge University Press.

Coupled multiple-scale approach: Hybrid models

In a study of the effect of stress on the growth of avascular tumor spheroids in an agarose gel^{12, 13} a hybrid model was developed where different descriptions of tumor cells were used in different regions of the spheroids. In the thin proliferating zone at the spheroid edge, an ABM was used where the discrete cells were represented as deformable ellipsoids, enabling a detailed description of intercellular dynamics, cell sizes and shapes, and cell-cell interactions. In the larger quiescent and necrotic regions in the spheroid interior, a continuum viscoelastic description was used. The coupling among the discrete and continuum components was limited to the incorporation of discrete cells into the continuum regions through mass and momentum fluxes.

Another hybrid approach has been used to simulate the growth of invasive glioma tumors¹⁴ where invading tumor cells were modeled using an ABM as discrete points (i.e., zero size) and a continuum model was used for the tumor bulk, assuming spherical symmetry. The coupling among the discrete and continuum models was limited to the production of discrete cells from the continuum field through mass fluxes at the tumor edge.

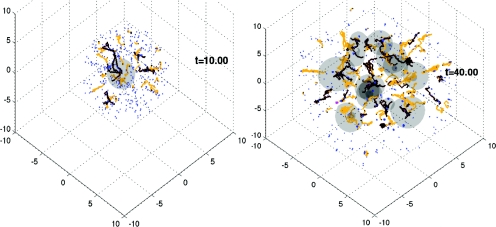
In a recent study of a hypoxia-induced epithelial-to-mesenchymal transition during tumor growth,¹⁵ an ABM for tumor cells was coupled directly to a continuum model for tumor volume fractions through mass and momentum exchanges between the two representations. Rules were posed to describe the conditions under which the discrete and continuum representations were used. Briefly, discrete cells were released in hypoxic regions, to model the epithelial-mesenchymal transition, and discrete cells were converted back to the continuum description at locations where their population exceeds a threshold (Fig. 2).

Figure 2.

Hybrid multiple-scale simulation of vascularized tumor growth.¹⁵ Discrete tumor cells (blue dots) are released from hypoxic areas of the continuum tumor regions (gray volumes). Vessel sprouts (light lines) and newly formed vessels (dark lines) releasing oxygen and nutrients are shown. Time is in proliferation time units.

Assessment of current approaches

The decoupled two-step approach does not allow for any dynamical exchange between cell- and tissue-scale models, which limits its applicability. The hybrid approaches improve over the decoupled methods in that there are interactions among the continuum and discrete cell representations. However, in both multiple-scale approaches the variables and fluxes considered at the macroscale (continuum) are pre-assumed and are not obtained by upscaling the cell scale (discrete) dynamics.

Multiscale modeling frameworks, such as the heterogeneous multiscale method¹⁶ and the equation-free approach,¹⁷ can be used to provide effective macroscale fluxes by numerically upscaling the results from models at the microscale. However, these methods do not provide analytical forms for these fluxes even if the macroscale continuum description is valid and the fluxes can be defined solely in terms of continuum variables. In the next section, we present a novel approach using dynamical density functional theory for modeling tissue and tumor growth, which provides a modeling framework for obtaining analytical expressions for the macroscale fluxes from the microscopic processes.

DYNAMIC DENSITY FUNCTIONAL THEORY FOR MULTICELLULAR SYSTEMS

Dynamic density functional theory (DDFT) provides a macroscopic continuum framework directly derived from the microscopic scale, where processes occurring at the microscale (i.e., in an interacting particle system) are integrated within the mesoscale description and incorporate correlations among the discrete components.^{1, 2} DDFT has been successfully used to describe Brownian dynamics of non-equilibrium colloidal particles, e.g., applied to crystal growth in single and binary component materials.^{18, 19, 20} The theory naturally incorporates elastic, plastic and viscoelastic deformations as well as defects.

As far as we are aware, DDFT has not been used in the context of multicellular systems. However, recent experiments on confluent epithelial cell sheets show that there are intriguing similarities between the dynamics of collective cell motion at high cell densities and the dynamics of supercooled colloidal and molecular fluids approaching a glass transition.²¹ In particular, at low cell densities it is found that the cells flow like a fluid. However, as the cells proliferate and compress, a critical density emerges above which solid-like behavior is observed and structural relaxations occur only over long time scales such as the mitosis time scale or longer (e.g., on the order of days). Accordingly, dynamic heterogeneities are seen to develop concomitant with a decrease in diffusive motion and the development of peaks in the dynamic structure factor. Together, these results suggest the importance of accounting for correlations among cells at the mesoscale, which makes DDFT a natural modeling choice. However, to model physiological tissues as multicellular systems, DDFT must be extended to account for cell proliferation (mitosis) and death (apoptosis/necrosis), as well as multiple cell types and phenotypes, which are also the main features needed to model malignant tissues.

Classical Dynamic Density Functional Theory

We briefly outline DDFT for the dynamics of N interacting (tumor) cells of a single species and outline the steps that allow for the derivation of equations describing the spatio-temporal evolution of the tissue-scale description. We describe the motion of each cell by the overdamped Langevin equation:

$$\frac{d{\mathbf{r}}_i}{dt}=\Gamma \left(\sum _{j=1}^N{\mathbf{F}}_{ij}^{int}+{\mathbf{F}}_i^{ext}\right)+\sqrt{2D}{\mathit{\eta }}_i\left(t\right),$$ (1)

where ${\mathbf{r}}_i={\left(r_i^{\alpha }\right)}_{\alpha =1\cdots d}\in {\Omega }^d$ is the position of the center of mass of the i-th cell in the d-dimensional physical domain Ω^d and Γ is the cell motility coefficient linked to the diffusion coefficient D by the Einstein relation D = Γ T (T is an effective temperature). To simplify the presentation, we assume no hydrodynamic interactions between the cells, i.e. no cell-cell friction, which could be included by adding a viscous drag force in the Langevin equations via a microscopic friction tensor acting on the relative velocity with neighboring cells.²² Although neglecting cell-cell friction may be more appropriate in the absence of active cell motion, cell-cell friction could easily be incorporated using a similar modeling framework. The forces ${\sum }_{j=1}^N{\mathbf{F}}_{ij}^{int}=-{\sum }_{j=1}^N{\nabla }_{{\mathbf{r}}_i}{V}_{int}\left(\right|{\mathbf{r}}_i-{\mathbf{r}}_j\left|\right)$ model cell-cell interactions (e.g., adhesion, repulsion) via a pair potential V_int that depends on the distance between two cells. We model microenvironmental influences (e.g., chemotaxis, haptotaxis, cell-ECM adhesion, etc) on cell movement by forces ${\mathbf{F}}_i^{ext}=-\nabla V_{ext}({\mathbf{r}}_i,t)$, where V_ext is an external potential depending on the microenvironment. The vector η_i(t) is a Gaussian noise satisfying $〈{\eta }_i^{\alpha }\left(t\right)〉=0$ and $⟨{\eta }_i^{\alpha }\left(t\right){\eta }_j^{\beta }\left(t^{\prime }\right)⟩={\delta }_{ij}{\delta }_{\alpha \beta }\delta (t-t^{\prime })$, where <· > is the averaging over different noise realizations, and α, β are coordinate indices. From Eq. 1 one can derive the equation for the N-particle position probability distribution P(r^N, t) (or N-body distribution function) by using the multivariable Ito formula of stochastic calculus²³ to obtain the Smoluchowski equation

$$\frac{\partial P({\mathbf{r}}^N,t)}{\partial t}=\sum _{i=1}^N{\nabla }_{{\mathbf{r}}_i}·\left[-\Gamma {\mathbf{F}}_i({\mathbf{r}}^N,t)+D{\nabla }_{{\mathbf{r}}_i}\right]P({\mathbf{r}}^N,t),$$ (2)

where r^N = {r_i}_{i = 1…N} is the N-dimensional position vector of cells and ${\mathbf{F}}_i={\sum }_{j=1}^N{\mathbf{F}}_{ij}^{int}+{\mathbf{F}}_i^{ext}$ denotes the sum of forces exerted on a single cell.

Summarizing the approach in Ref. 24, the discrete density field of the N-cell system is defined as $\overline{\rho }(\mathbf{r},t;{\mathbf{r}}^N)={\sum }_{i=1}^N\overline{\delta }({\mathbf{r}}_i\left(t\right)-\mathbf{r})$, where $\overline{\delta }$ is a coarse-grained delta function over a domain of characteristic length scale l, which lies between the cell size and the cell-density correlation length. The domain Ω^d is split into small subdomains (nodes) where a local density is defined with fluctuations around an equilibrium value. The cell density is evaluated around the position r ∈ Ω^d of a node of size l. The corresponding coarse-grained density ρ(r, t) is the limit of $\overline{\rho }(\mathbf{r},t;{\mathbf{r}}^N)$ for large N and small l. Let P[ρ, t] denote the probability of finding a specific realization of function ρ over the domain r ∈ Ω^d:

$$P[\rho ,t]=\int \delta \left(\rho -\overline{\rho }(·;{\mathbf{r}}^N)\right)P({\mathbf{r}}^N,t)d{\mathbf{r}}^N=\int \int \delta \left(\rho ({\mathbf{r}}^{\prime },t)-\overline{\rho }({\mathbf{r}}^{\prime },t;{\mathbf{r}}^N)\right)\delta \left({\mathbf{r}}^{\prime }-\mathbf{r}\right)P({\mathbf{r}}^N,t)d{\mathbf{r}}^{N}d{\mathbf{r}}^{\prime }.$$ (3)

Using the Smoluchowski equation 2 and the above definition, we can evaluate the temporal dynamics of the cell density distribution P[ρ, t]. The derivation involves the technique of projection operators and is based on the essential assumption that the density ρ(r, t) evolves with a time scale well-separated from the time scale corresponding to the evolution of the generalized position vector r^N. Finally, the time evolution of P[ρ, t] is described by the following functional Fokker-Planck equation:²⁴

$$\frac{\partial P[\rho ,t]}{\partial t}={\mathcal{L}}_{\mathcal{M}}[\rho ,t]P[\rho ,t].$$ (4)

Eq. 4 is a mesoscopic description of the initial system 1 and includes fluctuations that can be averaged out only for larger systems, where the first moment of P[ρ, t] (the cell density) is assumed to dominate the deterministic large-scale dynamics. In Eq. 4 the functional operator ${\mathcal{L}}_{\mathcal{M}}[\rho ,t]$ describes the dynamics of the coarse-grained density:²⁴

$${\mathcal{L}}_{\mathcal{M}}[\rho ,t]P[\rho ,t]=-\int d\mathbf{r}\frac{\delta }{\delta \rho (\mathbf{r},t)}\left\{\nabla ·\left[\rho (\mathbf{r},t)\nabla \left(D\frac{\delta }{\delta \rho (\mathbf{r},t)}+\Gamma \frac{\delta {\mathcal{F}}_{\mathcal{C}}\left[\rho (\mathbf{r},t)\right]}{\delta \rho (\mathbf{r},t)}\right)\right]P[\rho ,t]\right\},$$ (5)

where δ/δρ(r, t) is a functional derivative with respect to ρ and ${\mathcal{F}}_{\mathcal{C}}\left[\rho \right]$ is a coarse-grained free-energy functional, which is specific to the biophysical processes modeled and will be described in detail later. In order to derive a deterministic equation for the density, we multiply Eq. 4 by the density field and integrate, thereby performing an averaging procedure over the possible realizations of the density field. For appropriate boundary conditions, we integrate by parts and assume vanishing local fluctuations of the density field to obtain:

$$\frac{\partial \rho }{\partial t}(\mathbf{r},t)=\Gamma \nabla ·\left[\rho (\mathbf{r},t)\nabla \left(\frac{\delta {\mathcal{F}}_{\mathcal{C}}\left[\rho (\mathbf{r},t)\right]}{\delta \rho (\mathbf{r},t)}\right)\right].$$ (6)

Alternatively, one could derive the above result, starting again from Eq. 4, by using a free-energy minimization principle, as in Ref. 25. We remark that another option to derive Eq. 6 directly from Eq. 4 is proposed in Ref. 1, by defining $\overline{\rho }$ as the sum of noise-averaged delta functions without appealing to a free-energy minimization principle. However, we do not take this alternate approach here as it is more difficult to account for cell-proliferation as we will propose further in our paper.

The deterministic equation 6 captures the spatio-temporal dynamics of the cell density of a single cell type at the tissue level in the absence of cell proliferation, is physically-based, and takes the form of a continuity equation with the flux proportional to the gradient $\frac{\delta {\mathcal{F}}_{\mathcal{C}}\left[\rho \right]}{\delta \rho }$ of the coarse-grained free-energy functional. In general, this functional takes the form ${\mathcal{F}}_{\mathcal{C}}\left[\rho \right]={\mathcal{F}}^{id}\left[\rho \right]+{\mathcal{F}}^{ext}\left[\rho \right]+{\mathcal{F}}^{ex}\left[\rho \right].$ The first term corresponds to random cell motion and is given by ${\mathcal{F}}^{id}\left[\rho \right]=T\int d\mathbf{r}\rho \left(\mathbf{r}\right)\left[\ln \left(K\rho \right(\mathbf{r}\left)\right)-1\right]$, where the prefactor K is the analogue of the thermal de Broglie wavelength (i.e., the average distance between cells under the influence of stochastic fluctuations). The second term describes the response of cells to an external field, e.g. active cell movement, and is given by ${\mathcal{F}}^{ext}\left[\rho \right]=\int d\mathbf{r}\rho \left(\mathbf{r}\right)V_{ext}(\mathbf{r},t)$. The third term characterizes the excess free energy that arises from cell-cell interactions, which for pair potentials as used above, is given by^{26, 27}

$$\rho (\mathbf{r},t)\nabla \frac{\delta {\mathcal{F}}^{ex}\left[\rho (\mathbf{r},t)\right]}{\delta \rho (\mathbf{r},t)}=\int d{\mathbf{r}}^{\prime }{\rho }^{\left(2\right)}(\mathbf{r},{\mathbf{r}}^{\prime },t){\nabla }_{\mathbf{r}}{V}_{int}\left(\right|\mathbf{r}-{\mathbf{r}}^{\prime }\left|\right),$$ (7)

where ρ⁽²⁾(r, r′, t) is the two-particle density distribution function. Since ρ⁽²⁾ depends on ρ⁽³⁾, the three-particle distribution function, and so on, Eq. 6 is not closed. To close Eq. 6, the system needs to be truncated and ρ⁽²⁾ needs to be approximated. Several approximations as described briefly below are used.

Uncorrelated mean-field approximation

The simplest way to model ρ⁽²⁾ and close Eq. 6 is to neglect density correlations and take ρ⁽²⁾(r, r′, t) ≈ ρ(r, t) ρ(r′, t). This is known as the mean-field approximation.²⁸ In this case, Eq. 6 becomes

$$\begin{array}{ccc}\hfill \frac{\partial \rho }{\partial t}(\mathbf{r},t)& =& D{\nabla }^2\rho (\mathbf{r},t)+\Gamma \nabla ·\left[\rho (\mathbf{r},t)\nabla V_{ext}(\mathbf{r},t)\right]\hfill \\ & & +\Gamma \nabla ·\left[\rho (\mathbf{r},t)\int d{\mathbf{r}}^{\prime }\rho ({\mathbf{r}}^{\prime },t){\nabla }_{\mathbf{r}}{V}_{int}\left(\right|\mathbf{r}-{\mathbf{r}}^{\prime }\left|\right)\right].\hfill \end{array}$$ (8)

We note that similar formulations have been previously used to model cell-cell adhesion via the nonlocal operator.²⁹ Further, the mean field approximation fails when either the density is low, so that fluctuations are non-negligible, or when correlations are important, e.g., arising from long-range interactions. Interestingly, for a repulsive interaction potential, this leads to a version of Darcy's law since for a uniform density ρ = ρ_∞, the pressure is p(r) = ρ_∞Γ∫dr′V_int(|r − r′|).

Correlated mean-field approximation

In the DDFT framework rather than assuming that there are no correlations, the adiabatic approximation¹${\rho }^{\left(2\right)}(\mathbf{r},{\mathbf{r}}^{\prime },t)\approx {\rho }_{eq}^{\left(2\right)}(\mathbf{r},{\mathbf{r}}^{\prime })$ is used, where ${\rho }_{eq}^{\left(2\right)}$ is a two-particle density distribution function evaluated for a system with equilibrium density ρ₀(r) ≡ ρ(r, t). Although ${\rho }_{eq}^{\left(2\right)}$ is still not known in general, the corresponding excess energy ${\mathcal{F}}^{ex}\left[\rho \right]$ can be expanded around a constant reference density ρ_∞ to yield³⁰

$${\mathcal{F}}^{ex}\left[\rho (\mathbf{r},t)\right]\simeq {\mathcal{F}}^{ex}\left({\rho }_{\infty }\right)-\frac{D}{2\Gamma }\int d\mathbf{r}\Delta \rho (\mathbf{r},t)\int d{\mathbf{r}}^{\prime }\Delta \rho ({\mathbf{r}}^{\prime },t)c_{eq}^{\left(2\right)}(\mathbf{r}-{\mathbf{r}}^{\prime };{\rho }_{\infty }),$$ (9)

where Δρ(r, t) = ρ(r, t) − ρ_∞ and $c_{eq}^{\left(2\right)}(\mathbf{r}-{\mathbf{r}}^{\prime };{\rho }_{\infty })=-\frac{{\delta }^2{\mathcal{F}}_{ex}\left[\rho \right]}{\delta \rho \left(\mathbf{r}\right)\delta \rho \left({\mathbf{r}}^{\prime }\right)}{|}_{\rho (·)={\rho }_{\infty }}$ is the direct two-point correlation function of the uniform system, which is related to the total correlation function h(r), with r = |r|, by the Ornstein-Zernike (OZ) equation³¹

$$h\left(r\right)=c_{eq}^{\left(2\right)}(r;{\rho }_{\infty })+{\rho }_{\infty }\int d{r}^{\prime }h\left(r^{\prime }\right)c_{eq}^{\left(2\right)}\left(\right|\mathbf{r}-{\mathbf{r}}^{\prime }|;{\rho }_{\infty }),$$ (10)

where spherical symmetry is assumed. At this point, the system is still not closed and an additional closure relation needs to be imposed between h and $c_{eq}^{\left(2\right)}$ to be able to solve the Ornstein-Zernike equation 10. There are numerous examples of physically-based closure relations in the literature,³¹ which relate h, $c_{eq}^{\left(2\right)}$ and the interaction potential V_int; see Sec. 3C for an example of a specific closure relation. With these approximations, Eq. 6 becomes

$$\begin{array}{ccc}\hfill \frac{\partial \rho }{\partial t}(\mathbf{r},t)& =& D{\nabla }^2\rho (\mathbf{r},t)+\Gamma \nabla ·\left[\rho (\mathbf{r},t)\nabla V_{ext}(\mathbf{r},t)\right]\hfill \\ & & -D\nabla ·\left[\rho (\mathbf{r},t)\int d{\mathbf{r}}^{\prime }\left(\rho ({\mathbf{r}}^{\prime },t)-{\rho }_{\infty }\right){\nabla }_{\mathbf{r}}{c}_{eq}^{\left(2\right)}\left(\right|\mathbf{r}-{\mathbf{r}}^{\prime }|;{\rho }_{\infty })\right],\hfill \end{array}$$ (11)

where $c_{eq}^{\left(2\right)}$ remains to be evaluated via the OZ equation and a closure equation. We note that in both the uncorrelated and correlated mean-field models, the nonlocal terms may be further approximated and localized in space using gradient expansions. Next, we extend the DDFT framework to multicellular systems.

Multicellular Dynamic Density Functional Theory

As a first step towards the development of DDFT for multicellular systems, we extend the DDFT framework to account for different types of cells and cell phenotypes. We then develop an extension to birth/death processes.

Multiple cell types

We consider M_σ different cell species, identified by the index k, with each species having N_k cells with a common set of biophysical properties. The Langevin equation describing the motion of the i-th cell in population k, via its center of mass located at ${\mathbf{r}}_i^k$, reads

$$\frac{d{\mathbf{r}}_i^k}{dt}={\Gamma }^k\left(\sum _{l=1}^{M_{\sigma }}\sum _{j=1}^{N_k}{\mathbf{F}}_{ij}^{kl,int}+{\mathbf{F}}_i^{k,ext}\right)+\sqrt{2D_k}{\mathit{\eta }}_i^k\left(t\right),$$ (12)

where all the notation used in the previous section is generalized to account for the properties associated with a species k. The multispecies Eq. 12 is a straightforward generalization of the single species Eq. 1 where there are now cell-cell interactions among the different species k and l (e.g., to model differential adhesion) via the forces ${\mathbf{F}}_{ij}^{kl,int}$ and external forces in the microenvironment ${\mathbf{F}}_i^{k,ext}$, which act on each species individually (e.g., only a subset of the cell species may respond to particular microenvironmental forces).

The derivation of the deterministic counterpart (i.e., the equation for the continuous cell density ρ_k of each species) of the multispecies Langevin equations 12 is similar to the single species case presented in Section 3A. We use multivariable stochastic Ito calculus for each species to derive the corresponding Smoluchowski equation for each N_k-body distribution function. Then, we use Kawasaki's approach²⁴ and introduce the probability P_k[ρ_k, t] of finding a specic realization of ρ_k, whose dynamics is given by a functional Fokker-Planck equation. By averaging over all possible realizations, we obtain a deterministic continuity equation for the cell density ρ_k of each species k, which reads

$$\frac{\partial {\rho }_k}{\partial t}(\mathbf{r},t)={\Gamma }^k\nabla ·\left[{\rho }_k(\mathbf{r},t)\nabla \left(\frac{\delta {\mathcal{F}}_{\mathcal{C}}\left[\rho (\mathbf{r},t)\right]}{\delta {\rho }_k(\mathbf{r},t)}\right)\right],$$ (13)

where ${\mathcal{F}}_{\mathcal{C}}[\rho ]$ denotes the coarse-grained free-energy functional of the entire multispecies system of interacting cells, i.e., ${\mathcal{F}}_{\mathcal{C}}\left[\rho \right]$=${\mathcal{F}}_{\mathcal{C}}[{\rho }_1,\cdots ,{\rho }_{M_{\sigma }}]$. The energy associated with random cell motion and the external field are simply sums of the contributions from each species. The excess part of the free energy is the generalization of Eq. 7 and is given by

$${\rho }_k(\mathbf{r},t)\nabla \frac{\delta {\mathcal{F}}^{ex}\left[\rho (\mathbf{r},t)\right]}{\delta {\rho }_k(\mathbf{r},t)}=\sum _{l=1}^{M_{\sigma }}\int d{\mathbf{r}}^{\prime }{\rho }_{kl}^{\left(2\right)}(\mathbf{r},{\mathbf{r}}^{\prime },t){\nabla }_{\mathbf{r}}{V}_{kl,int}\left(\right|\mathbf{r}-{\mathbf{r}}^{\prime }\left|\right),$$ (14)

where ${\rho }_{kl}^{\left(2\right)}(\mathbf{r},{\mathbf{r}}^{\prime },t)$ describes cross-correlations between species k and l. Approximations and closure relations analogous to those described in Secs. 3A1, 3A2 can be used to complete and close the system of equations, yielding a system of coupled integrodifferential equations.

Multiple cell phenotypes

We next consider the case in which cells have different phenotypes. Recent experimental evidence suggests that phenotypic traits, such as the state of differentiation, are not necessarily fully hierarchical but rather a stochastically evolving, potentially reversible continuum.^{32, 33, 34, 35, 36} Similar to Refs. ^{36, 37}, where Markov processes have been used to model differentiation dynamics, we introduce a stochastic differential equation that governs the temporal evolution of a phenotype vector σ_i of cell i where each component of σ_i describes a cell phenotypic trait (e.g., differentiation, proliferation, etc):

$$\frac{d{\mathit{\sigma }}_i}{dt}={\mathbf{A}}_i({\mathbf{r}}^N,{\mathit{\sigma }}^N)+\sqrt{2D_{\mathit{\sigma }}}{\mathit{\eta }}_i^{\mathit{\sigma }}\left(t\right),$$ (15)

where A_i corresponds to evolutionary and external pressures and models drift forces driving the evolution of (the possibly interdependent) phenotypic traits of cell i. Similar to the definition of r^N (the generalized N-dimensional position vector of the whole set of cells), σ^N = {σ_i}_{i = 1…N} is the generalized N-dimensional phenotype vector of the whole set of cells. The second term in Eq. 15 accounts for uncorrelated random fluctuations of the phenotype (it is straightforward to extend the model to include correlated fluctuations).

Whereas Eq. 15 models the dynamics of the phenotype of cell i, the movement of that cell is still modeled via the Langevin equations. Assuming that the biophysics driving the cell spatio-temporal dynamics in the Langevin equations may depend on the cell phenotype, we shall consider Γ(σ_i), ${\mathbf{F}}_i({\mathbf{r}}^N,{\mathit{\sigma }}^N)={\sum }_{j=1}^N{\mathbf{F}}_{ij}^{int}({\mathbf{r}}_i,{\mathit{\sigma }}_i,{\mathbf{r}}_j,{\mathit{\sigma }}_j)+{\mathbf{F}}_i^{ext}({\mathbf{r}}_i,{\mathit{\sigma }}_i)$ and D(σ_i) in Eq. 1, which we rewrite for clarity as:

$$\frac{d{\mathbf{r}}_i}{dt}=\Gamma \left({\mathit{\sigma }}_i\right){\mathbf{F}}_i({\mathbf{r}}^N,{\mathit{\sigma }}^N)+\sqrt{2D\left({\mathit{\sigma }}_i\right)}{\mathit{\eta }}_i\left(t\right).$$ (16)

Equations 15, 16 form a discrete coupled system accounting for the stochastic dynamics of cell in both the physical and phenotypic spaces. Similar to the derivation performed in Section 3A, we introduce the generalized N-particle probability distribution $P({\mathbf{r}}^N,{\mathit{\sigma }}^N,t)$. Then, assuming that the interspecies noise terms ${\mathit{\eta }}_i^{\mathit{\sigma }}\left(t\right)$ are statistically independent, we apply the multivariate Ito formula to a function of the vector $({\mathbf{r}}^N,{\mathit{\sigma }}^N)$ to derive the Smoluchowski equation governing the spatio-temporal evolution of $P({\mathbf{r}}^N,{\mathit{\sigma }}^N,t)$. The rest of the derivation of a deterministic equation involves a new definition of the discrete density field, i.e. $\overline{\rho }(\mathbf{r},\mathit{\sigma },t;{\mathbf{r}}^N,{\mathit{\sigma }}^N)={\sum }_{i=1}^N\overline{\delta }({\mathbf{r}}_i\left(t\right)-\mathbf{r})\overline{\delta }({\mathit{\sigma }}_i\left(t\right)-\mathit{\sigma })$, with $\overline{\delta }$ being the coarse-grained delta function already introduced and σ the vector of continuous phenotype traits of cells at position r at time t. The application of Kawasaki's approach²⁴ to define the generalized coarse-grained density $\rho (\mathbf{r},\mathit{\sigma },t)$ as the limit of $\overline{\rho }(\mathbf{r},\mathit{\sigma },t;{\mathbf{r}}^N,{\mathit{\sigma }}^N)$ and to define the probability P[ρ, t], whose dynamics is governed by a functional Fokker-Planck equation, remains valid. Here the generalized density ρ depends on both spatial and phenotypic continuous variables r and σ. The averaging over all possible realizations yields the following deterministic equation for the generalized density ρ:

$$\begin{array}{ccc}\hfill \frac{\partial \rho }{\partial t}(\mathbf{r},\mathit{\sigma },t)& =& \Gamma \left(\mathit{\sigma }\right){\nabla }_{\mathbf{r}}·\left[\rho (\mathbf{r},\mathit{\sigma },t){\nabla }_{\mathbf{r}}\left(\frac{\delta {\mathcal{F}}_{\mathcal{C}}\left[\rho (\mathbf{r},\mathit{\sigma },t)\right]}{\delta \rho (\mathbf{r},\mathit{\sigma },t)}\right)\right]\hfill \\ & & +D_{\mathit{\sigma }}{\nabla }_{\mathit{\sigma }}^2\rho (\mathbf{r},\mathit{\sigma },t)-{\nabla }_{\mathit{\sigma }}·\left[\mathbf{A}(\mathbf{r},\mathit{\sigma })\rho (\mathbf{r},\mathit{\sigma },t)\right],\hfill \end{array}$$ (17)

where ∇_σ denotes the gradient with respect to the phenotype vector σ. Here, the functional free energy now involves integration over σ. In particular, the excess part of the free energy is now given by

$$\rho (\mathbf{r},\mathit{\sigma },t)\nabla \frac{\delta {\mathcal{F}}^{ex}\left[\rho (\mathbf{r},\mathit{\sigma },t)\right]}{\delta \rho (\mathbf{r},\mathit{\sigma },t)}=\int \int d{\mathit{\sigma }}^{\prime }d{\mathbf{r}}^{\prime }{\rho }^{\left(2\right)}\left((\mathbf{r},\mathit{\sigma }),({\mathbf{r}}^{\prime },{\mathit{\sigma }}^{\prime }),t\right){\nabla }_{\mathbf{r}}{V}_{int}\left(\right|\mathbf{r}-{\mathbf{r}}^{\prime }|,\mathit{\sigma },{\mathit{\sigma }}^{\prime }),$$ (18)

where ${\rho }^{\left(2\right)}\left((\mathbf{r},\mathit{\sigma }),({\mathbf{r}}^{\prime },{\mathit{\sigma }}^{\prime }),t\right)$ is a generalized two-particle density distribution function.

The first term on the right hand side of Eq. 17 corresponds to the transport of cells in the physical space (i.e., diffusion, advection by an external field, as in Eqs. 8, 11 with coefficients depending now on the phenotype σ). In addition, the transport may also be influenced by the nature of the interactions among cells of different phenotypes via the potential V_int (see Eq. 18). The second and third terms on the right hand side of Eq. 17 account for the phenotype dynamics that includes diffusion (e.g., for random mutations) and a drift term with velocity A (e.g., for evolutionary forces) within the phenotype space. Remark that those terms are to be compared with those of population dynamics models developed for cell differentiation^{37, 38} in which the level of differentiation is described by a continuous variable as suggested in Ref. 39.

While a similar approximation procedure as described in Sec. 3A2 can be used to close the system utilizing a multicomponent Ornstein-Zernike equation, it is not clear that the physically-based closure relations described in Ref. 31 are appropriate for this context. This is under study, see Sec. 4.

As an example, suppose that the phenotype is solely described by the state of differentiation of a cell. Then let σ = s be a scalar variable that denotes the differentiation state of a cell with s = 0 denoting the undifferentiated state and s = 1 the fully differentiated state. Then, the drift term A = A(r, s) is also a scalar, with A ⩾ 0 describing hierarchical forces driving differentiation and A ⩽ 0 describing de-differentiation. Feedback that modifies cell differentiation rates can be captured using this approach and a more detailed model that relates A to external (e.g., from the microenvironment) and interaction (e.g., among cells at different differentiation stages) forces analogous to those in Eq. 1, but now in the phenotype space.

Cell birth/death processes

We next describe the generalization of DDFT to include birth/death (BD) processes. We present the derivation for a single species, which can be generalized straightforwardly to a multispecies, multiphenotype system. The derivation of macroscopic descriptions of randomly moving reacting particles has a long history (see Ref. 23 for example). Only recently, rigorous mathematical results have been developed to treat stochastic spatially-distributed BD processes, e.g. Ref. 40.

We begin by considering only BD processes. Under the assumption of a local stochastic Markov process, cell birth/death can be classically modeled via the following Fokker-Planck equation:⁴¹

$$\begin{array}{ccc}\hfill \frac{\partial P[\rho ,t]}{\partial t}& =& {\mathcal{L}}_{\mathcal{BD}}[\rho ,t]P[\rho ,t],\mathrm{where}\hfill \end{array}$$ (19)

$$\begin{array}{ccc}\hfill {\mathcal{L}}_{\mathcal{BD}}[\rho ,t]P[\rho ,t]& =& \int d\mathbf{r}\frac{\delta }{\delta \rho \left(\mathbf{r}\right)}\left\{\left[-D_{\mathcal{BD}}^{\left(1\right)}\left[\rho \left(\mathbf{r}\right)\right]+\frac{1}{2}\frac{\delta D_{\mathcal{BD}}^{\left(2\right)}\left[\rho \left(\mathbf{r}\right)\right]}{\delta \rho \left(\mathbf{r}\right)}\right]P[\rho ,t]\right\},\hfill \end{array}$$ (20)

and the cell density functionals $D_{\mathcal{BD}}^{\left(i\right)}\left[\rho \right],i=1,2$, represent the first and the second moments of the BD process.

Next, we consider combined BD and cell-movement processes. We assume that the time scale of cell movement (i.e., from cell-cell interactions, external and random forces) across the length l is much smaller than the characteristic time of BD processes. That is, the ratio κ = τ_M/τ_BD ≪ 1, where τ_M and τ_BD are the time scales of the movement and BD processes, respectively. This implies that the system evolves during a time τ_BD under the composition of ${\mathcal{L}}_{\mathcal{BD}}$ and κ⁻¹ times of ${\mathcal{L}}_{\mathcal{M}}$, which yields:

$$P[\rho ,t+{\tau }_{BD}]=\left(\mathbf{1}+{\tau }_{BD}{\mathcal{L}}_{\mathcal{BD}}\right){\left(\mathbf{1}+{\tau }_M{\mathcal{L}}_{\mathcal{M}}\right)}^{{\kappa }^{-1}}P[\rho ,t].$$ (21)

For times much larger than τ_BD, and using the separation of BD and movement time scales, we derive a new functional Fokker-Planck equation that replaces Eq. 4:

$$\frac{\partial P[\rho ,t]}{\partial t}=\left({\mathcal{L}}_{\mathcal{M}}[\rho ,t]+{\mathcal{L}}_{\mathcal{BD}}[\rho ,t]\right)P[\rho ,t].$$ (22)

Following the steps of the derivation of Eq. 6 from Eq. 4, as described in Section 3A, an averaging procedure of the functional Fokker-Planck equation 22 over the possible realizations of the density field leads to a deterministic equation for the time evolution of the density:

$$\frac{\partial \rho }{\partial t}(\mathbf{r},t)=\Gamma \nabla ·\left[\rho (\mathbf{r},t)\nabla \frac{\delta {\mathcal{F}}_{\mathcal{C}}\left[\rho (\mathbf{r},t)\right]}{\delta \rho (\mathbf{r},t)}\right]+D_{\mathcal{BD}}^{\left(1\right)}\left[\rho (\mathbf{r},t)\right],$$ (23)

which describes both BD processes and cell movement simultaneously in a multicellular system.

Application to tumor growth

We illustrate the DDFT modeling framework by presenting an example that contains the basic phenomenology of tumor growth. We neglect many biophysical processes^{4, 42} and assume that tumor cell movement is mediated by random motion, cell-cell interaction forces and cell-extracellular matrix (ECM) interactions through haptotaxis, which can be modeled as an external force. In particular, let E denote the density of the ECM. Then, the external potential can be taken to be V_ext = −ξ_EE, which models movement of cells up gradients of ECM. We assume that ECM is degraded and produced by tumor cells. As a simple model of cell-cell interaction forces, one may use the Morse potential $V_M\left(r\right)={\overline{V}}_M{\left(1-e^{-a\left(r-r_e\right)}\right)}^2$, which describes short-range repulsion, e.g., resulting from cell-cell compression, and longer-range attraction, e.g., resulting from cell-cell adhesion. Here, ${\overline{V}}_M$ and a are parameters that control the well-depth and width, respectively, and r_e is an equilibrium distance. Of course, more sophisticated models of interactions may be used.⁴³ Accordingly, the overdamped Langevin equation 1 becomes

$$\frac{d{\mathbf{r}}_i}{dt}=-\Gamma \sum _{j=1}^N\nabla V_M\left(|{\mathbf{r}}_i-{\mathbf{r}}_j|\right)+{\chi }_E\nabla E\left({\mathbf{r}}_i\right)+\sqrt{2D}{\mathit{\eta }}_i\left(t\right),$$ (24)

where χ_E = Γξ_E. The ECM evolves according to

$$\frac{dE}{dt}={\lambda }_E\sum _{i=1}^N\delta \left(\mathbf{r}-{\mathbf{r}}_i\left(t\right)\right),$$ (25)

where λ_E is the net rate of ECM production, which is assumed to saturate at a specific value E_sat of ECM density, ${\lambda }_E={\overline{\lambda }}_{E,prod}{\left(E_{sat}-E\right)}_{+}-{\overline{\lambda }}_{E,degrade}E$, and the subscript + denotes the positive part.

The proliferation of tumor cells is dependent on the availability of nutrients with concentration n. As a simple model of BD, we assume that a single cell can undergo mitosis with a nutrient-dependent probability λ_m = λ_m(n), which we represent by means of the stoichiometric equation $X\stackrel{{\lambda }_m}{\leftrightarrow }2X$. We model cell death (e.g., apoptosis) as occuring with a constant probability λ_d, described by the stoichiometric equation $X\stackrel{{\lambda }_d}{\leftrightarrow }\varnothing$. This can be implemented as a Markov process and affects the number of cells in the population making N = N(t). The nutrient is provided by the vascular system, diffuses through the microenvironment and is uptaken by tumor cells, and thus satisfies the reaction-diffusion equation

$$\frac{\partial n}{\partial t}=D_n{\nabla }^{2}n+S_n-{\lambda }_n\sum _{i=1}^{N\left(t\right)}\delta \left(\mathbf{r}-{\mathbf{r}}_i\left(t\right)\right),$$ (26)

where D_n is the diffusion coefficient, S_n represents nutrient sources and λ_n is the nutrient uptake rate assumed to be proportional to n, ${\lambda }_n={\overline{\lambda }}_{n}n$.

Putting together the methodology described in the previous subsections, and using the fact that the first moment of the BD process described above is simply the result of two mass action laws, that is $D_{\mathcal{BD}}^{\left(1\right)}\left[\rho \right]={\lambda }_m\left(n\right)\rho -{\lambda }_d\rho$, we can derive the corresponding deterministic equation for the cell density ρ. Taking correlations into account, and using the approximations described in Sec. 3A2, the cell density equation becomes

$$\begin{array}{ccc}\hfill \frac{\partial \rho }{\partial t}(\mathbf{r},t)& =& D{\nabla }^2\rho (\mathbf{r},t)-{\chi }_E\nabla ·\left[\rho (\mathbf{r},t)\nabla E(\mathbf{r},t)\right]+\left[{\lambda }_m\left(n(\mathbf{r},t)\right)-{\lambda }_d\right]\rho (\mathbf{r},t)\hfill \\ & & -D\nabla ·\left[\rho (\mathbf{r},t)\int d{\mathbf{r}}^{\prime }\left(\rho ({\mathbf{r}}^{\prime },t)-{\rho }_{\infty }\right){\nabla }_{\mathbf{r}}{c}_{eq}^{\left(2\right)}\left(\right|\mathbf{r}-{\mathbf{r}}^{\prime }|;{\rho }_{\infty })\right].\hfill \end{array}$$ (27)

Due to cell proliferation, the reference density ρ_∞ should be time-dependent to reflect changes in correlations due to increased cell densities, as observed in Ref. 21. A simple way of implementing this is to define the reference density to be ρ_∞(t) = 1/ |Ω|∫drρ(r, t), where the integral is taken over the full domain Ω. Assuming no-flux boundary conditions, we obtain

$$\frac{d{\rho }_{\infty }}{dt}=\frac{1}{\left|\Omega \right|}\int d\mathbf{r}\left[{\lambda }_m\left(n(\mathbf{r},t)\right)-{\lambda }_d\right]\rho (\mathbf{r},t).$$ (28)

As described in Sec. 3A2, Eq. 27 is not closed and requires the direct two-point correlation function $c_{eq}^{\left(2\right)}$ that is determined as the solution of the Ornstein-Zernike equation (repeated here for clarity)

$$h\left(r\right)=c_{eq}^{\left(2\right)}(r;{\rho }_{\infty })+{\rho }_{\infty }\int d{r}^{\prime }h\left(r^{\prime }\right)c_{eq}^{\left(2\right)}\left(\right|\mathbf{r}-{\mathbf{r}}^{\prime }|;{\rho }_{\infty }),$$ (29)

together with a closure rule, which we may take, for example, to be the hypernetted chain closure³¹ (HNC) from the physical sciences,

$$h\left(r\right)=exp\left[-\frac{\Gamma }{D}{V}_M\left(r\right)+h\left(r\right)-c_{eq}^{\left(2\right)}(r;{\rho }_{\infty })\right]-1,$$ (30)

which relates the total correlation function h with $c_{eq}^{\left(2\right)}$ and the interaction potential V_M. Then, for the given potential V_M, Eqs. 29, 30 form a system of two nonlinear equations for the two unknowns h and $c_{eq}^{\left(2\right)}$, parameterized by the reference density ρ_∞ that changes dynamically due to Eq. 28, thus providing the direct two-point correlation function $c_{eq}^{\left(2\right)}$ to close Eq. 27.

Finally, the continuum equations for the ECM and nutrient concentration become

$$\begin{array}{ccc}\hfill \frac{dE}{dt}& =& \left[{\overline{\lambda }}_{E,prod}{\left(E_{sat}-E\right)}_{+}-{\overline{\lambda }}_{E,degrade}E\right]\rho ,\hfill \end{array}$$ (31)

$$\begin{array}{ccc}\hfill \frac{dn}{dt}& =& D_n{\nabla }^{2}n+S_n-{\overline{\lambda }}_{n}n\rho \hfill \end{array}$$ (32)

Thus far, we have outlined a stochastic, discrete model and its deterministic, continuum counterpart, which provide descriptions of the same processes occurring during tumor growth at different scales. These models can be used together to develop a hybrid continuum-discrete multiscale model using an adaptive mesh and algorithm refinement approach,^{44, 45} where the continuum model is used at coarse grid scales, while the discrete algorithm is used on the finest mesh where fluctuations are important (e.g., near the tumor-host interface). Further, feedback from continuum-scale to the microscale can be accommodated, for example, by assuming that the discrete forces depend on the cell density.

DISCUSSION AND OUTLOOK

We have proposed a modeling framework for multicellular systems by extending Dynamic Density Functional Theory (DDFT) to account for different cell types, phenotypes and birth/death processes. Analytical expressions were obtained for the biophysical fluxes that incorporate density correlations, which were modeled using several levels of approximation following a DDFT approach. We then applied these ideas to tumor growth and developed a stochastic, discrete model and a continuum DDFT-type counterpart that modeled the same biophysical processes at larger scales. We discussed how these continuum and discrete systems can be used to derive a hybrid continuum-discrete multiscale model that satisfies the essential properties of a multiscale approach as described in Sec. 1.

The primary difference between our framework and existing models is that the DDFT-based approach accounts for correlations at the continuum scale whereas existing models for multicellular systems tend to use uncorrelated mean-field approximations. As observed in recent experiments of collective cell motion,²¹ correlations become more important as cells proliferate and compress one another, leading to a transition from fluid-like to solid-like behavior. In growing tumors, where there is significant cell proliferation and compression, similar behavior may be expected. This cannot be captured in an uncorrelated mean-field model without phenomenological modifications of the biophysical fluxes (and constitutive laws) to separate fluid-like and elastic-like regimes using, for example, pre-imposed yield stresses.^{46, 47} In contrast, such transitions should be automatically captured in our approach, as has been observed in the physical sciences.^{48, 49, 50}

In the development of a DDFT for multicellular systems, several levels of approximations were used to close the system of equations including an adiabatic approximation and explicit closure relations, which relate the correlations to the microscopic interaction potential. While this approach has been used successfully in the physical sciences, it remains to be seen how appropriate these approximations are for biological systems. Alternatively, experimental measurements can be used to generate correlations by exploiting the relations between the structure factor and the correlations.⁵¹ For example, experimental measurements of the structure factor can be used to generate the total correlation function via the Fourier transform. Then, the direct two-point correlation function can be determined from the total correlation by solving the Ornstein-Zernike equation.

Further, the experiments discussed above on collective cell motion²¹ also underscore the potential importance of taking into account cell sizes and shapes, which are strongly influenced by compression and migration. While there is little known about DDFT for active, deformable objects, it may be possible to describe these effects as components in a phenotype vector, such as we have introduced here.

Because the DDFT-based model provides a description of processes at the mesoscale, further coarse-graining is needed to describe processes at the tissue scale. This should be possible by adapting and extending density-amplitude expansions developed in the physical sciences, where equations are derived for the amplitudes and phases of the density, which vary on much longer length scales.^{52, 53, 54}

While we have discussed the application of the DDFT framework to tumor growth, it is important to note that the framework can easily be made more general to accommodate more detailed tumor-stroma interactions. Further, heterogeneity and anisotropy associated with the ECM can be modeled using an approach analogous to that used in the development of a DDFT model of nematic liquid crystals.^{55, 56}