Abstract
Objectives
To define the mechanism of preserved ejection fraction (EF) despite depressed myocardial strains in hypertension (HTN).
Background
Concentric left ventricular (LV) remodeling in HTN may have normal or supra-normal EF despite depressed myocardial strains. The reason for such discordance is not clear. The aim of this study was to comprehensively evaluate the LV mechanics in a well defined HTN population to define underlying reasons for such a paradox.
Methods
67 patients with resistant HTN and 45 healthy control subjects were studied by cardiac magnetic resonance imaging and tissue tagging with 3-dimensional analysis. Amplitude and directional vector of longitudinal (Ell), circumferential (Ecc) and principal strain for maximal shortening (E3) were computed at basal, mid and distal LV levels respectively. LV torsion defined as the rotation angle of apex relative to base and LV twist which accounts for the effects of differential LV remodeling on torsion for comparison among the two groups, were also calculated.
Results
LV mass index and LV mass/LV end diastolic volume ratio were significantly higher in HTN compared to controls consistent with concentric LV remodeling. Ell and Ecc were significantly decreased in amplitude with altered directional vector in HTN compared to controls. However, the amplitude of E3 was similar in the two groups. Torsion and twist were significantly higher in HTN, which was mainly due to increase in apical rotation. HTN demonstrated significantly increased LV wall thickening compared to controls that resulted in greater LVEF in HTN compared to controls (70 vs. 65%, P <0.001 respectively).
Conclusions
In compensated LV remodeling secondary to HTN, there is increased LV wall thickening with preserved E3 and increased torsion compared to normal controls. This, therefore, contributes to supra-normal LVEF fraction in HTN despite depressed longitudinal and circumferential strains.
Keywords: Torsion, Strain, Hypertension, Left Ventricular Hypertrophy
Introduction
Hypertension (HTN) is the leading risk factor for the development of heart failure1. In response to the increased afterload of arterial hypertension the left ventricle (LV) undergoes concentric LV remodeling, which normalizes LV wall stress and maintains LVEF in a normal or even supernormal range2. Previous studies have shown that LV midwall shortening by echo and LV strains by magnetic resonance tagging are impaired in patients with hypertensive LV remodeling, suggesting cardiomyocyte dysfunction despite normal LVEF3–5. In usual circumstances, LV deformation as assessed by measurement of myocardial strains is directly correlated with LVEF. However in HTN with preserved EF, there appears to be discordance between measurement of regional myocardial strains and global ejection fraction (EF). The reason for such discordance is unclear.
Left ventricular systolic torsion is an important mechanism of wall thickening and a primary component of normal systolic function6–10. Some have also proposed an important role of transverse shear in the observed wall thickening11. Torsion represents the myocardial rotation gradient from the base to apex of the left ventricle. It acts to normalize LV wall stress by minimizing transmural gradients of fiber strain and thereby increase energy efficiency by reducing oxygen demand7, 12, 13. MRI tissue tagging techniques allow accurate non-invasive assessment of three dimensional (3D) – LV remodeling, myocardial strains and torsion14–17. The aims of the current study were twofold: 1) To comprehensively define regional and global cardiac mechanics and remodeling parameters using 3D-cardiac MRI with myocardial tagging in a well characterized HTN patient population and 2) To define the mechanism of preserved EF despite altered myocardial strains in such a patient population.
Methods
Study patients
This study prospectively evaluated consecutive patients referred for specialist evaluation of resistant hypertension. Control group comprised of volunteers who were healthy with no history of cardiovascular disease and not using any prescription medication. Resistant hypertension was defined as uncontrolled hypertension (> 140/90 mmHg) determined at two or more clinic visits in spite of the use of three or more antihypertensive medications at optimal doses. Patients with coronary artery disease or diabetes were also excluded from the study. Subjects with a history of congestive heart failure, chronic kidney disease (creatinine clearance < 60 ml/min) or chronic steroid therapy were excluded from study participation. Secondary causes of hypertension other than hyperaldosteronism, such as renovascular hypertension, pheochromocytoma or Cushing’s syndrome were excluded as clinically indicated. The HTN group consisted of 67 and control group 45 subjects. The study protocol was approved by our Institutional Review Board and informed consent obtained from all participants.
Magnetic Resonance Imaging
Magnetic resonance imaging was performed on a 1.5-T MRI scanner (GE Signa, Milwaukee, Wisconsin) optimized for cardiac application. Electrocardiographically gated breath-hold steady-state free precision technique was used to obtain standard 2-, 3-, 4-chamber and short-axis views with following general parameters: Prospective ECG gating, slice thickness 8 mm, zero interslice gap, field of view 40 × 40 cm, scan matrix 256 × 128, flip angle 45°, repetition/echo times 3.8/1.6 ms. 20 cardiac phases were reconstructed with 8–10 views per segment. Short axis stack was positioned from an end-diastolic four chamber image, centered parallel to mitral annulus and perpendicular to septum, starting 1cm proximal to mitral valve to 1 cm beyond the apex.
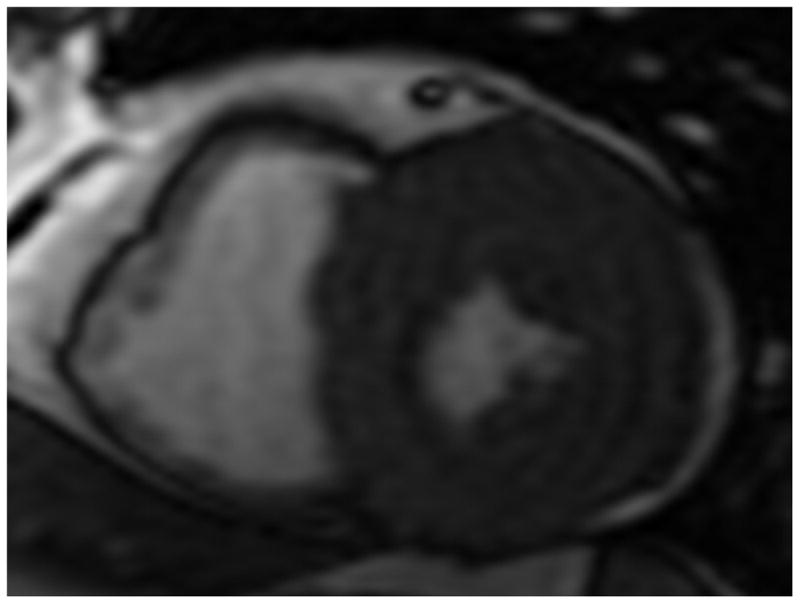
Tagged MRI was done on exact slice prescriptions as above by applying grid tagging to the short axis views and stripe tagging to long axis views using spatial modulation of magnetization encoding gradients method (FGR-SPAMM) as previously described18 with the following general parameters: Prospective ECG gating, slice thickness 8 mm, zero interslice gap, field of view 40 × 40 cm, scan matrix 256 × 128, flip angle 10°, repetition/echo times 8.0/4.2 ms, views per segment 8–10, tag spacing 7 mm, number of reconstructed cardiac phases 20 (Figure 1).
Figure 1.

Geometric Analysis
3D LV geometric parameters were measured from endocardial and epicardial contours manually traced on cine images acquired near end-diastole (LVED) and end-systole (LVES). The contours were traced to exclude the papillary muscles. The contour data were then transformed to a coordinate system aligned along the long-axis of the LV and converted to a prolate spheroidal coordinate system as described19. The prolate spheroidal coordinate system has one radial coordinate (λ) and two angular coordinates (μ,θ), and was used because surfaces of constant λ are ellipsoids, which more closely approximate the shape of the LV wall than cylinders or spheres. Cubic B-spline surfaces with 12 control points in the circumferential (θ) direction and 10 control points in the longitudinal direction (μ) were fit to the λ coordinates of the endocardial and epicardial contours for each time frame. The fit used the smoothing term described19 with α=0, β=0, γ=0.1.
3D surface curvatures were computed using standard formulas20 at the standard wall segments (excluding the apex)21. Myocardial mass was calculated by multiplying end-diastolic myocardial muscle volume by 1.05 g/cm3. 3D wall thickness was computed at the same segments by measuring the distance from a point on the epicardial surface to the closest point on the epicardial surface along a line perpendicular to the epicardial surface. The radius of curvature to wall thickness ratio (R/T), was computed by computing the reciprocal of the product of the endocardial circumferential curvature (κ) and wall thickness (h). End-systolic wall stress was computed according to the formula2:
where P is the end-systolic LV blood pressure measured by a cuff measurement at the time of the MR scan. The apex curvatures and apex curvature index22 were computed from endocardial contours drawn on 2 and 4-chamber view images at end-diastole and end-systole. The apex curvatures index was defined as the average of LV apex radius of curvature calculated from 2 and 4-chamber views divided by the LV inner radius. The sphericity index was defined as the ratio of LV long-axis length to LV inner diameter. The LV long-axis length was computed from LV endocardial contours drawn on a 4-chamber view.
Strain Analysis
3D- LV strain was measured from tagged images at end-systole, which was defined by visual inspection of the image data as the time frame with maximum contraction. Tag lines were tracked with the algorithm described in Denney et al23 and edited, if necessary, by an expert user. 3D deformation and Lagrangian strain was computed by fitting a B-spline deformation model in prolate-spheroidal coordinates to the tag line data24. Normal strains were computed in the radial, circumferential, and longitudinal directions. Principal strains and associated principal directions were also computed. The first principal strain (E1) was approximately aligned in the radial direction and is the maximum thickening strain. The second and third principal strains (E2 and E3) were approximately aligned with the longitudinal and circumferential directions respectively. The third principal strain (E3) is the maximum contraction strain.
3D LVES torsion angle was defined as the LVES rotation angle, ϕ, of the apex relative to the base. 3D LVES Twist, T, was computed from the rotation angle by the following formula25, 26 :
where ρ is the epicardial radius and L is the distance between the basal and apical slices.
All strains were computed at the mid-wall of all segments in the AHA 17-segment model21 except the apex (segment 17). For purposes of data analysis, the left ventricle was divided into 3 levels: base, mid and distal. The strain parameters at each individual level were obtained by averaging the ventricular segments encompassing the whole ventricular wall at that level (6 segments at the base and mid levels, 4 segments at the distal level).
Statistical Analysis
Continuous variables are reported in terms of means and standard deviations of means. Comparison was performed using unpaired t test. Normality of distribution was tested using Kolmogorov- Smirnov test. For variables that were not normally distributed, Mann-Whitney test was also performed. Since the results were similar, this data is not reported except for variables where the tests showed some difference where Mann-Whitney values are reported. The Fisher exact test was used for categorical variables. For all measurements, the level of significance was defined as p-value < set at 0.05. To minimize the inflation of the probability of a type 1 error due to multiple testing, Bonferroni adjustment was done where we divided the level of significance by number of tests. We also created multivariate model for torsional and strain parameters to adjust for age and BMI using linear regression models.
Results
Patient Demographics
Baseline patient characteristics for control subjects and HTN including details of anti-hypertensive therapy are outlined in Table 1. As expected, systolic and diastolic blood pressures were significantly higher in the HTN group despite taking an average of 4.15 antihypertensive medications. There were no significant differences in gender or race between the two groups. However the HTN group was more obese as reflected by body weight and BMI measurements.
Table 1.
Baseline Characteristics.
| Variable | HTN (n= 67 ) (±SD) | Control (n= 45) (±SD) | P value |
|---|---|---|---|
| Age (Yrs) | 55 (12.4) | 41 (12.6) | <0.001 |
| Age, Range (Yrs) | 26–76 | 20–69 | |
| % Females | 46.3 | 53.3 | NS |
| % Caucasians | 55.2 | 67.4 | NS |
| SBP (mmHg) | 144 (16) | 118 (13) | <0.001 |
| DBP (mmHg) | 88 (12) | 74 (11) | <0.001 |
| HR (/min) | 68 (12) | 72 (12) | 0.047 |
| Duration of HTN (Yrs) | 16.7(10) | 0 | |
| Number of anti-HTN medications | 4 (1) | 0 | |
| Beta Blocker (%) | 76.11 | 0 | |
| ACE-I (%) | 64.17 | 0 | |
| ARB (%) | 53.73 | 0 | |
| CCB (%) | 68.65 | 0 | |
| Diuretic (%) | 92.53 | 0 | |
| Other (%) | 40.29 | 0 | |
| BUN (mg/dl) | 13.8 (6) | 11.9 (3.7) | NS |
| Creatinine (mg/dl) | 1 (0.3) | 1 (0.2) | NS |
| Weight (lbs) | 208.4 (45.7) | 173.9 (43.1) | <0.001 |
| BMI (kg/m2) | 31.9 (5.8) | 26.3 (6) | <0.001 |
| BSA (m2) | 2.03 (0.27) | 1.92 (0.24) | 0.024 |
Significant P-value <0.05; NS= not significant
MRI-Derived Indices of LV Geometry and Torsion
Global parameters for assessment of left ventricular geometry for control subject and HTN groups are outlined in Table 2A. The HTN group had significantly higher EF as compared to controls. There were no significant differences in LVEDV and LVESV between controls vs. HTN. At end-diastole, LV in HTN compared to controls demonstrated lower sphericity index and higher apical curvature index. Torsional measurements indicated that both peak torsion and twist measured at end systole were significantly higher in HTN as compared to controls. Torsion and twist remained significantly higher despite adjusting for age alone (β coefficient 3.19, p= 0.002 and β coefficient 1.39, p< 0.001 respectively) or age and BMI together (β coefficient 3.60, p< 0.001 and β coefficient 1.62, p< 0.001 respectively). Furthermore, the effect on overall LV torsion and twist was predominantly due to distal LV segment rotation that was higher in HTN compared to controls. On subgroup analysis based on the gender (Table 2B and 2C) the differences in torsion and twist persisted in HTN compared to controls.
Table 2A.
LV Geometry and Torsion.
| Variable | HTN (±SD) | Control (±SD) | P value |
|---|---|---|---|
| LVEDD (cm) | 5.12 (0.58) | 5.01 (0.46) | NS |
| LVESD (cm) | 3.42 (0.62) | 3.52 (0.40) | NS |
| LVEDV (ml) | 139.3 (42.7) | 128.9 (26.5) | NS |
| LVESV (ml) | 43.1 (20.7) | 45.3 (12.7) | NS |
| LV ED Sphericity Index | 1.66 (0.22) | 1.78 (0.18) | 0.002 |
| LV ES Sphericity Index | 1.97 (0.39) | 1.97 (0.26) | NS |
| LV ED Apex Curvature (cm−1) | 1.38 (0.37) | 1.50 (0.32) | 0.049 |
| LV ES Apex Curvature (cm−1) | 3.84 (2.41) | 3.12 (1.07) | NS |
| LV ED Apex Curvature Index | 0.32 (0.08) | 0.28 (0.06) | 0.009 |
| LV ES Apex Curvature Index | 0.21 (0.1) | 0.21 (0.07) | NS |
| LV mass (g) | 132.88 (41.58) | 95.67 (25.56) | <0.001 |
| LV Mass Index 1(Mass/BSA) | 63.89 (17.59) | 49.69 (10.76) | <0.001 |
| LV Mass Index 2 (Mass/Ht2.7) | 30.24 ( 8.20) | 21.68 ( 5.06) | <0.001 |
| Mass/LVEDV (gm/ml) | 0.98 (0.25) | 0.75 (0.17) | <0.001 |
| LV EF (%) | 70 (8.3) | 65 (5.5) | <0.001 |
| LVES Torsion Angle (°) | 18.16 (4.50) | 14.05 (3.02) | <0.001 |
| LVES Twist (°) | 6.31 (1.51) | 4.56 (0.95) | <0.001 |
| LVES Rotation (distal) (°) | 14.42 (3.95) | 9.73 (3.56) | <0.001 |
Significant P-value <0.05; NS= not significant
Table 2B.
LV Geometry and Torsion (Male).
| Variable | HTN (±SD) | Control (±SD) | P value | |
|---|---|---|---|---|
| LVEDD (cm) | 5.28 (0.64) | 5.21 | (0.39) | NS |
| LVESD (cm) | 3.64 (0.59) | 3.60 | (0.38) | NS |
| LVEDV (ml) | 160.2 (49.7) | 138.9 | (25.3) | 0.078 |
| LVESV (ml) | 53.3 (21.1) | 47.9 | (12.1) | NS |
| LV ED Sphericity Index | 1.70 (0.20) | 1.78 | (0.16) | NS |
| LV ES Sphericity Index | 1.97 (0.42) | 2.00 | (0.27) | NS |
| LV ED Apex Curvature (cm−1) | 1.39 (0.43) | 1.52 | (0.38) | NS |
| LV ES Apex Curvature (cm−1) | 3.65 (2.43) | 3.18 | (0.96) | NS |
| LV ED Apex Curvature Index | 0.32 (0.08) | 0.28 | (0.06) | 0.057 |
| LV ES Apex Curvature Index | 0.21 (0.11) | 0.19 | (0.06) | NS |
| LV mass (g) | 157.62 (36.34) | 110.88 | (24.06) | <0.001 |
| LV Mass Index 1(Mass/BSA) | 68.73 (18.42) | 53.97 | (9.81) | 0.002 |
| LV Mass Index 2 (Mass/Ht2.7) | 29.74 (7.82) | 23.02 | (5.08) | <0.001 |
| Mass/LVEDV (gm/ml) | 1.02 (0.24) | 0.81 | (0.17) | 0.001 |
| LV EF (%) | 67 (6.8) | 66 | (4.5) | NS |
| LVES Torsion Angle (°) | 17.86(4.46) | 13.92 | (2.98) | <0.001 |
| LVES Twist (°) | 6.19 (1.53) | 4.48 | (0.90) | <0.001 |
| LVES Rotation (distal) (°) | 13.99 (4.44) | 9.88 | (3.22) | <0.001 |
Significant P-value <0.05; NS= not significant
Table 2C.
LV Geometry and Torsion (Female).
| Variable | HTN (±SD) | Control (±SD) | P value |
|---|---|---|---|
| LVEDD (cm) | 4.98 (0.50) | 4.84 (0.46) | NS |
| LVESD (cm) | 3.24 (0.59) | 3.45 (0.41) | 0.04 |
| LVEDV (ml) | 121.8 (25.4) | 120.1 (24.8) | NS |
| LVESV (ml) | 34.5 (16.1) | 43.0 (13.1) | 0.04 |
| LV ED Sphericity Index | 1.63 (0.22) | 1.79 (0.20) | 0.006 |
| LV ES Sphericity Index | 1.97 (0.38) | 1.95 (0.25) | NS |
| LV ED Apex Curvature (cm−1) | 1.37 (0.32) | 1.49 (0.28) | NS |
| LV ES Apex Curvature (cm−1) | 3.99 (2.42) | 3.06 (1.18) | NS |
| LV ED Apex Curvature Index | 0.32 (0.07) | 0.28 (0.06) | 0.04 |
| LV ES Apex Curvature Index | 0.21 (0.09) | 0.22 (0.08) | NS |
| LV mass (g) | 112.28 (34.00) | 82.37 (18.73) | <0.001 |
| LV Mass Index 1(Mass/BSA) | 59.77 (15.98) | 45.94 (10.32) | <0.001 |
| LV Mass Index 2 (Mass/Ht2.7) | 30.79 ( 8.69) | 20.50 ( 4.84) | <0.001 |
| Mass/LVEDV (gm/ml) | 0.94 (0.26) | 0.70 (0.15) | <0.001 |
| LV EF (%) | 72 (8.8) | 65 (6.3) | <0.001 |
| LVES Torsion Angle (°) | 18.41 (4.59) | 14.16 (3.11) | <0.001 |
| LVES Twist (°) | 6.41 (1.51) | 4.63 (1.00) | <0.001 |
| LVES Rotation (distal) (°) | 14.78 (3.51) | 9.60 (3.90) | <0.001 |
Significant P-value <0.05; NS= not significant
MRI-Derived Indices of Regional LV Remodeling and Wall Stress
Regional changes in LV shape and wall stress are described in Table 3. There were no differences in the end diastolic circumferential and longitudinal curvatures at various LV levels. LV wall thickness and thickening were higher in HTN as compared to controls at all levels and during both systole and diastole. Similarly the LV demonstrated concentric remodeling in HTN as compared to controls during both systole and diastole as measured by R/T ratio. LV wall thickening was increased in HTN compared to control. Furthermore, there was reduction in LV wall stress in HTN as compared to controls at end-systole. These changes therefore represent that the HTN group had compensated LV remodeling with higher EF as compared to controls.
Table 3.
Regional LV Remodeling and Wall Stress.
| Variable | Base | Mid | Distal | ||||||
|---|---|---|---|---|---|---|---|---|---|
| HTN (±SD) | Control (±SD) | P value | HTN (±SD) | Control (±SD) | P value | HTN (±SD) | Control (±SD) | P value | |
| LVED Circ. Curv. (cm−1) | 0.38 (0.04) | 0.38 (0.03) | NS | 0.40 (0.04) | 0.40 (0.03) | NS | 0.49 (0.06) | 0.50 (0.04) | NS |
| LVED Long. Curv.(cm−1) | 0.19 (0.02) | 0.19 (0.02) | NS | 0.07 (0.04) | 0.06 (0.03) | NS | 0.20 (0.04) | 0.18 (0.04) | 0.021(NS) |
| LVED Wall Thickness (cm) | 1.02 (0.21) | 0.78 (0.14) | <0.001 | 0.88 (0.18) | 0.69 (0.14) | <0.001 | 0.67 (0.14) | 0.57 (0.13) | <0.001 |
| LV Wall Thickening (%) | 58.4 (19.5) | 47.0 (14.8) | 0.001 | 78.3 (24.5) | 63.8 (16.5) | <0.001 | 100.7 (36.1) | 75.3 (27.7) | <0.001 |
| LVED R/T Ratio | 2.67 (0.58) | 3.47 (0.66) | <0.001 | 3.04 (0.73) | 3.79 (0.86) | <0.001 | 3.26 (0.85) | 3.77 (1.04) | 0.005(NS) |
| LVES R/T Ratio | 1.11 (0.30) | 1.65 (0.38) | <0.001 | 1.09 (0.36) | 1.61 (0.38) | <0.001 | 1.05 ( 0.41) | 1.47 ( 0.41) | <0.001 |
| LVES Wall Stress (1000N/m2) | 7.76 (2.94) | 10.53 (2.57) | <0.001 | 7.40 (3.48) | 9.83 (2.55) | <0.001 | 7.07 (3.86) | 8.80 (2.83) | 0.001 |
Significant P-value <0.0024; NS= not significant
MRI-Derived Regional Left Ventricular Strain Magnitude and Directionality
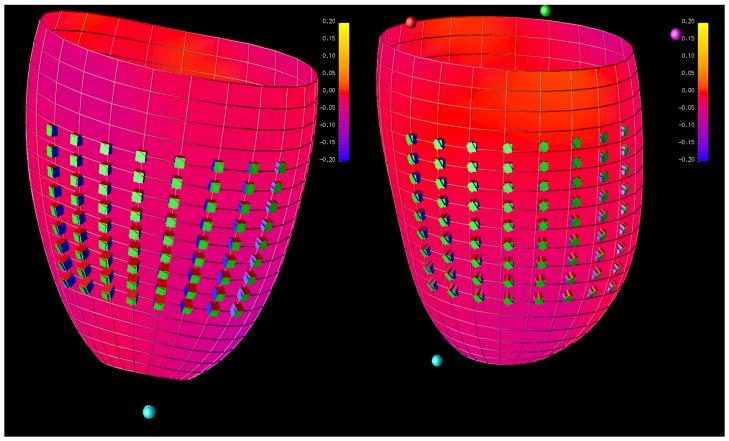
We calculated E3 (which is the principal strain in the direction of maximal shortening) and also longitudinal (Ell) & circumferential (Ecc) strains (these strain measurements are oriented with respect to the long axis of the left ventricle) at all three levels (Table 4). We found significant reduction in Ecc at mid and distal LV segments in HTN. Ell was also reduced at the basal and mid LV segment in HTN compared to controls. Results remained similar for Ecc when adjusted for age (β coefficient: −1.82, p = 0.003) or age and BMI together (β coefficient: −1.63, p = 0.02). Results for Ell also remained similar when adjusted for age (β coefficient: −2.07, p = 0.003). However the results were not statistically significant for Ell when adjusted for both age and BMI together (β coefficient: −1.43, p = 0.06). E3, i.e. the maximal shortening, was almost identical between the two groups at all three levels indicating that there may be changes in the directionality of strain tensors. Indeed, when we measured the directionality of the principal strain tensors, we found they were significantly less circumferential in the HTN relative to normal group as described in Table 5 and Figure 2.
Table 4.
Regional LV Strains.
| Variable | Base | Mid | Distal | ||||||
|---|---|---|---|---|---|---|---|---|---|
| HTN (±SD) | Control (±SD) | P value | HTN (±SD) | Control (±SD) | P value | HTN (±SD) | Control (±SD) | P value | |
| LVES Circ. Strain (Ecc) | 13.10 (2.62) | 13.99 (1.87) | 0.055(NS) | 14.24 (3.28) | 15.81 (1.65) | 0.004 | 13.97 (4.45) | 16.69 (2.63) | <0.001 |
| LVES Long. Strain (Ell) | 10.59 (3.37) | 13.16 (2.18) | <0.001 | 10.67 (3.45) | 12.33 (2.43) | 0.006 | 12.12 (4.66) | 11.78 (3.66) | NS |
| LVES Min. Principal Strain (E3) | 20.01 (2.31) | 19.72 (1.84) | NS | 19.90 (2.56) | 19.84 (1.95) | NS | 22.75 (3.26) | 22.59 (2.66) | NS |
P-value significant level is <0.0056; NS= not significant
Table 5.
Angles between Principal Strain Directions and Normal Strain (Circumferential, Longitudinal, and Radial) Directions is depicted in the table below.
| Variable | Base | Mid | Distal | ||||||
|---|---|---|---|---|---|---|---|---|---|
| HTN (±SD) | Control (±SD) | P value | HTN (±SD) | Control (±SD) | P value | HTN (±SD) | Control (±SD) | P value | |
| Ecc Angle (°) | 37.22 (4.03) | 36.08 (3.26 ) | NS | 33.86 (4.68) | 30.68 (4.87) | <0.001 | 35.41 ( 5.08) | 31.07 (5.27) | <0.001 |
| Ell Angle (°) | 38.49 (3.99) | 37.05 (3.72) | 0.06 (NS) | 35.16 (4.47) | 33.13 (6.20) | 0.004 | 36.46 (6.32 ) | 35.49 (7.42) | NS |
| Err Angle (°) | 15.91 (7.79) | 14.89 (7.41) | NS | 16.64 (6.41) | 14.97 (7.86) | NS | 26.57 (11.39) | 24.62 (11.22) | NS |
P-value significant level is <0.0056 ; NS= not significant
Figure 2.
Discussion
In the current study we have described a mechanistic rationale for supra-normal EF in a well characterized HTN patient population. To this objective, we have described global and regional LV mechanics and remodeling in HTN with normal EF. We demonstrate that there is increased torsional deformation in HTN as compared to controls which is predominantly due to increased rotation of the distal/apical segments of the LV. We have also confirmed that longitudinal (Ell) and circumferential (Ecc) strains are depressed at regional LV levels in the HTN. However we found that the principal strain representative of maximal shortening (E3) at the same corresponding levels is similar in the two groups. This apparent paradox may be accounted for by the change in the directions of principal components of strain tensors in HTN compared to controls. We also found that there is differential LV remodeling in HTN compared to controls which manifest not only as increase in LV mass and wall thickness, but also higher LV apical curvature index at end-diastole. Furthermore there is reduced end-systolic LV wall stress in HTN. Taken together these resulted in greater LV wall thickening and supra-normal EF in HTN despite lower longitudinal and circumferential strains.
Studies in individual myofibers have shown that a 15% fiber shortening leads to only an 8% increase in myocyte diameter (i.e. individual cell thickening), which cannot by itself account for the observed > 40% LV radial wall thickening and a > 60% LVEF27, 28. The increased wall thickness seen in hypertension with concentric remodeling has been shown to be associated with preserved EF and reduced circumferential shortening29. Recent research using theoretical models30, 31 and validated in humans31 has suggested that the geometric effects of increased radius to wall thickness ratio in concentric remodeling offset reductions in circumferential shortening allowing EF to be preserved. In our HTN group, we found increased LV wall thickening at all LV levels. This increased thickening in HTN occurred despite decrease in longitudinal and circumferential strains at various segments. Interestingly, we did not find any differences in the measurements of maximal shortening (E3) across various segments of the LV. This made us evaluate the directional vector of the strain tensors. We found that there were differences in the directional vector which may account for similar E3 in the two groups despite differences in Ell and Ecc. In contrast to our findings, recently investigators used 2D echocardiographic speckle tracking techniques to evaluate circumferential (Ecc), longitudinal (Ell) and radial strains (Err) at the papillary muscle level in patients with mild HTN. They demonstrated no difference in the measurements between normal and HTN32. However, other investigators using similar techniques such as ours have demonstrated depressed circumferential strains in HTN as compared to control population33.
We noted that LV torsion was increased in HTN that predominantly was due to increased rotation at the distal segment. Our current observations are consistent with the theoretical assumption that predicts a greater torsion in the presence of increased concentricity (decreased R/T ratio) due to increased mechanical torque advantage of subepicardial fibers over subendocardial fibers6, 7, 9, 34. In support of this hypothesis, previous studies in patients with aortic valve stenosis and preserved LVEF reported an increase in LV torsion35. Similarly in a small cohort of older individuals with higher BP compared to control, the investigators found greater systolic torsion using 3D- tagged MRI analytical technique 36. In patients with hypertrophic cardiomyopathy, torsion was increased in the presence of significantly decreased myocardial strains, which was attributed to the myofibrillar disarray of this condition17.
The major limitations of our study are that there were differences in the mean age and BMI of the two groups. We adjusted for these variables and still found significantly higher torsion and twist in HTN. In a large population cohort, one group has demonstrated an age dependence of Ecc37, in contrast other investigators have found no significant effect of aging on myocardial strains38, 39. All participants in HTN group by definition were on multiple anti-hypertensive medications including beta blockers and calcium channel blockers. These medications can affect the ventricular strains. However the effects of drugs would not explain the discordance in maximal shortening strains (E3) compared to Ell and Ecc in the two groups.
Conclusions
In HTN with preserved EF, we demonstrate increased LV torsion which is associated with concentric LV remodeling. Furthermore, despite depressed Ecc and Ell, LV wall thickening is increased in HTN that again is related to LV remodeling. Therefore compensated LV remodeling is the predominant factor for supra-normal EF in HTN.
Acknowledgments
Source of Funding:
NIH P50-HL077100 (LJD); NIH R01-HL104018 (HG)
Footnotes
Conflicts of Interest:
None
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Levy D, Larson MG, Vasan RS, Kannel WB, Ho KK. The progression from hypertension to congestive heart failure. Jama. 1996;275(20):1557–1562. [PubMed] [Google Scholar]
- 2.Grossman W, Jones D, McLaurin LP. Wall stress and patterns of hypertrophy in the human left ventricle. J Clin Invest. 1975;56(1):56–64. doi: 10.1172/JCI108079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.de Simone G, Devereux RB, Roman MJ, Ganau A, Saba PS, Alderman MH, Laragh JH. Assessment of left ventricular function by the midwall fractional shortening/end-systolic stress relation in human hypertension. J Am Coll Cardiol. 1994;23(6):1444–1451. doi: 10.1016/0735-1097(94)90390-5. [DOI] [PubMed] [Google Scholar]
- 4.Palmon LC, Reichek N, Yeon SB, Clark NR, Brownson D, Hoffman E, Axel L. Intramural myocardial shortening in hypertensive left ventricular hypertrophy with normal pump function. Circulation. 1994;89(1):122–131. doi: 10.1161/01.cir.89.1.122. [DOI] [PubMed] [Google Scholar]
- 5.Sadler DB, Aurigemma GP, Williams DW, Reda DJ, Materson BJ, Gottdiener JS. Systolic function in hypertensive men with concentric remodeling. Hypertension. 1997;30(4):777–781. doi: 10.1161/01.hyp.30.4.777. [DOI] [PubMed] [Google Scholar]
- 6.Arts T, Reneman RS. Dynamics of left ventricular wall and mitral valve mechanics--a model study. J Biomech. 1989;22(3):261–271. doi: 10.1016/0021-9290(89)90093-6. [DOI] [PubMed] [Google Scholar]
- 7.Arts T, Reneman RS, Veenstra PC. A model of the mechanics of the left ventricle. Ann Biomed Eng. 1979;7(3–4):299–318. doi: 10.1007/BF02364118. [DOI] [PubMed] [Google Scholar]
- 8.Gotte MJ, Germans T, Russel IK, Zwanenburg JJ, Marcus JT, van Rossum AC, van Veldhuisen DJ. Myocardial strain and torsion quantified by cardiovascular magnetic resonance tissue tagging: studies in normal and impaired left ventricular function. J Am Coll Cardiol. 2006;48(10):2002–2011. doi: 10.1016/j.jacc.2006.07.048. [DOI] [PubMed] [Google Scholar]
- 9.Lumens J, Delhaas T, Arts T, Cowan BR, Young AA. Impaired subendocardial contractile myofiber function in asymptomatic aged humans, as detected using MRI. American Journal of Physiology - Heart and Circulatory Physiology. 2006;291(4):H1573–H1579. doi: 10.1152/ajpheart.00074.2006. [DOI] [PubMed] [Google Scholar]
- 10.Sallin EA. Fiber orientation and ejection fraction in the human left ventricle. Biophys J. 1969;9(7):954–964. doi: 10.1016/S0006-3495(69)86429-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.LeGrice IJ, Takayama Y, Covell JW. Transverse Shear Along Myocardial Cleavage Planes Provides a Mechanism for Normal Systolic Wall Thickening. Circulation Research. 1995;77(1):182–193. doi: 10.1161/01.res.77.1.182. [DOI] [PubMed] [Google Scholar]
- 12.Beyar R, Sideman S. Effect of the twisting motion on the nonuniformities of transmyocardial fiber mechanics and energy demand--a theoretical study. IEEE Trans Biomed Eng. 1985;32(10):764–769. doi: 10.1109/TBME.1985.325491. [DOI] [PubMed] [Google Scholar]
- 13.Beyar R, Sideman S. Left ventricular mechanics related to the local distribution of oxygen demand throughout the wall. Circ Res. 1986;58(5):664–677. doi: 10.1161/01.res.58.5.664. [DOI] [PubMed] [Google Scholar]
- 14.Zerhouni EA, Parish DM, Rogers WJ, Yang A, Shapiro EP. Human heart: tagging with MR imaging--a method for noninvasive assessment of myocardial motion. Radiology. 1988;169(1):59–63. doi: 10.1148/radiology.169.1.3420283. [DOI] [PubMed] [Google Scholar]
- 15.Moore CCL-OC, McVeigh ER, Zerhouni EA. Three-dimensional systolic strain patterns in the normal human left ventricle: characterization with tagged MR imaging. Radiology. 2000;214(2):453–466. doi: 10.1148/radiology.214.2.r00fe17453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.O’Dell WGMC, Hunter WC, Zerhouni EA, McVeigh ER. Three-dimensional myocardial deformations: calculation with displacement field fitting to tagged MR images. Radiology. 1995;195(3):829–835. doi: 10.1148/radiology.195.3.7754016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Young AA, Kramer CM, Ferrari VA, Axel L, Reichek N. Three-dimensional left ventricular deformation in hypertrophic cardiomyopathy. Circulation. 1994;90(2):854–867. doi: 10.1161/01.cir.90.2.854. [DOI] [PubMed] [Google Scholar]
- 18.Castillo E, Osman NF, Rosen BD, El-Shehaby I, Li P, Jerosch-Herold M, Shenghan L, Bluemke DA, Lima JoAC. Quantitative Assessment of Regional Myocardial Function with MR-Tagging in a Multi-Center Study: Interobserver and Intraobserver Agreement of Fast Strain Analysis with Harmonic Phase (HARP) MRI. Journal of Cardiovascular Magnetic Resonance (Taylor & Francis Ltd) 2005;7(5):783–791. doi: 10.1080/10976640500295417. [DOI] [PubMed] [Google Scholar]
- 19.Young AA, Orr R, Smaill BH, Dell’Italia LJ. Three-dimensional changes in left and right ventricular geometry in chronic mitral regurgitation. Am J Physiol. 1996;271(6 Pt 2):H2689–2700. doi: 10.1152/ajpheart.1996.271.6.H2689. [DOI] [PubMed] [Google Scholar]
- 20.Lipshultz M. Differential Geometry. New York: McGraw-Hill; 1969. [Google Scholar]
- 21.Cerqueira MD, Weissman NJ, Dilsizian V, Jacobs AK, Kaul S, Laskey WK, Pennell DJ, Rumberger JA, Ryan T, Verani MS. Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart: a statement for healthcare professionals from the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association. Circulation. 2002;105(4):539–542. doi: 10.1161/hc0402.102975. [DOI] [PubMed] [Google Scholar]
- 22.Di Donato M, Dabic P, Castelvecchio S, Santambrogio C, Brankovic J, Collarini L, Joussef T, Frigiola A, Buckberg G, Menicanti L, the RG. Left ventricular geometry in normal and post-anterior myocardial infarction patients: sphericity index and ‘new’ conicity index comparisons. Eur J Cardiothorac Surg. 2006;29(Suppl_1):S225–230. doi: 10.1016/j.ejcts.2006.03.002. [DOI] [PubMed] [Google Scholar]
- 23.Denney TS, Jr, Yan BLGL. Unsupervised reconstruction of a three-dimensional left ventricular strain from parallel tagged cardiac images. Magnetic Resonance in Medicine. 2003;49(4):743–754. doi: 10.1002/mrm.10434. [DOI] [PubMed] [Google Scholar]
- 24.Li J, Denney TS., Jr Left ventricular motion reconstruction with a prolate spheroidal B-spline model. Phys Med Biol. 2006;51(3):517–537. doi: 10.1088/0031-9155/51/3/004. [DOI] [PubMed] [Google Scholar]
- 25.Aelen FWL, Arts T, Sanders DGM, Thelissen GRP, Muijtjens AMM, Prinzen FW, Reneman RS. Relation between torsion and cross-sectional area change in the human left ventricle. Journal of Biomechanics. 1997;30(3):207–212. doi: 10.1016/s0021-9290(96)00147-9. [DOI] [PubMed] [Google Scholar]
- 26.Rüssel I, Götte M, Bronzwaer J, Knaapen P, Paulus W, Rossum Av. Left ventricular torsion: an expanding role in the analysis of myocardial dysfunction. JACC Cardiovasc Imaging. 2009;2(5):648–655. doi: 10.1016/j.jcmg.2009.03.001. [DOI] [PubMed] [Google Scholar]
- 27.Rademakers FE, Rogers WJ, Guier WH, Hutchins GM, Siu CO, Weisfeldt ML, Weiss JL, Shapiro EP. Relation of regional cross-fiber shortening to wall thickening in the intact heart. Three-dimensional strain analysis by NMR tagging. Circulation. 1994;89(3):1174–1182. doi: 10.1161/01.cir.89.3.1174. [DOI] [PubMed] [Google Scholar]
- 28.Spann JF, Jr, Buccino RA, Sonnenblick EH, Braunwald E. Contractile state of cardiac muscle obtained from cats with experimentally produced ventricular hypertrophy and heart failure. Circ Res. 1967;21(3):341–354. doi: 10.1161/01.res.21.3.341. [DOI] [PubMed] [Google Scholar]
- 29.Aurigemma GP, Silver KH, Priest MA, Gaasch WH. Geometric changes allow normal ejection fraction despite depressed myocardial shortening in hypertensive left ventricular hypertrophy. J Am Coll Cardiol. 1995;26(1):195–202. doi: 10.1016/0735-1097(95)00153-q. [DOI] [PubMed] [Google Scholar]
- 30.Vandsburger MH, French BA, Helm PA, Roy RJ, Kramer CM, Young AA, Epstein FH. Multi-parameter in vivo cardiac magnetic resonance imaging demonstrates normal perfusion reserve despite severely attenuated Î2-adrenergic functional response in neuronal nitric oxide synthase knockout mice. European Heart Journal. 2007;28(22):2792–2798. doi: 10.1093/eurheartj/ehm241. [DOI] [PubMed] [Google Scholar]
- 31.Zha W, Lloyd SG, Gupta H, Dell’Italia LJ, Denney TSJ. Preserved Ejection Fraction in the Presence of Reduced LV Wall Strain in Hypertension: A Geometric Explanation Validated by MRI. Proceedings 19th Scientific Meeting of ISMRM; 2011. [Google Scholar]
- 32.Narayanan A, Aurigemma GP, Chinali M, Hill JC, Meyer TE, Tighe DA. Cardiac Mechanics in Mild Hypertensive Heart Disease: A Speckle - Strain Imaging Study. Circ Cardiovasc Imaging. 2009 doi: 10.1161/CIRCIMAGING.108.811620. CIRCIMAGING.108.811620. [DOI] [PubMed] [Google Scholar]
- 33.Biederman RWW, Doyle M, Young AA, Devereux RB, Kortright E, Perry G, Bella JN, Oparil S, Calhoun D, Pohost GM, Dell’Italia LJ. Marked Regional Left Ventricular Heterogeneity in Hypertensive Left Ventricular Hypertrophy Patients: A Losartan Intervention for Endpoint Reduction in Hypertension (LIFE) Cardiovascular Magnetic Resonance and Echocardiographic Substudy. Hypertension. 2008;52(2):279–286. doi: 10.1161/HYPERTENSIONAHA.108.109819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Van der Toorn A, Barenbrug P, Snoep G, Van der Veen FH, Delhaas T, Prinzen FW, Maessen J, Arts T. Transmural gradients of cardiac myofiber shortening in aortic valve stenosis patients using MRI tagging. American Journal of Physiology - Heart and Circulatory Physiology. 2002;283(4):H1609–H1615. doi: 10.1152/ajpheart.00239.2002. [DOI] [PubMed] [Google Scholar]
- 35.Stuber M, Scheidegger MB, Fischer SE, Nagel E, Steinemann F, Hess OM, Boesiger P. Alterations in the local myocardial motion pattern in patients suffering from pressure overload due to aortic stenosis. Circulation. 1999;100(4):361–368. doi: 10.1161/01.cir.100.4.361. [DOI] [PubMed] [Google Scholar]
- 36.Fonseca CG, Oxenham HC, Cowan BR, Occleshaw CJ, Young AA. Aging alters patterns of regional nonuniformity in LV strain relaxation: a 3-D MR tissue tagging study. American Journal of Physiology - Heart and Circulatory Physiology. 2003;285(2):H621–H630. doi: 10.1152/ajpheart.01063.2002. [DOI] [PubMed] [Google Scholar]
- 37.Cheng S, Fernandes VRS, Bluemke DA, McClelland RL, Kronmal RA, Lima JAC. Age-Related Left Ventricular Remodeling and Associated Risk for Cardiovascular Outcomes: The Multi-Ethnic Study of Atherosclerosis. Circ Cardiovasc Imaging. 2009;2(3):191–198. doi: 10.1161/CIRCIMAGING.108.819938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Marwick TH, Leano RL, Brown J, Sun J-P, Hoffmann R, Lysyansky P, Becker M, Thomas JD. Myocardial Strain Measurement With 2-Dimensional Speckle-Tracking Echocardiography: Definition of Normal Range. J Am Coll Cardiol Img. 2009;2(1):80–84. doi: 10.1016/j.jcmg.2007.12.007. [DOI] [PubMed] [Google Scholar]
- 39.Sun JP, Popovic ZB, Greenberg NL, Xu X-F, Asher CR, Stewart WJ, Thomas JD. Noninvasive quantification of regional myocardial function using Doppler-derived velocity, displacement, strain rate, and strain in healthy volunteers: effects of aging. Journal of the American Society of Echocardiography. 2004;17(2):132–138. doi: 10.1016/j.echo.2003.10.001. [DOI] [PubMed] [Google Scholar]