Contraction type influences the human ability to use the available torque capacity of skeletal muscle during explosive efforts

Abstract

The influence of contraction type on the human ability to use the torque capacity of skeletal muscle during explosive efforts has not been documented. Fourteen male participants completed explosive voluntary contractions of the knee extensors in four separate conditions: concentric (CON) and eccentric (ECC); and isometric at two knee angles (101°, ISO101 and 155°, ISO155). In each condition, torque was measured at 25 ms intervals up to 150 ms from torque onset, and then normalized to the maximum voluntary torque (MVT) specific to that joint angle and angular velocity. Explosive voluntary torque after 50 ms in each condition was also expressed as a percentage of torque generated after 50 ms during a supramaximal 300 Hz electrically evoked octet in the same condition. Explosive voluntary torque normalized to MVT was more than 60 per cent larger in CON than any other condition after the initial 25 ms. The percentage of evoked torque expressed after 50 ms of the explosive voluntary contractions was also greatest in CON (ANOVA; p < 0.001), suggesting higher concentric volitional activation. This was confirmed by greater agonist electromyography normalized to M_max (recorded during the explosive voluntary contractions) in CON. These results provide novel evidence that the ability to use the muscle's torque capacity explosively is influenced by contraction type, with concentric contractions being more conducive to explosive performance due to a more effective neural strategy.

1. Introduction

The capacity of the human neuromuscular system for explosive force/torque production, typically measured as rate of torque development (RTD), is considered functionally more important than maximal voluntary torque (MVT) during explosive movements, such as sprinting, jumping or restabilizing the body following a loss of balance [1–3]. An understanding of the neural and mechanical factors that limit explosive torque production will therefore have important implications for both health and sports performance. The influence of contraction type (i.e. isometric, concentric or eccentric) on MVT in vivo has been documented extensively via the MVT–velocity relationship [4–9]; however, little is known about the capability for explosive torque production during different types of contraction.

The majority of past studies have investigated RTD during isometric contractions [1–3,10], and occasionally during the acceleration phase of isoinertial dynamic contractions [11,12]. However, the latter provides an experimentally inconsistent situation, as the movement dynamics (acceleration, velocity and displacement) are not controlled and combine with the inertial properties of the system in a nonlinear manner, giving rise to torques that vary within and between trials and participants, and confound RTD measurements. In contrast, performing explosive concentric and eccentric contractions at a constant acceleration from stationary may provide a more controlled situation in which to investigate RTD during the acceleration phase of dynamic contractions.

A further complication with measuring dynamic RTD is that joint angle will change throughout the effort, and this change is in opposite directions for concentric and eccentric contractions. Consequently, it is not possible to match joint angle throughout the different types of contraction, apart from at a single time point/angle. The discrete influence of joint angle on explosive torque production can be evaluated by comparing isometric contractions at different angles; however, isolating the influence of the type of contraction is problematic. One approach is to normalize the explosive torque produced at any time point during the different types of contraction to the MVT available at that specific joint angle and angular velocity. This also enables us to investigate whether explosive torque production changes in proportion to MVT. Another approach is to normalize explosive voluntary torque to the maximum capacity for explosive torque production elicited during an evoked octet contraction (eight supramaximal pulses at 300 Hz; [2,13]) in identical contractile conditions. This provides an experimental approach that can dissociate between the neural and peripheral limitations of explosive torque production during different types of contraction.

While normalizing, explosive torque (via the above methods) will control for differences in joint kinematics between the different types of contraction, the behaviour of the series elastic component (SEC) may decouple the association between joint kinematics and muscle fibre behaviour [14]. Muscle modelling can be used to assess whether any measured effects of contraction type on explosive torque production are representative of muscle fibre performance, or due to the influence of the SEC.

There is limited evidence of the effect of joint angle on human RTD. During the initial 40 ms of explosive isometric contractions in humans, torque production has been reported to change with joint angle, but only in proportion to MVT [2]. In contrast, animal studies have found a faster time to peak force with decreasing muscle length [15–17], although this appears to primarily affect the later phases of explosive contractions [15,17]. Clearly, further work is required to understand the influence of joint angle on explosive torque production.

The primary aim of this study was to compare explosive torque production during concentric, eccentric and isometric contractions, and examine the neural and peripheral limitations to explosive torque production in these different contractile conditions. Two isometric angles were also studied to examine the discrete influence of joint angle on explosive torque production.

2. Methods

(a). Participants

Fourteen healthy male participants (age, 24 ± 6 years; height, 1.78 ± 0.05 m; mass, 75 ± 5 kg), ranging from elite explosive power athletes to low/moderately active individuals, gave informed consent to participate in the study, which was approved by the Loughborough University ethical advisory committee.

(b). Overview

Participants visited the laboratory on three occasions separated by 3–5 days to complete a series of voluntary and evoked contractions of the knee extensors on an isovelocity dynamometer. Session 1 involved: a series of isometric maximal voluntary contractions (MVCs) at different knee joint angles; electrically evoked concentric, eccentric and isometric octet contractions; and familiarization with explosive voluntary concentric, eccentric and isometric contractions. In session 2, surface electromyography (EMG) was collected from the three superficial quadriceps muscles while participants completed explosive voluntary concentric, eccentric and isometric contractions, and during electrically evoked supramaximal twitch contractions to elicit compound muscle action potentials (M-waves). In session 3, participants completed a series of concentric and eccentric isovelocity MVCs.

The isometric and isovelocity MVCs were used to determine joint angle and angular velocity-specific MVT for normalization of explosive voluntary torque measured under concentric, eccentric and isometric conditions. Likewise, concentric, eccentric and isometric explosive voluntary torque were also normalized to electrically evoked octet torque in the same contractile conditions. Finally, the M-waves recorded in session 2 were used for normalization of surface EMG data collected during the concentric, eccentric and isometric explosive contractions of the same session.

(c). Measurements

(i). Dynamometer and surface EMG

Shoulder and waist straps secured participants firmly in the seat of the dynamometer (Con-Trex; CMV Aargau, Switzerland) with the hip angle fixed at 95°. Single differential surface EMG electrodes (Delsys Bagnoli-4, Boston, MA, USA) were placed: over the belly of the rectus femoris (RF), vastus lateralis (VL) and vastus medialis (VM); parallel to the presumed orientation of the muscle fibres; and at approximately 50 per cent (RF), 55 per cent (VL) and 80 per cent (VM) of the distance between the greater trochanter and lateral femoral condyle. Analogue torque and crank angle (representing knee angle) signals from the dynamometer, and amplified EMG signals (×100, differential amplifier 20–450 Hz), were sampled at 2000 Hz with an analogue to digital converter and PC using Spike v. 2 software (CED micro 1401, CED, Cambridge, UK). Using a fourth order zero-lag Butterworth digital filter, torque and angle signals were low pass filtered at 21 Hz and 12 Hz, respectively, and EMG signals were band-pass filtered (6–500 Hz). Knee angular velocity was derived from the knee angle signal by numerical differentiation with a 1 ms epoch. Biofeedback was provided via a computer monitor.

(ii). Concentric, eccentric and isometric explosive voluntary contractions

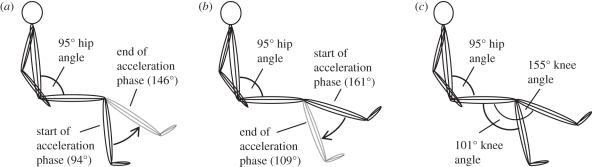
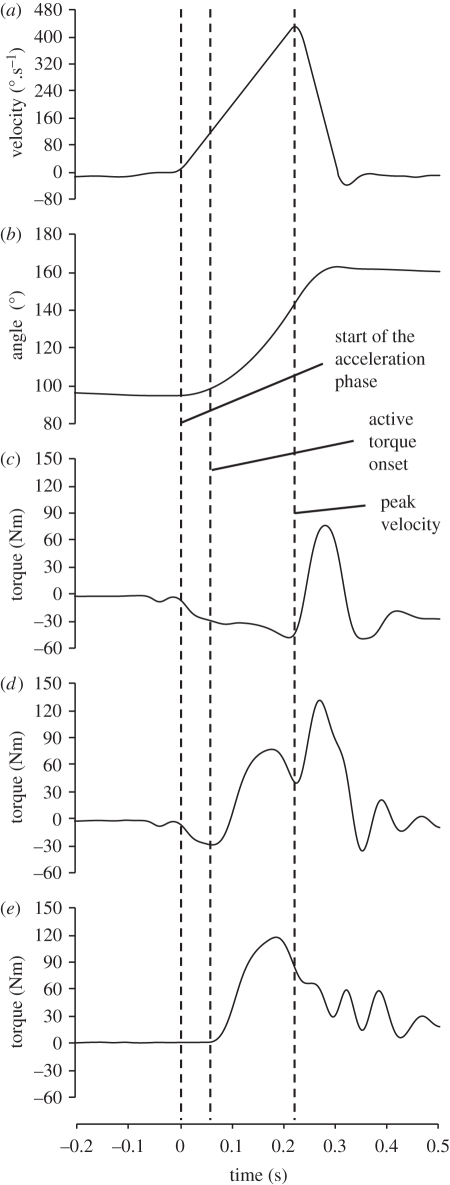
Explosive voluntary contractions were performed in four conditions; concentric (CON), eccentric (ECC), and isometrically at 101° (ISO101) and 155° (ISO155) knee joint angles (figure 1). During the concentric and eccentric conditions the crank arm was slowly moved (approx. 10°.s⁻¹) through the range of motion (94°–161°) to the start position for CON (94°) or ECC (161°). On reaching the start position, the crank arm accelerated from stationary, at a constant 2000°.s⁻², to a peak velocity of 450°.s⁻¹, moving 52° (94–146° in CON and 161°–109° in ECC) in 225 ms, before rapidly decelerating (−6000°.s⁻²) to stop 15° later (figures 1 and 2). In the CON and ECC conditions, participants performed approximately 15 explosive voluntary contractions (separated by approx. 30 s), when they were instructed to push as ‘fast and hard’ as possible at the start of the acceleration phase, from a completely relaxed state, and to keep pushing for the entire range of motion. The crank angle signal was displayed on the computer monitor with a cursor placed at the start position to indicate when the participant should start pushing. During extensive pilot testing, we found that participants typically started generating torque 50–70 ms into the acceleration phase due to a delayed response to the biofeedback. During three passive trials (no muscle activation) of the CON and ECC conditions, torque due to the acceleration and weight of the shank was recorded. In offline analysis (using Matlab; The MathWorks inc., Natick, MA, USA), the average torque-time curve of the three passive trials in each condition were time aligned with, and subtracted from, each active trial in the same condition, to calculate the torque due to muscle activation (figure 2).

Figure 1.

A schematic of the hip and knee angles during explosive knee extensions performed on an isovelocity dynamometer, in four separate conditions; (a) concentric (CON), (b) eccentric (ECC) and (c) two isometric positions (101° (ISO101) and 155° (ISO155)). During the dynamic conditions, the crank arm accelerated at 2000°.s⁻² from a knee angle of 94° to 146° (CON) and from 161° to 109° (ECC), before decelerating over a further 15° of motion.

Figure 2.

Kinetic and kinematic data recorded during passive and explosive voluntary concentric contractions of the knee extensors, completed on an isovelocity dynamometer. The crank arm was accelerated at a constant 2000°.s⁻² to a peak velocity of 450°.s⁻¹ (a), moving 52° in 225 ms (b). During the explosive voluntary contractions participants were instructed to push fast and hard at the start of the acceleration phase, but volitional torque onset typically occurred 50–70 ms later due to a delayed response to the biofeedback. The passive torque-time profile (c) was subtracted from the torque-time profile of the explosive voluntary contractions (d) to calculate the torque due to muscle activation (e). A similar protocol was used for explosive eccentric contractions.

In both ISO101 and ISO155, participants completed greater than or equal to 6 voluntary explosive contractions (separated by approx. 30 s), where they were instructed to push as ‘fast and hard’ as possible for 1 s, from a completely relaxed state. These specific joint angles were selected as they occurred during the early phase (approx. 75 ms into the acceleration phase) of CON and ECC explosive contractions to consider if joint angle effects were influencing the comparison of CON and ECC conditions.

Contractions performed in the CON and ECC conditions were disregarded if they did not meet the following criteria: baseline torque within ± 2 Nm; a change in baseline torque less than 2 Nm in the 200 ms prior to torque onset; and torque onset occurred 20–75 ms from the start of the acceleration phase. Contractions performed in the ISO101 and ISO155 conditions were disregarded if torque baseline changed by greater than 1 Nm in the 200 ms prior to torque onset. The three valid contractions in each condition with the greatest proportion of MVT (see below) at 100 ms from torque onset were chosen for further analysis, which involved measuring torque at 25 ms intervals up to 150 ms. Torque onset was defined as the point at which the first derivative of the torque-time curve crossed zero for the last time.

For comparison of explosive voluntary torques across the different types of contraction absolute torques were normalized, first to MVT: ISO101 and ISO155 torque values were normalized to measured isometric MVT at the same knee angle (see below); CON and ECC torque values were normalized to interpolated dynamic MVT at the same knee angle and angular velocity (interpolated from a dynamic MVT function; see below). Second, voluntary explosive torque at 50 ms from torque onset in each condition was normalized to evoked explosive torque at 50 ms (see below) in the same condition (voluntary/evoked). Furthermore, the voluntary/evoked ratio was established after each had been normalized to the relevant interpolated or measured MVT value, to control for any discrepancies in joint kinematics at the 50 ms time point between the voluntary and evoked trials.

During the explosive voluntary contractions agonist activation was assessed by measuring the root mean square (r.m.s.) amplitude of the EMG signal of each muscle in three consecutive 50 ms time windows (0–50 ms, 50–100 ms and 100–150 ms) from EMG onset. Agonist (RF, VL and VM) r.m.s. EMG values were normalized to M_max (see below) and averaged across the three muscles to give a mean agonist value. EMG onset was detected manually as detailed previously [3]. All explosive voluntary torque and EMG variables were averaged across the three contractions chosen for analysis in each condition.

(iii). Electrical stimulation

Using previously published methods [3,18], the femoral nerve was electrically stimulated (DS7AH, Digitimer Ltd., UK) with square wave pulses (0.1 ms duration) while participants were voluntarily passive to elicit explosive octet contractions (via eight pulses at 300 Hz) and compound muscle action potentials (M-waves; via a single pulse). At a knee angle of 101°, a series of single pulses were elicited at incremental current intensities until a maximal current intensity (simultaneous plateau in torque and M-wave response of each muscle) was achieved. Thereafter, supramaximal octet contractions and M-waves were elicited at 20 per cent above the maximal current intensity.

Three supramaximal octet (‘evoked’) contractions were elicited in both isometric conditions, and at 4° (approx. 60 ms) into the acceleration phase of CON and ECC, so that evoked torque onset would occur at a similar knee angle and angular velocity to that expected in the voluntary explosive contractions. Corrected, evoked torque in each condition was measured at 25 ms intervals up to 75 ms (75 ms was the shortest time to peak torque—CON). In ISO101 and ISO155 torque at 100 ms, peak torque, time-to-peak torque and half­-relaxation time were also recorded. For these isometric conditions, evoked torque at each time point was normalized to evoked peak torque. Measurements were averaged across the three evoked contractions in each condition.

The peak-to-peak amplitude of supramaximal M-waves (M_max) is affected by joint angle [19]. Therefore, three M_max were elicited at both 101° and 155° knee angles, and the average M_max at each angle was used to normalize volitional agonist EMG in these conditions. Three M_max were also elicited at 3°, 11° and 25° into the acceleration phase of CON and ECC conditions. Extensive pilot work had shown that these positions were typically in the centre of the consecutive 50 ms time windows after volitional EMG onset, and thus average M_max at each position was used to normalize volitional agonist EMG during the 0–50 ms, 50–100 ms and 100–150 ms time windows, respectively.

(iv). Isometric maximal voluntary contractions

Participants completed three isometric MVCs (separated by more than or equal to 90 s) at each of four different knee angles; 101°, 119°, 136° and 155° (12 MVCs overall). The instruction in each MVC was to push as hard as possible for 3–5 s. The largest measured extensor torque at each knee angle was defined as MVT at that angle. These measurements were used to establish a torque–angle relationship (defined by a quadratic function) that set the estimates and bounds of the dynamic MVT function (see below).

(v). Dynamic maximal voluntary torque function

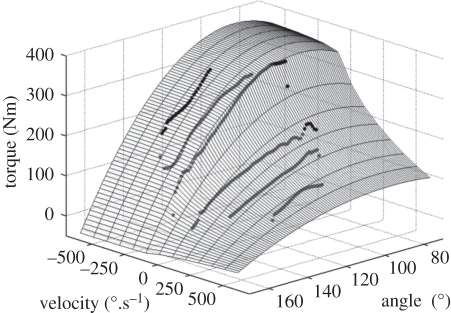
To establish dynamic MVT as a function of joint angle and angular velocity, participants completed a cycle of four reciprocal eccentric–concentric isovelocity MVCs at three angular velocities; 100, 250 and 400°.s⁻¹. This protocol is thought to ensure maximal voluntary activation, and thus MVT, throughout the entire range of motion [6,9,20,21], which was set at approximately 100° (70–170°), providing an isovelocity range of approximately 75°, 62° and 40° at 100, 250 and 400°.s⁻¹, respectively. Following familiarization at each velocity, participants were instructed to extend their knee as hard as possible throughout the entire cycle. If peak eccentric torque of at least two eccentric efforts in one cycle were not greater than or equal to 90 per cent of the largest recorded isometric MVT for that participant, the cycle was repeated. Active torque values were corrected for the effects of gravity using a sixth-order polynomial to describe the passive torque–angle relationship. For each velocity, the largest gravity corrected torque per degree of isovelocity movement was input into a nine parameter mathematical model [22] to establish a dynamic MVT function, defined as the product of torque–angular velocity [9], differential activation–angular velocity [9] and torque–angle [23] functions. The nine parameters were obtained by minimizing the weighted r.m.s. difference between interpolated and measured values using a simulated annealing algorithm [24]. A weighting for the r.m.s. difference score function which forced approximately 85 per cent of the measured values below the surface representing the dynamic MVT function (figure 3) was used, as errors in the measured data were thought to be predominantly one-sided (i.e. due to submaximal effort; [22]). The average weighted r.m.s. difference of all participants was 6 ± 2 Nm (1.3 ± 0.3% of maximum eccentric torque).

Figure 3.

An example of maximal voluntary torque (MVT) values measured during isovelocity contractions of the knee extensors at six velocities (black circles). The surface of the optimized nine parameter function describing dynamic MVT relative to knee angle and angular velocity was used to interpolate angle- and velocity-specific MVT values for normalization of dynamic explosive torque values. The r.m.s. difference between measured and interpolated values was weighted so that approximately 85% of the measured values were forced below the surface.

(vi). Generic muscle model

To assess whether any observed effects of contraction type on explosive torque production during the dynamic conditions were indicative of muscle fibre performance, the torque and kinematic data from CON, ECC and the dynamic MVCs were collapsed across all participants and input into a generic Hill-type muscle model [6]. This model consisted of an SEC and contractile component, and calculated fibre force, length and velocity of the RF, VL and VM during CON, ECC and the dynamic MVCs. Force in each muscle and at each 25 ms interval from force onset during CON and ECC was normalized to maximal voluntary force at the same muscle length and velocity, and averaged across the three muscles.

(d). Statistical analysis

The influence of condition (CON, ECC, ISO101 and ISO155) on all dependent variables measured in explosive voluntary and evoked contractions was analysed with a repeated measures ANOVA (four conditions). Paired t-tests and a stepwise Bonferroni correction were then used to determine paired differences between conditions at specific time points. Statistical analysis was completed using SPSS v. 17, and the significance level was set at p < 0.05.

3. Results

(a). Kinematics of the explosive contractions

During the dynamic explosive contractions, voluntary torque onset in the CON and ECC conditions occurred at similar angular displacements and angular velocities (table 1). In both CON and ECC, explosive voluntary torque onset typically occurred 5–10 ms earlier in the acceleration phase than evoked torque onset, as denoted by the overall tendency for angular displacement and velocity to be greater at torque onset in the evoked contractions (table 1). Voluntary EMG onset occurred at an angle of 96 ± 1° and an angular velocity of 74 ± 21°.s⁻¹ during the CON trials and at 159 ± 1° and −60 ± 39°.s⁻¹ during the ECC trials. Relative to these onsets M_max was recorded at 22 ± 11 ms, 65 ± 11 ms and 121 ± 10 ms into the CON trials, and 16 ± 25 ms, 65 ± 18 ms and 128 ± 22 ms into the ECC trials. This confirmed that M_max was typically recorded in the centre of each of the three consecutive 50 ms time windows from voluntary EMG onset in both CON and ECC conditions.

Table 1.

Knee joint angular displacement and angular velocity (kinematic parameters) at torque onset in explosive voluntary and evoked knee extensions completed in concentric (CON) and eccentric (ECC) conditions. p-values for paired differences between voluntary and evoked contractions are reported. Data are means ± s.d. (n = 14).

kinematic parameter	voluntary	evoked	p-value
CON angle	3.6 ± 1.2°	4.4 ± 0.8°	0.055
CON velocity	117 ± 24°.s−1	129 ± 16°.s−1	0.037
ECC angle	3.1 ± 1.6°	4.8 ± 1.6°	0.708
ECC velocity	−93 ± 38°.s−1	−123 ± 31°.s−1	0.086

(b). Volitional parameters

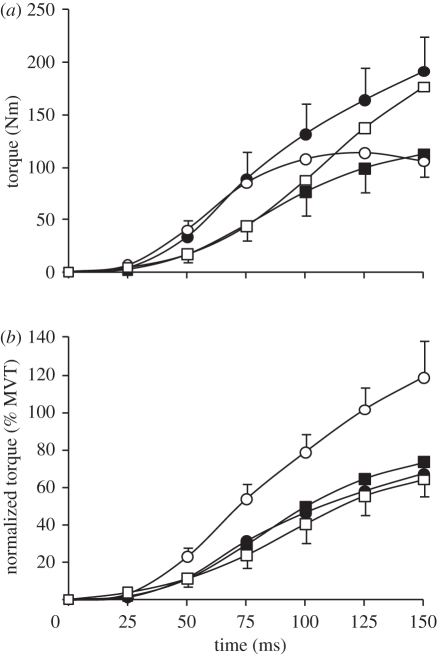
Absolute explosive voluntary torque was affected by condition at each of the six measured time points from torque onset (ANOVA, p < 0.001; figure 4a). These effects are consistent with the different joint kinematics of the separate conditions. ISO101 was performed close to optimal joint angle (θ_opt), and thus recorded the highest torque values after the initial 50 ms. CON torque was greater than ISO101, ISO155 and ECC in the initial 50 ms when angular velocity was relatively low, and joint angle was near θ_opt. ECC torque was greater than ISO155 and CON in the later phase of the contraction (greater than 100 ms), as angular velocity increased and the joint angle moved closer to θ_opt.

Figure 4.

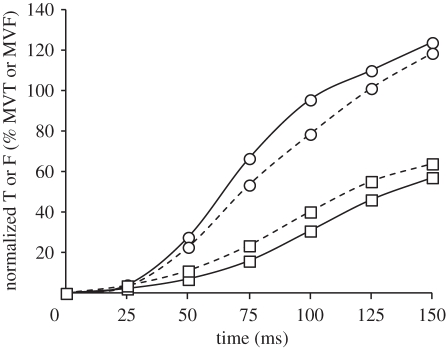
(a) Absolute and (b) normalized torque for 150 ms after torque onset during explosive voluntary knee extensions in four conditions: isometric at knee joint angles of 101° and 155° (ISO101 (filled circles) and ISO155 (filled squares), respectively); concentric (CON, open circles); and eccentric (ECC, open squares). CON and ECC conditions were completed at a constant 2000°.s⁻², and torque was corrected for the acceleration and weight of the shank. Normalized torque is expressed as a percentage of MVT at the relevant joint angle and angular velocity. Data are means ± s.d. on highest and lowest data points (n = 14).

Normalized explosive voluntary torque (relative to measured/interpolated MVT at the relevant joint angle and angular velocity) was also influenced by condition at each measured time point from torque onset (ANOVA, p < 0.001; figure 4b and table 2). Normalized CON torque was more than 60 per cent larger than all other conditions at all measured time points after 25 ms. Remarkably, after 125 ms explosive voluntary CON torque equalled MVT, and had exceeded MVT by 150 ms, being 119 per cent MVT. The considerably greater normalized torque in CON appears to be indicative of muscle fibre performance, as the generic muscle model results emulate the joint torque results (figure 5). In fact, the difference between CON and ECC conditions at a muscle fibre level appears to be just as large, if not larger, than those measured on a whole joint level. Normalized torque was similar in the ISO101, ISO155 and ECC conditions during the initial 75 ms of these explosive contractions, but during the later stages of contraction ISO155 was greater than ECC (75–150 ms), and ISO101 (125–150 ms).

Table 2.

Normalized torque at 25 ms intervals from torque onset during explosive voluntary knee extensions in four conditions: isometric at knee joint angles of 101° and 155° (ISO101 and ISO155, respectively); concentric (CON); and eccentric (ECC). Normalized torque is expressed as a percentage of MVT. Data are means ± s.d. (n = 14). Paired differences are denoted by capital (p < 0.01) or lower case (p < 0.05) letters; A (greater than ISO101 and ISO155), B (greater than all other conditions) C (greater than ECC) or D (greater than ISO101 and ECC).

	torque (% MVT)
time (ms)	ISO101	ISO155	CON	ECC
25	2 ± 1	2 ± 1	3 ± 1A	4 ± 2A
50	12 ± 5	11 ± 4	23 ± 6B	11 ± 4
75	31 ± 9C	29 ± 9C	54 ± 8B	24 ± 7
100	46 ± 11	50 ± 12C	79 ± 10B	40 ± 10
125	58 ± 12	65 ± 12D	101 ± 13B	55 ± 10
150	67 ± 11	74 ± 10d	119 ± 20B	64 ± 9

Figure 5.

Average normalized muscle fibre force of the rectus femoris, vastus lateralis and vastus medials (F) and normalized knee joint torque (T) during concentric (CON) and eccentric (ECC) explosive voluntary contractions of the knee extensors. Normalized F is a percentage of maximal voluntary fibre force (MVF) at the same fibre length and contractile velocity, while normalized T is a percentage of MVT at the same joint angle and angular velocity. Data are collapsed across all participants (n = 14). Circles with solid line denotes CON F; circles with dashed line, CON T; squares with solid line, ECC F; squares with dashed line, ECC T.

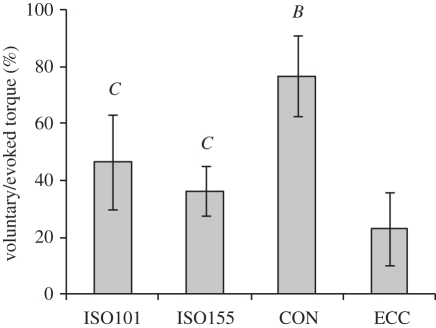
Voluntary/evoked torque at 50 ms after torque onset was dependent upon the contractile condition (ANOVA, both p < 0.001). Paired comparisons revealed that voluntary/evoked torque in CON (77 ± 17%) was substantially greater than all other conditions (p < 0.001; figure 6); ISO101 (46 ± 14%) tended to be greater than ISO155 (36 ± 13%; p = 0.054), and both isometric conditions were greater than ECC (23 ± 9%; p ≤ 0.002). These results were identical when both voluntary and evoked torques were first normalized to MVT prior to calculating the voluntary/evoked percentage.

Figure 6.

Absolute voluntary torque at 50 ms after torque onset as a percentage of absolute evoked torque at the same time point (voluntary/evoked), during explosive knee extensions in four conditions: isometric at knee joint angles of 101° and 155° (ISO101 and ISO155, respectively); concentric (CON); and eccentric (ECC). Data are means ± s.d. (n = 14). Paired differences are denoted by capital letters (p < 0.01); B (greater than all other conditions) and C (greater than ECC).

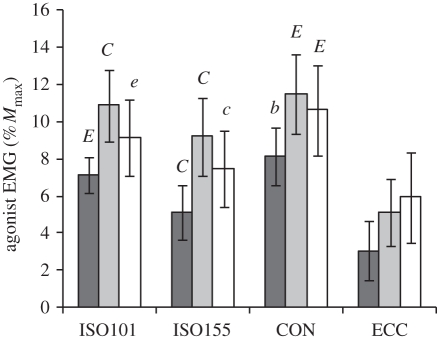
There was also a condition effect on the agonist normalized EMG during each 50 ms time window (0–50 ms, 50–100 ms and 100–150 ms) and over the whole 0–150 ms (ANOVA, p < 0.001). Over the whole 0–150 ms agonist normalized EMG was 10.1 ± 1.7 (CON), 9.0 ± 1.3 (ISO101), 7.3 ± 1.3 (ISO155) and 4.7 ± 1.5 (ECC) % M_max, and all conditions were significantly different from each other (paired t-tests, p < 0.032). Paired comparisons for the first 50 ms time window were similar to those for voluntary/evoked torque at 50 ms, where agonist normalized EMG differed between all of the conditions and was greatest in the CON followed by ISO101, ISO155 and ECC (p < 0.05; figure 7). Paired differences between conditions during the 50–100 ms and 100–150 ms time windows were less pronounced, but agonist normalized EMG remained greatest in CON and ISO101, and lowest in ECC.

Figure 7.

Agonist EMG over 0–50 ms (dark grey bars), 50–100 ms (light grey bars) and 100–150 ms (white bars) from EMG onset during explosive voluntary knee extensions in four conditions: isometric at knee joint angles of 101° and 155° (ISO101 and ISO155, respectively), concentric (CON) and eccentric (ECC). Agonist EMG is an average of the three superficial quadriceps muscles once normalized to maximal M-wave (M_max). Data are means ± s.d. (n = 14). Paired differences for each EMG time window are denoted by capital (p < 0.01) or lower case (p < 0.05) letters; B (greater than all other conditions), C (greater than ECC), E (greater than ISO155 and ECC).

(c). Evoked parameters

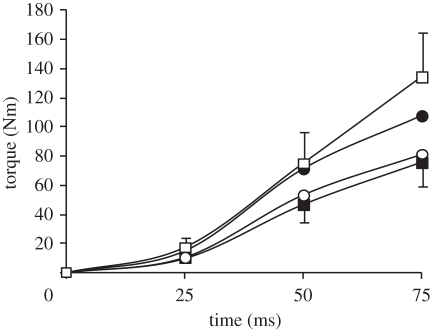
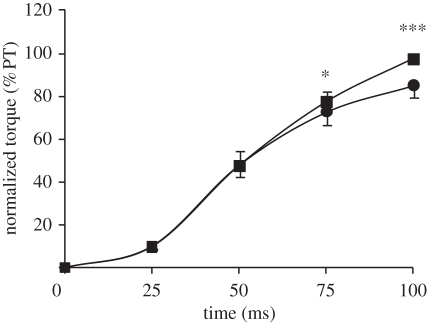
As expected given the different joint kinematics in each condition, absolute evoked torque at 25, 50 and 75 ms after torque onset was affected by condition (ANOVA, p < 0.001; figure 8), with evoked ECC and ISO101 torque greater than ISO155 and CON at all measured time points. Evoked torque in ISO101 and ISO155 normalized to evoked peak torque in the same condition was similar over the first 50 ms, but greater in ISO155 at 75 (+5%; paired t-test, p = 0.004) and 100 ms (+14%; paired t-test, p < 0.001) after torque onset (figure 9). Despite greater peak torque in ISO101, time-to-peak torque and half-relaxation time were shorter in ISO155 (table 3).

Figure 8.

Absolute torque recorded during evoked explosive voluntary knee extensions (supramaximal octet, eight pulses at 300 Hz) in four conditions; isometric at knee joint angles of 101° and 155° (ISO101 (filled circles) and ISO155 (filled squares), respectively); concentric (CON, open circles); and eccentric (ECC, open squares). CON and ECC conditions were completed at a constant 2000°.s⁻², and torque was corrected for the acceleration and weight of the shank. Data are means ± s.d. on highest and lowest data points (n = 14).

Figure 9.

Normalized torque during evoked isometric knee extensions (supramaximal octet, eight pulses at 300 Hz) at a 101° (ISO101, circles) and 155° (ISO155, squares) knee angle, expressed as a percentage of peak torque (PT) during the same contraction. Data are means ± s.d. (n = 14). Paired differences are denoted by asterisks (*p < 0.05 or ***p < 0.001).

Table 3.

Torque parameters recorded during the supramaximal evoked isometric knee extensions completed at a knee angle of 101° (ISO101) and 155° (ISO155). Data are means ± s.d. (n = 14). The p-value denotes differences between the two conditions.

	ISO101	ISO155	p-value
peak torque	148 ± 25 Nm	98 ± 19 Nm	<0.001
time-to-peak torque	137 ± 9 ms	112 ± 13 ms	<0.001
half-relaxation time	208 ± 21 ms	174 ± 12 ms	<0.001

4. Discussion

The results of the current study provide novel evidence that the ability of humans to use the available torque capacity of a muscle in an explosive situation is influenced by the type of contraction. Whether expressed relative to the available MVT or the maximum capacity for RTD during evoked contractions, explosive voluntary performance was clearly superior during concentric than isometric or eccentric actions. The proportion of MVT expressed during explosive concentric efforts was more than 60 per cent larger than for isometric or eccentric conditions after the first 25 ms of the contraction. Furthermore, participants achieved concentrically 77 per cent of their evoked torque after 50 ms, compared with 36–46 per cent isometrically and 23 per cent eccentrically. This greater concentric ability to use the available contractile capacity of the muscle indicates enhanced agonist activation and this was supported by the higher EMG amplitude throughout the explosive contraction.

(a). Effects of contraction type

The absolute voluntary and evoked torque-time curves appear to conform to the torque–angle–angular velocity relationship. Overall, absolute torque development was highest for ECC during the evoked contractions, but highest for ISO101 during the volitional contractions. This discrepancy is likely to reflect the differences typically observed between the torque/force–velocity relationships measured in vitro and voluntarily in vivo (i.e. eccentric to isometric torque/force for the same muscle length is normally greater than 1.5 in vitro and 0.9–1.1 in vivo [5,6,8]). Clearly, the absolute voluntary and evoked torque-time curves are primarily determined by the joint kinematics of each condition, and should therefore be normalized to a reference torque specific to that mechanical situation, in order to make a meaningful comparison between the different types of contraction.

Explosive voluntary torque normalized to joint angle- and angular velocity-specific MVT was consistently more than 60 per cent larger in CON than during the isometric or eccentric conditions, after the initial 25 ms. In fact, MVT was achieved only after 125 ms in CON, while torque in the other conditions did not exceed 73 per cent of MVT even after 150 ms. Previous studies have reported that it takes greater than 300 ms to achieve MVT in explosive isometric contractions performed from rest [1,25], and it is likely that this would have been the case in both the isometric and ECC conditions of the current study, had it been possible to measure torque beyond 150 ms. However, our results provide unique evidence that during explosive concentric contractions MVT can be achieved in less than 125 ms.

While the whole joint approach of this study makes its results directly relevant to functional human movement, caution should be taken when inferring muscle fibre performance from whole joint mechanics, owing to compliance of the SEC. The greater concentric ability to use the available torque generating capacity that we observed appears to be indicative of muscle fibre performance for two main reasons: (i) the generic muscle model which accounted for SEC compliance produced very similar results; and (ii) the percentage of evoked torque achieved voluntarily after 50 ms was also considerably greater in CON than any other condition (CON, 77%; ISO101, 46%; ISO155 36%; ECC, 23%). As these values are relative to the maximal involuntary explosive torque capacity in the same contractile conditions, they are indicative of substantial differences in neural drive to the agonist muscle. The greater agonist normalized EMG over the first 50 ms, as well as over the whole 150 ms from EMG onset, for CON supports this notion. The mechanistic explanation for this effect requires further investigation, but may be associated with neural inhibition during the isometric and ECC conditions that prevents full utilization of the high, and potentially harmful, rates of loading available in these contractions. Moreover, the condition effects on agonist activation we have observed occurred within the first 50 ms of crank arm acceleration, which is considered to be the minimum latency period for a reflex response to mechanical perturbation [26]. Therefore, our results support earlier evidence that the neural strategy employed at the start of the muscle contraction is pre-defined by the central nervous system according to the type of contraction [27].

The more effective neural strategy in CON appears to explain why this condition was considerably more conducive to explosive performance than any other condition. MVT was also exceeded by up to 19 per cent in the voluntary CON condition, suggesting that the greatest peak torque response in maximum voluntary concentric contractions is achieved when the focus is on producing explosive, rather than sustained maximal torque. This was an unexpected finding that was not replicated in any of the other conditions, and appears to be a consequence of the more effective neural strategy observed in the CON condition.

While this is the first study to compare agonist activation during different types of explosive contraction, previous studies have assessed agonist activation at MVT and reported greater activation in concentric than eccentric contractions [4,6,7,28,29], and in isometric than dynamic conditions [20,28]. Any differences in agonist activation at MVT between contraction types in this study could clearly have influenced the comparison of explosive voluntary torques when normalized to MVT. This may explain the marginal differences in normalized explosive torque between ECC and the isometric conditions (particularly ISO101), despite distinct levels of agonist activation indicated by both voluntary/evoked torque and EMG.

(b). Effects of joint angle

Absolute explosive voluntary and evoked torque-time curves for IS0101 and ISO155 conformed to the MVT–angle relationship, where torque at all measured time points from torque onset was greater in ISO101 (nearer θ_opt). However, when normalized to MVT at the same knee angle, voluntary torque was similar in ISO101 and ISO155 during the initial phase of the contraction (first 100 ms), but greater in ISO155 beyond 100 ms. Normalized explosive voluntary torque was also greater during the later stages of ISO155 (75 ms and onwards) compared with ECC. This is further evidence of an effect of knee angle during the later phase of the rising torque-time curve, given that ECC was accelerating into a more flexed knee position. These results suggest that differences in joint angle did not confound comparisons between the type of contraction in the first 100 ms, but may have contributed to greater normalized torque in the later phase of CON compared with ECC, when the knee was accelerating into more extended (CON) or flexed (ECC) positions.

The improved capacity for normalized voluntary torque production in ISO155 does not appear to be due to agonist activation, as agonist normalized EMG in the 100–150 ms time window, as well as over the whole 150 ms from EMG onset, was 21–23% greater in ISO101. Earlier studies have also reported reduced agonist activation during voluntary contractions at more extended knee angles [4,20,30,31], and this effect is thought to be a neural mechanism that protects the knee joint near full extension, where loading of the anterior cruciate ligament is greatest [32].

In a similar pattern to that observed in the normalized voluntary torque-time curves, normalized evoked torque (relative to peak evoked torque) was comparable for the two isometric conditions in the early phase of the contraction, but greater in ISO155 in the later phase (after 50 ms). This was associated with a shorter time to peak torque in ISO155, suggesting a mechanical explanation for improved normalized explosive torque in the extended position. Our results are consistent with earlier in vitro studies that found shorter muscle lengths to have a faster time to peak tension [15–17] and a steeper normalized tension-time curve during the later phase of the contraction [15,17]. However, this is the first study to measure a similar effect in vivo during both explosive voluntary and evoked contractions. The faster time to peak force at shorter muscle lengths has been attributed to: lower Ca²⁺ release or a reduced affinity of troponin C for Ca²⁺ [15] resulting in less efficient excitation–contraction coupling [16]; and/or overlapping of the actin filaments, which would interfere with cross-bridge formation [33]. Nevertheless, it is unclear why a faster time to peak torque at shorter muscle lengths would only affect the normalized torque-time curve during the later stages of the contraction.

In conclusion, the type of contraction influences the ability to use the muscles’ torque-producing capacity explosively, with concentric contractions being considerably more conducive to explosive performance than any other type of contraction, owing to more effective neural activation. Finally, a faster time to peak torque at more extended knee angles appears to increase the slope of the normalized voluntary and evoked torque-time curves at high, but not low torque levels. Collectively, the novel results of this study further our understanding of the neural and mechanical limitations of explosive torque production, and provide a platform for further research in this area that has important implications for health and sports performance.