Rise of dinosaurs reveals major body-size transitions are driven by passive processes of trait evolution

Abstract

A major macroevolutionary question concerns how long-term patterns of body-size evolution are underpinned by smaller scale processes along lineages. One outstanding long-term transition is the replacement of basal therapsids (stem-group mammals) by archosauromorphs, including dinosaurs, as the dominant large-bodied terrestrial fauna during the Triassic (approx. 252–201 million years ago). This landmark event preceded more than 150 million years of archosauromorph dominance. We analyse a new body-size dataset of more than 400 therapsid and archosauromorph species spanning the Late Permian–Middle Jurassic. Maximum-likelihood analyses indicate that Cope's rule (an active within-lineage trend of body-size increase) is extremely rare, despite conspicuous patterns of body-size turnover, and contrary to proposals that Cope's rule is central to vertebrate evolution. Instead, passive processes predominate in taxonomically and ecomorphologically more inclusive clades, with stasis common in less inclusive clades. Body-size limits are clade-dependent, suggesting intrinsic, biological factors are more important than the external environment. This clade-dependence is exemplified by maximum size of Middle–early Late Triassic archosauromorph predators exceeding that of contemporary herbivores, breaking a widely-accepted ‘rule’ that herbivore maximum size greatly exceeds carnivore maximum size. Archosauromorph and dinosaur dominance occurred via opportunistic replacement of therapsids following extinction, but were facilitated by higher archosauromorph growth rates.

1. Introduction

Body size is a trait that is fundamental to the biology of all animals [1–3] and covaries with key ecological, physiological and life-history traits such as range size, fecundity, metabolic efficiency and thermal physiology [4]. Body size has a complex interaction with individual fitness [5]; larger animals are often more successful in obtaining food, territory and mates [6,7], but are more susceptible to extinction, and in some cases predation, having lower fecundity, and requiring more resources per individual [7]. One of the longest noted trends in vertebrate evolution is a perceived tendency towards larger body sizes during the evolution of a clade: Cope's rule [8–10]. Cope's rule denotes an ‘active’ within-lineage directional trend of increase, generally held to be driven by selection for larger body size [7,11]. This results in increasing maximum and minimum body size through time within a clade [9]. In contrast, ‘passive diffusion’ denotes an increase in trait variance over evolutionary time without unidirectional selection, yielding an increase in maximum body size, but unaltered or decreasing minimum size [12,13]. Whether ‘active’ within-lineage processes, or ‘passive’ processes resulting from differential among-lineage effects are responsible for large-scale patterns of body-size evolution in deep time is an enduring question in evolutionary biology and palaeontology [9,14,15].

The effects of trophic interactions on body size are also of great interest to biologists [16]. In terrestrial faunas, the largest herbivores tend to be an order of magnitude larger than the largest closely related carnivores [17], and body size in carnivores and herbivores tends to correlate in time and space [18]. However, these ecological ‘rules’ are derived almost exclusively from the mammal-dominated fauna of the past 65 million years (Myr), and their general applicability has not been extensively tested.

The ca 100 Myr time span from the Late Permian (approx. 260 million years ago (Ma)) to the Middle Jurassic (approx. 160 Ma) provides an excellent case study of terrestrial vertebrate body-size evolution. This interval witnessed the ‘rise’ of dinosaurs and other archosauromorphs (birds, crocodiles and their extinct relatives including dinosaurs and pterosaurs, [19–21]) to more than 150 Myr of dominance as large-bodied terrestrial vertebrates, coincident with the ‘fall’ of the previously dominant therapsids (stem-group mammals; [22]). This landmark transition is bracketed by two of the largest mass extinctions in Earth's history, at the Permo-Triassic (approx. 252.2 Ma, [23,24]) and Triassic–Jurassic (approx. 201.5 Ma, [23,25]) boundaries [26,27]; it may be causally linked to these events, and to smaller extinction events within the Triassic [20,28,29]. Ornithodiran archosauromorphs included the largest land animals (sauropod dinosaurs) and the largest flying organisms (azhdarchid pterosaurs) ever to exist, and dinosaurs especially have long been icons of Cope's rule [30]. However, other analyses of body-size evolution in dinosaurs suggest a more complex situation [31], or the absence of selection-driven trends [32].

We examine body-size evolution in multiple clades over an extended time interval. Non-phylogenetic (time series) and phylogenetically informed modelling approaches are used to analyse more than 400 species from the two dominant clades of Late Permian–Middle Jurassic terrestrial vertebrates (Archosauromorpha and Therapsida). We test whether the major patterns in body-size evolution that accompanied the rise and decline of these clades (figure 1) are the result of clade-wide, ‘active’ within-lineage, directional trends towards increased or decreased body size (Cope's rule and its inverse). Moreover, we investigate the relationship between carnivore and herbivore body size within the time interval, and discuss its implications for the role of intrinsic, biological factors in body-size evolution.

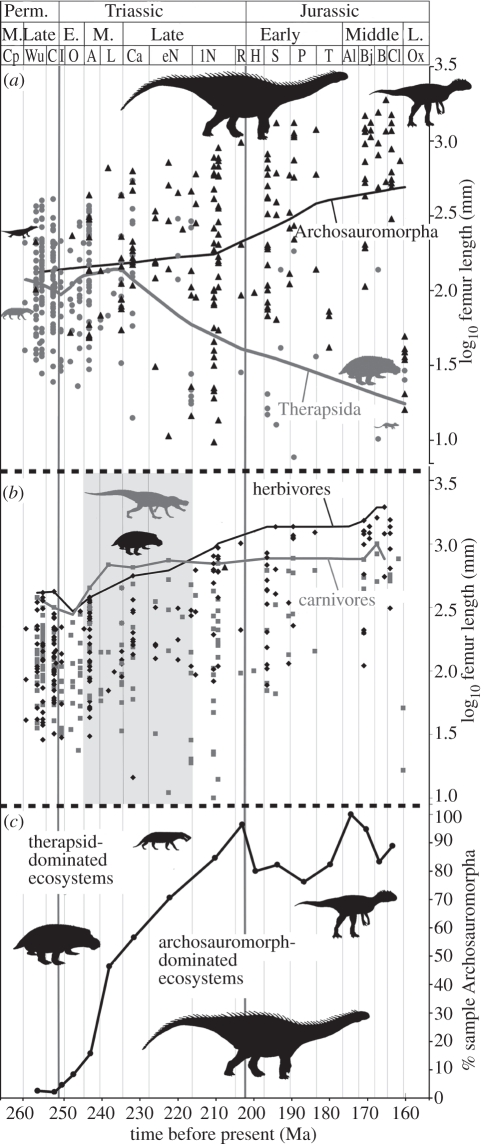
Figure 1.

(a) Log femur length (body size proxy) of archosauromorph (black triangles) and therapsid (grey circles) taxa from the Late Permian to Middle Jurassic plotted at the stratigraphic range midpoints for each taxon, with Lowess (locally adjusted) regression lines for archosauromorphs (black) and therapsids (grey). (b) Log femur length plotted at midpoints of stratigraphic ranges (points) and size maxima through time (lines) of herbivorous (black, rhomboid points) and carnivorous (grey, square points) taxa across the interval. From the Anisian to early Norian (light grey shading), the size of the largest carnivores exceeded that of the largest herbivores. (c) Proportion of archosauromorphs among archosauromorph and therapsid taxa sampled plotted through time. Perm., Permian, E., Early, M., Middle, L., Late. Stage abbreviations in the electronic supplementary material, table S2.

2. Material and methods

(a). Body mass proxy data

Femoral length was used as a body size proxy because it shows a consistent relationship with body mass in terrestrial vertebrates [33], and has been used in previous studies of archosauromorphs [31,32]. Femora have not been described for 77 per cent of the therapsids sampled, but use of femoral length was required to yield absolute values comparable with those of Archosauromorpha. Thus, for many therapsids, femoral length was estimated based on basal skull length using regression equations (see the electronic supplementary material). This is justified because basal skull length is tightly correlated (R² = 0.903, p < 0.001, n = 26) with femoral length for therapsids in which both were described from the same individual.

(b). Dating

Taxa were dated to geological stage (see the electronic supplementary material), with ranges representing either stratigraphic uncertainty or genuine observed ranges. Most taxa were assigned ranges based on age and formation assignments in the Paleobiology Database (http://paleodb.org/), updated with more recent information where appropriate. Absolute ages for stages were based on Walker & Geissman [23].

(c). Phylogenies

Phylogenies were compiled for Archosauromorpha and Therapsida using an informal supertree approach ([20,32,34], see the electronic supplementary material, figures S1 and S2 and table S1). Source phylogenies were chosen for their recentness and comprehensiveness of taxon and/or character sampling. The phylogenies were calibrated against time (see the electronic supplementary material), with taxa assigned absolute ages by taking the range midpoint. Unconstrained/zero length nodes/branches were given a date/length by setting a root length and sharing this time equally between unconstrained branches [19], using the date.phylo() function of Graeme Lloyd (http://www.graemetlloyd.com/methdpf.html).

(d). Time-series model fitting

Time-series models provide an approximation of the trajectory of mean body size within clades without reference to phylogeny or individual evolutionary lineages. Time-series analyses were carried out in R v. 2.13.1 [35] using the paleoTS package [36]. Data were binned by stage, with taxa placed in each bin that their stratigraphic range overlapped. Four models—generalized random walk (GRW), unbiased random walk (URW), an Ornstein–Uhlenbeck (OU) process and stasis—were fitted to mean body size and variance for each stage for 12 different clades (Gorgonopsia was not analysed alone owing to small sample sizes). GRW is a random walk with a non-zero step mean, corresponding to a directional evolutionary trend. URW is a random walk with a zero step mean corresponding to noticeable trait variation through time, but no consistent directional trend. An OU process is evolution towards an optimum, which becomes exponentially less attractive as the optimal value is neared. The Akaike information criterion (AICc) with correction for finite sample sizes was used to calculate Akaike weights and thus compare models (see the electronic supplementary material). To make assumptions more realistic for populations related by cladogenesis, and because variances showed significant heteroskedasticity, variances were not pooled between bins. Joint parameterization was used for all tests. Binning with uniform 5 Myr bins was carried out to assess sensitivity to the timescale used. Analyses were also repeated with binned means and variances for only the taxa present in the phylogenies to allow comparison with phylogenetic models (see the electronic supplementary material).

(e). Phylogenetic model fitting

Maximum-likelihood models were used to investigate body-size evolution [32,37]). Five models—Brownian motion (BM) with trend, BM, stasis, OU and early burst (EB)—were fitted to 13 clades. BM with trend is equivalent to a GRW (see §2d) and thus approximates directional within-lineage evolution (see [38]), BM is equivalent to an URW (see §2d), and EB is an exponentially decreasing rate of evolution through time. Model fitting was carried out in R using the package GEIGER [39]). The five models listed above were fitted for 13 clades. AICc was used to compare models. Analyses were also carried out in which species were dated using the lower bound of their stratigraphic range rather than the midpoint to assess the sensitivity of results to inaccuracies in dating (see the electronic supplementary material).

(f). Generalized least-squares regression of carnivore and herbivore size

Generalized least-squares regression models were analysed in R using the gls() function from the nlme package [40] with herbivore size as a predictor of carnivore size, and compared with a null model using AICc and Akaike weights, both with no autoregressive model (AR0, equivalent to ordinary least-squares regression) and with a first-order autoregressive (AR1) model. Data were again binned by stage.

3. Results

(a). Large-scale patterns of body-size evolution

Our body-size data clearly show a sustained increase in archosauromorph size and decrease in therapsid size over the study interval (figure 1a). Archosauromorphs attained large sizes only after extinction or decimation of therapsids of the same trophic guild. Thus, archosauromorph carnivores increased in size after the Permian–Triassic boundary extinction of gorgonospians (hypercarnivorous therapsids), and archosauromorph herbivores increased in size during the Triassic following extinction of most anomodonts (large herbivorous therapsids; see electronic supplementary material, figure S3). From the Anisian to the early Norian (245–216 Ma), carnivore maximum body size is larger than herbivore maximum body size (figure 1b), with archosauromorphs being the largest carnivores and therapsids the largest herbivores during this interval.

(b). Time-series model fitting

An URW model recorded the best AICc score for both Archosauromorpha and Therapsida. The fit of GRW models was non-negligible, with positive (Archosauromorpha) and negative (Therapsida) step means (µ), reflecting long-term body-size differentiation (figure 1a). For Dinosauromorpha and Theropoda (predatory dinosaurs), the GRW model fitted best, and µ was higher than for other archosauromorphs, reflecting more rapidly increasing mean body size than witnessed in non-dinosaurian archosauromorphs. An URW model fitted best for ornithischian dinosaurs, Pterosauria, Pseudosuchia (crocodilians and their stem group) and Cynodontia (the derived therapsid clade including mammals). An OU model fitted best for sauropodomorphs, aetosaurs (herbivorous/omnivorous Triassic pseudosuchians) and anomodonts, with a higher optimum body size (θ) in sauropodomorphs (3.031 log₁₀ mm) than anomodonts (2.484 log₁₀ mm) or aetosaurs (2.266 log₁₀ mm). At least one other model was non-negligible for all clades except Aetosauria and Pseudosuchia (table 1). Results using uniform 5 Myr time binning were similar but favoured more directional models (see the electronic supplementary material).

Table 1.

Summary of results for time-series model fitting for archosauromorph and therapsid clades. Higher Akaike weight (A.W.) indicates a better model fit. µ, step mean; σ², step variance; θ, trait mean for stasis; trait optimum for Ornstein–Uhlenbeck (OU), ω, trait variance; α, constraint parameter. Generalized random walk indicates an evolutionary trend, unbiased random walk indicates significant variation but no trend and OU indicates evolution towards an optimum. No shading and bold text, best model; light shading, non-negligible models (A.W. ≥1/8 best model), dark shading, negligible models (A.W. <1/8 best model).

clade	n	generalized random walk (GRW)		unbiased random walk (URW)		stasis		Ornstein–Uhlenbeck (OU)
		A.W.	μ, σ² (log mm)	A.W.	σ² (log mm)	A.W.	θ, ω (log mm)	A.W.	θ, α, σ² (log mm)
Archosauromorpha	194	0.210	0.005, 0.004	0.700	0.004	0.002	2.397, 0.064	0.088	2.508, 0.040, 0.005
Dinosauromorpha	107	0.585	0.012, 0	0.023	0.003	0.000	2.553, 0.077	0.392	3.198, 0.018, 0
Ornithischia	15	0.239	0.043, 0	0.410	0.004	0.349	2.174, 0	0.002	38.249, 0.001, 0
Theropoda	30	0.463	0.006, 0	0.436	0.001	0.095	2.540, 0.008	0.007	2.371, 0, 0.001
Sauropodomorpha	50	0.271	0.013, 0.002	0.222	0.003	0	2.844, 0.059	0.507	3.031, 0.059, 0.001
Pterosauria	17	0.026	−0.003, 0.002	0.791	0.002	0.184	1.690, 0.015	0	1.723, 0.105, 0
Pseudosuchia	35	0.099	−0.006, 0.003	0.853	0.003	0.044	2.218, 0.036	0.004	2.146, 0.051, 0.004
Aetosauria	7	0	−0.001, 0	0	0	0	2.286, 0	1.000	2.266, 1.317, 0
Therapsida	248	0.288	−0.003, 0.001	0.641	0.002	0.003	1.926, 0.023	0.069	1.590, 0.021, 0.002
Anomodontia	107	0.097	0.009, 0.001	0.418	0.002	0.013	2.322, 0.031	0.472	2.484, 0.097, 0
Cynodontia	68	0.143	−0.001, 0.002	0.630	0.002	0.037	1.781, 0.020	0.189	1.590, 0.021, 0.002
Therocephalia	33	0.032	−0.017, 0.000	0.676	0.001	0.292	1.913, 0.004	0	1.707, 0.091, 0

(c). Phylogenetic model fitting

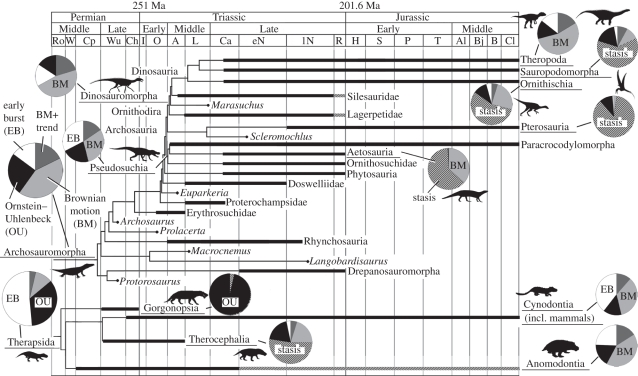
Maximum-likelihood models of body-size evolution demonstrate that active trends fit the phylogeny poorly compared with other models (figure 2 and table 2; modelled as BM with trend). BM, stasis and EB models provided the best fit (lowest AICc scores) for most clades (BM in Archosauromorpha, Dinosauromorpha, Theropoda and Anomodontia; stasis in Sauropodomorpha, Ornithischia, Aetosauria, Pterosauria and Therocephalia; EB in Pseudosuchia, Therapsida and Cynodontia), and an OU model fitted best for Gorgonopsia. At least one other model was non-negligible (Akaike weight greater than 1/8 that of the best model) for most clades (figure 2 and table 2). Results when lower range bounds were used as taxon ages were qualitatively similar to those based on range midpoints (see the electronic supplementary material).

Figure 2.

Simplified archosauromorph (top) and therapsid (bottom) phylogenies calibrated against time from the Permian to Jurassic with Akaike weights of phylogenetic models of body-size evolution displayed as pie charts next to clades for which analyses were carried out. Thick lines indicate observed stratigraphic range, thin lines indicate inferred range based on phylogeny, and thick lines with diagonal striping indicate uncertainty in observed range. Relationship between therapsid clades follows Liu et al. [41] (see the electronic supplementary material, table S1). Full phylogenies are given in the electronic supplementary material, figures S1 and S2 and stage abbreviations in the electronic supplementary material, table S2.

Table 2.

Summary of results for phylogenetic model fitting for archosauromorph and therapsid clades. Key as for table 1 except: r, decay rate for exponentially changing rate of evolution. Brownian motion (BM) with trend indicates an evolutionary trend, BM indicates significant variation but no trend, OU indicates evolution towards an optimum and early burst indicates exponentially decreasing evolutionary rate.

clade	n	Brownian motion with trend (BM+trend)		Brownian motion (BM)		stasis		Ornstein–Uhlenbeck (OU)		early burst (EB)
		A.W.	μ, σ², θ (log mm)	A.W.	σ² (log mm)	A.W.	θ, ω (log mm)	A.W.	α, ω (log mm)	A.W.	ω (log mm), r
Archosauromorpha	150	0.177	−0.001, 0.006, 2.079	0.422	0.006	0	2.300, 0.252	0.252	0.004, 0.006	0.149	0.006, 0
Dinosauromorpha	75	0.203	0.002, 0.006, 2.074	0.467	0.006	0	2.543, 0.169	0.172	0.002, 0.006	0.158	0.006, 0
Ornithischia	14	0.047	0.003, 0.005, 2.180	0.243	0.005	0.557	2.308, 0.087	0.109	0.044, 0.010	0.043	0.005, 0
Theropoda	24	0.163	−0.004, 0.007, 2.411	0.545	0.008	0.002	2.509, 0.151	0.145	0.003, 0.008	0.144	0.007, 0
Sauropodomorpha	28	0.079	0.006, 0.005, 2.265	0.103	0.005	0.616	2.844, 0.078	0.172	20.480, 3.177	0.029	0.005, 0
Pterosauria	12	0.003	0, 0.005, 1.596	0.022	0.005	0.861	1.674, 0.036	0.103	0.5000, 0.036	0.011	0.013, −0.050
Pseudosuchia	30	0.155	−0.005, 0.005, 2.403	0.304	0.005	0.003	2.321, 0.100	0.212	0.031, 0.008	0.326	0.009, −0.033
Aetosauria	7	0.003	−0.006, 0.005, 2.545	0.365	0.005	0.626	2.342, 0.072	0.004	50.000, 7.202	0.003	0.005, 0
Therapsida	138	0.036	−0.001, 0.011, 1.988	0103	0.011	0	2.009, 0.099	0.347	0.027, 0.012	0.514	0.016, −0.023
Anomodontia	50	0.160	0.009, 0.012, 1.857	0.418	0.012	0	2.060, 0.097	0.177	0.031, 0.014,	0.244	0.023, −0.062
Cynodontia	38	0.115	−0.003, 0.008, 1.859	0.347	0.008	0	1.807, 0.127	0.143	0.011, 0.009	0.395	0.011, 0.022
Therocephalia	19	0.048	0.015, 0.007, 1.900	0.202	0.007	0.524	1.933, 0.024	0.193	0.258, 0.013	0.032	0.007, 0
Gorgonopsia	37	0.000	−0.020, 0.014, 2.281	0.001	0.014	0.034	2.173, 0.025	0.964	0.534, 0.026	0	0.027, −0.064

(d). Regression of carnivore and herbivore size

A generalized least-squares regression model using herbivore maximum and mean body size to predict carnivore size substantially outperformed a null model when Therapsida and Archosauromorpha were examined together with no autoregressive model (AR0, equivalent to ordinary least-squares regression, table 3). However, the null model (though worse) was non-negligible for Archosauromorpha analysed alone, and outperformed the herbivore model for Therapsida analysed alone, suggesting inconsistent within-clade relationships through the study interval. When an autoregressive model (AR1) was implemented, the null model was best supported for most comparisons. Under this model, a strong, significant relationship, with substantially better (lower) AICc than the null model was only recovered for maximum body size, and only when considering Archosauromorpha and Therapsida together.

Table 3.

Summary of results for generalized least-squares regression models of carnivore maximum and mean size for both null models and models using herbivore size to predict carnivore size. The only model robustly better than null was maximum herbivore and carnivore size for both therapsid and archosauromorph taxa analysed together. AR1, first-order autoregressive model implemented to remove serial correlation. Bold Akaike weight (A.W.), herbivore models of carnivore size where null model was negligible (A.W. < 1/8 best model), bold model name, null model negligible under ordinary least squares, bold and italicized model name, null model negligible under ordinary least squares and generalized least squares with AR1.

	carnivore clade(s)	ordinary least squares		generalized least squares (AR1)		n
		null model A.W.	herbivore model A.W.	null model A.W.	herbivore model A.W.
maximum size	Therapsida+Archosauromorpha	0.0001	0.9999	0.0288	0.9712	18
	Therapsida	0.7266	0.2734	0.3591	0.6409	9
	Archosauromorpha	0.2952	0.7048	0.4362	0.5638	14
mean size	Therapsida+Archosauromorpha	0.0003	0.9997	0.5701	0.4299	18
	Therapsida	0.6075	0.3925	0.8821	0.1179	9
	Archosauromorpha	0.2222	0.7778	0.8781	0.1219	14

4. Discussion

Our phylogenetic results demonstrate that passive processes governed body-size evolution during a major reorganization of dominance in the terrestrial environment. Though Cope's rule has been supported for fossil mammals [10,42] and some dinosaurian clades [30,37], it did not occur in all dinosaurs [31,32], including Mesozoic birds [43]), and no neontological studies support its occurrence [3,44]). The results of our phylogenetic models provide little evidence for active trends towards higher (or lower) body sizes during the Late Permian–Middle Jurassic interval (approx. 260–160 Ma, figure 2 and table 2), despite overall increasing mean size in archosauromorphs, and decrease in therapsids (figure 1, and demonstrated by step means in non-phylogenetic random walk models, table 1). Within-lineage processes do not follow Cope's rule, or its inverse (a selection-driven decrease in body size). Instead, large-scale patterns are underlain by passive expansion of clades into smaller and larger body-size niches, with relative stasis within these niches (i.e. in less inclusive, less ecomorphologically varied clades). Thus, apparent ‘trends’ in body-size evolution resulted from changes in niche diversity, mediated by differential among-lineage processes such as origination followed by radiations of smaller- or larger-bodied subclades, and size-selective extinction. This agrees with previous work finding passive trends in size in more inclusive clades and longer time intervals and lack of trends at smaller scales and when phylogeny is taken into account [14,15,45].

The most inclusive clades examined—Archosauromorpha and Therapsida—both exhibit initial bidirectional passive expansion from an ancestral body size close to their absolute lower bound. Therapsid size evolution initially occurred rapidly, but younger therapsid subclades show relative stability, as indicated by strong support for an EB model of therapsid body-size evolution (table 2). Subsequent size reduction in therapsids resulted from selective extinction of larger bodied subclades (gorgonopsians, anomodonts and some cynodonts), and expansion of cynodonts into small-bodied niches. There was no evolutionary ‘trend’ of miniaturization across multiple lineages. Archosauromorph body-size expansion is best modelled as BM. This contrasts with the situation in therapsids, possibly owing to the delayed temporal occurrence of archosauromorph diversification, or greater variability in body size among archosauromorph subclades. Indeed, archosauromorphs exhibited repeated episodes of secondary size reduction, e.g. in drepanosauromorphs (small, superficially lizard-like archosauromorphs), basal pterosaurs and coelurosaurian theropod dinosaurs.

Four large and ecomorphologically varied subclades of Archosauromorpha (Dinosauromorpha, Theropoda and Pseudosuchia) and Therapsida (Anomodontia) favour a BM model, reflecting passive expansion into a range of niches. An EB model favoured for Cynodontia reflects their early ecological diversification into larger (‘non-probainognathan’) and smaller bodied (‘probainognathan’) subclades. The subclades best modelled by stasis or OU models have a limited ecomorphological variation (Sauropodomorpha, Ornithischia, Pterosauria, Aetosauria, Therocephalia and Gorgonopsia) during the study interval, and include the least inclusive clades examined. These clades thus exhibit the patterns expected of groups constrained within particular niche optima by selection.

The lack of evidence for within-lineage active trends of size increase among archosauromorphs and therapsids sheds new light on the enduring topic of reasons for archosaur and dinosaur ascent and therapsid downfall [19,20,28,29,32,46]. A major question is whether this replacement occurred via long-term evolutionary competition, or opportunistic replacement following chance extinctions of therapsids [32,46,47]. Evolutionary competition alone now seems unlikely for two reasons: (i) the absence of the driven trends that would be expected if size (in which archosauromorphs tended to exceed therapsids) per se were advantageous, and (ii) a delay between the decline of large-bodied therapsid predators (Gorgonopsia: extinct after the Late Permian), and herbivores (Anomodontia: decimated following the Carnian [32]), and the expansion of archosauromorphs into large-body-sized predatory (erythrosuchids, proterosuchids and Pseudosuchia, Early Triassic (approx. 252–245 Ma)) and herbivorous (Sauropodomorpha, Norian-Rhaetian (approx. 228–201.6 Ma)) niches, which suggests that contemporaneous therapsids and archosauromorphs were rarely competing for the same food resources. Archosauromorphs may, however, have possessed physiological adaptations conferring an exceptional ability to obtain large body size once therapsids vacated key niches. For example, archosauromorphs possess exceptional growth rates (e.g. in sauropodomorphs [48], later theropods [49], basal dinosauromorphs [50] and basal archosauriforms [51,52]) that have their origins in the Early Triassic [52], and a heterogeneous lung ventilated by efficient unidirectional flow [53], that is also capable of decoupling body size from overall mass via pneumatization (in dinosaurs: [54], and possibly more basal archosauromorphs: [55]). Failure of therapsids to reinvade large-bodied niches following extinction may even be explicable by higher growth rates and thus earlier sexual maturity in archosauromorphs [52,56,57], allowing a higher reproductive rate than in similarly sized therapsids. Prior to widespread therapsid extinction, this reproductive advantage could have been outweighed by the large incumbent advantage expected under neutral macroecological models [58]. Further elevation of growth rates may also in part explain dinosaurian ascent after extinction of many non-dinosaurian archosauromorphs (see [20,59]): only the basal crocodylomorph Terrestrisuchus [51] and some erythrosuchids [50,51] are currently known to have had growth rates comparable to those of dinosaurs and other ornithodirans.

Hypothesized physiological adaptations allowing higher maximum body-size thresholds in archosauromorphs are also supported by a unique and surprising situation that prevailed from the Anisian to early Norian (Middle–early Late Triassic (approx. 245-216 Ma)). During this interval, the largest terrestrial predators (including proterosuchid, erythrosuchid, pseudosuchian and phytosaurian archosauromorphs) reached maximum body sizes that exceeded the largest terrestrial herbivores (anomodont therapsids; figure 1b). This is inconsistent with the widely held ecological ‘rule’, whereby body size of the largest terrestrial herbivores should exceed that of the largest predators [17]. In fact, this ‘rule’ only applies when the largest predators and herbivores represent a single major clade, as in earlier (Middle–Late Permian (approx. 271–252 Ma)) therapsid-dominated ecosystems, and later Mesozoic (approx. 216–65.5 Ma, archosaur/dinosaur-dominated, [17]), and Cenozoic (65.5 Ma-present, mammal-dominated, [17,18]) times. The fact that the relationship between herbivore and predator maximum body sizes is supported only when archosauromorph and therapsid datasets are combined provides evidence that maximum body sizes between guilds tracked each other through time, regardless of affinities, suggesting co-evolution between ecotypes. If carnivore and herbivore maximum size were indeed linked via selection, and both guilds experienced similar environmental regimes, then intrinsic, biological differences provide the only remaining explanation of relatively small body sizes of the largest Triassic therapsid herbivores. Therapsids lacked key physiological adaptations of archosauromorphs (e.g. growth rates and ventilation system—see above), and were thus constrained to smaller body sizes, regardless of selective pressures.

Our results, spanning multiple higher clades and an extended time interval, fundamentally question the existence of consistent long-term, within-lineage active trends in vertebrate body-size evolution. Instead, size evolution is underlain by passive expansion coupled with constraining selection within ecological niches, and differential clade extinction. Within-clade body-size ranges are evolutionarily limited by intrinsic physiological constraints. Thus, archosauromorphs far exceeded the maximum body sizes of non-mammalian therapsids. Archosauromorphs only entered therapsid niches once they had been cleared by extinctions, but uniquely rapid growth and reproductive rates may have given archosauromorphs a competitive advantage in invading these vacated niches. We thus support a model for the rise of archosauromorphs and dinosaurs that was fundamentally opportunistic, but in which intrinsic physiological differences allowed archosauromorphs to be more successful than therapsids in taking advantage of opportunities for diversification.