Apex to Base Left Ventricular Twist Mechanics Computed From High Frame Rate Two-Dimensional and Three-Dimensional Echocardiography: A Comparison Study

Abstract

Background

The aim of this study was to compare two-dimensional (2D) and three-dimensional (3D) methods for computing left ventricular (LV) rotation.

Methods

A two-axis linear/rotary system was designed using rotary motors controlled through a digital interface, and 10 freshly harvested pig hearts were studied. Each heart was mounted on the rotary actuator with the base being rotated at different known degrees of rotation (10°, 15°, 20°, and 25°) and was passively driven by a pump with calibrated stoke volume (50 mL) at a constant rate (60 beats/min) simultaneously. Cardiac motion was scanned to acquire 2D short-axis views using a GE Vivid 7 system for assessing rotation, and 3D apical full-volume loops were acquired using a Toshiba Applio Artida ultrasound system. Full-volume 3D image loops were analyzed online with Toshiba Wall Motion Tracking software, and short-axis 2D images were analyzed offline for LV rotation in GE EchoPAC PC at corresponding LV levels.

Results

At each state, both 2D and 3D echocardiography detected the changes in LV rotation but overestimated the rotation degrees. The biases for overestimation from 3D imaging were smaller compared with 2D imaging at each LV level. Both methods, when compared with each other, showed a linear correlation (r = 0.84, P < .0001). Bland-Altman comparison showed 99% of data points within range, with a constant bias between both methods (adjusted values of 3D = 1.892 + 0.964 × 3D).

Conclusions

Although 3D echocardiography showed smaller bias, the results between 2D and 3D echocardiography were comparable.

Left ventricular (LV) twist is suggested as an important index of contractility and a potential marker of myocardial dysfunction in the diseased heart. As an index of systolic function, LV twist is computed from the net difference of counterclockwise apical and clockwise basal LV rotation during systole.^1–4 Rapid unwinding of this systolic twist has also been shown to have significant contribution in early diastolic filling.^5–8 An accurate quantification of twisting LV motion, therefore, can provide important information about both systolic and diastolic function of the heart.

A noninvasive imaging-based assessment of LV twist is of significant resource in the clinical evaluation of dynamic LV function. With the introduction of digital tracking of speckles in ultrasound image loops, high–frame rate two-dimensional (2D) echocardiography was tested for the computation of LV twist from short-axis (SAX) views and validated.^9–11 However, selection of optimal imaging planes for such computation is quite challenging, because of limited acoustic windows and oblique orientation of the heart in the patient’s chest cavity. Despite an accurate assessment of LV rotation with speckle tracking, the out-of-plane myocardial motion during 2D acquisition is a major source of error, especially near the LV base.

More recently, three-dimensional (3D) echocardiography has been introduced and is rapidly being integrated in clinical imaging because of its enhanced display of cardiac anatomy. New-generation matrix transducers have allowed the sequential acquisition of scan-line data with electrocardiographic gating and the reconstruction of 3D loops with a programmable degree of overlapping between successive volumes to suppress the through-plane motion, with resolution high enough to track speckle motion through the volumes for the computation of mechanical functions. The ability to obtain a full-volume image loop with a single acquisition from the same level and analyze the same volume at multiple levels avoids many difficulties of 2D echocardiographic methods. Digital feature tracking has also been tested to compute LV twist from high–frame rate 3D echocardiographic image loops and validated against sonomicrometry.^12,13 We sought to compare both 2D and 3D echocardiographic methods to quantify LV rotation at different levels using a custom-designed phantom.

METHODS

Heart Model

A two-axis linear/rotary torsion system was designed using rotary stepper motors to achieve both linear and rotary motion synchronized to each other, simulating base-to-apex linear and twisting cardiac motion. The rotary stepper motors were controlled using a six-step switching technique to allow for discrete commutation of the rotor and precision control of the position of each of the axis. An Atmel AT90CAN128 microcontroller (Atmel, San Jose, CA) was used to control the stepper motors and provide a digital interface (Figure 1). We studied 10 freshly harvested pig hearts. Each heart was mounted on the rotary actuator, with the base being rotated and the apex held fixed to avoid translational motion but permitting rotation. A pulsatile pump was connected to a balloon inserted into the LV cavity, and its rate of pumping was synchronized with the rate of rotation and linear motion. With each counterclockwise rotation as viewed from the LV apex, the base moved linearly toward the apex, which was held fixed, and the heart was emptied by synchronized negative suction of the pulsatile pump. The heart was filled with a positive upstroke of the pump with a known stroke volume and was synchronized with apex-to-base lengthening and clockwise untwisting, as viewed from LV apex. An electrocardiographic signal from the pulsatile pump was used to synchronize the pumping and torsion system. Linear motion of the torsion system was set to 20% of LV length for each heart. We studied different degrees of rotation (10°, 15°, 20°, and 25 °) at a constant rate of 60 beats/min and stroke volume of 50 mL.

Figure 1.

The model used in this study and a screen shot of the digital controls of the device. A freshly harvested pig heart is mounted on the rotary plate through the LV base with the apex stabilized and connected to a pulsatile pump through a balloon secured in the LV cavity. The digital interface was used to synchronize rotational, linear, and pulsatile motion to simulate physiologic motion of heart.

Data Acquisition

Full-volume 3D images were acquired from an apical window using a Toshiba Applio Artida ultrasound system (Toshiba, Tokyo, Japan) at a rate >22 volumes/sec. Frequency was optimized at 3.5 MHz, and scan range angle was set to 70° × 70° over six beats gated by the electrocardiographic signal generated from the pulsatile pump to acquire a complete dynamic image loop with uniform resolution quality throughout the depth of image. We used a Toshiba ultrasound system for the acquisition of 3D data sets, because it was the only system with released software to analyze 3D image loops for LV rotation at the time of the study. Similarly, a GE Vivid 7 Dimensions ultrasound system (GE Healthcare, Milwaukee, WI) was used to acquire 2D SAX views at two different LV levels with a 10S probe. The frame rate of acquisition was set at 80 to 90 frames/sec, and frequency was optimized to achieve uniform resolution quality throughout the depth of the image. Apical 2D SAX views were acquired from a distance equal to 20% of LV length from the apex, and basal 2D SAX views were acquired from a similar distance from the base of the heart. We used the GE Vivid 7 system for the acquisition of 2D data sets because a majority of published studies of LV rotation and twist have used this system.

Analysis

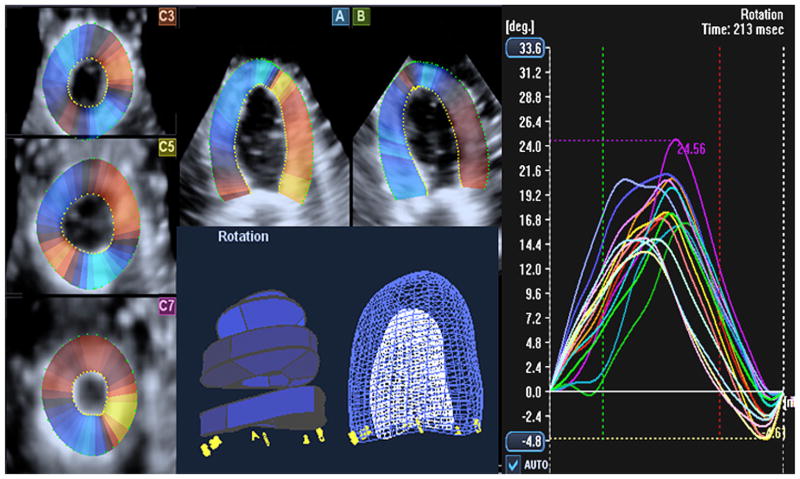
The 3D image data were analyzed for LV rotation using the new speckle tracking–based motion-detecting Wall Motion Tracking (WMT) program from Toshiba. One cycle of complete rotation and reversed motion was selected for resolution quality and complete inclusion of the LV wall. The WMT program shows 3D image data in two long-axis and three SAX 2D views that correspond to conventional two-chamber and four-chamber and parasternal SAX views (basal, middle, and apical). The program allows users to adjust the orientation of these 2D planes and draw an initial contour to define endocardial and epicardial borders on both long-axis views at the reference end-diastolic frame (Figures 2A and 2B). SAX planes are created by spline interpolation. The center of gravity of each SAX plane is created from the average of points defining SAX contour, and rotation center is defined by the center of gravity of each SAX plane in each frame. The software divides the LV wall into 16 segments and computes the degree of rotation globally and for each segment automatically, while tracking apex-to-base longitudinal motion (Figure 2). We computed planar rotation for the LV base and apex for comparison with 2D echocardiography by calculating the mean of their segments at each plane. The 2D image data were also exported to a Windows workstation for offline analysis of LV rotation using the 2DSR program embedded in EchoPAC (GE Healthcare). One cycle of complete rotation and reversed motion was similarly selected from image loop for rotation analysis. The 2D program requires the user to select an appropriate region of interest on the reference frame of image loop. To calculate LVrotation, a center of gravity is defined by averaging kernels within the region of interest around the circumference of the SAX view. The shift of selected points in the region of interest is calculated as angular displacements around the center of gravity. After processing the speckle motion in successive frames of a dynamic 2D grayscale image, the software calculates and displays both segmental and global LV rotation values. The direction of rotation with reference to the position of the probe is also shown (Figure 3). We used global rotation values at each 2D SAX planes.

Figure 2.

Depiction of how the WMT program from Toshiba processes and computes LV rotation from 3D echocardiographic cine loops. The program projects the 3D image data set into conventional 2D SAX and long-axis views. The user may adjust the orientation of planes and define the endocardial and epicardial borders on the reference frame for automated tracking through successive volumes of loop. The software computes and projects the results in all 16 segments, while tracking apex-to-base longitudinal motion.

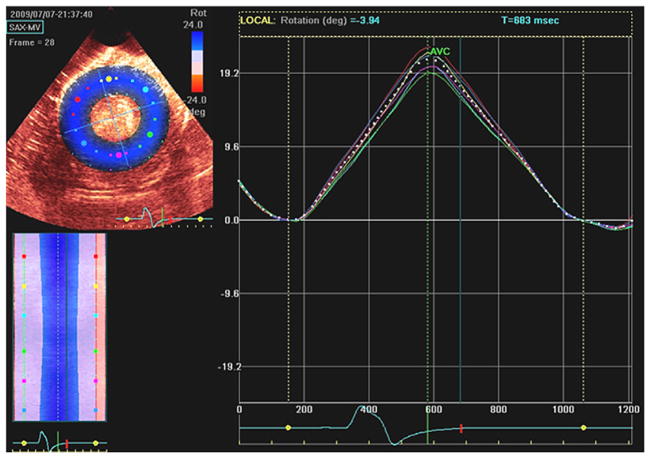
Figure 3.

Depiction of how the EchoPAC PC program from GE computes LV rotation from 2D echocardiographic cine loops. The software allows the user to draw a region of interest (ROI) on the reference frame of image encircling myocardium and tracks the myocardial motion within that ROI in successive frames of image loop. A center of gravity is defined by averaging kernels within the ROI around the circumference of the SAX view. LV rotation is computed as angular displacement of segments around that center of gravity.

Statistical Analysis

We used different statistical tools to compare our results of LVrotation from both 2D and 3D echocardiographic methods in this controlled phantom study.^14–19 We assessed the discrepancy between these two methods through the quantities of bias and mean square error. Nonparametric Wilcoxon’s signed-rand test was performed on the difference between echocardiography-derived LV rotation and reference measurements. In addition, a linear mixed effects model was used to correlate repeated measurements of LV rotation by both methods (2D and 3D echocardiography) at different states of the same pig heart. To assess the agreement between both 3D and 2D methods, we used Bland-Altman plots. We also used concordance correlation coefficient to avoid the bias in estimating the variance that may happen when using Pearson’s correlation coefficient. The concordance correlation coefficient combines measures of both precision and accuracy to determine how far the observed data deviate from the line of perfect concordance, that is, the line at 45° on a square scatterplot. Last, we determined intraclass correlation coefficients to access the reliability or consistency between these two methods (3D vs 2D echocardiography). P values < .05 were considered significant.

RESULTS

The results illustrated were derived from the images that were selected for their resolution quality and inclusion of complete LV walls within the pyramidal full-volume 3D and 2D cine loop. Planar rotation for each LV level was derived by averaging the angular displacement of each segment at that level for both 2D and 3D loops. Results are expressed as mean ± SD.

When the model was rotated, the LV base showed similar rotation being attached firmly to the rotary actuator. Moreover, apical levels of the left ventricle showed much lower degrees of rotation because the apex was essentially held fixed to avoid translational motion. Thus, there was a base-to-apex gradient in segmental rotation. Nonetheless, detected segmental rotation at all LV levels showed a strongly positive linear correlation with the actual degree of rotation imposed by the motor device. With increase in actual rotation at motor device, the degree of rotation at the LV base, middle, and apex also increased accordingly and was detected by both 2D and 3D echocardiographic methods (Table 1). The degree of rotation at the apex was smaller than that at the base and middle of actual heart rotation (both P values < .001), because it was partially restricted by the stabilizing apex. There was no statistically significant difference between the degree of rotation of the LV base and actual rotation at the motor device (all P values > .05). Each segment and the global rotation had good correlations with the actual rotation at the motor device (base r = 0.96, middle r = 0.93, and apex r = 0.68, all P values < .001 for the 3D method; base r = 0.95, middle r = 0.85, apex r = 0.85, all P values < .001 for the 2D method).

Table 1.

LV rotation (apex, base, and middle) computed by 2D and 3D echocardiography at each state of rotation

Reference rotation at motor device (°)	Measured rotation at LV base (°)		Measured rotation at LV middle (°)		Measured rotation at LV apex (°)
	3D	2D	3D	2D	3D	2D
10	11.25 ± 0.85	13.45 ± 2.55	8.19 ± 0.75	9.95 ± 1.85	7.20 ± 0.55	8.15 ± 2.61
15	16.86 ± 1.35	17.13 ± 1.58	12.83 ± 1.84	13.36 ± 0.99	9.25 ± 3.30	11.14 ± 2.18
20	21.29 ± 1.79	23.25 ± 1.62	17.65 ± 1.42	18.16 ± 1.28	12.82 ± 3.49	15.35 ± 2.63
25	26.18 ± 1.86	27.09 ± 1.41	23.15 ± 1.90	24.59 ± 2.14	14.59 ± 4.21	19.25 ± 3.75

We assessed the discrepancy of 2D and 3D echocardiographic methods by comparing the results obtained from each method at the LV base (attached firmly to the rotary actuator) to the reference values (actual rotation at the rotary actuator). Both methods overestimated the LV rotation at each state of rotation, but the 3D method showed relatively lower bias (1.18 ± 2.15) compared with the 2D method (2.09 ± 3.15). The discrepancy between both methods was further examined through the quantity of mean square error. The 3D method showed a smaller mean square error (35.98) than the 2D method (38.66), indicating that the 3D method had small discrepancy. We also performed Wilcoxon’s signed-rank test on the difference between echocardiography-derived rotation at LV base and reference measurements at each state of rotation and constructed the 95% confidence intervals of each difference (Table 2). Most confidence intervals for 3D measurements contained zero, indicating no difference between the 3D method and reference; we can infer that 3D measurements were similar to reference values. Similarly, because confidence intervals for most 2D echocardiographic measurements did not contain zero, we can infer that 2D measurements were different from reference values. At 15° rotation, both the confidence intervals for both 3D and 2D echocardiography contained zero, but the confidence intervals for 3D echocardiography were much narrower than those for 2D echocardiography, indicating higher precision in 3D measurements compared with 2D measurements. Similarly, at 10° rotation, both the confidence intervals of both 3D and 2D echocardiography did not contain zero, but the confidence interval for 3D imaging was narrower than for 2D imaging, indicating that the 3D method was more accurate than the 2D method.

Table 2.

Ninety-five percent confidence intervals of the difference between echocardiographic LV rotation and reference measurements at each state of rotation

Reference rotation (°)	95% confidence interval of difference between measured and reference rotation
3D echocardiographic rotation
10°	(0.1500 to 1.6750)
15°	(−2.0700 to 0.3950)
20°	(−1.0700 to 1.5700)
25°	(−1.1850 to 1.7200)
2D echocardiographic rotation
10°	(1.7500 to 4.0700)
15°	(−1.4850 to 2.1100)
20°	(0.1049 to 2.5001)
25°	(0.5351 to 2.8300)

The comparison of 2D and 3D echocardiographic rotation measurements using the linear mixed effects model was adjusted by the location (base, middle, or apex). The P value (.1961) indicates that either method (3D or 2D) is not significantly different. We could also say that both methods are relatively comparable. We also obtained the P value (.0014) of the adjusting location factor. This result indicates that the rotation values were significantly different from one location (i.e., base, middle, or apex) to the other LV levels.

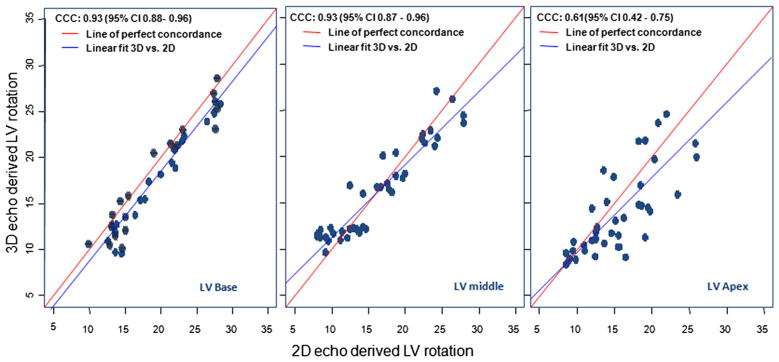
The concordance correlation coefficient estimates at the base, middle, and apex of the hearts were 0.923, 0.927, and 0.608, respectively (Figure 4). Although the concordance correlation coefficient at the apex was slightly weaker than those at the base and middle, this co-efficient is still in the reasonable range. The 95% confidence intervals for these coefficient estimates were 0.877 to 0.959, 0.875 to 0.957, and 0.411 to 0.752, respectively. These results indicate that the 3D and 2D methods were concordant. The estimated intraclass correlation coefficients were 0.931, 0.928, and 0.614 for the basal, middle, and apical locations of hearts, respectively. The bootstrap sample technique was used to construct 95% confidence intervals to draw an inferential statistical conclusion. The intervals were 0.8965 to 0.9544, 0.9032 to 0.9537, and 0.4627 to 0.7547 with respect to the three estimated intraclass correlation coefficients. None of these three confidence intervals contains zero, so we can infer that both the 3D and 2D methods were consistent.

Figure 4.

Concordance correlation coefficient estimates at the LV base, middle, and apex performed to assess the agreement on a continuous measure (LV rotation values) obtained by 3D and 2D echocardiography (to avoid the bias in estimating the variance that may happen when using Pearson’s correlation coefficient). The concordance correlation coefficient combines measures of both precision and accuracy to determine how far the observed data deviate from the line of perfect concordance (i.e., the line at 45° on a square scatterplot). Although the concordance correlation coefficient at the apex is weaker than those at the base and middle, it is still in the reasonable range. Our results indicate 3D and 2D echocardiography are quite strongly concordant.

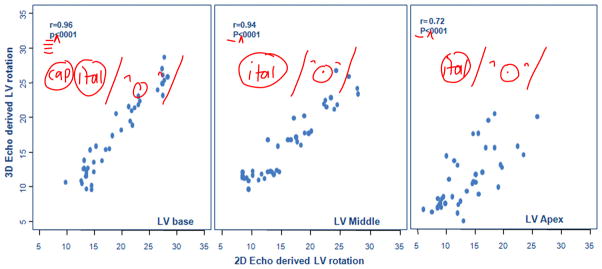
Pearson’s correlation coefficients also showed the 3D and 2D methods were strongly correlated (r = 0.9637, P < .0001, r = 0.9418, P < .0001, and r = 0.7215, P < .0001 for the base, middle, and apex, respectively; Figure 5). Thus, Bland-Altman analysis (Figure 6) was performed to explore the agreement between the 3D and 2D methods, showing the difference of 3D echocardiographic degrees of rotation and actual rotation at the motor device as the y axis and the average of both as the x axis. The scatterplot of points is between the upper and lower limit of agreement defined by the 2 standard deviations describing the range for 95% of comparison points. Despite some biases between the methods, almost all data points were within the confidence limits, except for a few points at high degrees of rotation. Therefore, if the mean of difference between 3D and 2D echocardiography within mean ± 2 SDs is not clinically important, the two methods may be used interchangeably.

Figure 5.

Linear relationships between 3D and 2D echocardiographic methods for computing rotation at each location (LV base, middle, and apex). All three show strong relationships between 3D and 2D echocardiographic methods, although the variations at the LV apex are slightly larger compared with other locations.

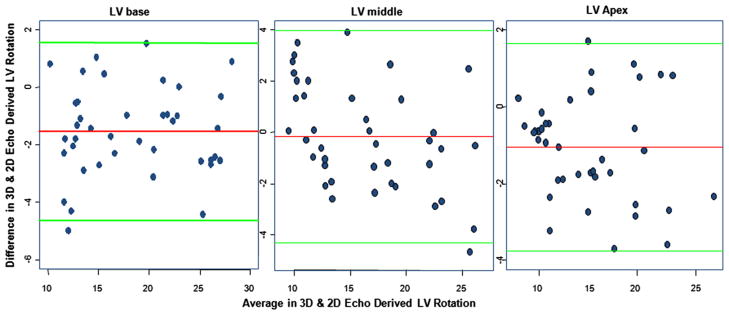
Figure 6.

Bland-Altman plots constructed to explore the agreement between 3D and 2D echocardiographic methods of computing LV rotation with respect to each location (base, middle, and apex). The vertical line (y axis) of each plot is the difference of rotation values obtained between the 3D and 2D methods, and the horizontal line (x axis) is the average of rotation values obtained by the 3D and 2D methods. Almost all data points are within the confidence limits, and <5% of these data points fall outside these boundaries. Such a low rate of falling outside the range limits is acceptable in this kind of analysis.

Reproducibility

To determine and compare the reproducibility of each method, inter-observer variability was determined by having a second observer measure LVrotation in 25 randomly selected 2D and 3D image loops. Intraobserver variability was determined by having one observer remeasure LVrotation in 25 image loops that were randomly reshuffled 1 month after initial analysis. Interobserver and intraobserver variability was calculated as correlation coefficients that were obtained using Pearson’s product and Spearman’s rank correlation. There was a strong linear association between the results from both observers. The calculated sample Pearson’s correlation coefficients were 0.92 (2D echocardiography) and 0.87 (3D echocardiography) (P < .05) for interobserver variability and 0.84 (2D echocardiography) and 0.77 (3D echocardiography) (P < .05) for intraobserver variability. Similar results were also obtained using Spearman’s rank correlation (intraobserver correlations of 0.88 for 2D echocardiography and 0.78 for 3D echocardiography, P < .0001; interobserver correlations of 0.81 for 2D echocardiography and 0.72 for 3D echocardiography, P < .0001).

DISCUSSION

The dynamic function of the heart is a complex and continuous interaction of linear and angular motion. Rotational LV motion is ascribed to oblique helical orientation of myocardial fibers that moves the LV apex counterclockwise and the base clockwise during systolic contraction.^20–24 Because the magnitude of LV twist is determined by contractile force, it is considered an important mechanical index of cardiac performance. This concept is supported by research, and many studies have linked the dynamics of LV twist to the systolic function of the heart, but none of the methods used in experimental work can be implemented in routine clinical practice for the evaluation of cardiac twist.^25–35 With the introduction of noninvasive imaging-based motion-detecting methods, many imaging scientists have developed interest in LV twist as a clinically usable mechanical index of dynamic heart function. Magnetic resonance imaging tagging was the first and probably only imaging method available until recently for the computation of LV rotation but was limited in clinical use for many reasons, including technical difficulties such as tag fading, high cost, and low temporal resolution.^36–39 With the advent of digital tracking of acoustic tags in scan-line echocardiographic image data, the computation of rotation in SAX planes was done using high-resolution dynamic 2D images and validated against more invasive methods. The ability to track tissue features in high-resolution 2D echocardiographic images created much optimism about the clinical implementation of LV twist. It was deemed a robust and convenient bedside method for the evaluation of cardiac twist. However, the forces resulting in twist also cause longitudinal shortening at the same time, which moves myocardial tissue out of the scanning plane during 2D acquisition of SAX view with a static scanner. Consequently, it results in tracking error and in plane decorrelation, leading to the inaccurate computation of twist. Nonuniform selections of imaging level and angle of incidence during multiple 2D acquisitions are other potential sources of error, which are difficult to optimize with 2D methods. Although modifications of magnetic resonance imaging tagging (complementary spatial modulation of magnetization) and image acquisition techniques (slice following imaging) have been suggested to suppress the effects of through-plane motion, no such methodology is proposed or possible with conventional 2D echocardiography.⁴⁰ Speckle tracking in 3D echocardiographic image loops also offers unique challenges. Despite recent advances in technology, 3D ultrasound images are still of relatively low spatiotemporal resolution, with artifacts such as attenuation, shadows, and signal dropout. These factors result in a higher degree of inconsistency of speckles between successive volumes of a 3D image loop. Despite these technical limitations, our study has demonstrated a comparable accuracy of the 3D method for the computation of LV rotation in a controlled experimental setup. Even though the results of our study are encouraging, we believe that more accurate and robust results will be achieved with continuing improved spatial and temporal resolution in 3D echocardiography that reduces the speckle pattern variability, making the 3D method more feasible for clinical implementation.

Limitations

We used a digital interface to coordinate linear, rotational, and pulsatile motion, ensuring the accuracy and automaticity of our phantom to simulate physiologic heart motion, which required us to use stepper motors. Unfortunately, the stepper motors exhibited relatively less precision and shaky motion at lower degrees of rotation that interfered with image analysis. For this reason, we were not able to study lower degrees (<10°) of rotation. It is unknown that how forced external twisting of nonliving heart tissue translates to the rotational mechanics in a living heart, and the same results may not be reproduced in vivo, which would require further studies. Although our phantom study allowed a reliable comparison between two methods, there may be limited clinical relevance between this relatively simple modeled dynamics, especially beyond physiologic limits, and what happens in a beating heart with more complex patterns of contraction and relaxation.

We used two entirely different ultrasound systems and motion analysis programs for comparison. To the best of our understanding, 2D and 3D speckle-tracking methods are entirely different even if the same ultrasound system is used for data acquisition. In the case of the 3D method, segmental rotation is computed from multiple SAX planes within the segment that covers one third of LV length. Each SAX plane in the segment is tracked dynamically depending on shortening motion to avoid through-plane motion, whereas LV rotation with the 2D method is derived from only one SAX plane that could be subject to through-plane motion. Therefore, the difference in results should not be attributed entirely to the two-dimensionality versus three-dimensionality of the data exploration.

The Toshiba 3D motion analysis program divides the LV wall at equal distance into 16 American Society of Echocardiography segments (four apical, six middle, and six basal), with each LV segment about 33% to 34% of the total apex-to-base distance. We used 20% and 80% of LV length for 2D imaging to approximate the center of 3D echocardiographically defined apical and basal segments, respectively. We understand that this is approximate and not an exactly similar location for comparison.

The results of this study are derived from the analysis of images acquired directly from the surface of pig heart in a water tank. Acquiring such uniform and artifact-free high–frame rate images may be difficult in clinical exams, especially in patients with poor acoustic windows. The quality of the electrocardiography signal that is used for gated reconstruction full-volume 3D image loops by stitching of pyramidal volumes may also be a limiting factor, especially in patients with arrhythmias. We compared the results of LV rotation obtained from both methods. Peak untwisting rate is another mechanical index suggested for diastolic function of heart. The relatively lower time resolution of 3D echocardiography may be a limiting factor for the accurate computation of this rate of change in LV rotation.

CONCLUSIONS

Although the 3D echocardiographic method showed relatively lower reproducibility and slightly better accuracy compared with the 2D method for the computation of LV rotation, both methods exhibited comparable results in this controlled phantom study. Despite relatively lower resolution, the comparable accuracy and reproducibility of the 3D echocardiographic method with the convenience of rotation analysis at different LV levels after a single acquisition may make it a better clinical tool for the evaluation of cardiac twist.

Abbreviations

LV

Left ventricular

SAX

Short-axis

3D

Three-dimensional

2D

Two-dimensional

WMT

Wall Motion Tracking