On Sharing Quantitative Trait GWAS Results in an Era of Multiple-omics Data and the Limits of Genomic Privacy

Abstract

Recent advances in genome-scale, system-level measurements of quantitative phenotypes (transcriptome, metabolome, and proteome) promise to yield unprecedented biological insights. In this environment, broad dissemination of results from genome-wide association studies (GWASs) or deep-sequencing efforts is highly desirable. However, summary results from case-control studies (allele frequencies) have been withdrawn from public access because it has been shown that they can be used for inferring participation in a study if the individual's genotype is available. A natural question that follows is how much private information is contained in summary results from quantitative trait GWAS such as regression coefficients or p values. We show that regression coefficients for many SNPs can reveal the person's participation and for participants his or her phenotype with high accuracy. Our power calculations show that regression coefficients contain as much information on individuals as allele frequencies do, if the person's phenotype is rather extreme or if multiple phenotypes are available as has been increasingly facilitated by the use of multiple-omics data sets. These findings emphasize the need to devise a mechanism that allows data sharing that will facilitate scientific progress without sacrificing privacy protection.

Introduction

Homer et al.¹ showed that it is possible to detect an individual's presence in a complex genomic DNA mixture even when the mixture contains only trace quantities of his or her DNA. The study considered the implications of its findings, motivated originally as an application to forensic science, in the context of genome-wide association studies (GWASs) from which aggregate allele frequencies for a large number of markers were being made publicly available. Shortly after this publication, a reduction in open access to aggregate GWAS results was implemented. Jacobs et al.² presented an improved method using a likelihood approach and showed that disease status could be inferred for participants of the study. Visscher et al.³ and Sankararaman et al.⁴ calculated power estimates to understand the limits of individual detection from sample allele frequencies. They showed that the power to detect membership is determined by the ratio between the number of markers and the number of participants in the study.

We present a method that can infer an individual's participation in a study when regression coefficients from quantitative phenotypes are available. This problem is especially relevant now that genome-wide system-level measurements of quantitative phenotypes (transcriptome, proteome, and metabolome) are being widely collected and analyzed. Undoubtedly, disseminating results from quantitative GWAS and deep-sequencing efforts could be of enormous benefit to research groups working on related traits. We explore several statistics that can discriminate study participants from nonparticipants. Notably, we find that the use of only the direction of effects (signs of the coefficients) enables membership inference with good accuracy. We show the results from applying the statistics to the Genetics of Kidneys in Diabetes (GoKinD) data set^5,6 to illustrate the level of information contained in aggregate data. We also provide quantification of the information content by computing the power of the method. Furthermore, we discuss a general framework that can be used for integrating our findings and earlier studies of genomic privacy based on sample allele frequencies. With the increasing use of high-throughput technologies to integrate multiple-omics data sets, these various statistics result in a more powerful approach to the identification problem than with the use of a single phenotype.

Material and Methods

Let us assume that we have the estimated regression coefficients for M independent SNPs, that we use data on n individuals in a GWAS (test sample), and that we also have the allelic dosage for $n^{\ast }$ individuals from a reference population such as HapMap^7,8 or 1000 Genomes Project.⁹

Membership Inference Method

We define a statistic (a function of available data) that has a different distribution depending on the membership status and use this difference to infer membership. We compute this statistic for the individual of interest, I, and for all individuals in the reference population. If the statistic falls well within the reference distribution we will conclude that the individual is not likely to have participated in the study, and if the statistic falls in the extremes of the distribution, we will conclude that the individual did participate in the study.

Let $\hat{Y}$ be defined as

$${\hat{Y}}_I=\frac{n}{M}\sum _{j=1}^M{\hat{\beta }}_j\left(X_{I,j}-{\hat{X}}_j\right),$$ (Equation 1)

where $X_{I,j}$ is the allelic dosage of individual I at SNP j, ${\hat{\beta }}_j$ is the estimated coefficient from fitting the model $Y_i={\alpha }_j+{\beta }_j{X}_{i,j}+e_i$, and ${\hat{X}}_j$ is the estimated mean of allelic dosage (twice the allele frequency) for SNP j computed with the reference group.

Conditional Mean and Variance of $\hat{Y}$

The expected value and the variance of the statistic ${\hat{Y}}_I$ conditional on the individual's genotype X_I and demeaned phenotype $Y_I-\mu$ and membership status (in or out) are as follows:

$$\begin{array}{c}E[\hat{Y}\mathrm{|}{X}_I,Y_I,in]\approx \left(Y_I-\mu \right)\\ E[\hat{Y}\mathrm{|}{X}_I,Y_I,out]\approx 0\\ \text{Var}[\hat{Y}\mathrm{|}{X}_I,Y_I,in]\approx {\sigma }^2\frac{n}{M}\\ \text{Var}[\hat{Y}\mathrm{|}{X}_I,Y_I,out]\approx {\sigma }^2\frac{n}{M}\end{array},$$ (Equation 2)

where σ² is the variance of the phenotype, and μ is the population mean of the phenotype Y. Note that for the method to work we do not need to make use of these expressions nor do we need to know σ² and μ because we rely on the empirical distribution from the reference population to determine membership. These expressions will serve to estimate the power of the method.

Unconditional on Y_I, the variance of the statistic $\hat{Y}$ is given by

$$\text{Var}\left(\hat{Y}\right)\mathrm{|}{X}_I,\mathit{in}\approx {\sigma }^2.$$

In computing these quantities we assume that the number of markers is much larger than the number of individuals in the test sample and the number of individuals in the reference group: $M>>n>>1\text{and}M>>n^{\ast }>>1$. Hardy Weinberg equilibrium is assumed. To derive these expressions, we used standard Taylor expansions and the law of iterative expectations. We tested the validity of these for finite samples (n between 100 and 1,000 and $M/n$ between 1,000 and 50,000) by fitting linear regressions with simulated genotypes and phenotypes and computing the sample mean and variances of the $\hat{Y}$ statistic. See Supplemental Data, available online, to find plots of the validation.

Power of the Method

To compute power, we define the null and alternative hypothesis. Under the null hypothesis the individual did not participate in the study (nor did any relatives of the individual), whereas under the alternative hypothesis, the individual did participate. Using the mean and variance under the null hypothesis and the corresponding mean and variance under the alternative hypothesis computed in Equation 2 and assuming $M>>n>>1,M>>n^{\ast }>>1$, normality of the statistic $\hat{Y}$, and the sign of $Y_I-\mu$ to be known, the power will be approximately given by

$$\text{power}\approx \Phi \left(\frac{\left|Y_I-\mu \right|}{\sigma }\sqrt{\frac{M}{n}}-z_{\alpha }\right),$$ (Equation 3)

where α is the type I error, $z_x={\Phi }^{-1}\left(1-x\right)$ is the $\left(1-x\right)$-quantile of the normal distribution, and Φ is the normal cumulative distribution function. If the sign of $\hat{Y}-\mu$ is not known, a two-sided test will be used in the derivation and the power will be given by

$$\text{power}\approx \Phi \left(\frac{\left|Y_I-\mu \right|}{\sigma }\sqrt{\frac{M}{n}}-z_{\alpha /2}\right).$$ (Equation 4)

See derivation in Appendix A. Because Φ is a strictly increasing function the power

• •increases when M, the number of SNPs, increases
• •decreases when n, the study's sample size, increases
• •increases when the individual's phenotype deviates more from the mean (scaled by the standard deviation)
• •increases when α, the type I error, increases

To facilitate comparison with Visscher et al.³ and Sankararaman et al.,⁴ let us express the one-sided power Equation 3 with the following (equivalent) implicit formula

$${\left(z_{\alpha }+z_{\beta }\right)}^2\approx {\left(\frac{Y_I-\mu }{\sigma }\right)}^2\frac{M}{n},$$ (Equation 5)

where $1-\beta$ is the power (note that in Sankararaman et al.⁴ β is defined as the power). Recall that in Visscher et al.³ and Sankararaman et al.⁴ power was given implicitly by

$${\left(z_{\alpha }+z_{\beta }\right)}^2\approx \frac{M}{n}.$$ (Equation 6)

Thus, the only difference between Equations 5 and 6 is the factor ${\left((Y_I-\mu )/\sigma \right)}^2$. If the phenotype of the person deviates more than one standard deviation away from the mean, i.e., $\left|Y_I-\mu \right|>\sigma$ and the sign of $Y_I-\mu$ is known, the power when regression coefficients are used is larger than it is when allele frequencies are used. If the person's phenotype is close to the mean, then the power will be much diminished. Although expectations are computed conditional on $Y_I-\mu$, we do not need to know its magnitude in order to achieve this power. However, we do need to know the sign of $Y_I-\mu$ in order to keep the test one-sided. If the sign is not used, $\left|Y_I-\mu \right|$ would need to be $1+\left(\right(z_{\alpha /2}-z_{\alpha })/\sqrt{M/n})$ times greater than the standard deviation in order to achieve greater power than the allele frequency case. As an example, if $\alpha =0.05$ and $M/n=100$, $\left|Y_I-\mu \right|$ would need to be greater than 1.031 times σ.

Individual Contribution to the Regression Coefficient

In order to get an intuitive understanding of the contribution of each individual from the sample, we can decompose the estimated regression coefficient into roughly the sum of individual contributions:

$$\begin{array}{c}{\hat{\beta }}_j={\left({\tilde{\mathbf{X}}}_j^{\prime }{\tilde{\mathbf{X}}}_j\right)}^{-1}{\tilde{\mathbf{X}}}_j^{\prime }\tilde{\mathbf{Y}}\\ {\hat{\beta }}_j\approx \frac{1}{n{\sigma }_j^2}{\tilde{X}}_{I,j}{\tilde{Y}}_I+\frac{1}{n{\sigma }_j^2}\sum _{i\ne I}{\tilde{X}}_{i,j}{\tilde{Y}}_i\\ {\hat{\beta }}_j\approx {\tilde{\beta }}_{I,j}+\sum _{i\ne I}{\tilde{\beta }}_{i,j}\end{array},$$ (Equation 7)

defining ${\tilde{\beta }}_{i,j}=(1/n{\sigma }_j^2){\tilde{X}}_{i,j}{\tilde{Y}}_i$ as the individual contribution to the regression coefficient and ${\sigma }_j^2$ as the variance of the allelic dosage (under Hardy Weinberg assumption ${\sigma }_j^2=2p_j\left(1-p_j\right)$ where p_j is the minor allele frequency of SNP j). We use the tilde $\tilde{X}$ for the demeaned variable that uses the mean from the sample. It is worth comparing with the decomposition for the case when minor allele frequencies for the sample are available: ${\hat{p}}_j\approx (p_{I,j}/n)+{\sum }_{i\ne I}(p_{i,j}/n)$, where ${\hat{p}}_j$ is the sample minor allele frequency and $p_{i,j}$ is the allelic dosage divided by 2 of individual i for SNP j. This similarity gives an intuitive understanding of the corresponding similarity in the dependence of power on the ratio of the number of SNPs and sample size of the study.

Combining Multiple Phenotypes

If results from multiple phenotypes such as eQTL (or other omics data) results are available, we can combine the information regarding the individual's membership by using a Fisher type of method (the sum of logarithms of p values).¹⁰

For each phenotype k, we can compute an empirical p value, p_k, defined as the proportion of reference individuals with magnitude of the $\left|\hat{Y}\right|$ greater than the individual's $\left|{\hat{Y}}_I\right|$. We can combine p values across different phenotypes by computing

$$-2\sum _{k=1}^{npheno}{\log }_{10}{p}_k$$

where $npheno$ is the number of phenotypes to be combined. In addition to accumulating evidence across phenotypes, this method avoids the problem of lack of power due to one particular phenotype being close to the population mean.

Covariate Adjustment

Usually other covariates such as age, sex, etc. are adjusted for when performing GWASs. If the allelic dosage is independent of the covariates (as will likely be the case for most SNPs) $\hat{Y}$ will converge to the covariate-adjusted phenotype instead of the actual phenotype. The standard deviation might change if the covariates explain a substantial portion of the phenotypic variability. However, the method will still work because under no participation $\hat{Y}$ will still be around 0, whereas if the individual participated in the study, $\hat{Y}$ will converge to the covariate-adjusted phenotype. The method does not require knowing the actual phenotype and it will work relative to this adjusted phenotype. For the purpose of re-identification using our method, the presence of covariates is only a nuisance and no additional power is achieved when they are present.

Sample Correlation Statistic

Equation 7 suggests that the sample correlation between the estimated beta and the individual's genotype might be useful because we would expect the correlation to be 0 if the individual was not in the sample and different from 0 if the individual was part of the study.

$$\hat{C}=\frac{\sum _{j=1}^M\left({\hat{\beta }}_j-\overline{\beta }\right)\left(X_{I,j}-{\hat{X}}_j-\overline{X_I-\hat{X}}\right)}{\sqrt{\sum _j{\left({\hat{\beta }}_j-\overline{\beta }\right)}^2\sum _j{\left(X_{I,j}-{\hat{X}}_j-\overline{X_I-\hat{X}}\right)}^2}},$$

where the long bar above an expression means the sample mean of the expression.

Sign Statistic

Equation 7 also shows that the sign of the correlation coefficient will be slightly more likely to match the sign of the demeaned allelic dosage if the person participated in the study than otherwise. Let $\hat{S}$ be defined as:

$$\hat{S}=\sum _{j=1}^M\text{sign}\left(\hat{\beta }\right)\text{sign}\left(X_{i,j}-{\hat{X}}_j\right)$$

We expect that strictly more than 50% of the times the product $\text{sign}\left(\hat{\beta }\right)\text{sign}\left(X_{i,j}-{\hat{X}}_j\right)$ will be positive (or negative) if the individual participated in the study and his or her phenotype is above (or below) average. By looking at the absolute value of the sign statistic we expect to gain information on whether the individual was part of the study or not.

Analysis Details

We used the PLINK software¹¹ and filtered out SNP markers that were not in Hardy Weinberg equilibrium (p < 0.001) and those that had minor allele frequencies less than 5%. Receiver operating characteristic (ROC) curves were generated by using the absolute value of the statistic as the predicting variable and membership in the sample as the labels by using the ROCR¹² package for the R statistical package.¹³ We used only individuals who self-reported as white both for sample and reference.

Results

We show the performance of the statistics defined in Material and Methods $\left(\hat{Y},\hat{S},\hat{C}\right)$ by using data from the GoKinD (Genetics of Kidney Disease) study.^5,6 The data set was downloaded from dbGaP¹⁴ and consisted of more than 1,800 probands with long-standing type 1 diabetes, over 300 dichotomous and quantitative phenotypes, and genotype from Affymetrix Genome-Wide Human SNP Array 5.0 platform. We used a subset of 1,644 individuals reported to be Caucasian.

We show results for two of the phenotypes: cholesterol level and body mass index (BMI). We also tested the method on a third simulated phenotype and found at least as good performance. The latter demonstrates that the method does not depend on any real effect of genotype on phenotype.

We randomly sampled 100, 500, and 1,000 individuals from each study's cohort and performed a GWAS including only individuals from each random sample. The remaining individuals were used as reference group. The statistics $\left(\hat{Y},\hat{S},\hat{C}\right)$ were computed for both sample and reference individuals.

Identifiability Statistic and Phenotype Reconstruction

Figure 1 shows $\hat{Y}$ versus the actual phenotype (rank normalized cholesterol levels). The blue dots correspond to individuals in the sample and the black dots correspond to individuals in the reference group. For individuals in the sample, $\hat{Y}$ lies close to the one-to-one line (perfect prediction line), whereas the individuals in the reference population lie close to a flat line around 0 (consistent with our calculations of mean and variances). The sample size was $n=1,000$ and the number of SNPs was $M=300,000$. The number of reference individuals was 644.

Figure 1.

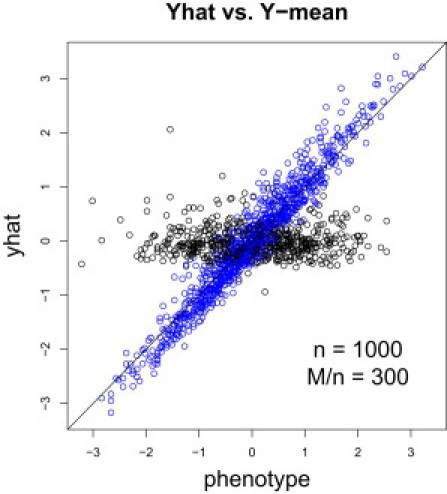
$\hat{Y}$ versus Y

$\hat{Y}$ versus the actual phenotype (cholesterol levels with normalizing transformation applied). The blue dots correspond to individuals in the sample and the black dots correspond to individuals in the reference group. For individuals in the sample $\hat{Y}$ lies close to the one-to-one line, whereas the individuals in the reference population lie close to a flat line around 0. The sample size was 1,000 and number of SNPs was 300,000.

This demonstrates that for individuals who participated in a study, their phenotype can be reconstructed with high accuracy using the $\hat{Y}$ statistic, whereas for nonparticipants what we get is mostly noise.

Distribution of Statistic by Membership Status and ROC Analysis

The left panel in Figure 2 shows the distribution of the absolute value of $\hat{Y}$ by membership status. As in Figure 1 nonmembers' values lie close to 0, whereas members' values are distributed in a large range of values. This difference in distributions is what will allow us to discriminate between members and nonmembers.

Figure 2.

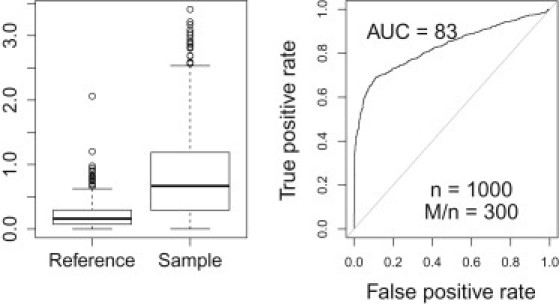
$\hat{Y}$ Distribution by Membership Status and Performance

(Left panel) The distribution of the absolute value of $\hat{Y}$ by membership status. As in Figure 1 nonmembers' values lie close to 0, whereas the values for participants are distributed similar to the actual phenotype.

(Right panel) The ROC curve, the true positive rate (sensitivity) versus the false positive rate (1-specificity) when we use $\left|\hat{Y}\right|$ to predict membership. A good test should yield a high true positive rate (sensitivity) while keeping the false positive rate low (1-specificity); ideally the AUC should be close to 1. For 300,000 SNPs and a sample size of 1,000, the AUC was 0.83, which is reasonably close to 1.

The right panel shows the ROC curve, the true positive rate (sensitivity or power) versus the false positive rate (1-specificity or type I error) when we use $\left|\hat{Y}\right|$ to predict membership. A good test should yield a high true positive rate (= sensitivity or power) while keeping the false positive rate low (= 1-specificity or type I error); ideally the area under the curve (AUC) should be close to 1. For 300,000 SNPs and a sample size of 1,000, the AUC was 0.83, which is much greater than 0.5, showing clear discrimination power. The poor performance relative to the allele frequency case is due to the fact that we do not assume the sign of the deviation from the mean to be known and that the phenotype values of some of the individuals in the test sample are close to the mean. Recall from Equation 3 that power (which is not equal to AUC but is a related measure of performance) is an increasing function of the absolute value of the difference between the phenotype and the mean. For average individuals (phenotype close to the mean) this method does not provide discrimination power.

Predictive Performance as Function of M/n

Figure 3 shows the area under the curve for different values of sample size (n) and number of SNPs (M). Consistent with our power calculation, we observe increasing performance as the ratio of number of SNPs to sample size increases. SNPs were chosen randomly from the full set of available SNPs. The lower AUC for larger sample sizes is probably because the independence of markers assumption fails more dramatically as the total number of markers increases.

Figure 3.

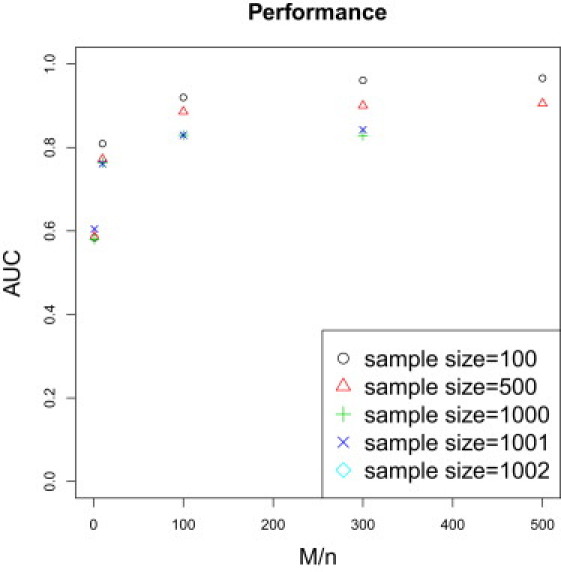
Performance by Sample Size and Number of Markers

The plot shows the area under the curve for different values of sample size (n) and number of SNPs (M). Consistent with the power calculation, we observe increasing AUC as the ratio of number of SNPs to sample size increases. The lower AUC for sample sizes of 1,000 is probably due to a more pronounced effect of linkage disequilibrium as we use more markers.

Performance of Other Statistics and Their Information Content

Figure 4 shows the distribution and performance of the sign statistic. The left panel shows the distribution of the sign statistic by membership status. The right panel shows the ROC curve when we use the absolute value of the sign statistic to predict membership. Notice that the area under the curve is 0.75, which still shows good discrimination power. This result suggests that a large portion of the information regarding the individual's participation is contained in the signs.

Figure 4.

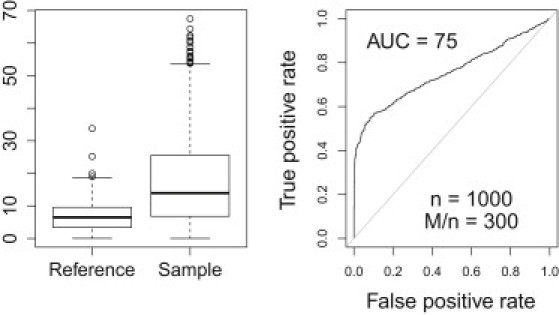
Sign Statistic Distribution and Performance

The left panel shows the distribution of the sign statistic by membership status. The right panel shows the ROC curve when we use the absolute value of the sign statistic to predict membership. The area under the curve is 0.75, a bit lower than the AUC when the actual estimated coefficients are used, but it still shows good discrimination. This suggests that a large portion of the information regarding individual's membership is contained in the signs rather than in the absolute value of the regression coefficient.

The performance of the correlation statistic is almost identical to the performance of $\hat{Y}$ as one might have expected.

Covariate Adjustments

Figure 5 shows the ROC curve for $\hat{Y}$ with rank normalized cholesterol levels as phenotype and sex and age as covariates in addition to allelic dosage. Note that the performance has not changed by adding the additional covariates. This was expected because our method is based on “over fitting” of the data.

Figure 5.

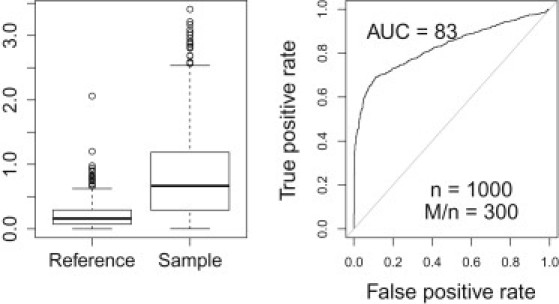
Performance with Covariate Adjustment

This figure shows the ROC curve for $\hat{Y}$ with rank normalized cholesterol levels as phenotype and sex, age, and allelic dosage as covariates. Note that the performance is not changed by adding the additional covariates.

In general access to the covariates or phenotypes for the participants is not available and so we did not attempt to improve our method by using them. If the allelic dosage is independent of the covariates (as will likely be the case for most SNPs), $\hat{Y}$ will converge to the covariate-adjusted phenotype, and our method will work relative to this adjusted phenotype. We do not expect the inclusion of covariates to affect the performance of the method. Also note that our method relies on “over fitting” of the data that occurs for individuals in the sample and not on any real relationship between genotype and phenotype. As previously mentioned, we found that the method worked equally well when a simulated phenotype was used.

Multiple Phenotypes

To illustrate the effect of combining more than one phenotype, we applied the Fisher type method (the sum of the log of empirical p values, see details in Methods) to cholesterol and Body Mass Index (BMI) regression coefficients. Figure 6 shows the ROC curves when single phenotypes were used compared to the curve when both were combined. Clearly, the combined method outperforms both single-phenotype methods. The AUC for each phenotype was 83% and 87%, whereas the combined AUC is 95%. The performance should improve as the number of phenotypes increases.

Figure 6.

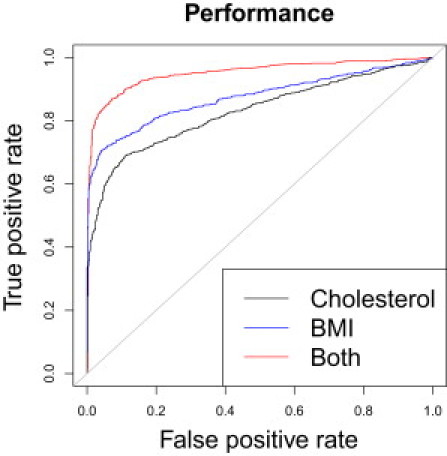
Performance with Multiple Phenotypes

To illustrate the effect of combining more than one phenotype, we applied the Fisher type method (the sum of the log p values) to cholesterol and BMI regression coefficients. This figure shows the ROC curves when each one of the phenotypes was used compared to the curve when both were combined. Clearly, the combined method outperforms both single-phenotype methods. The AUC for each phenotype was 83% and 87%, whereas the combined AUC is 95%.

Discussion

Given the increasing number of large-scale data sets in which very large numbers of phenotypes will be subject to GWAS or sequencing studies, it is of great interest to quantify the level of participant's private data contained in aggregate results. The insights gained from our study should be helpful in devising methods to facilitate broad dissemination of study results without compromising the participant's privacy.

We present three statistics that can discriminate between individuals who participated in a study and those who did not. We show the performance of the method by using real data from the GoKind GWAS. We also provide an approximate estimate of the power of the method when $\hat{Y}$ (the average of the regression coefficients times the allelic dosage) is used. Power is determined by the ratio between the number of markers and the sample size of the study, much like when allele frequencies are available. But the power is also modulated by the deviation from the mean of the individual's phenotype. This indicates that for individuals with extreme phenotypes (e.g., as expected from certain study designs), more power can be achieved (asymptotically) through the use of the regression coefficients than through the use of allele frequencies. But for a person with an average phenotype the method provides no power, which is expected because the average person contributes very little to the estimate of the regression coefficients. In an earlier study, Lumley and Rice¹⁵ considered the possibility that aggregate results from GWAS can reveal a participant's phenotype with high accuracy, even for quantitative phenotypes. However, the problem of phenotype reconstruction (the subject of Lumley et al.'s Commentary on quantitative traits¹⁵) for a participant of a study and the problem of identifiability are distinct problems; furthermore, the problem of identifiability was not theoretically explored. Here we quantified the power of our identification method for quantitative traits, demonstrated the existence of various statistics that can detect the presence of individual genotypes from summary data, and sought to provide a general framework for comparing the power with earlier studies^3,4 of genomic privacy based on sample allele frequencies.

The approximate decomposition of an individual contribution to the regression coefficients gives us an intuitive understanding of the level of information contained in these aggregate data. This decomposition shows the structural similarity with the case in which allele frequencies are used to infer membership.

Even though we do not claim that our method provides optimal discrimination, the striking similarity between our expression for power and the one obtained by Visscher et al.³ and Sankararaman et al.⁴ leads us to believe that it might not be far from optimal. In addition, the similarity between an individual contribution to the regression coefficients and the contribution to the sample allele frequency adds credence to our hypothesis.

Tests on several other GWAS data sets yielded similar results. As expected, we also found that the performance depends on the homogeneity of the study participants. Population structure would need to be taken into account if the GWAS results included a heterogeneous cohort.

Although not presented here, we have seen that the $\hat{Y}$ has a larger magnitude for relatives of study participants than for the reference population. Thus, the method presented here should be applicable to determine whether relatives of the individual participated in the study, albeit with reduced power.

We have derived and applied our method to an additive model but extension to other models (recessive, dominant, etc.) should be straightforward.

It is interesting to note that by using only the signs of the regression coefficients, we still maintain a large portion of the discrimination power of the method. We have seen similar effects in other data sets. One practical implication of this finding is that reducing the number of decimals in the published regression coefficients would not be an effective method to protect privacy.

If p values and signs were available, then regression coefficients could be computed and our method would identify participants. If only the p values are available, the absolute values of the regression coefficients can be calculated. The sign statistic suggests that we might be able to guess the sign of the regression coefficient slightly more often than 50% of the times. This would in principle allow us to compute $\hat{Y}$. However, the power is likely to be substantially reduced.

It is worth noting that the ability to predict the phenotype using $\hat{Y}$ and to infer membership is not related to any real effect of genotype on phenotype. We have seen that the method works as well or better with simulated phenotypes. We note that genotypic information is being used to infer study membership and to reconstruct trait value used in the estimates of regression coefficients; no prediction of phenotypic status in new individuals is being done.

Sensitivity and specificity give us information on the probability of false positives or false negatives given the individual participated in the study. In many cases, it might be more relevant to look at false positive or negative rates provided the individual was positive or negative according to our testing method. These are represented by positive or negative predictive values. The positive predictive value can become very small if the prior probability of the individual participating in the study is very low. For example, if all we know about the individual is the person's gender, this probability could be as low as ${10}^{-5}$ or ${10}^{-6}$ (e.g., 1,000 participants out of 159 million male individuals from the USA). In this context, given that the individual was positive in the test, the false negative rate might still be very high. Naturally, because investigators have no control over how much prior information someone can come up with, this argument cannot be used to ignore the possible breach of confidentiality.

Results from massively parallel sequencing (in the form of low frequency or rare genetic variations) might enable increased power of identification. If results from multiple phenotypes are available, as would be the case if, for example, gene expression associations were also conducted (and accompanying results made available), the information from each phenotype can be combined to achieve much greater power as suggested by the results from combining just two phenotypes. Although the single-phenotype method has no power for individuals with an average phenotype, it is unlikely a person will have an average phenotype for all the phenotypes considered.

A recent study¹⁶ of temporal trends in the availability of results from GWAS classified published studies according to level of risk for potential misuse and highlights the ongoing importance of clearer guidelines on how “data products” can be appropriately shared.

With the increasing trend to collect and analyze multiple-omics data, the need to share large amounts of quantitative GWAS results becomes more urgent. In addition, given our finding that multiple phenotypes can be combined to increase the power to infer membership, protecting privacy by limiting the number of significant hits published is becoming less feasible.

Because fluid sharing of results among researchers for legitimate scientific use would be highly desirable, our study emphasizes the urgent need to devise protocols and methods that facilitate this process without compromising a participant's privacy.

One mechanism to address this problem would be to implement an annual certification process, which would grant the certified researcher unrestricted access to study results with the condition that the data could only be used for research goals that do not compromise the participants' privacy. A researcher who does not abide by these rules could be penalized by withdrawing further access to data.

Appendix A

Power Calculation

To compute power, we use the same assumptions as for the conditional mean and variance, i.e., that the number of markers is much larger than the number of individuals in the test sample and the number of individuals in the reference group: $M>>n>>1\text{and}M>>n^{\ast }>>1$. Hardy Weinberg equilibrium is assumed. Under these assumptions, it can be shown that $\hat{Y}$ converges to a normal variate with mean and variance given in Equation 2.

We define the null and alternative hypothesis as follows. Under the null hypothesis, the individual did not participate in the study (nor did any relatives of the individual), whereas under the alternative hypothesis, the individual did participate.

If the method uses the sign of the difference $Y_I-\mu$, and we assume that the difference is greater than 0, we will reject the null hypothesis if ${\hat{Y}}_I$ is greater than $z_{\alpha }\sigma \sqrt{n/M}$, where α is the type I error and $z_{\alpha }$ is the $\left(1-\alpha \right)$ quantile of the normal distribution. The power will be given by the probability under the alternative that ${\hat{Y}}_I>z_{\alpha }\sigma \sqrt{n/M}$

$$\begin{array}{c}power=P_{in}\left({\hat{Y}}_I>z_{\alpha }\sigma \sqrt{\frac{n}{M}}\right)\\ =1-\Phi \left(\frac{z_{\alpha }\sigma \sqrt{\frac{n}{M}}-\left(Y_I-\mu \right)}{\sigma \sqrt{\frac{n}{M}}}\right)\end{array}$$ (Equation 8)

$$=1-\Phi \left(z_{\alpha }-\frac{Y_I-\mu }{\sigma }\sqrt{\frac{M}{n}}\right)$$ (Equation 9)

$$=\Phi \left(\frac{Y_I-\mu }{\sigma }\sqrt{\frac{M}{n}}-z_{\alpha }\right)$$ (Equation 10)

where in Equation (8) we have used the fact that ${\hat{Y}}_I$ is normally distributed with mean $Y_I-\mu$ and variance ${\sigma }^{2}n/M$ and in Equation (10) we have used the property of the normal CDF $\Phi \left(x\right)=1-\Phi \left(-x\right)$.

If $Y_I-\mu <0$, similar arguments will give

$$power=\Phi \left(\frac{-\left(Y_I-\mu \right)}{\sigma }\sqrt{\frac{M}{n}}-z_{\alpha }\right).$$

Thus more generally we have

$$power=\Phi \left(\frac{\left|Y_I-\mu \right|}{\sigma }\sqrt{\frac{M}{n}}-z_{\alpha }\right).$$ (Equation 11)

If the sign of the difference $Y_I-\mu$ is not used, the rejection region will be defined as $\left|{\hat{Y}}_I\right|>z_{\alpha /2}\sigma \sqrt{n/M}$. The alternative distribution will be an equally weighted mixture of normal distributions with means $\left|Y_I-\mu \right|$ and $-\left|Y_I-\mu \right|$. Note that any weight other than 1/2 would mean that we have information on whether it is more likely that the sign is positive or negative. For example, if we knew it was more likely to be positive, then we would give higher weight to the normal distribution with mean $\left|Y_I-\mu \right|$. The power when we do not make use of the sign of $\left|Y_I-\mu \right|$ is given by

$$\begin{array}{c}power=P_{in}\left(\left|{\hat{Y}}_I\right|>z_{\alpha /2}\sigma \sqrt{\frac{n}{M}}\right)\\ =P_{in}\left({\hat{Y}}_I>z_{\alpha /2}\sigma \sqrt{\frac{n}{M}}\right)+P_{in}\left({\hat{Y}}_I<-z_{\alpha /2}\sigma \sqrt{\frac{n}{M}}\right)\end{array}$$ (Equation 12)

$$=\frac{1}{2}\left(1-\Phi \left(\frac{z_{\alpha /2}\sigma \sqrt{\frac{n}{M}}-\left|Y_I-\mu \right|}{\sigma \sqrt{\frac{n}{M}}}\right)\right)+\frac{1}{2}\Phi \left(\frac{-z_{\alpha /2}\sigma \sqrt{\frac{n}{M}}+\left|Y_I-\mu \right|}{\sigma \sqrt{\frac{n}{M}}}\right)$$ (Equation 13)

$$=\frac{1}{2}\Phi \left(\frac{-z_{\alpha /2}\sigma \sqrt{\frac{n}{M}}+\left|Y_I-\mu \right|}{\sigma \sqrt{\frac{n}{M}}}\right)+\frac{1}{2}\Phi \left(\frac{-z_{\alpha /2}\sigma \sqrt{\frac{n}{M}}+\left|Y_I-\mu \right|}{\sigma \sqrt{\frac{n}{M}}}\right)$$ (Equation 14)

$$=\Phi \left(\frac{\left|Y_I-\mu \right|}{\sigma }\sqrt{\frac{M}{n}}-z_{\alpha /2}\right).$$ (Equation 15)