Abstract
Multi-shot spiral imaging is a promising alternative to echo-planar imaging for high-resolution diffusion-weighted imaging and diffusion tensor imaging. However, subject motion in the presence of diffusion-weighting gradients causes phase inconsistencies among different shots, resulting in signal loss and aliasing artifacts in the reconstructed images. Such artifacts can be reduced by using a variable-density spiral trajectory or a navigator echo, however at the cost of a longer scan time. Here, a novel iterative phase correction method is proposed to inherently correct for the motion-induced phase errors without requiring any additional scan time. In this initial study, numerical simulations and in vivo experiments are performed to demonstrate that the proposed method can effectively and efficiently correct for spatially linear phase errors caused by rigid-body motion in multi-shot spiral diffusion-weighted imaging of the human brain.
Keywords: inherent, motion correction, multi-shot, spiral, diffusion-weighted imaging
Introduction
Spiral imaging has emerged as a promising alternative to echo-planar imaging for diffusion-weighted imaging (DWI) and diffusion tensor imaging (DTI), because of its more efficient k-space coverage, higher signal-to-noise ratio (SNR), and lower sensitivity to flow artifacts (1–6). Multi-shot spiral trajectories are typically used to achieve a high spatial resolution, while maintaining a short readout duration to reduce the blurring due to off-resonance effects and T2 relaxation. However, subject motion in the presence of diffusion-weighting gradients causes phase errors that vary from shot to shot. In particular, rigid-body motion (e.g., bulk head motion) causes spatially linear phase errors (7), whereas nonrigid motion (e.g., pulsatile brain motion during the cardiac cycle) causes spatially nonlinear phase errors (8). These phase inconsistencies among different shots result in signal loss and aliasing artifacts in the reconstructed images, which in turn lead to errors in DWI and DTI metrics, such as the apparent diffusion coefficient (ADC) or fractional anisotropy, as well as in fiber tractography.
A variable-density spiral trajectory oversampling the central k-space is typically used to generate a low-resolution estimate of the motion-induced phase error for each shot and to correct for the resulting artifacts (1–5). However, to ensure a sufficient oversampling, the readout duration is increased by up to 70% (2), at the cost of more severe off-resonance effects, or the number of shots is nearly doubled to maintain the same readout duration, at the cost of a substantially longer scan time, which can be impractical for pediatric and patient populations or when many diffusion-weighting directions are used (9). Alternatively, a low-resolution single-shot spiral navigator echo can be acquired by adding a second 180° refocusing pulse to the spin-echo sequence to estimate the motion-induced phase error for each shot, but also results in a longer scan time (6).
Here, we propose a novel iterative phase correction method for multi-shot spiral DWI and DTI that can inherently correct for the motion-induced phase errors without requiring a variable-density spiral trajectory or a navigator echo, and hence without increasing the scan time. In this initial implementation, we apply this method to correct for spatially linear phase errors caused by rigid-body motion in multi-shot spiral DWI of the human brain.
Theory
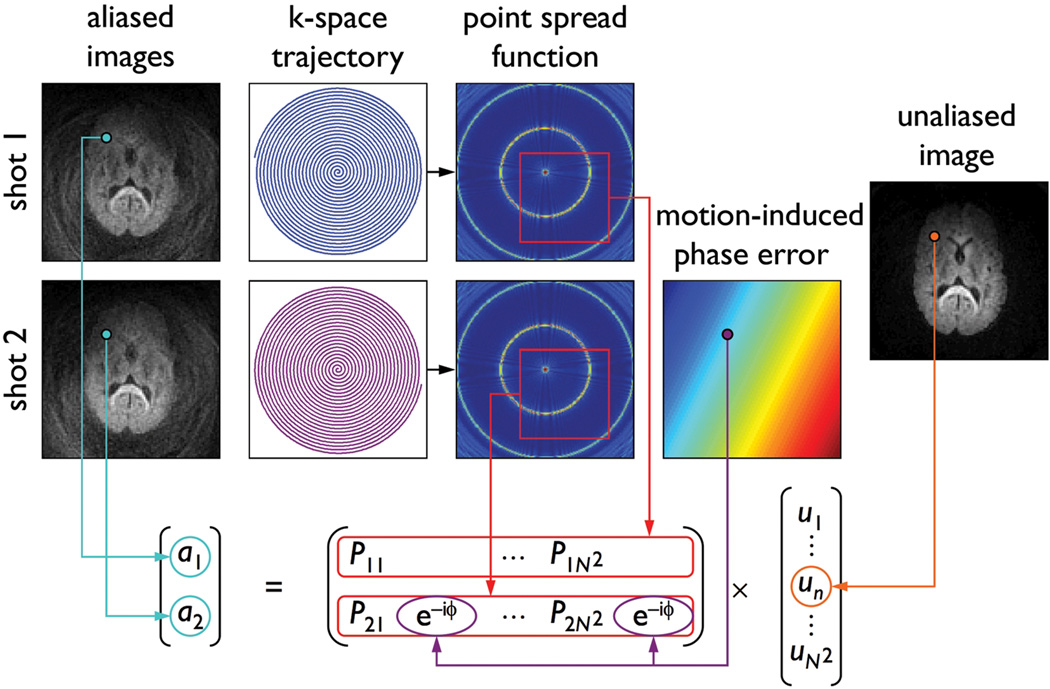
For simplicity, we consider a two-shot spiral acquisition, but the proposed method can also be extended to multi-shot spiral acquisitions with more than two shots. We first propose a new theoretical framework relating the two aliased images obtained by reconstructing the k-space data from each shot separately (by zero-filling the missing data from the other shot), the point spread function (PSF) computed from the k-space trajectory, the motion-induced phase error between the two shots, and the unaliased image to be reconstructed (Fig. 1). For each pixel (x0, y0) of an N×N image, this relationship can be expressed as:
| [1] |
where a is a 2×1 array containing the pixel values from the aliased images, u is a N2×1 array whose (x0, y0)th element contains the pixel value from the unaliased image, and E is a 2×N2 matrix whose rows contain the values from the following N×N subsets of the PSF:
| [2] |
FIG. 1.
Schematic diagram showing the relationship among the aliased images reconstructed from each shot, the spiral k-space trajectory, the PSF, the motion-induced phase error between the two shots, and the unaliased image to be reconstructed.
For each shot m, the PSF is computed as follows:
| [3] |
where DCF is the density compensation function (10) and (kx, ky) is the spiral k-space trajectory. In the presence of motion, each element in the second row of E is multiplied by an additional phase term exp[−iϕ(x0, y0)], where ϕ is the motion-induced phase error between the two shots. Thus, if ϕ is known (e.g., from a navigator echo), the unaliased image can be determined by solving Eq. [1] for each pixel (x0, y0).
However, since ϕ is generally unknown, we propose a novel iterative phase correction method, which consists in reconstructing a series of images by solving Eq. [1] with different ϕ values and choosing the image with the least amount of aliasing. In this initial implementation, we assume that ϕ is spatially linear:
| [4] |
and step through different ϕo, gx, and gy values, where ϕo is a global phase offset caused by translational motion, whereas gx and gy are linear phase gradients caused by rotational motion (7). This model is therefore sufficient to correct for spatially linear phase errors caused by rigid-body motion, but can also be extended to correct for spatially nonlinear phase errors caused by nonrigid motion. Note that the phase varies from shot to shot, but is assumed to remain constant within each readout window.
Among all images reconstructed with different ϕ values, the image with the least amount of aliasing is then chosen as the one that has the lowest background energy, which is defined as the sum of the signal intensity in all pixels contained in the background. The background region is determined by thresholding a corresponding non-diffusion-weighted image, which is not affected by motion-induced phase errors and is always acquired in DWI or DTI along with the diffusion-weighted images.
Because reconstructing a series of images with all possible ϕ values would be very time-consuming, we propose three strategies to drastically reduce the computation time. First, the phase optimization is performed by reconstructing low-resolution images from the central k-space, rather than high-resolution images from the full k-space, with different ϕ values. Once the ϕ value yielding the minimum background energy among these low-resolution images has been determined, the final image is then reconstructed at full resolution with this value.
Second, the phase optimization is performed iteratively, by starting with a large step size for the ϕo, gx, and gy values. Once an estimate for these parameters has been found, this procedure is repeated with a step size reduced by half and a smaller range centered on these estimates until the background energy reaches the noise level.
Third, the phase optimization is performed by solving Eq. [1] only for the background pixels, since only those pixels contribute to the background energy. Once the ϕ value yielding the minimum background energy has been determined, the final image is then reconstructed in all pixels with this value.
Methods
Simulations
We first performed numerical simulations to validate the proposed method. Specifically, a non-diffusion-weighted two-shot spiral image, acquired as described below and unaffected by motion artifacts, was used as a reference image. The corresponding k-space data from each shot were reconstructed separately, resulting in two aliased images, and a spatially linear phase was added to the second image to simulate a motion-induced phase error. This phase was randomly chosen such that |ϕ 0| ≤ π, |gx| ≤ π (in m−1), and |gy| ≤ π (in m−1), which includes the range of motion-induced phase errors measured experimentally. The iterative phase correction was then applied to these simulated data and the normalized root mean square error (NRMSE) between the reference image and the corrected image was computed to quantitatively assess the performance of the proposed method. This procedure was repeated for ten different random phase errors and for different slices across the entire brain.
In addition, to validate the first two strategies proposed for reducing the computation time and to determine the optimal parameters, the iterative phase correction was performed with four different spatial resolutions and five different iteration schemes (see Table 1). The third strategy was always used, because identical results are obtained whether Eq. [1] is solved for all pixels or only for the background pixels, since only the latter contribute to the background energy. Finally, to assess the sensitivity of the proposed method to noise, simulations were also performed with Gaussian noise added to the simulated data with an SNR of 10, 20, or 30, which includes the range of values measured experimentally in the diffusion-weighted images (typically 15).
Table 1.
Computation time of the iterative phase correction performed with different spatial resolutions (rows) and iteration schemes (columns) and by solving Eq. [1] only for the background pixels
| π/16 (a) | π/8 | π/4 | π/2 | π | |
|---|---|---|---|---|---|
| 1 (b) | 2 | 3 | 4 | 5 | |
| 96×96 | 6.5 days | 22 h | 3.5 h | 55 min | 36 min |
| 48×48 | 11 h | 1.6 h | 15 min | 3.9 min | 2.6 min |
| 24×24 | 1.1 h | 9.1 min | 1.4 min | 23 s | 15 s |
| 12×12 | 10 min | 1.4 min | 13 s | 3.6 s | 2.4 s |
initial step size,
number of iterations
Experiments
We studied three healthy volunteers, who provided written informed consent as approved by our Institutional Review Board, on a 3T HD MRI scanner (GE Healthcare, Milwaukee, WI) equipped with an eight-channel phased-array head coil and a gradient system with 40 mT/m maximum amplitude and 150 T/m/s slew rate. Foam padding was used to restrain the head within the coil and the subjects were instructed to remain still. High-order shimming was applied to minimize the global B0 inhomogeneity.
Axial DWI images of the brain were acquired with a spin-echo spiral imaging pulse sequence and the following parameters: repetition time = 5 s, echo time = 56 ms, field of view = 24×24 cm, matrix size = 96×96, slice thickness = 2.5 mm, and number of slices = 20. The k-space trajectory was a two-shot constant-density spiral-out trajectory with a readout duration of 21.5 ms (11). One image volume was acquired without diffusion-weighting and three image volumes were acquired with diffusion-weighting gradients successively applied along the x, y, and z axes with the following parameters: amplitude = 39.4 mT/m, duration (δ) = 20.5 ms, separation (Δ) = 27.2 ms, and b-factor = 1000 s/mm2.
In this initial implementation, the iterative phase correction was only used to correct for rigid-body motion. While pulsatile motion artifacts can be minimized with cardiac gating (3,4,6), we used a slightly different, but equivalent, approach in this proof-of-concept study, because it did not require any pulse sequence modification. Specifically, ten DWI datasets (each consisting of one non-diffusion-weighted and three diffusion-weighted image volumes) were successively acquired during a 6:40 min scan, while the cardiac waveform was simultaneously recorded with a finger pulse oximeter (BIOPAC Systems Inc., Goleta, CA) and the CIGAL software (12). The delay between the acquisition of each shot and the preceding peak in the cardiac waveform was then computed and a pair of shots that were acquired at exactly the same delay was selected for each slice and each diffusion-weighting direction to generate a new DWI dataset, while the remaining data were discarded.
The iterative phase correction was applied to this dataset with the optimal parameters determined from the simulations. Residual blurring artifacts caused by susceptibility effects near air/tissue interfaces and time-varying eddy currents induced by the diffusion-weighting gradients were corrected with a dynamic B0 mapping and off-resonance correction method (13). ADC maps were computed from the two-shot spiral DWI data and from single-shot spiral DWI data acquired with the same parameters (except for the readout duration), which are not affected by motion-induced phase errors. ADC values were then compared in 3×3 regions-of-interest (ROIs) randomly chosen across the entire brain. All image reconstruction and post-processing were performed in Matlab (The MathWorks, Natick, MA).
Results
Simulations
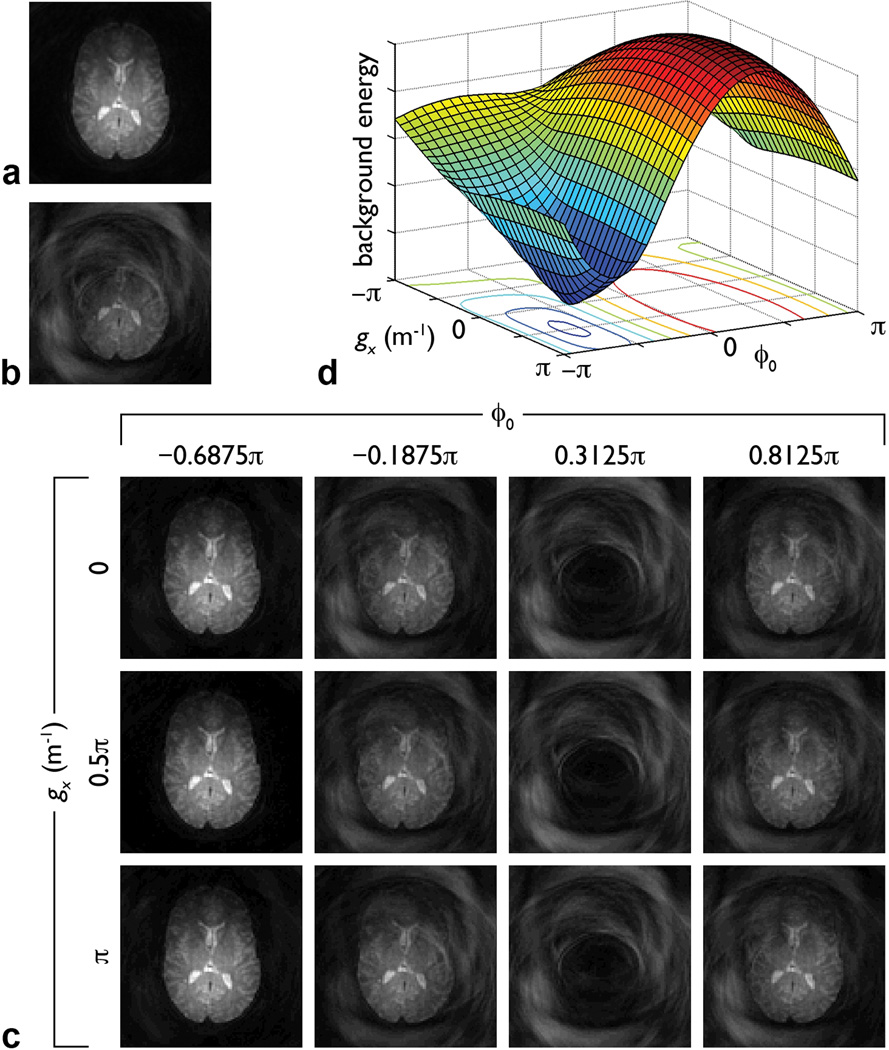
Representative results are shown in Fig. 2. As expected, the reference image has no motion artifacts (Fig. 2a), whereas the image simulated by adding a random spatially linear phase error suffers from severe signal loss and aliasing artifacts (Fig. 2b). Images reconstructed from the simulated data with different ϕo, gx, and gy values and a step size of π/16 (a subset of which are shown Fig. 2c) have highly variable patterns of aliasing artifacts. Among all of these images, the background energy reaches a global minimum for ϕo = −0.6875π, gx = 0.5π m−1, and gy = 0.6875π m−1 (Fig. 2d). These values are identical (within half the step size) to those used to generate the simulated image and the corresponding image in Fig. 2c (i.e., the one identified by the proposed method) is virtually identical to the reference image (NRMSE = 1.37×10−4).
FIG. 2.
a: Non-diffusion-weighted two-shot spiral image. b: Image simulated by separately reconstructing each shot of image (a), adding a random spatially linear phase to the second image (with ϕo = −0.6848π, gx = 0.5025π m−1, and gy = 0.6814π m−1), and summing the two resulting images. c: Images subsequently reconstructed from these simulated data with different ϕo and gx values and a fixed gy value of 0.6875π m−1. All images in (a–c) have the same scaling. d: Background energy (in arbitrary units) in images (c) and similar images reconstructed with other ϕo and gx values (with a step size of π/16) and the same gy value. The image with the least artifacts in (c) and the minimum background energy in (d) both correspond to ϕo = −0.6875π and gx = 0.5π m−1. The gy value used in (c–d) is the optimal value determined from the iterative phase correction. Similar results are obtained when using the optimal ϕo or gx value, while varying the other two parameters.
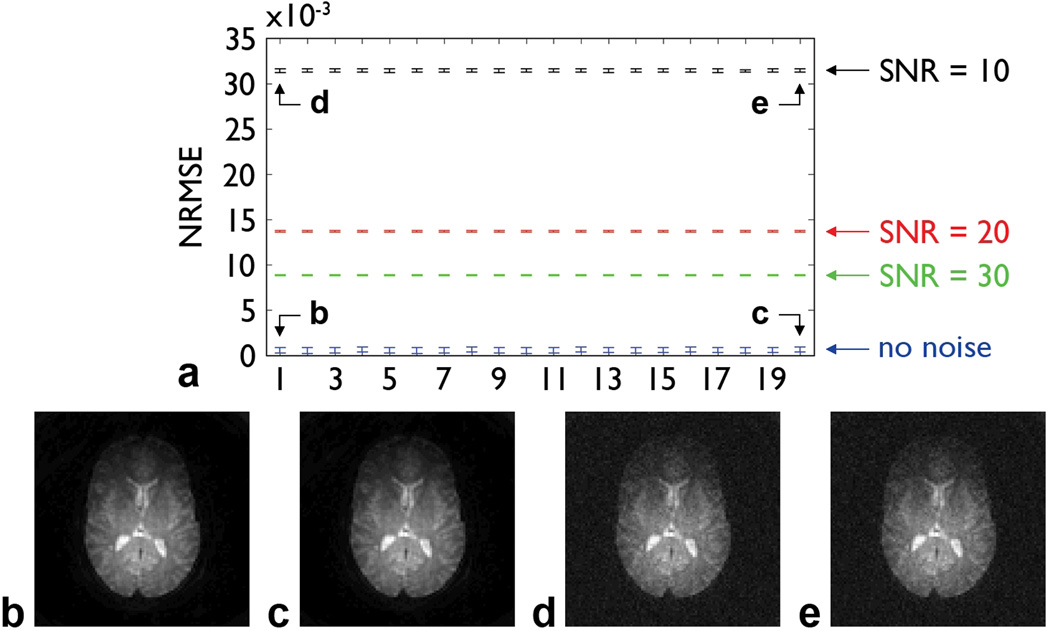
The results of simulations performed with different random phase errors, slices, spatial resolutions, iteration schemes, and SNRs are summarized in Fig. 3. Virtually identical NRMSEs (Fig. 3a) and images (e.g., Figs. 3b,c) are obtained for all phase errors, spatial resolutions, and iteration schemes tested. As expected, the NRMSE increases as the SNR decreases, but the iterative phase correction can still effectively correct for the signal loss and aliasing artifacts for all SNRs tested (e.g., Figs. 3d,e). Altogether, these results validate the proposed method, including the first two strategies proposed for reducing the computation time, and demonstrate that its performance is not sensitive to the choice of parameters or to noise.
FIG. 3.
a: NRMSE (mean ± standard deviation) between each reference image and the images simulated by adding different random spatially linear phase errors (and optionally noise) and subsequently corrected with different spatial resolutions and iteration schemes (shown on the horizontal axis in the same order as in Table 1 from left to right and from top to bottom). b: Fig. 2b corrected with a resolution of 96×96, an initial step size of π/16, and one iteration. c: Fig. 2b corrected with a resolution of 12×12, an initial step size of π, and five iterations. d: Fig. 2b with added noise (SNR = 10) and corrected with a resolution of 96×96, an initial step size of π/16, and one iteration. e: Fig. 2b with added noise (SNR = 10) and corrected with a resolution of 12×12, an initial step size of π, and five iterations.
By performing the phase optimization at a resolution of 12×12 instead of 96×96, by using five iterations with a variable step size instead of a single iteration, and by solving Eq. [1] only for the background pixels, the computation time can be reduced by a factor 915, 260, and 2, respectively, from 13 days to only 2.4 s, without affecting the accuracy of the results (Table 1). For comparison, the reconstruction time for a single-shot spiral image performed with gridding and fast Fourier transform is 0.15 s. In this work, each image was reconstructed in parallel on a Linux cluster, so that the total computation time is identical to that of a single image.
Experiments
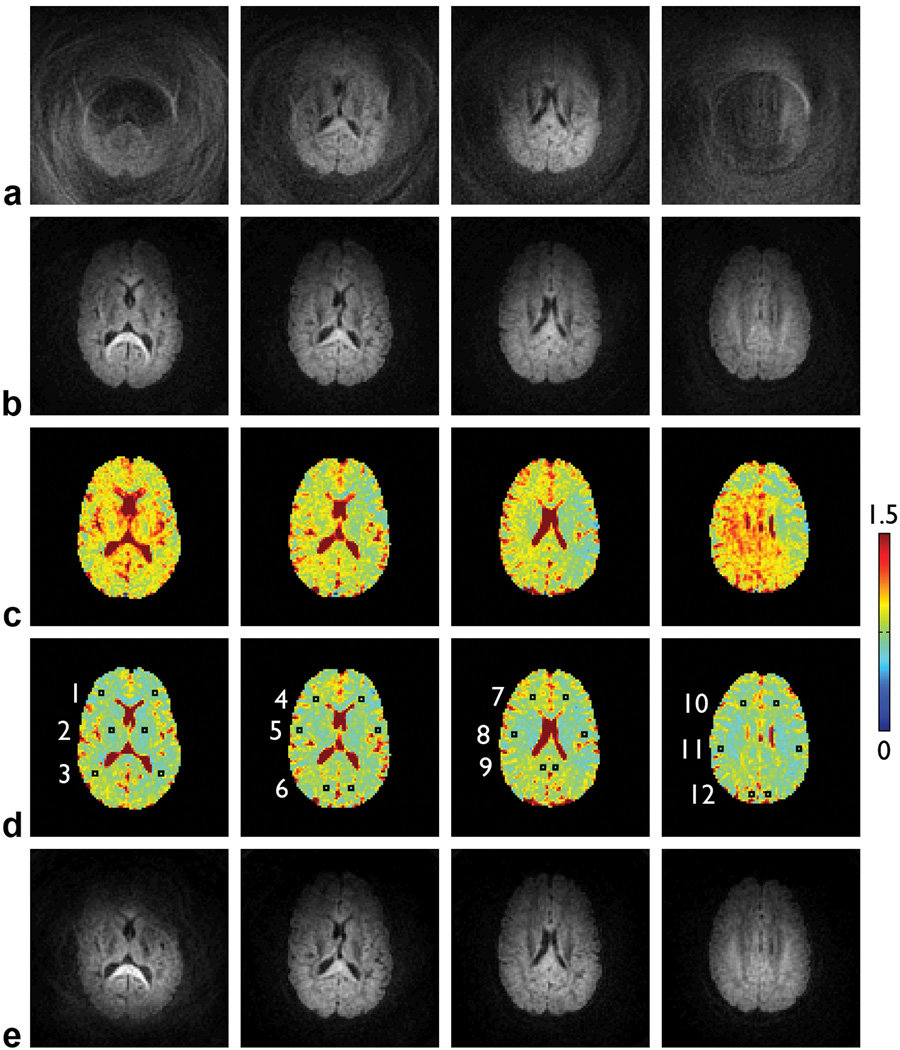
Representative results are shown in Fig. 4. Even though the subjects were instructed to remain still and their head was restrained with padding, residual motion still causes extensive signal loss and aliasing artifacts in the diffusion-weighted images (Fig. 4a). This signal loss therefore leads to an overestimation of the ADC values (Fig. 4c). The iterative phase correction can effectively correct for these artifacts and significantly improve the image quality (Fig. 4b). The resulting ADC values in representative ROIs (Fig. 4d) are identical to those derived from single-shot DWI data acquired with the same parameters, which are not affected by motion-induced phase errors (Table 2). Similar results are obtained across the entire brain. These results thus further validate the proposed method experimentally. Note that when applying this method to diffusion-weighted images reconstructed from two consecutive shots (i.e., irrespective of the cardiac cycle), the artifacts can still be largely reduced, but there remain residual artifacts caused by nonlinear phase errors (Fig. 4e).
FIG. 4.
Two-shot spiral diffusion-weighted images in four representative slices: uncorrected (a) and corrected with a spatial resolution of 12×12, an initial step size of π, and five iterations (b). ADC maps (in 10−3 mm2/s) derived from the uncorrected (c) and corrected (d) DWI data, overlaid with 12 bilateral ROIs (see Table 2). e: Two-shot spiral diffusion-weighted images reconstructed from two consecutive shots (i.e., irrespective of the cardiac cycle) and corrected with the same parameters as in (b). All images in (a,b,e) have the same scaling.
Table 2.
| ROI | two-shot spiral DWI (uncorrected) |
two-shot spiral DWI (corrected) |
single-shot spiral DWI (uncorrected) |
|---|---|---|---|
| 1 | 0.91 ± 0.09 | 0.77 ± 0.08 | 0.77 ± 0.11 |
| 2 | 0.89 ± 0.07 | 0.66 ± 0.05 | 0.66 ± 0.08 |
| 3 | 0.92 ± 0.11 | 0.77 ± 0.11 | 0.77 ± 0.07 |
| 4 | 0.79 ± 0.08 | 0.74 ± 0.06 | 0.76 ± 0.08 |
| 5 | 0.76 ± 0.09 | 0.68 ± 0.06 | 0.70 ± 0.11 |
| 6 | 0.83 ± 0.08 | 0.75 ± 0.07 | 0.75 ± 0.09 |
| 7 | 0.84 ± 0.05 | 0.77 ± 0.05 | 0.75 ± 0.07 |
| 8 | 0.80 ± 0.11 | 0.71 ± 0.08 | 0.70 ± 0.08 |
| 9 | 0.78 ± 0.06 | 0.74 ± 0.05 | 0.73 ± 0.08 |
| 10 | 0.80 ± 0.09 | 0.74 ± 0.05 | 0.74 ± 0.05 |
| 11 | 0.83 ± 0.14 | 0.67 ± 0.09 | 0.67 ± 0.08 |
| 12 | 0.98 ± 0.08 | 0.79 ± 0.11 | 0.78 ± 0.13 |
All differences between the ADC values derived from the uncorrected and corrected two-shot spiral DWI data are statistically significant (two-tailed t-test, P < 0.05), whereas all differences between the ADC values derived from the corrected two-shot and uncorrected single-shot spiral DWI data are not.
Discussion and Conclusions
The numerical simulations and in vivo experiments performed in this study demonstrate that the proposed iterative phase correction method can inherently and effectively correct for the spatially linear phase errors, as well as the resulting signal loss and aliasing artifacts, caused by rigid-body motion in multi-shot spiral DWI of the human brain. This method does not require any additional scan time and is therefore more efficient than alternative methods based on a variable-density spiral trajectory or a navigator echo (1–6). A similar method was previously proposed to correct for rigid-body motion in multi-shot echo-planar DWI (14).
Here, we discuss a few limitations of this proof-of-concept study as well as possible extensions of the proposed method to address them. First, this initial implementation is only applicable to two-shot spiral acquisitions, but can be extended to M-shot spiral acquisitions by using an M×1 array a and an M×N2 matrix E, where the 2nd to Mth rows of E each contain a different motion-induced phase term. Second, this initial implementation only corrects for spatially linear phase errors caused by rigid-body motion, but can also be extended to correct for spatially nonlinear phase errors caused by nonrigid motion.
Both of these extensions are theoretically straightforward, but may be limited by a long computation time in practice. However, the proposed method can be combined with parallel imaging and off-resonance correction methods to achieve a high spatial resolution and spatial fidelity, while maintaining a limited number of shots. In addition, the computation time may be further reduced by using faster algorithms, such as gradient search methods, for the background energy minimization and by combining the iterative phase correction with a variable-density spiral acquisition to obtain an initial estimate of the motion-induced phase error from the oversampled central k-space. Importantly, since only an estimate rather than an accurate measurement of the phase error is needed, the amount of oversampling would not have to be as large as when a variable-density spiral acquisition is used alone for the motion correction (1–5), resulting in a smaller increase in scan time. Nevertheless, further work is needed to investigate whether or not the proposed method can be extended to M-shot spiral acquisitions and to the correction of spatially nonlinear phase errors with a reasonable computation time.
As for other two-dimensional motion correction methods (1–4), the proposed method can correct for in-plane motion, but not for through-plane motion. Furthermore, as for other retrospective motion correction methods (1–6), it cannot correct for severe misregistration among different shots caused by gross subject motion from uncooperative subjects. Such errors need to be addressed with other approaches, such as prospective motion correction methods. Finally, the proposed method can be used as long as a background region is available to compute the background energy, which is always the case for whole-brain imaging, but not necessarily for applications using outer volume suppression or inner volume imaging, where the sample may occupy the entire field-of-view.
In conclusion, we have developed a novel iterative phase correction method for multi-shot spiral DWI and DTI that can inherently correct for motion-induced phase errors without increasing the scan time. This method should be particularly useful for high-resolution DWI and DTI studies in pediatric or patient populations who cannot tolerate long scan times.
Acknowledgments
We thank Susan Music for her assistance with MRI scanning. This work was, in part, supported by grants NS41328, NS65344, EB09483, and EB12586 from the National Institutes of Health.
References
- 1.Liu C, Bammer R, Kim D-H, Moseley ME. Self-navigated interleaved spiral (SNAILS): Application to high-resolution diffusion tensor imaging. Magn Reson Med. 2004;52:1388–1396. doi: 10.1002/mrm.20288. [DOI] [PubMed] [Google Scholar]
- 2.Li T-Q, Kim D-H, Moseley ME. High-resolution diffusion-weighted imaging with interleaved variable-density spiral acquisitions. J Magn Reson Imaging. 2005;21:468–475. doi: 10.1002/jmri.20287. [DOI] [PubMed] [Google Scholar]
- 3.Van AT, Karampinos DC, Georgiadis JG, Sutton BP. K-space and image-space combination for motion-induced phase-error correction in self-navigated multicoil multi-shot DWI. IEEE Trans Med Imaging. 2009;28:1770–1780. doi: 10.1109/TMI.2009.2023212. [DOI] [PubMed] [Google Scholar]
- 4.Karampinos DC, Van AT, Olivero WC, Georgiadis JG, Sutton BP. High-resolution diffusion tensor imaging of the human pons with a reduced field-of-view, multishot, variable-density, spiral acquisition at 3T. Magn Reson Med. 2009;62:1007–1016. doi: 10.1002/mrm.22105. [DOI] [PubMed] [Google Scholar]
- 5.Frank LR, Jung Y, Inati S, Tyszka JM, Wong EC. High efficiency, low distortion 3D diffusion tensor imaging with variable density spiral fast spin echoes (3D DW VDS RARE) NeuroImage. 2010;49:1510–1523. doi: 10.1016/j.neuroimage.2009.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Van AT, Hernando D, Sutton BP. Motion-induced phase error estimation and correction in 3D diffusion tensor imaging. IEEE Trans Med Imaging. 2011 doi: 10.1109/TMI.2011.2158654. (in press). [DOI] [PubMed] [Google Scholar]
- 7.Anderson AW, Gore JC. Analysis and correction of motion artifacts in diffusion weighted imaging. Magn Reson Med. 1994;32:379–387. doi: 10.1002/mrm.1910320313. [DOI] [PubMed] [Google Scholar]
- 8.Miller KL, Pauly JM. Nonlinear phase correction for navigated diffusion imaging. Magn Reson Med. 2003;50:343–353. doi: 10.1002/mrm.10531. [DOI] [PubMed] [Google Scholar]
- 9.Frank LR. Anisotropy in high angular resolution diffusion-weighted MRI. Magn Reson Med. 2001;45:935–939. doi: 10.1002/mrm.1125. [DOI] [PubMed] [Google Scholar]
- 10.Meyer CH, Hu BS, Nishimura DG, Macovski A. Fast spiral coronary artery imaging. Magn Reson Med. 1992;28:202–213. doi: 10.1002/mrm.1910280204. [DOI] [PubMed] [Google Scholar]
- 11.Glover GH. Simple analytic spiral k-space algorithm. Magn Reson Med. 1999;42:412–415. doi: 10.1002/(sici)1522-2594(199908)42:2<412::aid-mrm25>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- 12.Voyvodic JT. Real-time fMRI paradigm control, physiology, and behavior combined with near real-time statistical analysis. NeuroImage. 1999;10:91–106. doi: 10.1006/nimg.1999.0457. [DOI] [PubMed] [Google Scholar]
- 13.Truong TK, Chen NK, Song AW. Dynamic correction of artifacts due to susceptibility effects and time-varying eddy currents in diffusion tensor imaging. NeuroImage. 2011;57:1343–1347. doi: 10.1016/j.neuroimage.2011.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Robson MD, Anderson AW, Gore JC. Diffusion-weighted multiple shot echo planar imaging of humans without navigation. Magn Reson Med. 1997;38:82–88. doi: 10.1002/mrm.1910380113. [DOI] [PubMed] [Google Scholar]