Identifying multidrug resistant tuberculosis transmission hotspots using routinely collected data

SUMMARY

In most countries with large drug resistant tuberculosis epidemics, only those cases that are at highest risk of having MDRTB receive a drug sensitivity test (DST) at the time of diagnosis. Because of this prioritized testing, identification of MDRTB transmission hotspots in communities where TB cases do not receive DST is challenging, as any observed aggregation of MDRTB may reflect systematic differences in how testing is distributed in communities. We introduce a new disease mapping method, which estimates this missing information through probability–weighted locations, to identify geographic areas of increased risk of MDRTB transmission. We apply this method to routinely collected data from two districts in Lima, Peru over three consecutive years. This method identifies an area in the eastern part of Lima where previously untreated cases have increased risk of MDRTB. This may indicate an area of increased transmission of drug resistant disease, a finding that may otherwise have been missed by routine analysis of programmatic data. The risk of MDR among retreatment cases is also highest in these probable transmission hotspots, though a high level of MDR among retreatment cases is present throughout the study area. Identifying potential multidrug resistant tuberculosis (MDRTB) transmission hotspots may allow for targeted investigation and deployment of resources.

INTRODUCTION

In 2010, approximately 650,000 of the twelve million prevalent cases of tuberculosis had multidrug resistant disease (MDRTB: resistance to at least isoniazid and rifampin) [1]. The worldwide burden of MDRTB, coupled with reports of increasingly drug-resistant disease outbreaks (e.g. extensively drug resistant TB, XDRTB: defined as MDR plus additional resistance to a fluoroquinolone and capreomycin, amikacin, or kanamycin) [2], raise concern that drug resistance might undermine control [3]. Many countries with the heaviest burden of TB have witnessed a rise in the absolute incidence of MDRTB; this rise is most disturbing where the rate of increase in MDRTB incidence exceeds that of drug sensitive TB [4].

Peru is one such setting. Since 1996, data indicate the average absolute rate of increase of MDR incidence was 4.5% per year, while overall TB incidence was decreasing at 3.7% per year [4]. The reasons for the continued increase of MDRTB in the context of a declining TB epidemic are not clear. While the precise contributions of acquired and transmitted drug resistance are not easily quantified, recent analysis suggests that the onward transmission of MDRTB from infectious source cases may play an important role in Lima’s current situation. A recent study that compared the relative spatial aggregation of the home locations of treatment-naïve patients based on drug-resistance phenotype found that those with documented MDRTB were more aggregated than those without MDRTB at a scale of approximately 4 to 7 kilometers [5]. Based on those findings, we propose that identification of specific geographic areas where there is a high risk of transmitted MDRTB (i.e. MDR transmission “hotspots”) may inform focused confirmatory studies and the deployment of additional resources (e.g. wider coverage and use of rapid drug resistance testing, more rapid access to second-line drugs, and improved infection control) to confront this threat.

Identifying MDR transmission hotspots in communities where all individuals with TB do not receive drug sensitivity testing (DST) is challenging. In most countries with sizable drug resistant TB epidemics, only cases at highest probability of having MDRTB or doing poorly if infected will receive a DST at the time of diagnosis. For example, in Peru, previous guidelines specified routine drug sensitivity testing at the time of diagnosis among risk groups (e.g. individuals with known MDRTB contacts, prior TB treatment, or coinfection with HIV). Selective use of DST is efficient because those tested are at highest risk of MDRTB [6]. Yet since testing is 1) not done on all incident cases and 2) not done on a representative sample of cases, cluster detection methods do not allow inference from programmatic data about the levels of resistance or locations of MDRTB transmission.

We apply a new disease mapping approach to identify areas of increased MDRTB transmission risk using routinely collected data in two districts of Lima over three consecutive years. We demonstrate the use of programmatic data to generate maps identifying areas where there is a higher-than-expected-probability of MDR disease among incident cases of TB.

METHODS

Study setting

Described further in another publication [5], our study population includes 11,711 patients diagnosed with tuberculosis in two of the four health districts in Lima, Peru between January 1, 2005 and December 31, 2007. TB cases notified to the Peruvian National Tuberculosis Program within Lima Ciudad and several spatially contiguous health center catchment areas of Lima Este were included. Clinical and demographic data were collected retrospectively from TB registration records at 57 health centers. Laboratory information (i.e. drug sensitivity test results) was obtained from a web-based laboratory information system. Using home address data from medical records, study workers identified precise patient home locations on high-resolution Google Earth maps. IRB approval was obtained from the National Institute of Health in Peru and the Partners HealthCare System in the United States.

Of the 11,711 TB cases in our study, there were 376 DST confirmed MDRTB cases. We excluded 134 TB cases from this analysis because previous treatment status was not recorded, leaving a total of 11,577 TB cases, of which 368 have DST confirmed MDRTB.

Drug resistance testing

District reference laboratories of Lima Ciudad and Lima Este and the national reference laboratory (Instituto Nacional de Salud) performed DSTs by standard methods described previously [5].

Peruvian guidelines required drug sensitivity testing (DST) of patients at increased risk of MDRTB or when first-line treatment fails [7]; accordingly, drug sensitivity is confirmed only among a subset of patients. In the following subsection we describe our methods to detect resistance hotspots where drug sensitivity testing was performed only among a non-random sample.

In the three-year study period, 10.14% of the 11,577 TB cases received a DST. Among the 552 previously untreated TB cases that received DST, MDR was detected in 118 cases (21.38% prevalence). Among the 622 retreatment TB cases that received DST, MDR was detected in 250 cases (40.19% prevalence).

A TB drug resistance survey conducted in the same time frame and area of Lima [8] collected a representative sample of cases and produced estimates of the proportion MDRTB among previously untreated cases of 5.23% and among retreatment cases of 24.22%. Comparison of the survey estimates to those measured in the programmatic data reveal that routinely collected DSTs were done preferentially among individuals at increased risk of MDR.

Data description

We created maps of all notified TB cases in the study area using Google Maps (details in [5]). Our first analyses produced maps illustrating geographic risk of MDR for new and retreatment TB cases based on TB cases in whom DSTs were done. These maps represent the conditional risk of MDR for those tested through routine programmatic activities. Ideally, in order to locate MDR hotspots, we would also be able to map the risk of MDR among all new and retreatment TB cases throughout our study area (i.e. not conditional on having received a DST).

In a second set of analyses, we assume that all TB cases not receiving DSTs are not MDR; this allows us to generate maps showing risk of MDR among new and retreatment cases for all TB cases. However, this approach is naïve since many TB cases that do not receive DST through routine program activities have undetected MDR.

Based on the survey data, we expect 5.23% of 7962 patients without previous treatment would have MDR disease (417 previously untreated MDR cases) and that 24.22% of 3615 patients with prior TB treatment would have MDR (876 previously treated MDR cases). We note that routine, programmatic testing identified only 118 (28.29%) of the expected number of MDR cases without previous treatment and 250 (28.54%) of the expected number of previously treated MDR cases. These data are described in Table 1.

Table 1.

Summary of identified MDRTB cases and expected numbers of MDRTB cases for both previously untreated cases and cases with prior TB treatement.

	Total number of observed cases (a)	Estimated MDRTB prevalence (b)	Expected number of MDRTB cases (c=a*b)	Number of MDRTB cases identified (d)	Estimated number of unidentified MDRTB cases (c-d)
Previously untreated	7962	5.23%	417	118	299
Prior TB treatment	3615	24.22%	876	250	626

Since the majority of all expected MDR cases in the region were not identified by programmatic DST, for our third set of analyses, we reassigned the MDR status among those untested cases to generate simulated populations in which the total number of MDR cases among those with and without previous treatment reflected the survey estimates. We reassigned these untested cases in two different ways. First (as was done in [5]), we based MDR reassignment weights on the inverse probability of each untested case receiving DST at their given location. Using the inverse probability weights (IPW) to preferentially reassign untested TB cases located in regions of reduced testing reflects an assumption that in areas where testing was common, individuals most at risk were tested. As such, this method preferentially assigns those in areas where testing was less likely to MDRTB status. We calculated these reassignment probability weights separately for previously untreated and retreatment groups. This procedure, where we reassigned 626 untested retreatment cases and 299 untested new cases to MDRTB status (in order to match overall resistance levels reported in the survey), was repeated 1000 times to create 1000 augmented data sets. As a second approach, we reassigned these untested cases randomly without regard to the spatial variation in DST (i.e. without IPW weights), re-ran our disease mapping algorithms, and repeated this process 1000 times.

Disease Mapping

To examine the spatial variation of the risk of MDRTB in each of these maps, we use Jeffery’s disease mapping method [9] that identifies geographic areas where the incidence of “cases” differs significantly from the incidence of “controls”. We defined cases as individuals with MDRTB and controls as individuals with drug-sensitive TB. Jeffery’s method is used to examine the distances between the cases of MDRTB and fixed points located outside of the region of interest, and compares the distribution of these distances to a null distribution, representing the appropriate background population.

We compared the bivariate cumulative distribution functions (CDF) of the observed incident MDRTB cases, denoted F₁, to the expected CDF of the incident cases, under the null hypothesis of no association between location and MDR status, denoted F₀. Let x_i, i= 1…N, be the location of a TB case in the study region, containing N₁ MDRTB cases and N₀ non-MDRTB controls, such that N=N₁+N₀. For ease of notation, let x_i^* be the locations of the N₁ MDRTB cases. Let c_j, j= 1…M, be the location of a fixed point outside of the study region. Jeffery et al. show that F₁ can be estimated by F_1j, the cumulative distribution function of the distances between the N₁ MDRTB cases and c_j [9,10]. Denoting the Euclidean distance between any two points, x_i and c_j, as d(x_i,c_j), F_1j(d)=SUM_i(I(d(x_i^*,c_j) <= d)), where I(X)=1 if X is true and I(X)=0 otherwise. Similarly, we define F_0j as F_0j(d)=SUM_i(I(d(x_i,c_j) <= d)).

We quantify the comparison between the observed and expected distribution functions at any location in our study region, y, by examining the difference between F_1j and F_0j for a small set of distances around d(y,c_j), (d(y,c_j)−h/2, d(y,c_j)+h/2). We repeat these steps for several fixed points surrounding the study region and average the observed differences at each location y. We call this average difference at each location the score, which summarizes the spatial variability of the region.

Consider a large number of MDRTB cases located in a circular cluster of radius h/2, centered at a distance d from the fixed point c_j. When one examines F_1j, there will be a larger jump in the observed distribution function on the interval (d−h/2, d+h/2) than in the expected distribution function, calculated from the controls. This area, corresponding to a cluster of increased risk of MDRTB, will impact each individual F_1j calculated from all M fixed locations. Consequently, the marginal scores based on each fixed point will be large, and result in a large overall score for any location y in the cluster area, highlighting this location as an area of increased risk.

The null distribution is the distribution of distances one would expect if there were no association between location and MDR status; it is characterized by the distribution of the distances between all TB cases and those same fixed points located outside of the region. Essentially, this method will use a background population to determine how many cases are expected to be located at a given distance from a fixed point. We partition the study region into a 100×100 grid, and each cell in the grid is then given a score, similar to a risk difference. A relatively large score is indicative of more cases within that cell than expected. From these scores, we create color-coded maps that highlight areas with more cases than expected under the null distribution. An advantage of this mapping method is that it does not require the pre-specification of any potential hotspot locations, and can easily be modified to analyze weighted locations. We use this method to map the underlying risk of MDRTB among confirmed TB cases in the Ciudad and Este districts of Lima, Peru. For each augmented data set generated as described above, we calculate the Distance Based Mapping (DBM) scores based on the particular sample of cases. Once all 1000 sets of scores are calculated for each sample, a consensus map is obtained by plotting the average of the scores across all simulations.

To obtain the color scale, which is specific to the population distribution F₀, we calculate 100 permutations of scores generated under the null hypothesis of no association between location and MDR status. Using the random labeling hypotheses [11] we permute the case/control status of each subject in the study to randomly select N1 subjects out of the N(=N1+N2) total subjects to be cases. We then use the remaining N−N1 subjects as the controls and calculate the DBM scores for the same 100×100 grid. At each score recalculation, we store the maximum and the minimum score of that particular map. To define an extreme value in our observed data, we define the upper cut-off, the color Red, as an observed score greater than the maximum of every score calculated in the null distribution. We define the lower cut-off, the Dark Blue, as an observed score lower than the minimum of every score calculated in the null distribution. From Turquoise to Orange is defined as a score that is above the 5^th percentile of the minimum null scores and below the 95^th percentile of the maximum null scores.

RESULTS

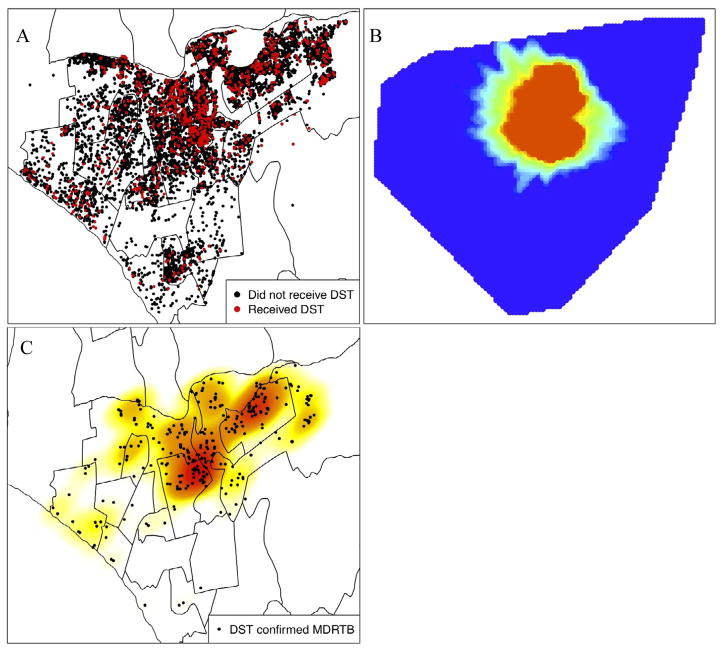
Figure 1a illustrates spatial distribution of TB cases in the two study districts and the subset of cases in who received DST; a previous study showed that DST is not homogeneously distributed, but there was no statistically significant association between the frequency of testing done within a health facility and the proportion of cases with detected drug resistance [5]. We apply Jeffery’s disease mapping technique to characterize the spatial distribution of retreatment cases in the study population. Because we have complete data on the retreatment status of each case in our study, we do not need to create any probability-weighted samples for this map; we use the collected data to generate Figure 1b. Following the method described above, we examine the spatial variation of the distribution of retreatment cases (F₁) among all lab confirmed TB cases (F₀). This map reveals a circular region in the center of the study area in which retreatment cases are concentrated. Figure 1c shows all 368 detected MDR cases and a kernel density estimate [12] displays areas of observed MDRTB concentration (Figure 1c).

Figure 1.

(A) Spatial locations of all tuberculosis cases with known retreatment/previous untreated status. (B) The DBM algorithm applied to retreated TB cases (F₁, in disease mapping notation) versus all TB cases in the study (F₀). (C) Kernel density estimate of DST confirmed multidrug resistant TB cases.

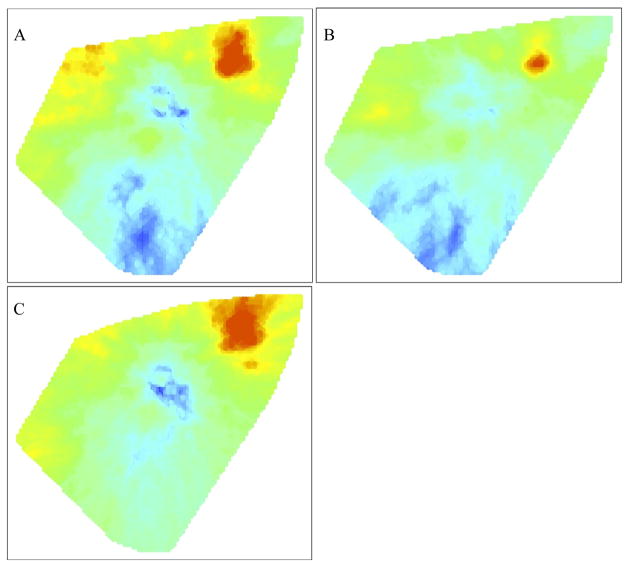
When we map the risk of MDR (F₁) among all incident TB cases receiving DST (F₀), we observe an elevated risk of MDR in the Este region of the study area (Figure 2a). We note that drug resistance among treatment naïve cases unambiguously signals transmitted resistance, while resistance among previously treated cases represents a combination of both transmitted resistance and resistance acquired as a result of previous inadequate therapy. When the maps are split to examine the risks of MDR among new (Figure 2b) and retreatment cases (Figure 2c) that actually received DST, we see that the risk of MDR conditional on DST is highest for each of these groups in the eastern sector of the study region. Interestingly, a trough in the estimated risk of MDR among retreatment cases in the center of the study area suggests the risk of MDR among retreatment cases tested in this location is lower in comparison to the rest of the region.

Figure 2.

The DBM algorithm applied only to those TB cases that received drug sensitivity testing (DST). (A) Map of the risk of a TB case that received DST being positive for MDR (F₁), compared to all TB cases that received DST (F₀). (B) Map of the risk of a previously untreated TB case that received DST being positive for MDR (F₁), compared to all previously untreated TB cases that received DST (F₀). (C) Map of the risk of a retreatment TB case that received DST being positive for MDR (F₁), compared to all retreatment TB cases that received DST (F₀).

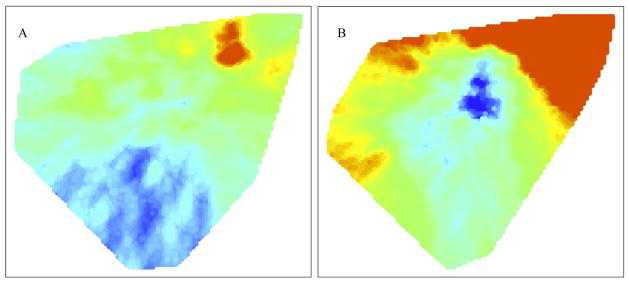
We are more interested in understanding the risk of MDR among all TB cases in these study areas, not just the risk among those who received a DST. When we first assume that all TB cases that did not receive DST were not MDR, we generate maps showing risk of MDR among new (Figure 3a) and retreatment cases (Figure 3b). These maps are constructed by treating the MDR confirmed subjects as the cases (F₁) and all TB cases as the background population, (F₀). These maps are not conditional on a case receiving testing, but are naïvely constructed since we know from drug resistance surveying that the number of notified cases detected as MDR is much smaller than the actual number of notified cases that are MDR.

Figure 3.

The DBM algorithm applied all TB cases in our study, assuming cases not receiving DST have drug sensitive TB. (A) Map of the risk of a previously untreated TB case that received DST being positive for MDR (F₁), compared to all r previously untreated TB cases (F₀). (B) Map of the risk of a retreatment TB case that received DST being positive for MDR (F₁), compared to all retreatment TB cases (F₀).

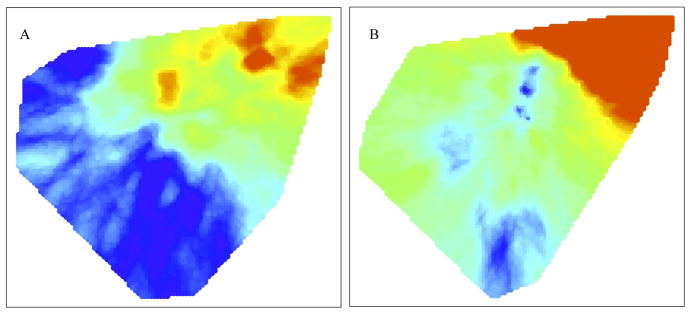
Attempting to correct for this underestimate, we reassigned those untested cases to MDR status as described in the Methods. Figures 4a and 4b display the risk of MDR among new and retreatment TB cases, respectively, using IPW reassignment of untested cases to MDR status. We believe these maps best permit inference about highest risk locations among all new and retreatment TB, even though our data only allow us to observe resistance among the non-randomly selected subset of patients that actually received DSTs. In this analysis, cases used to estimate the distribution F₁ are resampled from all TB cases according to their probability of being MDR positive. The controls, used to estimate the background distribution, F₀, are all TB cases in our study. These maps of MDR risk in previously untreated cases reveal several concentrated areas of probable MDR transmission in the eastern part of the study area and another, less dramatic elevation in risk of transmitted MDR in the center of the study area (Figure 4a). We also find transmitted MDR is less common in the western and southern regions. The risk of MDR among retreatment cases is also highest where MDR transmission hotspots seem to be concentrated, though high levels of MDR among retreatment cases is present everywhere (Figure 4b). Supplementary Figures 1 and 2 repeat these analyses with untested cases randomly reassigned (in contrast to IPW) to MDR status to match the prevalence reported in the survey.

Figure 4.

Maps created from repeated applying the DBM algorithm to the data that was augmented by including samples of non-DST cases as MDR-positive cases based on the calculated inverse probability weights. (A) Map of the risk of a previously untreated TB case that received DST being positive for MDR, based on lab-confirmed MDRTB cases and IPW selected non-DST TB cases (F₁), compared to all previously untreated TB cases (F₀). (B) Map of the risk of a retreatment TB case that received DST (F₁) being positive for MDR, based on lab-confirmed MDRTB cases and IPW selected non-DST TB cases, compared to all retreatment TB cases (F₀).

DISCUSSION

Using programmatic data from a high TB incidence urban community and a new disease mapping method to identify potential hotspots of MDRTB transmission, we found use of routine data in which a non-random sample of drug resistant cases are detected, in combination with estimates of the true underlying burden of drug resistant disease, might help identify important patterns of spatial heterogeneity which can be used to inform public health responses.

Simple analysis of the spatial variation of MDRTB in settings where DST is not done for every TB patient (or at random) does not reveal the actual distribution of drug resistant disease in the community. Since the resources for DST have been limited in most settings with a high burden of TB, methods to infer the possible distribution of risk from programmatic data are valuable. This paper demonstrates an inverse probability weighted approach for adjusting for missing DST data, though other models for the weights can be easily accommodated. As with all augmentation methods, our findings are dependent on (and limited by) our assumptions of the mechanisms leading to missingness in our data. Our model assumes that cases not tested in areas where increased testing was done were less likely to actually have drug resistant disease. In the absence of this assumption about missingness, we would have resorted to assigning the missing MDRTB cases at random (see Supplemental Material for details). The differences between these two sets of maps demonstrate the sensitivity of this method to the missingness assumptions. While neither of these maps is likely to exactly mirror the true distribution of MDRTB in the community, they do demonstrate the difference, and potentially the improvement, made when information related to the missingness mechanism is incorporated into the analysis. That we found any spatial pattern when nearly 90% of the data was augmented in a random fashion (i.e. imposing an assumption of an absence of clustering), and that the underlying patterns were similar to that given in the IPW approach gives us increased confidence that this method is robust against the choice of weights. We used Jeffery’s disease mapping technique primarily because it allows us to incorporate the inverse probability weights in our comparisons, which is not straightforward with other spatial cluster detection methods. As demonstrated in our results, when a substantial fraction of the data must be augmented, random assignment may be overly conservative, thus the ability to incorporate a weighted probability that any given individual is a case is crucial.

Identification of possible MDRTB transmission hotspots in the eastern part (and less dramatically in the center) of the study area is important because it suggests that resources necessary to interrupt the transmission of resistant disease should be prioritized in these regions. Additional investigation (e.g. a molecular epidemiological study) might validate this finding and uncover the causes or specific locations of relatively increased risk of transmission. For example, these locations might be areas where infectious MDRTB patients are not diagnosed and treated promptly, resulting in longer infectious periods and increased transmission. Alternatively, MDRTB patients might live in more dense conditions or may have more respiratory contacts in this area. It is also possible that particularly transmissible MDR strains are circulating in this region. Because the disease mapping method we used identifies areas of high risk of MDRTB, if some locations have implemented especially effective methods of preventing the transmission of drug-sensitive disease, these areas may be detected as possible MDRTB hotspots. We note that this analysis is based on home location; if location of exposure and transmission is far from the home location, we would expect that our ability to detect hotspots to be eroded. The fact that are able to detect areas of increased risk does not confirm that transmission is only happening in and around home location, but does suggest that interventions targeting particularly concerning geographic areas may be effective. Further investigation of possible hotspots revelaed by this type of analysis can help identify the actual causes of case aggregation and thus facilitate appropriate and targeted interventions.

We estimated that routine testing detected less than one-third of the expected MDRTB cases within the study’s timeframe. This suggests that far greater emphasis on detection of MDRTB is required to adequately confront this problem. Since the beginning of 2011, Peruvian National Tuberculosis Program guidelines require all diagnosed TB patients to receive DST.

In addition to the drug resistance results, the dramatic sub-regional variation in the relative frequency of previously untreated compared with retreatment TB in Lima begs further exploration (Figure 1b). Retreatment case concentration in the center of the study area may reflect a difference in local transmission dynamics (e.g. a relative increase in the risk of reinfection in this area), diagnostic practices (e.g. better notification of retreatment cases in this area), treatment practices (e.g. more aggressive initiation of retreatment regimens for suspected treatment failures), or treatment outcomes (e.g. a higher risk of failure, default, or abandonment or a lower risk of death in this area). Identifying the most probable explanation for the concentration of retreatment TB in this area could help inform a rational public health response.

On a per-case basis, MDRTB risk among retreatment cases is lower in the central region than it is in the eastern region. However, the high burden of retreatment cases in central Lima (Figures 1a and 1b) results in a local concentration of MDRTB (Figure 1c). From a programmatic perspective, this means that resources for detecting and treating existing cases of MDRTB should be concentrated in this central area.

Supplementary Material

01. Supplementary Figure 1.

Maps created from repeated applying the DBM algorithm to the data that was augmented by reassigning samples of non-DST cases as MDRTB cases based on random sampling, without replacement. (A) Map of the risk of a previously untreated TB case that received DST being positive for MDR, based on lab-confirmed MDRTB cases and randomly selected non-DST TB cases (F₁), compared to all previously untreated TB cases (F₀). (B) Map of the risk of a retreatment TB case that received DST (F₁) being positive for MDR, based on lab-confirmed MDRTB cases and randomly selected non-DST TB cases, compared to all retreatment TB cases (F₀).