Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Apr 11;2:358. doi: 10.1038/srep00358

Critical Dipole Length for the Wetting Transition Due to Collective Water-dipoles Interactions

Chunlei Wang 1, Bo Zhou 1,2, Yusong Tu 3, Manyi Duan 4, Peng Xiu 5, Jingye Li 1, Haiping Fang 1,6,a
PMCID: PMC3323886  PMID: 22496954

Abstract

The wetting behavior of water on the solid surfaces is fundamental to various physical, chemical and biological processes. Conventionally, the surface with charges or charge dipoles is hydrophilic, whereas the non-polar surface is hydrophobic though some exceptions were recently reported. Using molecular dynamics simulations, we show that there is a critical length of the charge dipoles on the solid surface. The solid surface still exhibited hydrophobic behavior when the dipole length was less than the critical value, indicating that the water molecules on the solid surface seemed not “feel” attractive interactions from the charge dipoles on the solid surface. Those unexpected observations result from the collective interactions between the water molecules and charge dipoles on the solid surface, where the steric exclusion effect between water molecules greatly reduces the water-dipole interactions. Remarkably, the steric exclusion effect is also important for surfaces with charge dipole lengths greater than this critical length.

A microscopic understanding of the wettability of solid surfaces is fundamental to various physical1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20, chemical21,22,23,24,25,26,27 and biological processes28,29,30,31,32,33, such as microfluidics34,35 and sensing36,37. Particularly, the hydrophobic effect plays a key role in protein folding38,39,40, nano-scale dewetting transition41,42,43 and self-assembly of amphiphiles44,45. However, the physics of the hydrophilic or hydrophobic effects is not fully understood because the hydrophilicity or hydrophobicity of a surface is usually subject to various factors, including temperature46 and morphology47. Conventionally, the surface with charge dipoles is hydrophilic, whereas the non-polar surface is hydrophobic. However, some exceptions were recently reported. Zangi and Berne48,49 showed that a high value (e.g., 1.5 e) of electrolyte particles in solution can induce hydrophobic particles to be more hydrophobic. Giovambattista et al.50 performed a series of simulations on polar hydroxylated silica (Si-OH) surfaces, finding that the surface is macroscopically hydrophobic, even though the dipole moment magnitude equaled to 41% that of the water molecule. The topography of the surface was also found to play a significant role in the wetting behavior of the protein surface or hydroxylated silica surface51,52. Boron-nitrogen nanotubes with a partial charge of ~0.4e53 have been shown to still exhibit hydrophobicity54. Moreover, in 2006, Li et al.55 showed that van der Waals interactions are the dominant interactions between the superhydrophobic surface molecule CF3(CF2)x(CH2)y and the water molecules on the surface with a charge of −0.2 e in CF3 groups. Very recently, we showed that hydrophobic-like behavior occurs on extremely polar hexagonal surfaces due to the ordered water monolayer for very large partial charges4,56, which was recently confirmed experimentally57. However, a relatively complete picture about the effect of the surface charges and charge dipoles on the wetting property is still lacking.

Here, using molecular dynamics simulations, we show that the length of the charge dipoles on the solid surface plays a key role on the wetting behavior. Moreover, there is a critical length of the charge dipoles on the solid surface, below which the charge dipoles on the solid surface plays unexpectedly negligible role in the wetting property. The solid surface still exhibits hydrophobic behavior when the dipole length is less than the critical value, indicating that the water molecules on the solid surface seem not to “feel” attractive interactions from the charge dipoles on the solid surface, no matter how large the moment magnitude of the charge dipoles is. Those unexpected observations result from the collective interactions between the water molecules and charge dipoles on the solid surface, where the steric exclusion effect between water molecules prevents those hydrogen atoms of water molecules from staying very close to the negative charge and those oxygen atoms of water molecules from staying very close to the positive charge, reducing the interactions between the water molecules and the charge dipoles. Interestingly, the steric exclusion effect was also important for surfaces with charge dipole lengths greater than this critical length. When the charge dipole lengths are greater than this critical length, it is found that the surfaces become more hydrophilic with the dipole lengths increase. We note that the bond lengths of most of common materials are less than the critical lengths, suggesting that the observation should be of general importance to the surface wetting properties.

The geometry of the solid surface system is shown in Fig. 1(a,b) together with snapshots of some water molecules. Positive and negative charges of the same magnitude, q, were assigned to every bonding atom of the hexagonal arrangement, represented by green and blue triangles, respectively, which was similar to the graphene and boron-nitrogen monolayer. The surface was neutral. The length of charge dipoles was denoted as l. Initially, 924 water molecules in a rectangular shape were located on solid surface composed of 2376 atoms in a box. Each system was simulated by molecular dynamics (MD) for 10 ns, and the data of the last 2 ns were collected for analysis. For all simulations, the water slab was in phase-level coexistence with the vapor at 300 K.

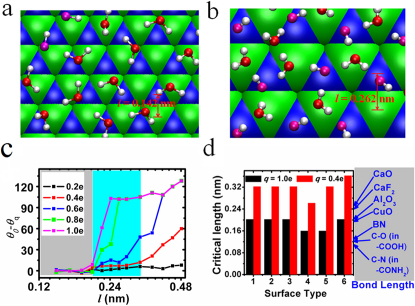
Figure 1. Introduction to the model system and its wetting behaviour.

Figure 1

Open in a new tab

(a,b) Structure of the model surface with l = 0.142 nm and 0.262 nm at q = 1.0 e together with snapshots of some water molecule. The green and blue triangles represent the atoms on the solid surface with positive charges and negative charges, respectively. The oxygen and hydrogen atoms of the water molecules are shown by (bright or soft) red and white spheres. The oxygen atom of a water molecule with one OH bond pointing downward is shown by soft red. (c) Contact angle discrepancy (θ0−θq) with respect to the dipole length (l) for the charge (q) 0.2 e (black), 0.4 e (red), 0.6 e (blue), 0.8 e (green), and 1.0 e (magenta). θq and θ0 are the contact angles of the liquid droplets on the surface with a charge of q and without any charge, respectively. The saturation values of θ0−θq increases from ~102° for l = 0.242 nm to ~130° for l = 0.482 nm due to the modification of the lattice length, which correspond to complete wetting of the surface (θq = 0). (d) Critical lengths for some typical surfaces of binary compound crystals. Here, the critical length is defined as the dipole length below which the contact angle discrepancy (θ0−θq) is less than 15° for all q value in the interval of [0, 1.0 e], or in the interval of [0, 0.4 e], denoted by lC and lC0.4 and shown by black and red columns, respectively. The first surface type is the structure shown in (a,b). The other surface types, increasing from 2 to 6, corresponds to the square, rhombic and rectangle lattice, (110) surface of a face-centered cube, and (110) surface of a body centered tetragonal, respectively (see Fig. S1 in Supplementary Information).

Results

Generally, the existence of polarity on the surface enhances the hydrophilicity. Surprisingly, our simulation shows that the contact angles of the liquid water droplets on the solid surfaces are always close to, even larger than 90° when l ≤ 0.202 nm, for all q value in the interval of [0, 1.0 e]. In Fig. 1(c), we show the contact angle discrepancy (θ0−θq) values associated with the parameter l for different q, where θq and θ0are the contact angles of the liquid droplets on the surface with the charge of q and without any charge, respectively. For l ≤ 0.202 nm, θq is very close to θ0 for all charges less than 1.0 e, indicating that the effect of the charge dipoles on the wetting property of the surface is negligible. From Fig. 1(c), one can observe that θ0−θq increases as l increases from 0.202 nm. The larger the value of q, the faster θ0−θqincreases. The increase of θ0−θq is very quick for q ≥ 0.6 e, and it reaches its maximal value, which corresponds to the water completely wetting the solid surface (θq = 0), for q = 1.0 e at l ≥ 0.242 nm, for q = 0.8 e at l ≥ 0.262 nm, and for q = 0.6 e at l ≥ 0.402 nm. A longer dipole length is clearly required to achieve complete wetting of the solid surface for a smaller charge. However, we find that the water could not complete wet the solid surface for q ≤ 0.4 e, even if l is very large (0.482 nm). Interestingly, for q = 0.4 e, the contact angle increases significantly only from l ≈ 0.3 nm. Thus, the wetting properties of the solid surface significantly depend on the length of the dipole. We note that, when l ≤ 0.202 nm, the surface always shows hydrophobic (θq≈ 90°) when the dipole moment magnitude is very large, even larger than 3 times of that of the water molecule. In order to better characterize the behavior, we define a critical length as the dipole length below which the contact angle discrepancy (θ0−θq) is less than a critical value, i.e., 15°, for all q value in the interval of [0, 1.0 e], or in the interval of [0, 0.4 e], denoted by lC and lC0.4, respectively. lC = 0.202 nm and lC0.4 = 0.302 nm, which are shown by grey and light blue shadows in Fig. 1(c), respectively. We note the bond lengths of many common materials are smaller than lC = 0.202 nm and most of common materials are smaller than l < lC0.4 = 0.302 nm (see Fig. 1d and the Table S1 in the Supporting Information). This also explains that boron-nitrogen nanotubes still exhibit hydrophobicity although there are partial charges of ~0.4e on the boron nitrogen atoms53.

Discussions

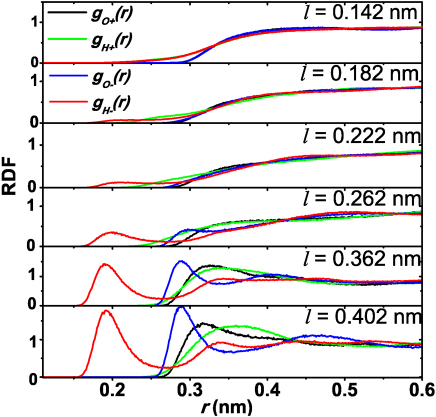
In order to understand the mechanism underlying this behavior, we have calculated radial distribution functions (RDF) between water oxygen (O) and hydrogen (H) atoms and the surface positive and negative charged atoms, denoted as gO+(r), gH+(r), gO−(r) and gH−(r), respectively. Some typical results for q = 0.4 e are shown in Fig. 2. Interestingly, the RDF profiles are almost independent of the charge positivity or negativity; gO+(r) ≈gO−(r), and gH+(r) ≈ gH−(r) for all r values when l is very small (0.142 nm). The peaks of all the RDF profiles are at r = ~0.4 nm. We have shown that the RDFs of the O and H for q = 0 are consistent with the RDFs for q = 1.0 e when l = 0.142 nm (see Fig. S1 in the Supporting Information). In fact, we find that the RDF profiles are almost independent of the charge for q ≤1.0 e, suggesting that the dynamics of the surface water is independent of the quantity of the charge dipoles on the surface for l = 0.142 nm. In Fig. 1(a) we show the snapshot of the water molecules in the layer with a thickness of 0.5 nm from the top view for l = 0.142 nm at q = 1.0 e. These water molecules do not show any ordering structure, indicating that water molecules seem not “see” the surface charges even q = 1.0 e. The RDF profiles for l = 0.182 nm were quite similar to the RDF profiles for l = 0.142 nm. When l = 0.222 nm, a clear but small peak appears at r = 0.20 nm for gH−(r). At l = 0.362 nm, clearer peaks appears at r ≈ 0.18 nm for gH−(r) profiles and at r ≈ 0.27 nm for gO−(r) profiles. The two peaks become clearer for l = 0.402 nm. The distance between those two peaks is found to be about 0.09 nm, which is very close to the bond length of O-H in the SPC/E water model of 0.1 nm used here. Careful examination finds that most of the O atoms near the peak at r ≈ 0.27 nm chemically bond H atoms near the peak r ≈ 0.18 nm. This explains the observation that the peak in the RDF profile of gO−(r) moves towards left as l increases since the first peak of gH−(r) moves towards left. From the snapshot for l = 0.262 nm at q = 1.0 e shown in Fig. 1(b), one can observe that the water molecules close to the solid surface show clear structure ordering, i.e, the water molecules above the negatively charged atoms have one OH bond pointing downward to the surface, and the water molecules above the positively charged atoms have neither OH bond pointing downward, indicating that the oxygen atoms are nearest to the positively charged atoms on the surface. Thus, the water molecules on the surface with l = 0.262 nm behaves qualitatively different from the water molecules on the surface with l = 0.142 nm, consistent with the RDF profiles. There is also a peak for the RDF profile of gH+(r) at r = 0.32 nm. As l increases more, the locations of the peaks in the profile of gO+(r) moves towards smaller values of r, whereas the profiles of gH+(r) show different characteristics. All of these observations show that the charge dipoles on the sold surface have a more profound effect on the distribution of the water orientation on the solid surface when l is larger. Due to the small van de Waals radius of an H atom, H is much closer to the negative charges compared to the distance from the positive charges to O atoms.

Figure 2. Radial distribution functions (RDF) of water oxygen O and hydrogen H atoms with respect to the surface positive and negative charged atoms for the surfaces considered, respectively, for various dipole lengths l at q = 0.4 e.

Figure 2

Open in a new tab

The black lines and green lines correspond to the RDF profiles for the oxygen (O) and hydrogen (H) to the positive charges, denoted by gO+(r) and gH+(r), respectively. Blue lines and red lines correspond to the RDF profiles for the oxygen (O) and hydrogen (H) to the negative charges, denoted by gO−(r) and gH−(r), respectively.

The interactions between water molecules and the solid surface are usually regarded as the key factor in determining the wetting property of the surface. We have computed the average electrostatic interaction energy between each single charge (average value from both cases of positive and negative charges) on solid surface and all the water molecules near the charge, with respect to l for various q, denoted as Eelectro (see Fig. 3). Eelectro is very small for l ≤ lC (the the grey shadows in Fig. 3). The water on the solid surface seems not to “feel” the attractive interactions from the charge on the solid surface, contrary to intuition, but consistent with our simulation results that solid surfaces with charge dipoles still exhibit hydrophobic behavior for l ≤ lC. As l increases from lC, the electrostatic interaction increases monotonically. We have also computed the electrostatic interaction energies from the RDFs of water oxygen O and hydrogen H atoms, denoted by Etheory. Herein, the partial charges on an oxygen and hydrogen atoms are −0.8476 e and 0.4238 e, respectively, from the SPC/E water model. As shown in Fig. 3, Etheory agrees with Eelectro very well.

Figure 3. Electrostatic interaction energy between water molecules and each charge on the solid surface with respect to the dipole length (l) for the charge (q) 1.0 e (magenta), 0.8 e (green), 0.6 e (blue), 0.4 e (red), and 0.2 e (black).

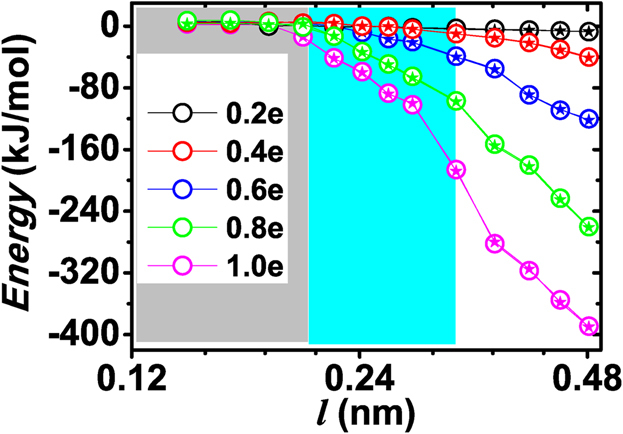
Figure 3

Open in a new tab

The open circles are determined directly from numerical simulations (denoted by Eelectro) and the filled stars represent the electrostatic interactions energy calculated from the radial distribution function (denoted by Etheory).

Now we may capture the physics behind this unexpected behavior. The key is the collective effect of the interaction of the water molecules with the charge dipoles on the solid surface, where the steric exclusion effect between the water molecules may become of importance. When l is large enough, the negative charges on the solid surface attract the H atoms and the positive charges attract the O atoms so that some of the H atoms are very close to the negative charges and some of the O atoms are very close to the positive charges. When l decreases to a smaller value, the steric exclusion effect prevents those hydrogen atoms from staying very close to the negative charge and those oxygen atoms from staying very close to the positive charge. The electrostatic interactions between water molecules and surface charge dipoles decrease correspondingly. When l is small enough, it becomes almost impossible to arrange the positions and orientation of the water molecules so that the O atoms are close to the positive charges while the H atoms are close to the negative charges. It is clear that this value of l should be comparable or smaller than the size of the water so that the positions and orientations of the water molecules near the solid surface cannot be arranged according to the charges on the surfaces. Our numerical results have shown that the critical surface dipole length lC = 0.202 nm and lC0.4 = 0.302 nm are close to the diameter of a water molecule (~0.28 nm). Consequently, when l ≤ lC, the atom densities are almost independent of the signs and the qualities of the charges and the water molecules on the solid surface seem not to “see” the charges on the solid surface.

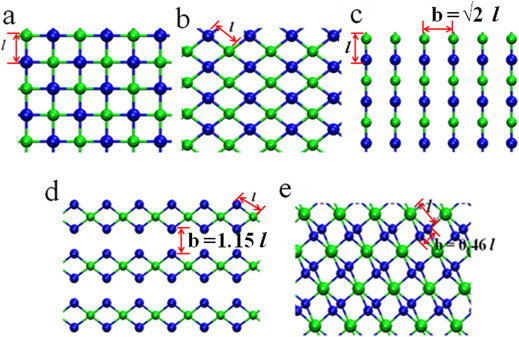
The existence of the critical length is universal. We have studied the wetting behavior of the surfaces of other five typical types. Three of them have 1:1 ratio, and the other two have 1:2 ratio of the number of positively charged atoms to the number of negatively charged atoms. Explicitly, the three typical types of surfaces of 1:1 ratio are the type 2 surface obtained from (100) surface of a face-centered cube (such as the NaCl(100) surface), the type 3 surface obtained from (110) surface of simple cube (such as the CsCl(110) surface) and the type 4 surface obtained from (110) surface of face-center cube (such as the NaCl(110) surface), which are shown in Fig. 4(a)(b)(c), respectively. The other two typical types of surfaces of 1:2 ratio are the type 5 surface obtained from (110) surface of a face-centered cube (such as the CaF2(110) surface) and the type 6 surface obtained from (110) surface of a body centered tetragonal (such as the BaO2(110) surface), as shown in Fig. 4(d)(e), respectively. For the two typical types of surfaces of 1:2 ratio, in order to keep the system charge neutral, we set the quantity of each positive charge twice of the quantity of each negative charge. Thus, for easy description, the notion q in the contexts below corresponds to the quantity of the positive charge for the two types of 1:2 ratio. The structure shown in Fig 1(a) is denoted as type 1. In Fig. 1(d), we show the critical lengths of the charge dipoles for various types of the solid surfaces. One can observe that the explicit value of the critical value depends on the geometry of the solid surface and the dipole structures. Explicitly, the critical length of the charge dipoles on the solid surface is lC = 0.202 nm for q = 1.0 e and lC0.4 = 0.302 nm for q = 0.4 e for the types 1–3. For the type 4, the critical length of the charge dipoles on the solid surface is lC = 0.162 nm for q = 1.0 e and lC0.4 = 0.262 nm for q = 0.4 e, which are smaller than the case of type 1–3. As for the type 5 and 6, the critical length of the charge dipoles on the solid surface is lC1.0 = 0.162 nm for q = 1.0 e and lC0.4 = 0.302 nm for q = 0.4 e; lC1.0 = 0.202 nm for q = 1.0 e and lC0.4 = 0.362 nm for q = 0.4 e, respectively. The close values of the critical lengths in the solid surfaces of the first three types may be attributed to that there is only one characteristic length for each type. For the type 4 solid surface, there are two characteristic lengths, where the longer one is √2 times larger than the shorter one. Here we only consider the shorter one as the critical length so that the critical length shows a smaller value. As for the types 5 and 6, the number of positively charged and negatively charged atoms is different and there are also two characteristic lengths so that the critical lengths show different behavior from those in the surfaces of the first three types. The lengths of the chemical bonds of some typical binary compound crystals or chemical groups are shown in Fig. 1(d), including the lengths of the C-O bond in –COOH group, C-N bond in –CONH2 group, and the bonds of BN, CuO, Al2O3, CaF2 and CaO. It is clear that all of them are less than lC0.4 and most of them are less than lC. This demonstrates that the observations should be of general importance.

Figure 4. Other five typical surfaces of binary compound crystals, which correspond to the surface type number = 2, 3, 4, 5 and 6, respectively.

Figure 4

Open in a new tab

The green and blue spheres represent positively and negatively charged atoms, respectively.

In summary, we have shown that the wetting properties of a solid surface significantly depend on the surface topology parameter, which can be characterized by the length of the charge dipoles l. Counter to intuition, the length of the charge dipoles on the solid surface plays a key role on the wetting behavior and there is a critical length of the charge dipoles, below which the charge dipoles on the solid surface have a negligible role in the wetting property. The solid surface still exhibits hydrophobic behavior when the dipole length is less than the critical value, indicating that the water molecules on the solid surface seem not to “feel” attractive interactions from the charge dipoles on the solid surface, no matter how large the moment magnitude of the charge dipoles is. Those unexpected observations result from the collective interactions between the water molecules and charge dipoles on the solid surface, where the steric exclusion effect between water molecules prevents those hydrogen atoms of water molecules from staying very close to the negative charge and those oxygen atoms of water molecules from staying very close to the positive charge, reducing the interactions between the water molecules and the charge dipoles. Remarkably, the steric exclusion effect is also important for surfaces with charge dipole lengths l greater than this critical length. When charge dipole lengths are greater than this critical length, the surfaces become more hydrophilic with the dipole lengths increase. We note that the bond lengths of most of common materials are less than the critical lengths, suggesting that the observation should be of general importance to the surface wetting properties. We further note that the critical length of the surface still exists for different Lennard-Jones parameters of the atoms on the substrate within a reasonable range (see Table S2 in the Supplementary Information). Moreover, when the charge dipoles are provided from planting groups, such as –COOH, the critical values will be smaller due to the flexible behavior of the groups, which decreases the steric exclusion effect. These findings also have biological significance and are helpful for interfacial engineering, new functional material design including carbon and silicon nanostructures, and offer insights into many unexpected observations on wetting behavior.

Methods

A constant temperature and constant volume (NVT ensemble) MD simulation was performed using a time step of 1.0 fs with Gromacs 3.3.158. The periodic boundary conditions were applied in all directions. The selection of a vapor-liquid coexistence system was used to maintain the ambient conditions, and a Berendsen thermostat59 with a time constant of 1.0 ps for coupling was used to maintain the temperature of the water at 300 K. The solid atom with Lennard-Jones parameters εss = 0.105 kcal/mol and σss = 3.343 Å, and the SPC/E water model was used as the explicit solvent. A cutoff of 10 Å was used for both the particle-mesh Ewald method60 with a real space to model long-range electrostatic interactions, and for the van der Waals interactions. The contact angle of a water droplet was calculated from the density profile. For simplicity, when all of the water molecules completely spread on the surface, we assumed that the contact angle was 0. In the computation of the radial distribution function (RDF) of the water molecules next to a given surface and the interaction between those water molecules and the surface, we considered the solid surface with 1664 atoms immersed in the center of a water box with 4 nm thickness of water layer, where periodic boundary conditions apply along the three dimensions52.

Author Contributions

C.L.W. performed most of the numerical simulations. H.P.F. and C.L.W. carried out most of the theoretical analysis. B.Z., Y.S.T., M.Y.D. and P.X. carried out some numerical simulations and theoretical analysis. H.P.F, C.L.W. and J.Y.L. contributed most of the ideas and wrote the paper. All authors discussed the results and commented on the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information for Critical Dipole Length for the Wetting Transition Due to Collective Water-dipoles Interactions

srep00358-s1.doc (294KB, doc)

Acknowledgments

We gratefully acknowledge Drs. Ruhong Zhou, Yi Gao, Guanghong Zuo and Rongzheng Wan for their helpful discussions. This work was supported by the National Science Foundation of China under grant No. 10825520 and 11105088, the National Basic Research Program of China under grant No. 2012CB932400, Shanghai Leading Academic Discipline Project (B111), E-Institutes of Shanghai Municipal Education Commission, the Knowledge Innovation Program of the Chinese Academy of Sciences, Innovation Program of Shanghai Municipal Education Commission (No. 11YZ20), China Postdoctoral Science Foundation (No. 20100480645), Shanghai Postdoctoral Scientific Program (No. 11R21418100) and Shanghai Supercomputer Center of China.

References

  1. Chandler D. Interfaces and the driving force of hydrophobic assembly. Nature 437, 640–647 (2005). [DOI] [PubMed] [Google Scholar]
  2. Han S. H., Choi M. Y., Kumar P. & Stanley H. E. Phase transitions in confined water nanofilms. Nature Phys. 6, 685–689 (2010). [Google Scholar]
  3. Wang B. & Král P. Chemically Tunable Nanoscale Propellers of Liquids. Phys. Rev. Lett. 98, 266102 (2007). [DOI] [PubMed] [Google Scholar]
  4. Wang C. L. et al. Stable Liquid Water Droplet on a Water Monolayer Formed at Room Temperature on Ionic Model Substrates. Phys. Rev. Lett. 103, 137801 (2009). [DOI] [PubMed] [Google Scholar]
  5. Strekalova E. G., Mazza M. G., Stanley H. E. & Franzese G. Large decrease of fluctuations for supercooled water in hydrophobic nanoconfinement. Phys. Rev. Lett. 106, 145701 (2011). [DOI] [PubMed] [Google Scholar]
  6. Raschke T. M., Tsai J. & Levitt M. Quantification of the hydrophobic interaction by simulations of the aggregation of small hydrophobic solutes in water. Proc. Natl. Acad. Sci. USA 98, 5965–5969 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Weiss D. R., Raschke T. M. & Levitt M. How hydrophobic buckminsterfullerene affects surrounding water structure. J. Phys. Chem. B 112, 2981–2990 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hummer G., Rasaiah J. C. & Noworyta J. P. Water conduction through the hydrophobic channel of a carbon nanotube. Nature 414, 188–190 (2001). [DOI] [PubMed] [Google Scholar]
  9. Ashbaugh H. S. & Pratt L. R. Colloquium: Scaled particle theory and the length scales of hydrophobicity. Rev. Mod. Phys. 78, 159–178 (2006). [Google Scholar]
  10. Stone H. A., Stroock A. D. & Ajdari A. Engineering flows in small devices microfluids towards a lab-on-a-chip. Annu. Rev. Fluid Mech 36, 381 (2004). [Google Scholar]
  11. Zhu Y. & Granick S. Rate-dependent slip of newtonian liquid at smooth surfaces. Phys. Rev. Lett. 87, 096105 (2001). [DOI] [PubMed] [Google Scholar]
  12. Briscoe W. H. et al. Boundary lubrication under water. Nature 444, 191–194 (2006). [DOI] [PubMed] [Google Scholar]
  13. Meng S., Zhang Z. Y. & Kaxiras E. Tuning solid surfaces from hydrophobic to superhydrophilic by submonolayer surface modification. Phys. Rev. Lett. 97, 036107 (2006). [DOI] [PubMed] [Google Scholar]
  14. Sedlmeier F., Horinek D. & Netz R. R. Nanoroughness, Intrinsic Density Profile, and Rigidity of the Air-Water Interface. Phys. Rev. Lett. 103, 136102 (2009). [DOI] [PubMed] [Google Scholar]
  15. Ogasawara H. et al. Structure and bonding of water on Pt(111). Phys. Rev. Lett. 89, 276102 (2002). [DOI] [PubMed] [Google Scholar]
  16. Huang D. M., Sendner C., Horinek D., Netz R. R. & Bocquet L. Water Slippage versus Contact Angle: A Quasiuniversal Relationship. Phys. Rev. Lett. 101, 226101 (2008). [DOI] [PubMed] [Google Scholar]
  17. Li J. Y. et al. Electrostatic gating of a nanometer water channel. Proc. Natl. Acad. Sci. USA 104, 3687–3692 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Yuan Q. Z. & Zhao Y. P. Precursor Film in Dynamic Wetting, Electrowetting, and Electro-Elasto-Capillarity. Phys. Rev. Lett. 104, 246101 (2010). [DOI] [PubMed] [Google Scholar]
  19. Yang J. J., Meng S., Xu L. F. & Wang E. G. Water adsorption on hydroxylated silica surfaces studied using the density functional theory. Phys. Rev. B 71, 035413 (2005). [Google Scholar]
  20. Meng X. W., Wang Y., Zhao Y. J. & Huang J. P. Gating of a Water Nanochannel Driven by Dipolar Molecules. J. Phys. Chem. B 115, 4768–4773 (2011). [DOI] [PubMed] [Google Scholar]
  21. Verdaguer A., Sacha G. M., Bluhm H. & Salmeron M. Molecular structure of water at interfaces: Wetting at the nanometer scale. Chem Rev 106, 1478–1510 (2006). [DOI] [PubMed] [Google Scholar]
  22. Ball P. Water as an active constituent in cell biology. Chem Rev 108, 74–108 (2008). [DOI] [PubMed] [Google Scholar]
  23. Godawat R., Jamadagni S. N. & Garde S. Characterizing hydrophobicity of interfaces by using cavity formation, solute binding, and water correlations. Proc. Natl. Acad. Sci. USA 106, 15119–15124 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Koishi T., Yasuoka K., Fujikawa S., Ebisuzaki T. & Zeng X. C. Coexistence and transition between Cassie and Wenzel state on pillared hydrophobic surface. Proc. Natl. Acad. Sci. USA 106, 8435–8440 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Gu W. et al. Design of a gated molecular proton channel. Angew. Chem. Int. Ed. 50, 768–771 (2010). [DOI] [PubMed] [Google Scholar]
  26. Das P. & Zhou R. H. Urea-Induced Drying of Carbon Nanotubes Suggests Existence of a Dry Globule-like Transient State During Chemical Denaturation of Proteins. J. Phys. Chem. B 114, 5427 (2010). [DOI] [PubMed] [Google Scholar]
  27. Janecek J. & Netz R. R. Interfacial water at hydrophobic and hydrophilic surfaces: Depletion versus adsorption. Langmuir 23, 8417–8429 (2007). [DOI] [PubMed] [Google Scholar]
  28. Tajkhorshid E. et al. Control of the Selectivity in the AQP Water Channel Family by Global Orientational Tuning. Science 296, 525–530 (2002). [DOI] [PubMed] [Google Scholar]
  29. Raschke T. M. Water structure and interactions with protein surfaces. Curr. Opin. Struct. Biol. 16, 152–159 (2006). [DOI] [PubMed] [Google Scholar]
  30. Cheung M. S., Garcia A. E. & Onuchic J. N. Protein folding mediated by solvation: Water expulsion and formation of the hydrophobic core occur after the structural collapse. Proc.Natl. Acad. Sci. USA 99, 685–690 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. VanVeen H. W. et al. Multidrug resistance mediated by a bacterial homolog of the human multidrug transporter MDR1. Proc. Natl. Acad. Sci. USA 93, 10668–10672 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wimley W. C. & White S. H. Experimentally determined hydrophobicity scale for proteins at membrane interfaces. Nature Struct. Biol. 3, 842–848 (1996). [DOI] [PubMed] [Google Scholar]
  33. Titov A. V., Kral P. & Pearson R. Sandwiched Graphene-Membrane Superstructures. ACS Nano 4, 229–234 (2010). [DOI] [PubMed] [Google Scholar]
  34. Bocquet L. & Charlaix E. Nanofluidics, from bulk to interfaces. Chem. Soc. Rev. 39, 1073–1095 (2010). [DOI] [PubMed] [Google Scholar]
  35. Whitby M. & Quirke N. Fluid flow in carbon nanotubes and nanopipes. Nature Nanotech. 2, 87–94 (2007). [DOI] [PubMed] [Google Scholar]
  36. Squires T. M. & Quake S. R. Microfluidics: fluid physics at the nanoliter scale. Rev. Mod. Phys. 77, 977 (2005). [Google Scholar]
  37. Besteman K., Lee J. O., Wiertz F. G. M., Heering H. A. & Dekker C. Enzyme-coated carbon nanotubes as single-molecule biosensors. Nano Lett. 3, 727–730 (2003). [Google Scholar]
  38. Shea J. E., Onuchic J. N. & Brooks C. L. Probing the folding free energy landscape of the src-SH3 protein domain. Proc. Natl. Acad. Sci. USA 99, 16064–16068 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Zhou R. H., Huang X. H., Margulis C. J. & Berne B. J. Hydrophobic collapse in multidomain protein folding. Science 305, 1605–1609 (2004). [DOI] [PubMed] [Google Scholar]
  40. Hua L., Huang X., Liu P., Zhou R. & Berne B. J. Nanoscale Dewetting Transition in Protein Complex Folding. J. Phys. Chem. B 111, 9069–9077 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Berne B. J., Weeks J. D. & Zhou R. H. Dewetting and Hydrophobic Interaction in Physical and Biological Systems. Annu. Rev. Phys. Chem. 60, 85–103 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Li J. Y. et al. Hydration and dewetting near graphite-CH3 and graphite-COOH plates. J. Phys. Chem. B 109, 13639–13648, 10.1021/jp044090w (2005). [DOI] [PubMed] [Google Scholar]
  43. Huang X., Margulis C. J. & Berne B. J. Dewetting-induced collapse of hydrophobic particles. Proc. Natl. Acad. Sci. USA 100, 11953–11958 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Charles T. Hydrophobic free energy, micelle formation and the association of proteins with amphiphiles. J. Mol. Bio. 67, 59–74, 10.1016/0022-2836(72)90386-5 (1972). [DOI] [PubMed] [Google Scholar]
  45. Israelachvili J. N., Mitchell D. J. & Ninham B. W. Theory of self-assembly of hydrocarbon amphiphiles into micelles and bilayers. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics 72, 1525–1568 (1976). [Google Scholar]
  46. Wang H. J., Xi X. K., Kleinhammes A. & Wu Y. Temperature-induced hydrophobic-hydrophilic transition observed by water adsorption. Science 322, 80–83 (2008). [DOI] [PubMed] [Google Scholar]
  47. Cheng Y. K. & Rossky P. J. Surface topography dependence of biomolecular hydrophobic hydration. Nature 392, 696–699 (1998). [DOI] [PubMed] [Google Scholar]
  48. Zangi R. & Berne B. J. Aggregation and dispersion of small hydrophobic particles in aqueous electrolyte solutions. J. Phys. Chem. B 110, 22736–22741 (2006). [DOI] [PubMed] [Google Scholar]
  49. Zangi R., Hagen M. & Berne B. J. Effect of ions on the hydrophobic interaction between two plates. J. Am. Chem. Soc. 129, 4678–4686 (2007). [DOI] [PubMed] [Google Scholar]
  50. Giovambattista N., Debenedetti P. G. & Rossky P. J. Effect of surface polarity on water contact angle and interfacial hydration structure. J. Phys. Chem. B 111, 9581–9587 (2007). [DOI] [PubMed] [Google Scholar]
  51. Giovambattista N., Lopez C. F., Rossky P. J. & Debenedetti P. G. Hydrophobicity of protein surfaces: Separating geometry from chemistry. Proc.Natl. Acad. Sci. USA 105, 2274–2279 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Giovambattista N., Debenedetti P. G. & Rossky P. J. Enhanced surface hydrophobicity by coupling of surface polarity and topography. Proc. Natl. Acad. Sci. USA 106, 15181–15185 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Won C. Y. & Aluru N. R. Structure and dynamics of water confined in a boron nitride nanotube. J. Phys. Chem. C 112, 1812–1818 (2008). [Google Scholar]
  54. Golberg D., Bando Y., Tang C. C. & Zhi C. Y. Boron nitride nanotubes. Adv Mater 19, 2413–2432 (2007). [Google Scholar]
  55. Li X., Li J. Y., Eleftheriou M. & Zhou R. H. Hydration and dewetting near fluorinated superhydrophobic plates. J. Am. Chem. Soc. 128, 12439–12447 (2006). [DOI] [PubMed] [Google Scholar]
  56. Wang C. L., Zhou B., Xiu P. & Fang H. P. Effect of Surface Morphology on the Ordered Water Layer at Room Temperature. J. Phys. Chem. C 115, 3018–3024 (2011). [Google Scholar]
  57. James M. et al. Nanoscale condensation of water on self-assembled monolayers. Soft Matter 7, 5309–5318 (2011). [Google Scholar]
  58. Lindahl E., Hess B. & van der Spoel D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. 7, 306–317 (2001). [Google Scholar]
  59. Berendsen H. J. C., Grigera J. R. & Straatsma T. P. The missing term in effective pair potentials. J. Phys. Chem. 91, 6269–6271 (1987). [Google Scholar]
  60. Darden T., York D. & Pedersen L. Particle mesh ewald - an N.LOG(N) method for ewald sums in large systems. J. Chem. Phys. 98, 10089–10092 (1993). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information for Critical Dipole Length for the Wetting Transition Due to Collective Water-dipoles Interactions

srep00358-s1.doc (294KB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES