A unified framework for non-Brownian suspension flows and soft amorphous solids

Abstract

While the rheology of non-Brownian suspensions in the dilute regime is well understood, their behavior in the dense limit remains mystifying. As the packing fraction of particles increases, particle motion becomes more collective, leading to a growing length scale and scaling properties in the rheology as the material approaches the jamming transition. There is no accepted microscopic description of this phenomenon. However, in recent years it has been understood that the elasticity of simple amorphous solids is governed by a critical point, the unjamming transition where the pressure vanishes, and where elastic properties display scaling and a diverging length scale. The correspondence between these two transitions is at present unclear. Here we show that for a simple model of dense flow, which we argue captures the essential physics near the jamming threshold, a formal analogy can be made between the rheology of the flow and the elasticity of simple networks. This analogy leads to a new conceptual framework to relate microscopic structure to rheology. It enables us to define and compute numerically normal modes and a density of states. We find striking similarities between the density of states in flow, and that of amorphous solids near unjamming: both display a plateau above some frequency scale ω^∗ ∼ |z_c - z|, where z is the coordination of the network of particle in contact, z_c = 2D where D is the spatial dimension. However, a spectacular difference appears: the density of states in flow displays a single mode at another frequency scale ω_min ≪ ω^∗ governing the divergence of the viscosity.

Suspensions are heterogeneous fluids containing solid particles. Their viscosity in the dilute regime was computed early on by Einstein and Batchelor (1). However, as the packing fraction ϕ increases, steric hindrance becomes dominant and particles move under stress in an increasingly coordinated way. For non-Brownian particles, the viscosity diverges as the suspension jams into an amorphous solid. This jamming transition is a nonequilibrium critical phenomena: the rheology displays scaling laws (2–8) and a growing length scale (2, 3, 9, 10). Jamming occurs more generally in driven materials made of repulsive particles, such as in aerial granular flows (11) with similar rheological phenomenology (12), and where large eddies are observed as jamming is approached (9). This phenomenology bears similarity with that of the glass transition, where steric hindrance increases upon cooling, and where the dynamics becomes increasingly collective as relaxation times grow (13). In dense granular materials and in supercooled liquids, the physical origin of collective dynamics and associated rheological phenomena remain elusive.

Recent progress has been made on a related problem, the unjamming transition where a solid made of repulsive soft particles is isotropically decompressed toward vanishing pressure (14–20). In this situation, various properties of the amorphous solid, such as elasticity, transport, and force propagation, display scaling with the distance from threshold (14, 21, 22) and are characterized by a diverging length scale (17, 18). The packing geometry also displays scaling: the average number of contacts or coordination z of jammed particles is observed to converge (5) to the minimal value allowing mechanical stability z_c derived by Maxwell (23). Theoretically, these observations can be unified by the realization that the vibrational spectrum of these simple amorphous solids must display a crossover at some threshold frequency (15), distinct from Anderson localization, above which vibrational modes are still extended but poorly transport energy (16). This threshold frequency, corresponding to the so-called boson peak ubiquitously observed in glasses (24), is governed by coordination and applied pressure (25) and vanishes at the unjamming threshold.

Under an imposed shear flow, materials near the jamming transition are strongly anisotropic and particles receive a net force from particles they are in contact with. When an amorphous solid is decompressed toward its unjamming transition however, configurations are isotropic and forces are balanced. Despite these significant differences, both transitions deal with the emergence or disappearance of rigidity, and it is natural to seek a common description of these phenomena. Such a framework would unify the elastic and vibrational properties of amorphous solids, much studied in the context of granular materials, glasses (24) and gels of semiflexible polymers (26), with the rheology of suspension flows. Herein we build the foundation of this framework, by focusing on a model of a suspension flow of non-Brownian hard particles where hydrodynamic interactions are neglected (2). The relationship between this model and real suspensions is not obvious. Here we furnish numerical observations and physical arguments to support the contention that this model captures the relevant physics near jamming. The next step is to show that for this model we can build a formal analogy between rheology and elasticity. This analogy allows us to simulate accurately and to measure with high precision key aspects of the particle organization, in particular the packing coordination. More fundamentally, it enables us to define and compute, in flows of hard particles, normal modes and their density, which are the natural mathematical objects connecting geometry to rheology. We find striking similarities between the jamming and the unjamming transitions: the coordination converges to Maxwell’s value with a nontrivial scaling with pressure. Furthermore, the density of states displays a transition that is characteristic of vibrational properties of amorphous solids. However, a fundamental difference appears: the density of states displays biscaling instead of the simple scaling found near unjamming, with one mode at low frequency that strongly couples to shear, which is responsible for the rapid divergence in viscosity.

Constitutive Relations

Dimensional analysis implies that suspensions of overdamped hard particles are controlled by one dimensionless parameter (6), the viscous number 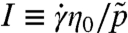where is the particle pressure, η₀ is the fluid viscosity and is the strain rate. For convenience we shall consider its inverse, the normalized pressure 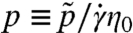. The steady-state rheology is then entirely determined by two constitutive relations that allow the computation of the flow in various geometries (6, 12): ϕ(p) describes the dilatency of the material, and 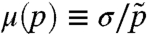its effective friction, where σ is the shear stress. Near jamming it is observed experimentally that:

[1]

[2]

with α ≈ 1/2 (6) and β ≈ 0.4 (10, 6, 27). Currently these constitutive relations are phenomenological and lack a microscopic theory.

The Affine Solvent Model

We consider a model of hard frictionless particles immersed in a viscous fluid that we call the affine solvent model (ASM). The dynamics is overdamped, and hydrodynamic interactions are neglected: the viscous drag on a particle is equal to the difference between the imposed velocity of the underlying fluid and the particle velocity times a coefficient ξ₀. The flow of the fluid phase is undisturbed by the particles and is chosen to be an affine shear of strain rate 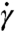. For hard particles at fixed packing fraction, changing 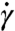simply rescales time and the stress tensor must therefore be proportional to 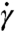(28). Note that for this model we can renormalize the pressure as 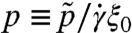in two dimensions and 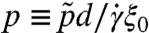in three dimensions, where d is taken to be the diameter of the small particles in our bidisperse numerics.

We constructed an event-driven simulation scheme [see (29) and Methods below] based on an exact equation of motion derived below, and on the actualization of the contact network, to simulate flow while carefully extracting the geometry of configurations visited. In Fig. 1 we present a snapshot of a configuration from our simulations in two-dimensions, and a typical stress-strain signal. A movie (Video S1) of our simulations can be found in the Supplementary Information.

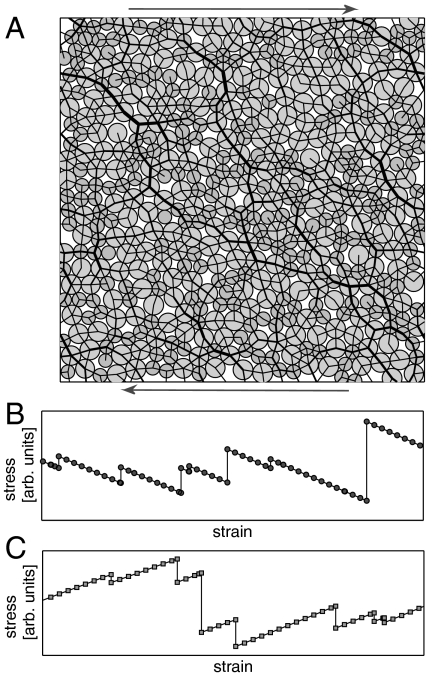
Fig. 1.

(A) Snapshot of a configuration visited under flow from simulations in two dimensions (see Methods for details). Small and large particles are represented in different colors. The width of the black segments connecting particles is proportional to the contact force. The arrows indicate the shear direction. (B) Example of the evolution of the stress with time. Instantaneous jumps upward correspond to the creation of new contacts. Stress relaxes smoothly, however, within periods where contacts do not change. Interestingly, this situation is opposite to the plasticity of amorphous elastic solids, where stress loads continuously before relaxing by sudden plastic events, as illustrated in (C) for compressed soft elastic particles under quasistatic shear.

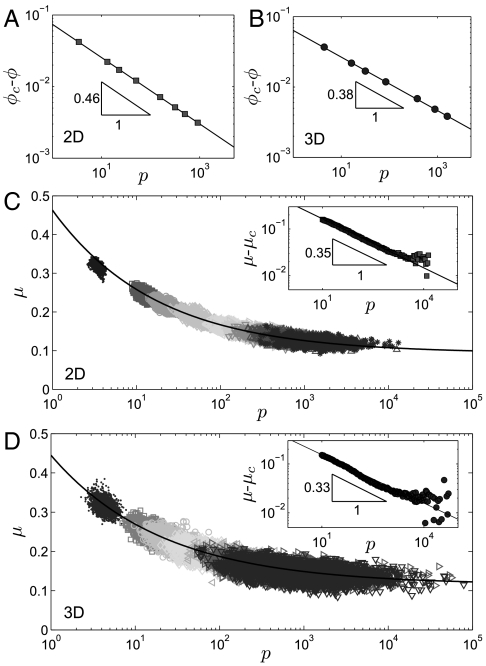
Our results for the constitutive relations are shown in Fig. 2. We first note that fluctuations in pressure for a given ϕ, proportional to the extent along the p-axis of the corresponding data-points cloud, diverge as jamming is approached, as expected from the observation that ϕ_c fluctuates in a finite size system (35). This finite size effect creates a difficulty to accurately extract the exponent α that characterizes the dilatancy, see Eq. 1. Our simulation method does not allow for the study of larger systems, which would improve our estimation of this exponent; nevertheless, our results in two-dimensions are in good agreement with previous work (2, 30, 31). Our results for three dimensions are similar to experimental observations: in three dimensions the friction law follows Eq. 2 with β ≈ 0.33, whereas dilatency follows Eq. 1 with α ≈ 0.38. These exponents are close to the experimentally observed exponents, supporting the claim that hydrodynamical interactions have weak effects, if any, on the critical behavior near jamming. Note that the exponents are found to be similar in two and three dimensions, raising the possibility that they are actually the same.

Fig. 2.

The relation ϕ(p) within ASM is computed by averaging the normalized pressure p at different packing fractions. This relation is well captured by Eq. 1 introduced to describe real suspension flows, with (A) ϕ_C ≈ 0.842 and α ≈ 0.46 for D = 2 and N = 4096 particles, (B) ϕ_C ≈ 0.647 and α ≈ 0.38 for D = 3 and N = 1000. The friction law μ(p) follows Eq. 2, with (a) μ_c ≈ 0.093 and β ≈ 0.35 for D = 2, and (b) μ_c ≈ 0.115 and β ≈ 0.33 for D = 3. The insets display μ - μ_c averaged at fixed pressure. The main plots show nonaveraged data; colors (and symbols) label the different packing fractions at which measurements were made, growing with increasing pressure (see Methods).

In sharp contrast with the fluctuations of pressure for a fixed packing fraction, the fluctuations in various quantities considered as a function of pressure are very limited, and seem to remain regular throughout the entire range of pressures simulated, see Figs. 2, 3 and 5. In addition, we detect no finite size effects when computing means as a function of pressure, see, for example, Fig. 5. Thus pressure is a much more suitable variable than packing fraction to quantify the distance from threshold and to study criticality in a finite system.

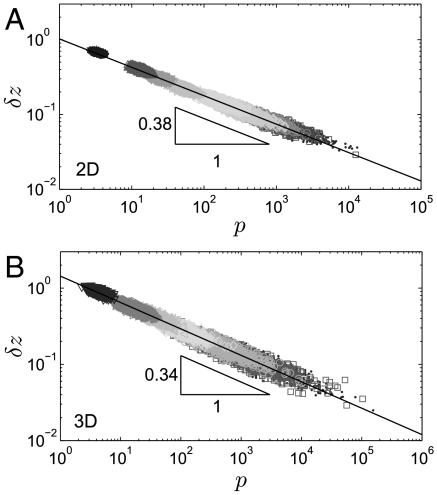
Fig. 3.

The coordination displays scaling near jamming δz ≡ z_c - z ∼ 1/p^δ in (A) two and (B) three dimensions. Particles barely connected to the contact network (making less than two contacts with their surroundings), the so-called rattlers, are removed from the analysis. Colors (and symbols) label different packing fractions (see Methods), growing with increasing pressure, and each data point pertains to a single configuration.

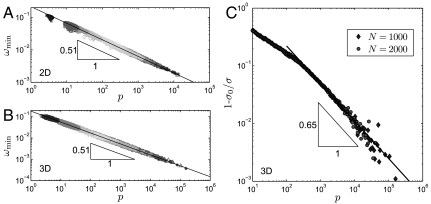
Fig. 5.

Scaling of the lowest frequency ω_min vs. normalized pressure p in (A) two and (B) three dimensions. This modes dominates the rheology near jamming, as can be seen by plotting the relative contribution (σ - σ₀)/σ of all the other modes to the stress, that vanishes as p^-0.65. The relative contribution is found to be independent of N.

Relationship Between Dynamics and Packing Geometry.

Within ASM the viscous drag force 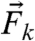acting on particle k at position 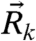is 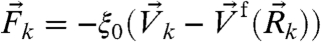, where 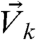and 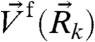are the particle and fluid velocities respectively, and ξ₀ characterizes the viscous drag. This linear relation can be written for all particles in compact notation:

[3]

where the uppercase ket notation 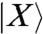indicates a vector of dimension ND, D being the spatial dimension and N the number of particles. 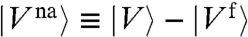is the so-called nonaffine velocity.

In addition to the viscous drag, a force 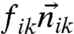is exerted on the kth particle from all particles i which are in contact with particle k, where 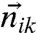is the unit vector along 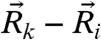. In the viscous limit considered here, forces are balanced 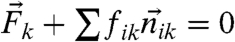, where the sum is over all particles i in contact with k. This equation can be written in compact notation:

[4]

where the lowercase ket notation 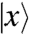indicates a vector of dimension N_c, the number of contacts. The linear operator is of dimension ND × N_c, its nonzero elements correspond to the vectors 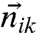, for particles i and k in contact.

The last condition defining ASM is that particles cannot overlap. This condition is best expressed by considering the network of contacts, as illustrated in Fig. 1. This network rewires by instantaneous events where contacts open or close (see Movie S1). In between these discrete events, the network is conserved, and the distance between particles in contact is fixed. This condition implies that

[5]

for all contacts. The N_c linear constraints in the form of Eq. 5 (one constraint for each pair of particles in contact) can be written in compact notation as:

[6]

where 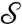is the N_c × ND linear operator that computes the change in pairwise distances 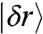between particles in contact, induced by a displacement of the particles 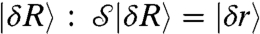. A direct inspection of the elements of 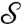indicates that it is the transpose of .

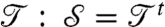Now we may derive an expression for the viscosity. Operating with 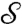on Eq. 3, and using Eqs. 4 and [6], we obtain:

[7]

where 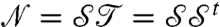is a N_c × N_c symmetric operator, which is generally invertible when the viscosity is finite (see below). 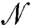contains the information on the topology of the contact network (who is in contact with whom) and the contact orientations. 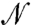characterizes how a contact force field 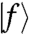is unbalanced 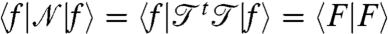. The term 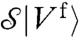on the right-hand side of Eq. 7 is not singular near jamming, as it is the rate at which the contacts lengths would change (generating gaps or overlaps between particles) if particles were following the affine flow of the fluid. One can thus introduce the notation 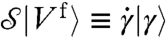. For a pure shear in the (x,y) plane, the components of 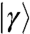are 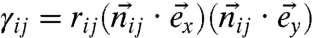, where r_ij is the distance between particles i and j. Inverting Eq. 7 and using this notation we derive an expression for the contact forces:

[8]

This result, together with Eqs. 3 and [4] yields an expression for the dynamics: 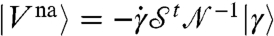. The shear stress σ carried by the particles is related to the contact forces by the relation (36) 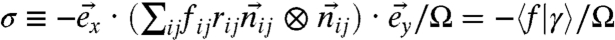, where Ω is the volume of the system. We thus obtain from Eq. 8 the suspension viscosity η:

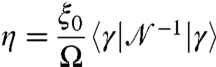[9]

Eq. 9 is a key result, as it shows that all the singularities that appear near jamming within ASM are contained in a single operator, 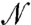, which connects rheology to geometry.

Analogy Between Elasticity and Rheology

The operator 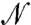bears similarities with the well-studied stiffness matrix 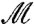that plays a central role in elasticity. By definition, the quadratic expansion of the energy in any elastic system is 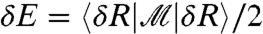. Consider the case of an elastic network of unstretched springs of unit stiffness. Labeling a spring by α, the energy can be expressed in terms of the spring elongation δr_α, namely:

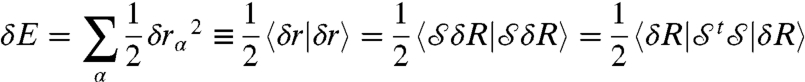[10]

Together with the definition of 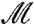, Eq. 10 implies that 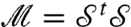. This expression is closely related to 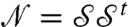, building a connection between rheological properties of suspended hard particles and the elasticity of spring networks with identical geometry. In particular, the spectra of 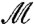and 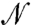are identical for positive eigenvalues λ ≡ ω², where ω is referred to as the mode frequency. To see this let us assume that 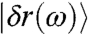is a normalized eigenvector of 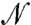, then

[11]

Operating on the above equation with 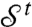we find:

[12]

implying that 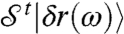is an eigenvector of 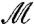with the same eigenvalue ω². Thus, there is a one-to-one correspondence between eigenvectors of 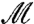and 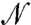for positive eigenvalues.

This observation suggests that the analytical techniques that were developed to study elasticity in random media apply as well to rheology of suspensions, at least within ASM. Here we shall take another route by studying empirically the spectrum of 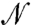, identifying what the spectral signatures of the singularities are in the rheological laws, and compare those with the known singularity in the spectrum of 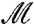near the unjamming transition.

Microscopic Analysis of Flow Configurations

A key variable that characterizes steric hindrance is the average number of contacts per particle, or the coordination z = 2N_c/N. This intuition is substantiated by Eq. 9, which indicates that the viscosity diverges when 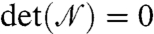. Since 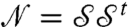, 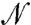must display zero-modes if 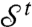does, which must occur if N_c > ND, as 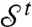is of dimension ND × N_c. For the coordination this argument implies that jamming must occur if z > 2D ≡ z_c, a necessary condition for rigidity derived by Maxwell (23). Earlier numerical work (32) considered the scaling of the coordination with ϕ, where it was found that for ϕ < ϕ_c, z₀ - z ∼ ϕ - ϕ_c with z₀ = 3.8. However, this analysis is hampered by the rather large fluctuations of ϕ_c in finite size systems (35), in addition to errors originating from the inclusion of rattlers. Our numerical procedure allows for a careful measurement of the coordination, displayed in Fig. 3. We find instead:

[13]

with z_c = 2D, δ ≈ 0.38 and δ ≈ 0.34 in two and three dimensions respectively.

Density of States

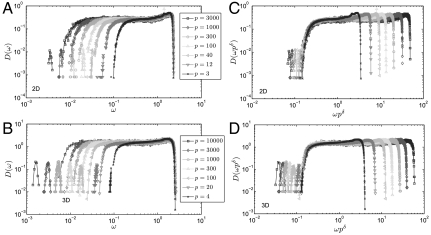
The symmetric operator 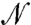is readily obtained from the contact network, and its spectrum is computed numerically. The frequency spectra, or densities of states D(ω) defined as the number of modes per unit frequency per particle, are shown in Fig. 4 as jamming is approached. They consist of two structures: a plateau of modes appearing above some frequency threshold ω^∗, and a gap at lower frequency, containing only one isolated mode of frequency ω_min. Strikingly, this plateau is also present in the vibrational spectrum of simple amorphous solids (14, 17), where its onset frequency scales as z - z_c (15, 16). To determine if this scaling law holds in configurations visited in flows as well, we rescale the frequency axis by δz ∼ 1/p^δ. Fig. 4 displays a striking collapse of the plateau in the density of states, emphasizing the strong connection between elasticity near unjamming and the rheology of dense flows.

Fig. 4.

Spectral analysis of the operator 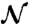governing flow as jamming is approached. The density of states D(ω) averaged over 500 configurations for each pressure indicated in the legend, in (A) two and (B) three dimensions. The amplitude of the peak at low-frequency was rescaled to make it visible. Since it consists of one mode only, this amplitude vanishes in the thermodynamic limit. If the frequency axis is rescaled by the excess coordination p^δ ∼ δz, as in (C, D), the emergence of a plateau in D(ω) collapses, indicating that the frequency at which this plateau appears follows ω^∗ ∼ δz.

The sole exception is the isolated mode at low frequency that does not collapse with this rescaling. Rather, its frequency scales as ω_min ∼ 1/p^ϵ with ϵ ≈ 0.51 independently of the spatial dimension, as shown in Fig. 5. Such biscaling is a new feature of flow not present in the elasticity of solids near unjamming, and it is of critical importance for the rheology.

Using Eq. 9 we can separate the contributions of the first mode σ₀ and of the plateau σ - σ₀ to the shear stress σ. Denoting the lowest-frequency mode as 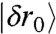, and the rest of the modes by 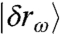, we obtain:

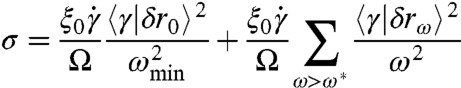[14]

We find that the first term of Eq. 14, denoted σ₀, dominates stress near jamming: σ → σ₀. This stems from the fact that the first eigenvector has a very strong projection on a shear that does not vanish as the number of particle increases: 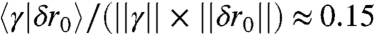in three dimensions. Using that ||γ|| ∼ N and that ||δr₀|| = 1 leads to 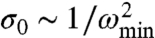. Since σ₀ ∼ σ ∼ p we obtain 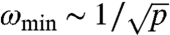or ϵ = 1/2, very close to the observation ϵ ≈ 0.51.

Note that the strong coupling between 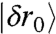and 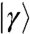implies, together with Eq. 8, that 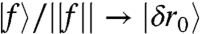as p → ∞. Thus Fig. 1A and Movie S1, that display respectively an example of 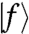and its evolution under shear very close to threshold, are very accurate representations of .

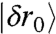The relative contribution of the rest of the density of states, corresponding to the second term in Eq. 14, vanishes as (σ - σ₀)/σ ∼ p^-0.65, as shown in Fig. 5. This exponent can also be rationalized by a simple scaling estimate, similar to arguments previously introduced for isotropic configurations near the unjamming transition (22, 33). Assuming that the modes 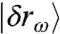forming the plateau in D(ω) have random orientations with respect to a shear (22) leads to 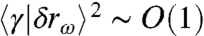. Thus

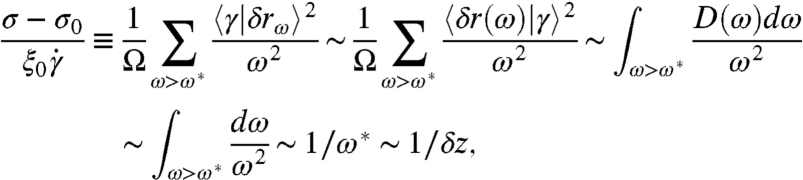implying (σ - σ₀)/σ ∼ δz/σ ∼ δz/p ∼ p^δ-1 which is indeed p^-0.65 in three dimensions. Thus most of the spectrum contributes less and less to the divergence of stress as jamming is approached. This contribution may nevertheless play an important role in the corrections to scaling, such as those leading to a varying friction law in Eq. 2. We shall explore this possibility in future work.

Discussion

We have shown that the rheological properties of ASM flows are described by a single operator 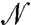, which is closely connected to the stiffness matrix of elastic networks. This result allows us to characterize flow in terms of the spectrum of a single operator 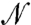. This spectrum presents remarkable features: it displays the plateau of modes controlling the anomalous elastic properties of amorphous solids near the unjamming transition, but also one mode at low-frequency responsible for the sharp divergence of the viscosity. Future work necessary to build a description of flow near jamming should explain (i) what configurations can generate such a biscaling spectrum, (ii) why such configurations are selected by the dynamic, and (iii) what fixes the relationship between ϕ and z.

It is likely that such a description will be of mean-field character. Near the unjamming transition the fact that a frequency scale ω^∗ scales linearly with the excess coordination δz in any dimension reflects the fact that spatial fluctuations of coordination are weak and irrelevant. The unjamming transition is in some sense a mean-field version of rigidity percolation where bonds are deposited randomly on a lattice and where fluctuations are important (34), as a mean-field description of the latter gives the correct elastic behavior near unjamming (16). Our finding that some frequency scale ω^∗ also scales like δz in ASM flows suggests that spatial fluctuations of coordination are irrelevant in dense suspensions too. This is also supported by our observation that more generally, exponents appear to depend weakly, if at all, on spatial dimension.

To conclude, we discuss the generality of our results. Constitutive relations in ASM appear quantitatively similar to experiments in real suspensions. This result might seem surprising at first glance, since the fluid is certainly strongly disturbed by flow near jamming, unlike what ASM assumes. We speculate why these two problems may fall in the same universality class. In real flow dissipation is dominated by the viscous friction resulting from lubrication between neighboring particles. The corresponding tangential friction coefficient has a weak (logarithmic) dependence on the gap between particles, whereas the normal friction coefficient diverges as the inverse of the gap. However evidences (37, 27) support that due to the finite elasticity and/or roughness of the particles, real contacts are eventually formed (37, 27). If so, one expects that the divergence of the normal friction coefficient will have a cutoff, and that the viscosity will be proportional to the square of the relative velocities between particles. In ASM, the viscosity is proportional to the square of the nonaffine velocities. However, we have checked that both quantities are approximately proportional to each other as jamming is approached, supporting that this model is appropriate to describe the scaling properties of suspension flows near jamming. Further support comes from a recent work on the viscoelasticity of amorphous solids near unjamming (33), showing that variations in the dissipation mechanism need not alter the scaling relations for the viscoelastic properties.

Methods

The simulations are based on the ASM equations of motion, which prescribes a velocity to each particle for a given configuration. We propagate the system forward in time over small time steps, while carefully monitoring the formation of new contacts or the destruction of existing contacts. For a complete description of the simulation employed see (29).

We simulated systems of N_2D = 4096 particles in two dimensions, at packing fractions ϕ_2D = 0.82, 0.825, 0.83, 0.835, 0.837, 0.838, 0.839, and 0.840. We also simulated systems of N_3D = 1000 and 2,000 particles in three dimensions, at packing fractions ϕ_3D = 0.61, 0.625, 0.63, 0.635, 0.640, 0.642, and 0.643. In all simulations we used a square box with Lees-Edwards periodic boundary conditions (36) that allows for homogeneous shear flow profiles throughout the simulation cell. Our systems consist of a 50∶50 mixture of small and large particles, where the ratio of the diameters d of the large and small particles is d_large/d_small = 1.4. We add a slight poly-dispersity of 3% in the particle sizes to avoid hexagonal patches in the two-dimensional systems (29). Normal modes are calculated with the LAPACK software package (http://www.netlib.org/lapack/).