Robust averaging during perceptual judgment is not optimal

de Gardelle and Summerfield (1) claimed that, when judging the mean of a set of stimuli, it is optimal to downweight outliers, and that human subjects follow this robust averaging strategy. Here, we show that, in their task, the optimal observer would equally weight all observations. In ref. 1, subjects were presented with a set of eight colors that are denoted by a vector x = (x₁, …, x₈) and drawn independently from a Gaussian distribution on a red–blue color axis with variance σ² and mean of either μ (blue) or −μ (red). On a given trial, μ was set randomly to one of two values, and σ² was set randomly to one of three values. The subject indicated whether the mean was blue (C = 1) or red (C = −1). When the prior probabilities are equal, the optimal decision is based on the likelihoods of both options [i.e., p(x|C = 1) and p(x|C=−1)]. Because μ and σ² are unknown to the observer, the optimal observer computes these likelihoods by averaging (marginalizing) over all six possibilities (Eq. 1):

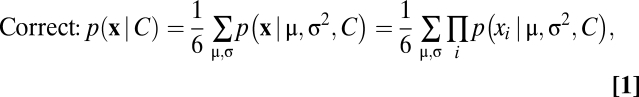where in the last step, we have used the conditional independence of the observations given μ and σ². The work by de Gardelle and Summerfield (1), however, computed the likelihoods by first factorizing and then marginalizing (Eq. 2):

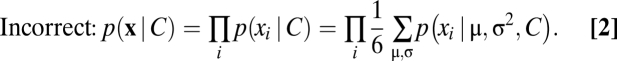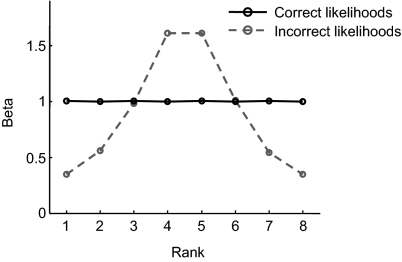
The first step in Eq. 2 is a mathematical mistake, because the observations are only independent when conditioned on μ and σ². They strongly covary otherwise, because the same μ and σ² are used for all observations on a given trial. de Gardelle and Summerfield recognized this mistake in their SI Methods but failed to realize that their main model prediction was a direct consequence of it. Indeed, when we simulate decisions based on the incorrect likelihood (Eq. 2) and then perform logistic regression as in ref. 1, we find downweighting of observations x_i with a larger magnitude (Fig. 1, dashed), consistent with the model predictions in ref. 1. By contrast, the decision based on the correct likelihood (Eq. 1) is to report blue whenever Σ_i x_i is positive (i.e., a simple averaging rule). Thus, the optimal observer equally weights all observations (Fig. 1, solid). The moral of the story is that not applying marginalization and conditional independence rules in the correct order can have severe consequences.

Fig. 1.

Weight given to an observation (normalized logistic regression coefficient) as a function of the rank of the observation obtained by simulating the optimal observer. On each trial, observations were ranked by their values. Downweighting of more outlying values occurs only when incorrect likelihoods (grey, dashed line) but not when correct ones (black, solid line) are used.

The experimental data presented in ref. 1, if reliable, should be taken as evidence against the hypothesis that humans accumulate evidence optimally in this task. That being said, robust averaging is a known concept in perception (2) and can be optimal when the observer considers multiple possible generative processes for the data (3). It remains to be seen whether this explanation applies to the current data. An alternative explanation could be that the stimulus spaces used in ref. 1 were not perceptually uniform.