Phase II Cancer Clinical Trials with Heterogeneous Patient Populations

SUMMARY

The patient population for a phase II trial often consists of multiple subgroups in terms of risk level. In this case, a popular design approach is to specify the response rate and the prevalence of each subgroup, to calculate the response rate of the whole population by the weighted average of the response rates across subgroups, and to choose a standard phase II design such as Simon’s optimal or minimax design to test on the response rate for the whole population. In this case, although the prevalence of each subgroup is accurately specified, the observed prevalence among the accrued patients to the study may be quite different from the expected one because of the small sample size, which is typical in most phase II trials. The fixed rejection value for a chosen standard phase II design may be either too conservative (i.e., increasing the false rejection probability of the experimental therapy) if the trial accrues more high-risk patients than expected or too anti-conservative (i.e., increasing the false acceptance probability of the experimental therapy) if the trial accrues more low-risk patients than expected. We can avoid such problem by adjusting the rejection values depending on the observed prevalence from the trial. In this paper, we investigate the performance of the flexible designs compared with the standard design with fixed rejection values under various settings.

1 Introduction

A typical single-arm phase II trial is to evaluate the efficacy of an experimental therapy compared to a historical control before it proceeds to a large scale phase III trial to be compared to a prospective control. The patient population for a phase II trial often consists of multiple subgroups, also called cohorts, with different prognosis although the study therapy is expected to be similarly beneficial for all subgroups. In this case, the final decision on the study treatment should adjust for the heterogeneity of the patient population.

Suppose that we want to evaluate the tumor response of CD30 antibody, SGN-30, combined with GVD (Gemcitabine, Vinorelbine, Pegylated Liposomal Doxorubicin) chemotherapy in patients with relapsed or refractory classical Hodgkin lymphoma (HL) through a phase II trial. In a previous study, GVD only has led to responses in 65% of patients with relapsed or refractory HL patients who never had a transplant and 75% in the transplant group. About 50% of patients in the previous study never had a transplant. Combining the data from the two cohorts, the response rate (RR) for the whole patient population is estimated as 70%(= 0.5 × 0.65 + 0.5 × 0.75).

Using this outcome as historical control data, the new study is designed as a single-arm trial for testing

$$H_0:p\le 70\%\text{against}{H}_a:p>70\%,$$ (1)

where p denotes the true RR of the combination therapy in the patient population combining the two subgroups, one for those with prior transplants and the other for those without one.

A standard design to account for the heterogeneity of the patient population is a single-arm trial based on a specified prevalence for each cohort for testing hypotheses (1). For the example study, we consider an increase in RR by 15% or larger clinically significant for each cohort. So, we will not be interested in the combination therapy if the true RR, p, is lower than p₀ = 70% and will be strongly interested if the true RR is higher than p_a = 85%. Then, the Simon’s (1989) two-stage optimal design for testing

$$H_0:p_0=70\%\text{against}{H}_a:p_a=85\%$$

with type I error no larger than α^* = 0.1 and power no smaller than 1−β^* = 0.9 is described as follows.

• Stage 1

  Accrue n₁ = 20 patients. If ā₁ = 14 or fewer patients respond, then we stop the trial concluding that the combination therapy is inefficacious. Otherwise, the trial proceeds to stage 2.

• Stage 2

  Accrue an additional n₂ = 39 patients. If more than ā = 45 patients out of the total n = 59(= n₁ + n₂) respond, then the combination therapy will be accepted for further investigation.

Assuming that the number of responders from the two stages are independent binomial random variables with probability of ‘success’ p_l under H_l (l = 0, a), we obtain the exact type I error and power of the two-stage design as 0.0980 and 0.9029, respectively.

In developing such a standard design, an accurate specification of the prevalence of each cohort is critical. If the prevalence is erroneously specified, the type I error of the statistical testing can not be accurately controlled. Even when the prevalence is accurately specified, the observed prevalence from the new study may be quite different from the true one. This can easily happen in phase II trials with mostly small sample sizes. If a new study accrues a larger number of high-risk (low-risk) patients than expected, then the trial will have a higher false negativity (positivity).

London and Chang (2005) resolve this issue by choosing rejection values based on a stratified analysis method. They adopt early stopping boundaries for both low and high efficacy cases based on a type I error rate and power spending function approach. Sposto and Gaynon (2009) propose a two-stage design with a lower stopping value only based on large sample approximations that may not hold well for phase II trials with small sample sizes. Wathen et al. (2008) propose a Bayesian method to test on the efficacy for each subgroup.

In this paper, we consider a similar design situation to those by London and Chang (2005) and Sposto and Gaynon (2009). The sample sizes are determined by a standard design, such as Simon’s minimax or optimal, based on a specified prevalence of each cohort, but the rejection value is adjusted depending on the observed prevalence from the trial. Conditioning on the observed prevalence, the rejection values are chosen by calculating the type I error rate and the power using the accurate probability distributions accounting for the small sample sizes of typical phase II trials. Using some real examples we show that our design accurately controls the conditional type I error rate and power in a wide range of the prevalence. In contrast, the conditional type I error of a standard design with fixed rejection values wildly fluctuates around the pre-specified level depending on the observed prevalence. Furthermore, the marginal type I error and power of the standard design can be heavily biased if the specified prevalence is different from the true prevalence.

The rejection values for a multi-stage phase II trial are chosen for the pre-determined sample size at each stage. However, due to dropouts or over-accrual, the realized sample size of the trial may be slightly different from the planned sample sizes. In this case, the chosen rejection values with respect to the planned sample size are not valid any more. To tackle this issue, we propose to calculate a p-value conditioning on the realized sample sizes and to conduct a statistical testing by comparing the conditional p-value with the pre-specified type I error rate. We also present a single-stage design for stratified phase II study analysis.

2 Single-Stage Designs

Suppose that we want to design a phase II trial on a new therapy with respect to a patient population with two cohorts of patients, called the high-risk cohort and the low-risk cohort. Cases with more than two cohorts will be discussed later. For cohort j(= 1, 2), let p_j denote the RR of the therapy and γ_j denote the prevalence (γ₁ + γ₂ = 1). The RR for the combined population is given as p = γ₁p₁ + γ₂p₂. Based on some historical control data, we will not be interested in the new therapy if its RR for cohort j is p_0j or lower, and will be highly interested in it if its RR is p_aj(= p_0j + Δ_j for Δ_j > 0) or higher. Let p₀ = γ₁p₀₁ + γ₂p₀₂ and p_a = γ₁p_a1 + γ₂p_a2.

2.1 Unstratified Designs

A standard single-stage design to test hypotheses H₀: p ≤ p₀ vs. H_a: p > p₀ is to accrue a certain number of patients, say n, and to reject the therapy, i.e. failing to reject H₀, if the observed number of responders is smaller than or equal to a chosen rejection value ā. Given pre-specified type I error rate α^*, power 1 − β^*, and clinically significant difference Δ_j for cohort j(=1,2), we choose the smallest n together with an integer ā satisfying

$$\alpha =\text{P}(X>\overline{a}\mid p=p_0)\le {\alpha }^{\ast }$$

and

$$1-\beta =\text{P}(X>\overline{a}\mid p=p_a)\ge 1-{\beta }^{\ast },$$ (2)

where X denotes the number of responders among n patients. Given ā, we usually calculate the exact type I error α and power 1−β by regarding X as a binomial random variable with n independent Bernoulli trials with probability of success p = γ₁p₁ + γ₂p₂, i.e. α = B(ā|n, p₀) and 1 − β = B(ā|n, p_a), where $B(x\mid n,p)={\sum }_{i=x+1}^{n}b(x\mid n,p)$ and

$$b(x\mid n,p)=\left(\begin{array}{c}n\\ x\end{array}\right)p^x{(1-p)}^{n-x}\text{for}x=0,1,\dots ,n.$$

We call (n, ā) a standard or unstratified design.

Let b(n, p) denote the binomial distribution with n independent Bernoulli trials with probability of success p. Let M_j be a random variable denoting the number of patients from cohort j among n patients. Assuming that the population consists of infinitely many patients, we have M₁ ~ b(n, γ₁) and M₂ = n − M₁. Conditioning on M₁ = m₁, the number of responders X_j among m_j patients from cohort j follows b(m_j, p_0j) under H₀. Hence, it is easy to show that above type I error for a standard design can be calculated also as

$$\alpha ={\text{E}}^{M_1}\text{P}(X_1+X_2>\overline{a}\mid p_{01},p_{02},M_1)=\sum _{m_1=0}^n\sum _{x_1=0}^{m_1}\sum _{x_2=0}^{n-m_1}I(x_1+x_2>\overline{a})b(x_1\mid m_1,p_{01})b(x_2\mid n-m_1,p_{02})b(m_1\mid n,{\gamma }_1).$$

Power (2) can be calculated similarly.

2.2 Stratified Designs

For a stratified single-stage design, we propose to choose a value a satisfying the α^*-condition given the observed m₁ value while fixing n(= m₁ + m₂) at the sample size of a standard design. Given M₁ = m₁ (m₂ = n − m₁), the conditional type I error for a rejection value a is calculated as

$$\alpha (m_1)=\text{P}(X_1+X_2>a\mid p_{01},p_{02},m_1)=\sum _{x_1=0}^{m_1}\sum _{x_2=0}^{m_2}I(x_1+x_2>a)b(x_1\mid m_1,p_{01})b(x_2\mid m_2,p_{02}).$$

Given m₁, we want to choose the maximal a = a(m₁) such that α(m₁) ≤ α^*. For the chosen rejection value a = a(m₁), the conditional power is calculated as

$$1-\beta (m_1)=\text{P}(X_1+X_2>a\mid p_{a1},p_{a2},m_1)=\sum _{x_1=0}^{m_1}\sum _{x_2=0}^{m_2}I(x_1+x_2>a)b(x_1\mid m_1,p_{a1})b(x_2\mid m_2,p_{a2}).$$ (3)

In summary, a stratified single-stage design for a population with two cohorts is chosen as follows:

• Step 1Specify γ₁, (p₀₁, p₀₂, p_a1, p_a2), and (α^*, 1 − β^*).
• Step 2Choose a reasonable n as follows.

  1. Calculate p₀ = γ₁p₀₁ + γ₂p₀₂ and p_a = γ₁p_a1 + γ₂p_a2.

  2. Choose a standard single-stage design (n, ā) for testing

     $$H_0:p=p_0\text{vs}.H_a:p=p_a$$

     under the (α^*, 1 − β^*)-condition. We choose this n (or a little larger number) as the sample size of the stratified design.

• Step 3For m₁ ∈ [0, n], choose the maximum a = a(m₁) satisfying α(m₁) ≤ α^*.
• Step 4Given (n, m₁, a), calculate the conditional power 1 − β(m₁) by (3).

The study protocol using a stratified design may provide a table of {a(m₁), α(m₁), 1−β(m₁)} for 0 ≤ m₁ ≤ n. When the study is over, we observe m₁ and x(= x₁ + x₂), and reject the study therapy if x ≤ a(m₁).

Noting that M₁ ~ b(n, γ₁), we can calculate the marginal type I error and power of the stratified design by

$$\alpha =\text{E}\{\alpha (M_1)\}=\sum _{m_1=0}^n\alpha (m_1)b(m_1\mid n,{\gamma }_1)$$

and

$$1-\beta =\text{E}\{1-\beta (M_1)\}=\sum _{m_1=0}^n\{1-\beta (m_1)\}b(m_1\mid n,{\gamma }_1),$$

respectively. Since, for each m₁ ∈ [0, …, n], we choose a = a(m₁) so that its conditional type I error does not exceed α^*, the marginal type I error will not exceed α^*.

2.3 Example 1

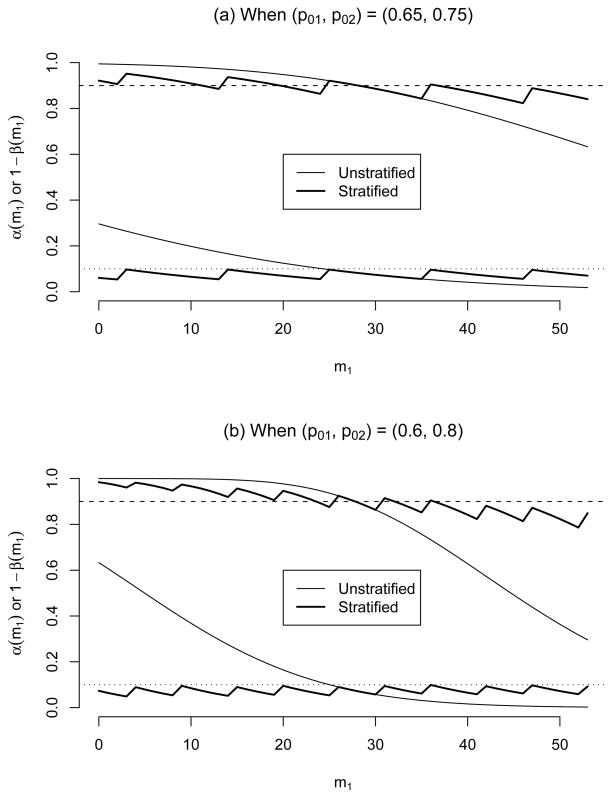
Let’s consider the study discussed in Section 1 using Δ₁ = Δ₂ = 0.15. Under γ₁ = γ₂ = 0.5 and response rates (p₀₁, p₀₂) = (0.65, 0.75), the hypotheses in terms of the population RR are expressed as H₀: p₀ = 0.7 and H_a: p₁ = 0.85. For (α^*, 1 − β^*) = (0.1, 0.9), the standard (unstratified) design with the minimal sample size is (n, ā) = (53, 41) which has α = 0.0906 and 1 − β = 0.9093. The type I error and power are valid only when the true prevalence is γ₁ = γ₂ = 0.5.

Suppose that the study observed (x₁, x₂) = (28, 13) and m₁ = 36. Note that the observed prevalence for the high-risk cohort, γ̂₁ = 36/53 = 0.68, is much larger than the expected γ₁ = 0.5. By the unstratified design, x = 41 equals the rejection value ā = 41, so that the therapy will be rejected. However, noting that m₁ = 36 is much larger than expected, the stratified design lowers the rejection value to a = 40, so that, with observation x = 41, the therapy will be accepted for further investigation. Similarly, the unstratified Simon’s design may falsely accept the therapy if γ̂₁ is much lower than the specified prevalence γ₁ = 0.5.

Table 1 lists the conditional type I error and power of the standard unstratified design for each m₁ ∈ [0, n]. Note that if m₁ is much larger than nγ₁, i.e. too many cohort 1 (high risk) patients are accrued, then the standard rejection value ā = 41 is so anti-conservative that the conditional type I error and power become smaller than the specified α^* = 0.1 and 1 − β^* = 0.9, respectively. On the other hand, if m₁ is too small compared to nγ₁, i.e. too many cohort 2 (low-risk) patients are accrued, then the standard rejection value ā = 41 is so conservative that the conditional type I error becomes larger than the specified α^* = 0.1 level. Figure 1(a) displays the conditional type I error rate and power of the standard (unstratified) design. We observe that the conditional type I error of the standard design widely varies between 0.0182 for m₁ = 53 and 0.2961 for m₁ = 0. Its conditional power also widely varies around 1 − β^* = 0.9.

Table 1.

Conditional type I error and power of single-stage standard (unstratified) and stratified designs with n = 53 for (p₀₁, p₀₂, Δ) = (0.65, 0.75, 0.15) and (α^*, 1 − β^*) = (0.1, 0.9). The standard design has a fixed critical value ā = 41.

m1	Unstratified		Stratified			m1	Unstratified		Stratified
	α	1 − β	a	α	1 − β		α	1 − β	a	α	1 − β
0	0.2961	0.9947	44	0.0606	0.9215	27	0.0869	0.9081	41	0.0869	0.9081
1	0.2852	0.9939	44	0.0569	0.9142	28	0.0823	0.9011	41	0.0823	0.9011
2	0.2746	0.9930	44	0.0535	0.9065	29	0.0780	0.8938	41	0.0780	0.8938
3	0.2641	0.9919	43	0.0972	0.9517	30	0.0738	0.8862	41	0.0738	0.8862
4	0.2540	0.9908	43	0.0920	0.9467	31	0.0699	0.8782	41	0.0699	0.8782
5	0.2440	0.9896	43	0.0870	0.9414	32	0.0661	0.8699	41	0.0661	0.8699
6	0.2343	0.9882	43	0.0822	0.9357	33	0.0625	0.8612	41	0.0625	0.8612
7	0.2249	0.9866	43	0.0776	0.9296	34	0.0590	0.8523	41	0.0590	0.8523
8	0.2157	0.9849	43	0.0733	0.9232	35	0.0557	0.8430	41	0.0557	0.8430
9	0.2067	0.9830	43	0.0691	0.9163	36	0.0526	0.8334	40	0.0961	0.9049
10	0.1980	0.9810	43	0.0651	0.9091	37	0.0496	0.8236	40	0.0913	0.8981
11	0.1895	0.9787	43	0.0614	0.9015	38	0.0468	0.8134	40	0.0867	0.8909
12	0.1813	0.9763	43	0.0578	0.8935	39	0.0441	0.8029	40	0.0822	0.8835
13	0.1734	0.9736	43	0.0544	0.8851	40	0.0415	0.7922	40	0.0780	0.8757
14	0.1656	0.9707	42	0.0969	0.9368	41	0.0391	0.7812	40	0.0739	0.8677
15	0.1582	0.9676	42	0.0919	0.9311	42	0.0367	0.7699	40	0.0701	0.8593
16	0.1510	0.9642	42	0.0870	0.9250	43	0.0346	0.7584	40	0.0664	0.8506
17	0.1440	0.9606	42	0.0823	0.9186	44	0.0325	0.7467	40	0.0628	0.8417
18	0.1373	0.9566	42	0.0779	0.9119	45	0.0305	0.7347	40	0.0594	0.8325
19	0.1308	0.9525	42	0.0736	0.9048	46	0.0287	0.7225	40	0.0562	0.8230
20	0.1245	0.9480	42	0.0696	0.8973	47	0.0269	0.7102	39	0.0955	0.8886
21	0.1185	0.9432	42	0.0657	0.8895	48	0.0252	0.6977	39	0.0908	0.8813
22	0.1127	0.9382	42	0.0620	0.8813	49	0.0237	0.6850	39	0.0864	0.8738
23	0.1071	0.9328	42	0.0585	0.8727	50	0.0222	0.6722	39	0.0820	0.8659
24	0.1017	0.9271	42	0.0551	0.8638	51	0.0208	0.6592	39	0.0779	0.8578
25	0.0966	0.9211	41	0.0966	0.9211	52	0.0195	0.6462	39	0.0739	0.8495
26	0.0916	0.9148	41	0.0916	0.9148	53	0.0182	0.6330	39	0.0701	0.8408

Figure 1.

Conditional type I error and power of standard (unstratified) and stratified designs with n = 53 for (α^*, 1 − β^*, Δ) = (0.1, 0.9, 0.15). The standard design has a fixed critical value ā = 41. The upper lines are conditional powers and the lower lines are conditional type I error.

The second part of Table 1 reports the conditional rejection value a(m₁) and its {α(m₁), 1− β(m₁)} for each m₁ ∈ [0, n]. The conditional rejection value a(m₁) decreases from 44 to 39 as m₁ increases. Note that ā = a(m₁) = 41 for m₁ values around nγ₁ = 26.5. Figure 1(a) also displays the conditional type I error rate and power of the stratified design. While the conditional type I error of the stratified design α(m₁) is closely controlled below α^*, the conditional power is also well controlled around 1 − β^* = 0.9. If we want 1 − β to be larger than 1 − β^* for all m₁ ∈ [0, n], we have to choose a slightly larger n than 53.

If the difference of the response probabilities between two cohorts |p₀₁ − p₀₂| is larger, then the range of the rejection values for the stratified design will be wider, and the conditional type I error and power of the standard design will vary more widely. Let’s consider (p₀₁, p₀₂) = (0.6, 0.8) and Δ₁ = Δ₂ = 0.15. Under (γ₁, α^*, 1 − β^*) = (0.5, 0.1, 0.9), the standard design will be the same as above, (n, ā) = (53, 41), but the stratified rejection value a(m₁) decreases from 47 to 37 as m₁ increases from 0 to 53. Figure 1(b) displays the conditional type I error rate and power of the standard and stratified designs. Comparing Figures 1(a) and (b), we observe that the stratified design controls its conditional type I error rate and power closely to their nominal levels regardless of |p₀₁ − p₀₂| value, but those of the standard design change further away from their specified levels with a larger difference. We also observe that, with a larger |p₀₁ − p₀₂| value, the conditional type I error and power of the stratified design fluctuate more often because the conditional critical value changes more frequently, see Figure 1(b).

Let’s investigate the impact of an erroneously specified prevalence on the study design. Suppose that the true prevalence is γ₁ = 0.3, but the study is designed under a wrong specification of γ₁ = 0.5. Let’s assume (p₀₁, p₀₂) = (0.65, 0.75), Δ₁ = Δ₂ = 0.15, and (α^*, 1 − β^*) = (0.1, 0.9) as above. Under the erroneously specified prevalence, the standard and stratified designs will be the same as above, as shown in Table 1. The standard design has marginal type I error and power (α, 1 − β) = (0.1530, 0.9631) and the stratified design has (α, 1 − β) = (0.0767, 0.9116). Under the true γ₁ = 0.3, p₀ = γ₁p₀₁ + γ₂p₀₂ = 0.72 and p₁ = γ₁p_a1 + γ₂p_a2 = 0.87 are farther away from 1/2 than those under the specified γ₁ = 0.5, so that the marginal power for the stratified design is still larger than 1 − β^* even though the marginal type I error is much below α^* = 0.1. The marginal type I error for the standard design is much larger than the specified α ^* = 0.1. Under a wrong projection of the prevalence, the type I error of a standard design can be heavily biased, but that of the stratified design will be always controlled below α^*.

Now, suppose that the true prevalence is γ₁ = 0.7, but the study is designed under a erroneously specified γ₁ = 0.5. In this case, the standard design has marginal type I error and power (α, 1−β) = (0.0501, 0.8209) and the stratified design has (α, 1−β) = (0.0768, 0.8762). The power for the stratified design is slightly smaller than 1−β^* because of the conservative adjustment of conditional type I error. However, the power for the standard design is much smaller than 1 − β^*. The impact of erroneously specified prevalence on the bias of marginal type I error and power will be larger with a larger difference between p₀₁ and p₀₂.

3 Two-Stage Designs

Because of ethical and economical issues, two-stage designs have been more popular for phase II cancer clinical trials than single-stage designs. We may stop a trial early when the RR of a study treatment turns out to be either too low or too high (e.g., London and Chang, 2005), but we consider the more popular design with an early stopping due to a low RR only here. If the experimental treatment is efficacious, we usually do not have a compelling ethical argument to stop the trial early and want to continue collecting more data to be used in designing a future phase III trial. Furthermore, this simplifies the computations and makes the statistical testing easier when the final sample size is different from a pre-determined one. Under a two-stage design, we accrue n_k patients during stage k(= 1, 2). Let n = n₁ + n₂. For stage k(= 1, 2) and cohort j(= 1, 2), let M_kj and X_kj be random variables denoting the number of patients and the number of responders, respectively. Note that n_k = m_k1 + m_k2.

3.1 Unstratified Designs

An example standard (unstratified) two-stage design is demonstrated in Section 1. Given (α^*, 1−β^*), a standard design (n₁, n₂, ā₁, ā) is chosen among the two-stage designs to satisfy α ≤ α^* and 1 − β ≥ 1 − β^*, where α and 1 − β are obtained assuming that X₁ = X₁₁ + X₁₂ and X₂ = X₂₁ + X₂₂ are independent binomial random variables with probability of success p₀ under H₀ and p_a under H_a, respectively, refer to e.g. Simon (1989) and Jung et al. (2001).

3.2 Stratified Designs

Given (M₁₁, M₂₁) = (m₁₁, m₂₁), a design (n₁, n₂, a₁, a) has conditional type I error

$$\begin{array}{c}\alpha (m_{11},m_{21})=\text{P}(X_{11}+X_{12}>a_1,X_{11}+X_{12}+X_{21}+X_{22}>a\mid p_{01},p_{02})\\ =\sum _{x_{11}=0}^{m_{11}}\sum _{x_{12}=0}^{m_{12}}\sum _{x_{21}=0}^{m_{21}}\sum _{x_{22}=0}^{m_{22}}I(x_{11}+x_{12}>a_1,x_{11}+x_{12}+x_{21}+x_{22}>a)\\ \times b(x_{11}\mid m_{11},p_{01})b(x_{12}\mid m_{12},p_{02})b(x_{21}\mid m_{21},p_{01})b(x_{22}\mid m_{22},p_{02})\end{array}$$ (1)

and power

$$\begin{array}{c}1-\beta (m_{11},m_{21})=\text{P}(X_{11}+X_{12}>a_1,X_{11}+X_{12}+X_{21}+X_{22}>a\mid p_{a1},p_{a2})\\ =\sum _{x_{11}=0}^{m_{11}}\sum _{x_{12}=0}^{m_{12}}\sum _{x_{21}=0}^{m_{21}}\sum _{x_{22}=0}^{m_{22}}I(x_{11}+x_{12}>a_1,x_{11}+x_{12}+x_{21}+x_{22}>a)\\ \times b(x_{11}\mid m_{11},p_{a1})b(x_{12}\mid m_{12},p_{a2})b(x_{21}\mid m_{21},p_{a1})b(x_{22}\mid m_{22},p_{a2}).\end{array}$$ (4)

We want to find a two-stage stratified design {n₁, n₂, a₁(m₁₁), a(m₁₁, m₂₁)} whose conditional type I error is smaller than or equal to α^* for each combination of (m₁₁, m₂₁) in m_k1 ∈ [0, n_k]. In order to simplify the computation associated with the search procedure, we fix (n₁, n₂) at the first and second stage sample sizes for a standard two-stage design based on a specified prevalence γ₁, such as Simon’s (1989) minimax or optimal design, or admissible design by Jung et al. (2004). Given M₁₁ = m₁₁, we also propose to fix a₁ = a₁(m₁₁) at [m₁₁p₀₁ + m₁₂p₀₂], where [c] denotes the largest integer not exceeding c. In other words, we reject the experimental therapy early if the observed number of responders from stage 1 is no larger than the expected number of responders under H₀. Now, the only design parameter we need to choose is a, the rejection value for stage 2. Given {α^*, n₁, m₁₁, n₂, m₂₁, a₁(m₁₁)}, we choose the largest a = a(m₁₁, m₂₁) satisfying α(m₁₁, m₂₁) ≤ α^*. Its conditional power, 1 − β(m₁₁, m₂₁), is calculated by (4).

If the observed prevalence is close to the specified one (i.e., m₁₁/n₁ ≈ γ₁ and m₂₁/n₂ ≈ γ₁), then the conditional rejection values {a₁(m₁₁), a(m₁₁, m₂₁)} will be the same as the unstratified rejection values (ā₁, ā). As in single-stage designs, the conditional power may be smaller than 1 − β^* for some (m₁₁, m₂₁). If we want to satisfy 1 − β ≥ 1 − β^* for all combinations of {(m₁₁, m₂₁), 0 ≤ m₁₁ ≤ n₁, 0 ≤ m₂₁ ≤ n₂}, then we have to choose a slightly larger n than that of a standard design.

When the true prevalence of cohort 1 is γ₁, M_k1 for k = 1, 2 are independent random variables following b(n_k, γ₁). Given (M₁₁, M₂₁) = (m₁₁, m₂₁), let α(m₁₁, m₂₁) and 1 −β(m₁₁, m₂₁) denote the conditional type I rate and power for conditional rejection values {a₁(m₁₁), a(m₁₁, m₂₁)}, respectively. Then, the marginal (unconditional) type I error and power are obtained by

$$\begin{array}{c}\alpha =\sum _{m_{11}=0}^{n_1}\sum _{m_{21}=0}^{n_2}\alpha (m_{11},m_{21})b(m_{11}\mid n_1,{\gamma }_1)b(m_{21}\mid n_2,{\gamma }_1)\\ 1-\beta =\sum _{m_{11}=0}^{n_1}\sum _{m_{21}=0}^{n_2}\{1-\beta (m_{11},m_{21})\}b(m_{11}\mid n_1,{\gamma }_1)b(m_{21}\mid n_2,{\gamma }_1),\end{array}$$

respectively. In summary, a phase II trial with a stratified two-stage design is conducted as follows.

• Step 1Specify (p₀₁, p₀₂, p_a1, p_a2) and (α^*, 1 − β^*).
• Step 2Choose sample sizes for two stages (n₁, n₂) by:

  1. Specify γ₁, the prevalence for cohort 1.

  2. For p₀ = γ₁p₀₁ + γ₂p₀₂ and p_a = γ₁p_a1 + γ₂p_a2, choose a standard (unstratified) two-stage design for testing

     $$H_0:p=p_0\text{vs}.H_a:p=p_a$$

     that satisfies the (α^*, 1 − β^*)-condition. We use (n₁, n₂) for the chosen standard design as the stage 1 and 2 sample sizes of the stratified design.

• Step 3After stage 1, calculate a₁ = a₁(m₁₁) = [m₁₁p₀₁ + m₁₂p₀₂] based on the observed m₁₁. We reject the therapy if x₁ = x₁₁ + x₁₂ is smaller than or equal to a₁(m₁₁). Otherwise, we proceed to stage 2.
• Step 4After stage 2, choose the maximum a = a(m₁₁, m₂₁) satisfying α(m₁₁, m₂₁) ≤ α^* based on (m₁₁, m₂₁). Accept the therapy if x = x₁₁ +x₁₂ +x₂₁ +x₂₂ is larger than a(m₁₁, m₂₁).
• Step 5The conditional power 1 − β(m₁₁, m₂₁) for a two-stage design (n₁, m₁₁, n₂, m₂₁, a₁, a) is calculated by (4).

Note that the description of the whole procedure and the design parameters listed in Steps 1 and 2 should be included in the study protocol.

3.3 Example 2

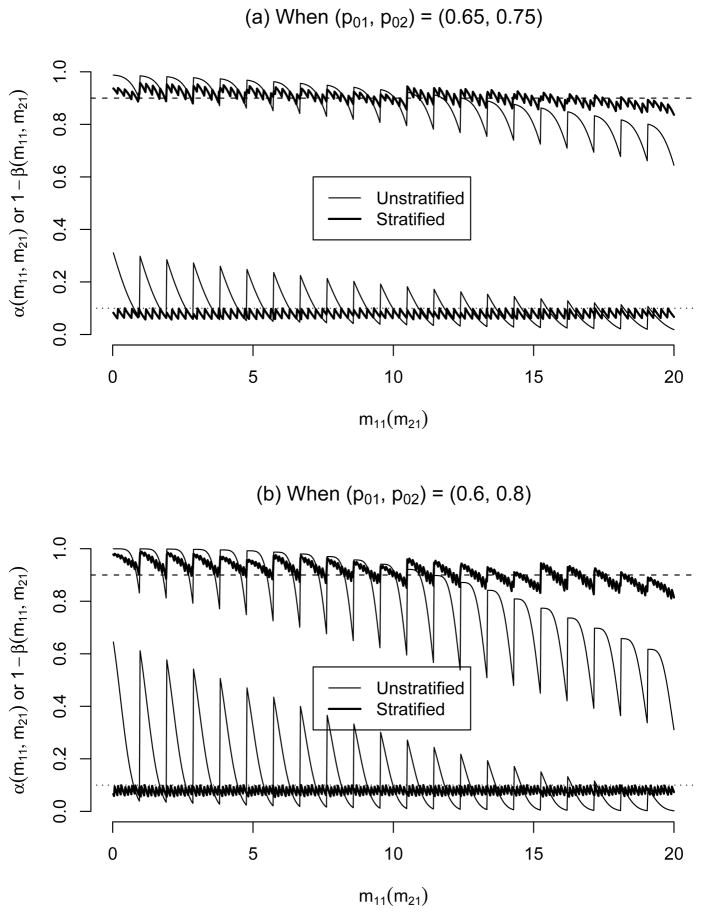
Let’s consider the design setting of Example 1 with (p₀₁, p₀₂, Δ₁, Δ₂) = (0.65, 0.75, 0.15, 0.15), γ₁ = 0.5 and (α^*, 1−β^*) = (0.1, 0.9). Under the setting, the Simon’s optimal two-stage design is given as (n₁, n, ā₁, ā) = (20, 59, 14, 45). We choose (n₁, n) = (20, 59) for our stratified two-stage design.

Suppose that the study observed (x₁, x) = (15, 45) and (m₁₁, m₂₁) = (14, 28). Note that much larger number of patients than expected are accrued from the high-risk group, cohort 1. By the Simon’s design, x = 45 equals ā = 45, so that the therapy will be rejected. However, the stratified critical values for (m₁₁, m₂₁) = (14, 28) are given as (a₁, a) = (13, 44), so that, with observations (x₁, x) = (15, 45), the therapy will be accepted for further investigation.

Figure 2(a) displays the conditional type I error and power of the Simon’s optimal design (marked as ‘Unstratified’) and the stratified design under the design settings. While the conditional type I error of the stratified design is closely controlled below α^*, that of the unstratified design wildly fluctuates between 0.0185 and 0.3110 depending on (m₁₁, m₂₁). Also, the conditional power of the stratified design is closely maintained around 1 − β^*, but that of the Simon’s design widely changes between 0.6447 and 0.9876. In the x-axis of Figure 2(a) (Figure 2(b) also), only m₁₁ values are marked, but actually m₂₁ values run from 0 to n₂ = 39 between consecutive m₁₁ values. Consequently, the conditional type I error rate and power, especially for the standard unstratified design, regularly fluctuate between consecutive m₁₁ values.

Figure 2.

Conditional type I error and power of two-stage standard (unstratified) and stratified designs under (α^*, 1 − β^*, Δ) = (0.1, 0.9, 0.15). The unstratified design has (n₁, n, ā₁, ā) = (20, 59, 14, 45). The upper lines are conditional powers and the lower lines are conditional type I error.

Figure 2(b) displays the conditional type I error and power of the two designs when the two cohorts have a larger difference in RR, (p₀₁, p₀₂) = (0.6, 0.8), with other parameters fixed at the same values as above. Note that, with γ₁ = 0.5, Simon’s optimal design will be identical to that for (p₀₁, p₀₂) = (0.65, 0.75). As in the single-stage design case (Figure 2(b)), we observe that the conditional type I error and power of the the unstratified design fluctuate more wildly than those with (p₀₁, p₀₂) = (0.65, 0.75), whereas the performance of the stratified design is almost the same.

If the true prevalence is accurately specified, then the Simon’s optimal design has marginal type I error and power of (α, 1 − β) = (0.0954, 0.9010), and the stratified design has (α, 1 − β) = (0.0792, 0.9044) if (p₀₁, p₀₂) = (0.65, 0.75) and (α, 1 − β) = (0.0788, 0.9159) if (p₀₁, p₀₂) = (0.6, 0.8). Both designs satisfy (α^*, 1 − β^*) = (0.1, 0.9). However, if the true prevalence of cohort 1 is γ₁ = 0.3 but γ₁ = 0.5 is specified in designing the study, then the Simon’s design has (α, 1 − β) = (0.1618, 0.9521) if (p₀₁, p₀₂) = (0.65, 0.75) and (α, 1 − β) = (0.2548, 0.9798) if (p₀₁, p₀₂) = (0.6, 0.8). Note that the Simon’s design has a more biased marginal type I error when two cohorts are more different in RR. On the other hand, the stratified design always controls the marginal type I error below α^* and power close to 1 − β^* even under an erroneously specified prevalence, e.g. (α, 1 − β) = (0.0776, 0.9203) if (p₀₁, p₀₂) = (0.65, 0.75) and (α, 1 − β) = (0.0782, 0.9481) if (p₀₁, p₀₂) = (0.6, 0.8).

4 Some Extensions

In this section, we present some extended concepts of stratified designs that are discussed above.

4.1 Conditional P-value

In the previous sections, a stratified two-stage design is determined by the sample sizes (n₁, n₂) and the rejection value a₁, a) conditioning on the number of patients from each cohort at each stage at the design stage. When the trial is completed, however, the number of patients accrued to the study may be slightly different from the predetermined sample size. This happens since often some patients drop out or turn out to be ineligible after registration. Because of this, we usually accrue a slightly larger number of patients than the planned sample size, say 5% more. So, the total number of eligible patients at the end of a trial may be different from the planned n. In this case, sample size is a random variable, and the rejection value chosen for the planned sample size may not be valid any more. As a flexible testing method for two-stage phase II trials, we propose to calculate the p-value conditioning on the observed sample size as well as the observed prevalence from each cohort, and to reject H₀ when the conditional p-value is smaller than the pre-specified α^* level.

If a trial is stopped due to lack of efficacy after stage 1, then usually we are not interested in p-value calculation. Suppose that the trial has proceeded to stage 2 to observe (x₁, x) together with (n₁, m₁₁, n₂, m₂₁). Then, the interim testing after stage 1 will be conducted using the rejection value a₁ = [m₁₁p₀₁ + m₁₂p₀₂]. Given m_kj (m_k1 + m_k2 = n_k), X_kj ~ b(m_kj, p_0j) under H₀. Hence, the p-value for an observation (x₁₁, x₁₂, x₂₁, x₂₂) conditioning on (n₁, m₁₁, n₂, m₂₁) is obtained by

$$\text{p}-\text{value}=\sum _{i_{11}=0}^{m_{11}}\sum _{i_{12}=0}^{m_{12}}\sum _{i_{21}=0}^{m_{21}}\sum _{i_{22}=0}^{m_{22}}I(i_{11}+i_{12}>a_1,i_{11}+i_{12}+i_{21}+i_{22}\ge x)\prod _{j=1}^2\prod _{k=1}^{2}b(i_{kj}\mid m_{kj},p_{0j}).$$

We reject H₀ if p-value < α^*. Note that the calculation of a conditional p-value does not require specification of the true prevalence. In order to avoid informative sampling issue, the final sample size should be determined without knowing the number of responders from the study.

Let’s revisit Example 2 with (p₀₁, p₀₂) = (0.65, 0.75). Suppose that, at the design stage, we chose (n₁, n) = (20, 59) based the Simon’s optimal design, but the study accrued a slightly larger number of patients (n₁, n₂) = (20, 40), among whom (m₁₁, m₂₁) = (12, 25) were from cohort 1 and (x₁, x) = (15, 46) responded. For the original sample size (n₁, n) = (20, 59), the stratified rejection values are (a₁, a) = (13, 45) with respect to (m₁₁, m₂₁) = (12, 24) or (12, 25). Hence, we could accept the therapy if the number of responders (x₁, x) = (15, 46) was observed from the design as originally planned, (n₁, n) = (20, 59). However, by having one more eligible patient from stage 2, it became unclear whether we should accept the therapy or not. To resolve this issue, we calculate the p-value for (x₁, x) = (15, 46) conditioning on (n₁, n₂) = (20, 40) and (m₁₁, m₂₁) = (12, 25), p-value = 0.1089. The conditional p-value is marginally larger than α^* = 0.1, so that we may consider accepting the therapy for further investigation.

Jung et al. (2006) propose an exact p-value calculation method for two-stage phase II designs with homogeneous patient populations.

4.2 When there are more than two cohorts

Suppose that there are J(≥ 2) cohorts with RR p_j for cohort j(= 1, …, J). We consider two-stage designs here. We accrue n₁ and n₂ patients for stages 1 and 2, respectively. The response rates for J cohorts are specified as p₀ = (p₀₁, …, p_0J ) under H₀ and p_a = (p_a1, …, p_aJ ) under H_a. Let (M_k1, …, M_kJ ) denote the random vector representing the numbers of patients from the J cohorts among n_k patients accrued during stage $k({\sum }_{j=1}^J{M}_{kj}=n_k,k=1,2)$, and (m_k1, …, m_kJ ) denote their observed values. Let X_kj denote the number responders among M_kj patients from cohort j during stage k. Then, given m_kj, X_kj is a random variable with b(m_kj, p_j).

Let M_k = (M_k1, …, M_kJ ) and m_k = (m_k1, …, m_kJ ) for stage k = 1, 2. Given (m₁, m₂), the conditional type I error and power for chosen rejection values (a₁, a) are calculated as

$$\begin{array}{c}\alpha ({\mathbf{m}}_1,{\mathbf{m}}_2)=\text{P}\{\sum _{j=1}^J{X}_{1j}>a_1,\sum _{j=1}^J(X_{1j}+X_{2j})>a\mid {\mathbf{p}}_0,{\mathbf{m}}_1,{\mathbf{m}}_2\}\\ =\sum _{x_{11}=0}^{m_{11}}\cdots \sum _{x_{1J}=0}^{m_{1J}}\sum _{x_{21}=0}^{m_{21}}\cdots \sum _{x_{2J}=0}^{m_{2J}}I\{\sum _{j=1}^J{x}_{1j}>a_1,\sum _{j=1}^J(x_{1j}+x_{2j})>a\}\\ \times \prod _{j=1}^{J}b(x_{1j}\mid m_{1j},p_{0j})b(x_{2j}\mid m_{2j},p_{0j})\end{array}$$

and

$$\begin{array}{c}1-\beta ({\mathbf{m}}_1,{\mathbf{m}}_2)=\text{P}\{\sum _{j=1}^J{X}_{1j}>a_1,\sum _{j=1}^J(X_{1j}+X_{2j})>a\mid {\mathbf{p}}_a,{\mathbf{m}}_1,{\mathbf{m}}_2\}\\ =\sum _{x_{11}=0}^{m_{11}}\cdots \sum _{x_{1J}=0}^{m_{1J}}\sum _{x_{21}=0}^{m_{21}}\cdots \sum _{x_{2J}=0}^{m_{2J}}I\{\sum _{j=1}^J{x}_{1j}>a_1,\sum _{j=1}^J(x_{1j}+x_{2j})>a\}\\ \times \prod _{j=1}^{J}b(x_{1j}\mid m_{1j},p_{aj})b(x_{2j}\mid m_{2j},p_{aj}),\end{array}$$ (5)

respectively. A phase II trial with a stratified two-stage design is conducted as follows.

• Step 1Specify p₀, p_a and (α^*, 1 − β^*).
• Step 2Choose the sample sizes for two stages (n₁, n₂) by:

  1. Specify the prevalence for each cohort, (γ₁, …, γ_J ).

  2. For $p_0={\sum }_{j=1}^J{\gamma }_j{p}_{0j}$ and $p_a={\sum }_{j=1}^J{\gamma }_j{p}_{aj}$, choose a standard (unstratified) two-stage design for testing

     $$H_0:p=p_0\text{vs}.H_a:p=p_a$$

     that satisfies the (α^*, 1−β^*) condition. We choose (n₁, n₂) for the standard design as the stage 1 and 2 sample sizes of our stratified design.

• Step 3After stage 1, calculate $a_1=[{\sum }_{j=1}^J{m}_{1j}{p}_{0j}]$ based on the observed m₁. We reject the therapy and stop the trial if x₁ ≤ a₁, where $x_1={\sum }_{j=1}^J{x}_{1j}$. Otherwise, proceed to stage 2.
• Step 4After stage 2, choose the maximum integer a satisfying α(m₁, m₂) ≤ α^* based on the observed (m₁, m₂). We accept the therapy if x > a for further investigation, where $x={\sum }_{k=1}^2{\sum }_{j=1}^J{x}_{1j}$.
• Step 5Calculate the conditional power 1 − β(m₁, m₂) for the two-stage testing defined by (n₁, n₂, m₁, m₂, a₁, a) using (5).

Given sample sizes n₁ and n₂, M₁ and M₂ are independent multinomial random vectors with probabilities of ‘success’ for the J cohorts (γ₁, …, γ_J ) and n₁ and n₂ independent trials, respectively. The marginal type I error and power can be calculated by taking the expectations of α(M₁, M₂) and 1 − β(M₁, M₂) with respect to M₁ and M₂.

5 Discussions

Patient heterogeneity is an immensely important problem that arises frequently in most clinical trials. Accounting for the randomness of observed subgroup sample sizes arises in any test where patients are heterogeneous, so this issue is not limited to phase II. While this issue is well addressed in phase III clinical trials by stratified randomization, the issue in phase II trials that are traditionally conducted as single-arm trials has been widely ignored. We can avoid such issue by randomizing patients between the experimental arm and a prospective control (Jung, 2008; Rubinstein et al. 2005; Thall et al. 1989) as in phase III trials. Adopting a stratified randomization, a randomized phase II trial definitely guarantees an unbiased comparison, but it requires up to four times larger sample size compared to a single-arm trial under the same type I error rate and power.

When historical control data come from a small prior study, we may use the estimates from the prior study as the design parameters p_0j, but we should incorporate the variation of these control parameters in designing a new study (Makuch and Simon, 1980; Thall and Simon, 1990). If the RR for the control is very low, e.g. 0.05 or 0.1, then we may be comfortable with a single-arm trial even with design parameters with some variation. However, for stable diseases with a larger RR, we may consider a randomized phase II trial when the estimated design parameters are unreliable.

In this paper, we assume that there exist reliable historical data for each cohort of a study population as in a standard single-arm phase II trial case. Under the assumption, we propose a stratified design method for single-arm phase II trials with heterogeneous patient populations. Rejection values are chosen to control the conditional type I error depending on the numbers of patients accrued from different subpopulations. As a result, a stratified design always controls the type I error under the pre-specified level regardless of the realized prevalence of each cohort, while its power is maintained around the pre-specified level. In contrast, the standard (unstratified) designs can have much biased type I error if the prevalence is erroneously projected or the realized prevalence is far from the true one. The bias can be more serious if the difference in RR between cohorts is larger. A stratified single-arm phase II trial does not require a larger sample size than a standard single-arm phase II trial. For each cohort, we can measure the effect size between the historical control and the experimental therapy in terms of odds ratio, i.e. p_aj(1 − p_0j)/{p_0j(1 − p_aj)} for cohort j. If too many patients are entered from the cohort with a smaller effect size, then the conditional power may be lower than the specified level. So, in the end of study, we may calculate the conditional power with respect to the observed number of patients from each cohort, and slightly increase the sample size for an appropriate conditional power if necessary. In this case, the proposed conditional p-value can be useful to draw the final testing result based on the revised sample size.

In designing a two-stage trial, we consider early stopping for lack of efficacy as in the usual phase II clinical trial designs (Simon, 1989). The critical values are calculated using exact binomial distributions conditioning on the number of patients from each subpopulation at each stage. London and Chang (2005) propose similar two-stage designs with early stopping boundaries for both low and high efficacy cases. The stopping values are selected based on alpha- and power-spending criteria, so that their design algorithm requires a search for the upper and lower stopping values satisfying the assigned alpha and power levels allocated to the first stage. On the other hand, we fix the lower stopping value at the expected number of responders under the null hypothesis, so that our design algorithm requires much simpler computation. Although not reporting in this paper, we compared the conditional power between our designs and those by London and Chang (2005), and found that the two methods have almost identical powers. Sposto and Gaynon (2009) propose a two-stage design with a lower stopping value only as in our designs. They derive the critical values by minimizing an ad hoc objective function based on large sample approximations. Typically phase II trials have small sample sizes, so that a statistical testing based on large sample approximations may not control the type I error rate accurately. In Example 2 with (p₀₁, p₀₂, Δ₁, Δ₂) = (0.6, 0.8, 0.15, 0.15) and α = 0.1, the Sposto and Gaynon method controls the conditional type I error rate between 0.022 and 0.126 while ours control it between 0.054 and 0.100 (see Figure 2(b)). Sposto and Gaynon (2009) method repeatedly calculates double integrals using a numerical approach, so that it takes much more computing time than our exact method requiring computation of binomial probabilities.