Distortion products and backward-traveling waves in nonlinear active models of the cochlea

Abstract

This study explores the phenomenology of distortion products in nonlinear cochlear models, predicting their amplitude and phase along the basilar membrane. The existence of a backward-traveling wave at the distortion-product frequency, which has been recently questioned by experiments measuring the phase of basilar-membrane vibration, is discussed. The effect of different modeling choices is analyzed, including feed-forward asymmetry, micromechanical roughness, and breaking of scaling symmetry. The experimentally observed negative slope of basilar-membrane phase is predicted by numerical simulations of nonlinear cochlear models under a wide range of parameters and modeling choices. In active models, positive phase slopes are predicted by the quasi-linear analytical computations and by the fully nonlinear numerical simulations only if the distortion-product sources are localized apical to the observation point and if the stapes reflectivity is unrealistically small. The results of this study predict a negative phase slope whenever the source is distributed over a reasonably wide cochlear region and/or a reasonably high stapes reflectivity is assumed. Therefore, the above-mentioned experiments do not contradict “classical” models of cochlear mechanics and of distortion-product generation.

INTRODUCTION

Acoustic distortion products (DPs) are generated by the inner ear as a consequence of the nonlinearity of the basilar-membrane (BM) response. We focus here on the best-known cubic DP, generated at the frequency f_DP = 2f₁−f₂ by two primary tones at frequencies f₁ and f₂. We are interested both in the DPs that can be directly observed on the BM using laser interferometry in animal experiments and also in the DP otoacoustic emissions (DPOAEs), which can be recorded in humans and animals as acoustic signals in the ear canal. Both signals have been extensively studied, and their properties have been shown to be related to the cochlear physiology and pathology.

According to the “standard model” of DPOAE generation, a backward-traveling DP wave is first generated by a wave-fixed nonlinear distortion mechanism near the cochlear place x(f₂), whose characteristic frequency matches f₂ (x₂, in the following, for brevity), where the distortion generated by the overlap of the two primary wave amplitudes is maximum (Shera and Guinan, 1999). A second place-fixed DP source is also present at x(f_DP) (x_DP, in the following), due to linear reflection from the cochlear roughness of the forward DP wave that is also generated at x₂. Due to the different phase slope of the two sources, the vector sum of the two backward waves produces the characteristic interference pattern that known as “DPOAE fine-structure” (see, e.g., Talmadge et al., 1999), observed in humans and other mammals. The DPOAE fine structure often shows modulation amplitudes exceeding 20 dB, with typical frequency spacing between maxima corresponding to a small fraction (approximately one eighth to one tenth) of an octave. This is the same minimum spacing observed between spontaneous OAEs (SOAEs). This evidence supports the coherent reflection filtering (CRF) theory for the production of OAEs from linear reflection due to random cochlear roughness (Talmadge et al., 1998; Shera et al., 2005).

Direct measurements of BM vibrations at the DP frequency have been performed on rodents using several different paradigms. Recent measurements of the amplitude and phase of the BM vibration in gerbils at the DP frequency at different cochlear places (He et al., 2007) have been interpreted as a demonstration that there is no backward-traveling wave at the DP frequency. More recently, de Boer et al. (2008) performed a slightly different experiment on guinea pigs, in which the phase of the BM vibration at the DP frequency was recorded as a function of the varying primary frequency f₂, at constant primary frequency ratio f₂/f₁. The BM vibration was measured at a fixed cochlear place x(f₀) (x₀, in the following), which, for f₀>f₂ is basal to x₂. In a scale-invariant cochlea, the two experimental paradigms would be strictly related to each other. A negative phase slope (NPS in the following) is observed for the DP response, very similar to that observed at the same place for the f₂ primary frequency, which is obviously propagating forward. This evidence has been interpreted as a demonstration that the traveling wave at the DP frequency propagates along the cochlea as a forward wave, and de Boer et al. refer to this phenomenon as “inverted direction of wave propagation” (IDWP). On the other hand, the observation of DPOAEs in the ear canal implies that power at frequency f_DP, is effectively transmitted back to the cochlear base. If this transmission was associated with a backward-traveling wave on the BM, an increasing slope would have been expected [see, for example, de Boer et al. (2008), who base their predictions on frequency-domain quasi-linear estimates of the BM response]. For this reason, it has been suggested that the DPOAEs must be transmitted back to the cochlear base by some different mechanism. Fast longitudinal compression waves in the fluid are the natural candidate for accomplishing this task, but comparison between auditory-brainstem response (ABR) and OAE latencies suggests that OAE delays are too long for this to be the case (Moleti and Sisto, 2008; Harte et al., 2009). Other evidence, both direct (Dong and Olson, 2008) and indirect (Shera et al., 2007; Meenderink and van der Heijden, 2010), also supports the predominance of a slow backward-traveling wave at the DP frequency on the BM and not that of a fast wave in the fluid.

To remain more faithful to the actual output of the experiments and of the simulations, we discuss the results in terms of observed and predicted phase slopes, instead of speaking of the inferred direction of propagation, and its possible inversion. We prefer this because the nonlinear nature of the cochlea may affect the interpretations involving the behavior of a well-defined frequency component of the response. Indeed, for a nonlinear system, even the frequency response is not a well-defined concept. Our hypothesis is that the NPS is explained by two well-known features of the cochlear mechanics: the spatial extension of the DP source and the significant stapes reflectivity for backward-traveling waves. Even assuming a strict relation between phase slope and direction of propagation, the fact that the observed phase behavior in BM vibration observations is that expected for a forward-traveling wave, and not for a backward-traveling wave, actually implies only that there is a forward-traveling wave at the DP frequency, comparable in size with the backward-traveling wave, whose contribution is sufficient to invert the phase slope. The backward-traveling wave could still be associated with the backward propagation of OAEs, and the existence of a strong forward-traveling wave could be explained assuming a large stapes reflectivity, and/or some additional mechanism that transmits and amplifies the forward waves more effectively than the backward waves. Using frequency-domain solutions of linear spatial feed-forward cochlear models, de Boer and Nuttall (2009) have recently suggested that amplification based on the spatial feed-forward principle could provide such a mechanism. In spatial feed-forward models, the tilt of the outer hair cells (OHCs) produces a forward shift of the additional force on the BM produced by the active feedback mechanism. This forward shift introduces a directionality to the cochlear amplifier that amplifies forward-traveling waves while attenuating backward-traveling waves. One might argue that the attenuation of backward-traveling waves predicted by spatial feed-forward models contradicts the evidence for effective backward propagation provided by the existence of spontaneous OAEs (SOAEs). According to the theory proposed by Shera (2003, 2007), 20, round-trip gain higher than unity and path length equal to an integer number of wavelengths are necessary conditions for SOAE existence at a given frequency. The first condition could still be fulfilled if the forward gain is increased and the backward gain is decreased, as could happen in a spatial feed-forward model.

In this study, we use both frequency-domain and time-domain simulations of nonlinear and nonlocal cochlear models to analyze the DP phenomenology along the BM under a wide range of parameters and modeling choices. Due to the intrinsically nonlinear nature of the DP generation, accurate predictions of the DP phase in strongly nonlinear models cannot rely solely on standard frequency-domain formulations. Although Nobili and Mammano (1996) have demonstrated the accuracy of a perturbative frequency-domain method, based on the recursive sequences of linear equations in a class of nonlinear cochlear problems, we prefer using the time-domain approach, which is less subject to the pitfalls of linearization. On the other hand, for a large number of discrete elements, time-domain solutions can be computationally expensive. The optimized numerical solution scheme used in this study (Moleti et al., 2009; Bertaccini and Sisto, 2011) permits accurate and reasonably fast solutions. We compare the predictions of a spatial feed-forward nonlinear and nonlocal cochlear model with those of “diagonal” models, as regards the DP phase behavior at a fixed BM, as a function of the stimulus frequency. By diagonal we mean a model in which the additional OHC pressure triggered by the tectorial membrane-stereocilia interaction at a give cochlear position x acts back on the BM at the same location, with no longitudinal shift associated with the OHC tilt.

As noted by de Boer et al., (2008) the fixed-x, varying-frequency experiment should be equivalent, in a scale-invariant cochlea, to that in which the stimulus frequencies are kept constant, and the place of observation is moved along the cochlea. In physiological experiments, the first experiment is simpler than the second one, whereas the opposite is true in the world of numerical simulations.

Preview of the results

We performed numerical simulations of both kinds of experiments, using both diagonal and spatial feed-forward nonlinear active models. In these models an additional force on the BM is associated with the OHC feedback mechanism, whose effectiveness is a nonlinear function of the BM displacement level, superimposed on an underlying passive linear model, representing the cochlear response at very high stimulus levels. The nonlinearly saturating function of the BM displacement is chosen to get two asymptotic linear BM response regimes at a very low and very high stimulus levels, respectively, with high effective “active Q” and low effective “passive Q,” and a compressive nonlinear regime between them.

One could try to explain the observed NPS at the intermediate place x₀ by assuming that the DP source extends toward the base much more than is commonly believed, and there is mounting evidence to support this possibility (Martin et al., 2010). The computational ability to turn the nonlinearity and/or the roughness on and off in selected cochlear regions has been used in this study to get information about the localization of the distortion and reflection sources in the model, which were found to reside, as expected, in regions slightly basal to the x₂ and the x_DPplaces, respectively.

The stapes reflectivity, which is due to the impedance mismatch seen by backward-traveling waves looking out of the oval window, affects the DP phase slope. This effect has been evaluated in the model by varying the damping constant of the middle ear element, which changes the impedance mismatch, and therefore the stapes reflectivity.

We have computed analytical estimates of the DP phase slope using frequency-domain techniques applied to a linearized model, in which the DP generation is perturbatively introduced using a cubic distortion term (Talmadge et al., 1998, 2000, 30; Shera et al., 2005). These methods predict either positive phase slope (PPSs) or NPS, depending on the conditions. We verified that PPS holds only for high Q passive models, whereas for active linear models including time-delayed stiffness (which produces tall but also much broader activity patterns, and a less localized DP source) the predicted phase slope can become negative if a reasonably high stapes reflectivity is also assumed for the backward wave.

The results of this study also show that the NPS reported by the BM experiments is predicted by both diagonal and spatial feed-forward nonlinear cochlear models. The nonlinear model solutions predict a PPS only if one assumes an unreasonably high value (of order 50) of the quality factor Q of the local oscillators of the underlying passive cochlea, and/or an unreasonably low stapes reflectivity. The first condition implies very sharp resonance at all stimulus levels and, consequently, a point-like DP source, whose longitudinal extension is not dependent on the BM excitation level, as happens in low Q nonlinear models.

We have also used the numerical model as a computing tool to get solutions of a “hybrid” model, in which the solution for the primary tones is first predicted by the nonlinear numerical model, explicit source terms are included along the BM at a second step according to the primary profiles, and the evolution of the solution is computed again in the nonlinear model without the primary tones. The results of these simulations show that a NPS is obtained also in this case in a cochlear region basal to x₂ increasingly extended toward the base as the size of the generation region is extended.

MODELING THE COCHLEA AND THE DP GENERATORS

1-D box model

We will refer to a 1-D transmission line active box model. The underlying passive model is described by the basic equations:

$$\frac{\partial {}^{2}p(x,0,t)}{\partial x^2}=\frac{2\rho }{H}\stackrel{\mathrm{··}}{\xi }(x,t)$$ (1)

$$\stackrel{\mathrm{··}}{\xi }(x,t)+{\gamma }_{\mathrm{bm}}(x)\stackrel{·}{\xi }(x,t)+{\omega }_{\mathrm{bm}}^2(x)\xi (x,t)=\frac{p(x,t)}{{\sigma }_{\mathrm{bm}}}$$ (2)

where ρ is the fluid density, σ_bm is the BM surface density and ξ the BM transverse displacement at the longitudinal position x and time t. In the box model, the cochlear duct is assumed to have a rectangular cross section of half-height H and length L. Active terms will be added later as additional force terms to Eq. 2 to schematize the OHC feedback.

We used the relation between longitudinal position x, angular frequency, and passive damping constant predicted by Greenwood (1990) map:

$$\begin{array}{c}\multicolumn{1}{c}{{\omega }_{\mathrm{bm}}(x)={\omega }_0{e}^{-k_{\omega }x}+{\omega }_1{\gamma }_{\mathrm{bm}}(x)={\gamma }_0{e}^{-k_{\gamma }x}+{\gamma }_1}\end{array}$$ (3)

The local passive quality factor is defined as:

$$Q(x)=\frac{{\omega }_{\mathrm{bm}}(x)}{{\gamma }_{\mathrm{bm}}(x)}.$$ (4)

We set k_ω = k_γ, and ω₁ = γ₁ =0, so Q(x) = Q₀ = ω₀/γ₀ is a constant, to avoid an explicit breaking of the scaling symmetry.

Analytical approximations

Approximate solutions of nonlinear cochlear models can be obtained using frequency-domain techniques. The validity of such approximate solutions is presumably limited to perturbative regimes, in which the nonlinearity is relatively weak and can be treated as a small perturbation on some underlying linear behavior. Even for linear systems, the derivation (although not necessarily the actual accuracy) of analytical methods based on the Wentzel-Kramer-Brillouin (WKB) approximation requires that the fractional variation of the wavelength of the traveling wave over the distance of a wavelength be small. This condition may not be well satisfied close to the response peak in active models, so the BM response may require more accurate solutions in this region. A fully numerical alternative approach is therefore needed to check the accuracy of the predictions of analytical perturbative techniques.

The basic idea leading to the prediction that backward DP traveling waves should exhibit a PPS if observed at a fixed intermediate cochlear position, as in the de Boer et al. (2008) experiment, can be explained in simple terms: the WKB representation of the forward-traveling transpartition pressure wave is

$${\psi }_r(\omega ,x)=\sqrt{\frac{k(\omega ,0)}{k(\omega ,x)}}\mathit{exp}(-i\int 0x\mathit{dx}\text{'}k(\omega ,x\text{'})).$$ (5)

We follow here a convention in which the wave vector k is defined so that Re(k)>0 and the direction of propagation is set by the sign in front of the integral in the argument of the exponential. The wave is described by a function of the form: A(ω,x)exp(i(ωt+Φ(ω,x)), and $-\frac{\partial \Phi }{\partial \omega }$ represents its group delay.

Neglecting the small contribution to the phase coming from the factor under the square root, the phase of the primary waves at the x₂ place does not change with frequency, due to the assumed scaling symmetry, if the ratio between the primary frequencies is kept fixed during the frequency scan. Therefore, the initial phase of the DP source at x₂ is also independent of f. Apart from a constant term, the phase of the backward-traveling component of the DP wave generated at x₂, measured at a given more basal place x₀<x₂, is, in the WKB approximation

$${\Phi }_l({\omega }_{\mathrm{DP}},x_0)\cong \int x_2{x}_0\mathrm{Re}(k({\omega }_{\mathrm{DP}},\tilde{x}))d\tilde{x}.$$ (6)

Taking the frequency derivative of this integral at the fixed place x₀ (the derivative is applied also to the integration limit x₂), omitting for simplicity of notation to specify taking the real part of the wave vector, and using the assumed scaling symmetry to solve the integral, one gets:

$$\begin{array}{c}\multicolumn{1}{c}{\frac{\partial \Phi ({\omega }_{\mathrm{DP}},x_0)}{\partial {\omega }_{\mathrm{DP}}}\cong \int x_2{x}_0\frac{\partial k({\omega }_{\mathrm{DP}},)}{\partial {\omega }_{\mathrm{DP}}}d\tilde{x}-\frac{\partial x_2}{\partial {\omega }_{\mathrm{DP}}}k({\omega }_{\mathrm{DP}},x_2)}\\ \multicolumn{1}{c}{\cong \frac{1}{k_{\omega }{\omega }_{\mathrm{DP}}}\int x_2{x}_0\frac{\partial k({\omega }_{\mathrm{DP}},\tilde{x})}{\partial x}d\tilde{x}+\frac{1}{k_{\omega }{\omega }_{\mathrm{DP}}}k({\omega }_{\mathrm{DP}},x_2)=\frac{k({\omega }_{\mathrm{DP}},x_0)}{k_{\omega }{\omega }_{\mathrm{DP}}}}\end{array}$$ (7)

Thus, for a pure backward-traveling wave originating from a point source at x₂, the phase slope is positive (when observed at x₀<x₂).

More accurate estimates of the phase slope can be obtained by computing the WKB solution of the transmission line cochlear model, using perturbative techniques, such as the osculating parameters technique (Shera and Zweig, 1991; Talmadge et al., 1998, 2000, 30), or the Green’s function method (Shera et al., 2005). The underlying cochlear model is linear and smooth and the DP sources are added as “small” perturbations, injected into the model. The active term is also linear, introduced as an additional delayed-stiffness term, which can be either diagonal or feed-forward, with a spatial feed-forward distance δx (for the “diagonal” model, δx = 0). Equation 2 is then modified as follows:

$$\stackrel{\mathrm{··}}{\xi }(x,t)+{\gamma }_{\mathrm{bm}}(x)\stackrel{·}{\xi }(x,t)+{\omega }_{\mathrm{bm}}^2(x)\xi (x,t)+{\rho }_s{\omega }_{\mathrm{bm}}^2(x)\xi (x-\delta x,t-{\tau }_s)+{\rho }_f{\omega }_{\mathrm{bm}}^2\xi (x-\delta x,t-{\tau }_f)=\frac{p(x,t)}{{\sigma }_{\mathrm{bm}}}$$ (8)

As in Talmadge et al. (1998), we fine tune the two delay parameters to get effective damping and anti-damping terms (Zweig, 1991), with a region of overall negative damping located slightly basal to the resonant place. The result is similar to the empirical profiles of the impedance used by de Boer and Nuttall (2009), as obtained from measured BM responses using the inverse method.

By definition, the Green’s function G(x|x′) is simply the response at location x to a point source at x′. Assuming an initially forward-traveling (right-going) wave, the Green’s function for the smooth cochlea in absence of reflections from the boundaries can be written as (Shera et al., 2005):

$$\{\begin{array}{c}\multicolumn{1}{c}{G_{\infty }(x|x\text{'})=\gamma {\psi }_l(x){\psi }_r(x\text{'})\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}(x<x\text{'})}\\ \multicolumn{1}{c}{G_{\infty }(x|x\text{'})=\gamma {\psi }_r(x){\psi }_l(x\text{'})\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}(x>x\text{'})}\end{array}$$ (9)

where the ψ_r,l are the basis functions representing respectively a forward- and backward-traveling (right and left going) wave at location x along the BM:

$${\psi }_{r,l}(\omega ,x)\cong \sqrt{\frac{k(\omega ,0)}{k(\omega ,x)}}\mathit{exp}(\mp i\int 0x\mathit{dx}\text{'}k(\omega ,x\text{'}))$$ (10)

and γ is the inverse of the Wronskian determinant of the solutions at the base. As shown by Shera et al. [2005; Eq. 8], Eq. 9 must be modified in presence of reflections.

In particular, if reflections from the stapes are present, the expression for the Green function becomes:

$$G(x|x\text{'})=G_{\infty }(x|x\text{'})+\gamma R_{\mathrm{s}}{\psi }_r(x){\psi }_r(x\text{'}),$$ (11)

where R_s represents the cochlear reflectivity at the stapes. The DP generation source is of the type [Talmadge et al., 1998; Eq. (130)]

$$D({\omega }_1,{\omega }_2,x)=\rho ({\omega }_1,{\omega }_2){\xi }_r^2({\omega }_1,x){\xi }_r^{*}({\omega }_2,x),$$ (12)

where the ξ_r (ω,x) represents the BM displacement:

$${\xi }_{r,l}(\omega ,x)\cong \frac{k^2(\omega ,x)}{k^2(\omega ,0)}·{\psi }_{r,l},$$ (13)

associated with the propagation of the forward-traveling waves at the frequencies of the primaries.

The response to a DP source distributed along x as in the Eq. 12 can be written as the convolution integral of the Green’s function with the function representing the source term. If the term coming from stapes reflections is added to the Green’s function, the following expression is obtained for the pressure at the frequency of the DP, observed at a location basal to the generation point at x₂:

$$\begin{array}{c}{P}_d({\omega }_{\text{dp}},x)={\displaystyle \underset{0}{\overset{\infty }{\int }}d{x}^{\prime }G(x|x^{\prime })}D({\omega }_1,{\omega }_2,x^{\prime })=\gamma [{\psi }_r({\omega }_{\text{dp}},x){\displaystyle \underset{0}{\overset{x}{\int }}d{x}^{\prime }{\psi }_l({\omega }_{\text{dp}},x^{\prime })D({\omega }_1,{\omega }_2,x^{\prime })}+\\ {\psi }_l({\omega }_{\text{dp}},x){\displaystyle \underset{x}{\overset{\infty }{\int }}d{x}^{\prime }{\psi }_r({\omega }_{\text{dp}},x^{\prime })D({\omega }_1,{\omega }_2,x^{\prime })+R_{\text{stapes}}{\psi }_r({\omega }_{\text{dp}},x)}{\displaystyle \underset{0}{\overset{\infty }{\int }}d{x}^{\prime }{\psi }_r({\omega }_{\text{dp}},x^{\prime })D({\omega }_1,{\omega }_2,x^{\prime })}]\end{array}.$$ (14)

The terms coming from G_∞(x|x′) and from reflections off the stapes appear similar, but have opposite resulting phase: the first representing a backward-traveling wave and the second a forward-traveling wave generated by reflection at the stapes.

The discretized model and its numerical solutions

We refer here to a 1-D nonlinear nonlocal active cochlear model that has been extensively described in Moleti et al. (2009) and in Sisto et al. (2010), based on the state-space formalism, following and slightly modifying the state-space scheme proposed by Elliott et al. (2007). The discretized model, its numerical properties and integration strategies are discussed in Bertaccini and Sisto (2011). The parameter values necessary to reproduce our results are given in Sisto et al. (2010).

The discretized cochlear model consists of N elements. The first represents the middle ear and oval window dynamics:

$${\stackrel{\mathrm{··}}{\xi }}_{\mathrm{ow}}(t)+{\gamma }_{\mathrm{ow}}{\stackrel{·}{\xi }}_{\mathrm{ow}}(t)+{\omega }_{\mathrm{ow}}^2\xi (t)=\frac{p(0,t)+G_{\mathrm{me}}{P}_{\mathrm{dr}}(t)}{{\sigma }_{\mathrm{ow}}}$$ (15)

where, according to Eq. 10 of Talmadge et al. (1998), γ_ow, ω_ow, and σ_ow are, respectively, the middle ear-oval window effective damping constant, frequency and density, P_dr is the calibrated pressure in the ear canal (for a rigid ear drum), and G_me, is the mechanical gain of the middle ear. The middle ear is schematized as a bandpass filter with maximum transmission around 1000–1500 Hz. The BM is schematized as a set of N-2 discrete resonant elements, each described by Eq. 2, with mechanical parameters varying according to Eq. 3. The last cochlear element is the helicotrema, described by a simple pressure-release boundary condition:

$$p(L,z,t)=0$$ (16)

More details on the state-space formalism used in this solution scheme can be found in previous studies (Moleti et al., 2009; Sisto et al., 2010).

The key feature, and most delicate part of the solution method, is the schematization of the nonlinear and the nonlocal active feedback mechanism mediated by the OHCs. This mechanism can be schematized either as an explicit anti-damping term proportional to the BM velocity [as done, e.g., by de Boer and Nuttall (2009)] or as an additional pressure proportional to the total pressure on the BM [as suggested by Lim and Steele (2002)]. We considered two different models: an anti-damping diagonal model and a spatial feed-forward model. The response to pure-tone stimulation of these two models has already been discussed in detail in Sisto et al. (2010).

As regards the functional dependence of the cochlear amplifier gain on the BM displacement level, we have chosen a “universal” gain function (see Sisto et al., 2010 for more details) that can be tuned (using two parameters only, the active gain coefficient α₀ and the displacement threshold for nonlinear saturation of the active amplifier ξ_s) to approximately match the behavior experimentally observed in mammals, which is characterized by constant gain at both low and high BM displacements and a compressive regime at intermediate levels (Nobili and Mammano, 1996). At low BM displacement levels, an approximately cubic distortion term is present, similar to that of Eq. 12, which is used in the frequency-domain quasi-linear approximations.

Cochlear roughness is needed to get an OAE component from linear reflection. It can be schematized as a random spatial variation either of the local stiffness around the value corresponding to the Greenwood map (Talmadge et al., 2000) or of the effectiveness (gain) of the active mechanism. We explored the role of the linear reflection DP source by comparing the results of simulations obtained using different levels of cochlear roughness.

Among several other possibilities, explicit violation of scaling symmetry can result from departures from a purely logarithmic place/frequency mapping, or from an explicit dependence of cochlear tuning on characteristic frequency. Both conditions occur to some degree in the real cochlea. We evaluated their effect on the predicted DPOAE spectral features in the simulations.

The localization of the nonlinear DP sources is important to get a meaningful interpretation of the experimental and numerical simulation results. It can be easily studied in numerical models by artificially removing the DP source in a given cochlear region by locally canceling the nonlinear dependence of the OHC additional feedback force. By shifting the borders of the “linearized” region in this way, we obtained a DP source density profile.

RESULTS

This section demonstrates that the NPS is predicted by several reasonable cochlear models, and that the basic elements needed to get this prediction are significant stapes reflectivity and/or a reasonably wide DP source. The gain and location of the region of cochlear amplification also play an important role. Only extreme localization of the DP source and unrealistically low stapes reflectivity lead to the prediction of PPS. The results of the de Boer (2008) experiment do not therefore provide strong constraints, individually, on the value of the stapes reflectivity and on the width of the DP source, but rather indicate a wide region in this 2-D parameter space that is in agreement with the observed NPS. We have not systematically delimited the parameter region consistent with NPS in this study, but show that PPS requires values of stapes reflectivity which is well below 0.5, and very narrow DP generation profiles, typical of Q = 25 passive or anti-damping models. Most middle ear models (Puria, 2003) predict values of R_s between 0.5 and unity, and very high-Q passive and anti-damping models fail to reproduce the tall and broad activity patterns necessary to match well-established properties of the BM response (Zweig, 1991). This means that virtually all reasonable cochlear models would predict NPS. To check its robustness, we have verified this result using analytical quasi-linear approximations, using numerical solution of fully nonlinear models, and using hybrid semi-analytical solutions of the nonlinear model.

Frequency-domain analytical estimates

The basic assumption of de Boer et al. (2008) was that a backward wave, propagating from the DP generation place, either x₂ or x,_DPto the cochlear base should have a PPS at a fixed place, x₀. We have seen that this assumption can be justified by the arguments leading to Eq. 7. We show in this section that a more complete frequency-domain quasi-linear analysis that includes the effect of stapes reflectivity, cochlear amplification, and distributed DP sources usually leads to the opposite prediction. Forward waves from a point-like source, such as that of the f₂ stimulus coming from the base, do have NPS, but the notion that the occurrence of NPS at the DP frequency implies the absence of backward-traveling DP waves on the BM is not accurate.

At a first stage, we have tried to remain adherent to the experimental results, to understand which is the relevant feature of a cochlear model necessary to explain the experimental results. We performed a fully analytical perturbative calculation in the frequency domain using the Talmadge–Shera formalism (Shera et al., 2005). Their “classical” model is a diagonal model with delayed stiffness terms, which have been first introduced by Zweig (1991) to give realistic “tall and broad” activity patterns. The delayed stiffness active terms can also be switched off to get a passive model, and they can also be shifted along the x-axis to transform the model into a spatial feed-forward model. In our estimates we have neglected the presence of cochlear roughness, which would introduce a DP reflection source.

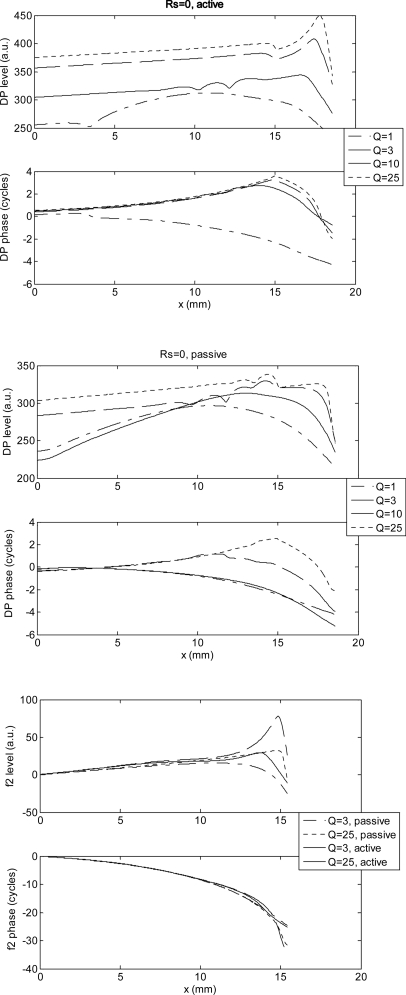
For simplicity, we choose to compute the DP phase as a function of cochlear position at a fixed frequency. We then exploit the scaling symmetry of the model and relate the computed slope to that measured in de Boer’s experiments at a fixed position place, x₀, as a function of frequency. When we take R_s = 0, the DP phase slope between the base and the DP generation place x₂ is positive for both the active and for the passive model, unless a very low quality factor is assumed (see top and mid panels of Fig. 1). This means that in the absence of reflections from the stapes, PPS is predicted if the DP source is well localized near the tonotopic place of the primary tone f₂. The spatial profile (forward basis function) of the primary tone f₂ is also shown for comparison in the bottom panel of Fig. 1, for two values (3 and 25) of the passive quality factor.

Figure 1.

DP level (arbitrary decibel units) and phase (in cycles) as a function of the cochlear longitudinal position x, for four different values of the passive quality factor Q, computed with the linearized perturbative method [i.e., from Eq. 14] with R_s = 0. Top panel: Active model: Mid panel: Passive model. The computed DP phase slope is positive, unless the quality factor is so small that the source extends up to a cochlear region close to the base. The level (in decibel) of the forward basis function of the primary wave of frequency f₂ is also shown for comparison, for two values of Q, in the bottom panel.

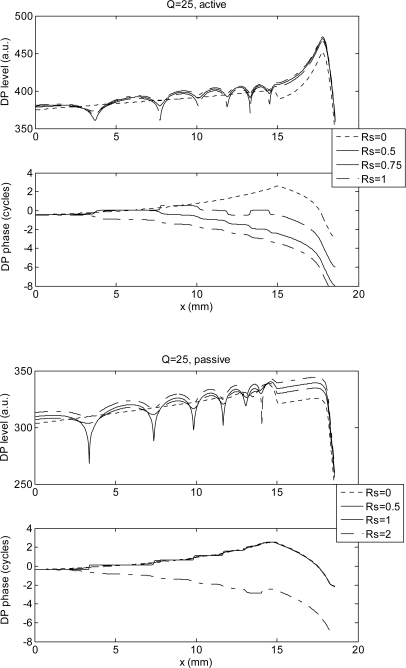
We obtain very different model predictions when a more realistic value of R_s is assumed: reasonably high-Q passive and active models exhibit a transition between PPS and NPS with increasing values of |R_s|. For the active model the transition is completed for |R_s| around 0.5, whereas for the passive model |R_s| ≈ 1 is necessary (Fig. 2). The oscillation of the amplitude, which is maximum for |R_s| = 0.5 and for |R_s| = 1 for active and passive models, respectively, shows the presence of stationary waves between the cochlear base and x₂ place. Although physically impossible in a passive system, apparent value of |R_s|>1 could be achieved by driving the system from the ear canal, so that the stapes acts as both a passive reflector and an active source. Values of |R_s| between 0.5 and 1 are fully reasonable in the mammalian ear (Puria, 2003), due to the impedance mismatch seen by the backward-traveling wave at the oval window. The lower value of |R_s| required to yield the NPS in active models is related to the additional boost provided by the cochlear amplifier. Introducing the spatial feed-forward shift δx=35 μm we do not see any change in the phase slope.

Figure 2.

DP level and phase as a function of x, including the effect of stapes reflectivity, for sharp cochlear passive tuning. NPS is observed starting from a cochlear position that is a decreasing function of |R_s|. For the active model (top panel), full inversion of the slope along the whole cochlea is progressively obtained with |R_s| between 0.5 and 1, with the maximum modulation amplitude (indicating stationary waves) obtained around the slope inversion place. For the passive model (whose activity pattern and DP source profile is much narrower), non-physical |R_s|>1 is necessary to get the NPS, with the largest stationary waves occurring for |R_s| = 1. The percentage phase jumps, associated with the minima of the amplitude, should not be considered when evaluating the phase slope, here and in the following figures.

The analytical results therefore suggest the following hypothesis: classical active models of the cochlea can explain the observed NPS if the DP source is not unrealistically point-like and/or the stapes reflectivity is not unrealistically low. Typical active models with a reasonably wide DP source require a minimum stapes reflectivity well below unity.

Time-domain numerical simulations of a fully nonlinear model

The numerical solutions of the fully nonlinear model were used to test the hypothesis formulated on the basis of the analytical estimates. In our model, the stapes reflectivity and the width of the DP generation can be varied by changing, respectively, the impedance of the middle ear, and the quality factor of the resonances in the underlying passive model. The role of the stapes reflectivity and of the width of the DP generation source has been confirmed by the numerical solutions of the nonlinear model, without the uncertainty associated with using linear approximations for solving a nonlinear problem. In a nonlinear system, the concept of frequency response is not even defined, and the phase behavior of the response in a complex experiment, involving nonlinear distributed sources, must be interpreted with much care, without trusting completely the previous hints provided by frequency-domain approximate analyses. The possible effects of spatial feed-forward asymmetry, roughness, scale invariance violation, etc., have also been evaluated using the full nonlinear model.

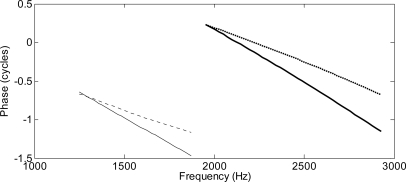
First we show that the numerical solutions of the fully nonlinear model reproduce some well-known features of the DP response at the cochlear base. In the top panels of Fig. 3 we show the spectrum (amplitude and phase) of the DP component at the cochlear base for an anti-damping model, with and without cochlear roughness, plotted as a function of the variable DP frequency. We recall that these spectra are actually obtained, by analogy with the standard experimental measurements of the DP fine structure, by performing a set of numerical simulations in which the frequency of the f₁ tone is changed in the range 1600–2400 Hz with a 20 Hz between each simulation, keeping a constant ratio between f₂ and f₁. For each simulation, only the Fourier component of the steady-state response at the correspondent DP frequency f_DPis considered. The model has passive Q = 4 and α₀ = 0.9, corresponding to a maximum active gain of order 20 dB. The stapes reflectivity associated with the middle ear model is of order 0.7 in the frequency range of interest. With no cochlear roughness, only the nonlinear distortion source is present. As a consequence of the scale invariance of the model, the phase at the base is expected to be constant. Apart from random fluctuations, presumably due to numerical errors in the computation, no slope can be seen indeed in the phase-frequency relation. Introducing cochlear roughness, the typical fine structure due to the interference between the two DP sources can be observed in the DP response amplitude at the base, as well as in the phase, which now oscillates about its previous value. When the roughness is larger (3%), the slope of the DP phase at the base becomes steep, indicating dominance of the reflection source. A similar phenomenology is observed, for slightly higher values of roughness, in the bottom panels of Fig. 3 for a spatial feed-forward model, with passive Q = 4, α₀ = 0.7, corresponding again to a maximum active gain of about 20 dB.

Figure 3.

Top: DP level and phase as a function of the DP frequency at the cochlear base, obtained from the numerical solution of the fully nonlinear nonlocal anti-damping model, with and without roughness. The typical fine structure and increasingly negative phase slope are obtained with increasing roughness, whereas the phase is approximately flat without roughness. Bottom: same for the spatial feed-forward model.

Figure 3 reproduces the expected behavior of the DP at the base, which is observed in the corresponding experimental DPOAE spectra. Therefore, we apply with some confidence the same models and numerical solution method to the study of the phase behavior of the BM response at other cochlear places, and, in particular, at a place that, as in the de Boer (2008) experiment, is basal to the DP generation region. Because we assume that the maximum distortion occurs near x₂, we choose x₀ so that its characteristic frequency (f₀) is 4 kHz, which is higher than the maximum f₂ frequency of the scan (2928 Hz). If f₀ is increased the absolute value of the slope decreased, as in the mentioned experiments (figure not shown). In Fig. 4 we show that the DP phase at these intermediate positions shows a NPS, as reported in the de Boer (2008) experiment. de Boer and Nuttall (2009) suggested that the possible feed-forward nature of the cochlea might be responsible for the unexpected negative slope of the experimental DP phase at the x₀ place. Our result is obtained both with anti-damping and with spatial feed-forward models, showing that the spatial feed-forward asymmetry is not necessary to explain the experimental results, as already suggested by the analytical approximations, provided that a reasonably high stapes reflectivity is assumed.

Figure 4.

Phase of the DP (thin lines) and of the primary tone at frequency f₂ (thick lines), computed at a fixed position x₀ = x(4 kHz), basal to the DP generation place, from the numerical solution of the fully nonlinear nonlocal anti-damping model (dotted lines), without roughness. NPS is found, with the absolute value of the slope decreasing with x₀ approaching the base (not shown). The is also shown. An identical phenomenology, with slightly steeper slope, is obtained for a spatial feed-forward model (solid lines).

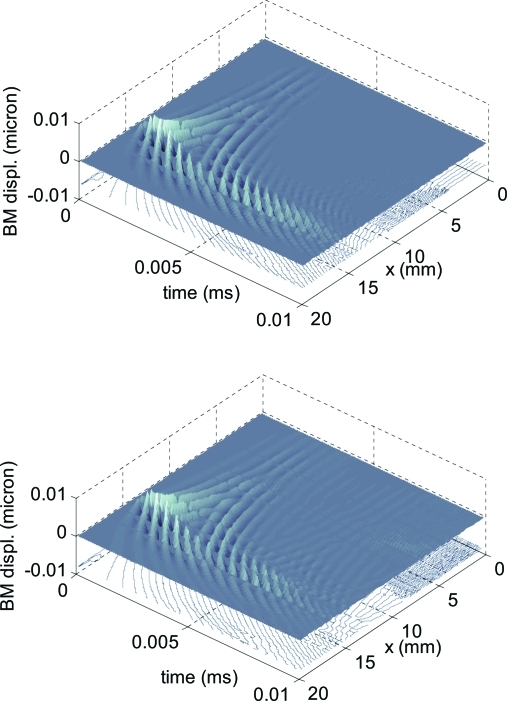
As shown by the frequency-domain analysis, an important feature of the model is the stapes reflectivity |R_s|, which, for the middle ear schematization used in our models is greater than 0.5 in the frequency range of interest. The numerical simulations permit us to estimate the reflection coefficient directly by exciting the BM at a given cochlear place x* directly with a sinusoidal stimulus and comparing the amplitudes of the backward- and forward-traveling waves for x between 0 and x*. For short tone bursts, the two waves are well separated close to the base (see Fig. 5, showing 3-D plot with the two waves, for |R_s| = 0.6).

Figure 5.

Backward and forward traveling waves are visually evident in the numerical solution of a cochlear model with high stapes reflectivity (|R_s| = 0.6). In this case, to make the reflected wave more evident, the stimulus is a 2 kHz gaussian tone burst fed at t = 1 ms at x =14 mm, slightly more basal than x₂. In the bottom panel, roughness has been added to the model to create multiple reflections, clearly visible between the base and the tonotopic place.

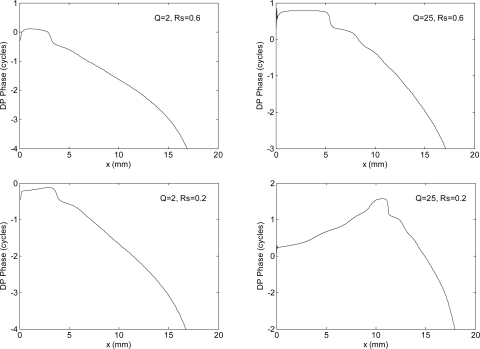
We have performed the same simulations with the spatial feed-forward model, using a different (and unreasonably high) middle-ear damping term, to decrease |R_s|, finding that the slope of the DP phase becomes positive if |R_s| is significantly decreased. The results show that the PPS is obtained only for very sharp tuning and exceedingly small stapes reflectivity. With high stapes reflectivity the slope is always negative over most of the cochlear region basal to x₂ (Fig. 6).

Figure 6.

DP phase (in cycles) as a function of the cochlear longitudinal position x, for two different values of the passive quality factor Q and of the stapes reflectivity |R_s|, from the numerical solution of the fully nonlinear nonlocal anti-damping model, without roughness. NPS is generally predicted in most of the cochlear region basal to the DP generation place, unless the source is very localized and |R_s| is underestimated, confirming the results of the approximate analytical solutions.

Therefore, the numerical simulation results confirm our hypothesis that the spatial extension of the DP source and/or a sufficiently high stapes reflectivity are the key elements needed to reproduce the experimental findings, although the possibly spatial feed-forward nature of cochlear amplification may also contribute. In addition to affecting the ratio of backward- to forward-traveling waves by preferentially amplifying forward-traveling waves, an indirect effect of the introduction of the spatial feed-forward push could be the broadening of the DP generation profiles, with respect to anti-damping models yielding the same active gain (see Sisto et al., 2010).

One could try to explain the observed phase slope suggesting that the nonlinear distortion DP source, instead of being localized near the x₂ place, actually extends closer to the cochlear base. However, we have verified, that NPS is also predicted by models in which the DP source does not significantly extend to cochlear regions basal to x₀, where the observation is made. To do this, we performed simulations in which the nonlinear anti-damping term that generates DPs was switched on only in a region extending from the base to some cochlear place x_l, using the cut-off function:

$${\alpha }_0(x)={\alpha }_0(1-\mathit{tanh}{}^4\left[\frac{x}{x_l}\right])$$ (17)

We have verified that the amplitude of the DP, either measured at an intermediate position x₀ or at the base, is almost negligible with increasing x_l, until x_l approaches x₂ within a distance of 1mm. Because x₂−x₀ is greater than 1 mm (e.g., 2–5 mm in Fig. 4), this means that the nonlinear DP generation source does not need to extend to cochlear regions substantially more basal than the observation point.

Hybrid semi-analytical solutions

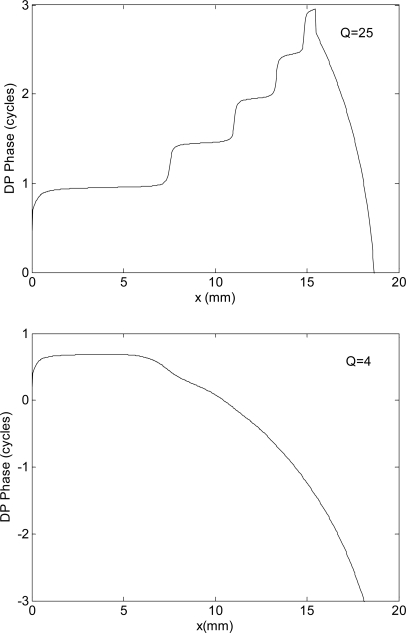
We have also tried to understand if the schematization of the nonlinear source as a simple cubic distortion, given by Eq. 12, affects the perturbative prediction of the phase slope. To do this, we have exploited the model capability of accepting a stimulus (a source term) not only at the base but also at any other cochlear place. We performed the following hybrid numerical computations, that we call semi-analytical: first the spatial profiles of the primaries were calculated with the full nonlinear anti-damping model, then the DP sources were directly injected with the functional form and spatial profile computed from Eq. 12, and the subsequent evolution of the DP waves was finally evaluated with the nonlinear anti-damping model, with no primary sources. In these simulations, fixed primary frequencies were used, and the phase computed as a function of x. We found results consistent with those of the numerical and analytical calculations. In a model with high stapes reflectivity |R_s| and passive Q = 25 (i.e., with an extremely localized DP source) the DP phase slope was positive in the region between the base and x₂. This behavior is shown in the top panel of Fig. 7. The behavior is different for passive Q = 4 (bottom panel of Fig. 7), where, with a much more reasonably wide DP source, the NPS is observed over most of the region basal to x₂. The effect of localization of the DP source has also been verified by artificially distributing the DP sources according to Eq. 12, but only on a given region around x₂. In the low passive Q model, the negative phase region progressively shrinks as the source is artificially localized.

Figure 7.

In a hybrid computation, in which a full nonlinear model is solved for |R_s| = 0.6, with the nonlinear DP source separately computed according to the perturbative approximation given by Eq. 12, the main results are confirmed: with reasonably high stapes reflectivity, the DP NPS is obtained when the source is not point-like (passive Q = 4, which means maximum effective Q = 40 in an anti-damping model with α₀ = 0.9). Only assuming an unreasonably high passive Q, the PPS is predicted.

Additional tests

Just to exclude other possible causes of the observed BM vibration phase behavior, we also investigated the sensitivity of the results to scaling symmetry violation and to different schematizations of the cochlear roughness, using the full nonlinear model, finding that they had no significant effect. We tested the phase slope dependence on the degree of violation of the scaling symmetry, obtained by adding a fictitiously large constant term to the Greenwood map, finding no significant effect on the DP phase slope. As discussed before, the NPS at the intermediate x₀ place was found both with and without roughness. Nevertheless, we have also checked the effect of a different schematization of roughness, consisting in a random fluctuation of the maximum OHC gain α₀(x) [Eq. (37) of Sisto et al. (2010)]. We found no significant difference in the computed DP phase between the models using the two schematizations of roughness.

DISCUSSION

We stress that the use of arguments and concepts that are fully valid only for linear systems (such as the system frequency response, and its predicted phase slope for forward and backward waves, but even the basic concept of a spectral component with well-defined amplitude and phase evolving independently from the others) is always dangerous, and implies some risk of circular reasoning. In principle, the phase slopes of nonlinearly and nonlocally generated spectral components should be considered as observable quantities that can be predicted only by sufficiently accurate time-domain solutions of nonlinear models. Nevertheless, there is a remarkable agreement between the results of the linearized analytical model and the numerical solutions of fully nonlinear models. This suggests that the perturbative approaches provide a fast access to useful information about the nonlinear cochlear behavior, although a final check should be made using a fully nonlinear numerical solution method. For this reason, in this discussion we will make use of the intuitive relation between direction of propagation and phase slope, always keeping in mind that this relation is strictly valid for linear systems only.

The modeling studies reported here address the counterintuitive experimental finding (Ren, 2002; He et al., 2007, 2008, 2010, 8, 9 ; de Boer and Nuttall, 2008) that the spatial phase profile of the DP traveling wave along the BM has a negative phase slope (NPS), implying that DP waves are traveling predominantly into the cochlea rather than out of it. The explanation proposed by Ren is that backward-traveling waves on the BM are small (or nonexistent) because the DP energy escapes from the cochlea via an alternative propagation mode (namely fast compressional waves in the fluid) that, unlike the transpartition pressure wave, couples only weakly (if at all) to the motion of the BM. In this model, fast compressional waves are partially converted into forward-traveling transpartition pressure waves visible on the BM by the impedance mismatch at the cochlear boundary with the middle ear. Although this compression-wave model for reverse DP propagation in the cochlea accounts for the measured phase slope, it appears inconsistent with a diverse array of other experimental findings (e.g., Shera et al., 2006; Shera et al., 2007; Moleti and Sisto, 2008; Dong and Olson, 2008; Harte et al., 2009; Meenderink and van der Heijden, 2010), and explanations for the paradoxical negative phase slope are thus reasonably sought elsewhere. (If no plausible alternative explanation could be found, the case for compression-wave DP propagation would be revived).

In a linearized model, when there are waves traveling in opposite directions along the BM, the sign of the total phase slope depends on which of the two waves is the larger at the point of measurement. Consequently, any aspect of the system that can affect the relative amplitudes of the two waves has the potential to influence the experimental outcome. Aside from the possibility of compression-wave propagation discussed above, a list of possible influences includes: (1) the spatial distribution of DP sources relative to the observation point (e.g., Shera et al., 2006; Zhang and Mountain, 2009), including the effective “directionality” of the radiation pattern emanating from the DP source region (Shera and Guinan, 2007); (2) the boundary conditions at the base of the cochlea (i.e., the value of R_s, which determines the amount of energy reflected back into the cochlea); (3) how much of the forward-traveling DP wave is reflected near its characteristic place (e.g., by roughness); (4) the amount and spatial location of traveling-wave amplification in the cochlea; and (5) any asymmetry in the amplification of forward- or backward-traveling waves (de Boer et al., 2008).

Computation of the frequency-domain traveling-wave Green’s function for a linearized cochlear model allows one to partially disentangle these many influences and deduce basic principles that can subsequently be tested in a fully nonlinear, time-domain model. Our results show that the behavior of the DP phase is largely related to the localization of the source and to the presence of significant reflectivity at the stapes for the DP traveling wave. These results apply both to the numerical solutions of the full nonlinear model, to the analytical perturbative calculations, and also to the semi-analytical “hybrid” solutions. We therefore conclude that the supposed discrepancy between the experimental results and theoretical expectations—a discrepancy used to question the existence of significant backward-traveling waves on the BM and thereby to support the dominance of DP propagation via fast compression waves—may in large part be attributed to the fact that naïve theoretical predictions either assume too point-like a localization of the DP source or underestimate the stapes reflectivity, or both. In these unrealistic conditions, both the time-domain and the approximate frequency-domain computations fail to reproduce the experimental results. Therefore, experiments that find NPS do not automatically contradict “classical” models of cochlear mechanics and of distortion-product generation (see also Vetesnik et al., 2006).

CONCLUSIONS

The negative phase slopes observed in BM vibration experiments (e.g., Ren, 2004; de Boer et al., 2008) are predicted by “classical” models of the cochlea under a wide range of parameters, if the stapes reflectance and the spatial distribution of the DP sources are taken into account. Therefore, the notion that the backward propagation of DPOAEs occurs predominantly via longitudinal compressional pressure waves in the cochlear fluid—an idea contradicted by other experimental evidence—cannot be justified on the basis of those BM vibration experiments alone.