Abstract
Case-cohort and nested case-control designs are often used to select an appropriate subsample of individuals from prospective cohort studies. Despite the great attention that has been given to the calculation of association estimators, no formal methods have been described for estimating risk prediction measures from these 2 sampling designs. Using real data from the Swedish Twin Registry (2004–2009), the authors sampled unstratified and stratified (matched) case-cohort and nested case-control subsamples and compared them with the full cohort (as “gold standard”). The real biomarker (high density lipoprotein cholesterol) and simulated biomarkers (BIO1 and BIO2) were studied in terms of association with cardiovascular disease, individual risk of cardiovascular disease at 3 years, and main prediction metrics. Overall, stratification improved efficiency, with stratified case-cohort designs being comparable to matched nested case-control designs. Individual risks and prediction measures calculated by using case-cohort and nested case-control designs after appropriate reweighting could be assessed with good efficiency, except for the finely matched nested case-control design, where matching variables could not be included in the individual risk estimation. In conclusion, the authors have shown that case-cohort and nested case-control designs can be used in settings where the research aim is to evaluate the prediction ability of new markers and that matching strategies for nested case-control designs may lead to biased prediction measures.
Keywords: cardiovascular diseases, case-cohort studies, nested case-control studies, risk prediction, sampling design
Prediction and prognostication of risk for disease is one of the main aims of many biomedical and clinical studies. Risk prediction equations are used clinically in different disease areas (1, 2). In cardiovascular disease (CVD) prevention, the Framingham risk score (2) is a standard tool to predict 10-year incidence of CVD in healthy individuals, and any suggested improvements in risk prediction by the addition of new biomarkers have usually been benchmarked against the Framingham risk score.
In recent years, a number of circulating biomarkers and genetic variants have been reported to be associated with CVD. However, statistical metrics other than measures of association are necessary to assess the clinical utility of these new markers. Metrics of reclassification, discrimination, and calibration are often reported to summarize improvement in prediction when adding a new risk marker to established risk factors, such as those included in the Framingham risk score (3). So far, no new biologic markers for CVD have been consistently shown across different studies and settings to improve the risk prediction of traditional risk factors, although several promising biomarkers need further assessment (4–6).
Population-based longitudinal cohort studies provide the ideal setting to study the prediction ability of new biomarkers. Many such studies have stored biologic samples (including DNA) from thousands of individuals who are being followed up over many years (7, 8). In addition, several new large initiatives in different countries are currently collecting baseline information from hundreds of thousands of individuals, such as LifeGene (9), Biobank in the United Kingdom (10), and LifeLines (11). In parallel with this development, emerging large-scale, high-throughput “-omics” technologies now allow researchers to assess thousands of genetic markers, proteins, and metabolites in small amounts of biologic specimens (12). The combination of huge study samples and high costs for these new technologies makes it unfeasible to measure these new markers on an entire cohort, so there is a clear need for efficient study designs that restrict the measurements to an appropriate subsample.
Case-cohort and nested case-control studies are 2 popular designs for sampling from a prospective cohort where disease outcomes and some baseline information are known for all the individuals (13). These designs may offer considerable cost savings, especially in settings where biologic specimens from baseline are stored for future analysis. Both designs include all individuals who develop the disease during follow-up (cases), but they differ in the selection of the control group. In case-cohort studies, controls come from a subcohort sampled from the entire cohort at baseline, while in nested case-control designs, controls are sampled from individuals at risk at the times when cases are identified.
Despite the great attention given to the calculation of appropriate association estimators, no formal methods have been described for estimating risk prediction measures from these 2 sampling designs. A few previous studies have used prediction measures in subjects sampled with nested case-control (14, 15) and case-cohort (16) designs from prospective cohort studies. However, the authors do not always seem aware of the issues related to using these measures in selected subsamples.
Recognizing the absence of a comprehensive description of the behavior of prediction measures in sampling designs, we aimed to investigate the ability to adequately estimate individual risk and risk prediction metrics in unstratified and stratified (matched) case-cohort and nested case-control designs. We did this by comparing these designs with realizations from the whole longitudinal cohort study (as “gold standard”) in 3 steps. First, we compared the accuracy of the estimates of association. Second, we estimated the cumulative individual risk of disease. Finally, we compared appropriate prediction metrics for survival data—the net reclassification improvement (for reclassification), the C-index (a measure of discrimination in survival analysis for discrimination), and the goodness-of-fit test (for calibration) developed by Grønnesby and Borgan (hereafter referred to as the “GB test”). We studied 1 real biomarker, high density lipoprotein cholesterol (HDL-C), and 2 simulated biomarkers, using data from the Swedish Twin Registry on 6,558 unrelated individuals free of diagnosed CVD at baseline.
MATERIALS AND METHODS
Study sample
TwinGene is a longitudinal substudy within the Swedish Twin Register (17) (www.tvillingregistret.se) that was initiated to examine associations between genetic factors and CVD in Swedish twins. Within this study, we selected 6,558 unrelated individuals (2,862 men, 3,696 women) and linked them with Swedish health registers to identify CVD events before December 2009. A detailed description of the study subjects can be found in the Web Appendix, posted on the Journal’s website (http://aje.oxfordjournals.org/).
All participants provided written informed consent, and the Stockholm Regional Ethical Review Board approved the study.
Biomarker simulation and measurements
The 2 biomarkers were generated to have mean and standard deviation equal to 6 in cases. To create a biomarker (BIO1) independently and highly associated with the outcome (hazard ratio per 1-standard deviation (SD) increase = 1.62; P < 0.0001 after multivariable adjustment), we set the average in controls equal to 3 and again used a SD = 6. The second biomarker (BIO2) was created to have a weaker association (hazard ratio per 1-SD increase = 1.25; P = 0.006 after adjustment) and to be correlated (rho = 0.5) with age, systolic blood pressure, and antihypertensive treatment. These relations were obtained by setting the average of BIO2 in controls equal to 4 (SD = 6) and using Cholesky decomposition to introduce the chosen correlation. In the comparisons of the different study designs, we used these simulated biomarkers and actual data on HDL-C.
Assessing performance of sampling designs
Calculation of prediction measures in the same sample used for model fitting introduces a risk of overestimation of the prediction ability and induces optimism about model performance (18). Internal validation techniques, such as bootstrapping, can be applied to reduce this source of bias. With this in mind, we designed our study using the following strategy: 1) From the original cohort of 6,558 unrelated individuals, we sampled with replacement (i.e., bootstrapped) a random sample of the same size (n = 6,558) that we will refer to as a “realization”; 2) from the realization, we sampled the stratified or unstratified case-cohort and nested case-control subsamples and implemented the appropriate analysis to calculate the measures of interest; and 3) we repeated this process 2,000 times, obtaining 2,000 realizations of the original cohort and consequently 2,000 case-cohort and nested case-control samples and the measures of interest they produced.
Description of study designs evaluated
For each of the case-cohort and nested case-control designs, we considered 2 sampling schemes:
Unstratified designs. For the case-cohort design, the subcohort was a random sample from the realization of the original cohort; for the nested case-control design, x controls were selected at random from individuals at risk at each case’s failure time.
Stratified designs. For the case-cohort design, we considered 4 strata (male or female and age higher or lower than the median) and randomly sampled from the realization of the original cohort a number of participants proportional to the number of cases in each of these strata. For each case in the nested case-control design, we selected x controls at risk with the same sex and age (fine matching).
Because it was not possible to have equal sample sizes for all designs, we chose the number of participants in the subcohort of the case-cohort sample so that the total number of unique individuals in the stratified case-cohort design was approximately equal to the number of unique subjects in the matched nested case-control design. Thus, equal sample sizes were achieved for these 2 designs, which were the main focus of our comparisons because of their superior performances in terms of study efficiency.
Comparison of estimators
We compared the average hazard ratios for BIO1, BIO2, and HDL-C in the realizations with the corresponding values obtained from the case-cohort and nested case-control designs. To estimate the efficiency of a sampling design, we compared the empirical variance of the parameter estimates obtained from the 2,000 realizations of the cohort with the empirical variance of the estimates obtained from the corresponding 2,000 case-cohort or nested case-control samples. The ratio of these variances is the empirical relative efficiency, and values close to 100% indicate that the sampling design provides estimators with precision similar to those of the full cohort analysis.
For case-cohort designs, we used a multivariable Cox proportional hazards model with the modifications referred to as “Prentice” (19), “Self and Prentice” (20), and “Barlow” (21) for unstratified designs and “Borgan I” (22), “Borgan II” (22), and “Breslow calibration” (23) for stratified designs. Briefly, these methods differ in the risk set definitions and in the weights used in the pseudo-likelihood estimation (described in detail in the Web Appendix). For the nested case-control design, coefficients were estimated by using multivariable conditional logistic regression. In the matched nested case-control design, we thus could not estimate the coefficients for age or sex. All analyses were adjusted for the components of the Framingham risk score, except HDL-C, which we omitted in order to have a common baseline model for all 3 markers (BIO1, BIO2, HDL-C).
Individual risk calculation
We determined the individual risk of CVD within 3 years for each sampled participant in each design and compared it with the individual risk obtained for the same individual from the realization of the original cohort. The building block for the calculation of the individual risk (the probability that the subject does not survive CVD free to 3 years) is the cumulative baseline hazard, which has a simple relation with the survival function (refer to the Web Appendix). This quantity can be calculated for both case-cohort and unmatched nested case-control designs by using a weighted modification of the Breslow estimator of the cumulative hazard. Special attention must be paid to the selection of the appropriate weights and to the definition of the risk sets and, in the Web Appendix, we provide an extended description of the methods we used. The individual risk for an individual, k, at a given time is a function of this cumulative baseline hazard, the values for the considered risk factors (z1,k, z2,k, …, z1,k) for the individual, and the coefficients for each of these factors. The sum of the product of these last 2 elements is called the “linear predictor” (β1z1,k + β2z2,k + …+ β1z1,k) for the subject, while the cumulative baseline hazard is common to all the subjects. We estimated the individual risk for matched nested case-control designs in the same way, except that age and sex could not be included in the linear predictor.
Another method for calculation of the predicted individual risk is to obtain the Breslow estimator of cumulative baseline hazard from the full cohort, adjusting for all covariates except the investigated biomarker. However, this estimator is calculated at the average values of the covariates in the whole cohort and, thus, to obtain an appropriate individual risk, the linear predictor for an individual in the case-cohort or nested case-control study must have this average subtracted from his or her covariates. Because the investigated biomarker is not available for the whole cohort, the average can be approximated by the average value among controls.
Prediction metrics assessment
To evaluate the improvement in model discrimination on adding a new marker (BIO1, BIO2, HDL-C), we calculated the C-index (24), which is equivalent to the receiver operating characteristic area under the curve, taking censorship into account. Risk reclassification was evaluated with net reclassification improvement (25) (categories of ≤5%, 6%–20%, >20% as suggested by Pencina et al. (26)). Calibration, the comparison between the predicted and observed number of events, was assessed with the GB test (27), using the implementation proposed by May and Hosmer (28). This test is similar to the Hosmer and Lemeshow test for logistic models but based on martingale residuals. The test is easily implemented in standard statistical software by adding group indicator variables (obtained as quintiles of the risk score) to a standard Cox model and testing, via a Wald test, the hypothesis that the coefficients of the group indicator variables are zero.
With the exception of the unstratified case-cohort design, the case-cohort and nested case-control designs include all cases and a sample of controls that is not fully representative of the original cohort. Although providing efficient estimates of association (hazard ratio), this biased sampling creates limitations in the assessment of prediction measures. To overcome the selective sampling, we used a weighted version of the C-index and net reclassification improvement, assigning a weight of 1 to cases and a weight equal to the inverse of the sampling probability to controls (specific weights for each design are described in the Web Appendix). In this way, we obtained prediction measures comparable with the corresponding measures in the original cohort. The GB calibration test for sampling designs is based on weighted martingale residuals and does not need any further reweighting (29).
Because case-cohort and nested case-control designs allow for multiple selections of the same individual, we took care not to include duplicated subjects in the calculations of prediction measures (refer to the Web Appendix).
Software
All simulations and analyses were conducted by using the R statistical package (version 2.11.0). To fit the model for the unstratified case-cohort design, we used the “coxph” function from the survival package (version 2.35-8) after appropriate rearrangement of the data structure as suggested by Langholz and Jiao (30) and Kulathinal et al. (31). The unmatched and matched nested case-control designs were analyzed with the coxph function by using an offset argument and “fake” entry time as shown by Langholz (http://hydra.usc.edu/timefactors) for the SAS statistical package (SAS Institute, Inc., Cary, North Carolina). The stratified case-cohort design was analyzed by using the 2-phase function from the R survey package (version 3.22-4) following the tutorial by Breslow (http://faculty.washington.edu/norm/IEA08.html).
RESULTS
Association of biomarkers with CVD
Two hundred and thirty-eight CVD events were observed during a median follow-up of 3.0 years. Table 1 presents baseline characteristics, along with the hazard ratios and confidence intervals of Framingham risk score covariates. Further, hazard ratios calculated in the full original cohort are reported in Web Table 1, the first of 3 Web tables and 1 Web figure in the Web Appendix). As expected, the average of the bootstrapped hazard ratios was almost identical to the values observed in the original cohort.
Table 1.
Baseline Descriptive Statistics and Average Associationsa (Confidence Intervals) With Cardiovascular Disease for Models With a Framingham Risk Score + High Density Lipoprotein Cholesterol, Biomarker 1, or Biomarker 2, TwinGene, 2004–2009
| Descriptive Statistics |
Association (Average Realization)b |
|||||||||||
| Characteristic | Men |
Women |
FRS + HDL-C |
FRS + BIO1 |
FRS + BIO2 |
|||||||
| No. | % | Mean (SD) | No. | % | Mean (SD) | HR | 95% CI | HR | 95% CI | HR | 95% CI | |
| Sex | 2,862 | 43 | 3,696 | 56 | 0.46*** | 0.34, 0.61 | 0.43*** | 0.33, 0.56 | 0.42*** | 0.32, 0.55 | ||
| Age, years | 65 (8) | 64 (8) | 1.07*** | 1.05, 1.09 | 1.06*** | 1.05, 1.08 | 1.06*** | 1.04, 1.08 | ||||
| Diabetes | 220 | 8 | 187 | 5 | 1.99** | 1.36, 2.92 | 2.11** | 1.43, 3.10 | 2.09** | 1.42, 3.07 | ||
| Current smokers | 401 | 14 | 617 | 17 | 1.75** | 1.25, 2.44 | 1.80** | 1.29, 2.51 | 1.77** | 1.27, 2.46 | ||
| Antihypertensive drugs | 491 | 17 | 668 | 18 | 1.69** | 1.27, 2.24 | 1.66** | 1.25, 2.21 | 1.71** | 1.28, 2.26 | ||
| Systolic blood pressure, mm Hg | 140 (19) | 138 | 20 | 1.01* | 1.00, 1.02 | 1.01* | 1.00, 1.02 | 1.01 | 1.00, 1.01 | |||
| Total cholesterol, mg/dL | 5.6 (1.1) | 6.0 (1.1) | 1.25** | 1.11, 1.41 | 1.22* | 1.08, 1.38 | 1.22* | 1.08, 1.37 | ||||
| HDL-C, mg/dL | 1.3 (0.3) | 1.6 (0.4) | 0.62* | 0.43, 0.91 | ||||||||
| BIO1 | 3.3 (5.9) | 3.0 (6.1) | 1.61c, *** | 1.42, 1.83 | ||||||||
| BIO2 | 35.9 (6.0) | 35.3 (6.2) | 1.24c, ** | 1.06, 1.45 | ||||||||
Abbreviations: BIO1, simulated biomarker 1; BIO2, simulated biomarker 2; CI, confidence interval; FRS, Framingham risk score; HDL-C, high density lipoprotein cholesterol; HR, hazard ratio; SD, standard deviation.
* P < 0.05; **P < 0.001; ***P < 0.0001.
Hazard ratios are obtained as the exponentiated average of the ln(HR) values from the 2,000 realizations, and confidence intervals are constructed with the average of 2,000 model-based standard errors for ln(HR).
All estimates reported are from Cox proportional hazard analyses adjusted for age, sex, systolic blood pressure, antihypertensive treatment, diabetes, current smoking, and total cholesterol.
For 1 − SD increase of the biomarker.
Estimates of association for BIO1, BIO2, and HDL-C with CVD are shown in Table 2 for the full realizations and the different study designs. Both case-cohort and nested case-control designs gave more accurate results when stratified/matched sampling was used. Stratified case-cohort and matched nested case-control designs were comparable in terms of accuracy and efficiency of estimates; unmatched nested case-control designs were more efficient than the unstratified case-cohort design.
Table 2.
Average Hazard Ratiosa (Empirical Relative Efficiencyb) for Associationc With Cardiovascular Disease, TwinGene, 2004–2009
| Marker | Average Realizations, the Gold Standard | Unstratified Case-Cohort Design |
Unmatched Nested Case-Control Design | Stratified Case-Cohort Design |
Matched Nested Case-Control Design | ||||
| Prentice (19)d | Self and Prentice (20)d | Barlow (21)d | Borgan I (22) d | Borgan II (22)d | Breslow Calibration (23)d | ||||
| BIO1e | 1.61 (100) | 1.73 (12) | 1.78 (9) | 1.78 (10) | 1.75 (20) | 1.71 (16) | 1.65 (26) | 1.67 (26) | 1.69 (27) |
| BIO2e | 1.24 (100) | 1.27 (18) | 1.28 (16) | 1.28 (16) | 1.30 (26) | 1.26 (25) | 1.25 (31) | 1.26 (31) | 1.26 (36) |
| HDL-Ce | 0.62 (100) | 0.61 (22) | 0.60 (21) | 0.60 (21) | 0.57 (31) | 0.60 (29) | 0.60 (31) | 0.61 (61) | 0.63 (42) |
| BIO1f | 1.61 (100) | 1.66 (28) | 1.67 (26) | 1.67 (26) | 1.69 (44) | 1.65 (42) | 1.63 (55) | 1.63 (54) | 1.66 (54) |
| BIO2f | 1.24 (100) | 1.25 (39) | 1.26 (38) | 1.26 (38) | 1.27 (54) | 1.25 (55) | 1.24 (60) | 1.24 (59) | 1.26 (65) |
| HDL-Cf | 0.62 (100) | 0.62 (49) | 0.62 (49) | 0.62 (49) | 0.59 (55) | 0.61 (60) | 0.61 (61) | 0.62 (82) | 0.63 (67) |
Abbreviations: BIO1, simulated biomarker 1; BIO2, simulated biomarker 2; HDL-C, high density lipoprotein cholesterol.
For 1 − SD increase of the biomarker. Hazard ratios are estimated by exponentiating the average of the ln(HR) values obtained from 2,000 realizations.
“Empirical relative efficiency” is defined as the ratio between the empirical variance of the ln(HR) calculated for 2,000 realizations from the entire cohort and the empirical variance calculated for each design, expressed as percentage.
All estimates reported are from Cox proportional hazard analyses or conditional logistic regression adjusted for age, sex, systolic blood pressure, antihypertensive treatment, diabetes, current smoking, and total cholesterol.
Reference number.
Sampling ratio: 1:1; subcohort size: n = 229. There were 459, 467, 454, and 454 individual subjects for the unstratified case-cohort design, the unmatched nested case-control design, the stratified case-cohort design, and the matched nested case-control design, respectively.
Sampling ratio: 1:3; subcohort size: n = 632. There were 847, 896, 835, and 833 individual subjects for the unstratified case-cohort design, the unmatched nested case-control design, the stratified case-cohort design, and the matched nested case-control design, respectively.
Estimates of individual risk
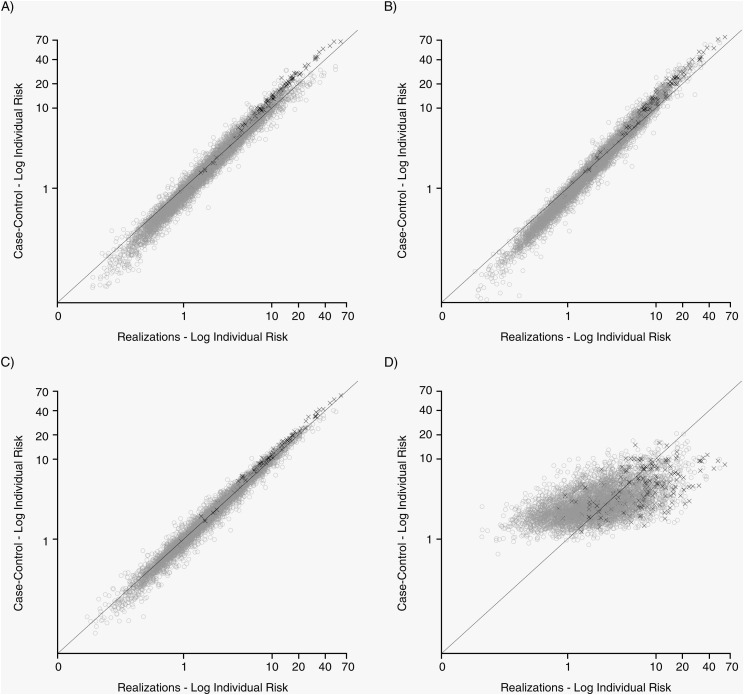
In Table 3, we present the median differences between individual risks calculated in the sampling designs and in the full realizations for the Prentice and Borgan II methods. Overall, median differences were small, ranging from 0.01% for stratified case-cohort designs to −0.64% for matched nested case-control designs. These results are also presented graphically in Figure 1 and Web Figure 1 where, for BIO1, we compared log-transformed individual risks from the realization (gold standard) with the value from the sampling designs with 1:1 and 1:3 sampling ratios, respectively. If the estimated risk in the sampling design is equal to that in the full realization, all points will fall on the bisector line. Deviation from this line indicates over- or underestimation of the individual risk. Our plots indicate serious deviations for the matched nested case-control design but unbiased estimates for the other designs. Similar results were observed for BIO2 and HDL-C (data not shown).
Table 3.
Median (5th–95th Percentile) Differences in Individual Risk at 3 Years Between Calculations From the Full Realizations (Gold Standard) and From the Sampling Design, TwinGene, 2004–2009
| Marker | Unstratified Case-Cohort Design |
Unmatched Nested Case-Control Design |
Stratified Case-Cohort Design |
Matched Nested Case-Control Design |
||||
| Median Difference, % | Rangea | Median Difference, % | Range | Median Difference, % | Range | Median Difference, % | Range | |
| BIO1b | 0.08 | −0.75 to 0.23 | 0.01 | −2.12 to 0.33 | 0.02 | −0.38 to 0.23 | −0.62 | −3.03 to 5.54 |
| BIO2b | 0.06 | −0.61 to 0.22 | 0.08 | −1.67 to 0.37 | 0.02 | −0.36 to 0.21 | −0.43 | −2.67 to 5.00 |
| HDL-Cb | 0.06 | −0.59 to 0.23 | 0.08 | −1.68 to 0.47 | 0.02 | −0.40 to 0.21 | −0.42 | −2.65 to 5.18 |
| BIO1c | 0.04 | −0.37 to 0.09 | 0.07 | −1.21 to 0.24 | 0.01 | −0.14 to 0.07 | −0.64 | −2.99 to 5.58 |
| BIO2c | 0.03 | −0.26 to 0.08 | 0.06 | −0.97 to 0.26 | 0.01 | −0.14 to 0.07 | −0.45 | −2.66 to 5.10 |
| HDL-Cc | 0.03 | −0.24 to 0.08 | 0.06 | −0.99 to 0.34 | 0.01 | −0.15 to 0.07 | −0.44 | −2.63 to 5.16 |
Abbreviations: BIO1, simulated biomarker 1; BIO2, simulated biomarker 2; HDL-C, high density lipoprotein cholesterol.
Range: 5th to 95th percentiles.
Sampling ratio: 1:1; subcohort size: n = 229.
Sampling ratio: 1:3; subcohort size: n = 632.
Figure 1.
Individual risk (plotted on the logarithmic scale) from sampling designs compared with the realizations (“gold standard”) for simulated biomarker 1 (BIO1) and a 1:1 sampling ratio, TwinGene, 2004–2009. Values on the bisector indicate perfect agreement between individual risk calculated in the sampling design and in the realization. Cases are represented by a black “X” and controls by gray hollow circles. A, realizations versus unstratified case-cohort design; B, realization versus unmatched nested case-control design; C, realizations versus stratified case-cohort design; D, realizations versus matched nested case-control study design.
Prediction measures
Measures of reclassification, discrimination, and calibration for models with BIO1, BIO2, and HDL-C are reported in Table 4. On average, BIO1 was able to correctly reclassify 9.1% of individuals in the full realizations compared with a model including only established risk factors. Moreover, it showed a significant improvement in the C-index (0.779 vs. 0.751; P = 0.0005). Improvements in reclassification and discrimination for BIO2 were not significant.
Table 4.
Weighted Prediction Measures (Empirical Relative Efficiency) of Cardiovascular Disease at 3 Years, TwinGene, 2004–2009
| Marker | Average Realizations, the Gold Standard | Unstratified Case-Cohort Design | Unmatched Nested Case-Control Design | Stratified Case-Cohort Design | Matched Nested Case-Control Design |
| Reclassificationa | |||||
| BIO1b | 9.1 (100)c | 8.6 (34) | 9.6 (39) | 8.5 (49) | 10.1 (31) |
| BIO2b | 2.0 (100) | 1.7 (55) | 2.1 (53) | 1.6 (67) | 4.0 (34) |
| HDL-Cb | 0.8 (100) | 1.2 (47) | 1.0 (48) | 1.1 (61) | 0.4 (49) |
| BIO1d | 9.1 (100) | 8.8 (56) | 9.5 (67) | 8.9 (71) | 9.7 (57) |
| BIO2d | 2.0 (100) | 1.7 (69) | 2.0 (80) | 1.8 (78) | 4.0 (57) |
| HDL-Cd | 0.8 (100) | 0.8 (77) | 0.7 (79) | 0.9 (88) | 0.5 (73) |
| Discriminatione | |||||
| BIO1b | 0.779 (100) | 0.777 (45) | 0.783 (48) | 0.780 (56) | 0.704 (25) |
| BIO2b | 0.756 (100) | 0.755 (46) | 0.760 (50) | 0.757 (62) | 0.679 (28) |
| HDL-Cb | 0.756 (100) | 0.756 (47) | 0.761 (51) | 0.758 (61) | 0.678 (24) |
| BIO1d | 0.779 (100) | 0.778 (72) | 0.782 (75) | 0.780 (77) | 0.701 (44) |
| BIO2d | 0.756 (100) | 0.755 (72) | 0.759 (76) | 0.756 (81) | 0.675 (46) |
| HDL-Cd | 0.756 (100) | 0.756 (72) | 0.760 (76) | 0.757 (80) | 0.674 (43) |
| Calibrationf | |||||
| BIO1b | 9.7 | 10.0 | 5.7 | 6.5 | 5.5 |
| BIO2b | 8.3 | 8.6 | 5.8 | 6.0 | 5.6 |
| HDL-Cb | 8.1 | 7.7 | 5.0 | 5.9 | 6.0 |
| BIO1d | 9.7 | 7.1 | 6.9 | 7.8 | 6.5 |
| BIO2d | 8.3 | 6.2 | 6.3 | 6.9 | 6.7 |
| HDL-Cd | 8.1 | 5.8 | 6.2 | 6.4 | 7.5 |
Abbreviations: BIO1, simulated biomarker 1; BIO2, simulated biomarker 2; HDL-C, high density lipoprotein cholesterol.
The net reclassification improvement percentage.
Sampling ratio: 1:1; subcohort size: n = 229.
Numbers in parentheses represent the “empirical relative efficiency,” defined as the ratio between the empirical variance calculated in 2,000 realizations and the empirical variance calculated for each design, expressed as percentage.
Sampling ratio: 1:3; subcohort size: n = 632.
The average of C-index, which is equivalent to the receiver operating characteristic area under the curve, taking censorship into account.
The Grønnesby and Borgan goodness-of-fit test statistic. Values higher than 9.5 indicate significant lack of calibration.
Overall, in all case-cohort designs and the unmatched nested case-control design, the estimates of the different prediction measures were similar to what was observed for the full realizations, but the variability was higher. The C-index for the matched nested case-control design was lowest, which was not surprising as the regression model did not include age and sex, thus leading to a poorer fit. All models including biomarkers that were calibrated in the realizations (gold standard) were also calibrated in the sample designs; however, we observed a tendency to overestimate the model goodness of fit for all designs. In Table 5, we report the mean changes in the C-index when the model with only established risk factors is augmented with one of the biomarkers, and we compare these changes with the changes in the realizations. The matched nested case-control design overestimated the changes, while the remaining designs were in close agreement with the gold standard and able to detect significant changes.
Table 5.
Average Difference in C-Indexa Between Base Model (FRS) and Base Model + Marker, TwinGene, 2004–2009
| Marker | C-Index Improvements Over the Base Model (C-Index = 0.751) |
||||
| Average Realizations, the Gold Standard | Unstratified Case-Cohort Design | Unmatched Nested Case-Control Design | Stratified Case-Cohort Design | Matched Nested Case-Control Design | |
| BIO1b | 0.028** | 0.026* | 0.027* | 0.027* | 0.044 |
| BIO2b | 0.004 | 0.004 | 0.004 | 0.004 | 0.018 |
| HDL-Cb | 0.005 | 0.005 | 0.005 | 0.005 | 0.018 |
| BIO1c | 0.028** | 0.027* | 0.027* | 0.028* | 0.045* |
| BIO2c | 0.004 | 0.004 | 0.004 | 0.004 | 0.019 |
| HDL-Cc | 0.005 | 0.005 | 0.005 | 0.005 | 0.018 |
Abbreviations: BIO1, simulated biomarker 1; BIO2, simulated biomarker 2; FRS, Framingham risk score; HDL-C, high density lipoprotein cholesterol.
* P < 0.05; **P < 0.001 (for test of difference).
C-index is equivalent to the receiver operating characteristic area under the curve, taking censorship into account.
Sampling ratio: 1:1; subcohort size: n = 229.
Sampling ratio: 1:3; subcohort size: n = 632.
DISCUSSION
In this study, we use data on 1 real and 2 simulated biomarkers in a large prospective cohort to compare individual risk and prediction measures between 2 popular sampling designs. Previous studies have used a weighting system to adjust for the skewed distribution of controls due to sampling, but none provided a formal and detailed description of how this was implemented. Interestingly, 2 editorials (32, 33) in different research areas (cardiovascular disease and breast cancer) identified similar limitations, and one of these suggested an adjustment using the entire cohort (33). We propose reweighting the prediction measures with the inverse of the sampling probabilities to obtain more precise estimators.
We performed our analyses in 3 steps. First, we studied the performance of the different designs in terms of estimates of association and confirmed previous findings (22, 34) that stratification or matching improves the accuracy and precision. Overall, the finely matched nested case-control design was comparable with the stratified case-cohort design. Different weighting methods have been proposed to estimate hazard ratios in the case-cohort design. Confirming results from a previous study (35), we found that the Prentice method (19) is the most accurate and precise among the unstratified methods. In 2009, Breslow et al. (23) suggested using a 2-stage calibration approach to recalculate the sampling weights in stratified case-cohort studies using the information available from the whole cohort. In our data, we found this method to be superior for 1 marker (HDL-C), which can be explained by its correlation with apolipoprotein AI, which was included in the model we used to recalibrate the weights (description in the Web Appendix). Thus, this method is useful in situations where information available for the whole cohort is correlated with markers measured in the subsample, but it may not improve efficiency where the investigated markers are unrelated to established risk factors.
In the second part of this work, we calculated the individual CVD risk at 3 years, using only subjects sampled in the case-cohort or nested case-control designs and reweighting by the cumulative baseline hazard. These methods are not routinely implemented in statistical packages and require some computational precautions. Langholz and Jiao (30) describe computational methods for case-cohort studies, and Langholz provides SAS macros for the calculation of absolute risks for case-cohort and nested case-control designs (http://hydra.usc.edu/timefactors).
Alternatively, the cumulative hazard can be calculated in the whole cohort adjusting for all covariates except the investigated biomarker. We applied this method to our data to recalculate the median differences in Table 3, and the results are provided in Web Table 2. Overall, the individual risk estimators were less precise than in Table 3, especially for larger subsamples (1:3 sampling ratio) and the more highly associated biomarker (BIO2). In general, we suggest calculating the baseline hazard using only subsampled subjects as proposed by Langholz and Borgan (36).
Finally, we calculated the 3 prediction measures suggested in the recent literature. These required reweighting of the controls so that the subsample was representative of the original cohort. Although this is straightforward for case-cohort designs where the subcohort is a random or stratified sample of the whole cohort, the appropriate weights for nested case-control designs are more complex as they are based on the inverse of the probability that a subject is ever selected as a control (37) (Web Appendix). In Web Table 3, we report the unweighted prediction measures for comparison. Estimates of the net reclassification improvement were similar to the weighted versions, indicating that the reclassification abilities of a new marker in a population can be estimated from a selected subpopulation enriched with high-risk subjects. However, C-indices were severely underestimated and clearly needed to be reweighted.
We experienced some problems in the calculation of individual risk for the matched nested case-control design and, consequently, the prediction measures were unsatisfactory. In this design, coefficients for matching variables are not estimable, resulting in a biased calculation of the individual risk and overestimation of the discriminative power introduced by the additional biomarker. This problem was previously reported by Janes and Pepe (38) for case-control designs. An alternative common practice is to include the matching variables in an unconditional logistic regression, a method often referred to as “breaking the matching.” This procedure is meant to adjust for the residual confounding not captured by a simple matched analysis. However, it is well known that the association coefficients for the matching variables are not correctly estimated. In a classic association study, the correct estimation of these coefficients is not of interest but, where the aim is the assessment of the predictive ability of new biomarkers, the individual risk (which is a function of all variables in the model) will be biased.
It has been suggested that calibration measures cannot be assessed within a nested case-control design (39). We showed that assessment of calibration is possible for case-cohort and nested case-control designs using the GB test. However, we noticed a tendency to overestimate the goodness of fit of the model (lower GB test values) compared with the realizations. This may be partially explained by the different definition of the quintiles used in the sampling designs, where the numbers of subjects in low risk ranges are reduced; weighted quintiles of risk may reconstruct the risk distribution observed in the realization. As an alternative, we suggest comparing the observed number of events with the expected number obtained from martingale residuals, within categories of clinical utility, using a standardized z statistic = (“observed” − “expected”)/(√“expected”) as suggested by May and Hosmer (28). Investigations of the performance of these suggested strategies are beyond the scope of the present paper.
Strengths of our study include the large, prospective cohort with data on relevant baseline variables, the use of bootstrapped samples to reflect uncertainty in the cohort parameter estimates, and the exploration of different scenarios using both real and simulated markers with widely different properties. For these reasons, although we concentrated on a specific disease (CVD), the main conclusions from our work are likely to be applicable to other settings. Most cardiovascular studies investigate the prediction ability of new markers using a 10-year individual risk. However, given the limited follow-up time of our study, we chose to assess the 3-year risk. This will not affect the comparison of prediction measures because the weights we used depend only on the sampling probability and not on the length of follow-up.
Some limitations of our study also need to be considered. We focused on a limited number of designs, considering only stratification and matching on age and sex. Although these designs reflect much of the epidemiologic literature, better stratification schemes might be used according to the purpose of the specific study. For example, in order to obtain better estimates of the individual risks in matched nested case-control studies, it is possible to enlarge the matching categories to calculate strata-specific cumulative hazards (13). Whether this will result in a reduction in efficiency is a matter for further investigation. Another aspect that was not investigated here is the behavior of the asymptotic variance estimators, as the purpose of our study was to assess design performance, which we did by comparing empirical variances.
Scientists are currently embarking on a new era, with the collection of biologic specimens within large prospective studies with hundreds of thousands of individuals. The high cost of laboratory assays makes it impractical to ascertain all measurements for all individuals within such cohorts and, hence, substudies need to be conducted on selected participants. Alternatively, specimen pooling strategies may be considered, and methods to deal with these have been developed for matched and unmatched case-control studies (40, 41).
In this paper, we have shown that case-cohort and nested case-control sampling designs not only provide accurate and efficient estimates of association but also can be used to calculate measures of reclassification, discrimination, and calibration. However, finely matched nested case-control studies may not be appropriate when the research aim is to evaluate the prediction ability of a new biomarker.
Supplementary Material
Acknowledgments
Author affiliations: Department of Medical Epidemiology and Biostatistics, Karolinska Institutet, Stockholm, Sweden (Andrea Ganna, Marie Reilly, Nancy Pedersen, Patrik Magnusson, Erik Ingelsson); and Institute of Environmental Medicine, Karolinska Institutet, Stockholm, Sweden (Ulf de Faire).
The Swedish Twin Registry is supported by the Ministry for Higher Education, the Swedish Research Council, and GenomEUtwin; the US National Institutes of Health; and the Swedish Foundation for Strategic Research. E. I. and A. G. were supported by the Swedish Foundation for Strategic Research (ICA08-0047), the Swedish Research Council (2009–2298), the Swedish Heart-Lung Foundation (20100401), and the Royal Swedish Academy of Science when working on this paper.
The authors thank Ørnulf Borgan, Bryan Langholz, Nathalie Støer, and Sven Ove Samuelsen for helpful advice regarding sampling designs and weighting strategies.
The sponsors had no role in the study design, analyses, writing, or decision to publish the manuscript.
Conflict of interest: none declared.
Glossary
Abbreviations
- BIO1 and BIO2
simulated biomarkers 1 and 2
- CVD
cardiovascular disease
- HDL-C
high density lipoprotein cholesterol
- SD
standard deviation
References
- 1.Gail MH, Brinton LA, Byar DP, et al. Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. J Natl Cancer Inst. 1989;81(24):1879–1886. doi: 10.1093/jnci/81.24.1879. [DOI] [PubMed] [Google Scholar]
- 2.Wilson PW, D’Agostino RB, Levy D, et al. Prediction of coronary heart disease using risk factor categories. Circulation. 1998;97(18):1837–1847. doi: 10.1161/01.cir.97.18.1837. [DOI] [PubMed] [Google Scholar]
- 3.Pencina MJ, D’Agostino RB, Vasan RS. Statistical methods for assessment of added usefulness of new biomarkers. Clin Chem Lab Med. 2010;48(12):1703–1711. doi: 10.1515/CCLM.2010.340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Melander O, Newton-Cheh C, Almgren P, et al. Novel and conventional biomarkers for prediction of incident cardiovascular events in the community. JAMA. 2009;302(1):49–57. doi: 10.1001/jama.2009.943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wang TJ, Gona P, Larson MG, et al. Multiple biomarkers for the prediction of first major cardiovascular events and death. N Engl J Med. 2006;355(25):2631–2639. doi: 10.1056/NEJMoa055373. [DOI] [PubMed] [Google Scholar]
- 6.Zethelius B, Berglund L, Sundström J, et al. Use of multiple biomarkers to improve the prediction of death from cardiovascular causes. N Engl J Med. 2008;358(20):2107–2116. doi: 10.1056/NEJMoa0707064. [DOI] [PubMed] [Google Scholar]
- 7.The Atherosclerosis Risk in Communities (ARIC) Study: design and objectives. The ARIC investigators. Am J Epidemiol. 1989;129(4):687–702. [PubMed] [Google Scholar]
- 8.Hays J, Hunt JR, Hubbell FA, et al. The Women’s Health Initiative recruitment methods and results. Ann Epidemiol. 2003;13(suppl 9):S18–S77. doi: 10.1016/s1047-2797(03)00042-5. [DOI] [PubMed] [Google Scholar]
- 9.Almqvist C, Adami HO, Franks PW, et al. LifeGene—a large prospective population-based study of global relevance. Eur J Epidemiol. 2011;26(1):67–77. doi: 10.1007/s10654-010-9521-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Elliott P, Peakman TC. The UK Biobank sample handling and storage protocol for the collection, processing and archiving of human blood and urine. Int J Epidemiol. 2008;37(2):234–244. doi: 10.1093/ije/dym276. [DOI] [PubMed] [Google Scholar]
- 11.Stolk RP, Rosmalen JG, Postma DS, et al. Universal risk factors for multifactorial diseases: LifeLines: a three-generation population-based study. Eur J Epidemiol. 2008;23(1):67–74. doi: 10.1007/s10654-007-9204-4. [DOI] [PubMed] [Google Scholar]
- 12.Schmid A, Blank LM. Systems biology: hypothesis-driven omics integration. Nat Chem Biol. 2010;6(7):485–487. doi: 10.1038/nchembio.398. [DOI] [PubMed] [Google Scholar]
- 13.Langholz B, Goldstein L. Risk set sampling in epidemiologic cohort studies. Stat Sci. 1996;11(1):35–53. [Google Scholar]
- 14.Mealiffe ME, Stokowski RP, Rhees BK, et al. Assessment of clinical validity of a breast cancer risk model combining genetic and clinical information. J Natl Cancer Inst. 2010;102(21):1618–1627. doi: 10.1093/jnci/djq388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kim HC, Greenland P, Rossouw JE, et al. Multimarker prediction of coronary heart disease risk: the Women’s Health Initiative. J Am Coll Cardiol. 2010;55(19):2080–2091. doi: 10.1016/j.jacc.2009.12.047. [DOI] [PubMed] [Google Scholar]
- 16.Folsom AR, Chambless LE, Ballantyne CM, et al. An assessment of incremental coronary risk prediction using C-reactive protein and other novel risk markers: the Atherosclerosis Risk in Communities Study. Arch Intern Med. 2006;166(13):1368–1373. doi: 10.1001/archinte.166.13.1368. [DOI] [PubMed] [Google Scholar]
- 17.Lichtenstein P, De Faire U, Floderus B, et al. The Swedish Twin Registry: a unique resource for clinical, epidemiological and genetic studies. J Intern Med. 2002;252(3):184–205. doi: 10.1046/j.1365-2796.2002.01032.x. [DOI] [PubMed] [Google Scholar]
- 18.Steyerberg EW, Harrell FE, Jr, Borsboom GJ, et al. Internal validation of predictive models: efficiency of some procedures for logistic regression analysis. J Clin Epidemiol. 2001;54(8):774–781. doi: 10.1016/s0895-4356(01)00341-9. [DOI] [PubMed] [Google Scholar]
- 19.Prentice RL. A case-cohort design for epidemiologic cohort studies and disease prevention trials. Biometrika. 1986;73(1):1–11. [Google Scholar]
- 20.Self SG, Prentice RL. Asymptotic distribution theory and efficiency results for case-cohort studies. Ann Stat. 1988;16(1):64–81. [Google Scholar]
- 21.Barlow WE. Robust variance estimation for the case-cohort design. Biometrics. 1994;50(4):1064–1072. [PubMed] [Google Scholar]
- 22.Borgan O, Langholz B, Samuelsen SO, et al. Exposure stratified case-cohort designs. Lifetime Data Anal. 2000;6(1):39–58. doi: 10.1023/a:1009661900674. [DOI] [PubMed] [Google Scholar]
- 23.Breslow NE, Lumley T, Ballantyne CM, et al. Using the whole cohort in the analysis of case-cohort data. Am J Epidemiol. 2009;169(11):1398–1405. doi: 10.1093/aje/kwp055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Harrell FE, Jr, Lee KL, Mark DB. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med. 1996;15(4):361–387. doi: 10.1002/(SICI)1097-0258(19960229)15:4<361::AID-SIM168>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 25.Pencina MJ, D’Agostino RB, Sr, D’Agostino RB, Jr, et al. Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond. Stat Med. 2008;27(2):157–172. doi: 10.1002/sim.2929. discussion 207–212. [DOI] [PubMed] [Google Scholar]
- 26.Pencina MJ, D’Agostino RB, Sr, Steyerberg EW. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Stat Med. 2011;30(1):11–21. doi: 10.1002/sim.4085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Grønnesby JK, Borgan O. A method for checking regression models in survival analysis based on the risk score. Lifetime Data Anal. 1996;2(4):315–328. doi: 10.1007/BF00127305. [DOI] [PubMed] [Google Scholar]
- 28.May S, Hosmer DW. A simplified method of calculating an overall goodness-of-fit test for the Cox proportional hazards model. Lifetime Data Anal. 1998;4(2):109–120. doi: 10.1023/a:1009612305785. [DOI] [PubMed] [Google Scholar]
- 29.Nair V, Doksum KA. Advances in Statistical Modeling and Inference: Essays in Honor of Kjell A. Doksum. Hackensack, NJ: World Scientific; 2007. [Google Scholar]
- 30.Langholz B, Jiao J. Computational methods for case-cohort studies. Comput Stat Data An. 2007;51(8):3737–3748. [Google Scholar]
- 31.Kulathinal S, Karvanen J, Saarela O, et al. Case-cohort design in practice—experiences from the MORGAM Project. Epidemiol Perspect Innov. 2007;4:15. doi: 10.1186/1742-5573-4-15. (doi:10.1186/1742-5573-4-15) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wang TJ. Multiple biomarkers for predicting cardiovascular events: lessons learned. J Am Coll Cardiol. 2010;55(19):2092–2095. doi: 10.1016/j.jacc.2010.02.019. [DOI] [PubMed] [Google Scholar]
- 33.Cook NR, Paynter NP. Genetics and breast cancer risk prediction—are we there yet? J Natl Cancer Inst. 2010;102(21):1605–1606. doi: 10.1093/jnci/djq413. [DOI] [PubMed] [Google Scholar]
- 34.Langholz B, Borgan O. Counter-matching: a stratified nested case-control sampling method. Biometrika. 1995;82(1):69–79. [Google Scholar]
- 35.Onland-Moret NC, van der A DL, van der Schouw YT, et al. Analysis of case-cohort data: a comparison of different methods. J Clin Epidemiol. 2007;60(4):350–355. doi: 10.1016/j.jclinepi.2006.06.022. [DOI] [PubMed] [Google Scholar]
- 36.Langholz B, Borgan O. Estimation of absolute risk from nested case-control data. Biometrics. 1997;53(2):767–774. [PubMed] [Google Scholar]
- 37.Samuelsen SO. A psudolikelihood approach to analysis of nested case-control studies. Biometrika. 1997;84(2):379–394. [Google Scholar]
- 38.Janes H, Pepe MS. Matching in studies of classification accuracy: implications for analysis, efficiency, and assessment of incremental value. Biometrics. 2008;64(1):1–9. doi: 10.1111/j.1541-0420.2007.00823.x. [DOI] [PubMed] [Google Scholar]
- 39.Chao C, Song Y, Cook N, et al. The lack of utility of circulating biomarkers of inflammation and endothelial dysfunction for type 2 diabetes risk prediction among postmenopausal women: the Women’s Health Initiative Observational Study. Arch Intern Med. 2010;170(17):1557–1565. doi: 10.1001/archinternmed.2010.312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Saha-Chaudhuri P, Umbach DM, Weinberg CR. Pooled exposure assessment for matched case-control studies. Epidemiology. 2011;22(5):704–712. doi: 10.1097/EDE.0b013e318227af1a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Weinberg CR, Umbach DM. Using pooled exposure assessment to improve efficiency in case-control studies. Biometrics. 1999;55(3):718–726. doi: 10.1111/j.0006-341x.1999.00718.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.