A new statistical approach to detecting differentially methylated loci for case control Illumina array methylation data

Abstract

Motivation: As an epigenetic alteration, DNA methylation plays an important role in epigenetic controls of gene transcription. Recent advances in genome-wide scan of DNA methylation provide great opportunities in studying the impact of DNA methylation on many human diseases including various types of cancer. Due to the unique feature of this type of data, applicable statistical methods are limited and new sophisticated approaches are desirable.

Results: In this article, we propose a new statistical test to detect differentially methylated loci for case control methylation data generated by Illumina arrays. This new method utilizes the important finding that DNA methylation is highly correlated with age. The proposed method estimates the overall P-value by combining the P-values from independent individual tests each for one age group. Through real data application and simulation study, we show that the proposed test is robust and usually more powerful than other methods.

Contact: Zhongxue.Chen@uth.tmc.edu

1 INTRODUCTION

DNA methylation, as an alteration of epigenetic control, plays a critical role in transcriptional regulation, chromosomal stability, genomic imprinting and X-inactivation (Kuan et al., 2010; Rakyan et al., 2008). It has been shown to be linked to many human diseases, including various types of cancer (Baylin and Ohm, 2006; Feinberg and Tycko, 2004; Jabbari and Bernardi, 2004; Jones and Baylin, 2002; Kulis and Esteller, 2010; Laird, 2010; Wang, 2011; Xu et al., 1999).

With the BeadArray technology, Illumina GoldenGate and Infinium Methylation Assays can generate genome-wide high-throughput methylation data which are widely used in research. After background correction and normalization for the raw fluorescent intensities, for each locus, a summarized value (called β-value) is generated based on ~30 replicates in the same array: max(M,0)/(max(M,0)+max(U,0)+100) , where M is the average signal from a methylated allele and U is from unmethylated allele. The range of the β-value is therefore, between 0 and 1, with 0 representing totally unmethylated and 1 representing completely methylated.

To detect differentially methylated loci between two groups of case and control, the commonly used statistical tests, such as t-test and linear regression-based methods may not be appropriate as the assumptions of those methods may not meet for this kind of data. For example, in a linear regression model, we usually assume the error terms are normally distributed with common variance. However, it has been shown that the β -value is highly associated with age; its mean and SD vary across subject's age (Christensen et al., 2009; Teschendorff et al., 2010). Simply treating age as a covariate in the linear regression model does not guarantee that the model assumptions are met.

Recently, Wang has proposed a model-based likelihood ratio test to detect differentially methylated loci for case and control data under the assumption that the β-value follows a three-component normal-uniform distribution (Wang, 2011). Through simulation, Wang showed that under some situations, their proposed test outperforms the simple t-test. However, the commonly used t-test cannot be the best test if data are from mixture distributions.

In this article, we propose a new statistical testing approach to detect differentially methylated loci for case control Illumina array methylation data. In the proposed test, we incorporate the important recent finding that the β-value is correlated with age. More specifically, we first group subjects into several age groups based on their age; then for each age group, a statistical test such as t-test will be conducted for the given locus and the two P-values each from one-sided test (one from left-side and the other from right-side) are recorded. An overall P-value for that locus will be estimated through combining the two sets of P-values. Using a real methylation data with two treatments and a simulation study, we show that the proposed test is robust and usually more powerful than other methods. In this article, all the t-tests used are based on the unequal variance assumption.

2 METHODS

Suppose we have k age groups; for each age group, a statistical test, such as t-test, will be used to detect the mean differences between the case and control groups. We have k P-values from the left-sided test, denoted by P_li(i= 1, 2,…, k), and k P-values from the right-sided test, P_ri=1−P_li(i=1, 2,…, k). Under the null hypothesis that there is no difference between the two treatment groups, all of the above P-values from the same one-sided tests are independent and identical uniform [0, 1] random variables. Therefore, according to Fisher (Fisher, 1932), we have the following results:

(1)

where χ_2k² is a chi-square random variable with df 2k; and

(2)

We define the following statistic:

(3)

Since statistics T₁ and T₂ are not independent, the null distribution of T is not easy to find. However, we can estimate the P-value of T based on the following theorem (Chen, 2011; Chen and Ng, 2012; Owen, 2009):

Theorem 1. —

Under the null hypothesis of no difference between the case and control groups, the P-value of statistic T satisfies:

(4)

Therefore, we can approximate the P-value of T by its upper bound 2α:

(5)

For small α, the approximation is very accurate.

Theorem 1 can be proved by using the concept of associated random variables due to Esary, Proschan and Walkup (Esary et al., 1967). More details can be found in (Owen, 2009).

We call the above proposed method ‘combined test based on one-sided t-test’. Similarly, we can use Fisher's method to combine independent P-value from two-sided t-tests, each for one age group; we call this test ‘combined test based on two-sided t-test’.

A regression model with age as covariate is also conducted to compare the treatment effect (case versus control); the P-value is obtained after adjusting for the age effect. We also calculate the P-value from the single t-test, which ignores the age information and uses pooled data.

3 RESULTS

3.1 Simulation study

In the simulation study, we assume there are six age groups; two treatment groups each with sample size 30 are simulated from normal distributions with standard deviations equal to 1. We assume the effect sizes can take four different values: −0.5, −0.1, 0.1 and 0.5. Table 1 gives the settings for each scenario of the simulation study. The degree of heterogeneity of the effect sizes decreases from scenario 1 to scenario 7, where all the effects have the same size. Scenario 8 is for the null hypothesis, where the effect sizes for all age groups are zeros. Table 1 also reports the estimated power for the single t-test, regression model adjusting for age effect and the combined tests based on one- and two-sided t-tests at significance level 0.05 using 10⁴ replicates. The type I error rates (scenario 8) from all the methods are close to the preset significance level of 0.05.

Table 1.

Number of the given effect sizes for each scenario in the simulation study and the estimated powers at significance level 0.05 using 10⁴ replicates

Scenario	Number of given effect sizes in the simulation					Power
	−0.5	−0.1	0	0.1	0.5	Single t-test	regression	Comb1a	Permb	Comb2c
1	2				4	0.297	0.297	0.856	0.846	0.975
2	1			2	3	0.437	0.436	0.749	0.743	0.837
3		3		1	2	0.225	0.223	0.447	0.431	0.508
4		1		3	2	0.451	0.450	0.571	0.558	0.503
5				4	2	0.596	0.598	0.654	0.645	0.523
6				5	1	0.329	0.327	0.361	0.350	0.255
7				6		0.155	0.154	0.138	0.140	0.089
8			6			0.049	0.048	0.051	0.048	0.049

^aCombined test based on one-sided t-test;

^bCombined test based on one-sided t-test and permutation;

^cCombined test based on two-sided t-test.

From the simulation study, we have the following observations. First, the performances of the single t-test and the regression model adjusting for age effect are very similar; the proposed method (comb1) and the method based on one-sided t-test and permutation test (perm) have very similar powers. Second, when the effects have different directions and both have large sizes (e.g. scenarios 1–3), the two combined tests have comparable power and both are more powerful than the single t-test. Third, when the effects have different directions but one direction has relatively small sizes (e.g. scenario 4), the proposed method based on one-sided t-test is more powerful than that based on two-sided t-test and the single t-test. Fourth, when the effects have the same directions but different sizes (e.g. scenarios 5–6), the proposed test outperforms the other two methods. Fifth, when all the effects have the same sizes (e.g. scenario 7), the proposed test and the single t-test have comparable power; both are more powerful than the combined test based on two-sided t-test.

3.2 A real data set

The United Kingdom Ovarian Cancer Population Study (UKOPS) (Teschendorff et al., 2010) with 274 controls and 131 pre-treatment cases will be used to compare the performance of the proposed test with the single t-test. All of the controls and the cases are women. Those methylation data with 27 578 loci were generated by the Illumina Infinium Huamn Methylaytion27 BeadChip and downloaded from the NCBI Gene Expression Omnibus (http://www.ncbi.nlm.nih.gov/geo) under accession number GSE19711.

For the data quality control, we remove 29 patient samples (15 controls and 14 treatment cases) with low bisulphite (BS) conversion efficiency (BS control intensity value <4000) or with coverage rate <95% (Teschendorff et al., 2010). For each locus, we perform a single t-test comparing the mean difference between the two treatment groups: control and pre-treatment. We also separate subjects into six age groups (50–55, 55–60, 60–65, 65–70, 70–75 and 75 and over), which was given by the original data, and calculate the overall P-value of the proposed test using (5). Table 2 gives the number of subjects in each treatment group by age group.

Table 2.

Number of subjects by age group and treatment group in the UKOPS data set

Treatment	Age group
	50–55	55–60	60–65	65–70	70–75	75+
Control	14	63	64	35	63	20
Pre-treatment	15	18	17	17	25	25

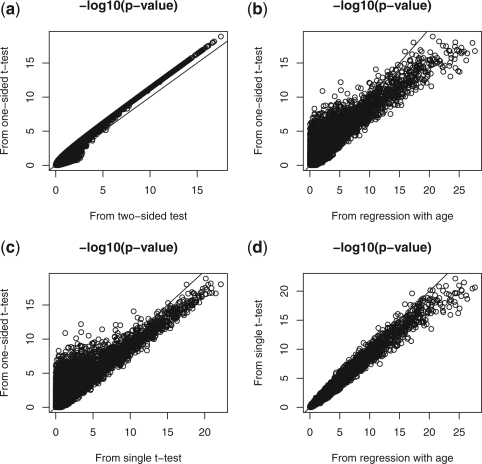
Figure 1 plots the negative log10 P-values from the combined test with one-sided t-test (i.e. the proposed test), the combined test with two-sided t-test, the regression model with covariate age and the single t-test. Figure 1a plots the −log10 P-values from the combined test based on one- and two-sided t-tests. It can be seen that for most loci with small P-values, the combined test based on one-sided t-test has smaller P-value, indicating it is more powerful than the combined test based on two-sided t-test. Figure 1b compares the P-values from the proposed test and those from regression model after adjusting for age. When a locus has small P-value from the regression model, it usually also has small P-value from the proposed method. However, there are many loci with small P-values from the proposed method while their P-values from the regression model are very large. For those loci, the proposed method is more powerful. Figure 1c compares the P-values from the proposed method with those from the single t-test. In the regression model, the single t-test is less powerful for many loci when compared with the proposed test. Figure 1d plots the P-values from the single t-test and the regression model. It shows that the regression-based method and the single t-test have very similar P-values. We therefore compare the proposed test mainly with the single t-test.

Fig. 1.

Negative log10 P-values from pair of methods when comparing controls and pre-treatment cases. (a) The proposed combined test based on one-sided t-test and the combined test based on two-sided t-test; (b) The proposed test and the regression model with covariate age; (c) The proposed test and the single t-test; (d) The regression model with covariate age and the single t-test. The proposed combined test statistic was obtained by (3) with k=6 (six age groups).

Indeed, the proposed method detects much more differentially methylated loci than the single t-test. Table 3 lists the number of loci detected by either and both of the two tests at different significance levels; 10⁻³, 10⁻⁴, 10⁻⁵ and 10⁻⁶. Clearly, most loci detected by single t−test are also detected by the proposed method. However, there are a lot of loci detected by the proposed method but not by the single t-test for given cutoff P-values.

Table 3.

Number of loci with P-values smaller than the given cutoff P-value from the single t-test and combined test when comparing control with pre-treatment

Cutoff P-value	Single t-test	Combined test	Both
10−3	1869	3215	1755
10−4	1360	2329	1298
10−5	1091	1707	1043
10−6	902	1334	866

Table 4 lists the estimated mean, standard deviation, effect size for each age group and those of pooled data for the five loci with P>0.01 from the single t-test and <10⁻⁸ from the proposed test. The effect size is defined as (m₁−m₂)/s, where m₁ is the mean of control, m₂ is the mean of pre-treatment group and s is the pooled standard deviation 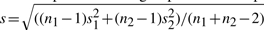, n_i and s_i are the sample size and estimated standard deviation for group i(i=1, 2). It shows that the effect sizes vary across age groups. Furthermore, the effects may even have different directions among the six age groups. Interestingly, the estimated effects from the age group of ‘75 and over’ for the five loci are all negative (control-pre-treatment) and their sizes are relatively small compared with other age groups. In addition, except for the age group of ‘75 and over’, all effects of the same locus from the other five age groups have the same direction. The single t-test fails to detect those loci with small overall effect sizes from the pooled data; however, the combined test can detect the mean differences by comparing the two treatments within each age group, where data are more homogeneous.

Table 4.

Estimated mean, standard deviation, effect size for each age group and those of pooled data for the five loci with P>0.01 from the single t-test but <10⁻⁸ from the proposed test

Age group			cg04956511	cg07380496	cg12998614	cg19168338	cg26728422
50–55	Control	Mean	0.0663	0.0406	0.1014	0.0865	0.1149
		SD	0.0188	0.0132	0.0243	0.0158	0.0273
	Pretreat	Mean	0.0618	0.0335	0.0847	0.0656	0.0752
		SD	0.0178	0.0102	0.0206	0.0158	0.0258
	Effect size		0.2338	0.5829	0.7148	1.2677	1.4381
55–60	Control	Mean	0.0655	0.0405	0.0898	0.0756	0.0931
		SD	0.0192	0.0162	0.0243	0.0176	0.0264
	Pretreat	Mean	0.0478	0.0344	0.0765	0.0664	0.0747
		SD	0.0087	0.0066	0.0233	0.0175	0.0360
	Effect size		0.9981	0.4107	0.5443	0.5203	0.6307
60–65	Control	Mean	0.0634	0.0430	0.0917	0.0779	0.1000
		SD	0.0241	0.0177	0.0224	0.0170	0.0305
	Pretreat	Mean	0.0466	0.0307	0.0711	0.0575	0.0720
		SD	0.0108	0.0053	0.0154	0.0103	0.0288
	Effect size		0.7554	0.7653	0.9611	1.2707	0.9172
65–70	Control	Mean	0.0656	0.0473	0.1018	0.0711	0.0985
		SD	0.0186	0.0185	0.0328	0.0189	0.0330
	Pretreat	Mean	0.0508	0.0368	0.0793	0.0593	0.0666
		SD	0.0206	0.0084	0.0217	0.0151	0.0156
	Effect size		0.7496	0.6433	0.7431	0.6493	1.0924
70–75	Control	Mean	0.0644	0.0456	0.0991	0.0683	0.0877
		SD	0.0212	0.0243	0.0301	0.0154	0.0269
	Pretreat	Mean	0.0510	0.0349	0.0782	0.0645	0.0785
		SD	0.0131	0.0072	0.0207	0.0196	0.0249
	Effect size		0.6828	0.5067	0.7421	0.2225	0.3457
75+	Control	Mean	0.0708	0.0391	0.0979	0.0694	0.0926
		SD	0.0271	0.0126	0.0306	0.0122	0.0303
	Pretreat	Mean	0.0753	0.0582	0.1040	0.0717	0.0985
		SD	0.0946	0.1048	0.1267	0.0850	0.1475
	Effect size		−0.0611	−0.2370	−0.0614	−0.0355	−0.0514
Alla	Control	Mean	0.0651	0.0432	0.0954	0.0739	0.0954
		SD	0.0214	0.0188	0.0273	0.0172	0.0293
	Pretreat	Mean	0.0564	0.0393	0.0834	0.0647	0.0791
		SD	0.0461	0.0491	0.0613	0.0414	0.0718
	Effect size		0.2773	0.1234	0.2910	0.3365	0.3458

^aCompare two groups: control and pre-treatment using pooled data.

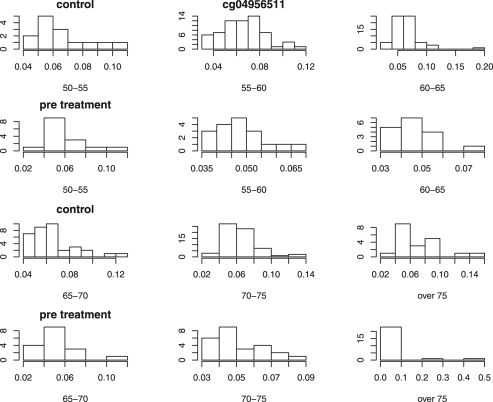
Figure 2 plots the distribution of the β-value of locus cg04956511, one of the five loci listed in Table 4, for both treatment groups by age group.

Fig. 2.

Histogram plots for a locus with large P-value from single t-test but small one from the combined test.

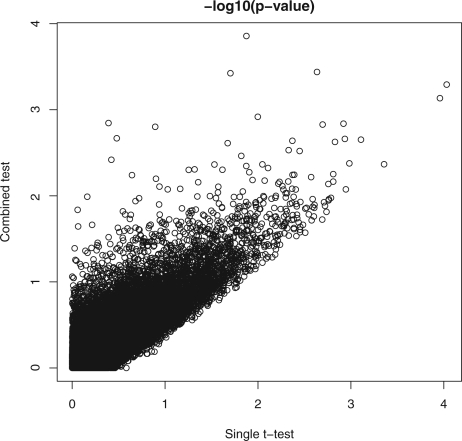
To investigate how well the proposed method controls type I error rate, for each age group, we randomly assign half of the controls into one group and the remaining controls into another group; then we apply the single t-test and the proposed method to the data of the two randomly assigned control groups. Since both groups contain only controls, the null hypothesis is true and not many small P-values should be expected from appropriate statistical tests. Figure 3 plots the negative log10 P-values from both the single t-test and the proposed method for each locus. As expected, only a few loci have P<10³ from either tests. This result indicates both the single t-test and the proposed method can control type I error rate well at small significance levels.

Fig. 3.

Negative log10 P-values from the single t-test and the proposed test when comparing two controls groups with randomly assigned controls.

4 DISCUSSION

The assumption that the β-value is normally distributed with constant variance across age may not be always appropriate; if this assumption is violated, the commonly used t-test and the regression method will lose power and alternative methods are desirable. It has been shown that the β-value is an age related measurement, both its mean and standard deviation may vary across age; we would expect that it is more homogeneous for subjects with similar age. Based on this idea, we propose a new statistical approach which separates subjects based on their age, conducts one-sided statistical test for each individual age group, and then combines P-values to obtain an overall P-value. The proposed method uses the one-sided, instead of two-sided tests for each age group because most of the time, the direction of the effects are expected to be the same (negative or positive). If the direction of the effects is the same and known for all age groups, we can even improve the power by only using test T₁ or T₂. However, in practice, the directions may be unknown even if they are the same; the proposed method is still powerful for this situation. From the results of our simulation study and the real data application, we can see that the proposed test is robust in the sense that it has reasonable power when the effects have different directions. In contrast, the single t-test will lose power dramatically when it is applied to the pooled data where the effects have different sizes and/or their directions are different.

The proposed method is based on the effect modifier: age, which is by far the strongest demographic risk factor for cancer (Teschendorff et al., 2010). However, there is no difficulty to extend the proposed method to other factors which are associated with methylation.

In this article, we use the commonly used t-test to compare the case and control groups for each age group; however, it can be replaced by any other appropriate test. Except for the Fisher's test, there are many different ways to combine P-values from independent tests (Chen, 2011; Chen and Nadarajah, 2011; Cousins, 2008; Whitlock, 2005); however, there is no uniformly most powerful approach. It remains an open topic to find the most appropriate approach for this kind of data. We recommend using Fisher's test since it is robust and is very powerful under many situations.

In summary, we have proposed a new approach to detect differentially methylated loci for case control Illumina array methylation data. Through simulation study and a real data application, we have shown that the proposed method is more powerful than the commonly used t-test and regression-based method.