Parental Compensatory Behaviors and Early Child Health Outcomes in Cebu, Philippines

Abstract

A dynamic optimization model of parents choosing investments in their children’s health motivates an empirical model of parents’ choices of health inputs for their children and the impacts of these decisions on their children’s subsequent health. Estimates of the child health input demand functions and the child health production functions from the Cebu Longitudinal Health and Nutrition Survey accord with the prediction that optimizing behavior results in higher levels of aggregate child health. Observable parental behaviors respond to the physical developmental status of their children. These parental responses appear to yield large and statistically significant improvements in children’s early physiological outcomes. However, because some health inputs choices are not observable, it is impossible to ascertain whether these measured effects are due solely to variations in the observed input choices.

1. Introduction

This study explores the determinants of parents’ behaviors that can influence their children’s early childhood development and the impacts of these actions on their children. It traces how birth outcomes and children’s growth over the first two years of life influence parents’ decisions about breast-feeding, supplemental feeding, preventative health care, maternal work decisions, and timely vaccinations. We assess how these endogenous, compensatory behaviors appear to affect the growth of children throughout these formative years, and we include a detailed discussion of some key issues in interpreting these estimated effects that arise because one cannot observe all of the inputs that parents choose to influence their children’s physiological development.

From a biomedical perspective, the first two years of life is a critical period for cognitive development, during which nutritional deficits are hypothesized to directly limit the growth and development of the brain (Smart 1998, Lozoff 1998). Biomedical scientists conclude that anthropometric indicators of poor nutritional status are consistently associated with poor cognitive outcomes. In less developed countries, the inadequate living environment poses a great threat to the child’s growth and cognitive development, which in turn could affect learning ability and school achievement, and ultimately limit the performance in the labor market. There has been a great deal of emphasis on early child development programs in less developed countries, as witnessed recently by large investments in such programs by the World Bank and the Asian Development Bank.

Social scientists also have concluded that there are strong effects of mothers’ education and household income on child health outcomes (see Behrman and Taubman 1990; Blau 1999; Duncan, Brooks-Gunn, and Klebanov 1994). Nevertheless, we have little understanding about the underlying relationship between these socioeconomic factors and parents’ health-related behaviors. At the same time, given that parents might determine the health inputs in response to their and their child’s observed and unobserved health-related characteristics, child health production studies without adequate control for endogeneity and unobserved heterogeneity can lead to biased estimates about the effects of health inputs. The limited understanding of the determinants of health-related behavior has undermined our ability to evaluate the health impact of these potential programs. In this paper we model and estimate the relationships among child outcomes, subsequent endogenous health inputs, and health outcomes. The results provide empirical evidence on the determinants of these health-related behaviors, as well as an assessment of the health consequences from parents adjusting their health behaviors in response to the child’s physiological development.

Using the Cebu Longitudinal Health and Nutrition Survey (CLHNS), a comprehensive longitudinal data set collected in the Philippines, this study incorporates prenatal care information, birth outcomes, important subsequent parental inputs, and multiple measures of early childhood health outcomes. While many studies have examined the effects of prenatal care on pregnancy outcomes, little attention has been given to the decision and timing of prenatal care. We hypothesize that ceteris paribus initiating prenatal care earlier tends to be more beneficial. Using the CLHNS data, numerous studies have assessed the associative relationships between health inputs in early childhood and subsequent child outcomes. For instance, Adair (1999) uses a discrete time duration model to study the impacts of various factors on the probability of recovery from stunting among children who were stunted at age 2. She concludes that children with great growth potential at birth, indicated by high birth length and tall maternal stature, are more likely to recover from stunting at age 2. Mendez and Adair (1999) and Daniels and Adair (2004) investigate the association between a child’s nutritional status at age 2 and her predicted academic achievements through high school. They find a lingering effect of the early childhood nutrition status through high school. While remaining statistically significant, these estimated associations become smaller when additional socio-economic factors are controlled for. More importantly, considering the potential endogeneity of health inputs is not accounted for in these studies, the estimated effects may be biased.

Several previously studies attempt to investigate the casual relationship between health-related goods (behaviors) and health outcomes measured by growth or morbidity. The common econometric strategy to address the endogeneity problems is an instrumental variables approach, but the lack of good instruments and strong functional form assumptions may likely have contributed to the inconsistency in results across studies. Adair, Popkin, and Guilkey (1993) investigate the impact of a set of socioeconomic and biological factors on the duration of full and partial breast-feeding. They allow time-varying independent variables to enter the hazard rate equation with a one-period lag. Most of these studies focus on estimating the overall effects of one or more health related parental behaviors on children’s health outcomes in a reduced-form health production function. The Cebu Study Team (1992) presents a structural model similar to the models suggested by Rosenzweig and Schultz (1983). The authors rely on a two-stage regression framework to directly estimate the models with endogenous variables on the right hand side. The unobserved heterogeneity specific to a given child is accounted for using a random effects generalized least squares estimator. There are two main shortcomings with their empirical results. First, every health outcome is estimated separately. Second, the standard errors reported in the paper fail to take into account the fact that pre-estimated explanatory variables are used in place of the actual variables. Additionally, the study does not focus on the compensatory behaviors in their empirical analyses.

This paper addresses the following two important questions: how do parents change their behavior in response to their children’s health outcomes and how effective are these changes. Guided by a dynamic economic model of parental investments in a child’s health, we propose a tractable empirical model that includes a set of parents’ demand functions for health inputs in conjunction with a set of health production functions for how a child’s physiological development responds to these inputs. We specifically allow unobserved heterogeneity across mothers and children to enter the health production functions as well as the health input demand functions, and we use flexible parametric forms to help uncover the dependence of behaviors on prior outcomes and the dependence of subsequent outcomes on these behaviors. The joint estimation of these parental behaviors and child health outcomes achieves more statistical efficiency than estimating separate equations by techniques such as two stage least squares.

We find that parents adjust their behaviors in response to their children’s observed health. Most importantly, our estimates indicate that these adjustments are statistically significant and, subject to the proviso that the estimated effects might be tainted because one cannot observe all of the behaviors parents make to help their children, they appear to yield substantively important improvements in child growth and health. While there is evidence of lingering impacts of low birth weight on some child outcomes, the mothers adjust their behaviors in response to low birth weight and contemporaneous adverse outcomes during the early life course. For instance, we find that a mother of a low birth weight child is less likely to work during the first year of the child’s life, feeds the child more calories per kilogram, and breast-feeds the child longer. Moreover, empirical analyses that ignore the interactions and endogeneity of parental behaviors and childhood health-related events provide biased estimates of the effectiveness of parental behavior towards their children.

The paper is organized as follows. Section 2 outlines a dynamic economic model and presents some testable implications of optimizing behavior. Section 3 describes the Cebu Longitudinal Health and Nutrition Survey data and the basic empirical specifications and goals. Section 4 describes the empirical models used in this analysis. Section 5 discusses key limitations in estimating health production functions like those examined here that arise because one cannot observed all of the choices parents make about the inputs to their children’s health. Section 6 presents the results of the estimation and policy simulations from the empirical model’s estimates. We provide a discussion and our conclusions in Section 7.

2. A Prototypical Economic Model of Parent’s Investments in Children’s Health

2.1 The Dynamic Optimization Problem

Suppose the parents of a single young child attempt to maximize the present discounted value of a time separable utility function subject to a per period budget constraint. Their utility flow depends on their current consumption and their perception of the well being or health of their child. Let U(c_t, h_t) be the per period utility function where c_t is the parents’ consumption during period t and h_t is the stock of child health at the start of this time period. We assume that this per period utility function is concave, that the marginal utility of child health is not increasing in the parents’ consumption, and that the price of consumption is normalized to one.

While parents cannot alter the health of their child within a period, they may make investments in their children that can lead to higher expected child health at the start of the subsequent time period. Let the deterministic component of the health production process be given by

$$h_{t+1}^d=H^d(h_t,f_t\mid t),$$

where we allow next period’s child health to depend on today’s actual health as augmented by the health investment inputs f_t purchased today by the parents at price p_t. We assume

$$\frac{\partial H^d}{\partial h_t}>0;\frac{\partial H^d}{\partial f_t}>0;\frac{{\partial }^2{H}^d}{\partial h_t^2}<0;\frac{{\partial }^2{H}^d}{\partial f_t^2}<0;\mathit{and}\frac{{\partial }^2{H}^d}{\partial h_t\partial f_t}<0.$$

This latter restriction, on the cross derivative, captures the notion that equally sized increases in health investments would do more to improve the health of less healthy children. Realized child health at the start of the next time period is given by the product of the deterministic component and an independent mean 1 health shock s_t+1, i.e., $h_{t+1}=s_{t+1}{h}_{t+1}^d$. The parents’ information about the distributions of future prices, incomes and health shocks is contained in the information set Ω_t.

2.2 Derivation of the Demands for Inputs to the Child Health Production Function

Using Bellman’s formulation under these conditions, the parents’ dynamic optimization problem at point of time t can be simplified to

$$\begin{array}{l}max{W}_t(h_t)=U(c_t,h_t)+\beta E_t[V_{t+1}(h_{t+1})\mid {\mathrm{\Omega }}_t]\\ \mathit{wrt}{f}_t,c_t\end{array}$$

subject to the above health production function and the per period budget constraint

$$y_t=c_t+p_t{f}_t.$$

The function V_t+1(h_t+1) is the optimized value function as of the start of period t+1, and β is a discount factor. The solution to this optimization problem implies a demand equation for inputs to the child’s health production process of the form:

$$f_t=D_t^f(y_t,h_t,p_t,{\mathrm{\Omega }}_t).$$

Even though this period t demand function is part of a dynamic optimization process, it only depends on variables observed by the parents as of time period t.¹ One can express the demand for the input f at each point in time t solely as a function of the state variables observed at that point in time. If the only uncertainty about the future comes from uncertainty about future incomes, prices, and health shocks, the future joint distribution of y_t and p_t, follows a first order Markov process, and the health shocks s_t are independent over time, then it is unnecessary to further condition the demand function on the information set Ω_t. Such simplifying assumptions are commonly made in many structural dynamic models (E.g. see Blundell et al, 1997). Mroz and Weir (2003) provides a more detailed discussion of the interpretation of dynamic formulations of this type.

While in general it will be impossible to solve for closed form solutions for the age specific demand functions, this economic framework provides important implications for an empirical analysis of parents’ choices of inputs to the child health production process and the estimation of the health production process. Most importantly, it implies that there is a well-defined demand function for health inputs that only depends on the state variables observed by the parents at time t. In our empirical analysis we exploit this fact and implement in the estimation a flexible functional form for the demand equations to approximate the actual solutions to the optimal investment in child’s health problem, if that is in fact how the parents make their choice about inputs to their children’s health. Additionally, provided one continues to condition the health demands on the relevant parts of the parent’s information set, the estimation approach could uncover arbitrary, or even irrelevant, rules of thumb. This framework does not require that parents solve an explicit maximization problem in order to solve for their demands for health inputs, but it can approximate the expected utility optimizing rules if that is how parents make their decisions.

2.3 Key Restrictions Implied by a Dynamic Optimization Model

The production process for expected child health in the next time period depends on two factors. The first is the child’s health state when entering the current time period, and the second is the amount of investment, f_t, the parents use to help produce more health for the child. In this dynamic optimization model parents are willing to trade their own current consumption for child health inputs that can raise their utility from the flow of future child well-being. Since the parents’ period specific utility function is concave, parents will receive less additional expected future utility from a given increment to their child’s health when their child’s current health is high than they would from the same health increment if their child’s health were low. As a consequence of optimizing behavior, ceteris paribus, parents will spend less on child health investments when their child’s health is good (and more on their own current consumption) than when their child’s health is poor, or $\partial D_t^f/\partial h_t<0$.

These differential investments by otherwise identical optimizing parents whose children have different health statuses at the start of period t will result in a population distribution of subsequent health of their children that is more concentrated than if they had treated all children equally regardless of the health status of the children when making investment and consumption decisions. Stated differently, optimizing behavior yields more equality in child outcomes. A somewhat stronger implication arises when one exploits the assumption that the production function for child well-being exhibits diminishing returns.

Suppose there is a non-degenerate distribution of child health at time t, and consider a population of parents of who are otherwise identical. If these parents were maximizing expected life cycle utility as in the above model, then the distribution of child health statuses h_t would induce a distribution of optimal parental inputs f_t in the population. Through the stochastic health production function, this distribution of parental actions would result in a distribution of child health in the subsequent time period. Let G_t(f) be the marginal distribution of these inputs in the population for children of age t. Now, suppose that instead of solving a dynamic optimization model to choose their investments f_t (which would depend on each child’s observed health status), that parents randomly choose their inputs from the marginal distribution G_t(f) without conditioning on their child’s health. Since optimizing parents allocated more resources towards those children whose health production functions had the higher expected marginal returns, the random allocation of child investments would result in fewer children in bad health, and more children in good health, receiving large health investments. This implies that the subsequent distribution of child health would have a lower expected value when parents randomly choose their child investments. In Section 6 we use the estimates of the parents’ investment demand functions and for the child health production function to assess whether the types of behavior parents exhibit in the Cebu data are consistent with this implication of the stochastic dynamic optimization model.

3. Data, Basic Empirical Specifications, and Identification

3.1. The Cebu Longitudinal Health and Nutrition Survey Data

This paper focuses on the CLHNS data, which have been analyzed extensively by scholars from numerous disciplines. The CLHNS is an ongoing longitudinal study of a cohort of Filipino children (and their mothers) who were born in 1983–84. Through a stratified and single-stage sampling procedure, a random sample was selected of 33 communities or barangays from the Metropolitan Cebu area, Philippines. A baseline survey took place for 3,327 women at a median gestation week of 30 (range 14–44). Postnatal interviews took place immediately after birth. Starting at age 2 months, interviews took place every two months until the child reached age two. The birth information survey revealed a total of 3,080 single live births among sample women.² Among these single live births, 2,873 infants had valid measurements of birth weight and length. The surveys collected information on anthropometric measures of the children (length and weight), infant breast-feeding and supplemental feeding practices, the incidence of diarrhea and respiratory illnesses, the labor supply and health care behaviors of the mother, and other important economic and demographic data. Concurrent with the sequence of household level interviews, the survey team collected community information on health facilities, health care personnel, food prices, and other community characteristics. There are too few infant deaths in this sample for one to carry out a meaningful analysis of the determinants of child mortality.

3.2 General Forms for the Dynamic Relationships

In our empirical strategy we utilize both health production functions and health input demand functions to characterize the health outcome trajectories of infants. Ideally, the production functions we estimate would describe the technical relationships between the health outcomes and health inputs, while the input demand functions would describe the parents’ possibly endogenous choices of health-related inputs. Let H(t) represent a set of child health outcomes, such as weight, length, and disease incidents at time t, and let M(t-1) be a health input vector, such as lagged choices of prenatal care, preventive health care, and breast-feeding practice. The health production process in time t is modeled as a function of a vector of exogenous child and family characteristics (X(t)), a vector of community characteristics relevant for the outcome under consideration (C(t)), lagged health (H(t−1)), lagged health inputs (M(t−1)), an unobserved heterogeneity term (μ_H ), and an independently distributed shock (ε_H(t)) according to the following formulation:

$$H(t)=H[X(t),C(t);M(t-1),H(t-1),{\mu }_H,{\epsilon }_H(t)].$$ (1)

The time index indicates the occurrence of interviews starting from the baseline, prenatal survey at t= −1. Following t = 0, which denotes the information collected about the day of birth, there were 12 bi-monthly longitudinal surveys (numbered 1 through 12). For each of these latter 12 survey dates we have information on the child’s health and growth and parental behaviors that could influence child outcomes.

We make two important assumptions about health production. First, the biological process involved in the production of health takes time and, therefore, the current health outcomes are determined typically by lagged inputs. Note that the only exception to this sequencing of events concerns the impacts of breast-feeding. For breast-feeding it is likely that a two month lag might conceal some of its key impacts. Further discussions about the identification of the effects of these health inputs are presented in Section 3.3. Second, we model all health outcomes as “value-added” functions, where we use lagged outcomes to substitute for all historical inputs.³ Given the relatively short window between interviews, we model each of the relevant parental behaviors (working away from home, breast-feeding, preventative health care for the child, and children’s caloric intakes) as a function only of lagged child outcomes. Mroz and Weir (2003) discuss how a sequential model of this type can be interpreted as an approximation to the solution of a stochastic dynamic optimization problem.

The permanent unobserved heterogeneity μ_H can be decomposed into two components, a mother-specific unobserved heterogeneity (μ₁ ) and a child-specific unobserved heterogeneity (μ₂ ). An “i” subscript that denotes the i^th mother-child pair is dropped to simplify the notation. A common set of contemporaneously measured exogenous variables are used as determinants of all health outcomes in a given bi-monthly survey after birth. For instance, the vector of child and family exogenous characteristics, X (t), includes child and mother’s demographic information and household composition; C(t) contains information about population density, deflated prices of important food items, and climate. As we discuss in more detail in Section 5, we include these contemporaneous family and community characteristics to control for unobserved inputs and unobserved changes in inputs that take place in the two month window between observation time periods t−1 and t. As discussed in that section and in Rosenzweig and Schultz (1983), unmeasured inputs to the health production process can limit one’s ability to interpret derivatives of equation (1) with respect to the health inputs M(t−1) as marginal products.

The input demands are specified as functions of exogenous child and family characteristics, community characteristics, lagged health outcomes, a time-varying heterogeneity term (μ_M ), and an independently distributed shock (ε_M ) as follows.

$$M(t)=M[X(t),C(t);H(t-1),{\mu }_M(t),{\epsilon }_M(t)],$$ (2)

where μ_M can vary over t; in particular, its child-specific heterogeneity component is not effective until the child is born.⁴ We specify μ_M as:

$${\mu }_M(t)={\rho }_{M1}{\mu }_1+{\rho }_{M2}{\mu }_{2}1(t\ge 0)$$ (3)

where 1(·) is an indicator function for the event in parentheses. As discussed in Section 5, these input demand functions do have standard interpretations as demand functions even when there are unmeasured healthy inputs, provided the prices of these inputs and other factors affecting their demands are controlled for in the vectors C(t) and X(t).

In order to facilitate the modeling of various outcomes and inputs, we have explicitly made assumptions about the timing of corresponding measurements. We assume that health outcomes are revealed at the end of period t (or the very start of t+1), while the decisions about health inputs are made at the beginning of t. In addition, i.i.d. random shocks ε_H and ε_M are assumed to be realized at the start of time t.⁵ Table 1 contains a description of the dependent variables modeled in this paper and Table 2 presents summary statistics for all variables used in the analysis of prenatal care and birth outcomes. Table 3 provides information on the endogenous and exogenous variables appearing in the empirical model of the dynamics of the child’s physiological development during the first two years of life.

Table 1.

Health Outcomes and Inputs Being Estimated

	Description	Survey Source	Timing (t)	Statistical Model	Freq
V(g, τ)	g measures the gestational age of first prenatal visit and τ represents the type of visit	Baseline survey	t = −1	Discrete time hazard model	1
bw	Birth weight	Birth date survey	t = 0	“Hazard” model	1
bl	Birth length	Birth date survey	t = 0	“Hazard” model	1
bf	Breast-feeding choices	Birth date, post-birth date, follow-up surveys	t =0,1,…,12	logit	13
wk	Mother working away home	Follow-up surveys	t = 1,…,12	logit	12
phc	Preventive health care, including immunization shots and any doctor visits	Follow-up surveys	t = 1,…,12	logit	12
cal	Calorie intake	Follow-up surveys	t = 1,…,12	“Hazard” model	12
fri	Incident of severe respiratory disease	Follow-up surveys	t = 1,…,12	logit	12
dia	Incident of diarrhea	Follow-up surveys	t = 1,…,12	logit	12
cw	Child weight	Follow-up surveys	t = 1,…,12	“Hazard” model	12
ch	Child length	Follow-up surveys	t = 1,…,12	“Hazard” model	12

Table 2.

Descriptive Statistics of variables during pregnancy

Variable Name	Description	Mean	(S.D.)
Prenatal care information
1st month of visit (g)	Timing of the first prenatal visit if it happens before than the end of 7th month; otherwise, individuals are treated as having no visits.	4.300	(1.362)
Traditional visit	1 = 1st prenatal visits occurs at a traditional care-giver; 0 = otherwise	0.351	(0.477)
Hospital visit	1 = 1st prenatal visits occurs at a hospital; 0 = otherwise	0.085	(0.278)
Clinic visit	1 = 1st prenatal visits occurs at a clinic; 0 = otherwise	0.358	(0.480)
Mother’s characteristics
Parity	Previous number of live births	2.235	(2.204)
Previous baby	1 = woman had live birth before current pregnancy; 0 = otherwise	0.789	(0.408)
Mother’s age	Age of the mother in 10 years	2.603	(0.596)
Mother’s height	Age of the mother in 10 centimeters	15.059	(0.500)
Education	Years of formal schooling	7.176	(3.314)
Family socioeconomic factors
Household assets	Total deflated real value of assets household owned in 1000’s 1978 pesos	12.275	(48.124)
Household size	Number of household members	5.615	(2.822)
Other HH members income	Sum of deflated weekly income of household members other than the pregnant woman in 1000’s 1978 pesos	0.221	(0.301)
Insurance coverage	1 = women’s prenatal care is covered by insurance; 0 = otherwise	0.104	(0.305)
Extended household	1 = extended household, either vertically or horizontally; 0 = nuclear	0.395	(0.489)
No. children 0–6	Number of children in this age group	1.515	(1.133)
Catholic	1 = husband and wife are Catholic; 0 = otherwise	0.947	(0.225)
Husband present	1 = husband/partner was living with the pregnant woman; 0 = otherwise	0.942	(0.235)
Ethnic origin (Cebuano)	1 = Cebuano spoken by husband and wife; 0 = otherwise	0.921	(0.270)
Community/health facility characteristics
Urban	1 = the barangay is classified as urban; 0 = rural	0.767	(0.423)
Population density	The population density of the barangay (1000 persons per km2)	14.020	(18.665)
Price of corn	Deflated price of corn (10 pesos per kg)	0.233	(0.036)
Price of cereal	Deflated price of cereal (10 pesos per kg)	0.307	(0.023)
Dry season	1 = birth occurred in dry season; 0 = otherwise	0.240	(0.427)
Wet season	1 = birth occurred in wet season; 0 = otherwise	0.517	(0.500)
Waiting time in hospital	Average waiting time in hospitals serving the barangay (min)	16.127	(6.556)
Waiting time in clinic	Average waiting time in clinics serving the barangay (min)	6.073	(9.390)
Cost in hospital	Average costs for a prenatal visit in hospitals serving the barangay in 1978 pesos	7.432	(3.015)
Cost in clinic	Average costs for a prenatal visit in clinics serving the barangay in 1978 pesos	2.697	(3.665)
Doctor/patient ratio in hospital	The doctor/patient ratio in hospitals serving the barangay	0.008	(0.013)
Part-time traditional caregiver	Percentage of traditional prenatal care providers that are part-time practitioners.	0.086	(0.084)
Health outcomes of pregnancy
Birth weight (bw)	Weight obtained within one hour postpartum (kg)	2.993	(0.429)
Birth length (bl)	Length obtained within one hour postpartum (cm)	49.076	(2.071)

Table 3.

Descriptive Statistics of Variables during Early Childhood

	Age of Child
	2 months Means (s.d.)	4–12 months Means (s.d.)	14–22 months Means (s.d.)	24 months Means (s.d.)
Endogenous health inputs
Mother working away	0.150 (0.357)	0.226 (0.418)	0.318 (0.466)	0.348 (0.476)
Preventive health care	0.125 (0.331)	0.143 (0.351)	0.035 (0.183)	0.018 (0.132)
Exclusive breast-feeding	0.262 (0.440)	0.036 (0.187)	0.000 (0.000)	0.000 (0.000)
Any breast-feeding	0.863 (0.343)	0.742 (0.438)	0.396 (0.489)	0.181 (0.384)
*Calorie intake (kcal/day)	0.109 (0.196)	0.319 (0.343)	0.624 (0.411)	0.735 (0.418)
Health outcomes
Diarrhea	0.067 (0.250)	0.206 (0.404)	0.205 (0.404)	0.180 (0.384)
FRI	0.109 (0.311)	0.168 (0.374)	0.169 (0.374)	0.153 (0.360)
Weight (kg)	4.881 (0.656)	7.162 (1.155)	8.818 (1.230)	9.790 (1.235)
Length (cm)	56.286 (2.379)	66.261 (4.374)	75.093 (3.877)	79.168 (3.674)
Community Characteristics
Urban	0.761 (0.427)	0.756 (0.430)	0.753 (0.431)	0.752 (0.432)
Population density(persons/km)	14.900 (19.121)	14.802 (19.125)	14.755 (19.194)	14.812 (19.245)
Dry season	0.222 (0.415)	0.257 (0.437)	0.266 (0.442)	0.202 (0.402)
Wet season	0.416 (0.493)	0.414 (0.493)	0.409 (0.492)	0.484 (0.500)
Average price of corn cereal	3.154 (0.319)	3.265 (0.284)	3.410 (0.465)	3.112 (0.934)
Minimum price of formula	3.640 (0.724)	3.621 (0.697)	3.465 (0.517)	3.107 (0.764)
N	2711	12713	12235	2426

Note:

^*This measure only accounts for the calories contained in the supplemental food.

3.3 Statistical Identification in this Dynamic Empirical Model

Each of the child outcomes and post-natal parental decisions depends on possibly endogenous explanatory variables, and it is important to assess whether the statistical model proposed here can identify the impacts of these lagged outcomes on current behaviors and outcomes. First, note that the CLHNS collected bi-monthly data on food and infant formula prices and local labor market conditions for each household’s barangay of residence. We incorporate cereal and formula prices, local wages and seasonality indicators, as well as period specific descriptors of each household’s composition, as time varying determinants of child outcomes and parental responses. Cebu is comprised of hundreds of small islands and the whole region underwent dramatic yet uneven economic development during the period when the surveys were conducted. Consequently, there were sizable variations of food prices and wage rates among our sample barangays cross-sectionally and over time. These prices as well as changes in family composition and seasonality of interviews provide important exogenous time-variants to our empirical models. The spatial and time variations in these determinants provide numerous exclusion restrictions in a dynamic empirical model.

Second, as discussed in Bhargava (1991), panel data relationships like those studied here implicitly provide many more over-identification restrictions than one might infer by simply listing the number of exogenous variables excluded from a single structural equation of interest. Bhargava’s (1991) paper considered a linear, dynamic structural equations estimator, and his careful examination of the reduced form equations revealed that every lag of each exogenous variable (i.e., the C(t′)’s and X(t′)’s in equation (1)) could have a separate impact on the “contemporaneous” value of an endogenous explanatory variable. The dynamic setting provides a multiplicity of exclusion restrictions when exogenous variables vary through time. Cameron and Trivedi (2005) also discuss the possible surfeit of exclusion restrictions in dynamic models.

Third, in nonlinear dynamic models, Mroz and Surette (1998) demonstrate how the time ordering of the exogenous variables and their interactions can provide even higher degrees of over-identification. As an example, consider using whether a child was being breast fed as an endogenous explanatory variable. First, note that both a household’s wealth and the price of infant formula are determinants of breast-feeding behavior at each point in time (Stewart and Guilkey, 2000), and that breast-feeding is nearly impossible to recommence after a temporary cessation. Previous research suggests that on average it takes a larger fall in the price of infant formula to induce a less wealthy mother to stop breast-feeding than it does for a mother in a wealthier household (Stewart and Guilkey, 2000; Rous, 2001). Under these conditions, the interactions of the timing of formula price and wealth changes matter for the cessation of breast-feeding in addition to the average levels of these variables. With several additional time-varying exogenous explanatory variables influencing the breast-feeding decision over time, there would be even more identification arising from interactions among the time series patterns of all these variables. The maximum likelihood framework we use to estimate the dynamic model optimally exploits all such dynamic, interactive, over-identifying conditions.

As an illustration of some of these identification sources, we estimate a simplified version of one child outcome equation in our model. In particular, we examine a two-stage least-squares regression of child weight outcomes regressed on three endogenous regressors: a low birth weight dummy variable, the child’s weight in the previous time period, and the child’s caloric intake in the previous time period. We also condition on a full set of assumed exogenous contemporaneous prices and descriptors of the household at that point in time. As instruments for the three endogenous explanatory variables we use four lags of the price and household descriptor measures.

Each of the three F-statistics for the relevance of the lagged values as predictors of the three endogenous explanatory variables exceed 10, and an Anderson IV relevance test (Canonical Correlation Test) resoundingly rejects the null hypothesis of under-identification (p-value < 0.001). In addition, a test of the overidentification conditions fails to reject the null hypothesis (Hansen J statistic p-value=0.15). It appears that even the limited time series variation in instrumental variables provides sufficient predictive power allow one to identify the impacts of three endogenous explanatory variables. Only one of the three estimated effects of the endogenous explanatory variables in this simple linear model, however, is statistically significantly different from zero at a conventional testing level. This might reflect the inefficiency of two stage least squares in this dynamic setting. In the full maximum likelihood model the implicit number of lags is greater and the interactions among the lagged exogenous variables are implicitly more complicated than what we use in this simple illustrative two stage least squares model. In addition, the maximum likelihood model incorporates the identifying information into the model without requiring the estimation of entirely new sets of coefficients as two-stage least squares does. It is likely that the identification sources in the maximum likelihood model are much richer than we see here for the two stage least squares model.

4. The Econometric Model

Empirically, we are estimating a sizable longitudinal model where prenatal visits, birth outcomes, and early childhood events are linked by child- and mother-specific heterogeneities and estimated simultaneously. Our statistical model starts with the mother’s decision about whether to use any prenatal care from a hospital, clinic, or traditional provider and the timing of when to first seek care. We then follow the mothers and children bimonthly from birth through age two. We model the dynamics of the child’s growth in both length and weight and the processes governing the bi-monthly incidence of severe respiratory infections and diarrhea. We focus on how parental behaviors such as exclusive breast-feeding, partial breast-feeding, supplemental feeding, mother’s working, and preventive health care respond to previous health and growth outcomes after continuing to control for correlated unobserved mother heterogeneity and unobserved heterogeneity specific to each child.

4.1 Maternal Inputs to Child Health

A primary goal of this paper is to explore whether parents adjust their behaviors that could affect their children’s growth in response to the observed developmental progress of their children. We model five separate parental behaviors: the commencement and type of prenatal care, and at each of the bimonthly interviews, the mother’s working away from home, preventative health care visits for the children, breast-feeding, and the child’s non-breast milk caloric intake. The empirical models for the mother working away from home and for the use of preventative health care visits since the last survey are standard logit models conditional on heterogeneity. These are discussed further in Appendix A. The modeling of the prenatal care, breast-feeding, and the child’s caloric intake are not standard, and we discuss them briefly in the following subsections.

Prenatal visits (V)

The choice of prenatal visits is characterized by a two-element vector V(g, τ), where g measures the gestational age at the first prenatal visit and τ represents the visit type if it occurs prior to the end of the sixth month of pregnancy. We impose the assumption that if a woman had not initiated prenatal care by the end of the second trimester that it would be unlikely that commencing prenatal care during the last trimester would have important beneficial effects on birth outcomes. We divide all prenatal visits during the first two trimesters into three categories: traditional prenatal care, modern care in a hospital, and modern care in a clinic. Detailed descriptions of these different visit types can be found in Table 2. See Appendix A for a complete description of the empirical model used to describe the timing and type of the first prenatal care visit.

The design of the original CLHNS induced a key data limitation, namely that prenatal care information was only collected at the time of the single prenatal interview. Let G_i be the time, in gestation age, of the prenatal interview. Researchers can only observe the timing and type of a woman’s first prenatal visit if the first visit took place at or prior to G_i. Women who were interviewed prior to the 6^th month of pregnancy and before a prenatal visit took place, for example, could have had their first prenatal care before the end of the 6^th month, but we would have no way to know whether it took place. In particular, there are 185 women who had not completed their 6^th month of pregnancy and who reported that they had not visited any prenatal care-giver, accounting for 6.4% of our estimation sample. In our empirical model we address this data truncation problem by integrating over all possible decisions about prenatal care, conditional on their not having had a first visit by the date of their prenatal interview. We describe this in our derivation of the likelihood function. Note that our solution to this truncation issue assumes that prenatal care visits are independent of the gestation age at which the prenatal survey took place after controlling for observed covariates and unobserved heterogeneity.

Breast-feeding (bf)

Breast-feeding behaviors have important effects on various infant health outcomes. In particular, exclusive and partial breast-feeding patterns are associated with enhanced child growth and reduced diarrhea morbidity. An array of factors may play a role in the decision to initiate or to continue breast-feeding. We model discrete choices of breast-feeding in a nested logit framework. A complete discussion of the empirical model of breast feeding choices is in Appendix A.

Caloric intake (cal)

Given that the CLHNS only collects data on the caloric contents of non-breast milk food for the infants, we only model the caloric intake for children who are not breast-fed exclusively⁶. The caloric intake measure we use is the number of calories per gram of the child’s weight at the prior interview. We adopt a flexible parameterization to specify the process that determines the quantity of caloric intake cal(t). More specifically, we follow the conditional density method proposed by Gilleskie and Mroz (2004). A key advantage of this approach is that it allows the empirical model of unobserved heterogeneity to more easily capture and control for the across equation error correlations that give rise to the endogenous explanatory variables. Additionally, this approach relaxes the restrictive assumptions about error distributions implied by other parametric specifications.

To do this we partition the normalized caloric intakes into ten discrete cells and model the conditional probability of an advance to a higher, discretized caloric level. Conditional on reaching at least a given level p, the probability of reaching at least the next highest level (i.e., 1 minus the hazard rate) is specified as:

$$\begin{array}{l}Pr[\text{Cell}(\text{cal}(t),t)>p\mid \text{Cell}(\text{cat}(t),t)\ge p,\text{bf}(t)\ne 1]=\text{Logit}[F_{\mathit{cal}}[X(t),C(t),H(t-1),M(t-1),{\mu }_1,{\mu }_2]+F_{\mathit{cal},b}(p)].\end{array}$$ (4)

cal(t) is the observed caloric intake per gram of weight at t and Cell(•,•) is the age -specific function mapping calories consumed at age t into a discrete cell. F_cal,b(p) represents the “baseline hazard” at caloric intake level p and F_cal captures the effects of covariates. The baseline hazard rate is specified as a third-order polynomial in the current caloric level p as follows:

$$F_{\mathit{cal},b}(p)=\sum _{n=1}^3\{{\theta }_{\mathit{cal},n}{[log(P-p)]}^n\},$$ (5)

where P is the highest caloric intake level, defined as 10 in this study. The covariate component is further specified as

$$F_{\mathit{cal}}[X(t),C(t);H(t-1),{\mu }_1,{\mu }_2]={\beta }_{\mathit{cal}}^{\prime }{X}_{\mathit{cal}}(t)+{\alpha }_{\mathit{cal}}^{\prime }{C}_{\mathit{cal}}(t)+{\gamma }_{\mathit{cal}}^{\prime }{H}_{\mathit{cal}}(t-1)+{\rho }_{\mathit{cal},1}{\mu }_1+{\rho }_{\mathit{cal},2}{\mu }_2+\text{interactions}\text{and}\text{higher}\text{order}\text{terms}$$ (6)

Because the caloric intake decision depends on the health status of the child and endogenous health inputs, we include the relevant lagged health inputs and outcomes, including mother’s working away, any breast-feeding, preventive health care, and incidents of diarrhea and febrile respiratory illness (FRI).

4.2 Child Health Outcomes

We focus on six measures of the child’s health. Birth weight and birth length are measured at t=0. Each of the other four is measured at the bimonthly interviews (t=1,…,12): the child’s length, its weight, any diarrhea during the past two months, and whether the child had febrile respiratory illness during the prior two months. Birth outcomes depend upon prenatal visits, and each of the latter four outcomes depends upon the child’s prior health status as well as on parental behaviors that could have been responding to prior observations on the child’s health. The bimonthly incidences of disease are simple logit models conditional on heterogeneity and we discuss them in Appendix A. The empirical models for the child size measures are not standard, and we discuss them in detail in this subsection.

To model the determinants of continuous measures in this maximum likelihood framework, we use flexible functional forms like those for caloric intakes. For the models of child weight and height, we group children of the same age (in months) into 10 equal-sized sets based on the age specific percentiles of their weights and lengths respectively (5:1–10, 15:11–20, …, 95:91–100), and model the determinants of how a child outcome measure “progresses” from one cell to the next highest cell through the logit hazard rate model described earlier in this section. The child’s weight depends on characteristics of the child such as his/her age and gender, characteristics of the mother such as her age, fertility history, presence of her spouse, schooling level, and community characteristics such as food prices and urbanization level. Additionally, child weight is also a function of lagged weight and length, prior health status, such as previous incidents of diarrhea and severe respiratory disease, breast-feeding practices, and their parents’ other health inputs, including previous maternal employment and preventive health care. The specification of the process of child length increase is modeled nearly identically to that of the child weight function.

We use a similar discretized empirical model for the two primary birth outcomes: birth weight and length. To test the hypothesis that the effect of the first prenatal visit on birth outcomes is a function of the timing of the visit during a woman’s pregnancy, we include as additional regressors interaction terms between visit type dummies and the gestational age when the first visit occurred.

4.3 The Likelihood Function

We use a quasi-maximum likelihood method with discrete factors to estimate this multi-equation system. All parameters in the dynamic statistical model are estimated jointly. Each individual’s contribution to the likelihood function comprises the joint probability of observing each of the aforementioned health inputs and outcomes. Instead of assuming a restricted multivariate parametric specification for the error terms that cause correlations across different equations, we use a semi-parametric formulation to approximate the distribution of the unobserved heterogeneity terms. Heckman and Singer (1981) as well as Mroz (1999) show that the discrete factor estimators often have a superior performance than tightly parameterized heterogeneity distributions like the normal and gamma distributions.

Given our specification of discrete distributions for mother-specific heterogeneity term μ₁ and child-specific heterogeneity term μ₂, where μ₁ takes on J₁ different values and μ₂ takes on J₂ different values, with corresponding probabilities Pr(μ_{1, j1}) and Pr(μ_{2, j2}), the likelihood contribution from woman i is then given by:

$$\begin{array}{l}{L}_i=\sum _{j_1=1}^{J_1}\sum _{j_2=1}^{J_2}Pr({\mu }_{j_1})Pr({\mu }_{j_2})\\ \left\{\begin{array}{l}{\left\{Pr({V_i}^{\ast }(g,\tau \mid {\mu }_{j_1},{\mathrm{\Omega }}_{i,-1})Pr\left[{H_i}^{\ast }(0)\mid {\mu }_{j_1},{\mu }_{j_2},{\mathrm{\Omega }}_{i,0}\right]\right\}}^{I(s_i=1)}\\ {\left\{\sum _{{\tau }^{\prime }=1}^3\sum _{g^{\prime }=C_i-1}^7\{Pr({V_i}^{\ast }(g^{\prime },{\tau }^{\prime }\mid {\mu }_{j_1},{\mathrm{\Omega }}_{i,-1})Pr\left[{H_i}^{\ast }(0)\mid g^{\prime },{\tau }^{\prime },{\mu }_{j_1},{\mu }_{j_2},{\mathrm{\Omega }}_{i,0}\right]\}\right\}}^{I(s_i=0)}\\ Pr\left[{M_i}^{\ast }(0)\mid {\mu }_{j_1},{\mu }_{j_2},{\mathrm{\Omega }}_{i,1}\right]\prod _{t=1}^{12}\left\{Pr[{H_i}^{\ast }(t)\mid {\mu }_{j_1},{\mu }_{j_2},{\mathrm{\Omega }}_{i,t}]Pr[{M_i}^{\ast }(t)\mid {\mu }_{j_1},{\mu }_{j_2},{\mathrm{\Omega }}_{i,t}]\right\}\}\end{array}\right\}\end{array}$$

We use a binary variable s_i as an indicator for prenatal care information truncation: s_i =1 for a woman i who had her first prenatal care visit before the time of the baseline interview (G_i), and s_i=0 otherwise. The second line of the likelihood function is the contribution to the likelihood from the prenatal care visits and birth outcomes of for women whose prenatal information was not truncated (s_i =1). In the third line we integrate over all possible combinations of timing and types of their first prenatal visit, including no visit at all before the end of the 6^th month of their pregnancy, and the birth outcomes associated with each of those possible timings and types of prenatal visits. This only takes place for those whose first visit timing was censored by the event of the prenatal interview (s_i =0). The last line of the likelihood contains the contribution of the maternal behaviors at birth and the child outcomes and parental behaviors at each of the 12 bimonthly surveys. There are J₁ points of support for the mother/family specific heterogeneity and J₂ points of support for the child specific heterogeneity. In the empirical model we set these to seven and four points of support, respectively. The heterogeneity terms μ₁ and μ₂ enter various equations as third order polynomial forms. These are quite flexible specifications of the unobserved heterogeneity.⁷ The coefficients on 1^st, 2^nd, and 3^rd order polynomials in μ₁ and μ₂ are similar to factor loadings.

5. Limitations of this Matching of the Empirical Model to the Theoretical Model

5.1 Unobserved Inputs to the Health Production Function

Rosenzweig and Schultz (1983) discuss the empirical consequences of estimating a health production function when all of the relevant inputs are not observed. Their insights can be easily displayed in the following simple description of the household’s choices of inputs and their impacts on the child health outcomes. Throughout this example, we assume parents are attempting to maximize a well-defined expected utility function subject to a per period budget constraint as discussed in Section 2.

For simplicity, we assume that there are only two inputs to the health production process; only one of these can be observed by the researcher. The deterministic dynamic health production function depends only on these two inputs and the current health state of the child:

$$h_{t+1}^d=H^d(f_{1t},f_{2t}\mid h_t).$$

The expected utility maximizing choice of the two health inputs are

$$f_{jt}=D_{jt}^f(p_{1t},p_{2t},y_t\mid h_t),j=1,2,$$

where the budget constraint is given by y_t = c_t + p_1t f_1t + p_2t f_2t and the price of the composite consumption good has been normalized to one. Suppose that the second input is not observed.

In general the optimal choice of the unobserved input can be obtained from a conditional demand function of the form

$$f_{2t}=D_{2t}^R(p_{2t},y_t-p_{1t}{f}_{1t},\mid h_t,f_{1t}),$$

which is evaluated at the optimal choice of the first input. Note that the functional form of this conditional demand is in equivalent to the rationed demand when the household is forced to consume (and pay for) a particular level of the first input. It differs from a standard two stage budgeting formulation because we do not assume separability of the two inputs in the production function. Non-separability implies that “impact” of the first input on the conditional demand for the second input need not be captured entirely through its impact on the budget constraint.

Replacing the unobserved input with its conditional demand in the health production function yields:

$$h_{t+1}^d=H^d(f_{1t},D_{2t}^R(p_{2t},y_t-p_{1t}{f}_{1t},\mid h_t,f_{1t})\mid h_t).$$

This is a restatement of the hybrid production function developed by Rosenzweig and Schultz (1983). Taking the derivative of this hybrid production function with respect to a change in the level of the first input yields

$$\frac{\partial h_{t+1}^d}{\partial f_{1t}}=\frac{\partial H^d}{\partial f_{1t}}+\frac{\partial H^d}{\partial f_{2t}}\left[{-p_{1t}\frac{\partial D_{2t}^R}{\partial y_t}+\frac{\partial D_{2t}^R}{\partial f_{1t}}|}_{y_t-p_{1t}{f}_{1t}}\right].$$ (7)

The expression in equation (7) corresponds to what one would estimate for the “partial effect” of f_1t on health if information on the level of the second input was not controlled for in the empirical analysis. It could differ substantially from the true partial effect of the first input, f_1t, on health, $\frac{\partial H^d}{\partial f_{1t}}$. Provided the second input has positive marginal effect and the income effect on the conditional demand is small (say due to its comprising at most a small budget share), then the empirical estimate of the effect of the first input will tend to be overstated when higher levels of the first input increase the marginal productivity of the second input (the two inputs are complements in production). In practice it will almost always be the case that the researcher cannot observe and control for some inputs to the health production process and therefore will be unable to obtain uncontaminated estimates of the impacts of the observed health inputs. Nevertheless, it may be possible to assess a priori the extent of possible biases from knowledge about the likely magnitudes of the three partial derivatives comprising the bias.

5.2 “Intermediate” Inputs

In the estimation of health production functions, researchers are frequently interested in the impacts of “intermediating” inputs such as doctor, hospital, and clinic visits on health outcomes. Consider, for example, the impact of prenatal care visits on birth weight. It is unlikely that the act of visiting a prenatal clinic by itself has any direct beneficial impact on the birth outcome. Rather, the impact of the prenatal visit would operate through the induced changes in more proximate inputs to the health production process such as better nutrition, more exercise, extended bed rest if necessary, tetanus shots, and lower levels of alcohol and cigarette consumptions⁸. If one were to estimate a health production function incorporating these more direct health inputs in addition to the input “any prenatal care visit,” it is likely that one would conclude that the ceteris paribus beneficial impact of a health care visit is at most trivial. Especially for the evaluation of potential policies aimed at increasing access to prenatal care, however, that ceteris paribus interpretation likely would not provide relevant information about the benefits of prenatal care that incorporate the several paths through which it might operate. Many pregnant women might have made different decisions about their choices of the other health inputs in the absence of a prenatal visit.

The most commonly used estimation strategy in such a situation is to substitute out for the more direct inputs (e.g., nutrition) and model the health production function as depending only on the occurrence of a prenatal visit. Typically one would also control for the prices and other determinants of the more direct inputs that would capture the levels of these inputs in the absence of the prenatal care visit intervention. This is the strategy used in this paper to model the impacts of prenatal care visits⁹. If the true ceteris paribus impact of the visit is indeed zero (i.e., the first term in equation (7) is zero), then in this instance one would presumably be estimating as the impact of prenatal care the entire second term in equation (7). The complementarity of the knowledge obtained from the prenatal visit with the other health inputs, acting through these more direct inputs’ marginal effects, would describe the relevant mechanism through which the prenatal care visits affect health outcomes. If the price of the observed input is low, or the conditional income effects for the unobserved inputs are small, then one should be able to obtain an informative estimate of the indirect physiological impact of the intermediating input on health outcomes.

5.3 Data Timing Issues

The ideal empirical economic analysis of a production relationship would entail one observing a complete set of production inputs and then observing the actual level of output associated with that particular set of instruments. It would provide, for the most part, a purely technical description of the mapping from the inputs to the outputs. Health production functions, however, do not fit neatly into that framework. Not only are there issues of unobserved and indirect inputs as discussed above, but there are also important timing issues as it typically takes a somewhat lengthy period for many health inputs to cumulate and have measurable impacts on health. Compounding these difficulties, it is typically the case that one only intermittently observes a set of inputs and the corresponding outputs. The issue of what types of effects one can estimate in the presence of such time-dated, intermediating inputs can be analyzed in the context of a model quite similar to that used above for the interpretation of effects estimated in the presence of unobserved inputs.

Suppose, in the context of a three period model, that preferences are intertemporally separable and there are no financial borrowings or savings across time periods. We assume that health stocks, h_t, and health inputs, f_t, can be observed at time periods 1 and 3, but are unobserved at time period 2. As above, health evolves over time as a function of the previous period’s health stock, the choices of inputs in the previous period, and a set of random health shocks as in

$$h_{t+1}=H_{t+1}^d(f_t,h_t)+{\epsilon }_{t+1}.$$

The input demand function at time period 2 is give by

$$f_2=F_2[h_2,p_2,y_2]=F_2[H_2^d(f_1,h_1)+{\epsilon }_2,p_2,y_2],$$

where p₂ is the price of the health input (the price of consumption is normalized to one) and y₂ is the household’s income at that time period. Preferences need not be myopic in this model, but if families are maximizing the expected present discounted value of lifetime utility, then one needs to assume that contemporaneous prices and incomes do capture the expectations of future economic variables. The first order Markov assumption used in nearly all micro-empirical stochastic dynamic programming models is a simple example of this type of restriction on the information set used in the production process.

The health stock observed at time period 3 as a function of the observable inputs, prices, incomes, and health shocks and observable health stocks is given by

$$h_3=H_3^d[F_2[H_2^d(f_1,h_1)+{\epsilon }_2,p_2,y_2],H_2^d(f_1,h_1)+{\epsilon }_2]+{\epsilon }_3$$

The derivative of this function with respect to the period 1 input is given by

$$\frac{\partial h_3}{\partial f_1}=\frac{\partial H_3^d}{\partial H_2}\frac{\partial H_2}{\partial f_1}+\frac{\partial H_3^d}{\partial f_2}\frac{\partial f_2}{\partial H_2}\frac{\partial H_2}{\partial f_1}$$ (8)

The first of these two terms defines the cumulative effect of increasing the period 1 input on observed health in period 3 holding constant the period 2 inputs. The second term describes how the additional inputs at period 1 affects the unobserved second period inputs (though their impact on health at period 2) and their subsequent impact on observed health in at time 3. The expectation of the derivative in equation (8) with respect to the distribution of ε₂ defines the observable impact of period 1 inputs on period 3 health holding constant health at period 1 and prices and incomes¹⁰.

Equation (8) provides key information for assessing the impacts of beneficial health inputs on subsequent health. First, increases in inputs at the early time period can be undone during the unobserved second period whenever higher health stocks lead to lower levels of health inputs $\left(\frac{\partial f_2}{\partial H_2}<0\right)$. Family behaviors that are responsive to health changes would imply that the estimated effect of period 1 inputs from equation (8) would tend to be smaller than the ceteris paribus effect. Second, the shorter the span of time between periods the more similar will be the input choices in the first two time periods $\left(\frac{\partial f_2}{\partial H_2}\frac{\partial H_2}{\partial f_1}=\frac{\partial f_2}{\partial f_1}\approx 1\right)$. In this situation the estimated effect would correspond more closely to a “two period” change in the health input rather than to a change in the first period’s input that could be “undone” in the second time period. The “omitted variable bias” resulting from not being able to control for the unobserved time period 2 input could mean that one estimates a quantity more like the impact of a longer term change in the input f than the effect of just an instantaneous change in the input. The two month interview horizons for the CLHNS data used here, consequently, are more likely to provide estimates corresponding to relatively constant changes in health inputs than would be obtained if one instead used data with information on inputs and health status collected every six or twelve months.

The above behavioral models suggest that the empirical models and data used here, while clearly imperfect, might be able to capture much of what economists hope to estimate from demand and production functions. For example, the effects on birth outcomes from prenatal care visits that we estimate do confound the complementarities of other health inputs with the “prenatal care.” Unobserved, relevant inputs to the production processes present the most formidable barriers to clean, precise interpretations of marginal effects. However this “contaminated” effect likely captures a policy relevant interpretation of the impact of receiving prenatal care.

In our birth outcome models the only major “input” considered in previous studies that we do not specify is smoking behaviors, which were only observed during the baseline pregnancy survey of the CLHNS. Recent evidence presented in Walker, Tekin, and Wallace (2007), however, suggests a large component of what most researchers have estimated as the impact of smoking on birth outcomes could be due to unobserved heterogeneity rather than to direct physiological effects. In light of the above discussion of intermediating inputs in Section 5.2, one might obtain a more policy relevant estimate of prenatal care impacts by not directly conditioning on smoking behaviors. Regardless of whether smoking is an important birth outcome determinant or not, our empirical model provides a framework to assess the “total” impact of prenatal care. We cannot, however, disentangle the paths through which it operates.

The production functions for post birth outcomes that we estimate do include many of the most important inputs to early child physiological development. We include breastfeeding and post breastfeeding nutritional inputs, constraints on the mother’s time as captured by her working outside the home, and preventive care visits for the child. We allow the previous health outcomes to affect both health input choices and the health production functions, as implied by the models we specified above. The estimations also condition on family characteristics, such as the mother’s age and education, the number of other adults in the household, whether a spouse is present, and the number of young children in the household, which likely affect the marginal technological efficiency of the health inputs. Because of the two month lag between observation periods we do include intervening prices in the production functions, as discussed above. Equations (7) and (8) provide a framework for assessing the interpretations of the production function estimates from imperfectly observed sets of inputs like those used here. In general the above analysis suggests that unless both the marginal impacts of the unobserved inputs are large and the income effects in their conditional demands are large, the biases arising from estimating the production functions with only the observed inputs might be small enough for one to obtain useful (but imperfect) inferences from the input demands and health production functions estimated in models like those considered here. As seen from the empirical results we present below, we do find there are some significant price effects.

5.4 Which Estimated Effects Are Robust to Missing Inputs?

The preceding discussion highlights important difficulties in obtaining simply interpretable estimates of production function effects when one cannot observe all relevant input choices. In general, the interpretation of estimated “marginal effects” when all inputs are not observed will require one to make assumptions about the magnitudes of quantities like conditional income effects and complementarities between observable and unobserved inputs. As discussed above, however, the evaluation of some potential policies might better be evaluated without conditioning on many chosen inputs, as those policies may best be thought of as operating through their impacts on the set of inputs chosen by the family. In addition, there are two classes of effects that can be calculated where the interpretations of the estimated effects are not hampered by one’s ability to observe all of the inputs to the health production process. For estimates to make sense in both of these general cases, it is necessary for one to be able to control for all of the prices and other factors affecting the demands for all of the observed and unobserved inputs to the health production process.

First, one can readily obtain estimates of the demand functions for each of the observable inputs. This follows directly from the definition of a demand function and the assumption that one observes all relevant prices and other factors affecting the input demands. In particular, one can obtain interpretable estimates of own and cross price effects, as well as of the impacts on the input demands of the child’s prior health status, family composition measures, and other factors that are not determined by the family simultaneously with the health inputs. Any of these measures that depends on unobserved heterogeneity that also influences the demand equation, prior health status for example, will need to be treated as endogenous in order to interpret any of the estimated demand effects as causal.

Second, it is possible to obtain readily interpretable effects of all of the factors affecting the demands for the observable inputs on the subsequent health outcomes. These effects are those that allow the family to re-optimize all inputs in response to changes in the “economically exogenous” demand factors. They measure the total effect of a change in the “constraint” on the health outcome, not a partial effect. To calculate these effects one must allow the observable input choices to vary in response to the changing constraints and then trace out how the changes in the observed input choices and constraints affect the hybrid demand system¹¹. That is precisely the approach used in several of the simulations presented below. The reason one can obtain interpretable estimates of such effects even with a hybrid production function is that the conditional demand functions for the unobserved inputs, after substituting in the functional forms of the optimal demands for the observed inputs, are functionally identical to the unconditional input demands for unobserved inputs.

6. Empirical Results

Given the nonlinear nature of this estimation framework, it is quite difficult to interpret directly the parameter estimates. Instead of discussing the actual point estimates, we use simulations from the estimated relationships to explore parental behaviors and the impacts on children. Appendix B, however, does contain point estimates and standard errors for all of the parameters estimated for our most general model¹². In this section we present the impacts of the timing of the commencement of prenatal care on birth outcomes, the determinants of the parents’ input decisions, and the impacts of parents’ responses on children’s health. At the end of this section we assess the benefits of parents using compensatory behaviors instead of making child care decisions that are unrelated to their children’s development.

6.1 Impacts of prenatal care on birth outcomes

Prenatal care is a key health behavior investigated in this study. It is important to recall the definition of the prenatal care effects that we estimate. Given that there are no other behavioral choices modeled as affecting birth outcomes, these prenatal care effects measure those discussed in section 5.2 and described in equation (7). In particular, these prenatal care effects measure the sum of the effects from the changes in all of the more direct birth outcome determinants that take place because the mother had a prenatal care visit. As seen from the first term within brackets in equation (7), these changes in the more direct inputs reflect the financial cost of the prenatal visit in addition to the more technological effects of changes in the unmeasured parental behaviors.

In this section we examine two general types of prenatal care effects. The first corresponds to an exogenous assignment of prenatal care to all pregnant mothers; it corresponds to an average treatment effect (ATE). The second measures the impact of prenatal care on those mothers who would be induced to receive prenatal care because of a change in a price or availability of prenatal care; these correspond to local average treatment effects (LATEs). It is important to note that the LATEs, since they are the overall responses to exogenous changes in constraints for an identifiable subgroup, do provide uncontaminated measures of the overall effect of the constraint changes on child health for this subset of the population, regardless of the precise mechanism through which the prenatal care operates. The LATEs are likely to be more relevant for evaluating new health policies, as they do correspond to possible policy changes which could be instituted in the hope of increasing prenatal care visits. The ATEs, on the other hand, measure the overall importance of prenatal care, but one would be hard pressed to posit an implementable public policy where an ATE would measure well the new policy’s impact.

As a baseline, consider a simplified model without heterogeneity controls that estimates the average treatment effects (ATEs) of various types of prenatal visits. Figure 1 displays the estimated impacts of these prenatal visits on the child’s birth weight. According to these estimates, it appears that delaying the onset of prenatal visits, or never receiving prenatal care (as measured by the 6+ category) almost always results in better birth outcomes. Consider, for example, a woman who would only receive prenatal care from a traditional provider. These simple estimates imply that if she postponed her first traditional visit from the first month of pregnancy to the sixth month her child’s birth weight would increase by about 80 grams.

Figure 1.

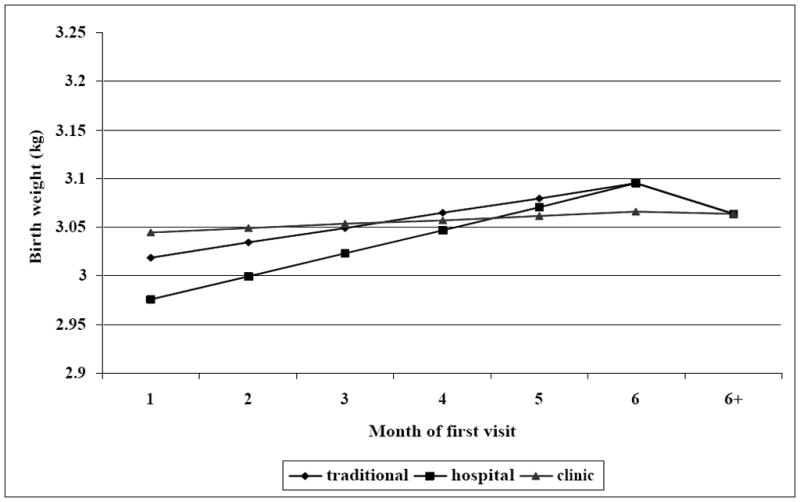
The impact of prenatal visit on birthweight (Full model without heterogeneity control)

Unobserved heterogeneity, perhaps due to pregnancy complications, could be leading to the rather counter-intuitive implications from the simple prenatal care model as displayed in Figure 1. When we use unobserved heterogeneity approaches to help control for the possible endogeneity of the timing of the first prenatal care visit, the implications change dramatically. As shown in Figure 2, postponing the first clinic visit from the first gestation month until the sixth would result in about a 120 gram reduction in birth weight, and never having a first visit would lead to a further reduction of almost 140 grams. According to these estimates there are clear and important benefits from mothers receiving early prenatal care. Surprisingly, having one’s first prenatal care visit at a hospital visit appears to be less effective at increasing birth weight than either traditional or clinic first prenatal visits. Possibly this could be due to incomplete controls for heterogeneity in fetal health, or it might reflect that first going to a hospital does not encourage women, or enable them as much, to receive regular, subsequent prenatal care.

Figure 2.

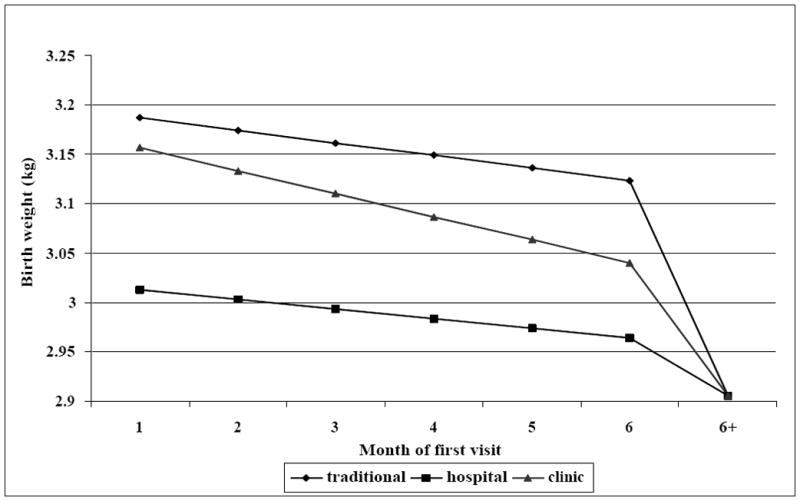
The impact of prenatal visit on birthweight (Full model with heterogeneity control)

We examine the impacts of several potential policies for increasing a mother’s willingness to start prenatal care at an earlier date. We do this by varying the value taken on by the price, availability, and convenience of prenatal care measures that influence the choice of prenatal care. By doing so we focus on that group of individuals who would be impacted by such potential policy changes, and consequently these effects can be interpreted as local average treatment effects (LATE). Table 4 contains simulation results for these experiments.

Table 4.

Simulation Results for Prenatal Visits and Birth Outcomes ¹

	(1) Half price hosp3 (36% with no prenatal care responded )		(2) No wait in clinic4 (9% with no care responded)		(3) Full-time trad care5 (21% with no care responded)
	Before	After	Before	After	Before	After
Mean 1st visit month2	-	4.4	-	4.8	-	4.7
Mean birth weight (kg)	3.05	3.06	3.02	3.05	3.04	3.08
Mean birth length (cm)	48.9	49.1	49.7	49.8	49.1	49.4

Note:

¹Using 2873 observations and full model parameter estimates to simulate a subsample of women who will not receive prenatal care at baseline but they will do so after environmental variables change.

²First visits that occurred after the 6^th month of gestation are re-coded into no visits;

³This change represents an average price drop of 3.7 pesos;

⁴This represents an average drop of 6 minutes in clinic for prenatal care;

⁵This represents an increase in full-time percentage of traditional care-givers from 91.4% to 100%.

After reducing the average cost of hospital visits by half, 36% of women who did not seek any prenatal care before the price drop would alter their decisions. The average weight of their newborns, however, increases by only 10 grams. The magnitude of increase is significantly less than the treatment effects indicated in Figure 2. These somewhat conflicting implications reflect the difference between average treatment effects and local average treatment effects. According to our estimates, those women who altered their behavior in response to the price change had unobserved characteristics that are positively associated with good pregnancy outcomes. There is much less room for improvements in their children’s birth outcomes from early prenatal visits than for the general population. Increasing the number of traditional caregivers yields somewhat stronger results. After an approximate 10% increases in the number of full-time traditional practitioners, 21% of women who would not seek prenatal care otherwise receive some type of prenatal care. The changed behavior is associated with an increase in average birth weights of 40 grams. Eliminating the waiting time in clinics only induced 9% of women into participating in prenatal care. However, the average improvement in birth weights of their newborns is about 30 grams. These simulated LATE results are modest compared to marginal treatment effects already discussed, but they are not inconsequential.

6.2 Parents’ compensatory behaviors

Table 5 contains estimates of parental behaviors under two scenarios: one where the child had low birth weight (2,000 grams) and the other where the child had an average birth weight (3,300 grams). We impose these two birth “initial conditions” and simulate separately a parent’s behaviors regarding work, preventative health care, breast-feeding, and supplemental feeding using a representative woman who otherwise has individual and community characteristics corresponding to the medians of those observed in the sample. As discussed in Section 5.4, these effects on the input demands should measure the average effect on the observable behavioral choices for the representative woman, provided that the empirical model controls for the prices and other determinants of all the behavioral decisions made by the family.

Table 5.

Simulation Results for Parental Behaviors in Response to Low Birthweights

Sample size: 30001
		(1) Low birthweight2 (S.E.)4	(2) Normal birthweight3 (S.E.)4	Parental response (1)–(2) (S.E.)4
Expected working months	up to year 1	2.251 (0.081)	2.641 (0.083)	−0.390 (0.034)
	up to year 2	5.901 (0.183)	6.634 (0.172)	−0.733 (0.082)
#of month w/preventive care5	up to year 1	1.507 (0.076)	1.315 (0.062)	0.192 (0.056)
	up to year 2	1.912 (0.096)	1.651 (0.082)	0.261 (0.072)
Duration of breast-feeding (months)6	Exclusive	0.684 (0.056)	0.725 (0.044)	−0.041 (0.054)
	Any	15.721 (0.252)	15.116 (0.208)	0.605 (0.173)
Caloric intake (calorie/kg)7	At end of year 1	54.412 (3.361)	53.128 (3.081)	1.284 (0.456)
	At end of year 2	70.873 (3.342)	69.642 (3.135)	1.231 (0.488)

Note:

¹The sample used in these simulation is comprised of 3000 replicates of a typical mother-child pair whose exogenous characteristics are median values of the estimation sample;

²The birth weight is set to be 2.0 kg and birth length is set to be 34.0cm;

³The birth weight is set to be 3.3 kg and birth length is set to be 51.0cm;

⁴Standard errors are obtained after bootstrapping using 1000 draws of parameters using estimated parameter vector and covariance matrix;

⁵Expected preventive visits within first year (6 bi-monthly surveys) and first two years (12 bimonthly surveys) respectively;

⁶Conditional on having initiated breast-feeding at the first follow-up survey;

⁷Caloric contents from breast milk are not included.

We simulate 3000 life courses for each child up to age two and construct summary measures from these simulations.¹³ To obtain standard errors of these summary statistics, we use a parametric bootstrap procedure. For each of 1000 sets of parameters drawn from the estimated asymptotic distribution of the parameter estimators, we recalculate these summary measures from the 3000 life course simulations. We report as standard errors the standard deviations of outcomes across these 1000 simulations.

The mother of the low birth weight child is less likely to work at all during the first year of the child’s life or during the first two years of the child’s life than the mother of the average birth weight child. While these effects are somewhat small, they are statistically significant. The mother of a low birth weight child had 16% more preventive care visits during the first two years of the child’s life than the mother whose child had an average birth weight, and this difference is statistically significant. On average, mothers of low birth weight children breast-feed (exclusively or non-exclusively) for about 0.6 month longer, conditional on having initiated breast-feeding at the first follow-up survey. The normal weight children are exclusively breast fed slightly longer than the low birth weight children, though this difference in exclusive breast-feeding practices is not statistically significant. At both the first and second birthdays, the low birth weight child receives about 1.2 more calories of food per kilogram in its weight than the child with an average birth weight. These estimates suggest that adverse birth outcomes have lingering impacts on parents in Cebu as they make work, health care, and infant and child feeding decisions during their children’s early childhood.

Table 6 contains estimates of how a representative parent responds to her child’s weight when making preventative care, nutrition, and work decisions. In this table we compare women whose child was at the 20^th percentile of each age-adjusted weight distribution to one at the 80^th percentile. Unlike the estimates just discussed, these do not incorporate the effect of having a birth weight below 2500 grams. If they are not breast-feeding, at age 12 months the parents of the smaller child provide about 7 more calories of nutritional intakes per kilogram of weight, and this difference is statistically significant. Parents of the smaller children are slightly more likely to take their children to preventative health care visits, and this difference is also statistically significant. Mothers of the smaller children are somewhat more likely to be working when the child is four months old, but the effect is not statistically significant. It is, however, difficult to put a clear interpretation on this result.

Table 6.

Simulated Maternal Responses to Different Levels of Lagged Weights and Lengths

Sample size: 30001
	(1) 20th pctile2 (S.E.)4	(2) 80th pctile3 (S.E.)4	Parental response (1)–(2) (S.E.)4
Expected calories/kg at year 15	84.713 (3.138)	77.521 (3.080)	7.192 (0.667)
Prob(preventive care) at year 1	0.116 (0.012)	0.109 (0.011)	0.007 (0.003)
Prob (working away) at month 4	0.172 (0.013)	0.167 (0.014)	0.005 (0.004)

Note:

¹The sample used in these simulation is comprised of 3000 replicates of a typical mother-child pair whose exogenous characteristics are median values of the estimation sample;

²Lagged weight and length are held at 20^th percentile of population weights and lengths respectively. The values are equivalent to 5371.3 grams and 58.7cm in month 4 and 6953.1 grams and 67.8cm in year 1;

³Lagged weight and length are held at 80^th percentile of population weights and lengths respectively. The values are equivalent to 6669.0 grams and 62.8cm in month 4 and 8691.3 grams and 72.8cm in year 1 ;

⁴Standard errors are obtained after bootstrapping using 1000 draws of parameters using estimated parameter vector and covariance matrix;

⁵The simulation is carried out conditional on no breast-feeding.

6.3 Impacts of Parental Behaviors on Child Outcomes

Figure 3 presents the estimates of the impacts of breast-feeding on the child’s weight gain over the first year of life using a representative sample to simulate the trajectory of child weights after birth. As discussed in Section 5.1, if there are important, costly, and unmeasured inputs affecting the child’s health, then these effects obtained from a hybrid production function do not capture just the ceteris paribus impact of changes in the observed inputs. Instead, they also incorporate the effects of changes in the unobserved inputs brought about because they are complements or substitutes for the observed inputs, in conjunction with the changes in the unobserved inputs resulting from “loss” of income because one is forced to utilize more of the observed inputs.

Figure 3.

Simulated infant weight with different types of breast-feeding practice

The top curve in Figure 3 represents the average weight of children who exclusively breast fed during the first four months of life and thereafter continued to breast-feed with supplemental food through the remainder of the first year of life. Exclusively breast fed children at first gain weight more rapidly than those who only partially breast fed. At month four, these children are about 200 grams heavier. Additionally, these children at age four months are about 400 grams heavier than children who were never breast fed. These differences, however, start to diminish after age four months. By age six months or later there is almost no discernable difference in weight between the children who were exclusive breast fed for the first four months and those who were only partially breast fed. By age 12 months, the children who were never breast fed have nearly caught up with those children who had been breast fed; they are only about 180 grams lighter at that age.

Table 7 presents the estimated impacts of other parental behaviors on the children’s probability of contracting diseases and their weights and lengths when they are age four months. Holding month two child health outcomes and each of the other health inputs constant, we simulate the expected child outcomes at month four in response to parents’ different choices about breast-feeding, maternal working, preventive health care, and caloric intake respectively. Similar to the results shown in Figure 3, significant health benefits are associated with exclusive breast-feeding. The children who are exclusively breast fed up to month four will outgrow those who are not breast-fed after month two by about 240 grams and nearly 0.2 cm in length from month two to month four. The exclusively breast-fed children are also less likely to contract diarrhea and FRI. These latter improvements are somewhat less statistically significant. A mother staying at home at month two and seeking preventive health care at month two appears to have positive effects on children’s weights and lengths at month four, albeit with much smaller magnitudes in contrast to the impacts of exclusive breast-feeding. Preventive health care only reduces the probability of contracting diseases slightly, and the benefits are not statistically significant. However, by increasing caloric intake level at month two from the 20^th percentile to the 80^th percentile, average children gain an extra 147 grams in weight between months two and four.

Table 7.

Simulation Results for the Effects of Health Inputs on Child Health Outcomes at Month 4

Simulation sample size: 30001
	Prob(Diarrhea) (S.E.)2	Prob(FRI) (S.E.)2	Weight(kg) (S.E.)2	Length(cm) (S.E.)2
(1) Exclusive Breast-feeding	0.218 (0.036)	0.155 (0.024)	6.502 (0.105)	61.411 (0.113)
(2) No Breast-feeding	0.240 (0.036)	0.167 (0.020)	6.262 (0.105)	61.220 (0.115)
(3)Effect of Breast-feeding = (1) – (2)	−0.022 (0.013)	−0.012 (0.014)	0.240 (0.015)	0.191 (0.018)
(4) Working Away from Home	0.224 (0.036)	0.165 (0.018)	6.400 (0.104)	61.250 (0.114)
(5) Not working away	0.232 (0.036)	0.159 (0.017)	6.418 (0.104)	61.266 (0.013)
(6) Effect of Working Away from Home = (4) – (5)	−0.008 (0.006)	0.006 (0.007)	−0.018 (0.005)	−0.016 (0.008)
(7) Preventive care	0.228 (0.036)	0.156 (0.018)	6.417 (0.104)	61.221 (0.113)
(8) No preventive care	0.232 (0.035)	0.159 (0.016)	6.415 (0.103)	61.268 (0.114)
(9) Effect of Preventative Care = (7) – (8)	−0.003 (0.007)	−0.003 (0.008)	0.002 (0.006)	−0.047 (0.011)
(10) 80th pctl supplemental calorie consumption	-	-	6.451 (0.106)	61.281 (0.112)
(11) 20th pctl supplemental calorie consumption	-	-	6.304 (0.105)	61.222 (0.111)
(12) Effect of Extra Calorie Supplementation = (10) – (11)	-	-	0.147 (0.007)	0.059 (0.019)

Note:

¹The sample used in these simulation is comprised of 3000 replicates of a typical mother-child pair whose exogenous characteristics are median values of the estimation sample;

²Standard errors are obtained after bootstrapping using 1000 draws of parameters using estimated parameter vector and covariance matrix.

As was the case for the analysis of the effects of breastfeeding, equation (7) implies that these measured effects of the parental behaviors are contaminated by the parents changing their use of the unmeasured inputs as one exogenously varies the observed health inputs. It is possible to use equation (7) to assess the extent of the possible bias. Suppose there is a single unobserved input with positive marginal product and that this input is a normal good in its conditional demand equation. Under these assumptions, the effects discussed above will underestimate the actual marginal impacts of these inputs unless the observed inputs are strong complements to the unobserved inputs (as measured in the conditional demand). With multiple unobserved inputs, one can derive somewhat similar though more complex, conditions under which the marginal effect from the hybrid demand function will yield underestimates of the true marginal effects. In general, it is likely that these estimates provide lower bound estimates of the true marginal effects, provided there are not large complementarities between the observed and unobserved inputs.

6.4 The Importance of Parental Compensatory Behaviors

The preceding two subsections suggest that parents in Cebu do alter their behaviors in response to their children’s early health outcomes and that these parental behaviors can have beneficial impacts on their children. In this subsection we compare simulations of parental behaviors and outcomes based on estimates from our full model to those from a set of simulations of child outcomes based on situations where parents randomly make their work, breast-feeding, preventative care, and caloric supplementation decisions. The economic model presented in Section 2 predicted more favorable child outcomes, on average, for parents who chose their behaviors “optimally” as opposed to those who picked their behaviors “randomly.” One could clearly pick alternative definitions of non-responsive, counterfactual behaviors, but this one seems to convey well the notion that parents may vary in their behaviors even when they are not motivated by the potential impacts of these behaviors on their children.

If parents do solve a dynamic optimization problem like that described in Section 2, then the estimates we obtain from the CLHNS data should reflect the implications of theoretical model. To assess whether the observed data are in accord with these theoretical predictions, we simulate the estimated dynamic relationships under two scenarios where children vary in initial (birth) status. The first simulates the parents’ behavioral responses as functions of their children’s health status over time and uses these responses as “inputs” to the estimated health production functions. This yields a distribution of child outcomes over time that should correspond to whatever types of decision rules parents actually use for deciding how take care of their children. The second simulated scenario assumes that parents do not takes their children’s observed health status into account when making their when making their health investment decisions. Instead, they “randomly” choose a set of health investments from the observed distribution of parental behaviors from the data set at each age. We use these as inputs to the estimated health production functions in the dynamic simulations.¹⁴

We compare the simulated distributions of health outcomes under these two scenarios to assess whether the estimated behavioral relationships appear to yield outcomes that are in accord with the predictions of the dynamic optimization model. A finding that the simulated health outcomes do not differ between the two scenarios in a way that is consistent with the predictions of the theoretical model could be considered a rejection of theory. However, a finding that the results appear to be in accord with the theoretical predictions should not be interpreted as conclusive evidence of optimizing behavior, as the implications we examine are only necessary conditions. Other behaviors, not necessarily ones following from stochastic dynamic optimizing decision rules, could also satisfy the necessary conditions.

Table 8 presents estimates of the consequences of compensatory behaviors for the incidence of diarrhea and respiratory illness. We carry out this analysis separately by whether the child was low birth weight as examined above. For both types of illnesses, we see that the incidence of disease is lower when parents make their behavioral decisions by taking into account the actual health status of their children, though the results are much more striking for the incidence of diarrhea. Nevertheless, all these differences are statistically significant. Additionally, we see that it is the low birth weight children who benefit the most from parents being able to adjust behaviors in response to each child’s progress.

Table 8.

Simulation Results for the Impacts of Early Childhood Outcomes and Health Inputs on Child Health Outcomes (Standard errors in parentheses)

Simulation sample size: 30001
		Low birthweight2		(3) Compensation Effect (1)–(2) (S.E.)6	Normal birthweight3		(6) Compensation Effect (4)–(5) (S.E.)6	(7) Differential Compensation Effect (3)–(6) (S.E.)6
		(1) with compensation4 (S.E.)6	(2) without comensationp5 (S.E.)6		(4) with compensation4 (S.E.)6	(5) without compensation5 (S.E.)6
Expected months w/diarrhea	in yr 1	2.326 (0.076)	2.412 (0.078)	−0.086 (0.026)	2.151 (0.043)	2.228 (0.056)	−0.077 (0.029)	−0.009 (0.001)
	in yr 1,2	4.824 (0.156)	4.976 (0.162)	−0.152 (0.036)	4.468 (0.204)	4.580 (0.207)	−0.112 (0.036)	−0.040 (0.007)
Expected months w/FRI	in yr 1	1.972 (0.108)	2.017 (0.115)	−0.045 (0.018)	1.874 (0.082)	1.901 (0.088)	−0.027 (0.012)	−0.018 (0.004)
	in yr 1,2	4.060 (0.152)	4.136 (0.178)	−0.076 (0.024)	3.946 (0.206)	4.004 (0.214)	−0.035 (0.028)	−0.041 (0.013)

Note:

¹The sample used in these simulation is comprised of 3000 replicates of a typical mother-child pair whose exogenous characteristics are median values of the estimation sample;

²The birth weight is set to be 2.0 kg and birth length is set to be 34.0cm;

³The birth weight is set to be 3.3 kg and birth length is set to be 51.0cm;

⁴Both health outcomes and health inputs are simulated using the full model estimates;

⁵Health inputs are randomly drawn from sample;

⁶Standard errors are obtained after bootstrapping using 1000 draws of parameters using estimated parameter vector and covariance matrix.

Figures 4 and 5 examine the consequences of compensatory behavior for normal birth weight children on their weight gain and length increases over the first two years of life. Children whose parents alter their behaviors in response to their child’s development on average have a two-year weight gain 300 grams higher than that for children whose parents do not adjust their behaviors. Similarly, children whose parents’ behaviors respond to the child’s health grow an additional 0.6 centimeters on average over the first two years of life. The estimates we obtain indicate that parents adjust their behaviors in response to their children’s observed health. Most importantly, these adjustments appear to bring about key aggregate improvements in child growth and health. These are precisely the predictions of the dynamic optimization model presented in Section 2.

Figure 4.

Simulated weights for children with normal birth weights

Figure 5.

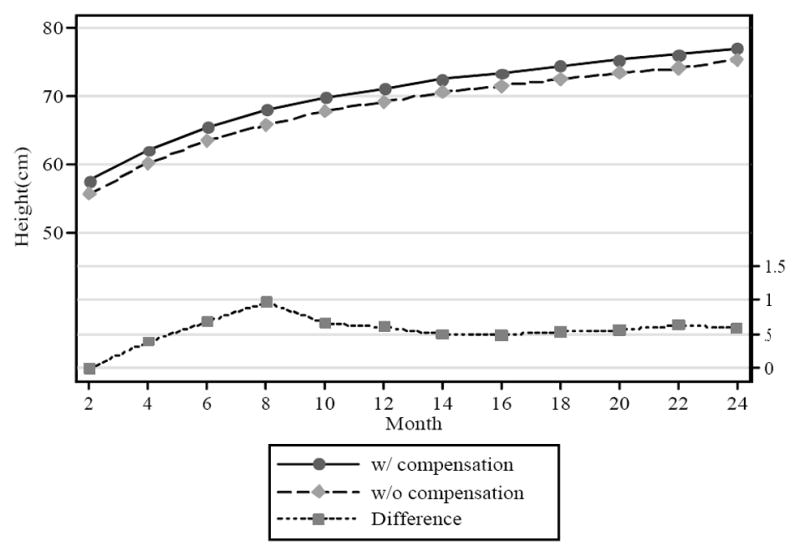
Simulated lengths for children with normal birth weights

The analysis in Section 5 revealed, even when there are unmeasured health inputs, that the empirical model can provide uncontaminated estimates of the physiological outcomes resulting from changes in baseline constraints and conditions. Consequently, the columns and graphs labeled “with compensation” in Table 8 and Figures 4 and 5 should provide accurate estimates of the child outcomes when the parents follow their own behavioral rules. The simulations labeled “without compensation,” as implied by equation (7), do not necessarily yield health outcomes corresponding to random allocations of all health production function inputs. Consequently, these comparisons of outcomes with and without compensation likely provide biased estimators of the impacts of the parent’s targeted responses on health outcomes.

It is important to recognize that the empirical model implicitly allows parents to select optimally the unobserved health inputs for any constrained, specified levels of the observed inputs. If the parents are making utility optimizing health input decisions, then the simulations where only the observed inputs are randomly assigned implicitly allow the parents in these counter factual situations to choose purposefully new optimal levels of all the unobserved health inputs. We suspect, but have not proven, that in many cases the choices of the unobserved inputs subject to the randomly chosen constraints will result in health outcomes more closely related to optimally chosen ones without the random constraints, on average, than would be the case if it were possible to assign randomly all health inputs.

If this were indeed the case, then the simulations “without compensation” likely overstate the average health outcomes relative to the case where all inputs would be randomly assigned. In this case, the effects presented in Table 8 and Figures 4 and 5 would understate the true effects of compensating behaviors. Additionally, with diminishing marginal utility of child health and diminishing returns to health inputs, parents who were randomly assigned more observable health inputs than they would have chosen without the constraint would likely choose fewer of the unobserved health inputs than in an unconstrained optimal choice, unless there were quite high production complementarities between the observed and the unobserved inputs. Similarly, parents assigned fewer healthy inputs than they would have optimally chosen without a constraint would compensate by purchasing more of the unobserved health inputs than in the unconstrained case. If this were the case, then the differential compensation effects presented in Table 8 would likely be under-estimates of the true health differential compensation effects that would appear when all inputs were randomly assigned. Compensating behaviors might be even more important for improving health and reducing inequality than the estimates presented in this paper.

7. Discussion and Conclusions

Our simulation results indicate that parental behaviors importantly affect early child health outcomes in Cebu, Philippines. After including controls for unobserved heterogeneity across women, prenatal care results in better birth outcomes in terms of birth length and weight. Early initiation of prenatal care during pregnancy appears to be most beneficial. We find that the event of having been a low birth weight baby has lingering effects even after allowing adjustments in parental behaviors to compensate for this adverse early childhood outcome. Mothers of low birth weight children tend to breast-feed longer relative to mothers whose currently identically sized children had not been low birth weight. Mothers of low birth weight babies are less likely to work; they are more likely to seek preventive health care for their children; and their children consume more calories per kilogram in weight.

While there is evidence of lingering impacts of low birth weight on some child outcomes, the mother’s responses to low birth weight and contemporaneous adverse outcomes during the early life course suggest that there are important compensatory behaviors taking place. For instance, the parents will significantly increase the caloric intake and preventive care visits when their child’s growth appears slow. Analyses that ignore the interactions and endogeneity of parental behaviors and childhood health-related events provide biased estimates of the efficacy of parental behavior towards their children.

Ideally, the characteristics of other children within the family could help researchers understand better the allocation of resources among the family. The CLHNS, however, regularly collected detailed information only on one child for each woman. This limitation makes it difficult to study the family health production process. At the same time, it is also possible that the genetic endowments of low-birth weight children are associated with their parents’ unobserved heterogeneity, which partially determines household resources available to support child growth. Also important might be the fact that we imposed somewhat arbitrary exclusion restrictions and timing conventions on the sequencing of parental behaviors and child outcomes. We did, however, examine alternative conventions and found quantitatively similar results.

It is clear that we have not been able to include all of the relevant health inputs in our empirical analysis. As trenchantly observed by Rosenzweig and Schultz (1983), the resulting hybrid health production function relationships need not correspond well to what economists usually consider as health production functions. Our statistical models do not adjust for these possible factors, and therefore the interpretations placed on the estimated impacts of maternal decisions on child outcomes need to be interpreted with caution. We do, however, present a theoretical analysis of the consequences of missing health inputs and argue that our estimated relationships provide useful, though imperfect, measures of the health production functions.

According to our estimates, mothers in Cebu make work decisions, infant feeding decisions, and preventative child health care decisions based in part on their children’s growth and health. Their tailored behavioral responses appear to be quite effective in improving child outcomes, but it is impossible to disentangle completely the effects of their observable behavioral responses from those due to the hidden behavioral responses in the choices of unobserved health inputs. Overall, there appears to be substantial evidence that these parents are not passive receptors to their children’s progress as they adjust their child care actions in a way that enhances their children’s outcomes. In particular, mothers with the worst off children, as measured by low birth weight and low weight for age, appear to make extra efforts to help their children overcome these developmental deficiencies.

Appendix A—Included here only for Reviewers; this should appear on the web for readers. Additional Empirical Modeling Specifications

Prenatal Care Visits

We use a discrete-time hazard model to help describe the mother’s prenatal care decision and investigate how the probability of commencing professional prenatal care evolves over the course of the pregnancy and how that probability is affected by observed and unobserved characteristics of the mother, the family, and the community where they lived. Conditional on having a prenatal visit, we also model the probability of selecting each one of the three care types.

To facilitate the modeling of this hazard, we use an auxiliary time line, t′, which starts at the initiation of pregnancy and ends when the gestational age is 7 months. The hazard rate for starting prenatal care at time t′ is defined as the probability that she initiated prenatal care at t′ given that she had not done so before t′. This probability is given by:

$$Pr[v(t^{\prime })=1\mid v(t^{\prime }-1)=0,\dots ,v(t_0^{\prime })=0]=F_{\mathit{any}}(X_v,C_v,{\mathbf{t}}^{\prime },{\mu }_{\mathbf{1}}),$$

where t′₀ represents the starting time of pregnancy. We model this probability as:

$$F_{\mathit{any}}(X_v,C_v,t^{\prime },{\mu }_1)=\mathit{Logit}[{\beta }_v^{\prime }{X}_v+{\alpha }_v^{\prime }{C}_v+\sum _{t^{″}=2}^{T^{\prime }}{\delta }_{v,t^{″}}I(t^{″}=t^{\prime })+{\rho }_{v,1}{\mu }_1],$$

where Logit[x] = exp(x)/[1+ exp(x)], and T′, here equaling 6, represents the assumed maximum gestational age (measured in months) for the first prenatal visit to have a meaningful impact on birth outcomes. To capture arbitrary forms of duration dependence in this hazard function we include a set of time dummies within the hazard rate specification where the omitted period is the first.

In each period t′, we use a nested logit model to characterize the choice of the prenatal care provider, where the first-level alternative is a binary choice of having any prenatal visit (v=0 if not) and the bottom-level alternatives conditional on having any visit are traditional (v=1), hospital (v=2) and clinic (v=3, omitted). For instance, given that a first visit of any type happens at time t′, the probability that this first visit is with a traditional health care provider is modeled by the function

$$Pr[\tau (t^{\prime })=1\mid v(t^{\prime })=1]=F_{\tau ,1}(X_{\tau },C_{\tau },{\mu }_{\mathbf{1}})=\text{Logit}[{\beta }_{\tau 1}^{\prime }{X}_{\tau }+{\alpha }_{\tau 1}^{\prime }{C}_{\tau }+\sum _{t^{″}=2}^{T^{\prime }}{\delta }_{\tau 1,t^{″}}I(t^{\prime }=t^{″})+{\rho }_{\tau 1}{\mu }_1].$$

Breast-feeding (bf)

Like the prenatal care visits, discrete choices of breast-feeding are modeled in a nested logit framework, where the first-level alternative is a binary choice of practicing any breast-feeding (bf=1) and the bottom-level alternatives conditional on any breast-feeding are exclusive breast-feeding (bf=2) and partial breast-feeding (bf=3, omitted).

The probabilities of observing breast-feeding practice type k, Pr(bf_t = k| μ₁, μ₂) are given by:

$$\begin{array}{l}{F}_{bf,1}(X{(t)}_{\tau },C{(t)}_{\tau },H(t-1),{\mu }_{\mathbf{1}},{\mu }_{\mathbf{2}})=Pr(\text{bf}(t)=1\mid {\mu }_{\mathbf{1}},{\mu }_{\mathbf{2}})\text{for}k=1;\\ [1-Pr(\text{bf}(t)=1\mid {\mu }_1,{\mu }_2,{\mathrm{\Omega }}_t)]F_{bf,2}(X{(t)}_{\tau },C{(t)}_{\tau },H(t-1),\text{M}(\text{t}-1),{\mu }_1,{\mu }_2)\text{for}k=2;\end{array}$$

and for k =3,

$$[1-Pr(bf(t)=1\mid {\mu }_1,{\mu }_2,{\mathrm{\Omega }}_t)][1-Pr(bf(t)=2\mid {\mu }_1,{\mu }_2,{\mathrm{\Omega }}_t)]·F_{bf,3}(X(t),C(t),H(t-1),M(t-1),{\mu }_1,{\mu }_2),$$

where each of these binary events is modeled as

$$\begin{array}{l}{F}_{bf,k}(X{(t)}_{\tau },C{(t)}_{\tau },H(t-1),M(t-1),{\mu }_{\mathbf{1}},{\mu }_{\mathbf{2}})=\\ \text{Logit}[{\beta }_{bf,k}^{\prime }{X}_{bf}(t)+{\alpha }_{bf,k}^{\prime }{C}_{bk}(t)+{\gamma }_{bf,k}^{\prime }H(t-1)+{\varphi }_{bf,k}^{\prime }{M}_{bf}(t-1)+{\rho }_{\rho f,k,1}{\mu }_1+{\rho }_{bf,k,2}{\mu }_2].\end{array}$$

The choice of working away from home can impose great constraints on decisions about breast-feeding and, in addition, a recent preventive care can have an impact on the breast-feeding choices. To take into account these constraints, we include the lagged choices of working away and preventive care (M) as an explanatory variable in the breast-feeding equations.

Birth Outcomes

After we discretize the measures of birth weight and length, we use the conditional density/hazard rate approach to specify the probability of observing certain birth outcomes. For example, the probability for a newborn’s weight or length to reach a higher discrete level of value conditional on achieving a given level is given by

$$Pr[bo>q\mid bo\ge q]=\text{Logit}[F_{bo}[X_{bo}(-1),C_{bo}(-1),V(g,\tau ),{\mu }_1,{\mu }_2]+F_{bo,b}(q)],$$ (16)

where bo=bw or bl, and the baseline hazard is defined as

$$F_{bo,b}(q)=\sum _{n=1}^4\{{\theta }_{bo,n}{[log(Q-q)]}^n\}.$$ (17)

The covariate component of the hazard rate specification for each birth outcome is given by

$$F_{bo}[•]={\beta }_{bo}^{\prime }{X}_{bo}(-1)+{\alpha }_{bo}^{\prime }{C}_{bo}(-1)+{\varphi }_{bo}^{\prime }V(g,t)+{\rho }_{bo,\mathbf{1}}{\mu }_{\mathbf{1}}+{\rho }_{bo,\mathbf{2}}{\mu }_{\mathbf{2}}+\text{interactions}\text{and}\text{higher}\text{order}\text{terms},$$

for bo=bw, bl.

Weight gain and length increases

We use a similar model for the discretized child outcomes length and weight measured at each of the 12 post-birth surveys. In particular, we model:

$$Pr[co(t)>r\mid co(t)\ge r]=\text{Logit}[F_{co}[X(t-1),C(t-1);M(t-1),H(t-1){\mu }_1,{\mu }_2]+F_{co,b}(r)]$$

where co=cw(child weight) or ch (child length), and the baseline hazard is defined as

$$F_{co,b}(r)=\sum _{n=1}^4\{{\theta }_{co,n}[-log{(R-r)}^n]\}·\sum _{i=1}^n{X}_i{Y}_i$$

The covariate component of the hazard rate specification for each outcome is given respectively by

$$F_{cw}[•]={\beta }_{cw}^{\prime }{X}_{cw}(t-1)+{\alpha }_{cw}^{\prime }{C}_{cw}(t-1)+{\gamma }_{cw}^{\prime }{H}_{cw}(t-1)+{\varphi }_{cw}^{\prime }{M}_{cw}(t-1)+{\rho }_{cw,1}{\mu }_1+{\rho }_{cw,2}{\mu }_2+\text{interactions}\text{and}\text{higher}\text{order}\text{terms}.$$

and

$$F_{ch}[•]={\beta }_{ch}^{\prime }{X}_{ch}(t-1)+{\alpha }_{ch}^{\prime }{C}_{ch}(t-1)+{\gamma }_{ch}^{\prime }{H}_{ch}(t-1)+{\varphi }_{ch}^{\prime }{M}_{ch}(t-1)+{\rho }_{ch,1}{\mu }_1+{\rho }_{ch,2}{\mu }_2+\text{interactions}\text{and}\text{higher}\text{order}\text{terms}.$$

Maternal labor supply (wk)

We specify the probability of mother being working away from home,

Pr[wk (t) =1| μ₁,μ₂, Ω_t] as:

$$\text{Logit}[{\beta }_{wk}^{\prime }{X}_{wk}(t)+{\alpha }_{wk}^{\prime }{C}_{wk}(t)+{\gamma }_{wk}^{\prime }{H}_{wk}(t-1)+{\varphi }_{wk}^{\prime }{M}_{wk}(t-1)+{\rho }_{wk,1}{\mu }_1+{\rho }_{wk,2}{\mu }_2].$$ (A.1)

Here, X_wk (t) contains exogenous child and family characteristics, including child age, child gender, family members, and mother’s demographic variables. The low birth weight status, lagged weight, and lagged heights are included in vector H_k(t−1).

Preventive health care (phc)

We define the preventive health care as any preventive checkup or immunization shots, Pr( phc(t) =1| μ₁, μ₂, Ω_t ),by

$$\text{Logit}[{\beta }_{\mathit{phc}}^{\prime }{X}_{\mathit{phc}}(t)+{\alpha }_{\mathit{phc}}^{\prime }{C}_{\mathit{phc}}(t)+{\gamma }_{\mathit{phc}}^{\prime }{H}_{\mathit{phc}}(t-1)+{\varphi }_{\mathit{phc}}^{\prime }{M}_{\mathit{phc}}(t-1)+{\rho }_{\mathit{phc},1}{\mu }_1+{\rho }_{\mathit{phc},2}{\mu }_2]$$ (A.2)

Given that timely immunization shots and physical checkups are important to child’s health outcomes at various stages of their lives, we have included a measure of the time interval between last preventive care and the current month in X_phc(t). This term is also interacted with the current child age so that we can capture any age trend of the impacts of the missed preventive health care treatments. To account for the fact that working mothers can increase their children’s exposure to pathogens brought from outside, we also include a term that measures whether the mother worked away from home at t−1. For women whose work information is missing, we measure this work variable with a predicted probit probability.

Diarrhea (dia)

Diarrhea can have serious consequences for young children, including death. The statistical specification used in this study allows for the identification of a number of important susceptibility and exposure inputs significantly related to the incidence of diarrhea over the first two years of the child’s life. The probability of the child contracting diarrhea at t,

Pr[dia(t) = 1| H (t − 1), M (t − 1, t), μ₁, μ₂] is given by

$$\text{Logit}[{\beta }_{\mathit{dia}}^{\prime }{X}_{\mathit{dia}}(t)+{\alpha }_{\mathit{dia}}^{\prime }{C}_{\mathit{dia}}(t)+{\gamma }_{\mathit{dia}}^{\prime }{H}_{\mathit{dia}}(t-1)+{\varphi }_{\mathit{dia}}^{\prime }{M}_{\mathit{dia}}(t-1)+{\rho }_{\mathit{dia},1}{\mu }_1+{\rho }_{\mathit{dia},2}{\mu }_2]$$ (A.3)

where M_dia(t−1,t) is a vector that comprises a set of endogenous health inputs, including current breast-feeding choice, and lagged values of preventive health care and maternal employment.¹⁵ We hypothesize that these health inputs are results of parents’ compensatory behaviors. In particular, parents respond to adverse birth outcomes or other health outcomes they have observed in past periods by modifying the time spent at home (proxied by the choice of working away from home), and preventive health measures. Note that we make an exception about the duration of breast-feeding as its contemporaneous value is used instead of lagged value per discussion presented in Section 2.

Febrile respiratory infection (FRI)

FRI is an important negative health outcome in developing countries. Like diarrhea, this illness is a major cause of infant mortality. However, not only FRI might be caused by different pathogens but also the two diseases have different effects on child development. The probability of any incidence of FRI at t, Pr[fri (t) = 1| H (t − 1), M (t − 1,t), μ₁, μ₂], is given by

$$\text{Logit}[{\beta }_{\mathit{fri}}^{\prime }{X}_{\mathit{fri}}(t)+{\alpha }_{\mathit{fri}}^{\prime }{C}_{\mathit{fri}}(t)+{\gamma }_{\mathit{fri}}^{\prime }{H}_{\mathit{fri}}(t-1)+{\varphi }_{\mathit{fri}}^{\prime }{M}_{\mathit{fri}}(t-1)+{\rho }_{\mathit{fri},1}{\mu }_1+{\rho }_{\mathit{fri},2}{\mu }_2]$$ (A.4)

Similar to the specification for the incidence probability of diarrhea, M_fri includes contemporaneous breast-feeding choice, and the lagged values of preventive health care, and maternal employment and their interaction terms.

Appendix B—Included here only for Reviewers; this should appear on the web for readers

Point Estimates and Standard Errors

B.1.

Any Prenatal Visit Equation

	Coeff.	S.E.
intercept	−3.2038	0.5187
waiting time in hospital	0.1159	0.1504
waiting time in clinic	−0.0743	0.0521
mean cost of hospital visit	−0.3217	0.3085
mean cost of clinic visit	−0.0529	0.1156
doctor/patient ratio hospital	0.0083	0.0046
doctor/patient ratio clinic	0.3672	0.5008
doctor/staff ratio hospital	0.1449	0.1484
trad. caregiver part-time pct	−0.2352	0.1274
# male in HH age 13+	−0.0178	0.0373
# female in HH age 13+	0.0229	0.0402
extended family	0.0716	0.0772
# children b/n 0–6 in HH	−0.1531	0.0276
spouse present	0.3359	0.1255
speaking cebu dialect	−0.1653	0.1007
catholic	−0.0281	0.1350
other HH members income	0.1018	0.1783
HH wealth	0.0010	0.0006
mother hlth insurance	0.1171	0.0883
mother highest grade	0.0586	0.0096
mother age	0.0049	0.0509
cereal price	−1.6464	1.2632
corn price	0.8583	0.8432
urban	−0.0083	0.0904
gestation month 2	0.4407	0.1508
gestation month 3	1.6294	0.1312
gestation month 4	1.8718	0.1321
gestation month 5	3.1890	0.1282
gestation month 6	3.2850	0.1393
loading on 1st order μ1	−0.8642	0.9988
loading on 2nd order μ1	2.0874	2.3189
loading on 3rd order μ1	−1.6832	1.5026

B.2.

Traditional Care Prenatal Visit Equation

	Coeff.	S.E.
intercept	1.5241	0.9593
mean wait time in hospital	0.1012	0.2831
mean waiting time in clinic	0.0096	0.0883
mean cost of hospital visit	−0.1917	0.5766
mean cost of clinic visit	−0.2181	0.2092
doctor/patient ratio hospital	0.0010	0.0082
doctor/patient ratio clinic	−1.4374	0.8820
doctor/staff ratio hospital	−0.1265	0.2697
trad. caregiver part-time pct.	0.2024	0.2259
# males in HH age 13+	−0.0170	0.0642
# females in HH age 13+	−0.0472	0.0723
extended family	−0.1108	0.1350
# children b/n 0–6 in HH	0.0744	0.0464
spouse present	0.0470	0.2343
speaking cebu dialect	0.1422	0.1895
catholic	0.4980	0.2326
other HH members income	−0.0368	0.2858
HH wealth	0.0001	0.0008
mother hlth insurance	−0.5856	0.1819
mother highest grade	−0.1697	0.0186
mother age	−0.2348	0.0939
cereal price	0.8390	2.3244
corn price	−3.2306	1.4674
urban	−0.3164	0.1566
gestation month 2	−0.2997	0.3183
gestation month 3	0.1276	0.2813
gestation month 4	−0.1697	0.2802
gestation month 5	0.0873	0.2683
gestation month 6	−0.1820	0.2772
loading on 1st order μ1	1.6184	1.7107
loading on 2nd order μ1	−2.7457	3.9830
loading on 3rd order μ1	1.6407	2.5983

B.3.

Hospital Prenatal Visit Equation

	Coeff.	S.E.
intercept	−2.6137	1.8277
mean waiting time in hospital	0.4814	0.7556
mean waiting time in clinic	−0.0678	0.1868
mean cost of hospital visit	−2.7443	1.4875
mean cost of clinic visit	1.0955	0.3729
doctor/patient ratio hospital	−0.0002	0.0195
doctor/patient ratio clinic	−3.3542	2.6624
doctor/staff ratio hospital	−1.6629	0.4870
# males in HH age 13+	−0.0618	0.1087
# females in HH age 13+	−0.0443	0.1344
extended family	0.3373	0.2460
# children b/n 0–6 in HH	−0.2349	0.0982
spouse present	−0.6769	0.3504
speaking cebu dialect	−0.2454	0.2844
catholic	0.1484	0.3249
other HH members income	−0.3396	0.3890
HH wealth	0.0009	0.0019
mother hlth insurance	−0.0520	0.2404
mother highest grade	0.1836	0.0316
mother age	0.1633	0.1782
cereal price	6.9607	4.7710
corn price	−3.5714	2.9767
urban	0.4319	0.5194
gestation month 2	−0.5921	0.5252
gestation month 3	0.4789	0.3875
gestation month 4	0.2422	0.4011
gestation month 5	0.3985	0.3864
gestation month 6	0.4878	0.4143
loading on 1st order μ1	−4.1047	3.1056
loading on 2nd order μ1	8.4240	8.0826
loading on 3rd order μ1	−5.6046	5.6789

B.4.

Birth Weight Equation

	Coeff.	S.E.
Intercept	−7.6586	0.9175
cereal price	2.3825	1.2905
corn price	−0.0363	0.7468
parity X previous baby	0.0554	0.0188
previous baby	0.3440	0.0766
mother age	0.0524	0.0648
mother height	0.0431	0.0053
dry season at interview	0.0327	0.0794
wet season at interview	0.0092	0.0581
sex of child	0.0741	0.0511
urban	0.2321	0.0630
clinic care	0.2445	0.1639
traditional care	0.4197	0.3165
hospital care	0.1705	0.1455
clinic care X month of visit	−0.0424	0.0339
trad care X month of visit	−0.0496	0.0685
hosp care X month of visit	−0.0153	0.0297
loading on 1st order μ1	−3.6243	0.9288
loading on 2nd order μ1	6.1173	2.0610
loading on 1st order μ1	−4.3450	1.2893
loading on 2nd order μ2	−0.9869	0.6364
loading on 3rd order μ2	0.7428	0.8940
loading on 3rd order μ2	0.5330	0.4387
1st order baseline hazard	0.1054	0.0703
2nd order baseline hazard	2.4697	0.8052
3rd order baseline hazard	−5.0244	2.0832
4th order baseline hazard	2.4647	1.3635

B.5.

Birth Height Equation

	Coeff.	S.E.
intercept	−9.4864	0.9582
cereal price	0.4248	1.2476
corn price	2.8800	0.7852
parity X previous live baby	0.0082	0.0184
previous live baby	0.1328	0.0781
mother age	0.1202	0.0657
mother height	0.0534	0.0055
dry season at interview	−0.0974	0.0772
wet season at interview	−0.0137	0.0615
sex of child	0.2148	0.0529
urban	0.2604	0.0614
clinic care	0.1060	0.1673
traditional care	0.2479	0.1347
hospital care	0.1007	0.3264
clinic care X month of visit	−0.0177	0.0337
trad care X month of visit	−0.0466	0.0274
hosp care X month of visit	−0.0156	0.0694
loading on 1st order μ1	−3.0574	0.9447
loading on 2nd order μ1	5.2561	2.1210
loading on 3rd order μ1	−3.9619	1.3407
loading on 1st order μ2	4.6884	0.8212
loading on 2nd order μ2	−9.7967	2.0925
loading on 3rd order μ2	4.8447	1.3621
1st order baseline hazard	−0.3764	06290
2nd order baseline hazard	1.2144	0.8790
3rd order baseline hazard	0.6042	04319
4th order baseline hazard	0.0991	0.0693

B.6.

Any Breast-feeding Equation

	Coeff.	S.E.
intercept	−5.2773	10.0890
child age	−0.2542	0.0444
child age squared	0.0032	0.0012
# children 0–6	0.0009	0.0283
density of community	0.0061	0.0021
# females in HH age13+	−0.0490	0.0376
# males in HH age 13+	0.1026	0.0345
mother height	−2.0684	0.6461
mother highest grade	−0.0861	0.0098
mother age	0.0160	0.0054
previous live baby	0.3310	0.0891
sex of child	−0.1112	0.0594
urban	−0.2005	0.0893
cereal price	−0.1269	0.0691
lowest formula price	0.1072	0.0539
other HH members inc	−0.0741	0.0947
extended family	−0.0832	0.0600
spouse present	0.0901	0.0845
dry season at interview	0.0437	0.0675
wet season at interview	0.1827	0.0606
distance to City Hall	−0.1323	0.0984
prevailing unskilled wage rate	−0.0964	0.0895
prevailing female wage rate	−0.1016	0.2773
travel time to nearest health facilities	0.0027	0.0027
average waiting time in clinics	0.0395	0.0323
low birth weight	0.1507	0.0919
log(lagged weight)	0.3331	1.1571
log(lagged weight)2	0.6294	0.3370
log(lagged height)	11.6603	11.4542
log(lagged height)2	−3.5877	3.0840
birth day interview	−5.8677	0.2565
first followup interview	−0.6247	0.2455
lagged working away	−0.1347	0.0691
lagged preventive health care	−0.0743	0.1133
lagged diarrhea	−0.1672	0.0746
lagged FRI	−0.0929	0.0826
loading on 1st order μ1	3.2509	0.9781
loading on 2nd order μ1	−6.2673	2.2127
loading on 3rd order μ1	4.2331	1.4235
loading on 1st order μ2	0.1712	0.8704
loading on 2nd order μ2	2.4846	2.2970
loading on 3rd order μ2	−2.4903	1.4973

B.7.

Exclusive Breast-Feeding Equation

	Coeff.	S.E.
intercept	−3.8953	22.2504
child age	1.9009	0.7065
child age squared	−0.3291	0.0754
# children 0–6	0.0396	0.0483
density of community	0.0071	0.0035
# females in HH age 13+	−0.0630	0.0694
# male in HH age 13+	0.0692	0.0617
mother height	0.4628	0.9317
mother highest grade	−0.1671	0.0180
mother age	−0.0518	0.0090
previous live baby	0.3424	0.1587
sex of child	−0.3095	0.0914
urban	−0.9695	0.1258
cereal price	0.0076	0.1595
lowest formula price	0.1377	0.0655
other HH members inc	0.0799	0.2220
extended family	−0.0486	0.1070
spouse present	0.4287	0.1748
dry season at interview	−0.0970	0.1201
wet season at interview	−0.0984	0.1063
distance to City Hall	−0.1094	0.1464
prevailing unskilled wage rate	0.2747	0.1361
prevailing female wage rate	0.2008	0.4299
travel time to nearest health facility	0.0075	0.0033
average waiting time in clinics	0.1320	0.0520
low birth weight	0.1216	0.1546
log(lagged weight)	−0.0592	2.1120
log(lagged weight)2	0.3337	0.7892
log(lagged height)	−4.3825	27.5899
log(lagged height)2	1.5546	8.3203
first followup interview	1.6172	0.6888
lagged working away	0.1680	0.2515
lagged preventive health care	−0.1130	0.2409
lagged diarrhea	−0.1766	0.3163
lagged FRI	−0.1421	0.2331
loading on 1st order μ1	0.3075	1.6054
loading on 2nd order μ1	1.5179	3.5433
loading on 3rd order μ1	−1.0359	2.2520
loading on 1st order μ2	1.5960	1.9769
loading on 2nd order μ2	17.6457	3.9170
loading on 3rd order μ2	−17.4876	2.2798

B.8.

Preventive Care Equation

	Coeff.	S.E.
intercept	−24.9318	8.5382
child age	−0.1065	0.0420
child age squared	−0.0019	0.0014
# children 0–6	−0.0732	0.0255
density of community	−0.0048	0.0017
# females in HH age 13+	0.0538	0.0308
# males in HH age 13+	−0.0047	0.0290
mother height	0.5710	0.5245
mother highest grade	0.0730	0.0080
mother age	0.0007	0.0048
previous live baby	−0.0625	0.0748
sex of child	−0.1419	0.0504
urban	0.5736	0.0909
cereal price	−0.0462	0.0811
lowest formula price	−0.0916	0.0487
other HH members inc	0.0559	0.0772
extended family	−0.1032	0.0562
spouse present	−0.0956	0.0787
dry season at interview	0.2232	0.0663
wet season at interview	0.1846	0.0599
distance to City Hall	−0.0946	0.1002
prevailing unskilled wage rate	−0.0326	0.0858
prevailing female wage rate	1.1876	0.2459
travel time to nearest health facility	−0.0040	0.0028
average waiting time in clinics	−0.3153	0.0351
low birth weight	0.1294	0.0786
log(lagged weight)	3.0252	1.0818
log(lagged weight)2	−0.5781	0.3184
log(lagged height)	21.1641	10.1088
log(lagged height)2	−5.5282	2.7977
lagged working away	−0.1341	0.0735
lagged preventive health care	0.4072	0.0908
lagged diarrhea	−0.1150	0.0737
lagged FRI	0.0789	0.0730
duration since last care	−0.4308	0.0595
age X duration	0.0304	0.0063
loading on 1st order μ1	−0.2065	0.8073
loading on 2nd order μ1	1.1896	1.9239
loading on 3rd order μ1	−1.0378	1.2929
loading on 1st order μ2	−0.4647	0.7757
loading on 2nd order μ2	0.0222	1.9479
loading on 3rd order μ2	0.3845	1.2483

B.9.

Working Away From Home Equation

	Coeff.	S.E.
intercept	−0.0518	7.9031
child age	0.1356	0.0358
child age squared	−0.0024	0.0010
# children 0–6	0.0329	0.0193
density of community	−0.0016	0.0013
# females in HH age 13+	0.0350	0.0246
# males in HH age 13+	−0.0140	0.0226
mother height	0.3132	0.4147
mother highest grade	0.0262	0.0058
mother age	0.0342	0.0034
previous live baby	−0.1239	0.0614
sex of child	0.0846	0.0394
urban	0.1551	0.0605
cereal price	−0.0448	0.0538
lowest formula price	0.0449	0.0381
other HH members inc	−0.1468	0.0400
extended family	0.1286	0.0435
spouse present	−0.0194	0.0580
dry season at interview	−0.0231	0.0535
wet season at interview	−0.0339	0.0485
distance to City Hall	0.0732	0.0608
prevailing unskilled wage rate	0.0976	0.0534
prevailing female wage rate	−0.0527	0.1706
travel time to nearest health facilities	0.0068	0.0017
average waiting time in clinics	−0.0203	0.0214
low birth weight	−0.1707	0.0603
log(lagged weight)	−0.5598	1.0817
log(lagged weight)2	−0.1594	0.3078
log(lagged height)	−1.4161	9.2069
log(lagged height)2	0.0434	2.4674
lagged working away	3.6719	0.0348
lagged preventive health care	0.1142	0.0803
lagged diarrhea	0.0720	0.0599
lagged FRI	0.0173	0.0604
loading on 1st order μ1	−1.4538	0.5712
loading on 2nd order μ1	0.6137	1.3208
loading on 3rd order μ1	0.1711	0.8705
loading on 1st order μ2	−3.2073	0.5708
loading on 2nd order μ2	3.7475	1.4826
loading on 3rd order μ2	−1.0438	0.9571

B.10.

Diarrhea Equation

	Coeff.	S.E.
intercept	−12.2108	7.1138
child age	0.0033	0.0284
child age squared	−0.0019	0.0008
# children 0–6	0.0122	0.0145
density of community	0.0054	0.0008
# females in HH age 13+	−0.0762	0.0187
# males in HH age 13+	0.0298	0.0169
mother height	−1.8312	0.3298
mother highest grade	−0.0414	0.0052
mother age	−0.0071	0.0026
previous live baby	−0.0257	0.0446
sex of child	0.0842	0.0311
urban	0.0768	0.0363
cereal price	0.1012	0.0426
lowest formula price	−0.1633	0.0320
other HH members inc	−0.0464	0.0538
extended family	0.0072	0.0328
spouse present	−0.0343	0.0479
dry season at interview	−0.0898	0.0458
wet season at interview	0.0948	0.0399
low birth weight	0.0311	0.0445
log(lagged weight)	1.0214	1.0721
log(lagged weight)2	−0.0061	0.2839
log(lagged height)	12.6017	8.3219
log(lagged height)2	−3.2086	2.1758
age X any BF	0.0171	0.0063
age X exclusive BF	0.1214	0.1118
exclusive BF	−0.6005	0.3070
any BF	−0.4164	0.0865
lagged working away	−0.0255	0.0380
lagged preventive health care	−0.0052	0.0601
loading on 1st order μ1	0.0940	0.4875
loading on 2nd order μ1	0.6789	1.0911
loading on 3rd order μ1	−0.2235	0.7162
loading on 1st order μ2	1.8284	0.4428
loading on 2nd order μ2	−4.8991	1.1018
loading on 3rd order μ2	3.2175	0.7091

B.11.

Febrile Respiratory Illness Equation

	Coeff.	S.E.
intercept	−3.8651	6.7524
child age	−0.0018	0.0298
child age squared	−0.0007	0.0008
# children 0–6	0.0304	0.0171
density of community	0.0001	0.0009
# females iin HH age 13+	−0.0319	0.0219
# males in HH age 13+	0.0412	0.0197
mother height	−0.6480	0.3625
mother highest grade	−0.0379	0.0057
mother age	0.0065	0.0030
previous live baby	0.0290	0.0529
sex of child	0.0739	0.0353
urban	0.1427	0.0417
cereal price	0.0998	0.0458
lowest formula price	0.0244	0.0323
other HH members inc	0.0305	0.0532
extended family	0.0547	0.0373
spouse present	−0.0112	0.0539
dry season at interview	−0.0261	0.0476
wet season at interview	−0.0287	0.0422
low birth weight	0.0038	0.0495
log(lagged weight)	−1.0488	0.9229
log(lagged weight)2	0.2583	0.2528
log(lagged height)	2.7776	7.7935
log(lagged height)2	−0.4150	2.0671
age X any BF	0.0013	0.0070
age X exclusive BF	0.1443	0.0475
exclusive BF	−0.4763	0.1878
any BF	−0.1474	0.1048
lagged working away	0.0744	0.0411
lagged preventive health care	−0.0412	0.0651
loading on 1st order μ1	−0.3592	0.5837
loading on 2nd order μ1	1.7963	1.2871
loading on 3rd order μ1	−1.1841	0.8234
loading on 1st order μ2	2.0884	0.5013
loading on 2nd order μ2	−6.0085	1.2724
loading on 3rd order μ2	3.9608	0.8249

B.12.

Caloric Intake Equation

	Coeff.	S.E.
intercept	−15.4131	1.6463
child age	0.1074	0.0159
child age squared	−0.0035	0.0005
# children 0–6	−0.0238	0.0125
density of community	0.0037	0.0009
# females in HH age 13+	0.0244	0.0168
# males in HH age 13+	−0.0389	0.0157
mother height	−0.2600	0.2748
mother highest grade	0.0975	0.0044
mother age	0.0242	0.0022
previous live baby	−0.3132	0.0421
sex of child	0.2001	0.0244
urban	0.3931	0.0335
cereal price	−0.0911	0.0318
lowest formula price	−0.0594	0.0189
other HH members inc	0.0325	0.0431
extended family	0.0084	0.0257
spouse present	−0.0703	0.0414
dry season at interview	−0.0546	0.0307
wet season at interview	−0.0290	0.0263
distance to City Hall	0.1564	0.0415
prevailing unskilled wage rate	0.0989	0.0425
prevailing female wage rate	0.2985	0.1206
travel time to nearest health facility	−0.0085	0.0010
average waiting time in clinics	−0.0459	0.0139
low birth weight	0.0113	0.0389
log(lagged weight)	0.3642	0.4872
log(lagged weight)2	−0.3029	0.1463
log(lagged height)	30.4222	3.9453
log(lagged height)2	−7.6010	1.0891
any bf	−15.4131	1.6463
lagged working away	−0.0050	0.0321
lagged preventive care	−0.0155	0.0410
lagged diarrhea	0.1337	0.0347
lagged FRI	0.0851	0.0354
1st order baseline hazard	4.0612	0.5437
2nd order baseline hazard	−6.8270	0.9870
3rd order baseline hazard	5.2690	0.6161
4th order baseline hazard	−1.2166	0.1257
loading on 1st order μ1	−0.9738	0.4005
loading on 2nd order μ1	0.4064	0.9167
loading on 3rd order μ1	0.5128	0.5992
loading on 1st order μ2	−3.3163	0.2960
loading on 2nd order μ2	−7.4179	0.6962
loading on 3rd order μ2	9.1297	0.4432

B.13.

Weight Equation

	Coeff.	S.E.
intercept	−11.3768	0.6572
child age	−0.6600	0.0187
child age squared	0.0129	0.0005
# children 0–6	−0.1073	0.0197
density of community	−0.0069	0.0011
# females in HH age 13+	0.0897	0.0240
# males in HH age 13+	−0.1288	0.0231
mother height	10.4594	0.3977
mother highest grade	0.1315	0.0065
mother age	0.0122	0.0035
previous live baby	−0.3713	0.0632
sex of child	1.1325	0.0402
urban	0.0729	0.0481
cereal price	−0.0770	0.0259
lowest formula price	0.0143	0.0181
other HH members inc	−0.0638	0.0428
extended family	0.0797	0.0242
spouse present	−0.0736	0.0366
dry season at interview	0.0008	0.0286
wet season at interview	−0.1429	0.0239
low birth weight	−0.5494	0.0625
log(lagged weight)	−11.6773	0.2823
log(lagged weight)2	5.6933	0.0930
exclusive BF	0.4855	0.0516
any BF	1.2055	0.1203
log(lagged calorie/gram)	−0.1273	0.0277
log(lagged calorie/gram)^2	0.3110	0.0386
lagged working away	0.0095	0.0302
lagged preventive care	−0.0329	0.0317
lagged diarrhea	−0.5507	0.7903
lagged FRI	6.5557	4.0048
log(lagged calorie/g) X any BF	−2.6040	0.3630
age X any BF	−0.1227	0.0093
age X any BF X log(lagged cal/g)	0.4290	0.0337
log(lagged cal/g) X 0–6 months	−2.6736	0.2643
log(lagged cal/g) X 7–12 months	−2.2087	0.1563
1st order baseline hazard	0.6845	0.3005
2nd order baseline hazard	5.5748	0.5943
3rd order baseline hazard	−4.4990	0.3919
4th order baseline hazard	1.2283	0.0835
loading on 1st order μ1	−16.3379	0.5280
loading on 2nd order μ1	28.9373	1.2071
loading on 3rd order μ1	−20.3668	0.7665
loading on 1st order μ2	0.1113	0.48138
loading on 2nd order μ2	2.9761	1.20737
loading on 3rd order μ2	−3.1704	0.78399

B.14.

Height Equation

	Coeff.	S.E.
intercept	62.4437	2.3480
child age	−1.0259	0.0175
child age squared	0.0168	0.0005
# children 0–6	−0.1183	0.0129
density of community	−0.0020	0.0007
# females in HH age 13+	0.0600	0.0153
# males in HH age 13+	−0.0645	0.0151
mother height	8.8000	0.2695
mother highest grade	0.0829	0.0043
mother age	0.0097	0.0023
previous live baby	−0.2132	0.0416
sex of child	0.5697	0.0255
urban	−0.0192	0.0309
cereal price	−0.0286	0.0240
lowest formula price	−0.0001	0.0150
other HH members inc	0.0065	0.0385
extended family	0.0935	0.0211
spouse present	0.0112	0.0303
dry season at interview	0.0306	0.0232
wet season at interview	−0.1335	0.0214
low birth weight	−0.2706	0.0382
log(lagged height)	−108.5019	2.6205
log(lagged height)2	37.8897	0.7503
lagged exclusive BF	0.5764	0.0440
lagged any BF	0.0711	0.0752
log(lagged calorie/g)	−0.0897	0.0256
log(lagged calorie/g)^2	0.1405	0.0309
lagged working away	−0.1064	0.0271
lagged preventive care	−0.0244	0.0273
lagged diarrhea	2.1423	0.9651
lagged FRI	2.2280	4.1186
log(lagged calorie/g) X lagged any BF	0.0323	1.1646
age X any laggedd BF	0.0102	0.0057
age X any BF X lagged(lagged cal/g)	0.0421	0.0955
log(lagged cal/g) X age 0–6 months	−4.3009	0.7127
log(lagged cal/g) X age 7–12 months	−4.5082	0.5007
1st order baseline hazard	1.1848	0.2918
2nd order baseline hazard	3.0667	0.5802
3rd order baseline hazard	−2.5627	0.3817
4th order baseline hazard	0.7342	0.0810
loading on 1st order μ1	−7.7425	0.3829
loading on 2nd order μ1	14.2328	0.8648
loading on 3rd order μ1	−10.3500	0.5542
loading on 1st order μ2	6.5951	0.3374
loading on 2nd order μ2	−13.5458	0.8419
loading on 3rd order μ2	6.3459	0.5399

B.15.

Parameters Defining Probabilities of Child-Specific Heterogeneity Factor

Support Point	Coefficient	Standard Error	Implied Probability
0	0.5311	0.0302	0.1636
1/3	−0.6775	0.0198	0.2610
2/3	−0.6999	0.0197	0.2779
1	-	-	0.2975

B.16.

Parameters Defining Probabilities of Mother-Specific Heterogeneity Factor

Support Point	Coefficient	Standard Error	Implied Probability
0	−0.7674	0.0586	0.0706
1/6	−1.0166	0.0781	0.1192
1/3	1.1364	0.1293	0.1463
1/2	−1.4625	0.1047	0.2248
2/3	4.8695	0.1075	0.2126
5/6	1.1509	0.1117	0.1496
1	-	-	0.0769