Abstract
It is now widely accepted that instrumental actions can be either goal-directed or habitual; whereas the former are rapidly acquire and regulated by their outcome, the latter are reflexive, elicited by antecedent stimuli rather than their consequences. Model-based reinforcement learning (RL) provides an elegant description of goal-directed action. Through exposure to states, actions and rewards, the agent rapidly constructs a model of the world and can choose an appropriate action based on quite abstract changes in environmental and evaluative demands. This model is powerful but has a problem explaining the development of habitual actions. To account for habits, theorists have argued that another action controller is required, called model-free RL, that does not form a model of the world but rather caches action values within states allowing a state to select an action based on its reward history rather than its consequences. Nevertheless, there are persistent problems with important predictions from the model; most notably the failure of model-free RL correctly to predict the insensitivity of habitual actions to changes in the action-reward contingency. Here, we suggest that introducing model-free RL in instrumental conditioning is unnecessary and demonstrate that reconceptualizing habits as action sequences allows model-based RL to be applied to both goal-directed and habitual actions in a manner consistent with what real animals do. This approach has significant implications for the way habits are currently investigated and generates new experimental predictions.
1. The problem with habits
There is now considerable evidence from studies of instrumental conditioning in rats and humans that the performance of reward-related actions reflects the interaction of two learning processes, one controlling the acquisition of goal-directed actions, and the other of habits (Balleine & O’Doherty, 2010; Dickinson, 1994). This evidence suggests that, in the case of goal-directed actions, action selection is governed by encoding the association between the action and its consequences or outcome. In contrast, the performance of habitual actions depends on forming an association between an action and antecedent stimuli, rather than its consequences. As a consequence, being stimulus bound, habitual actions are relatively inflexible or reflexive and are not immediately influenced by manipulations involving the outcome. They differ from goal-directed actions, therefore, in two ways: (i) in their sensitivity to changes in the value of the outcome (Adams, 1982); and (ii) in their sensitivity to changes in the causal relationship between the action and outcome delivery (Dickinson, Squire, Varga, & Smith, 1998).
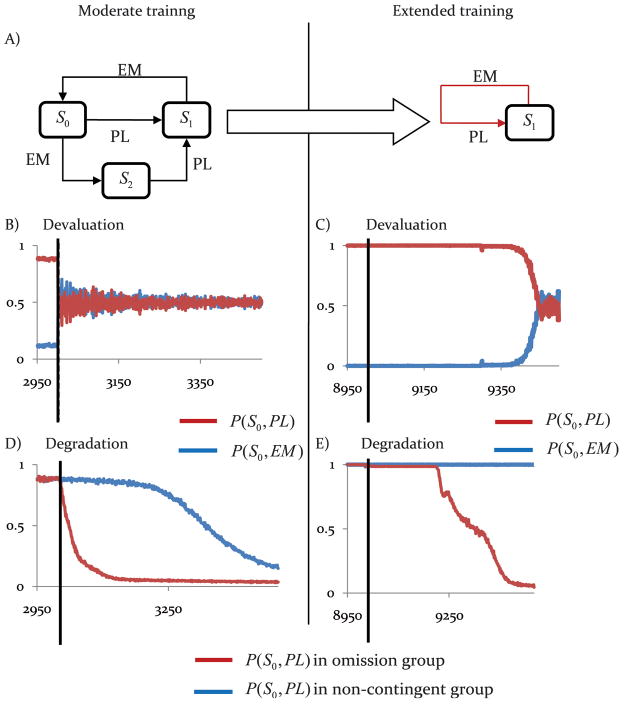
Although many replications of these effects exist in the literature, we describe, for illustration, data from a recent study in which we were able to observe both effects in the same animals in the same experiment comparing moderately trained and overtrained actions for their sensitivity to devaluation, induced by outcome-specific satiety, and contingency degradation, induced by the imposition of an omission schedule in rats. These data are presented in Figure 1 (see caption for details). Rats were trained to press a lever for sucrose and, after the satiety treatment, given a devaluation test (Figure 1A). After retraining, they were given the contingency degradation test (Figure 1B). In the first test, moderately trained rats showed a reinforcer devaluation effect; those sated on the sucrose outcome reduced performance on the lever relative to those sated on another food. In contrast, groups of overtrained rats did not differ in the test. In the second test, rats exposed to the omission contingency were able to suppress the previously trained lever press response to get sucrose but only if moderately trained. The performance of overtrained rats did not differ from the yoked, non-contingent controls. These data confirm, therefore, the general insensitivity of habitual actions to changes in both outcome value and the action-outcome contingency.
Figure 1.
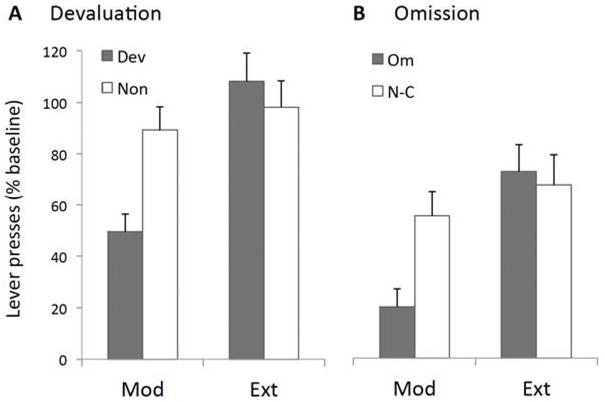
Four groups of rats (n=8) were trained to lever press for a 20% sucrose solution on random-interval schedules (RI1, RI15, RI30, RI60) with moderately trained rats allowed to earn 120 sucrose deliveries and overtrained rats 360 sugar deliveries (the latter involving an additional 8 sessions of RI60 training with 30 sucrose deliveries per session). (A) For the devaluation assessment, half of each group was then sated either on the sucrose or on their maintenance chow before a 5-min extinction test was conducted on the levers. As shown in the figure (panel A), moderately trained rats showed an reinforcer devaluation effect; those sated on the sucrose outcome reduced performance on the lever relative to those sated on the chow. In contrast, groups of overtrained rats did not differ in the test. Statistically we found a training x devaluation interaction, F(1,28)=7.13, p<0.05, and a significant devaluation effect in the moderately trained, F(1,28)=9.1, p<0.05 but not in the overtrained condition (F<1). (B) For the contingency assessment, after devaluation all rats received a single session of retraining for 30 sucrose deliveries before the moderately trained and overtrained rats were randomly assigned to either an omission group or a yoked, non-contingent control group. During the contingency test the sucrose outcome was no longer delivered contingent on lever pressing and was instead delivered on a fixed time 10 sec schedule. For rats in the omission groups, responses on the lever delayed the sucrose delivery by 10 sec. Rats in the yoked groups received the sucrose at the same time as the omission group except there was no response contingency in place. As is clear from the figure (panel B), rats exposed to the omission contingency in the moderately trained group suppressed lever press performance relative to the non-contingent control whereas those in the overtrained groups did not. Statistically, there was a training x degradation interaction, F(1,28)=5.1, p<0.05, and a significant degradation effect in the moderately trained, F(1,28)=7.8, p<0.05, but not in the overtrained condition (F<1).
The neural bases of goal-directed and habitual actions have also received considerable attention. Based on the results of a number of studies, it appears that, whereas the acquisition of goal-directed actions is controlled by a circuit involving medial prefrontal cortex and dorsomedial striatum (or caudate nucleus), habitual actions involve connections between sensory-motor cortices and dorsolateral striatum (or putamen) (Balleine & O’Doherty, 2010; Balleine, Delgado, & Hikosaka, 2007). Importantly, these two forms of action control have been argued to be at least partly competitive; at the level of the striatum, lesions or pharmacological manipulations aimed at blocking activity in dorsomedial striatum (DMS) render goal-directed actions habitual whereas blocking activity in dorsolateral striatum (DLS) renders otherwise habitual actions goal-directed by the measures described above (Yin, Knowlton, & Balleine, 2005, 2006). In addition, there is clear evidence for the involvement of a number of neuromodulators associated with these networks, particularly the input from dopamine neurons in the substantia nigra pars compacta to DLS which has been found to play an essential role in learning-related plasticity in the dorsolateral region and, indeed, in habits (Faure, Haberland, Condé, & El Massioui, 2005; Reynolds, Hyland, & Wickens, 2001). Generally, therefore, although there is tremendous complexity in the circuitry and in the necessary conditions for plasticity associated with the goal-directed and habit learning processes, they appear to depend on distinct, parallel cortico-basal ganglia networks that likely constitute functional loops connecting cortex, striatum and midbrain regions with feedback to the cortex via midline thalamus (Alexander & Crutcher, 1990; Kelly & Strick, 2004).
The functional specificity of these anatomical loops has provided fertile ground for computational models of action control (Frank & O’Reilly, 2006; O’Reilly, Herd, & Pauli, 2010). Given the functional complexity of the circuitry involving dorsal striatum, a key issue has been how well these computational models capture the difference between goal-directed and habitual actions. Perhaps the most influential approach has come from recent developments in a sub-field of computational theories collectively known as reinforcement learning (RL) (Sutton & Barto, 1998). The core feature of such RL models is that, in order to choose optimally between different actions, an agent needs to maintain internal representations of the expected reward available on each action and then subsequently choose the action with the highest expected value. Importantly, two forms of RL have been argued to be necessary accurately to model goal-directed and habitual actions (Daw, Niv, & Dayan, 2005), known generally as ‘model-based’ and ‘model-free’ RL, respectively (Daw et al., 2005; Rangel, Camerer, & Montague, 2008; Redish, Jensen, & Johnson, 2008). The essential difference between these forms of RL lies in how they compute the values of actions. As its name implies, model-based RL depends on developing a model of the world from which values for different actions are worked out on-line by taking into account knowledge about the rewards available in each state of the world in which an animal finds itself, and the transition probabilities between those states. It then works iteratively across states to establish the value of each available action option, much as a chess player might work out which chess move to make by thinking through the consequences of various possible moves. On this view, the performance of an action depends both on its relationship to the final (what might be called the ‘goal’) state and the value of that state. As such, model-based RL can be applied to goal-directed actions in a relatively straightforward manner and, indeed, this model has been applied to prefrontal cortical control of decision-making and executive functions generally (Daw et al, 2005).
In contrast, model-free RL does not form a model of the world but rather caches action values within states, allowing an agent to select an action based on its reward history rather than its consequences. According to the model-free RL approach, action selection involves two interacting components: one that learns to predict reward value, and another that forms a policy as to which action to select in a particular state. The goal of the model is to modify the policy stored in the actor such that over time, the action selected in a state is associated with the highest predicted reward. This is accomplished by means of a prediction error signal that computes the changes in predicted reward as the agent moves from state to state. That signal is then used (i) to update the value predictions for each state, and (ii) to update the policy in that state. If an action moves the agent to a state predicting greater reward (a positive prediction error), then the probability of choosing that action in the future is increased. Conversely, if an action moves the agent to a state predicting less reward (a negative prediction error) then the probability of choosing that action again is decreased. As such, the policy and value signal function to bring together a state-action associative process with an error correction feedback signal to acquire and shape actions, something that strongly approximates the classic stimulus-response/reinforcement theory long postulated to support habit learning in the behaviorist era (Hull, 1943; Spence, 1956). Furthermore, analogies have been drawn in several influential papers between the anatomy and connections of the basal ganglia and possible neural architectures for implementing reinforcement learning models (Montague, Dayan, & Sejnowski, 1996; O’Doherty et al., 2004). A key aspect of these suggestions is that the ventral striatum learns values, whereas the dorsal striatum acquires the policies and, indeed, both of these regions receive strong inputs from the midbrain dopamine neurons thought to mediate the critical error prediction signal (W. Schultz & Dickinson, 2000; W. Schultz, Dayan, & Montague, 1997).
Although Daw et al (Daw et al., 2005) proposed that model-free RL, such as that encapsulated in the actor-critic framework, can be applied directly and successfully to habits (and so were motivated to introduce a dual-process model of action control), on closer inspection this turns out not to be true. It is clear that the model-free approach anticipates the insensitivity of habitual actions to the effects of reinforcer devaluation. This is because the values that determine action selection are cached within the state, meaning that a policy can only be changed once feedback regarding a change in value is given. As tests of habit learning are conducted in extinction, no such feedback is provided. So far, so good. The problem for traditional RL approaches to habit, however, doesn’t lie in their application to devaluation but in their application to contingency degradation. As shown in Figure 1B, after a period of overtraining, during which a particular policy should have been very strongly established, the change in contingency – actually, in the case of omission, the reversal of the contingency – fails to induce any immediate change in lever press performance in the rats. From the perspective of the model-free RL, however, the error signal used to alter the policy should function perfectly well to modify performance; indeed, when an omission schedule is imposed at the end of a long period of overtraining, at which point any error should be at a minimum, the impact of both the negative error signal generated as a consequence of performing the habitual action (which now delays the reward) and the large positive error generated when the animal stops performing the action (which allows reward to be delivered), should be anticipated to have a correspondingly large effect on performance. As shown in Figure 1B, however, the performance of real animals fails to adjust to the change in contingency, opposing this prediction of the model.
Variants of model-free RL can be designed to address the failure of this approach to deal with habits. For example, it can be argued that long periods of exposure to the stationary situation of training, makes the update rate of values and policies slow (Dayan & Kakade, 2001; Dayan, Kakade, & Montague, 2000), rendering them rigid and reluctant to change in new environmental conditions. According to this account, contingency manipulations do not affect behavior because after overtraining, animals cannot learn new values and policies. However, since the test is conducted in extinction, in which there is no feedback provided about the change in value, this argument does cannot also explain reinforcer devaluation experiments, and habits of this kind cannot be attributed to the effect of low learning rates.
It is possible that other variants of model-free RL could be designed that account for insensitivity to both contingency degradation and reinforcer devaluation phenomena. Alternatively, perhaps the reason RL has difficulty developing a common account for both of these effects is rooted in the general equation of the representation of goal-directed and habitual actions within the model-based and model-free approach. In this paper, we are concerned with exploring this second possibility. Habits, we contend, are more complex than goal-directed actions and reflect the association of a number of, initially variably produced, actions into rapidly executed action sequences. For modeling sequences of this kind we develop a model in which we essentially preserve model-based RL and propose a new theoretical approach that accommodates both goal-directed and habitual action control within it. This model, we will show, is not only more parsimonious, it also provides a means of modeling sequences. Importantly, it also provides a model that uses the prediction error signal to construct habits in a manner that accords with the insensitivity of real animals to both reinforcer devaluation and contingency degradation. Finally, it makes several important predictions about the structure of habit learning and the performance of habitual actions generally that we believe will provide a guide to future experimentation in this area and we discuss these issues in the final section.
2. Sequence learning: From closed-loop to open-loop action control
The flexibility of goal-directed actions reflects, therefore, the need for immediate, or at least rapidly acquired, solutions to new problems and, indeed, evidence suggests that in novel environments there is a strong tendency for animals to generate behavioral variation and to resist immediately repeating prior actions or sequences of actions (Neuringer, 2004; Neuringer & Jensen, 2010). Of course, the need to explore new environments requires behavioral variation; once those solutions are found, however, exploiting the environment is best achieved through behavioral stability; i.e. by persisting with a particular behavioral response. It is important to recognize that, with persistence, actions can change their form, often quite rapidly. Errors in execution and the inter-response time are both reduced and, as a consequence, actions previously separated by extraneous movements or by long temporal intervals are more often performed together and with greater invariance (Buitrago, Ringer, Schulz, Dichgans, & Luft, 2004; Buitrago, Schulz, Dichgans, & Luft, 2004; Willingham, Nissen, & Bullemer, 1989). With continuing repetition these action elements can become linked together and run off together as sequence; i.e. they can become chunked (Graybiel, 1998; Terrace, 1991). Practice appears, therefore, to render variable, flexible, goal-directed actions into rapidly deployed, relatively invariant, components of action sequences suggesting that an important way in which the form of a goal-directed action can change as it becomes habitual is via the links that it forms with other actions to generate sequences.
Generally, sequence learning and habit formation are assessed using different behavioral tasks, and are considered to be distinct aspects of automatic behavior. However, neural evidence suggests that habit learning and action sequence learning involve similar neural circuits: thus, in the first stages of learning both sequences and goal-directed actions appear to involve the prefrontal cortex and associative striatum (Bailey & Mair, 2006, 2007; Lehéricy et al., 2005; Miyachi, Hikosaka, Miyashita, Kárádi, & Rand, 1997; Poldrack et al., 2005). However, as they become more routine in their expression, performance of both habits and action sequences involves the sensorimotor striatum (Lehéricy et al., 2005; Miyachi, Hikosaka, & Lu, 2002; Miyachi et al., 1997; Poldrack et al., 2005; Yin, Knowlton, & Balleine, 2004; Yin et al., 2006). Evidence suggests that a cortico-striatal network parallel to that implicated in goal-directed action involving sensorimotor cortices together with the DLS in rodents mediates the transition to habitual decision processes associated with stimulus-response learning (Barnes, Kubota, Hu, Jin, & Graybiel, 2005; Jog, Kubota, Connolly, Hillegaart, & Graybiel, 1999). Changes in the DLS appear to be training related (Costa, Cohen, & Nicolelis, 2004; Hernandez, Schiltz, & Kelley, 2006; Tang, Pawlak, Prokopenko, & West, 2007) and to be coupled to changes in plasticity as behavioral processes become less flexible (Costa et al., 2006; Tang et al., 2007). Correspondingly, whereas overtraining causes performance to become insensitive to reinforcer devaluation, lesions of DLS reverse this effect rendering performance once again sensitive to devaluation treatments (Yin et al., 2004). Likewise, muscimol inactivation of DLS has been found to render otherwise habitual performance sensitive to changes in the action-outcome contingency (Yin et al., 2006) and to abolish the stimulus control of action selection during discrimination learning (Balleine, Liljeholm, & Ostlund, 2009; Featherstone & McDonald, 2004, 2005). Importantly, there is recent evidence that the DLS is involved in sequence learning. For example, Jin & Costa (2010) trained rats to make a fixed number of lever presses to earn food and not only found evidence of response sequencing and chunking on this task, they also recorded neuronal activity in DLS where they found phasic changes in the activity of neurons associated with either the first and last response in a sequence. They also observed a reduction in neuronal ensemble variability in the DLS at sequence boundaries. This start/stop activity was not a function of action value or of timing.
The most important feature of sequence learning is the interdependency of actions (Shah, 2008). Through the process of sequence learning, action control becomes increasingly dependent on the history of previous actions, and independent of environmental stimuli, to the point that, given some triggering event, the whole sequence of actions is expressed as an integrated unit. Take, for example, a typical sequence learning experiment such as the serial reaction time task (SRTT) (Nissen & Bullemer, 1987). In this task a subject is required to elicit a specific action in response to a specific cue. For example, cues can be asterisks that are presented on a computer screen and the corresponding responses require the subject to press the keys that spatially match the cues’ positions that can appear in either a random or sequential order. In the ‘sequential trials’ condition, the position of the cues is repeated in a pattern such that the position of the next stimulus can be predicted given the previous one. In the ‘random trials’ condition, stimuli are presented in random order, and thus, given the previous stimuli, the next one cannot be predicted.
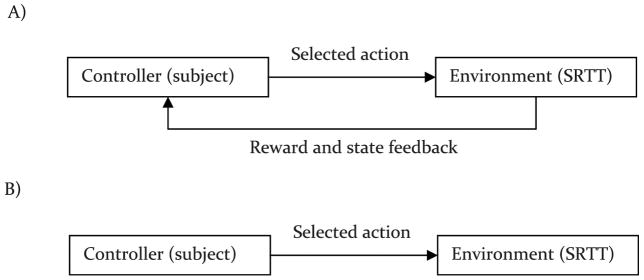
On a simple conception of the learning process in the SRTT, the subject takes an action and, if it is successful, the association between that action and the cue strengthens. Then, the subject waits for the next cue, and takes the action that has the strongest association with the cue. From a control theory point of view, this learning process can be characterized as a closed-loop control system in which, after each response, the controller (here the subject), receives a feedback signal from the environment to guide future actions. In the SRTT, after taking an action the subject receives two types of feedback: reward feedback and state feedback. Reward feedback is the reward received after each response, e.g., a specific amount of juice, and is used for learning stimulus-response associations. State feedback is given by the presentation of the next cue after the response that signals the new state of the environment, and is used by the subject to select its next action. The term ‘closed-loop’ commonly refers to the loop created by the feedback path (Figure 2A). In the absence of this feedback, the control system is called open-loop (Figure 2B) (Astrom & Murray, 2008), according to which the actions that the subject takes are not dependent on the presented cues or the received rewards.
Figure 2.
(A) A closed-loop control system. After the controller executes an action it receives cues regarding the new state of the environment and a reward. (B) An open-loop control system in which the controller does not receive feedback from the environment.
Clearly, closed-loop control is crucial for learning. Without feedback, the agent cannot learn which response is correct. It also needs state feedback from the environment because the correct response differs in each state and, as such, without knowing the current state, the agent cannot make the correct response. However, in the ‘sequential trials’ condition of the SRTT, the subject could potentially maintain a high level of performance without using the state feedback; indeed, evidence suggests that is exactly what they do in accord with open-loop control. Reaction time, defined as the time between the stimulus onset and the onset of the behavioral response, is the primary measure in the SRTT. Evidence from rodents (Schwarting, 2009), non-human primates (Desmurget & Turner, 2010; Hikosaka, Rand, Miyachi, & Miyashita, 1995; Matsuzaka, Picard, & Strick, 2007), and humans (Keele, Ivry, Mayr, Hazeltine, & Heuer, 2003; Nissen & Bullemer, 1987) suggests that, after training, reaction times are shorter in the ‘sequential trials’ than the ‘random trials’ condition. In fact, if the subject is permitted to respond during the inter-trial delay, then the reaction time can even be negative; i.e. the next action is often executed before the presentation of the next stimulus (Desmurget & Turner, 2010; Matsuzaka et al., 2007). Matsuzaka et al., (2007) reported that with increasing training, the number of these predictive responses increases up to the point that in almost all trials, the subject responds in a predictive manner without the visual cue (see also Miyashita, Rand, Miyachi, & Hikosaka, 1996), indicating that the number of predictive responses increases as a sequence becomes well learned.
The occurrence of very short or negative reaction times in ‘sequential trials’ implies that, after sufficient learning, selection of an action is mostly dependent on the history of previous actions and less dependent on the external stimuli (visual cues). In fact, even if the subject does not respond predictively before stimulus presentation, it is clear that the decision as to which action to take on the next trial is made before stimulus presentation. In a sequential button-push task, Matsumoto et al (1999) trained a monkey to execute a series of three button pushes in response to illumination of the buttons in a fixed cued sequence. After training, the monkey was tested in a condition in which the third button in the sequence was located in a position different from its position during training. They found that, during the first and sometimes the second trial, the monkeys would continue to push the third button of the learned sequence even if one of the other targets was illuminated. Similarly, Desmurget & Turner, (2010) reported when the first stimuli of a random trial follow, by coincidence, the pattern of stimuli from a learned sequence, the animal responded as if the next stimuli will be drawn from the learned sequence.
It appears, therefore, that, during the first stages of training, the subject learns the association between cues and responses. At this stage, action selection is under closed-loop control and relies on the observation of the cues. In the case of random trials, action selection remains closed-loop through the course of learning. In ‘sequential trials’, however, with further learning, action selection switches to open-loop control in which the execution of successive actions is not related to the current state of the environment, something that leads to the expression of action ‘chunks’ (Lashley, 1951; Sakai, Kitaguchi, & Hikosaka, 2003). When actions are expressed in chunks, both state identification, based on visual cues, and action evaluation appear to be bypassed. Endress and Wood (Endress & Wood, 2011), for example, note that successful sequence learning requires view-invariant movement information; i.e. rather than depending on the relation between visual cues and movement information in allocentric space, as goal-directed actions do (Willingham, 1998), sequential movements appear to depend on position-based encoding in egocentric space. Hence, chunked in this way, the performance of sequential movements is largely independent of environmental feedback allowing for very short reaction times in the open-loop mode.
Another line of evidence consistent with the cue-independency notion of habitual behavior comes from place/response learning tasks in animals (Restle, 1957; Tolman, Ritchie, & Kalish, 1946). In this type of task, rats begin each trial at the base of a T-maze surrounded by environmental cues (e.g., windows, doors) and are trained to find food at the end of one arm (e.g., the right, or east arm). Following this training period, they are given probe tests in which the maze is rotated 180° (with respect to the cues), and thus the start point will be at the opposite side of the maze. Results show that after moderate training, at the choice point the animal turns in the opposite direction to that previously learned (i.e., towards the west arm; place strategy), suggesting that action control is state-dependent and based on the environmental cues (closed-loop action control). However, after overtraining, rats switch and at the test they take the same action that they learned in the initial training (i.e. they turn right; a response strategy), indicating that overtraining renders action selection at the choice point independent of the environmental cues and the state identification process (open-loop action control) (Packard & McGaugh, 1996; Ritchie, Aeschliman, & Pierce, 1950). Similarly, in more complex mazes in which a sequence of actions is required to reach the goal, removal of environmental cues does not affect performance of a learned sequence of egocentric movements (body turns), but disrupts the use of a place strategy (Rondi-Reig et al., 2006). Learning the maze in a cue-deficient environment, but not in a cue-available environment, in which decision-making should minimally rely on state-guided action control is impaired by inactivation of DLS (Chang & Gold, 2004). Few studies have addressed functional differences between the DLS and DMS in place/response learning, however, in general it seems that the DMS is involved in goal-directed decision-making (the place strategy), and the DLS is involved in habitual responses (the response strategy) (Devan & White, 1999; Devan, McDonald, & White, 1999; Moussa, Poucet, Amalric, & Sargolini, 2011; Yin & Knowlton, 2004) (see Section 5.1 for more discussion), consistent with the role of these striatal sub-regions in instrumental conditioning and SRTT.
Based on the mentioned similarities in neural and behavior aspects of increasing automaticity in SRTT (‘sequential trials’), maze learning, and instrumental conditioning, we assume that action sequence formation is the underlying process of these modalities of habitual behavior. In order to formalize this assumption, in the next section we use RL to provide a normative approach to modeling changes in performance during action sequence learning. Next, in the results section we show that how this model applies to the different forms of habitual behavior.
3. An alternative perspective: Reinforcement learning and action sequence formation
3.1. Overview of the decision-making process
RL is a computational approach to learning different types of instrumental associations for the purpose of maximizing the accrual of appetitive outcomes and minimizing aversive ones (Sutton & Barto, 1998). In the RL framework, stimuli are referred to as “states”, and responses as “actions”. Here after we use these terms interchangeably.
A typical RL agent utilizes the following components for the purpose of learning and action selection: (i) State identification – the agent identifies its current state based on the sensory information received from its environment (e.g., visual cues); (ii) action selection – given its current state, and its knowledge about the environment, the agent evaluates possible actions then selects and executes one of them; (iii) learning – after executing an action, the agent enters a new state (e.g., receives new visual cues) and also receives a reward from the environment. Using this feedback, the agent improves its knowledge about the environment. This architecture is a closed-loop decision-making process because the action selection process is guided by the current state of the agent, which is identified based on sensory inputs received from the environment. As we discussed in the previous section, action selection in sequence learning is not guided by environmental stimuli, and so does not require a state identification process. To explain sequence learning, therefore, we need to modify this framework. In sections 3.3 and 3.4 we will introduce a mixed open-loop/closed-loop architecture for this purpose. Before turning to that issue, we shall first take a closer look at the learning process in the RL.
3.2. Average reward reinforcement learning
We denote the state of the agent at time t as st. In each state, there is a set of possible actions, and the agent selects one of them for execution, that we denote with at. The agent spends dt time steps in state st (commonly referred to as the state dwell time), and after that, by taking at, it enters a new state, st+1, and receives reward rt. The next state of the agent, the amount of reward received after taking an action, and the state dwell times, depend on the dynamics of the environment, which are determined respectively by the transition function, the reward function, and transition time function. The transition function, denoted by Psa (s′) indicates the probability of reaching state s′ upon taking action a in state s. R(s) denotes the reward function, which is the amount of reward the agent receives in state s. Finally, D(s), the transition time function, is the time spent in state s (dwell time). The time that the agent spends in a state is the sum of the time it takes the agent to make a decision, and the time it takes to new stimuli appears after executing an action.
The goal of the agent is to select actions that lead to a higher average reward per time step, and this is why this formulation of the RL is called average reward RL (Daw & Touretzky, 2002; Daw & Tourtezky, 2000; Mahadevan, 1996; Tsitsiklis & Roy, 1999). This average reward, denoted by R̄, can be defined as the total rewards obtained, divided by the total time spent for acquiring those rewards:
| (1) |
To choose an action amongst several alternatives, the agent assigns a subjective value to each state-action pair. This subjective value is denoted by Q(s, a), and represents the value of taking action a in state s (Watkins, 1989). These Q-values are learned such that an action with a higher Q-value leads to more reward in a shorter time compared to an action with a lower Q-value.
The first determinant of Q(s,a) is the immediate reward that the agent receives in s, which is R(s). Besides the immediate reward the agent receives, the value of the next state the agent enters is also important: actions through which the agent reaches a more valuable state, are more favorable. Thus, assuming that the agent reaches state s′ by taking action a, the value of the next state, V(s′), is the second determinant of Q(s, a) and is assumed to be proportional to the reward the agent gains in the future by taking its best action in the state s′. In general, for any state s, V(s) is defined as follows:
| (2) |
The final determinant of Q(s, a) is the amount of time the agent spends in the state. If the agent spends a long time in a state, then it will lose the opportunity of gaining future rewards. In fact, losing D(s) time steps in state s is equal to losing D(s)R̄ reward in the future. Given these three determinants, the value of taking an action in a state can be computed as follows:
| (3) |
Where the expectation in the last term is over s′:
| (4) |
As the above equation implies, computing Q-values, requires knowledge of the transition probabilities, the reward functions, and the state dwell times, which together constitute a model of the environment. However, without a prior model of the environment, the agent can estimate these quantities through its experience with the environment. For example R(s) can be estimated by averaging immediate reward received in state s. In the same manner, D(s) can be computed as the average of waiting times in state s. An estimation of Psa(s′) can be made by counting the number of times taking action a in state s leads to state s′. Given the model of the environment, Q-values can be derived from Equation (4) using dynamic programming algorithms such as value-iteration (Mahadevan, 1996; Puterman, 1994). Because these methods of value computation rely on the model of environment, they are called model-based value computation methods. Using these state-action pairs, agent can guide its actions toward ones that lead to a higher average reward rate.
Returning to the overview of the decision-making process in the RL, in (i) the agent identifies its current state, st and then feeds st, is fed into equation (4), allowing the value of different actions, Q-values, to be computed. These Q-values guide the action selection process, and the agent takes the appropriate action (ii). By taking an action, the agent enters a new state, receives a reward, and measures the time from entering the previous state, st, to entering the new state, st+1. Finally, using these quantities, the model of the environment is updated (iii).
3.3. Action sequence formation
When an agent starts learning in a new environment all the decisions are based on model-based action selection; i.e., after entering a new state, the agent computes Q-values using the process introduced in the previous section and chooses one of the actions that tends to have the higher Q-value. Under certain conditions, however, it may be more beneficial for the agent to execute actions in a sequence without going through the action selection process. First, we discuss the process of sequence formation and in the next section, how action sequences interact with the model-based action selection.
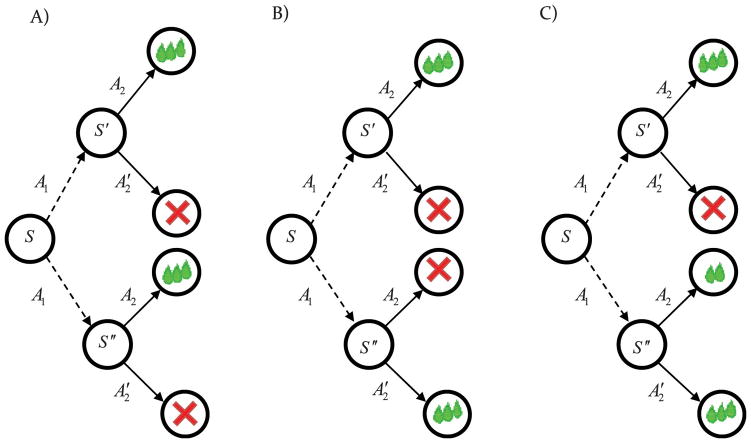
We start by reviewing the environmental conditions in which action sequences form. Figure 3 shows three environments in which, by taking action A1 in state S, the agent enters state S′ or S″ with equal probability. In states S′ and S″ two actions are available, A2 and . Figure 3A provides an example of the kind of environment in which an action sequence forms; i.e. in states S′ and S″, action A2 is the best action. An example of this environment is the situation in which pressing a lever (action A1), leads to the illumination of, say, a light (state S′) or a tone (state S″) with equal probability, both of which signal that by entering the magazine (action A2), the rat can gain a desirable outcome, and by not entering the magazine (action ) it gains nothing. As a consequence, after taking action A1 in S the agent does not need to check the upcoming state but can execute A2 irrespective of the next state, either S′ or S″ (light or tone). In this situation, actions A1 and A2 form an action sequence consisting of A1 and A2. Here after, we call these action sequences macro actions, and denote them, for example in this situation, with {A1A2}. Actions that are not macro, e.g., A1 or A2, are called primitive actions.
Figure 3.
Environmental constraints on sequence formation. (A) An example of an environment in which action sequences will form. Action A1 leads to two different states with equal probability, in both of which action A2 is the best action, and thus action sequence {A1A2} forms. (B) An example of an environment in which action sequences do not form. Action A1 leads to two different states with equal probability in one of which action A2 is the best action and, in another, action is the best action. As a consequence, an action sequence {A1A2} does not form. (C) An example of an environment in which the process of sequence formation is non-trivial. Action A1 leads to two different states with equal probability in one of which action A2 is best action, but in the other action is the best action (although it is a little bit worse than the rival best action).
Figure 3B shows a situation in which an action sequence does not form. In state S′, action A2 is the best action, but in state S″, action is the best. In the context of the previous example, illumination of the light indicates that by entering the magazine, the animal will gain a desirable outcome; but, presentation of the tone indicates that entering the magazine is not followed by a desirable outcome. Here, after taking A1 in S, the animal cannot select an action without knowing the upcoming state, and thus a macro action does not form.
Figure 3C shows a more challenging example. In state S′, A2 is the best action. In state S″, A2 is not the best action, but it is slightly worse than the best action, (e.g., two drops of a liquid reward, versus one drop of liquid reward). Does a sequence form in this case? To answer this question, we need a cost-benefit analysis: i.e. what the agent gains by executing actions A1 and A2 in sequence and what it looses. Assume it decides to always execute A2 after A1. If the next state is S′, then it loses nothing, because action A2 is the best action in state S′. But, if the next state be S″, by taking A2 instead of the best action, , the agent looses some of the future rewards. The amount of these reward losses is equal to the different between the value of action A2, Q(S″, A2), and the value of the best action, V(S″), which will be Q(S″, A2)−V(S″) that we denote by A(S″, A2). A(S″, A2) can be interpreted as the advantage of taking action A2 in state S″ instead of the best action (Baird, 1993; Dayan & Balleine, 2002). In this example, because agent enters state S″ after state S only half the time, the total cost of executing A1 and A2 in sequence will be 0.5A(S″, A2).
Generalizing from the previous example, the cost of executing macro action {aa′} in state s is equal to:
| (5) |
where expectation over next state, s′, given the previous action and the previous state, is:
| (6) |
Using the above equation, the term C(s, a,a′) can be computed based on the model-based approaches described in the section 3.2. The agent computes Q(s′,a′) and V(s′) using equation (4), and then C(s, a, a′) is calculated by equation (6). However, this means that at each decision point, deciding whether to execute an action sequence, equation (6) should be evaluated for all currently possible actions, and all possible subsequent actions. This will likely impose a heavy processing load on the decision-making process, and could considerably increase the latency of action selection. It turns out, however, that C(s, a,a′) can be estimated efficiently using samples of the temporal difference error signal(TD error signal).
The TD error signal experienced after taking action at in state st is defined as follows:
| (7) |
Based on equation (3), the term rt − dtR̄ + V(st+1) is a sample of Q(st,at). Thus, δt will be a sample of A(st,at), and hence C(s, a,a′) can be estimated using samples of the TD error signal. By taking action at−1 in state st−1, and action at in state st, C(st−1, at−1, at) will be updated as follows:
| (8) |
where ηC is the learning rate, and αt is a factor, which equals one when the environment is deterministic (see Appendix 6.1 for more details). As mentioned above, extensive evidence from animal and human studies suggest that the TD error signal is coded by the phasic activities of mid-brain dopamine neurons (W. Schultz & Dickinson, 2000; W. Schultz et al., 1997). Thus, besides being more efficient, utilizing the error signal for the purpose of sequence learning provides a neurally plausible way for computing the cost of sequence-based action selection, C(s, a,a′).
Up to now, we have only considered one side of the trade off, which is the cost of sequence-based action selection. What are the benefits of sequence-based action selection? As discussed in the previous section, expression of a sequence of actions is faster than selecting actions one by one, based on the action evaluation process. This can be for several reasons; e.g., identification of the current state by processing environmental stimuli can be time consuming; and the evaluation of actions using a model-based process is slower than having solely to select the next action from the sequence. Besides being faster, executing actions without going through the decision-making process makes it possible to perform a simultaneous task that requires decision-making resources. Here, we focus on the first advantage of sequence learning.
Assume that selecting the next action of the current sequence is τ time steps faster than selecting an action based on the action evaluation process. Saving τ time steps is equivalent to gaining R̄τ more reward in the future(Niv, Daw, Joel, & Dayan, 2007). This provides the other side of the trade off: if the benefit of sequence-based action selection, R̄τ, exceeds its costs, −C(s, a, a′), then the macro action {aa′} replaces action a in state s. Otherwise, if the macro action is already formed, it decomposes to its constitute actions, and action a replaces the macro action {aa′}:
| (9) |
After a macro action is added, it can be concatenated with other actions, to form a longer macro action. For example, macro action {aa′} can be concatenated with another action, say a″, and form the macro action {aa′a″}. It is important to recognize that, during execution of a macro action, primitive actions are not evaluated and thus the TD error signal is not computed, which means the cost of the action sequence, C(s, a,a′), is not updated after it is formed. This implies that a sequence should only form after the agent is certain about the estimated costs and benefits of the sequence, otherwise, the agent could stick to a sub-optimal sequence for a long period of time. This implies that action sequences should not form during early stages of instrumental learning because a high degree of certainty requires sufficient experience of the environment and hence more training time. In the current example, we did not model the agent’s certainty about its estimations. Instead we assumed a large initial value for the cost of sequence formation, and chose a slow learning rate for that cost (ηC), something that ensures sequences form only after the environment is well learned.
3.4. A mixed model-based and sequence-based architecture
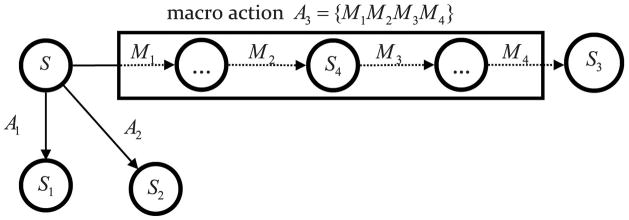
Assume that the agent is in state S in which several choices are available (Figure 4), two of which are primitive actions (A1 and A2), and one of which is a macro action (A3). In state S the agent uses model-based action evaluation, and selects one of the available actions for execution, which can be either a primitive action, or a macro action. After completion of a primitive action the agent enters a new state in which it again uses a model-based evaluation for selecting subsequent actions. However, if the selected action is the macro action, A3, its execution is composed of taking a sequence of primitive actions (M1…M4). Nevertheless, upon completion of the macro action, the agent identifies its new state (S3), and uses model-based action evaluation again for selection of the next action.
Figure 4.
Mixed model-based and sequence-based decision-making. At state S0, three actions are available: A1, A2, A3, where A1 and A2 are primitive actions, and A3 is a macro-action composed of primitive actions M1 … M4. If at state S, the macro action is selected for execution, the action control transfers to the sequence-based controller, and actions M1 … M4 become executed. After the termination of the macro-action control returns back to model-based decision-making at state S3.
The above scenario involves mixed model-based and sequence-based action control. At the choice points, actions are selected based on the model-based evaluations. However, during the execution of a sequence of actions, they are selected based on their sequential order, without going through the evaluation process. As discussed in the previous section, this sequence-based action selection can lead to higher average reward rates, in comparison to a pure model-based decision-making system, which is the benefit of sequence-based action selection. However, it can lead to a maladaptive behavior if the environment changes after action sequences have formed. For example, assume that, after the macro action {aa′} has formed, the environment changes so that the execution of action a′ after action a, no longer satisfies the cost-benefit analysis presented in the previous section – say the change causes the value of the state to which action a′ leads to decrease significantly – as a consequence, taking action a′ after action a will no longer be the best choice. If action control is sequence-based it is the previous action that determines the next action and not the consequences of the action. Hence, the agent will continue to take action a′ even though it is not the most appropriate action.
Ultimately, in this situation, we expect the macro action to decompose to its components so that the agent can consider other alternative actions other than action a′. However, this does not happen instantly after the environment has changed, and thus at least for a while, the agent will continue behaving maladaptively. As mentioned in the previous section, after the macro action has formed, its cost, C(s, a,a′), is not updated, because the system is working on the open-loop mode and the TD error signal is not computed to update C(s, a, a′). As a consequence, the cost side of the sequence formation tradeoff is relatively insensitive to environmental changes. The other side of the trade-off, R̄τ, however, is sensitive to environmental changes: if the environment changes so that executing the macro action leads to a decrease in the average reward the agent experiences, R̄, then this circumstance motivates decomposition of the macro. In fact, this model predicts that, if the environmental changes do not alter the average reward, then the agent will continue to take action a′ after a, even if the change introduces better alternatives other than taking action a′. Nevertheless, if the change causes a decrease in the average reward, then the macro action will decompose, and the responses will adapt to the new situation. However, this cannot happen instantly after the change because it takes several trials before the average reward adapts to the new condition.
The above feature of the model implies different sensitivity of sequence-based responses of the model after an environmental change compared to the situation where responses are under model-based control. As an example, in Figure 4 assume that the action A1 is the best action, i.e., it has the highest Q-value among actions A1, A2 and A3, and so the agent takes action A1 more frequently than the others. Now, assume that the environment changes, and the value of the state that action A1 leads to (state S1) dramatically decreases. The next time that the agent is making a decision in state S, it evaluates the consequences of action A1 using equation (3), and finds out that A1 is no longer the best action, and adapts its behavior instantly to the new conditions. Evidence for the effect of this type of environmental changes on the behavior comes from an experiment (Ostlund, Winterbauer, & Balleine, 2009) in which rats were trained on two action sequences for two outcomes; i.e. R1→R2→O1 and R2→R1→O2. After this training, either O1 or O2 was devalued, and performance of the two sequences (macro actions {R1R2} and {R2R1}) were assessed in extinction. Results show that the performance of the sequence that leads to the devalued outcome decreases, which implies that performance of a macro action (e.g., {R1 R2}) is immediately sensitive to the value of the states to which it leads (O1). It is worth mentioning that although the values of individual actions in the sequence are not updated, the total reward gained by executing the action sequence is learned by the model-based system.
Compare the above situation with one in which an environmental change causes a decrease in the value of one of the states visited during a sequence, e.g., state S4. Here, an action other than M2 would now be more optimal but, because action selection is under sequence-based control, the choice of M2 is derived by its previous action, M1, rather than the value of the state that M2 leads to, i.e., S4. After several trials, because taking action M2 does not lead to reward, the average reward that the agent experiences decreases, and the sequence should then decompose to its elements. At this point, the control of actions will return to the model-based system and choices adapt to the new environmental conditions. In the next section we show that insensitivity to reinforcer devaluation and contingency degradation is due to this type of environmental change.
4. Simulation of the model: Sequence learning and habit formation
Having described the model, we are now in a position to establish whether it can provide an accurate account of (i) sequence learning, such as that observed in SRTT, and (ii) instrumental conditioning, particularly the shift in sensitivity of instrumental actions to reinforcer devaluation and contingency degradation during the course of over training (see Appendix 6.2 for implementation details).
4.1. Sequential and Random Trials of Sequence Learning
As noted in section 2, when a sequence of stimuli is predictable, such as in the ‘sequential trials’ of the SRTT, along with the progress of learning as a result of sequence-based action selection, reaction times decline. In contrast, when the sequence of stimuli is random, as it is in the ‘random trials’ condition of SRTT, reaction times do not decrease substantially during the course of learning. Here, we simulated the model described in section 3 in a task similar to SRTT. After each correct button press the model receives one unit of reward. In the ‘sequential trials’ condition, after each correct button press the next stimulus in a fixed sequence is presented otherwise the sequence restarts and the first stimulus is presented. Here, we assume that the order of stimuli is S0 to S3, where the correct button press in S0 is B0, B1 in S1 and so on. In the ‘random trials’ condition, the next stimulus is selected randomly. It is assumed that it takes 400ms to make a decision using the model-based method, and 100ms to elicit a response under sequence-based action control.
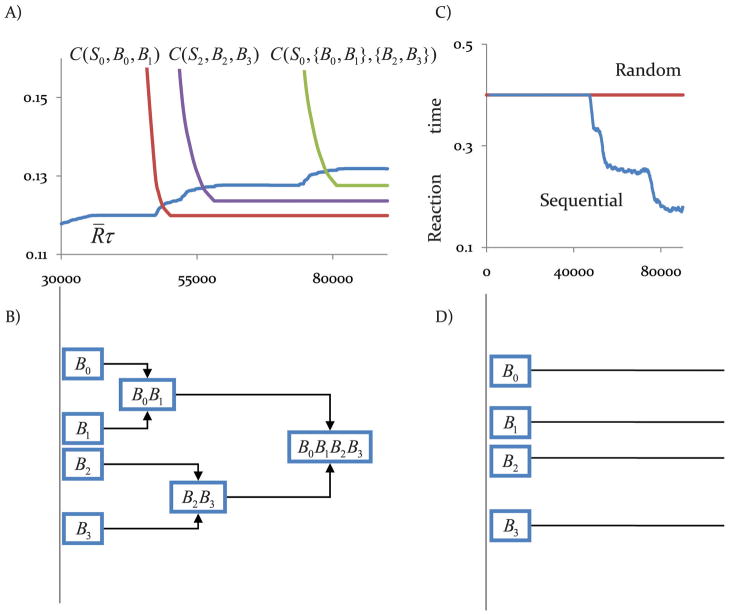
The temporal dynamics of sequence formation is depicted in Figure 5. After several learning trials, the agent learns the model of the environment (the rewards in states, delays in states, and the consequences of each action), and, as a consequence, the probability of taking the correct actions increases, which implies that the agent gains more rewards and thus, the average reward that the agent receives, R̄, increases. This increase in the average reward implies that a significant number of the rewards that could have been gained in the future are being lost due to time taken for model-based action selection, and this favors the transition of action control to the sequence-based method, which is faster. At the same time, the cost of sequence-based action selection, C(S0, B0, B1) decreases (Figure 5A) which means that the agent has learned B1 is always the action that should be taken after B0. Eventually, the benefit of sequence-based action selection becomes larger than its cost and, at that stage, the macro action {B0B1} replaces the B0 action (Figure 5B). Later, actions B2 and B3 form the macro action {B2B3}, and finally, the two previously formed macro actions concatenate, and the macro action {B0B1B2B3} is formed. In addition, as shown in Figure 5A, after a macro-action is formed the average reward that the agent gains increases due to faster decision-making.
Figure 5.
The dynamics of sequence learning in sequential and random trials of SRTT. (A, B) As the learning progresses, the average reward that the agent gains increases, indicative of a high cost of waiting for model-based action selection. At the same time, the cost of sequence-based action selection decreases (top panel), which means that the agent has discovered the correct action sequences. Whenever the cost becomes less than the benefit, a new action sequence forms (bottom panel). The abscissa axis shows the number of action selections. (C) Reaction times decrease in sequential trials as a result of sequence formation but they remain constant in the random trials of SRTT because, as panel (D) shows, no action sequence forms. Data reported are means over 10 runs.
Figure 5C shows the reaction times. As the figure shows, by forming new action sequences, reaction times decrease up to the point that only selection of the action sequence is based on model-based action control, and all subsequent button presses during the sequence are based on sequence-based action control. Figure 5C also shows the reaction times in the case of ‘random trials’, which remain constant largely because the sequence of stimuli is not predictable and the cost of sequence-based action selection remains high so that no action sequence forms (Figure 5D).
4.2. Instrumental Conditioning
In this section, we aimed to validate the model in instrumental conditioning paradigms. Figure 6A depicts a formal representation of a simple instrumental conditioning task. The task starts in state S0 and the agent has two options: the press lever (PL) action, and enter magazine (EM) action. By taking action PL, and then action EM, the agent enters state S0 in which it receives one unit of reward (r= 1). All other actions, e.g., taking action EM before action PL, leads to no reward. Entering state S1 is cued for example by a “click” produced by the pellet dispenser, or “buzz” of the pump if sucrose solution is the reward.
Figure 6.
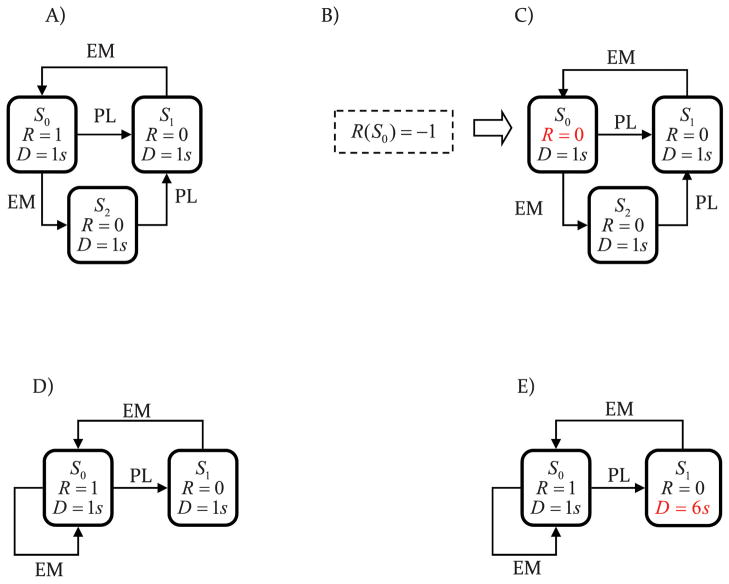
Formal representation of instrumental conditioning tasks. (A) Instrumental learning: By taking the press lever (PL) action, and then enter magazine (EM) action, the agent earns a reward of magnitude one. By taking EM action in state S2 and PL action in state S1, agent remains in the same state (not shown in the figure). (B,C) Reinforcer devaluation: The agent learns that the reward at state S0 is devalued, and then is tested in extinction in which no reward is delivered. (D) Non-contingent training: Unlike panel A, reward is not contingent on the PL action, and the agent can gain the reward only by entering the magazine. (E) Omission training: Taking the PL action causes a delay in the reward delivery, and agent should wait 6s before it can gain the reward by entering the magazine.
After several learning trials, the agent learns the model of the environment; the value of the PL action exceeds the value of action EM, and the probability of taking action PL increases. As the probability of taking PL increases, the agent gains more rewards, and, hence, the average reward, R̄ increases. Simultaneously, the cost of sequence-based action selection decreases which means the agent has learned that PL is always the action that should be taken after the EM action, an, as a consequence, the macro action {E M,P L} replaces the EM action (Figure 7A). From that point, the action PL is always taken after EM.
Figure 7.
Sensitivity of the model to reinforcer devaluation and contingency manipulations before and after sequence formation. (A) In the moderate training condition, actions are selected based on the model-based evaluation (left panel) but, after extended training, the selection of the PL action is potentiated by its previous action (here EM) (right panel). (B) After the devaluation phase (shown by the solid-line), the probability of pressing the lever decreases instantly if the model is moderately trained. The abscissa axis shows number of action selections. (C) After the devaluation phase behavior does not adapt until the action sequence decomposes and control returns to the model-based method. (D) In a moderately trained model the probability of selecting action PL starts to decrease in the contingency degradation condition, although the rate of decrease is greater in the case of omission training. (E) When training is extensive, behavior does not adjust and the non-contingent and omission groups perform at the same rate until the sequence decomposes. Data reported are means over 3000 runs.
The schematic representation in Figure 6A corresponds to a continuous reinforcement schedule (CRF) in which each lever press is followed by a reinforcer delivery (e.g., Adams, 1982). However, in most experimental settings, animals are required to execute a number of lever presses (in the case of ratio schedules), or press the lever after an amount of time has passed since the previous reward delivery (in the case of interval schedules) in order to obtain reward. One approach to analyzing these kinds of experiments using the paradigm illustrated in Figure 6A is through application of the ‘response unit hypothesis’ (Mowrer & Jones, 1945; Skinner, 1938), according to which the total set of lever presses required for reward delivery is considered as a single unit of response. For example, in the case of fixed ratio schedules, if ten lever presses are required to produce reinforcement, the whole ten lever presses are considered as a single unit, corresponding to the action PL in Figure 6A. In ratio schedules this hypothesis is supported by the observation that, early in learning, the animal frequently takes the EM action which, with the progress of learning, tends to occur only after the last lever press (Denny, Wells, & Maatsch, 1957; Overmann & Denny, 1974; Platt & Day, 1979). Following this training, animals are given an extinction test, in which rewards are not delivered (but in which state S1 is cued). During the course of extinction, the response unit mainly preserves its form and only the last response is likely to be followed by the EM action (Denny et al., 1957). Further, the average number of executed response units in extinction is independent of the number of lever presses required for reinforcer delivery, indicating that the whole response unit is being extinguished, and not individual lever presses (Denny et al., 1957; Overmann & Denny, 1974; Platt & Day, 1979). In the case of interval schedules, because reinforcement of a lever press depends on the time that has passed since the previous reward delivery, the ‘response unit hypothesis’ has to be generalized to temporal response unit structures in which the animal continues to lever press for a certain amount of time (instead of for a certain number of times), in the form of ‘bouts’ of lever pressing (Shull & Grimes, 2003), or nose poking (Shull, Gaynor, & Grimes, 2002).
In fact, in the previous section, in the course of analyzing SRTT, we applied the ‘response unit hypothesis’ by treating the action of pressing the button as a single response unit, which of course can be broken into smaller units. Similarly, in the case of maze learning, the action of reaching the choice point from starting point can be thought as a sequence of steps. Is the formation of such response units (e.g., PL action composed of homogenous set of responses) through the action sequence formation method proposed in the previous section, or they form in a level different from in which macro action {E M,P L} forms? We leave answer to this question for future works.
In the next two sections, we investigated the behavior of the model, based on Figure 6A, when an environmental change occurs both before and after sequence formation.
4.3. Reinforcer devaluation before vs. after action sequence formation
As described above, in reinforcer devaluation studies, the value of the outcome of an action is reduced offline through some treatment (such as specific satiety or taste aversion learning) and the performance of the action subsequently assessed in extinction. There is a considerable literature demonstrating that, with moderate training, instrumental performance is sensitive to this change on value whereas after more extended training it is not (cf. Figure 1A).
To assess the accuracy of the model it was simulated using the procedure depicted in Figure 6. The procedure has three steps. The first step, Figure 6A, is the instrumental learning phase, described in the previous section. The next step, Figure 6B, models the devaluation phase in which the model learns that the reward obtained in state S0 is devalued (r=−1). The third phase is the test conducted under extinction conditions; i.e., reward is not delivered in state S0 (r= 0). The critical question here is whether the model chooses action PL in state S0. As noted previously, experimental evidence shows that after moderate training, the agent chooses action PL whereas after extended training, it does not. Figure 7B shows the probability of taking action PL after moderate training (in this case after 3000 action selections). As the figure shows, because action selection is under model-based control, when the reward in state S0 is devalued, the value of taking PL action in state S0 is immediately affected and, as such, the probability of taking action PL decreases.
The same is not true of overtrained actions. Figure 7C shows the sensitivity of responses to devaluation after extended training (9000 action selections). At this point the action sequence {E M,P L} has been formed and, as the figure shows, unlike moderate training the agent continues taking action PL after reinforcer devaluation. This is because action selection is under sequence-based action control and selecting action PL is driven by the previous action (EM) rather than the value of the upcoming state. After several learning trials, because the experiment is conducted in extinction and no reward is received, the average reward decreases, which means deciding faster is not beneficial, and causes the macro action {E M,P L} to decompose to action EM and action PL. At this point, behavioral control should return to the model-based system, and the probability of taking action PL should adjust to the new conditions induced by devaluation. It is worth noting that the prediction that extensive devaluation testing in extinction will cause habitual behavior to revert to goal-directed control has not been assessed experimentally largely because extinction usually produces such a profound suppression of performance that any change in behavioral control would be difficult to detect.
4.4. Contingency degradation before vs. after action sequence formation
In the first section we began by pointing out that habits are not just insensitive to reinforcer devaluation but also to the effects of degrading the instrumental contingency. A good example of this is the failure of habits to adjust to the imposition of an omission schedule as shown in Figure 1B. Having learned that lever pressing delivers food, the omission schedule reverses that relationship such that food becomes freely available without needing to lever press to receive it. However, in the experimental group, lever pressing delays free food delivery; hence the rats now have to learn to stop lever pressing to get the reward. The ability to stop responding in the omission group is compared with rats given exposure to a zero contingency between lever pressing and reward delivery (the non-contingent control). As shown previously (e.g. Dickinson et al., 1998; Figure 1B) in this situation, rats who are given moderate instrumental training are able to withhold their lever press action to get food; the omission group responds less than the control group when the omission schedule is introduced. When lever pressing has been overtrained, however, the rats are insensitive to omission and cannot withhold their lever press responses compared to the control group.
For the simulation of non-contingent reward delivery in the control condition, the model underwent the instrumental conditioning procedure described in the previous section (Figure 6A) and then the model was simulated in the task depicted in Figure 6D. The agent can obtain reward by taking action EM without performing action PL, and hence reward delivery is no longer contingent upon action PL. For the simulation of the omission schedule, after instrumental training (Figure 6A), the agent was exposed to the schedule depicted in Figure 6E. The difference between this schedule and the non-contingent schedule is that, after pressing the lever, the model must wait 6s before obtaining the reward by taking action EM, which models the fact that rewards are delayed if the animal chooses action PL under the omission schedule. The behavior of the model after moderate training is depicted in Figure 7D. As the figure shows, after the introduction of the degradation procedure, the probability of taking action PL starts to decrease. The rate of decrease is faster in the case of the omission schedule, in comparison to the non-contingent schedule. This is because the final value of action PL in the omission condition is lower than the final value of the non-contingent condition, and, therefore, the values adjust faster in the omission case.
Figure 7E shows the effect of omission and degradation after more extended training when action selection is under sequence-based control. As the figure shows, in both the control and omission conditions, the probability of selecting the action fails to adjust to the new conditions and the agent continues selecting action PL. However, in the omission condition, because rewards are delayed as a result of pressing the lever, the average reward starts to decrease and, after sufficient omission training, the action sequence decomposes, and behavior starts to adapt to the new conditions. In the case of non-contingent reward delivery, because the average reward remains constant, the model predicts that the agent will continue pressing the lever, even after extended exposure to the non-contingent schedule. Again, this prediction has not been assessed in the literature again largely because exposure to non-contingent reward tends to have a generally suppressive effect on performance as competition from EM responding increases and action LP begins to extinguish. As is the case after reinforcer devaluation testing, it can be challenging to assess changes in performance when responding has reached a behavioral floor.
Although somewhat idealized relative to the effects observed in real animals, it should be clear that, in contrast to simple RL, sequence learning and habitual actions are both accurately modeled by this mixed model-based and sequence-based architecture. The implications of this model for the behavior of real animals and for theories of goal-directed and habitual action control are described below.
5. The implications of the model
The development of the mixed model-based and sequence-based architecture we describe and simulate here was motivated by the fact that simple RL fails accurately to model the performance of habitual instrumental actions. One reason of this failing, we believe, lies in the way model-free RL treats the TD error signal during the acquisition of habitual actions. When applied to a specific action, the TD error actually ensures that overtrained, habitual actions will be more sensitive to degradation of the instrumental contingency than goal-directed actions. This is the opposite pattern of results to that observed in real animals (see Figure 1). We also argued that the problem lies in the way that habitual actions are described; i.e. they are typically regarded as essentially identical to goal-directed actions in their representational structure; a response (whether a button push, handle turn, lever press etc) can be nominally either goal-directed or habitual in the usual case. We propose, to the contrary, that as goal-directed actions become habitual they grow more complex in the sense that they become more thoroughly integrated, or chunked, with other motor movements such that, when selected, these movements tend to run off in a sequence. Under this scheme, rather than establishing the value of individual actions, the TD error provides feedback regarding the cost of this chunk or sequence of actions, an approach that we show successfully models the insensitivity of overtrained actions to both reinforcer devaluation and degradation of the instrumental contingency.
5.1. Implications and predictions: Habitual responses
The solution we propose to the issue that habits pose to RL is, therefore, to view them as a form of action sequence under the control of a model-based RL process. There are two important implications, and sets of predictions, generated by this kind of approach. The first is for the nature of habits themselves. Viewed as sequences of movements, as opposed to action primitives, habitual responses should be anticipated to have qualities that differentiate them from goal-directed actions, many of which will be similar to those of skilled movements (Buitrago, Ringer, et al., 2004; Newell, Liu, & Mayer-Kress, 2001). First, we should anticipate observing a reduction in the variation in the movements around the action; e.g. if, say, lever pressing is chunked with other movements, the frequency of those movements should increase whereas the incidence of other extraneous movements should decline. Second, the inter-response interval between any candidate set of sequential movements should decline with practice. More critically: (i) the incidence of these factors should be predicted to correlate with the acquisition of habits by other measures, such as reduced sensitivity to reinforcer devaluation and contingency degradation; and (ii) manipulations known to affect habits, such as lesions or inactivation of dorsolateral striatum (Yin, Ostlund, & Balleine, 2008) or of the dopaminergic input to this region from the substantia nigra pars compacta (Faure et al., 2005), should be expected to affect these measures and alter actions to make their performance more similar to that observed when demonstrably goal-directed.
In fact, there is already considerable evidence for some of these effects in the literature examining the acquisition of skilled movements (Wolpert & Flanagan, 2010; Wolpert, Ghahramani, & Flanagan, 2001), although it is well beyond the scope of the current paper to review that literature here. Of greater direct relevance is evidence from studies examining the performance of animals in various mazes, particularly those that have been heavily utilized to study the acquisition of habitual performance such as the T-maze. For example, Jog et al. (1999) overtrained rats in a T-maze and found that, as component responses performed between start and end points in the maze declined in latency, neural activity in dorsolateral striatum specific to those points also gradually declined to the extent that task-related activity was limited to the first and last responses in the maze; i.e. the points at which any response sequence or chunk should have been initiated and terminated. Similar effects have been observed by Barnes et al. (2005) and indeed, using response reversals, they were also able to observe a collapse of the sequence; i.e. both inter-maze responses and neural activity initially associated with those responses reemerged along with task irrelevant movements. The inter-maze responses again declined with continued training post-reversal. Hence, changes in both striatal unit activity and incidental behavioral responses tracked the development of the sequence as has been observed recently using a homogeneous sequence of lever press responses, described above (X. Jin & Costa, 2010), and in a head movement habit (Tang et al., 2007). Finally, Kubota et al (2009) reported observing electrophysiological effects associated with both the overall response sequence and the component response primitives as these were rapidly remapped onto new stimuli presented during the course of T-maze performance, suggesting that the mice (in this case) maintained separate representations of the sequence and component movements. Interestingly, Redish and colleagues (Johnson, van der Meer, & Redish, 2007; Schmitzer-Torbert & Redish, 2004) reported neural signals in striatum associated with sequence learning in a novel navigation task composed of a series of T-mazes reordered across days. Striatal activity differed across different sequences of turns in the maze but was also highly correlated across repeated sequences suggesting, again, the co-occurrence of movement-specific and sequence-specific activity in striatum.
The role of sensorimotor striatum in action sequences is not without controversy (Bailey & Mair, 2006; Turner & Desmurget, 2010). For example, inactivation of the globus pallidus internus, the principal output of sensorimotor striatum, does not increase the reaction time in the ‘sequential trials’ of SRTT (Desmurget & Turner, 2010), which suggests performance of action sequences is not dependent on the sensorimotor striatum. However, although execution, as opposed to the encoding, of sequence-based actions may not be dependent on sensorimotor striatum, it can be argued that transfer of control to sequence-based action control can be independent its output in the pallidum. Based on this assumption, disrupting the output should not necessarily be accompanied by an increase in the reaction time, because it does not cause transfer of control to model-based action control, but should result in an increase in the number of errors because it cannot exert control over the motor control circuitry, consistent with the experimental observation (Desmurget & Turner, 2010).
5.2. Implications and predictions: Action sequences
The second implication of the current analysis is for the way in which the processes controlling goal-directed and habitual actions should be thought to interact. A number of investigators have noted the apparently competitive nature of these forms of action control and some have suggested that these processes may compete for access to the motor system. Using this general approach, previous computational accounts have successfully explained the effect of reinforcer devaluation on instrumental responses in different stages of learning (Daw et al., 2005; Keramati, Dezfouli, & Piray, 2011), the effect of habit formation on reaction times (Keramati et al., 2011), and the effect of the complexity of state identification on the behavioral control (Shah & Barto, 2009). All these approaches shares a common ‘flat’ architecture in which the goal-directed and the habitual systems work in parallel at the same level, and utilize a third mechanism, called an arbitration mechanism, to decide whether the next action will be controlled by the goal-directed or the habit process. They differ from the hierarchical architecture used here in which the goal-directed system stands at a higher level, with the role of the habit process limited to efficiently implementing decisions made by the goal-directed system in the form of macro actions. This structural difference itself raises some important behavioral predictions. For example, in the hierarchical structure, the goal-directed system treats macro actions as integrated units, and thus the action evaluation process is blind to the change in the value of states visited during execution of the macro action. Thus, in Figure 4, goal-directed action evaluation in state S0, depends only on the value of states S1, S2, S3 and the total reward obtained through executing the macro action. As a consequence, changing the value of state S4 has no immediate impact on the decisions made at state S0. In contrast, in a ‘flat’ architecture, goal-directed action selection is conducted by searching all the consequences of possible actions, and thus, a change in the value of state S4 should immediately affect action selection in state S0. Another prediction of a sequence-based conception of habits is that, if an agent starts decision-making in a state in which an action sequence has been learned (state S0), it will immediately show habit-like behavior, such as insensitivity to outcome devaluation. In contrast, if it starts decision-making somewhere in the middle of a sequence (e.g., in the test phase the task starts in an intermediary state such as S4), it will not show habit-like behavior. This is because in the current conception of the model, an action sequence can be launched only in the state in which is has been learned.
The problem of mixed closed-loop and open-loop decision-making has been previously addressed and discussed in the literature but the solutions proposed differ from that suggested here. In the model proposed here, the inputs for the mixed architecture come from fast action control in the open-loop mode, whereas, in previous work, it has come from a cost associated with sensing the environment (Hansen, Barto, & Zilberstein, 1998), or the complexity of modeling the environment (Kolter, Plagemann, Jackson, Ng, & Thrun, 2010). From a control point of view, in most situations (especially stochastic environments), open-loop action control is considered to be inappropriate. As such, in hierarchical approaches to RL, the idea of macro-actions is usually generalized to closed-loop action control (Barto & Mahadevan, 2003). Behavioral and neural signatures of this generalized notion have been found in previous studies (Badre & Frank, 2011; Botvinick, 2008; Botvinick, Niv, & Barto, 2009; Frank & Badre, 2011; Haruno & Kawato, 2006; Ribas-Fernandes et al., 2011). Here, instead of using this generalized hierarchical RL, we utilized a hierarchical approach with a mixed open-loop and closed-loop architecture that allows us to incorporate the role of action sequences in habit-learning. Further, to examine the potential neural substrates of this architecture, we developed a method based on the TD error for learning macro-actions, though various alternative methods have also been proposed for this purpose (Iba, 1989; Korf, 1985; Mcgovern, 2002; Randløv, 1999).
With regard specifically to sequences, the effect of overtraining on reaction times has been addressed in instrumental conditioning models (Keramati et al., 2011) which often interprets them as the result of transition to habitual control which, because it is fast, results in a reduction in reaction times. However, that model predicts a decrease in reaction times in both ‘random’ and ‘sequential trials’ of SRTT. This is because, on that approach, a habit forms whenever the values of the available choices are significantly different, irrespective of whether the sequence of states is predictable. As such, because, in both ‘sequential’ and ‘random trials’ of SRTT, the values of correct and incorrect responses are different, the model predicts that habits will form and reaction times decrease in both cases, which is not consistent with the evidence. In the sequence learning literature, the issue of learning sequences of responses and stimuli using TD error has been addressed (Bapi & Doya, 2001; Berns & Sejnowski, 1998; Bissmarck, Nakahara, Doya, & Hikosaka, 2008; Nakahara, Doya, & Hikosaka, 2001). However, because these models are generally developed for the purpose of visuo-motor sequence learning, it is not straightforward to apply them to instrumental conditioning tasks. Likewise, the effect of the predictability of stimuli (i.e., random vs. sequential trials in the SRTT) on reaction times is not directly addressed in these models, which makes it hard to compare them in SRTT.
One important restriction of the proposed model relates to the fact that it may seem implausible to assume that, after an action has been formed, the individual actions are always executed together. To address this issue it can, for example, be assumed that, occasionally, the model-based controller interrupts execution of actions during the performance of an action sequence in order to facilitate learning of new action sequences. Along the same lines, it can be assumed that action sequences do not replace primitive actions (as proposed in this paper), but are added as new actions to the list of available actions. Finally, investigating why some kinds of reinforcement schedules lead to habits (action sequences) whilst others do not, is an interesting issue and each of these will be addressed in future work.
Acknowledgments
The research described here and the preparation of this paper was supported by grants from the Australian Research Council#FL0992409, the National Health & Medical Research Council #633267, and the National Institute of Mental Health #MH56446.
6. Appendix
6.1. Estimating the cost of sequence-based action selection
We aim to estimate C(s, a,a′) by the samples of the error signal experienced by taking action a′, after action a in state s.
C(s, a,a′) is defined as:
| (10) |
We maintain that:
| (11) |
This follows from:
| (12) |
P(a′|s,a) and P(a′|s′) can be estimated directly by counting number of times action a′ has been taken after s, a and after s′ respectively. Given these, C(s, a,a′) can be estimated by averaging over the samples of the error signal multiplied by the factor αt:
| (13) |
αt is in fact percentage of taking action a′ after s and a is due to being in state s′. If action a′ is not available in state s′, we assume this factor is infinity. Given αt, the cost function is estimated using equation (8).
6.2. Implementation details
The implementation of the mixed architecture is similar to model-based hierarchical reinforcement learning. After execution of a macro-action finished, the characteristics of the underlying semi-Markov Decision Process (MDP) are updated. That is, the total reward obtained through executing the macro action, and the total time spent for executing the macro action are used for updating the reward, and transition delay functions. Here, since we assumed that reward function depends on the states, and not state-action pairs, the total reward obtained through the macro action cannot be assigned to the state in which the macro action was launched. This is because the total reward obtained through the macro action can be different from the reward of the state. For addressing this problem, when an action sequence was formed, a temporary extended auxiliary state is added to the MDP, to which the agent enters when the macro action starts, and exits when the macro action finished. The transition delay and reward function of this auxiliary state is updated using the rewards obtained through executing the macro action, and the time spent to take the macro action.
Since according to the Bellman equation for average reward semi-Markov RL, the Q-values satisfy equation (3) (Puterman, 1994), when a non-exploratory action is taken (the action with highest value is taken), we update the average reward as follows:
| (14) |
Where σ is the learning rate of the average reward. For the action selection (in the model-based system), soft-max rule is used:
| (15) |
Where parameter β determines rate of exploration. For computing model-based values, a tree-search algorithm was applied with the depth of search of three levels. After this level, goal-directed estimations are replaced by model-free estimations.
Due to the fluctuations of C(s, a, a′) and R̄τ at the point they meet, a series of sequence formation/decomposition may happen before the two curves become separated. To address this issue, an asymmetric rule for sequence decomposition is used, and a sequence decomposes only if −C(s, a,a′)>1.6R̄τ. Also, for simplicity, we assumed that macro-actions could not be cyclic.
Internal parameters of the model are shown in Table 1.
Table 1.
Free parameters of the model, and their assigned values.
| parameter | value |
|---|---|
| Update rate of the reward function | 0.05 |
| Update rate of the average reward (σ) | 0.002 |
| Update rate of the cost of sequence-based control (ηC) | 0.001 |
| Initial value of the cost of sequence-based control | −2 |
| Rate of exploration (β) | 4 |
References
- Adams CD. Variations in the sensitivity of instrumental responding to reinforcer devaluation. The Quarterly Journal of Experimental Psychology Section B. 1982;34B:77–98. [Google Scholar]
- Alexander GE, Crutcher MD. Functional architecture of basal ganglia circuits: neural substrates of parallel processing. Trends in neurosciences. 1990;13(7):266–71. doi: 10.1016/0166-2236(90)90107-l. [DOI] [PubMed] [Google Scholar]
- Astrom KJ, Murray RM. Feedback Systems: An Introduction for Scientists and Engineers. Princeton, NJ: Princeton University Press; 2008. [Google Scholar]
- Badre D, Frank MJ. Mechanisms of Hierarchical Reinforcement Learning in Cortico-Striatal Circuits 2: Evidence from fMRI. Cerebral cortex. 2011 doi: 10.1093/cercor/bhr117. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey KR, Mair RG. The role of striatum in initiation and execution of learned action sequences in rats. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2006;26(3):1016–25. doi: 10.1523/JNEUROSCI.3883-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey KR, Mair RG. Effects of frontal cortex lesions on action sequence learning in the rat. The European journal of neuroscience. 2007;25(9):2905–15. doi: 10.1111/j.1460-9568.2007.05492.x. [DOI] [PubMed] [Google Scholar]
- Baird LC. Wright-Patterson Air Force Base. Ohio: Wright Laboratory; 1993. Advantage updating (No. WL--TR-93–1146) [Google Scholar]
- Balleine BW, O’Doherty JP. Human and rodent homologies in action control: corticostriatal determinants of goal-directed and habitual action. Neuropsychopharmacology: official publication of the American College of Neuropsychopharmacology. 2010;35(1):48–69. doi: 10.1038/npp.2009.131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balleine BW, Delgado MR, Hikosaka O. The role of the dorsal striatum in reward and decision-making. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2007;27(31):8161–5. doi: 10.1523/JNEUROSCI.1554-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balleine BW, Liljeholm M, Ostlund SB. The integrative function of the basal ganglia in instrumental conditioning. Behavioural brain research. 2009;199(1):43–52. doi: 10.1016/j.bbr.2008.10.034. [DOI] [PubMed] [Google Scholar]
- Barnes TD, Kubota Y, Hu D, Jin DZ, Graybiel AM. Activity of striatal neurons reflects dynamic encoding and recoding of procedural memories. Nature. 2005;437(7062):1158–61. doi: 10.1038/nature04053. [DOI] [PubMed] [Google Scholar]
- Barto AG, Mahadevan S. Recent advances in hierarchical reinforcement learning. Discrete Event Dynamic Systems. 2003;13(1–2):41–77. [Google Scholar]
- Botvinick MM. Hierarchical models of behavior and prefrontal function. Trends in cognitive sciences. 2008;12(5):201–8. doi: 10.1016/j.tics.2008.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botvinick MM, Niv Y, Barto AG. Hierarchically organized behavior and its neural foundations: a reinforcement learning perspective. Cognition. 2009;113(3):262–80. doi: 10.1016/j.cognition.2008.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buitrago MM, Ringer T, Schulz JB, Dichgans J, Luft AR. Characterization of motor skill and instrumental learning time scales in a skilled reaching task in rat. Behavioural brain research. 2004;155(2):249–56. doi: 10.1016/j.bbr.2004.04.025. [DOI] [PubMed] [Google Scholar]
- Buitrago MM, Schulz JB, Dichgans J, Luft AR. Short and long-term motor skill learning in an accelerated rotarod training paradigm. Neurobiology of learning and memory. 2004;81(3):211–6. doi: 10.1016/j.nlm.2004.01.001. [DOI] [PubMed] [Google Scholar]
- Chang Q, Gold PE. Inactivation of dorsolateral striatum impairs acquisition of response learning in cue-deficient, but not cue-available, conditions. Behavioral neuroscience. 2004;118(2):383–8. doi: 10.1037/0735-7044.118.2.383. [DOI] [PubMed] [Google Scholar]
- Costa RM, Cohen D, Nicolelis MAL. Differential corticostriatal plasticity during fast and slow motor skill learning in mice. Current biology: CB. 2004;14(13):1124–34. doi: 10.1016/j.cub.2004.06.053. [DOI] [PubMed] [Google Scholar]
- Costa RM, Lin SC, Sotnikova TD, Cyr M, Gainetdinov RR, Caron MG, Nicolelis MAL. Rapid alterations in corticostriatal ensemble coordination during acute dopamine-dependent motor dysfunction. Neuron. 2006;52(2):359–69. doi: 10.1016/j.neuron.2006.07.030. [DOI] [PubMed] [Google Scholar]
- Daw ND, Touretzky DS. Long-term reward prediction in TD models of the dopamine system. Neural computation. 2002;14(11):2567–83. doi: 10.1162/089976602760407973. [DOI] [PubMed] [Google Scholar]
- Daw ND, Tourtezky DS. Behavioral considerations suggest an average reward TD model of the dopamine system. Neurocomputing. 2000;32–33(1–4):679–684. [Google Scholar]
- Daw ND, Niv Y, Dayan P. Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nature neuroscience. 2005;8(12):1704–11. doi: 10.1038/nn1560. [DOI] [PubMed] [Google Scholar]
- Dayan P, Balleine BW. Reward, motivation, and reinforcement learning. Neuron. 2002;36(2):285–98. doi: 10.1016/s0896-6273(02)00963-7. [DOI] [PubMed] [Google Scholar]
- Dayan P, Kakade S. Explaining away in weight space. In: Leen TK, Dietterich TG, Tresp V, editors. Advances in Neural Information Processing Systems. Vol. 13. 2001. pp. 451–457. [Google Scholar]
- Dayan P, Kakade S, Montague PR. Learning and selective attention. Nature neuroscience. 2000;3:1218–23. doi: 10.1038/81504. [DOI] [PubMed] [Google Scholar]
- Denny MR, Wells RH, Maatsch JL. Resistance to extinction as a function of the discrimination habit established during fixed-ratio reinforcement. Journal of Experimental Psychology. 1957;54(6):451–456. doi: 10.1037/h0040155. [DOI] [PubMed] [Google Scholar]
- Desmurget M, Turner RS. Motor sequences and the basal ganglia: kinematics, not habits. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2010;30(22):7685–90. doi: 10.1523/JNEUROSCI.0163-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devan BD, White NM. Parallel information processing in the dorsal striatum: relation to hippocampal function. The Journal of neuroscience: the official journal of the Society for Neuroscience. 1999;19(7):2789–98. doi: 10.1523/JNEUROSCI.19-07-02789.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devan BD, McDonald RJ, White NM. Effects of medial and lateral caudate-putamen lesions on place- and cue-guided behaviors in the water maze: relation to thigmotaxis. Behavioural brain research. 1999;100(1–2):5–14. doi: 10.1016/s0166-4328(98)00107-7. [DOI] [PubMed] [Google Scholar]
- Dickinson A. Actions and Habits: The Development of Behavioural Autonomy. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences. 1985;308(1135):67–78. [Google Scholar]
- Dickinson A. Instrumental conditioning. In: Mackintosh NJ, editor. Animal cognition and learning. London: Academic Press; 1994. pp. 4–79. [Google Scholar]
- Dickinson A, Nicholas DJ, Adams CD. The effect of the instrumental training contingency on susceptibility to reinforcer devaluation. The Quarterly Journal of Experimental Psychology Section B Comparative and Physiological Psychology. 1983;35(1):35–51. [Google Scholar]
- Dickinson A, Squire S, Varga Z, Smith JW. Omission learning after instrumental pretraining. The Quarterly Journal of Experimental Psychology B: Comparative and Physiological Psychology. 1998;51B(3):271–286. [Google Scholar]
- Endress AD, Wood J. From movements to actions: Two mechanisms for learning action sequences. Cognitive psychology. 2011;63(3):141–171. doi: 10.1016/j.cogpsych.2011.07.001. [DOI] [PubMed] [Google Scholar]
- Faure A, Haberland U, Condé F, El Massioui N. Lesion to the nigrostriatal dopamine system disrupts stimulus-response habit formation. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2005;25(11):2771–80. doi: 10.1523/JNEUROSCI.3894-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Featherstone RE, McDonald RJ. Dorsal striatum and stimulus-response learning: lesions of the dorsolateral, but not dorsomedial, striatum impair acquisition of a stimulus-response-based instrumental discrimination task, while sparing conditioned place preference learning. Neuroscience. 2004;124(1):23–31. doi: 10.1016/j.neuroscience.2003.10.038. [DOI] [PubMed] [Google Scholar]
- Featherstone RE, McDonald RJ. Lesions of the dorsolateral striatum impair the acquisition of a simplified stimulus-response dependent conditional discrimination task. Neuroscience. 2005;136(2):387–95. doi: 10.1016/j.neuroscience.2005.08.021. [DOI] [PubMed] [Google Scholar]
- Frank MJ, Badre D. Mechanisms of Hierarchical Reinforcement Learning in Corticostriatal Circuits 1: Computational Analysis. Cerebral cortex. 2011 doi: 10.1093/cercor/bhr114. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank MJ, O’Reilly RC. A mechanistic account of striatal dopamine function in human cognition: psychopharmacological studies with cabergoline and haloperidol. Behavioral neuroscience. 2006;120(3):497–517. doi: 10.1037/0735-7044.120.3.497. [DOI] [PubMed] [Google Scholar]
- Graybiel AM. The basal ganglia and chunking of action repertoires. Neurobiology of learning and memory. 1998;70(1–2):119–36. doi: 10.1006/nlme.1998.3843. [DOI] [PubMed] [Google Scholar]
- Hansen EA, Barto AG, Zilberstein S. Advances in Neural Information Processing Systems NIPS. Vol. 9. The MIT Press; 1998. Reinforcement Learning for Mixed Open-Loop and Closed Loop Control; pp. 1026–1032. [Google Scholar]
- Haruno M, Kawato M. Heterarchical reinforcement-learning model for integration of multiple cortico-striatal loops: fMRI examination in stimulus-action-reward association learning. Neural networks: the official journal of the International Neural Network Society. 2006;19(8):1242–54. doi: 10.1016/j.neunet.2006.06.007. [DOI] [PubMed] [Google Scholar]
- Hernandez PJ, Schiltz Ca, Kelley AE. Dynamic shifts in corticostriatal expression patterns of the immediate early genes Homer 1a and Zif268 during early and late phases of instrumental training. Learning & memory. 2006;13(5):599–608. doi: 10.1101/lm.335006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hikosaka O, Rand MK, Miyachi S, Miyashita K. Learning of sequential movements in the monkey: process of learning and retention of memory. Journal of neurophysiology. 1995;74(4):1652–61. doi: 10.1152/jn.1995.74.4.1652. [DOI] [PubMed] [Google Scholar]
- Hull CL. Principles of Behavior. New York: Appleton; 1943. [Google Scholar]
- Iba Ga. A heuristic approach to the discovery of macro-operators. Machine Learning. 1989;3(4):285–317. [Google Scholar]
- Jin X, Costa RM. Start/stop signals emerge in nigrostriatal circuits during sequence learning. Nature. 2010;466(7305):457–62. doi: 10.1038/nature09263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jog MS, Kubota Y, Connolly CI, Hillegaart V, Graybiel AM. Building neural representations of habits. Science. 1999;286(5445):1745–9. doi: 10.1126/science.286.5445.1745. [DOI] [PubMed] [Google Scholar]
- Johnson A, van der Meer MAA, Redish AD. Integrating hippocampus and striatum in decision-making. Current opinion in neurobiology. 2007;17(6):692–7. doi: 10.1016/j.conb.2008.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keele SW, Ivry R, Mayr U, Hazeltine E, Heuer H. The cognitive and neural architecture of sequence representation. Psychological review. 2003;110(2):316–39. doi: 10.1037/0033-295x.110.2.316. [DOI] [PubMed] [Google Scholar]
- Kelly RM, Strick PL. Macro-architecture of basal ganglia loops with the cerebral cortex: use of rabies virus to reveal multisynaptic circuits. Progress in brain research. 2004;143:449–59. doi: 10.1016/s0079-6123(03)43042-2. [DOI] [PubMed] [Google Scholar]
- Keramati M, Dezfouli A, Piray P. Speed/Accuracy Trade-Off between the Habitual and the Goal-Directed Processes. PLoS computational biology. 2011;7(5):e1002055. doi: 10.1371/journal.pcbi.1002055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolter Z, Plagemann C, Jackson DT, Ng A, Thrun S. A Probabilistic Approach to Mixed Open-loop and Closed-loop Control, with Application to Extreme Autonomous Driving. Proc. of the IEEE Int.Conf.on Robotics & Automation (ICRA); Anchorage, Alaska, USA. 2010. [Google Scholar]
- Korf RE. Macro-Operators: A Weak Method for Learning. Artificial Intelligence. 1985;26(1):35–77. [Google Scholar]
- Lashley KS. The problem of serial order in behavior. In: Jeffress LA, editor. Cerebral Mechanisms in Behavior. Wiley; 1951. pp. 112–136. [Google Scholar]
- Lehéricy S, Benali H, Van de Moortele PF, Pélégrini-Issac M, Waechter T, Ugurbil K, Doyon J. Distinct basal ganglia territories are engaged in early and advanced motor sequence learning. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(35):12566–71. doi: 10.1073/pnas.0502762102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahadevan S. Average Reward Reinforcement Learning: Foundations, Algorithms, and Empirical Results. Machine Learning. 1996;22(1):159–195. [Google Scholar]
- Matsuzaka Y, Picard N, Strick PL. Skill representation in the primary motor cortex after long-term practice. Journal of neurophysiology. 2007;97(2):1819–32. doi: 10.1152/jn.00784.2006. [DOI] [PubMed] [Google Scholar]
- Mcgovern EA. Autonomous Discovery Of Temporal Abstractions From Interaction With An Environment. University of Massachusetts; Amherst: 2002. [Google Scholar]
- Miyachi S, Hikosaka O, Lu X. Differential activation of monkey striatal neurons in the early and late stages of procedural learning. Experimental brain research. 2002;146(1):122–6. doi: 10.1007/s00221-002-1213-7. [DOI] [PubMed] [Google Scholar]
- Miyachi S, Hikosaka O, Miyashita K, Kárádi Z, Rand MK. Differential roles of monkey striatum in learning of sequential hand movement. Experimental brain research. 1997;115(1):1–5. doi: 10.1007/pl00005669. [DOI] [PubMed] [Google Scholar]
- Miyashita K, Rand MK, Miyachi S, Hikosaka O. Anticipatory saccades in sequential procedural learning in monkeys. Journal of neurophysiology. 1996;76(2):1361–6. doi: 10.1152/jn.1996.76.2.1361. [DOI] [PubMed] [Google Scholar]
- Montague P Read, Dayan P, Sejnowski TJ. A framework for mesencephalic dopamine systems based on predictive Hebbian learning. The Journal of neuroscience: the official journal of the Society for Neuroscience. 1996;16(5):1936–47. doi: 10.1523/JNEUROSCI.16-05-01936.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moussa R, Poucet B, Amalric M, Sargolini F. behavior Contributions of dorsal striatal subregions to spatial alternation behavior. Learning & Memory. 2011:444–451. doi: 10.1101/lm.2123811. [DOI] [PubMed] [Google Scholar]
- Mowrer OH, Jones H. Habit strength as a function of the pattern of reinforcement. Journal of Experimental Psychology. 1945;35(4):293–311. [Google Scholar]
- Neuringer A. Reinforced variability in animals and people: implications for adaptive action. The American psychologist. 2004;59(9):891–906. doi: 10.1037/0003-066X.59.9.891. [DOI] [PubMed] [Google Scholar]
- Neuringer A, Jensen G. Operant variability and voluntary action. Psychological review. 2010;117(3):972–93. doi: 10.1037/a0019499. [DOI] [PubMed] [Google Scholar]
- Newell KM, Liu YT, Mayer-Kress G. Time scales in motor learning and development. Psychological review. 2001;108(1):57–82. doi: 10.1037/0033-295x.108.1.57. [DOI] [PubMed] [Google Scholar]
- Nissen MJ, Bullemer P. Attentional Requirements of Learning: Performance Measures Evidence from. Cognitive Psychology. 1987;19(1):1–32. [Google Scholar]
- Niv Y, Daw ND, Joel D, Dayan P. Tonic dopamine: opportunity costs and the control of response vigor. Psychopharmacology. 2007;191(3):507–20. doi: 10.1007/s00213-006-0502-4. [DOI] [PubMed] [Google Scholar]
- Ostlund SB, Balleine BW. On habits and addiction: An associative analysis of compulsive drug seeking. Drug discovery today. Disease models. 2008;5(4):235–245. doi: 10.1016/j.ddmod.2009.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostlund SB, Winterbauer NE, Balleine BW. Evidence of action sequence chunking in goal-directed instrumental conditioning and its dependence on the dorsomedial prefrontal cortex. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2009;29(25):8280–7. doi: 10.1523/JNEUROSCI.1176-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Overmann SR, Denny MR. The free-operant partial reinforcement effect: A discrimination analysis. Learning and Motivation. 1974;5(2):248–257. [Google Scholar]
- O’Doherty JP, Dayan P, Schultz J, Deichmann R, Friston K, Dolan RJ. Dissociable roles of ventral and dorsal striatum in instrumental conditioning. Science. 2004;304(5669):452–4. doi: 10.1126/science.1094285. [DOI] [PubMed] [Google Scholar]
- O’Reilly RC, Herd Sa, Pauli WM. Computational models of cognitive control. Current opinion in neurobiology. 2010;20(2):257–61. doi: 10.1016/j.conb.2010.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Packard MG, McGaugh JL. Inactivation of hippocampus or caudate nucleus with lidocaine differentially affects expression of place and response learning. Neurobiology of learning and memory. 1996;65(1):65–72. doi: 10.1006/nlme.1996.0007. [DOI] [PubMed] [Google Scholar]
- Platt JR, Day RB. A hierarchical response-unit analysis of resistance to extinction following fixed-number and fixed-consecutive-number reinforcement. Journal of Experimental Psychology: Animal Behavior Processes. 1979;5(4):307–320. [Google Scholar]
- Poldrack Ra, Sabb FW, Foerde K, Tom SM, Asarnow RF, Bookheimer SY, Knowlton BJ. The neural correlates of motor skill automaticity. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2005;25(22):5356–64. doi: 10.1523/JNEUROSCI.3880-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puterman ML. Markov Decision Processes. New York: Wiley Interscience; 1994. [Google Scholar]
- Randløv J. Advances in Neural Information Processing Systems. Vol. 11. MIT Press; 1999. Learning Macro-Actions in Reinforcement Learning; pp. 1045–1051. [Google Scholar]
- Rangel A, Camerer C, Montague PR. A framework for studying the neurobiology of value-based decision making. Nature reviews neuroscience. 2008;9(7):545–56. doi: 10.1038/nrn2357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redish AD, Jensen S, Johnson A. A unified framework for addiction: vulnerabilities in the decision process. The Behavioral and brain sciences. 2008;31(4):415–37. doi: 10.1017/S0140525X0800472X. discussion 437–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Restle F. Discrimination of cues in mazes: a resolution of the place-vs.-response question. Psychological review. 1957;64(4):217–28. doi: 10.1037/h0040678. [DOI] [PubMed] [Google Scholar]
- Reynolds JN, Hyland BI, Wickens JR. A cellular mechanism of reward-related learning. Nature. 2001;413(6851):67–70. doi: 10.1038/35092560. [DOI] [PubMed] [Google Scholar]
- Ribas-Fernandes JJF, Solway A, Diuk C, McGuire JT, Barto AG, Niv Y, Botvinick MM. A neural signature of hierarchical reinforcement learning. Neuron. 2011;71(2):370–9. doi: 10.1016/j.neuron.2011.05.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritchie BF, Aeschliman B, Pierce P. Studies in spatial learning: VIII. Place performance and the acquisition of place dispositions. Journal of Comparative and Physiological Psychology. 1950;43:73–85. doi: 10.1037/h0055224. [DOI] [PubMed] [Google Scholar]
- Rondi-Reig L, Petit GH, Tobin C, Tonegawa S, Mariani J, Berthoz A. Impaired sequential egocentric and allocentric memories in forebrain-specific-NMDA receptor knock-out mice during a new task dissociating strategies of navigation. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2006;26(15):4071–81. doi: 10.1523/JNEUROSCI.3408-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakai K, Kitaguchi K, Hikosaka O. Chunking during human visuomotor sequence learning. Experimental brain research. 2003;152(2):229–42. doi: 10.1007/s00221-003-1548-8. [DOI] [PubMed] [Google Scholar]
- Schmitzer-Torbert N, Redish AD. Neuronal activity in the rodent dorsal striatum in sequential navigation: separation of spatial and reward responses on the multiple T task. Journal of neurophysiology. 2004;91(5):2259–72. doi: 10.1152/jn.00687.2003. [DOI] [PubMed] [Google Scholar]
- Schultz W, Dickinson A. Neuronal coding of prediction errors. Annual review of neuroscience. 2000;23:473–500. doi: 10.1146/annurev.neuro.23.1.473. [DOI] [PubMed] [Google Scholar]
- Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275(5306):1593–9. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- Schwarting RKW. Rodent models of serial reaction time tasks and their implementation in neurobiological research. Behavioural brain research. 2009;199(1):76–88. doi: 10.1016/j.bbr.2008.07.004. [DOI] [PubMed] [Google Scholar]
- Shah A. Biologically-Based Functional Mechanisms of Motor Skill Acquisition. University of Massachusetts; Amherst: 2008. [Google Scholar]
- Shah A, Barto AG. Brain research. Vol. 1299. Elsevier B.V; 2009. Effect on movement selection of an evolving sensory representation: a multiple controller model of skill acquisition; pp. 55–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shull RL, Grimes Ja. Bouts of responding from variable-interval reinforcement of lever pressing by rats. Journal of the experimental analysis of behavior. 2003;80(2):159–71. doi: 10.1901/jeab.2003.80-159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shull RL, Gaynor ST, Grimes Ja. Response rate viewed as engagement bouts: resistance to extinction. Journal of the experimental analysis of behavior. 2002;77(3):211–31. doi: 10.1901/jeab.2002.77-211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skinner BF. The behavior of organisms. New York: Appleton-Century-Crofts; 1938. [Google Scholar]
- Spence KW. Behavior theory and conditioning. New Haven: Yale University Press; 1956. [Google Scholar]
- Sutton RS, Barto AG. Reinforcement learning: an introduction. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- Tang C, Pawlak AP, Prokopenko V, West MO. Changes in activity of the striatum during formation of a motor habit. The European journal of neuroscience. 2007;25(4):1212–27. doi: 10.1111/j.1460-9568.2007.05353.x. [DOI] [PubMed] [Google Scholar]
- Terrace HS. Chunking during serial learning by a pigeon: I. Basic evidence. Journal of Experimental Psychology: Animal Behavior Processes. 1991;17(1):81–93. doi: 10.1037//0097-7403.17.1.81. [DOI] [PubMed] [Google Scholar]
- Tolman EC, Ritchie BF, Kalish D. Studies in spatial learning: II. Place learning versus response learning. Journal of Experimental Psychology. 1946;36:221–229. doi: 10.1037/h0060262. [DOI] [PubMed] [Google Scholar]
- Tsitsiklis JN, Roy BV. Average Cost Temporal-Difference Learning. Automatica. 1999;35:1799–1808. [Google Scholar]
- Turner RS, Desmurget M. Basal ganglia contributions to motor control: a vigorous tutor. Current opinion in neurobiology. 2010;20(6):704–16. doi: 10.1016/j.conb.2010.08.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watkins CJCH. Learning from Delayed Rewards. Cambridge University; 1989. [Google Scholar]
- Willingham DB. A neuropsychological theory of motor skill learning. Psychological review. 1998;105(3):558–84. doi: 10.1037/0033-295x.105.3.558. [DOI] [PubMed] [Google Scholar]
- Willingham DB, Nissen MJ, Bullemer P. On the development of procedural knowledge. Journal of experimental psychology. Learning, memory, and cognition. 1989;15(6):1047–60. doi: 10.1037//0278-7393.15.6.1047. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Flanagan JR. Motor learning. Current biology: CB. 2010;20(11):R467–72. doi: 10.1016/j.cub.2010.04.035. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Ghahramani Z, Flanagan JR. Perspectives and problems in motor learning. Trends in cognitive sciences. 2001;5(11):487–494. doi: 10.1016/s1364-6613(00)01773-3. [DOI] [PubMed] [Google Scholar]
- Yin HH, Knowlton BJ. Contributions of striatal subregions to place and response learning. Learning & memory (Cold Spring Harbor, NY) 2004;11(4):459–63. doi: 10.1101/lm.81004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin HH, Knowlton BJ, Balleine BW. Lesions of dorsolateral striatum preserve outcome expectancy but disrupt habit formation in instrumental learning. The European journal of neuroscience. 2004;19(1):181–9. doi: 10.1111/j.1460-9568.2004.03095.x. [DOI] [PubMed] [Google Scholar]
- Yin HH, Knowlton BJ, Balleine BW. Blockade of NMDA receptors in the dorsomedial striatum prevents action-outcome learning in instrumental conditioning. The European journal of neuroscience. 2005;22(2):505–12. doi: 10.1111/j.1460-9568.2005.04219.x. [DOI] [PubMed] [Google Scholar]
- Yin HH, Knowlton BJ, Balleine BW. Inactivation of dorsolateral striatum enhances sensitivity to changes in the action-outcome contingency in instrumental conditioning. Behavioural brain research. 2006;166(2):189–96. doi: 10.1016/j.bbr.2005.07.012. [DOI] [PubMed] [Google Scholar]
- Yin HH, Ostlund SB, Balleine BW. Reward-guided learning beyond dopamine in the nucleus accumbens: the integrative functions of cortico-basal ganglia networks. The European journal of neuroscience. 2008;28(8):1437–48. doi: 10.1111/j.1460-9568.2008.06422.x. [DOI] [PMC free article] [PubMed] [Google Scholar]