Abstract
In carbon capture and storage (CCS), CO2 is captured at power plants and then injected underground into reservoirs like deep saline aquifers for long-term storage. While CCS may be critical for the continued use of fossil fuels in a carbon-constrained world, the deployment of CCS has been hindered by uncertainty in geologic storage capacities and sustainable injection rates, which has contributed to the absence of concerted government policy. Here, we clarify the potential of CCS to mitigate emissions in the United States by developing a storage-capacity supply curve that, unlike current large-scale capacity estimates, is derived from the fluid mechanics of CO2 injection and trapping and incorporates injection-rate constraints. We show that storage supply is a dynamic quantity that grows with the duration of CCS, and we interpret the lifetime of CCS as the time for which the storage supply curve exceeds the storage demand curve from CO2 production. We show that in the United States, if CO2 production from power generation continues to rise at recent rates, then CCS can store enough CO2 to stabilize emissions at current levels for at least 100 y. This result suggests that the large-scale implementation of CCS is a geologically viable climate-change mitigation option in the United States over the next century.
Keywords: carbon sequestration, pressure dissipation, residual trapping, solubility trapping
Carbon dioxide is a well-documented greenhouse gas, and a growing body of evidence indicates that anthropogenic CO2 emissions are a major contributor to climate change (1). One promising technology to mitigate CO2 emissions is carbon capture and storage (CCS) (2–4). In the context of this study, CCS involves capturing CO2 from the flue gas of power plants, compressing it into a supercritical fluid, and then injecting it into deep saline aquifers for long-term storage (4, 5). Compared with other mitigation technologies such as renewable energy, CCS is important because it may enable the continued use of fossil fuels, which currently supply >80% of the primary power for the planet (6, 7). We focus on CO2 produced by power plants because electric power generation currently accounts for >40% of worldwide CO2 emissions (8) and because power plants are large, stationary point sources of emissions where CO2 capture technology will likely be deployed first (4). We further restrict our analysis to coal- and gas-fired power plants because they emit more CO2 than any other type of plant: Since 2000, they have emitted ∼97% by mass of the total CO2 produced by electricity-generating power plants in the United States (9). We focus on storing this CO2 in deep saline aquifers because they are geographically widespread and their storage capacity is potentially very large (4, 5).
We define the storage capacity of a saline aquifer to be the maximum amount of CO2 that could be injected and securely stored under geologic constraints, such as the aquifer's size and the integrity of its caprock. Regulatory, legal, and economic factors such as land-use constraints and the locations of power plants will ultimately play an important role in limiting the degree to which this capacity can be utilized (10–12), but they do not contribute to the estimates of storage capacity in this study.
Although CCS has been identified as the critical enabling technology for the continued use of fossil fuels in a carbon-constrained world (7), the role it can play within the portfolio of climate-change mitigation options remains unclear. This ambiguity is due in part to uncertainty in the total amount of CO2 that CCS could store and therefore uncertainty in the time span over which it could be extended into the future. Storage capacity estimates for the United States, for example, range over almost four orders of magnitude: from ∼5 (13) to 20,000 billion metric tons (Gt) of CO2 (11), with other estimates falling in between (14). This uncertainty in capacity leads to large uncertainty in the potential lifetime of CCS: At a storage rate of 1 Gt CO2/y, which is about one-sixth of US emissions (9), CCS could operate from 5 to 20,000 y.
An important factor contributing to the uncertainty in storage capacity is the high level of uncertainty in the hydrogeologic data for deep saline aquifers—recent estimates (11) make use of much larger and more sophisticated datasets than earlier estimates (13). The large range is also due to the complexity of the storage process: Because the subsurface fluid dynamics of CO2 storage are complicated, studies use different simplifying assumptions and methodologies to estimate large-scale capacity, such as assuming that the entire pore volume of an aquifer is saturated with dissolved CO2 (14) or extrapolating storage capacities from an ensemble of local-scale simulations (10, 11). Moreover, the impact of injection-rate constraints due to pressure buildup is not clear. For example, some studies of CO2 injection support the adoption of CCS with injection-rate management (15), whereas others conclude that injection constraints render CCS infeasible (16).
Here, we clarify the potential of CCS to mitigate emissions in the United States. We develop a storage capacity model that advances previous efforts by explicitly capturing the fluid dynamics of CO2 storage as well as injection-rate constraints. We treat geologic capacity as a supply of storage space and the amount of CO2 that needs to be stored as a demand for that space. We then interpret the lifetime of CCS in the United States as the time for which supply exceeds demand.
CO2 Migration and Pressure Buildup both Constrain Storage Capacity
CO2 Trapping and Migration-Limited Capacity.
To develop the geologic storage supply curve, we first consider how much CO2 can be trapped in the pore space of an aquifer. Trapping is essential to prevent upward leakage of the buoyant CO2 to shallower formations or the surface (17, 18). Although trapping can be analyzed over a wide range of length scales, we consider trapping at the large scale of an entire geologic basin because large volumes of CO2 will need to be stored to offset emissions (3). We consider residual trapping, in which blobs of CO2 become immobilized by capillary forces (19), and solubility trapping, in which CO2 dissolves into the groundwater (20, 21), because these mechanisms operate over relatively short timescales and provide secure forms of storage (Fig. 1 A and B). To estimate capacity at the basin scale, we develop an upscaled model for CO2 migration and trapping that is simple, but captures the key macroscopic physics of these pore-scale trapping processes. The model also incorporates CO2 migration due to the aquifer slope and natural head gradient, because migration critically impacts trapping. For example, the tendency of CO2 to migrate in a long, thin tongue along the caprock reduces the effectiveness of residual trapping, which occurs in the wake of the plume, but increases the effectiveness of solubility trapping, which occurs primarily along the underside of the plume (Fig. 1C). Modeling migration is also essential to ensure that the mobile CO2 becomes fully trapped before traveling to leakage pathways such as outcrops, large faults, or high-permeability zones in the caprock. We make many simplifying assumptions in deriving the trapping model, including homogeneity of the reservoir and vertical-flow equilibrium, and arrive at a nonlinear partial differential equation (PDE), which we solve analytically in some limiting cases, but numerically in general (22) (SI Appendix). Although the model is complex enough to permit aquifer-specific capacity estimates on the basis of >20 parameters, it is simple enough to be applied quickly to a large number of aquifers.
Fig. 1.
Residual and solubility trapping are the key trapping mechanisms that contribute to CO2 storage capacity. (A) Shows blobs of gas immobilized by residual trapping in an experimental analog system: a glass-bead pack saturated with water. (B) Shows solubility trapping in a different analog system: a Hele–Shaw cell saturated with water, topped with a source of dense, dyed water. As in the CO2 system, in which the brine with dissolved CO2 is denser than the ambient brine, dissolution occurs via finger-like protrusions of dense fluid. (C) We model trapping at the large scales relevant to a nationwide analysis and account for the injection and migration of CO2. We consider a linear arrangement of injection wells in a deep section of the aquifer (28). Initially, each well produces a radial CO2 plume, which grows and eventually interferes with those from neighboring wells, leading to a problem that can be approximated as 2D on a vertical cross section. Trapping occurs primarily after injection, when the CO2 migrates due to the aquifer slope and the natural head gradient. As the buoyant plume of mobile CO2 (dark gray) rises and spreads away from the well array, residual trapping immobilizes blobs of CO2 in its wake (light gray) (19, 29, 30), and solubility trapping shrinks the plume from below (blue) (20, 21).
Pressure Dissipation and Pressure-Limited Capacity.
Although an aquifer's trapping-based storage capacity may be large, it may be impossible to use the entire capacity due to limitations on the injection rate (15, 16). If the injection rate is too high, the rise in pressure may create fractures or activate faults. Fracturing and fault activation could induce seismicity or could create or enhance pathways by which CO2 could leak (ref. 4, Chap. 5).
We translate sustainable injection rates into pressure-limited storage capacities (SI Appendix). We calculate the pressure-limited capacity of an aquifer as the total amount of CO2 that can be injected over a duration T without causing a tensile fracture in the caprock (23). We neglect multiphase flow effects on the pressure evolution, motivated by the observation that the buoyant CO2 will spread mostly along the top of the aquifer and thereby occupy a small fraction of the aquifer volume. Rather than assuming that aquifers are closed (16), we account for pressure dissipation vertically through the geologic basin and interpret geologic cross sections to determine appropriate lateral boundary conditions (15). As with the trapping model, the pressure model is a PDE that we solve analytically in some limiting cases, but numerically in general (SI Appendix).
Whereas the trapping-based supply curve of an aquifer is independent of time, the pressure-limited supply curve is dynamic, growing approximately as 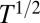 for short injection durations. This scaling reflects the diffusive character of pressure dissipation in porous media. The trapping-based and pressure-limited supply curves always exhibit a crossover as a function of injection duration, and the complete storage supply curve is the lower of these two curves: It is the pressure-limited supply curve for short injection times, but is the migration-limited supply curve for long injection times (SI Appendix).
for short injection durations. This scaling reflects the diffusive character of pressure dissipation in porous media. The trapping-based and pressure-limited supply curves always exhibit a crossover as a function of injection duration, and the complete storage supply curve is the lower of these two curves: It is the pressure-limited supply curve for short injection times, but is the migration-limited supply curve for long injection times (SI Appendix).
US Storage Capacity.
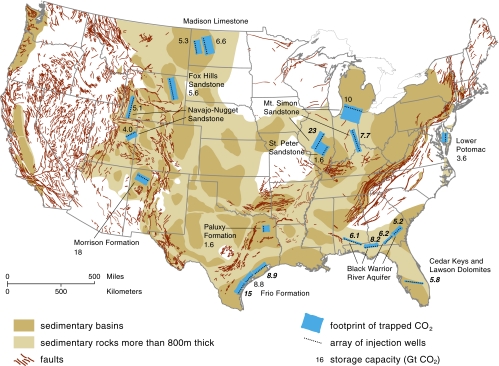
We calculate the storage supply curve for the entire United States as the sum of the supply curves for 11 major deep saline aquifers, assuming that CO2 injection begins simultaneously in each aquifer. The footprints of trapped CO2 in the aquifers studied illustrate the geographic distribution of storage capacity in the United States (Fig. 2). We characterize the geology and hydrogeology of each aquifer to determine which portions are suitable for sequestration, considering several criteria that include the following: (i) The depth must exceed 800 m so that CO2 is stored efficiently as a high-density, supercritical fluid; (ii) the aquifer and caprock must be laterally continuous over long distances; and (iii) there must be very few faults that could serve as leakage pathways (SI Appendix). Although abandoned wells can also serve as leakage pathways (18), data about their locations and integrity are not sufficient to incorporate them into this large-scale study.
Fig. 2.
We estimate the nationwide storage capacity from 20 arrays of injection wells in 11 aquifers. We select these aquifers because they are large, exhibit few basin-scale faults, and have been relatively well characterized (31). This map shows the locations of the aquifers and their storage capacities for an injection period of 100 y (capacities for different injection periods are in SI Appendix, Table S29). Capacities in italic boldface type are constrained by pressure; otherwise, they are constrained by migration. The map also shows the ultimate CO2 footprints for those capacities, which correspond to the areas infiltrated by migrating, free-phase CO2 before it becomes completely trapped.
Our results for the storage supply of individual aquifers agree well with published estimates. For the portion of the Mt. Simon Sandstone located within the Illinois basin (Region a, SI Appendix), the National Energy Technology Laboratory (NETL) Sequestration Atlas (11) reports a migration-limited capacity of 11–151 Gt, and Birkholzer et al. (15) estimate a pressure-limited capacity of ∼13 Gt for an injection time of 50 y. These values compare well with our estimates: Our estimate of the migration-limited capacity is 88 Gt, which falls in the center of the range reported by the NETL, and our estimate of the pressure-limited capacity for an injection time of 50 y is 15 Gt, which is ∼15% higher than the estimate by Birkholzer et al.
In addition to calculating a baseline storage supply, we perform a sensitivity and uncertainty analysis for each aquifer. Although there are many types of uncertainty in storage supply, we consider the impact of statistical uncertainty in the input parameters to estimate the standard deviation (SD) in storage supply (SI Appendix).
Storage Demand vs. Supply Dictates CCS Lifetime
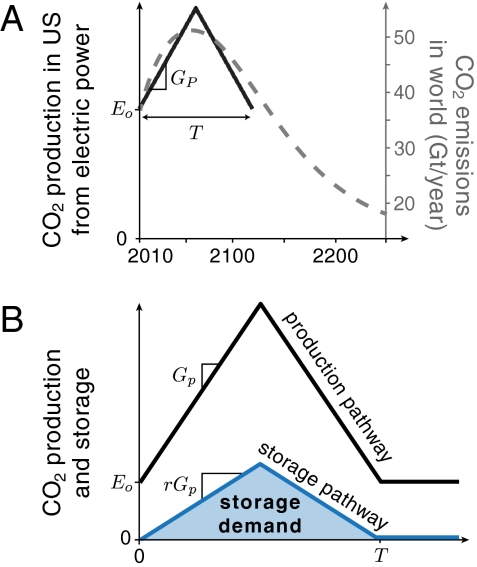
To estimate the demand for CO2 storage, we first model future CO2 production from coal- and gas-fired power plants. We assume that the rate of CO2 production from these plants will increase linearly, reach a maximum, and then decrease linearly with equal and opposite slope until returning to the current rate (Fig. 3A). Although future CO2 production trends will likely be complex, we use this simple model because it captures the essential features expected in future trends: an increase in the rate of production as energy demand grows and fossil fuels continue to supply the energy and then a decrease as low-emissions energy sources begin to replace fossil fuels. We assume that the CO2 injection rate in each aquifer also follows this ramp-up, ramp-down trend.
Fig. 3.
(A) Worldwide emission pathways that would stabilize the atmospheric concentration of CO2 exhibit a characteristic shape: Emissions rise to a maximum, decrease, and then level off (dashed gray curve, for stabilization at 750 ppm CO2) (25). Our model of CO2 production pathways in the United States (solid black curve) is a simplification of the initial part of that shape. The model is parameterized by two variables: the time required to return to current production rates, T, and the slope of the linear increase, Gp. E0 is the current production/emission rate. (B) We model the CO2 storage rate as a fraction, r, of the CO2 produced from coal- and gas-fired power plants at rates above the current rate. The storage demand is the cumulative CO2 stored over a storage pathway, which is the total area under the pathway (shaded blue).
This CO2 production model has two key parameters: the slope of the linear increase, Gp, and the time at which production returns to the current rate, T. On the basis of data from the electricity sector in the United States over the past four decades, we estimate the recent growth rate in production to be Gp ∼ 45 million tons of CO2 per year per year (Mt/y2) (24). This rate has slowed recently (∼30 Mt/y2 over the past two decades or ∼20 Mt/y2 over the past decade), in part due to growth coming more and more from gas-fired plants instead of coal-fired plants. However, we choose the higher historic rate on the basis of our expectation that the deployment of CCS and the abundance of coal will promote the construction of coal-fired plants at rates similar to those in previous decades and that those plants will be capture ready. The variable T describes different trajectories of the CO2 production rate, which we call production pathways in analogy to emission pathways (25).
We define the CO2 storage rate to be a constant fraction, r, of the surplus CO2 production rate or the rate at which CO2 is produced above the current rate. As a result, storage pathways exhibit the same shape as production pathways: The rate of storage increases linearly, reaches a maximum at the same time production reaches a maximum, and then decreases linearly, returning to zero when production returns to the current rate. The storage demand is the cumulative mass of CO2 stored over an entire storage pathway: 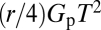 (Fig. 3B). This formula indicates that r can also be used to capture uncertainty in the production growth rate, Gp.
(Fig. 3B). This formula indicates that r can also be used to capture uncertainty in the production growth rate, Gp.
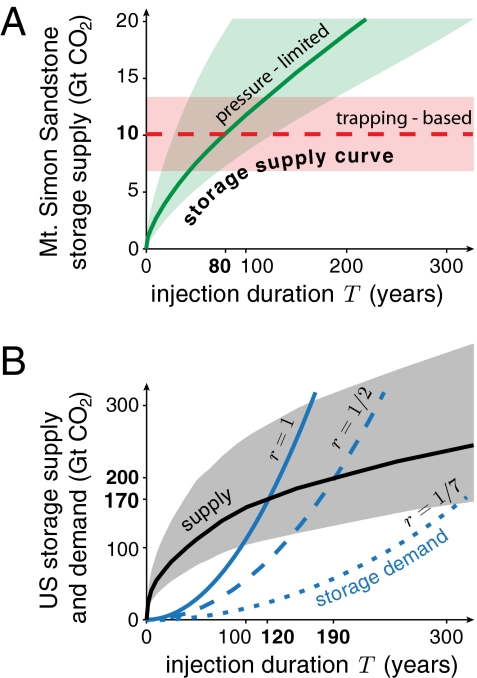
The time span over which CCS can be extended is the time for which the storage supply curve exceeds the storage demand curve. The storage demand curve is concave, growing approximately as T1/2 for short injection times when most aquifer capacity is pressure-limited, and flattening for long injection times when most aquifer capacity is migration-limited (Fig. 4A). The time at which the curves intersect corresponds to the longest storage pathway for which there is sufficient storage supply. If the storage demand is all of the surplus CO2 produced (r = 1), the demand curve crosses the supply curve at T = 120 y, with a range of T = 95–165 y (Fig. 4B). If the storage demand is one-half of CO2 produced (r = 0.5), the intersection occurs at T = 190 y, with a range of T = 145–250 y. If the storage demand is one-seventh of the CO2 production, as proposed in ref. 3, the crossover time is at least 300 y.
Fig. 4.
(A) The storage supply curve of a deep saline aquifer is constrained by both CO2 trapping and pressure buildup. For short injection times, pressure buildup is the more limiting constraint, and the supply curve increases approximately as the square root of the injection duration, 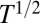 (SI Appendix). For longer injection times, trapping is the more limiting constraint and the capacity becomes independent of injection time. This crossover is shown for Region b of the Mt. Simon Sandstone, where trapping becomes limiting after about 80 y. The shaded areas are uncertainty envelopes based on 1 SD (SI Appendix). (B) The storage supply curve for the entire United States (black curve) is the sum of the supply curves of all of the aquifers. The uncertainty envelope again represents 1 SD (shaded gray). The storage demand curves represent storing 100%, 50%, and 15% of all of the surplus CO2 produced at the recent growth rate of 45 Mt/y2. The intersection of these curves with the capacity curve marks the maximum time over which CCS can be extended. For a storage demand of all surplus production, the demand curve intersects the supply curve at ∼120 y, indicating that CCS can stabilize atmospheric emissions in the United States for at least 100 y.
(SI Appendix). For longer injection times, trapping is the more limiting constraint and the capacity becomes independent of injection time. This crossover is shown for Region b of the Mt. Simon Sandstone, where trapping becomes limiting after about 80 y. The shaded areas are uncertainty envelopes based on 1 SD (SI Appendix). (B) The storage supply curve for the entire United States (black curve) is the sum of the supply curves of all of the aquifers. The uncertainty envelope again represents 1 SD (shaded gray). The storage demand curves represent storing 100%, 50%, and 15% of all of the surplus CO2 produced at the recent growth rate of 45 Mt/y2. The intersection of these curves with the capacity curve marks the maximum time over which CCS can be extended. For a storage demand of all surplus production, the demand curve intersects the supply curve at ∼120 y, indicating that CCS can stabilize atmospheric emissions in the United States for at least 100 y.
Discussion
We have shown that in the United States, the storage supply from 11 major deep saline aquifers is sufficient to store large quantities of CO2 for long times. If the task of stabilizing emissions is divided among several technologies such that the storage demand for CCS is one-seventh of the CO2 produced, CCS can operate for >300 y. If the storage demand is all of the surplus CO2 produced, CSS can operate for at least 100 y. This result suggests that geologic storage supply will enable CCS to play a major role within the portfolio of climate-change mitigation options.
Although the storage supply is large, many regulatory and economic factors will play an important role in determining the degree to which this storage supply can be utilized. The successful large-scale deployment of CCS will require, for example, detailed exploration for site selection (26) and comprehensive policy to establish safety and monitoring regulations and drive adoption. Absence of comprehensive policy, in particular, has been identified as the key barrier to the deployment of CCS (27).
Understanding the lifetime of CCS is essential for informing government policy. Because storage supply depends fundamentally on the duration of CCS, policymakers should consider the total time over which CCS will be deployed to identify storage targets or deployment rates that comply with geologic constraints. Alternatively, policymakers should set storage targets, recognizing that they can be achieved only for a finite time. Policy for the development of low-emissions energy sources should also consider the lifetime of CCS, which constrains the timescales over which these technologies must be deployed to eventually replace fossil fuels.
Supplementary Material
Acknowledgments
We thank Bradford Hager, Daniel Rothman, and two anonymous reviewers for their comments. Funding for this work was provided by the US Department of Energy under Grant DE-FE0002041, the Massachusetts Institute of Technology Energy Initiative, the Reed Research Fund, the Martin Family Society of Fellows for Sustainability, and the Atlantic Richfield Company (ARCO) Chair in Energy Studies.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1115347109/-/DCSupplemental.
References
- 1.Falkowski P, et al. The global carbon cycle: A test of our knowledge of earth as a system. Science. 2000;290:291–296. doi: 10.1126/science.290.5490.291. [DOI] [PubMed] [Google Scholar]
- 2.Lackner KS. Climate change. A guide to CO2 sequestration. Science. 2003;300:1677–1678. doi: 10.1126/science.1079033. [DOI] [PubMed] [Google Scholar]
- 3.Pacala S, Socolow R. Stabilization wedges: Solving the climate problem for the next 50 years with current technologies. Science. 2004;305:968–972. doi: 10.1126/science.1100103. [DOI] [PubMed] [Google Scholar]
- 4.IPCC . In: Special Report on Carbon Dioxide Capture and Storage. Metz B, et al., editors. Cambridge, UK: Cambridge Univ Press; 2005. [Google Scholar]
- 5.Orr FM., Jr Onshore geologic storage of CO2. Science. 2009;325:1656–1658. doi: 10.1126/science.1175677. [DOI] [PubMed] [Google Scholar]
- 6.Hoffert MI, et al. Advanced technology paths to global climate stability: Energy for a greenhouse planet. Science. 2002;298:981–987. doi: 10.1126/science.1072357. [DOI] [PubMed] [Google Scholar]
- 7.MIT . In: The Future of Coal – An Interdisciplinary MIT Study. Deutch J, Moniz EJ, editors. Cambridge, MA: MIT Press; 2007. [Google Scholar]
- 8.International Energy Agency CO2 emissions from fuel combustion – highlights. 2011. Available at http://www.iea.org/co2highlights/. Accessed September 1, 2011.
- 9.US Energy Information Administration, US Department of Energy Emissions of greenhouse gases in the United States 2008. Report no. DOE/EIA-0573(2008) 2009. Available at http://www.eia.gov/oiaf/1605/ggrpt/pdf/0573(2008).pdf. Accessed September 1, 2011.
- 10.Bachu S, et al. CO2 storage capacity estimation: Methodology and gaps. Int J Greenh Gas Control. 2007;1:430–443. [Google Scholar]
- 11.National Energy Technology Laboratory Carbon Sequestration Atlas of the United States and Canada, 3rd Ed. 2010. Available at http://www.netl.doe.gov/technologies/carbon_seq/refshelf/atlas/. Accessed September 1, 2011.
- 12.Dooley JJ. Valuing national and basin level geologic CO2 storage capacity assessments in a broader context. Int J Greenh Gas Control. 2011;5:177–178. [Google Scholar]
- 13.Bergman PD, Winter EM. Disposal of carbon dioxide in aquifers in the U.S. Energ Convers Manage. 1995;36:523–526. [Google Scholar]
- 14.Dooley JJ, et al. A CO2 storage supply curve for North America and its implications for the deployment of carbon dioxide capture and storage systems. In: Rubin ES, et al., editors. Proceedings of the 7th International Conference on Greenhouse Gas Control Technologies. Elsevier; 2005. Vol 1: Peer-Reviewed Papers and Plenary Presentations, pp 593–601. [Google Scholar]
- 15.Birkholzer JT, Zhou Q, Tsang CF. Large-scale impact of CO2 storage in deep saline aquifers: A sensitivity study on pressure response in stratified systems. Int J Greenh Gas Control. 2009;3:181–194. [Google Scholar]
- 16.Ehlig-Economides C, Economides MJ. Sequestering carbon dioxide in a closed underground volume. J Petrol Sci Eng. 2010;70:118–125. [Google Scholar]
- 17.Bickle M, Chadwick A, Huppert HE, Hallworth M, Lyle S. Modeling carbon dioxide accumulation at Sleipner: Implications for underground carbon storage. Earth Planet Sci Lett. 2007;255:164–176. [Google Scholar]
- 18.Nordbotten JM, Kavetski D, Celia MA, Bachu S. Model for CO2 leakage including multiple geological layers and multiple leaky wells. Environ Sci Technol. 2009;43:743–749. doi: 10.1021/es801135v. [DOI] [PubMed] [Google Scholar]
- 19.Juanes R, Spiteri EJ, Orr FM, Jr, Blunt MJ. Impact of relative permeability hysteresis on geological CO2 storage. Water Resour Res. 2006;42:W12418. [Google Scholar]
- 20.Ennis-King J, Paterson L. Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. Soc Pet Eng J. 2005;10:349–356. [Google Scholar]
- 21.Riaz A, Hesse M, Tchelepi HA, Orr FM., Jr Onset of convection in a gravitationally unstable, diffusive boundary layer in porous media. J Fluid Mech. 2006;548:87–111. [Google Scholar]
- 22.MacMinn CW, Szulczewski ML, Juanes R. CO2 migration in saline aquifers. Part 2. Capillary and solubility trapping. J Fluid Mech. 2011;688:321–351. [Google Scholar]
- 23.Zoback MD. Reservoir Geomechanics. Cambridge, UK: Cambridge Univ Press; 2007. [Google Scholar]
- 24.International Energy Agency Electricity generation by fuel in the United States (1972–2008) 2011. vailable at http://www.iea.org/stats. Accessed September 1, 2011.
- 25.Wigley TML, Richels R, Edmonds JA. Economic and environmental choices in the stabilization of atmospheric CO2 concentrations. Nature. 1996;379:240–243. [Google Scholar]
- 26.Friedmann SJ, Dooley JJ, Held H, Edenhofer O. The low cost of geological assessment for underground CO2 storage: Policy and economic implications. Energy Convers Manage. 2006;47:1894–1901. [Google Scholar]
- 27.Report of the Interagency Task Force on Carbon Capture and Storage. 2010. Available at http://www.epa.gov/climatechange/policy/ccs_task_force.html. Accessed September 1, 2011.
- 28.Nicot J-P. Evaluation of large-scale CO2 storage on fresh-water sections of aquifers: An example from the Texas Gulf Coast Basin. Int J Greenh Gas Control. 2008;2:582–593. [Google Scholar]
- 29.Hesse MA, Orr FM, Jr, Tchelepi HA. Gravity currents with residual trapping. J Fluid Mech. 2008;611:35–60. [Google Scholar]
- 30.Juanes R, MacMinn CW, Szulczewski ML. The footprint of the CO2 plume during carbon dioxide storage in saline aquifers: Storage efficiency for capillary trapping at the basin scale. Transp Porous Media. 2010;82:19–30. [Google Scholar]
- 31.Hovorka SD, et al. Sequestration of greenhouse gases in brine formations. 2003. Available at http://www.beg.utexas.edu/environqlty/co2seq/dispslsalnt01.htm. Accessed August 1, 2011.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.