Phosphorus-31 MRI of hard and soft solids using quadratic echo line-narrowing

Abstract

Magnetic resonance imaging (MRI) of solids is rarely attempted. One of the main reasons is that the broader MR linewidths, compared to the narrow resonance of the hydrogen (¹H) in free water, limit both the attainable spatial resolution and the signal-to-noise ratio. Basic physics research, stimulated by the quest to build a quantum computer, gave rise to a unique MR pulse sequence that offers a solution to this long-standing problem. The “quadratic echo” significantly narrows the broad MR spectrum of solids. Applying field gradients in sync with this line-narrowing sequence offers a fresh approach to carry out MRI of hard and soft solids with high spatial resolution and with a wide range of potential uses. Here we demonstrate that this method can be used to carry out three-dimensional MRI of the phosphorus (³¹P) in ex vivo bone and soft tissue samples.

Magnetic resonance imaging (MRI) has become an invaluable tool for clinical medicine, fundamental biomedical research, the physical sciences, and engineering (1). Typically, MRI detects only the signal from free water, using just a single nuclear isotope (¹H). Extending the reach of MRI to the study of other elements, and to hard or soft solids, opens new frontiers of discovery. One example is phosphorus (³¹P), which is abundant in both bone mineral and cell membranes, so ³¹P MRI of tissues is, in principle, possible. In practice, however, the slower motion of ³¹P in those environments (compared to ¹H in water) results in much broader MR spectra (Fig. S1), limiting both the attainable spatial resolution and the signal-to-noise ratio (2). In this paper, we describe the use of a pulse sequence to narrow the ³¹P MR spectrum of solids to that of a liquid (3), making high-resolution imaging possible. This line-narrowing MR sequence was discovered in the course of basic research (3–6) initiated by Kane’s proposal (7) to build a quantum computer using phosphorus spins in silicon. Applying field gradients in synch with this sequence, we have obtained high-resolution 3D MR images of the ³¹P in a variety of ex vivo animal bone samples. This is a unique probe of a key element in bone mineral, which complements existing assessments of bone quality. Using the same approach, we have obtained 3D MR images of ³¹P in several ex vivo soft tissues.

Bone is a composite material (8), containing approximately 45% bone mineral by volume (9). Bone mineral is similar to calcium hydroxyapatite (i.e., Ca₁₀(OH)₂(PO₄)₆), but it is less crystalline, and it has a unique stoichiometry (10). The spatial distribution, composition, and quantity of bone mineral are primarily responsible for the compressive strength and stiffness of bone (8–10). While a few ³¹P MRI studies have successfully targeted in vivo (10–12) and ex vivo (10, 13, 14, 15) bone, the broad MR spectra have limited the achievable spatial resolution to no better than 0.5 mm (15) and more typically in the range of 2 mm. There is currently a great need to probe the internal composition of bone on the sub-0.1 mm length scale (16, 17), both to study normal features (osteons, Haversian canals, trabeculae) and to look for signs of disease (i.e. changes in microarchitecture–cortical pores and trabecular perforations, as well as changes in mineral composition). Despite the obvious importance of the mineral fraction to the biomechanical properties of skeletal tissue, few useful nondestructive technologies are available to evaluate changes in its chemical structure and functional microarchitecture. Micro-CT provides high spatial resolution 3D imaging of the electron density (dominated by calcium in the bone mineral; see SI Text) but does not reveal the chemical information provided by MRI. In bone mineral, up to 14% of the phosphate groups are replaced by carbonate groups, and several recent Fourier transform infrared (FTIR) and Raman spectroscopy studies (18, 19) have reported a spatial dependence of the CO₃∶PO₃ ratio that correlates with bone tissue age (e.g., radially out from an osteon center), as well as with nano-indentation measurements of indentation modulus and hardness. Our approach (3)—which has line-narrowed the solid ²⁹Si spectrum by a factor of 70,000—has the potential to push the 3D ³¹P MRI spatial resolution down to the sub-0.1 mm length-scale (isotropic), for ex vivo bone samples.

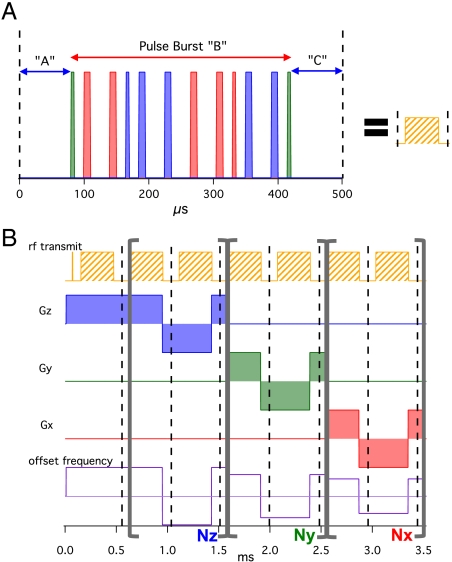
Our technique adopts the spatial encoding strategy pioneered by earlier line-narrowing approaches to the MRI of solids: Repeated pulse blocks null out the internal spin Hamiltonian, while applied magnetic field gradients add in the external spin Hamiltonian (20–23). The key difference is that our pulse block (Fig. 1A) uses a quadratic echo (3) to refocus both the Zeeman (H_Z) and dipolar (H_ZZ) terms in the internal spin Hamiltonian, so it has the unique advantage of working best in the limit H_Z≥H_ZZ (see SI Text). In contrast, the well-known magic echo pulse sequence (24) works best if there is no magnetic shift or broadening (H_Z ≈ 0) during the pulse burst (22, 23). Thus, our pulse block (3) is a better choice to null out the internal spin Hamiltonian of ³¹P in bone [because H_Z≥H_ZZ (25)], and stronger gradients may be used since they can be left on during the pulse burst (see SI Text).

Fig. 1.

Schematic of our imaging sequence. (A) The main pulse block used in our imaging sequences with 90° (thin) and 180° (thick) pulses along the Y (green), X (red), and -X (blue) directions. (B) Diagram depicting the 3D MRI sequence with our pulse block where the loop counters: N_z, N_y, and N_x determine the k-space trajectory. The offset frequency can be set for each loop to place the image center off-center in the FOV. A single k-space point is sampled at each dashed line.

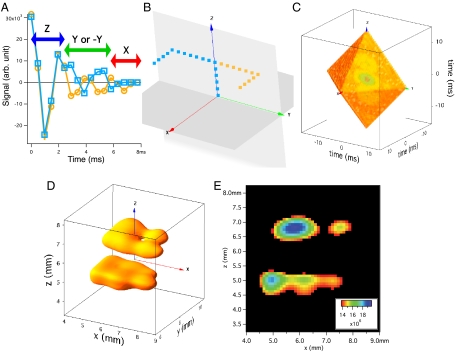
We use these fundamental pulse blocks to build a 3D MRI pulse sequence, shown in Fig. 1B. A nonselective 90° pulse excites the full sample volume, and we acquire a single point in k space after each pulse block. These stroboscopically detected points oscillate due to the effective applied field gradient and pulse frequency offset, f_offset, like a pseudo free induction decay (FID), so this sequence is a hybrid of echo (for internal fields) and FID (for external fields) imaging approaches (26), which enables high spatial resolution. Synchronizing a modulated applied field gradient with the pulse block achieves the desired spatial encoding while eliminating the internal H_Z Hamiltonian (see SI Text). Starting at k = (0,0,0), we sample k space uniformly along Cartesian grid trajectories by systematically varying the loop parameters, N_x, N_y, and N_z (with N_x + N_y + N_z = constant). The real parts of two measured pseudo-FIDs are plotted in Fig. 2A, (although only the first 17 windows of each pseudo-FID are plotted here). They are the same through the N_z loop (equal steps along +k_z), but they diverge in the N_y loop, with steps along +k_y (-k_y) for the yellow (blue) points due to flipped G_y modulation patterns. They have the same G_x modulation in the final N_x loop (steps along +k_x). The two trajectories through 3D k space are depicted in Fig. 2B and for simplicity we will refer to their loop patterns as {Z,Y,X} (yellow) and {Z,-Y,X} (blue). Each pseudo-FID is a distinct experiment requiring time, T_rep, per repetition.

Fig. 2.

Figure showing the mapping of acquired data onto k space and the resulting image. (A) Plot showing real data acquired (from the dry bovine bone sample) in the first 17 windows for two different trajectories in k space. Starting at k = (0,0,0), both the yellow-circle and blue-square points take five steps forward along the positive k_z direction (N_z = 5). Next the yellow circles (blue squares) move seven steps forward (backward) along the positive k_y direction (N_y = 7). Finally, both the yellow circles and blue squares step forward along the positive k_x direction (N_x = 19), for a total of 32 points. (B) A 3D plot of these two trajectories in k space. See Movie S1 to see how this mapping takes place. (C) Three-dimensional octahedron of k-space points measured with our imaging scheme (plotting the magnitude of the complex points in the time domain). The imaging time was just under 47 h. (D) Isosurface rendering of the 3D image of ³¹P in two dry bovine bone blocks separated by a 1.1-mm gap obtained by Fourier transformation of Fig. 2C. The spatial resolution is 0.428 × 0.428 × 0.353 mm³. Note the thru-hole in the top block, which was drilled using a 0.343-mm-diameter drill bit. The sample dimensions are 4.9 × 2.6 × 1.4 mm³ (bottom bone) and 4.2 × 2.4 × 1.4 mm³ (top bone). The isosurface value was chosen to show the presence of the thru-hole and is 65% of the maximum signal value. See Movie S2 for a better view of this 3D isosurface. (E) A 2D slice of the 3D data (zero-filled by a factor of four) with thickness of 0.107 mm. The cutoff for the minimum of the color scale is the isosurface value used in Fig. 2D to clearly show the thru-hole in the top bone and two partial holes in the bottom bone, made by the same 0.343-mm-diameter drill bit.

We vary the k-space trajectories sampled by a set of 1D pseudo-FIDs (i.e., varying N_z,N_y,N_x), in order to fill a Cartesian grid in 3D k space. First, we co-add the “p” complex data points that should correspond to the same k value. Second, we divide the sum at each k value by the corresponding p (e.g., in Fig. 2B, p = 2 for the co-added data at k = (0,0,0), while p = 1 at the other end of the trajectories). Fig. 2C shows an octahedron of 3D k-space points filled in this manner. The upper half of the octahedron lying in octants 1–4 is directly filled using the loop patterns: {Z,Y,X},{Z,Y,-X},{Z,-Y,X},{Z,-Y,-X}, respectively. The same data is used to complete the lower half of the octahedron (in octants 5–8), using the Hermetian symmetry of k space (26). A total of N_pnts = 32 points were acquired in each of the 1D pseudo-FIDs, which defines the octahedron’s surface (0 ≤ N_z,N_y,N_x ≤ 31 for each trajectory, with the constraint N_z + N_y + N_x = 31). This loop pattern uses a total of (N_pnts/2)(N_pnts + 1) = 528 pseudo-FIDs to fill each octant.

Fourier transformation of the k-space data yields a 3D ³¹P MR image (Fig. 2 D and E). Because our pulse block removes constant resonance offsets, susceptibility broadening, chemical shifts, and displacements from the isocenter are not issues. Our method also can easily be adapted to radial sampling of k space, rather than Cartesian, because the k = (0,0,0) point is measured particularly well by the first pulse block of our sequence.

Results

The images in Fig. 2 D and E, obtained using our pulse sequence, show the features of a sample composed of two dry blocks of bovine cortical bone separated by a 1.1-mm masking tape spacer (see Materials and Methods). The upper block has one thru-hole, and the lower block has two partial holes made by a #80 drill bit (0.343 mm-diameter). The threshold value chosen for the isosurface and 2D slice gives a clear view of the hole but does not depict the outer-surface of the blocks. However, after checking various 2D slices and different isosurface values, the image does match the spatial dimensions of the sample. These findings are consistent with our estimate of the spatial resolution of 0.428 × 0.428 × 0.353 mm³, the best yet reported for ³¹P MRI in bone.

This demonstrates that the achievable spatial resolution of the image is no longer limited by the natural linewidth. For comparison, if we were to implement “solid-state ³¹P MRI” (15) on our system (see Materials and Methods) using the same 30 mT/m gradients, the natural ³¹P linewidth would limit the spatial resolution to (5.9 mm)³, which is larger than the entire volume shown in Fig. 2D. Because quadratic echo line-narrowing overcomes this limitation, the achievable spatial resolution of our technique is limited only by the specifications of our MRI system (see Materials and Methods), which can and will be improved upon in the future.

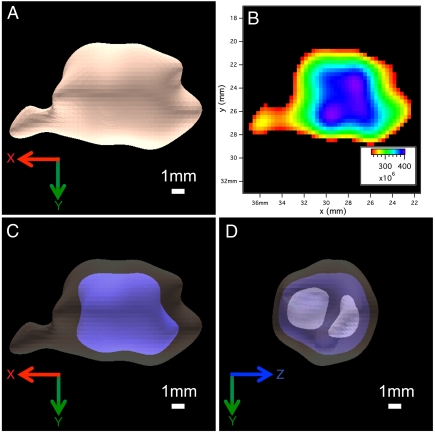
Our approach works just as well (or better, due to a shorter T₁) on wet, marrow-filled bones. Our ³¹P MRI has been applied to store-bought sections of a pork rib (mostly cortical bone), shown in Fig. 3, and a rabbit femoral head (largely trabecular bone), shown in Fig. 4; both are imaged in a sealed plastic cryotube, filled with phosphate buffered saline (PBS) solution (see Materials and Methods). In the pork rib, the thick outer shell of cortical bone that surrounds the marrow space dominates both the 3D surface plot (Fig. 3B) and the 2D slice (Fig. 3C). The trabecular bone in the marrow space is not visible, given the relatively low spatial resolution, (1.19 mm)³. On the other hand, the interconnected plates of trabecular bone on the interior of the rabbit femoral head (seen in the micro-CT 2D slice shown in Fig. 4B) are clearly visible in both the 3D surface plot (Fig. 4C) and a 2D slice (Fig. 4D), given the higher spatial resolution of that dataset, approximately (0.46 mm)³. A series of 2D slices (Fig. 4 E–J) show a virtual sectioning of the 3D rabbit femoral head dataset, which demonstrates the potential of this technique to provide nondestructive quantitative maps of phosphorus on the interior of complex 3D samples.

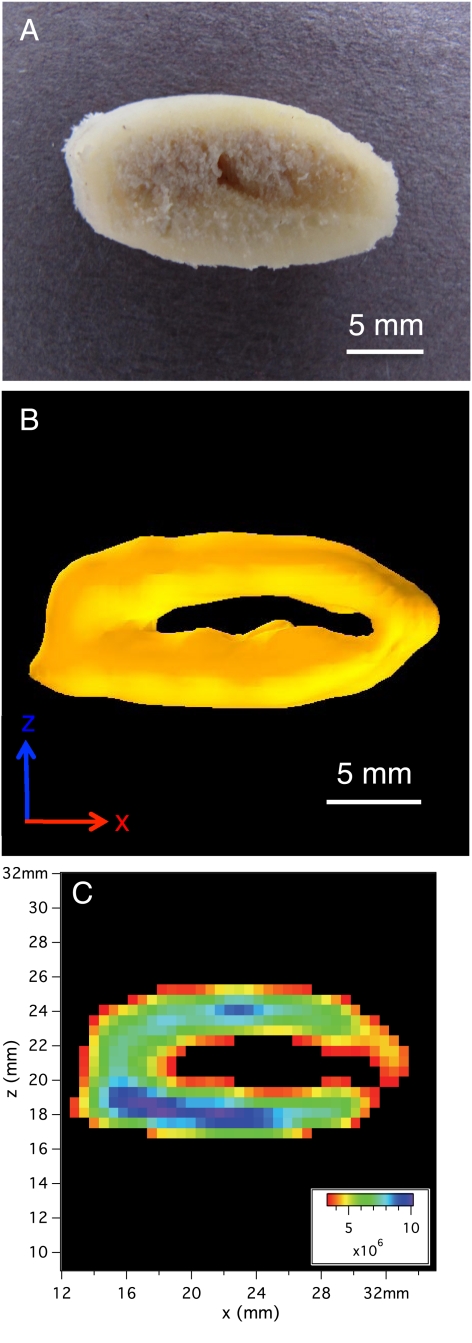
Fig. 3.

Images of the ex vivo pork rib sample. (A) Photo of the marrow-filled pork bone sample. (B) Isosurface rendering of the 3D image of ³¹P in pork rib in PBS solution. The isosurface value is 33% of the maximum signal value and shows the thick cortical bone ring. The spatial resolution is (1.19 mm)³ and the imaging time was 35.2 h. See Movie S3 for a better view of this 3D isosurface. (C) A 2D slice of the 3D data shown in Fig. 3B (zero-filled by a factor of two) with thickness of 0.595 mm.

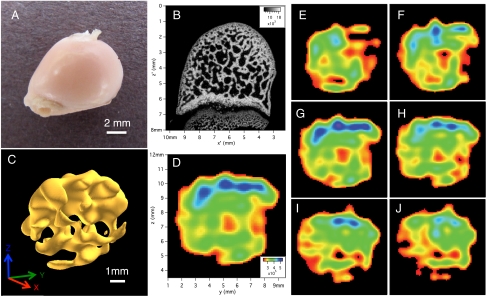
Fig. 4.

Images of the ex vivo rabbit femoral head sample. (A) Photo of the rabbit femoral head sample. (B) Two-dimensional slice of micro-CT data. The 2D resolution is (0.0185 mm)² and the slice thickness is 0.0185 mm. (C) Isosurface rendering of the 3D image of ³¹P in rabbit femoral head in PBS solution. The isosurface value is 60% of the maximum signal value and shows trabecular bone. The spatial resolution is 0.458 × 0.458 × 0.422 mm³ and the imaging time was 70.4 h. (D) A 2D slice of the 3D data shown in Fig. 3C (zero-filled by a factor of four) with thickness of 0.115 mm. Note that these axes are different from those used in Fig. 4B and the orientation of the bone is different than in both Fig. 4 A and B. Here the “flat end” of the bone is on the right edge. (E–J) Multiple 2D slices (each 0.115 mm thick) cutting along the x axis going in the positive x direction (with a 0.458-mm step size) through the 3D dataset shown in Fig. 4C, using the same color scale and FOV as in Fig. 4D. The 2D slice shown in Fig. 4D is between slices shown in Fig. 4G and Fig. 4H.

The theoretical foundation (3) of our technique shows that it is immediately applicable to any spin-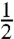 with a Hamiltonian where H_Z≥H_ZZ. As another potential biomedical target, soft tissues have phosphorus concentrated in the membranes, metabolites, RNA and DNA of cells (Fig. S2). This leads to a complicated, multipeak ³¹P MR spectrum (including a broad membrane peak and narrow metabolite peaks), which would ordinarily be a poor choice for high-resolution MRI (27). However, our quadratic echo pulse block (Fig. 1A) narrows the entire ³¹P spectrum into a single peak (see SI Text), enabling high-resolution imaging. Using our sequence, we have carried out 3D ³¹P MRI on a variety of ex vivo soft tissue samples, including fixed neural stem cell-endothelial cell hydrogel co-cultures, mouse liver, mouse heart, and a variety of mouse brains. Fig. 5 shows the ex vivo 3D ³¹P MR image of a mouse brain in PBS (see Materials and Methods). This is a functionally different kind of MR image, because conventional ¹H MRI probes the intracellular and extracellular free water (26). A rough calculation of the phosphorus reservoirs in a typical cell suggests that the membrane signal represents approximately 75% of the total ³¹P MRI signal, depending on the density of mitochondria (Fig. S2). This membrane signal is rarely studied due to its broad MR linewidth but may provide new insights into cellular and tissue function that compliments the information revealed by ¹H MRI.

Fig. 5.

Three-dimensional ³¹P MR image of an ex vivo mouse brain. (A) Isosurface rendering of the 3D image of ³¹P in mouse brain in PBS solution. The isosurface value is 50% of the maximum signal value and shows the brain stem on the left. The spatial resolution is (1.33 mm)³ and the imaging time was 88.7 h. (B) A 2D slice of the 3D data shown in Fig. 5A (zero-filled by a factor of four) with thickness of 0.332 mm. The cutoff for the minimum of the color scale is the isosurface value used in Fig. 5A. (C) Two isosurface renderings of the 3D image of ³¹P in mouse brain in PBS solution. The highlighted inner isosurface value is 70% of the maximum signal value and the outer isosurface is the same as in Fig. 5A. (D) Three isosurface renderings of the 3D image of ³¹P in mouse brain in PBS solution, now rotated by 90° relative to those shown in Fig. 5 A and C. The highlighted most inner isosurface value is 90% of the maximum signal value, the middle isosurface is the same as in Fig. 5C, and the outer isosurface is the same as in Fig. 5A. See Movie S4 for a better view of all three of the 3D isosurfaces depicted.

Discussion

Unlike conventional ¹H MRI—which often use T₁ or T₂ weighting to provide contrast (26)—all the ³¹P MR images shown here reveal the ³¹P density in each sample. Additional contrast mechanisms will be explored in future work. These images do not represent the ultimate resolution limits of our line-narrowing approach, rather they represent what is currently achievable with our existing 4 Tesla MRI system (see Materials and Methods). At 12 Tesla, we project that image resolution will improve by another factor of 1,000, if the line-narrowing of ³¹P in bone works as well as it did for ²⁹Si in crystalline silicon (3). This may require adding some form of proton decoupling to achieve resolution on the 0.001 mm length scale in bone. Of course, other factors will impact the limit of resolution such as sample size, gradient slew rate, signal-to-noise ratio (SNR), and imaging time, but pushing 3D ³¹P MRI toward, or below, the resolution limit of micro-computed tomography (micro-CT), FTIR, Raman, etc. is now feasible and of considerable importance (16–19).

While our method has great promise, it also has limitations. First, in vivo MRI cannot use the strong rf pulses and rapid gradient changes shown in Fig. 1B, for reasons of safety (26). Consequently we are initially focusing on applications that can use ex vivo methods such as our ³¹P MRI of bone. A recent review (16) summarized 15 state-of-the-art methods to assess bone quality and listed 12 as primarily or exclusively ex vivo techniques. Our data indicate that ³¹P microstructure will provide important new information that complements what can be learned from these existing techniques. Second, despite making the MR spectrum as narrow as that of a liquid, one still needs to address the long spin-lattice relaxation time (T₁) of a solid (e.g., 52 s for dry bone, 26 s for wet bone, and 3.4 s for the mouse brain at 4 Tesla). For example, the data in Fig. 2 used a repetition time 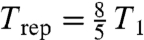, meaning that it took 47 h to acquire without signal averaging. Several acceleration strategies are currently being investigated (see SI Text) including: (a) using T_rep ≪ T₁, (b) using a driven equilibrium technique, and (c) using sparse MRI to undersample the k space in a pseudo-random fashion (28). We have very encouraging preliminary results using this third strategy—an image obtained in just 88 min with sparse sampling (Fig. S3) looks similar to Fig. 2D, which took 47 h using normal, dense sampling. Third, the SNR depends on a sample’s solid fraction (e.g., for soft tissue, the ³¹P content of a cell is approximately 1% of the ¹H in free water; Fig. S2). Practically speaking, this means that less dense solid samples will require larger voxel dimensions or more signal averaging.

We have shown here, and in previous work (3), that our quadratic echo line-narrowing technique works in a wide variety of samples with H_Z≥H_ZZ—from a nearly perfect crystalline silicon sample to very complicated biological samples with phosphorus located in bone mineral or cell membranes. This sequence offers a solution to the long-standing problem of MR imaging of solids (2). In addition to biomedical applications, this approach may be applied to the study of geological samples (29), archaeological artifacts (30, 31), and granular physics (32, 33), to name but a few examples. Very generally, quadratic echo imaging represents the ultimate limit of Hamiltonian design: The entire internal Hamiltonian is removed, and the desired external Hamiltonian is added to drive the coherent evolution of a quantum system. Only a small portion of the available parameter space has been explored to date, and new applications of the quadratic echo are very likely to emerge in future work.

Materials and Methods

All three of the bone samples used in this report were purchased at local grocers. The sample depicted in Fig. 2 and Fig. S3 is composed of two dry blocks of bovine cortical bone, which were each cut from a segment of white, cleaned bovine femur (a natural dog chew purchased at Petco, Hamden, CT). The two blocks are separated by a ≈1.1 mm masking tape spacer. The upper block has one thru-hole, and the lower block has two partial holes made by a #80 drill bit (0.343-mm diameter). Teflon tape was wrapped around the outside of the two-block assembly to hold it together and to center it in the solenoidal coil. Movie S2 shows a surface plot of the bovine bone block image, rotating in place.

The sample used in Fig. 3 and Figs. S5 and S6 is a marrow-filled section of a pork rib bone, which was cut from a whole fresh pork rib (purchased at Ferraro’s Market, New Haven, CT). The soft tissue was removed, the rib surface was washed by hand, and the marrow space was left intact. The rib bone section was placed in a cryotube vial (NUNC, catalog # 368632), which was then filled to volume with phosphate buffered saline (PBS) solution to keep the sample hydrated. The thick outer shell of cortical bone that surrounds the marrow space dominates both the 3D surface plot (Fig. 3B) and the 2D slice (Fig. 3C). The trabecular bone in the marrow space is not visible, given the relatively low spatial resolution (1.19 mm)³. Figs. S5 and S6 highlight this issue by comparing micro-CT and ³¹P MRI images of the same specimen. Movie S3 shows a surface plot of the pork rib image, rotating in place. Fig. 3A shows a photo of this sample taken several months after we have imaged it using MRI or micro-CT. It was kept in a refrigerator in the interim and then gently washed with soap and water and dried in order to take the photo.

The sample used in Fig. 4 is a marrow-filled rabbit femoral head. The femoral head was cut from one femur of a whole frozen rabbit (purchased at Ferraro’s Market, New Haven, CT). The sample was thawed, the soft tissue was removed, the surface of the femur washed by hand, and the marrow space was left intact. The rabbit femoral head was placed in a cryotube vial, which was then filled to volume with PBS. The plate-like trabecular architecture of the interior femoral head is clearly visible in both the 3D surface plot (Fig. 4C) and 2D slices (Fig. 4 D–J), given the high spatial resolution of that dataset (0.458 mm)³. Fig. 4A shows a photo of this sample taken several months after we have imaged it using MRI or micro-CT. It was kept in a refrigerator in the interim and then gently washed with soap and water and dried in order to take the photo.

The sample used in Fig. 5 (and Movie S4) is an ex vivo brain from a CD-1 mouse. CD-1 mice were bred and housed at the Yale University Animal Care facilities in accordance with approved procedures and were obtained from laboratory stock derived through breeders from Charles River Laboratories (Wilmington, MA). All animal studies were performed with approval and in full compliance with the Yale University Animal Care committee (protocol 2008-07366) and with National Institutes of Health regulations. A mature adult (12-week-old) CD-1 mouse was injected with ketamine (100 mg/kg) and xylazine (10 mg/kg) 5 min prior to sacrifice. Intracardiac perfusion was performed with PBS, immediately followed by 4% paraformaldehyde in PBS. The brain was excised, then postfixed with 4% paraformaldehyde in PBS overnight. The fixed brain was rinsed with PBS and inserted into a cryotube using small pieces of teflon as spacers to position it in the center of the vial, which was then filled to volume with PBS.

All ³¹P MR images reported here were acquired at the Yale University Medical Schools Magnetic Resonance Research Center (MRRC), using the Bruker Avance 4.0 Tesla/31 cm animal system, running ParaVision 3.0.1. (See specs at http://mrrc.yale.edu/resources/magnets/animal/bruker40t.aspx.) The 15-cm bore, actively shielded, Magnex gradient coil set has a maximum gradient strength of 150 mT/m for all three axes, although the largest gradient magnitude used for imaging in this paper was 30 mT/m (see Table S1). Each gradient coil (X, Y, Z) is connected to its own AE Techron 8607 gradient amplifier (150 V/ 130 A). The Bruker’s “ramp off” mode was used to achieve the fastest possible transients (about 0.06 ms to switch from +30 mT/m to -30 mT/m). At 4 Tesla, the ³¹P resonance frequency is 68.94 MHz, and the signal was detected using home-built solenoidal coils (matched to the sample sizes). The same coils were used to generate the rectangular pulses used (e.g., in Fig. 1A), with T₉₀ in the range of 0.004–0.008 ms. The imaging data were acquired stroboscopically (e.g., in Fig. 1B, Fig. 2 A and B and Movie S1) using the Bruker’s analog acquisition mode. Short bursts of 5 complex points were sampled using an external dwell time of 0.002 ms, around the end of each pulse block of duration ≈0.5 ms (Fig. 1 and Fig. S4). The built-in 125-kHz low-pass filter of the Bruker Avance system was supplemented by a second inline filter (a Krohn-Hite Model 3940, dual-channel, 15-kHz low-pass Bessel) inserted just before the HADC/2.