Fluorescence microscopy for simultaneous observation of 3D orientation and movement and its application to quantum rod-tagged myosin V

Abstract

Single molecule fluorescence polarization techniques have been used for three-dimensional (3D) orientation measurements to observe the dynamic properties of single molecules. However, only few techniques can simultaneously measure 3D orientation and position. Furthermore, these techniques often require complex equipment and cumbersome analysis. We have developed a microscopy system and synthesized highly fluorescent, rod-like shaped quantum dots (Q rods), which have linear polarizations, to simultaneously measure the position and 3D orientation of a single fluorescent probe. The optics splits the fluorescence from the probe into four different spots depending on the polarization angle and projects them onto a CCD camera. These spots are used to determine the 2D position and 3D orientation. Q rod orientations could be determined with better than 10° accuracy at 33 ms time resolution. We applied our microscopy and Q rods to simultaneously measure myosin V movement along an actin filament and rotation around its own axis, finding that myosin V rotates 90° for each step. From this result, we suggest that in the two-headed bound state, myosin V necks are perpendicular to one another, while in the one-headed bound state the detached trailing myosin V head is biased forward in part by rotating its lever arm about its own axis. This microscopy system should be applicable to a wide range of dynamic biological processes that depend on single molecule orientation dynamics.

Single molecule fluorescence imaging techniques are being increasingly used to observe the dynamic properties of single molecules like spatial orientation, which provides information on a protein’s three-dimensional (3D) motility and its conformational changes (1, 2). These techniques can be grouped into two different classes: intensity distribution techniques and interference pattern techniques. In the first class, 3D orientation is determined by comparing fluorescence intensities among several excitation or detection polarizations. For example, in single-molecule fluorescence polarization microscopy (3), the dye is excited by multiple polarized beams incident from different directions. The resulting emission is split with respect to its polarization and detected with avalanche photodiodes, which allows for sensitivity to the 3D orientation of a single dye’s transition dipole moments. The second class takes advantage of single molecule emission patterns created by defocusing. Defocused imaging reveals additional structures in single-molecule emission patterns that depend on the orientation of the emitting dipole (4–7). The 3D orientation is obtained by comparing the defocused images with corresponding calculated model images. This technique can be used to determine both the position and orientation of the dye. However, because the defocused image is spread over a greater number of pixels, the image inherently has poor position accuracy. Furthermore, in most orientation-determination techniques, time consuming fitting procedures are required. Consequently, the limitations of these techniques necessitate the development of more general methods suited for visualizing 3D orientation dynamics.

Here we describe one such microscopy system that compares four fluorescence polarization components of a single molecule to determine the fluorescence anisotropy, which is then used to calculate the 3D orientation of the molecule (8). This method requires only that one collect fluorescence counts at four different polarizations followed by relatively simple mathematical analysis. To show the effectiveness of this technique, we observed the axial rotation of actin filaments sliding over myosin molecules fixed onto a glass surface by measuring the polarization of individual rhodamine phalloidin fluorophores sparsely bound to the filaments. We also applied quantum rods (Q rods), which exhibit linearly polarized emissions, as an alternative probe to study myosin molecular dynamics, as Q rods allow for better accuracy when simultaneously measuring position and 3D orientation. Finally, we measured Q rods bound to the stalk of single myosin V molecules to investigate rotation around the myosin axis. These observations led us to identify previously unseen features of myosin translocation that should help clarify its walking mechanism.

Results

3D Orientation Measurement.

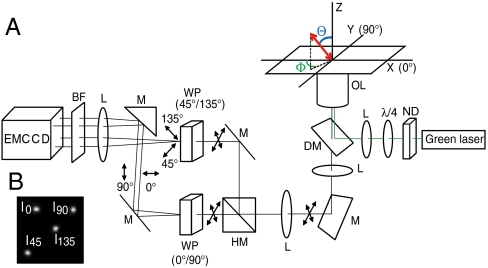
A schematic of our optical system is shown in Fig. 1. Q rod-conjugated myosin V movement and actin filament sliding were imaged by epiillumination. The fluorescent probe was excited at 532 nm by a laser beam that was circularly polarized by a quarter-wave plate. The fluorescence was collected by an objective lens and split equally into two beams by a half-mirror. Each beam was further split into two perpendicular polarization components (0° and 90°, 45° and 135°, respectively) by a pair of Wollaston prisms. The four polarization components (0°, 45°, 90°, and 135°) were focused onto an EMCCD camera through a focal length lens and emission bandpass filter. Angular values of the in-plane and tilt angles (Φ, Θ) in the microscope coordinate frame were rotated into the actin filament coordinate frame (β, α) by defining the direction of the probe motion as the polar axis in the actin frame of reference (2). β is the polar angle with respect to the forward moving end of the actin filament and α is the azimuthal angle around the filament. Due to twofold rotational symmetry in a single fluorescent probe’s dipole moment, there is a fourfold degeneracy in the determined orientation, meaning Φ and Θ are indistinguishable from 180° + Φ and 180°−Θ, respectively. Similarly, the azimuthal and axial angles in the actin frame, α and β, are indistinguishable from α-180° and 180°-β, respectively.

Fig. 1.

(A) Experimental apparatus. Cartesian coordinates: the z-axis is parallel to the optical axis; the x- and y-axes are in the plane of the glass. Polar coordinates: the tilt angle, Θ, is the angle of the probe with respect to the +z axis; the in-phase angle, Φ, is the azimuthal angle of the probe in the x - y plane. The fluorescence is equally split into two beams by a half-mirror. Each beam is further split into two polarization components by a Wollaston prism resulting in four polarization components (0°, 45°, 90°, and 135°) that are focused onto an EMCCD camera through an emission bandpass filter and focal length lens. ND, neutral density filter; λ/4, quarter-wave plate; L, lens; DM, dichroic mirror; OL, objective lens; M, mirror; HM, half mirror; WP, Wollaston prism; BF, emission bandpass filter. (B) Fluorescent image of a fluorescent latex bead.

Polarization Factor of Q Rods.

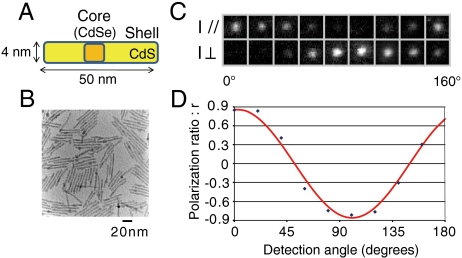
It has been reported that emissions from Q rods with aspect ratios greater than 10∶1 approximate linear polarization (9). Our synthesized Q rods have an average aspect ratio of 13∶1 (Fig. 2 A and B). Luminescence images from one such Q rod show the relative intensity between the two perpendicular polarization directions changes with the detection angle (Fig. 2 C and D). The polarization factor, ρ, for this Q rod was determined to be 86% (Materials and Methods). Because we used an objective lens with a large numerical aperture (N.A. = 1.45) to depolarize the light, our experimental setup has a ρ limit of approximately 90%, which confirms emissions from our synthesized Q rods have linear polarization.

Fig. 2.

Quantum rods. (A) Schematic of a synthesized CdSe/CdS Q rod. (B) Transmission electron microscopy image of Q rods. The Q rod has an aspect ratio of 13∶1. (C) Luminescence images of a single Q rod simultaneously recorded in two perpendicular polarization directions at detection angles ranging from 0° to 160°. (D) The intensity ratio, r = (I // -I⊥)/(I // +I⊥), for the luminescence images in (C) (blue dots) fitted with a sinusoidal function (red line).

Orientation of Q Rods on a Glass Surface and Angle Determination Accuracy.

Φ and Θ of a given Q rod attached to a glass surface were measured with 33 ms time resolution. The results show that Φ distributed almost uniformly from 0° to 180°, while Θ mostly converged to 90°. These results suggest that Q rods attach to a glass surface with their long axis parallel to the surface, whereas their directions are random (Fig. S1).

Noise in the system risks causing the calculated orientation to deviate from its true values. The extent of the error, (δΦ, δΘ), depends on the intensity fluctuations, δI, and the orientation itself. Surface plots for δΦ and δΘ are shown in Fig. S2. The vertical axis represents the standard deviation of a calculated quantity at a specific orientation (Φ, Θ). δΦ contains singularities at Θ = 0° and 180°. This result is because the function for δΦ has a sin²Θ factor in the denominator. Unlike δΦ, δΘ has an additional singular region at Θ = 90°, because a sin 2Θ factor rather sin²Θ appears in the denominator (10).

Axial Rotation of the Actin Filament.

Several reports have indicated that under various conditions, myosin produces a torque in conjunction with axial force production while stepping along the actin filament (11–14). In order to test our method, we observed actin filaments rotations about the filament axis while the filaments were sliding over myosin molecules fixed onto a glass surface by measuring the polarization of individual rhodamine phalloidin fluorophores sparsely bound to the filaments with time resolutions between 100 and 300 ms (Movie S1). The 3D orientation was measured in the microscope coordinate frame (Φ, Θ) and in the actin filament coordinate frame (β, α) (Fig. 3A). For a filament that is uniformly rotating about its axis, β should be approximately constant and constrained between 0° and 90°, while α should increase (right-handed pitch) or decrease (left-handed pitch) linearly and be constrained within −180° and 180°. Orientations in a given frame were determined based on the orientations measured in the previous frame such that the degree of rotation was minimized. Both Φ and Θ should oscillate 90° over time because β was constant at 45° (Fig. 3B). In fact, Θ only oscillated 45° (Fig. 3C). This result is because of the twofold rotational symmetry discussed above, which cannot distinguish angles between 90°+x and 90°-x (0° ≤ x ≤ 90°). For similar reasons, α is periodic rather than linear. Despite twofold rotational symmetry making α periodic rather than linear and therefore preventing us from determining the direction of rotation, we confirmed that an actin filament rotates about its axis during translocation at an average rotational pitch of 0.59 ± 0.3 μm (mean ± SD) by measuring the angular change of the probe during myosin motility, a result consistent with a previously reported value (14).

Fig. 3.

Axial rotation of actin filaments. (A) Reference frame of the actin filament. β is the polar angle with respect to the forward moving end (+Z_A) of the actin filament; α is the azimuthal angle around the actin filament. (B), (C) Angles in the actin frame (β, α) and microscope frame (Φ, Θ) are plotted over time. Both Φ and Θ oscillate with time, whereas in the actin frame, β is constant (45°) while α oscillates. The rotation pitch in this example is 0.5 μm. Error bars are SD.

Myosin V Rotation Around Its Own Axis.

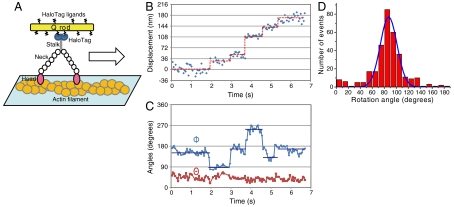
We also observed the rotation of myosin molecules around their axis by measuring the orientation of Q rods attached to myosin V stalks at 50 ms time resolution (Fig. 4A and Movie S2). Myosin V is a dimeric motor protein that takes 36 nm processive steps along actin filaments in a hand-over-hand manner by using the chemical energy from ATP hydrolysis (15–18). Myosin V consists of two identical heavy chains, each of which composes a motor domain that hydrolyzes ATP, a neck domain that serves as a lever arm, a coiled-coil domain (stalk) with which the two heavy chains interact, and a globular cargo-binding domain (19).

Fig. 4.

Displacement and 3D orientation of Q rod-tagged myosin V at 2 μM ATP. Data were acquired every 50 ms. (A) Schematic showing how myosin V rotation around its own axis was measured. A Q rod was bound to the myosin V via two HaloTags at the C terminus. (B) Myosin V position. Blue circles, raw position data analyzed by FIONA; red lines, the average position within a dwell period. (C) Changes in Φ and Θ. Blue circles, raw Φ values; blue lines, dwell-averaged Φ. Φ changes 90° per step. Red circles, raw Θ values. Error bars are SD. (D) Histogram of the average Φ rotation during myosin V stepping. Peak is 87° (n = 320).

We observed 49 Q rods that processively moved with a regular 36 nm step. Of these 49 Q rods, 43 Q rods showed 90° rotations. Only these 43 Q rods were used in the analysis. The remaining 6 Q rods may have been incorrectly attached to myosin V so that their angles were insensitive to any rotations.

Fig. 4B shows the position of a Q rod-conjugated myosin V translocating at 2 μM ATP, while Fig. 4C shows the corresponding time trajectories of Φ and Θ. These results show the myosin molecule rotated approximately 90° around its own axis during each step. Sometimes rotational motions not associated with normal steps were also detected (Fig. S3B, arrows). Fig. 4D shows a histogram of Φ per step, with the average being 87 ± 12° (mean ± SD). Θ was stable at 40°. However, our method is influenced by the degree of anisotropy in the fluorescence when estimating Θ. If a fluorescent molecule wobbles faster than the measurement time, it will be excited and emit fluorescence at different orientations during a measurement, which will cause the degree of anisotropy in the fluorescence to be small relative to the static fluorescent molecule resulting in an underestimated Θ. This concern does not apply to Φ because the different orientations cancel out.

Discussion

We here used single molecule fluorescence polarization to measure the orientation of individual Q rod probes. Unlike other methods, ours does not require obtaining a spatially distributed intensity pattern. Instead, it collects a sufficient number of photons at four different polarizations. Orientation can then be calculated by a relatively simple set of equations. Further, our method does not need to use excitation polarization. To illuminate a probe uniformly in the x - y plane, we used epiillumination and a circularly polarized beam for the orientation measurements. This method should be applicable to probes that produce linear polarizations such as gold nanorods (20).

The error surfaces, δΦ and δΘ, exhibit different orientation dependencies (Fig. S2), consistent with their trigonometric periodicities. Both show large deviations when Θ is near 0° or 180°, while δΘ also shows large deviations when Θ is near 90°. This large deviation is because the A/(G - B) term in Eq. 3 (Materials and Methods) is not restricted to the range of (0, 1) due to noise in the system, giving no solution for sin Θ when Θ is close to 90° (10). However, we estimated the orientation by using a fitting procedure that minimizes the deviations of the predicted and measured polarized fluorescence intensities so that the orientation (Φ, Θ) can be estimated even when Θ is close to 90°.

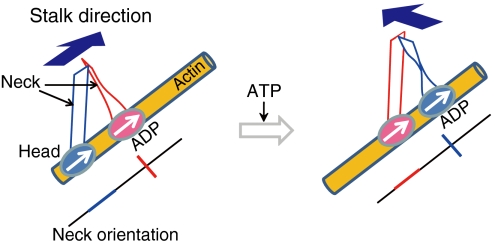
We previously found that a fluorescently labeled actin filament can be rotated by myosin V fixed to a glass surface (21). In the present study, we directly observed myosin rotations by simultaneously measuring myosin steps and orientations, finding myosin V rotates 90° for each 36 nm step. Based on these results, we assume that the two neck domains make a 90° angle at the neck-neck junction and that during the two-headed bound state the neck in the lead head is perpendicular to the actin filament (Fig. 5). This assumption is consistent with several crystal structure studies of myosin II, which have indicated different nucleotide-dependent twists in the myosin light chain domains that may represent the pre- and postpower stroke states (22–24).

Fig. 5.

Myosin rotation during steps. Myosin V is represented by two ovals and two ribbons, which correspond to the head and neck domains, respectively. The orientation of each neck is indicated by the red and blue lines below each cartoon. The actin filament is represented by the yellow cylinder. In the two-headed bound state, the angle between the two necks is 90° at the neck-neck junction. Arrows inside the ovals and above the ribbons indicate the directions of the heads and stalk, respectively.

When ATP binds to the myosin, the rear head (blue) dissociates from the filament, releasing strain on the lead head (pink). This release biases the detached head toward the forward site where it uses Brownian motion to search and bind the forward actin binding site (25, 26). The detached head must twist 90 ° to bind to the actin filament so that myosin can again take the two-headed bound state. The binding is facilitated by a recovery stroke, which entails an angle change at the head-neck junction of the detached head (27).

Our model suggests there exists an axial component in the power stroke and that strain release caused by the rotation of the leading head results in the entire molecule rotating. This myosin molecule differs from another motor protein, kinesin which has been suggested to either not rotate its stalk or rotate it 180° (28).

However, we cannot determine the handedness of the rotation because (i) 36 nm steps were completed within a single video frame, meaning the rotational motion during a single step could not be resolved, and (ii) twofold rotational symmetry of the dipole prevented us from determining the rotational direction.

We also observed rotational motion by myosin that did not associate with stepping (Fig. S3B, arrows). This result suggests that rotational motion can occur when a head dissociates from the actin filament spontaneously. High speed atomic force microscope (29) and fluorescence microscopy (30) have shown that in the two-headed bound state, each head briefly dissociates from the actin filament and that these dissociations may associate with < 10 nm steps, suggesting tiny hops between neighboring actin sites. Our results indicate the stalk rotates during these hops too. Thus, it is possible the myosin rotation angle varies with the landing position of the trailing head. This flexibility in the rotation angle may be functionally advantageous, as it should help myosin avoid any obstructions in the crowded actin network of a cell by allowing it to adopt to different conformations to maximize the probability that the heads will alternate between the lead and rear positions during motility. Our model can also explain why in our previous study (21) an actin filament underwent two 90° Brownian rotations per 36 nm myosin V step, while in the present study only one 90° rotation was seen. In the previous study, myosin V was fixed onto a glass surface at its tail end, whereas in this one the tail end is free. This difference would cause the heads to be antiparallel in ref. 21, but perpendicular here when myosin V is in the one-head bound state.

In conclusion, we have developed a technique for measuring the three-dimensional orientation of a fluorescent probe. By labeling myosin V molecules with Q rods, we propose an asymmetric hand-over-hand model in which the detached trailing myosin head is biased forward in part by rotating the lever arm about its own axis. This microscopy system should have particular applicability to biophysical studies that investigate single molecule orientation dynamics.

Materials and Methods

Theoretical Model for 3D Orientation Measurements.

Our 3D orientation measurements were based on the theory by Fourkas (8). Fluorescence from the molecule is collected by an infinity-corrected and polarization-preserving high-N.A. objective with a light-collection cone angle of α = sin^-1(N.A./n), where in our experiments N.A. = 1.45 and the refractive index n = 1.51. We define the z-axis as the optical axis. By defining Φ as the in-plane angle and Θ as the tilt angle from the optical axis, the dipole orientation (Φ, Θ) can be determined (Fig. 1). Intensities collected at four different polarizations, 0°, 45°, 90°, and 135° have been shown to have the following respective forms:

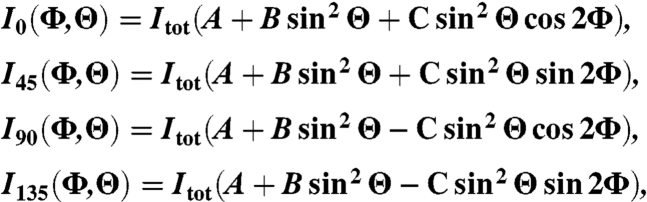[1]

where

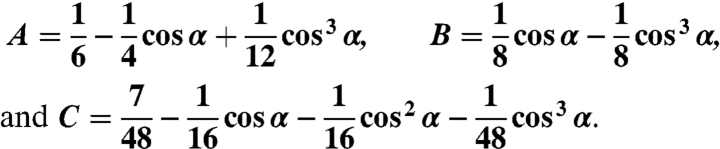The dipole orientations, Θ and Φ, as well as the total intensity, I_tot, emitted during the period of measurement can be obtained by solving the above four intensity equations to give:

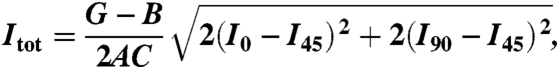[2]

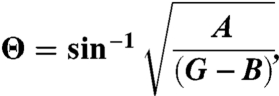[3]

[4]

where

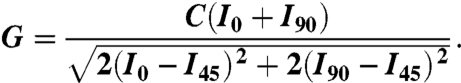Because the measured values for I₀, I₄₅, I₉₀, and I₁₃₅ all contain errors, the absolute value of (A/(G - B)) in Eq. 3 can be larger than 1, which results in no solution for Θ. Therefore we fit Θ and Φ to minimize the squared error, J, shown below with the Levenberg-Marquardt algorithm:

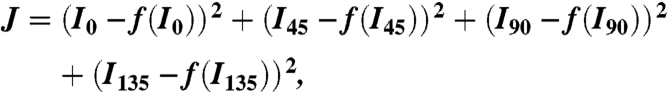where I and f(I) are the measured and predicted polarized fluorescence intensities, respectively.

The errors, δΦ and δΘ, that propagate from (δI₀, δI₄₅, δI₉₀, and δI₁₃₅) were calculated by using Eqs. 1, 3, and 4 such that

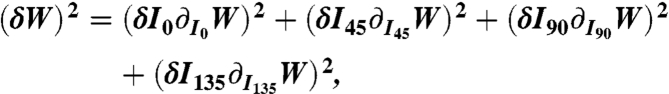[5]

where W = Φ or Θ, and δI = the shot noise + background noise. I_tot = 5,000.

Experimental Setup.

The experimental arrangement for obtaining the four polarizations is shown schematically in Fig. 1. The fluorescent probe was excited at 532 nm by a laser beam (Coherent, Compass 415M) that was circularly polarized by a quarter-wave plate. The excitation power was approximately 4 mW at the sample for the Q rod-conjugated myosin V motility assay, and approximately 20 mW for the actin filament sliding assay, covering a sample area of 60 μm in diameter. Fluorescence was collected by an infinity-corrected and polarization-preserving 150×, 1.45 N.A. oil immersion objective lens (Olympus). The fluorescence was split equally into two beams by a half-mirror. Each beam was further split into two perpendicular polarization components by a Wollaston prism (Halbo Optics). The four polarization components (0°, 45°, 90°, and 135°) were focused onto an EMCCD camera (Andor, DV887ECS-BV) through a 200 mm focal length lens. An emission bandpass filter (FF01-593/40-25, Semrock) was put in front of the camera. Image acquisition was performed by commercial software (Andor, SOLIS software). Exported data were imported into a custom written program using Visual C++ (Microsoft). In Q rod-conjugated myosin V experiments, the position of a single Q rod was determined as follows. The spot center for each of the four bright spots was determined using a two-dimensional Gaussian fit by fluorescence imaging with one nanometer accuracy (FIONA) (31, 32) followed by determining the centroid of the quadrangle made by the four spot centers.

Q Rods.

CdSe/CdS shell quantum nanorods were synthesized as previously described (33) and coated with glutathione (GSH) to make them soluble in water (34). HaloTag ligands (Promega, P6711) were conjugated to the carboxyl groups on the surface of the GSH coated Q rods by using EDC [1-ethyl-3-(3-dimethylamino-propyl)carbodiimide)] mediated coupling. GSH coated Q rods (567 nM, 500 μL) were incubated with EDC (1 mM, 28 μL) for 20 min and sulfo-NHS (1 mM, 56 μL) for 1.5 h at room temperature and dialyzed to remove unreacted EDC and sulfo-NHS. HaloTag ligands (20 mM, 5.6 μL) were incubated with the dialyzed solution and left for 2 h at room temperature. Unreacted HaloTag ligands were removed by dialysis (300 kDa cellulose acetate membrane, Harvard Apparatus). Synthesized Q rods have an emission peak at 596 nm.

Polarization Factor of Q Rods.

A dilute solution of Q rods in chloroform was cast onto a quartz substrate. We used a 532 nm laser to excite the Q rods and a polarizing beam splitter to split the luminescence light into two perpendicularly polarized beams. The two split images could be simultaneously recorded with a single CCD camera. By rotating the polarizing beam splitter, polarizations along any pair of angles could be determined. The polarization factor, ρ, for this rod sample was determined by fitting the polarization ratio, r = (I // -I⊥)/(I // +I⊥), vs. detection angle with a sinusoidal function. (I // is the horizontally polarized fluorescence and I⊥ is the vertically polarized fluorescence.)

Myosin-Q Rod Conjugation.

A Q rod-HaloTag ligand conjugate was bound to the myosin V via two HaloTag at the C terminus. Q rod-HaloTag ligand conjugates and HaloTag-myosin V were mixed at a 2∶1 molar ratio for 2 h at room temperature. Q rods did not affect myosin V motility (SI Text and Fig. S4).

Data Analysis.

We obtained fluorescent images from fluorescent latex beads showing isotropic emissions. I₀ + I₉₀ was set equal to I₄₅ + I₁₃₅ by using a correction factor, R, such that I₀ + I₉₀ = R ∗ (I₄₅ + I₁₃₅), to correct for the different detection efficiencies of the two beam paths created by the half-mirror in our optical system. Characteristic vectors, which describe the relative positions of the four bright spots originating from a single bead, were extracted from the fluorescent images. Polarized fluorescence intensities were obtained by adding pixel intensities from a 4 × 4 pixel grid with its central focus defined as the position of the Q rod based on the two-dimensional Gaussian fit and then subtracting the background. The raw intensity traces were corrected for artifacts that arose from differences in the transmission rate and reflection rate between two optical paths by applying a correction factor obtained from the latex bead fluorescent images, as R ∗ I₄₅ and R ∗ I₁₃₅, instead of I₄₅ and I₁₃₅, respectively, when calculating the orientation. 3D orientation of the probe was estimated by the Levenberg-Marquardt algorithm to fit the measured polarized fluorescence intensities.