Modelling and Analysis of Central Metabolism Operating Regulatory Interactions in Salt Stress Conditions in a L-Carnitine Overproducing E. coli Strain

Abstract

Based on experimental data from E. coli cultures, we have devised a mathematical model in the GMA-power law formalism that describes the central and L-carnitine metabolism in and between two steady states, non-osmotic and hyperosmotic (0.3 M NaCl). A key feature of this model is the introduction of type of kinetic order, the osmotic stress kinetic orders (g_OSn), derived from the power law general formalism, which represent the effect of osmotic stress in each metabolic process of the model.

By considering the values of the g_OSn linked to each metabolic process we found that osmotic stress has a positive and determinant influence on the increase in flux in energetic metabolism (glycolysis); L-carnitine biosynthesis production; the transformation/excretion of Acetyl-CoA into acetate and ethanol; the input flux of peptone into the cell; the anabolic use of pyruvate and biomass decomposition. In contrast, we found that although the osmotic stress has an inhibitory effect on the transformation flux from the glycolytic end products (pyruvate) to Acetyl-CoA, this inhibition is counteracted by other effects (the increase in pyruvate concentration) to the extent that the whole flux increases. In the same vein, the down regulation exerted by osmotic stress on fumarate uptake and its oxidation and the production and export of lactate and pyruvate are reversed by other factors up to the point that the first increased and the second remained unchanged.

The model analysis shows that in osmotic conditions the energy and fermentation pathways undergo substantial rearrangement. This is illustrated by the observation that the increase in the fermentation fluxes is not connected with fluxes towards the tricaboxylic acid intermediates and the synthesis of biomass. The osmotic stress associated with these fluxes reflects these changes. All these observations support that the responses to salt stress observed in E. coli might be conserved in halophiles.

Flux evolution during osmotic adaptations showed a hyperbolic (increasing or decreasing) pattern except in the case of peptone and fumarate uptake by the cell, which initially decreased. Finally, the model also throws light on the role of L-carnitine as osmoprotectant.

Introduction

Stress responses and their underlying mechanisms are of foremost interest not only because they are critical for determining cell physiology and metabolism in such conditions but also because they reveal some conserved features that are largely independent of the organism [1].

Extensive investigation into E. coli stress responses [2]–[5] has shown that major components of the general and specific response regulate key cellular processes. However, most of the studies on the E. coli response to osmotic stress environmental changes refer to the transcription level. Despite some analyses [6]–[10], the mechanisms involved in the adaptation of the central and energy metabolism of bacteria to osmotic conditions remain largely unstudied. Important in this regard is the fact that, contrary to most cases where signaling is involved, the osmoregulation signals which eventually translates into changes in metabolism and physiology, are of a physicochemical rather that of chemical nature [11]. This paper deals with the osmoregulation of E. coli at the metabolic level; that is, the changes in metabolic processes which, prompted by signals associated with the new osmolarity conditions, occur during adaptation to increasingly saline environments.

Important in this regard are some aspects that greatly determine the scope of our study. First, attention should be drawn to the distinction between the osmoregulatory mechanisms acting in the long term (when the system has reached a steady state in constant osmolarity conditions), and short term mechanisms, of a transient nature that occur in changing osmolarity conditions. Interestingly, little information is available concerning the long-term effects of salt stress exposure on the central metabolism of E. coli. In addition, in the case of hyperosmotic stress in E. coli, one well observed homeostatic mechanism is the synthesis of some osmoprotectants, non-toxic molecules that help compensate the osmotic pressure by accumulating in the intracellular medium. These osmoprotectants include K⁺, amino acids such as glutamate and proline, and trehalose and zwitterionic organic solutes like L-carnitine, [12], [13] a trimethylammonium compound well described as osmoprotectant in this microorganism [14], [15]. Further, experimental evidence on the important role played by salt stress on the energetic state and the main metabolic pathways of the cells during metabolic biotransformations of trimethylammonium compounds in E. coli has been shown [6].

Starting with the results of an anaerobic culture of a L-carnitine E. coli overproducing strain subjected to an osmotic stress [10], we have constructed a mathematical model which reproduces both the non-osmotic and hyperosmotic steady states, as well as the observed dynamic behavior of the transition between them. Our aim was to quantify the signals and observed changes in fluxes; in particular, we wished to contribute to the elucidation and quantification of the response generated in E. coli by hyperosmotic stress as regards the primary metabolism (central carbon) and its relationship with the synthesis of an osmoprotectant, L-carnitine, produced by a secondary metabolism.

Materials and Methods

Experimental Methods

The experimental set up and data used to construct and verify the model were taken from [10]. In the experimental set up used by these authors, an L-carnitine overproducer E. coli (O44K74AS) strain adapted to high salt concentration was used. After removal of the storage medium, the bioreactor was operated in the presence of this strain and a standard complex medium at a fixed dilution rate. Once the initial steady state under standard salt conditions (control, 0.085 M NaCl) was reached, a gradual osmotic up-shift was carried out by feeding the culture with a medium containing 0.3 or 0.5 M NaCl until a new, hyperosmotic medium steady state was reached. This new steady state was reached 70 h after switching the medium. This time period of 70 hours can be considered a long-term E. coli cell adaptation period [10], [16] since at least 12 generations were produced to keep the cell population steady within the bioreactor. This number of cell divisions meant that many changes and protein turn-overs, the result of gene expressions and adaptations, had occurred to reach the steady state within the reactor at the new salt concentration [10]. The osmotic up-shift was carried out when the culture had reached the steady state.

Mathematical modeling

The approach used to model this biochemical system involves mathematical models in ordinary differential equations in the power-law formalism. In this formalism [17] the processes that conforms the biochemical networks are modelled using power-law expansions in the variables of the system and are then included in non-linear ordinary differential equations with the following structure, called Generalized Mass Action (GMA):

(1)

In Equation 1, X_i represents the model variables (concentrations of compounds of the investigated network: metabolites, salt medium, bacterial concentration, etc.), n_d is the number of model variables, and γ'_j (rate constants) and g_jk (kinetic orders) are different kinds of parameters defining the dynamics of the system. Unlike in conventional kinetic models, where the kinetic orders are always integer numbers, power-law models admit non-integer values.

In order to deal with the description and quantification of the effect of the osmotic stress in the metabolic processes we use a new type of kinetic order, the osmotic stress kinetic orders (g_OSn), derived from the power law general formalism. In the definition of this system parameter, we follow a similar approach to that presented by Fonseca et al. [18] for the study and quantification of the temperature dependence of the system. While these authors introduce a parameter that represents the change in enzymatic activity brought about by an increase in temperature, our kinetic orders (g_OSn) represent the change caused by the osmotic stress.

In our case, the rate constants γ'_j can be expressed as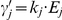, where k_j depends on the properties of the molecular medium, such as the pH, temperature or salt concentration (in our case only the salt, 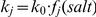and E_j is the enzyme concentration. The enzyme concentration, E_j, under stress conditions also changes, 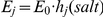. Accordingly, 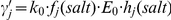. In the phenomenological approach here proposed the effect of osmotic stress in the rate constant and the enzyme activity is aggregated into a single characteristic power-law term:

Therefore Equation 1 in the osmotic stress conditions under consideration becomes:

(2)

The most notable property of these power-law equations is that two such equations with the same structure can be used to describe totally different dynamics (from inhibitory processes to the description of cooperativity) simply by modifying the numerical values of the kinetic orders involved [19]. Moreover, this type of representation has been shown to be suitable and effective for the modelling of dynamic signalling structures. It has been shown that virtually any linear or non-linear system can be represented accurately by a GMA of higher dimension through algebraic equivalence transformations of variables in a process called recasting [20].

Delay definition

A time-delay was applied to the model to represent the different time scale between some distinct qualitative processes within the cell (cell death, gene expression, etc.). This delay was modeled using the linear chain trick [21], whereby the delay was described using time-dependent fiction variables (in our case, Delay_{name 1} and Delay_{name 2}, where name is the name of the variable to which the delay is applied). The features of distributed time-delay (average value and standard deviation) depend on the number of fictitious variables used and the value assigned to the rate constant K_delay. We noticed that more sophisticated strategies are available to introduce time delay in ordinary differential equation models (see for example, [22]). However, our initial analysis indicated that the simple strategy used to model time-delay was sufficient for our case study.

Parameter estimation

The numerical values for the parameters γ _i and g_jk are determined using an evolutionary algorithm called simple genetic algorithm (SGA) adapted to determine the values of parameters in power law models [23], [24]. This algorithm starts with a population of individuals, which are the set of parameters that generates a solution of the model. The population is mutated and recombined; the convergence stems from minimization of the value of the objective function (Fobj):

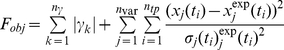(3)

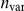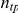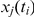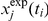In Equation 3, and are the model variables and time points, respectively; n_γ is the number of rate constants of the model and are the value of variable j at time i based on the simulation of the model and the experimental data of the variable j at time i, respectively; 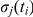is the standard deviation of the experimental value of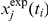. Furthermore, an additional term in Equation 3 was introduced in order to obtain a more restrictive objective function. This term is the sum of the γ's, in absolute values, which allow the value of these parameters in the solutions to be reduced. γ is associated with the enzyme concentration; the enzyme concentration (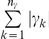) is minimized in the data fitting process.

The initial point integrating for the variables should be at the same time an experimental and analytical steady state value. The last condition is fulfilled by a set of system parameters satisfying equations 3.

(4)

In the search for a solution, SGA was run through 10,000 iterations using the 0.3 M salt concentration time series data. Initially, a first set of γ_j and g_jk parameters was found within the range searched (γ_j = [0, 20]; g_jk = [−3, 3]), showing a low value of Fobj. Then, the previously obtained parameter solution was used in the subsequent searches within a 95% of the first solution, the Fobj between 25% and 60% of the initial Fobj in all cases.

Stability analysis

All eligible solutions should show initial and final stable steady states. The stability of the steady states was checked by analyzing the behavior of the model against small perturbations.

Dynamic sensitivity analysis

Sensitivity analysis is a general analysis tool useful for evaluating robustness and characterizing system dynamics. Since our model studies the system dynamics, it is possible to identify those parameters with a major influence on the transient dynamics. For this purpose we used a modified version of previously defined dynamic sensitivity [24], the System Dynamic Sensitivity, S_pk ^Xi, as indicated in equation 5:

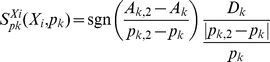(5)

In the above expression, Xi is the considered variable, while pk is the parameter under scrutiny. Ak,2 is the area below the solution curve, after a change of pk to pk,2. Ak is the area under the solution curve using the original value pk. Dk is the area between the two solution curves, using pk and pk,2, respectively. We have considered changes in two kinds of parameter, the kinetic orders and the rate constants. The S_pk ^Xi value corresponds to the variation of the area under the variable time course after perturbation in parameter space. For each model variable the absolute values of the area A_k, A_k2 and D_k were calculated using the trapezoidal method. Positive sensitivity means that the area under the ÒnewÓ curve is greater than the area under the original curve i.e. that the parameter pk has a positive influence on variable Xi. Negative sensitivity means the opposite. Zero sensitivity means that small changes in the parameter have no influence on the variable. All sensitivities were computed for standardized variables.

Kinetic processes

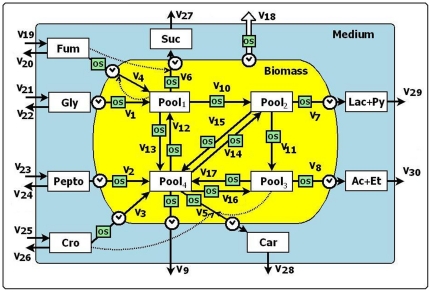
Figure 1 shows the simplified version of the central metabolism of E. coli applicable both to normal and osmotic stress conditions where the intracellular variables are connected to the external measured ones.

Figure 1. Schematic representation of the central metabolism of a L-carnitine overproducing E. coli strain applicable both to normal and osmotic stress conditions.

Solid lines represent rate processes and dotted arrows represent regulatory interactions. The empty arrow represents the output flux of biomass. The “clock” symbols represent a time-delay in a process whose value is a parameter estimated during the model calibration. The OS boxes represent the influence of the osmotic stress on the flux rate. See text for detail.

Since our objective here is to analyze the effect that changes in the salt concentration of the medium provoke in the dynamics of the system, we focused our attention on the main central metabolism fermentation processes. We also pay attention to the mass flux looking at the metabolite accumulation and biomass production and the flux exchanges among the cell cultures, the medium and the bioreactor. Accordingly, four variables aggregate all the intracellular compounds. As is shown in Figure 1, three pools (Pool₁, Pool₂ and Pool₃) connect the carbon source (glycerol, Gly) with the fermentation products lactate and pyruvate (Lac+Py) and acetate and ethanol (Ac+Et) as well as with the fumarate (Fum) reduction into succinate (Suc). Pool₄, on its own, aggregates the rest of the components of the cell and it is connected with the rest of the Pools. Presented in this way the model is simple enough to be defined and to be user friendly, but still provide information on the influence of the osmotic stress on the metabolic rearrangement.

More specifically, Pool₁ represents the intracellular concentration of phosphoenolpyruvate, succinate, fumarate, malate and oxaloacetate; Pool₂ includes pyruvate and lactate; Pool₃, acetyl CoA, acetyl-P, acetate, acetaldehyde and ethanol, while Pool₄ is a variable representing the rest of the intracellular cell compounds; among them, the rest of the intermediates of the tricarboxilyc acid cycle. Biomass, which is not directly represented in Figure 1, where the yellow area represents the variable biomass as the sum of all the variables within it, is an auxiliary variable, defined as the summation of the four intracellular Pool_i variables. Thus defined, Biomass serves to represent the mass of microorganism in the reactor. Biomass is defined as the whole population in the reactor, and it is measured as the total cell dry weight (mg)/ml of the reactor bulk liquid. During the different cell divisions biomass adapts to the new steady state after the salt up-shift [10], [25]. Therefore, the individual cell content was adapted to the new conditions and can be represented by the summation of the Pools, and the total amount of cells can be represented by the total cell dry weight (mg)/ml of the reactor bulk liquid. Since the biomass changes during the transition, fluxes were normalized to the biomass unit, so that they are referred to milligrams of cell mass.

The reactor medium and the extracellular metabolite concentrations are represented by Lac+Py, the combined concentrations of lactate and pyruvate; Ac+Et is the summation of pyruvate, acetate and ethanol; Gly, is the glycerol concentration, and Pepto represents the concentration of peptone.

Quantification of direct and indirect influence of osmotic stress on metabolism

In this model the influence of osmotic stress conditions on the flux values is represented by of the power law term Salt^gOSj (indicated as OS, green boxes in Figure 1). In this expression Salt is the normalized salt concentration (NaCl) of the medium with respect to the control conditions (0.085 M). Salt quantifies the osmotic stress, being 1 in control conditions, 3.53 in 0.3 M NaCl conditions and 5.88 in 0.5 M.

The exponential terms g_OSj are the osmotic kinetic orders. These are phenomenological parameters, that quantify the combined effect on the fluxes (V_j) of the mediating mechanisms between the medium salt concentration (the osmotic stress) and the fluxes. These mechanisms are of a physicochemical and transcriptional (changes in enzyme concentrations) nature. The term g_OSj can have positive or negative values, reflecting an increase or decrease of the flux due to the osmotic stress. This modelling strategy permits us to separately quantify the influence of osmotic stress (through the g_OSj) and of the metabolite concentration (g_jk) on the fluxes

Transport and central metabolic processes

The central metabolism and the glycerol and peptone uptake by cells are also depicted in Figure 1. V₁ is the glycolytic flux (glycerol to phosphoenolpyruvate, indicate by Pool₁); V₁₀ the transformation from Pool₁ (mainly phosphoenolpyruvate) to Pool₂ (pyruvate) through pyruvate kinase, and, V₁₁ is the transformation from Pool₂, namely pyruvate, into Pool₃ (acetyl CoA) through pyruvate dehydrogenase. Fluxes V₁₂, V₁₄ and V₁₆ are catabolic fluxes mediated by enzymes: V₁₂ is associated with the phosphoenolpyruvate carboxykinase activity and also represents the thehalose degradation processes that yield pyruvate from any other precursor, particularly the TCA intermediates and the amino acid degradation; V₁₄ represents the synthesis of pyruvate from other metabolites. V₁₆ represents different processes leading to the synthesis of Pool₃ from precursors other than glycerol (lipids and/or proteins and L-carnitine). V₁₃, V₁₅ and V₁₇ are anabolic processes. V₁₃ is associated with the intracellular production of trehalose, the net flux between Pool₁ and Krebs cycle intermediates, the PEP-carboxylase activity and the transformation of these intermediates into Biomass [10]; V₁₅ represents the transformation of the pyruvate component of Pool₂ into some precursors (amino acids and osmoprotectants). V₁₇ is related with the flux through citrate synthase, including glutamate biosynthesis. V₇ is the combined transformation/excretion of pyruvate and lactate (Pool₂), which is mediated by the reference enzyme lactate dehydrogenase, while V₈ is the combined transformation/excretion of Pool₃ into acetate and ethanol (Ac+Et) mediated by the reference enzymes Acetyl-CoA synthetase and Phosphotransacetylase. V₂ is the input flux of peptone into the cell and V₉ is the biomass output flux (for instance in the form of NH₄ ⁺ and/or CO₂ release).

Fumarate reduction and succinate production

Fumarate (Fum) is antiported with intracellular succinate and it is not used as carbon source [26] . Once fumarate is within the cell, it is reduced and transformed (V₄) into internal succinate (Pool₁), which eventually leaves the cell, V₆. The positive regulatory influence of fumarate on V₆ collects its role as substrate in the production of succinate [10].

Bioreactor system

The whole system (open and continuous) has overall input and output fluxes. V₁₉ to V₃₀ represent the influxes and the outflows of the corresponding variables, all of which are mediated by the dilution rate (K_d = 0.1 h⁻¹). V₁₈ (empty arrow) represents the output of biomass from the reactor.

L-carnitine transport, production and degradation

Cell crotonobetaine (Cro) uptake flux from the reactor medium is represented by V₃; V₅ is the transformation/output flux of L-carnitine from the cell to the reactor medium (Car). V₅ is linked to the variables Pool₃ and Cro through activating regulatory interactions in accordance [14].

Model Equations

In accordance with the model scheme shown in Figure 1, the system model equations are as follows.

Mass Balance

The mass balance equations of the processes take the following form:

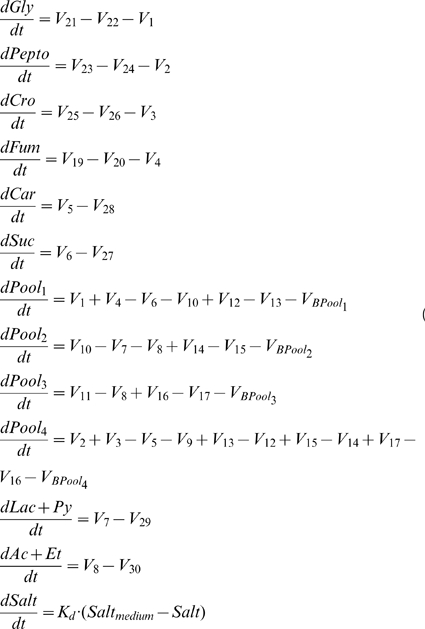(6)

As said above, biomass is the sum of Pool_i (i = 1, 2, 3, 4). In Figure 1, V₁₈ represents the output of biomass, but since biomass is a variable composed of four terms, V₁₈ is the sum of four biomass contributions coming from each one of the internal variables of Pool_i, namely V_BPool1, V_BPool2, V_BPool3 and V_BPool4. Accordingly, these fluxes are represented in the corresponding Pool_i differential equations (see Equations 6).

Salt_medium is the normalized concentration of salt with respect to the control condition in the input medium to the reactor and Salt as defined above.

Delay equations

The delay equations that describe the longer temporal hierarchies of the enzyme expression processes are modelled using a three-equation linear chain trick. Delay is applied to the variable Biomass, which is the sum of the variables of the model Pool₁, Pool₂, Pool₃ and Pool₄, so this delay is applied to each of these variables as a proportional part of the biomass that they conform (Equations 6).

(7)

Power law rate equations

The rate equations in power law form corresponding to the different fluxes are:

(8)

System parameters and constants

In this model approach the rate constants (γ_j) are associated with the net enzyme activity of each process and are considered to remain constant. It should be noted here that since the osmotic kinetic orders measures the effect on the fluxes of the mechanisms that mediate between the osmotic stress and the fluxes, they include in their values the effects on the fluxes associated with the changes that occurs in enzymes (concentration, effectors, coenzymes etc.). Kinetic orders (g_jk) measure the effect of each variable on the flux V_j. Gly_medium, Peptone_medium, Cro_medium and Fum_medium are the concentration of glycerol, peptone, crotonobetaine and fumarate in the input medium to the reactor, respectively, which are kept constant.

Identifiability of solutions

Many set of parameters showing similar values of the objective function were found. In order to select the most representative ones, a selection criterion was applied. The selection criterion used ensures that the fitting of each variable is independent from the remaining variables. Since the objective function can give solutions with a poor fitting in one of the variables if another variable has a very good fit, the criterion mentioned above eliminate these kinds of solutions. According with this criterion only was admitted as solutions for the osmotic steady state (0.3 M) those in which the values of the dependent variables were within the range ±1.5 SD of the experimental values of osmotic steady state, except in the case of Lac+Py and Car (±3 SD) and Biomass (±4.5 SD). The value of the ranges was estimated from the standard deviation of the data.

Model validation

The model was validated using a new set of data which were not used in the parameter fitting procedure. This data were obtained at 0.5 M salt concentration. Solutions obtained by fitting with the 0.3 M data were tested against the experimental data obtained at 0.5 M NaCl. In these conditions the only solutions admitted were those in which the dependent variables were within the range ±3 SD of the experimental values. In the case of the variables Lac+Py and Car and Biomass the range was ±6 SD and ±9 SD, respectively.

Results and Discussion

Model fitting and verification

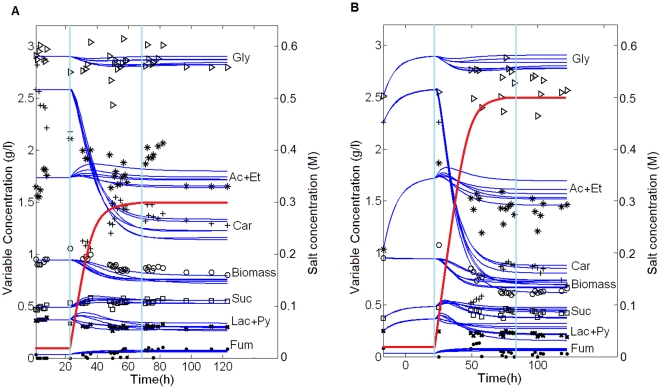
Figure 2 shows the simultaneous integration of the six selected solutions obtained with the procedures described above; this representation shows the differences between them. Panel A shows the model data fitting in 0.3 M of NaCl conditions; panel B shows a comparison of the model predictions with the experimental time series data in 0.5 M of NaCl conditions. In all cases the first vertical line (23 hours) indicates the moment when salt switching begins (at the initial 0.085 M NaCl control steady state), and the second one (70 hours) the moment when the system reaches the final steady state (0.3 or 0.5 M NaCl, respectively). The mean values of the parameters of the six solutions as well as the whole set of parameter solutions for each of the solutions are shown in Tables S1 and S2 of Supporting Information files, respectively. The model fits the experimental data well (Fobj = 195.82±20.84) and is able to predict the general behavior in different, more saline conditions (0.5 M NaCl).

Figure 2. Model fitting and verification.

In all panels continuous lines represent the six best model solutions are represented (they are represented simultaneously in order to see the differences between them). The first vertical line indicates the moment (23 hours) when the medium switch begins by NaCl addition, while the second one indicates when the final steady state is reached (70 hours). Red lines represent the salt concentration in the extracellular medium. A. Model fitting in conditions of 0.3 M of final NaCl concentration. B. Model verification in conditions of 0.5 M of final NaCl.

Sensitivity and stability analysis

All solutions were in a stable steady state before and after the salt concentration switch. Variable sensitivities for parameter changes and initial conditions showed distinct pattern distribution for the different solutions considered. However, all sensitivity values were in the range [1.0825, −0.7377], 99% of all sensitivities being between −0.1 and 0.1 (data not included). This indicates that the selected solutions are robust for changes in parameters and initial conditions.

Concentrations change in variables

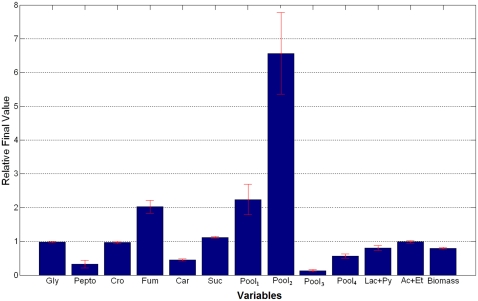
Figure 3 shows the relative changes in variables concentrations between the final (0.3 M NaCl) and the initial steady state. It can be seen that the concentration of all the variables increased in osmotic conditions. In particular Pool₂ increased more than 6 times with respect to its value in nonosmotic conditions and Pool₁ and Fum doubled in concentration.

Figure 3. Relative variable concentration changes.

Mean values of the variables concentration changes for the selected solutions between the final, osmotic stress (0.3 M NaCl) and the initial steady state. Values were calculated as the ratio between the final and the initial steady states. All values are normalized with respect to the initial steady state values.

Kinetic order distribution for metabolic changes and osmotic stress

In previous studies [6], [10] it was shown that, as a result of long-term exposure to NaCl, the metabolism of E. coli adapts to stress conditions, the adaptation being mediated by changes in enzyme activities and cofactor levels. Integration of the experimental data into a comprehensive model provides new evidences regarding the actual flux distribution.

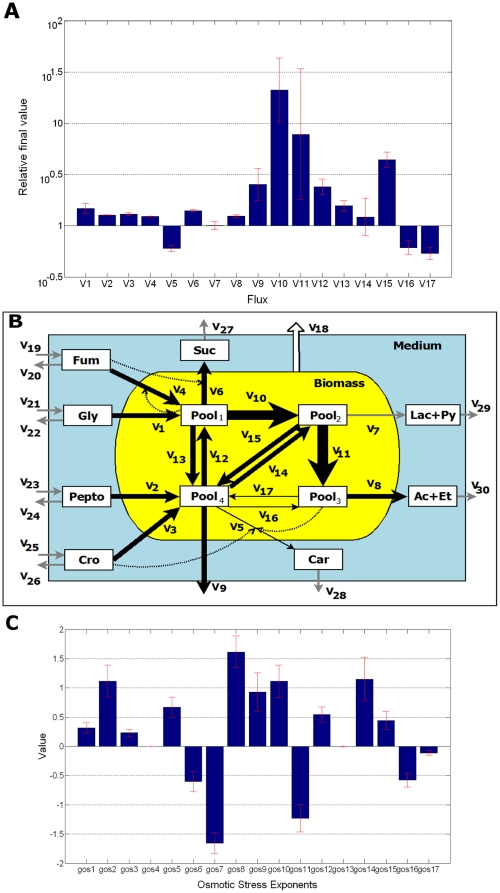
Figures 4A and 4B show the magnitude of the flux changes from different perspectives. It can be seen that the fluxes showing the increases in the 0.3 M steady state were V₁₀ and V₁₁. To a lesser degree, V₁, V₂, V₃, V₄, V₆, V₈, V₉, V₁₂, V₁₃, V₁₄ and V₁₅, also decreased. Some fluxes (V₅, V₁₆ and V₁₇) decreased when in osmotic conditions while V₇ remained practically unchanged.

Figure 4. Flux changes and osmotic stress kinetic order distribution in osmotic conditions (0.3 M).

A. Mean flux changes in logarithmic scale of (the mean of) the selected solutions. Relative change was calculated as the ratio between the flux values (normalized by the biomass and the flux at the initial steady state) in the osmotic steady state and the corresponding normalized flux in the initial steady state. B. The magnitude of the flux changes are indicated by the thickness arrows. Thicker arrows represent fluxes which increase their value in stress condition; thinner ones are the fluxes that decrease their value after the salt switch, while the gray ones correspond to unchanged fluxes. All fluxes are normalized to the concentration of the biomass. C. g_OS kinetic order value (mean values).

Figure 4C show the estimated g_OS kinetic orders. As stated above the value of these parameters measure the effect of osmotic stress on the corresponding fluxes. As can be seen, all of them are within the [−2, 2] range value. Those showing higher positive values, indicating a major positive influence of the osmotic conditions on the corresponding fluxes, are g_OS2 (V₂), g_OS8 (V₈), g_OS9 (V₉), g_OS10 (V₁₀) and g_OS14 (V₁₄). Also positive but of minor magnitude are g_OS1 (V₁), g_OS3 (V₃), g_OS5 (V₅), g_OS12 (V₁₂) and g_OS15 (V₁₅). On the other hand, the g_OS showing the greatest negative values are g_OS7 (V₇) and g_OS11 (V₁₁). Negative too, but less so, were: g_OS6 (V₆), g_OS16 (V₁₆) and g_OS17 (V₁₇). Parameters g_OS4 (V₄) and g_OS13 (V₁₃) have zero values.

As stated above, the influence of osmotic stress conditions on the flux values is represented by the term Salt^gOSn. Examination of this term in the context of each flux rate equation (see Equations 7) allows us to analyse the magnitude and significance of the osmotic associated interactions on each of the fluxes. The main results of this section are summarized in Figure 4.

One observed change after the salt switch was the increase in the flux V₁. This flux is dependent on Gly and Salt and represents the flux from external glycerol (Gly_medium) to internal Pool₁. The corresponding kinetic order g_OS1 is 0.3, meaning that the osmotic stress has a moderate positive effect in the input of glycerol. Since variable Gly remains constant (see Figure 2), we conclude that the osmotic stress is responsible for this flux increase. This result shows that there is a mechanism which relates osmotic stress with the entrance and transformation of glycerol into Pool₁.

Another result arises from the change in the fluxes V₁₀ and V₁₁. V₁₀, which increase its value in osmotic conditions, represents the transformation from Pool₁ to Pool₂. Its value is dependent on Pool₁ and Salt through the kinetic orders g₁₀₇ (1.6) and g_OS10 (1.1), respectively. Since both kinetic orders are positive and the values of Pool₁ and Salt are higher in osmotic conditions (Figure 3) the positive influence of the osmotic stress must be added to the positive effect of the other variables. A different situation is observed in the case of V₁₁, the flux representing the transformation from Pool₂ to Pool₃. V₁₁ depends on Pool₂ and Salt through the kinetic orders g₁₁₈ (1.7) and g_OS11 (−1.2), respectively. In this case, despite the negative value of g_OS11, V₁₁ increased, the positive effect of the combined Pool₂ increased and its greater kinetic order g₁₁₈ being enough to compensate the negative influence of Salt^gOS11 term. It may be suggested that the increase in V₁₀ is to meet the energy requirements, while the increase in V₁₁ serves to compensate Pool₂ accumulation. This would permit increased energy synthesis in order to resist the selective pressure imposed and would explain the increased rates of generation of fermentation products.

V₈, the combined transformation/excretion of Pool₃ into Ac+Et, reflects a different situation. This flux, which is dependent on Pool₃ and Salt through the kinetic orders 1 and g_OS8 (1.6), increases in osmotic conditions. In the stressed steady state, Pool₃ decreases significantly (87%) although the strong and positive influence of Salt^gOS8 causes this flux to increase its value. This behavior correlates with an increase in energy production as a result of substrate level phosphorylation under osmotic stress.

V₄, the fumarate uptake, increases and the associated osmotic kinetic order (g_OS4) is null. Thus, the osmotic stress does not affect V₄. Since the other terms affecting V₄ either decrease (Pool₁ ^g47; g₄₇ being negative) or increases (Fum) the observed increase is due to the increase of Fum. In the same vein, V₆, which represents Fum respiration and succinate output, increases its value. This increase in flux cannot be attributed to an osmotic stress mechanism since its influence is negative (g_OS6 = −0.6) and must be attributed to the positive influence of the increase of Fum (g₆₄ = 0.12) and Pool₁.

V₁₅, which represents the anabolic use of pyruvate, increase its value more than 4 times. In this case the osmotic stress kinetic order is positive (g_OS6 = 0.44), as is the effect of Pool₂, whose concentration increases more than 5 times (g₁₅₈ = 0.37).

Flux V₉ represents the loss of biomass in the form of CO₂ and NH₄ ⁺. This flux increases in osmotic conditions. Since the Pool₄ value decreases, the increase in V₉ arises from an osmotic stress response mechanism (g_OS9 = 0.93).

V₁₂, the flux through the phosphoenolpyruvate carboxykinase activity (also linked to the trehalose degradation), increases due to the osmotic stress (g_OS12 = 0.54). Contrary to the observed increase in V₁₃, a aggregated process, which is not influenced by the osmotic stress (g_OS13 = 0).

Finally, V₇, which integrates the production and export of lactate and pyruvate does not change. In this case, the osmotic stress has a negative effect (g_OS7 = −1.65), but is compensated by the positive effect of Pool₂.

The role of osmoregulators

The effects of osmotic stress on different systems pertaining to many, if not all, biological kingdoms are essentially the same [11]. The main and most common mechanism observed in such systems, aiming to keep within the physiologically acceptable boundaries the intracellular milieu, consists of the accumulation of nontoxic compatible solutes in the cytoplasm. These compatible solutes (osmolytes) can be either produced by the cell or assimilated from the extracellular medium.

In many instances, the first event in osmotic stress adaptation is the uptake of K⁺. The increase in K⁺ concentration not only serves to decrease the osmotic pressure, but is a primer signal for the production of other compatible solutes. One of these is glutamate, whose accumulation quickly reflects the K⁺ concentration increase, thus helping to neutralize the increase of positive charges. In a second phase, these K⁺ and glutamate concentrations decrease (the first one through excretion and the second one through its metabolic transformation), while trehalose is synthesized in a process that usually marks the end of metabolic osmotic adaption.

In the assayed experimental system the culture medium contained crotonobetaine, which, after uptake, yields a potent osmoregulator, L-carnitine. In our model V₃ represents the input of crotonobetaine to produce L-carnitine (Pool₄). We observed that this flux increases by 30%, its related osmotic stress kinetic order being positive (g_OS3 = 0.23). Since Cro remains unchanged, the single reason for the increase in crotonobetaine input is the salt stress response mechanism.

In our model the production of glutamate is represented by flux V₁₇, which is dependent on Pool₃ and Salt through the corresponding kinetic orders g₁₇₉ (0.3) and g_OS17 (−0.1), respectively (see Table S1; Supplementary Materials). After the salt switch, a decrease in this flux occurs, indicating that glutamate is not significantly synthesized in response to the salt rise. This suggests that there is, instead, an accumulation of other compatible solutes from the extracellular medium, such as the trimethylammonium compounds involved in the medium (Cro and Car).

L-carnitine metabolism is inhibited in osmotic stress conditions [10]. In our model, the catabolism of L-carnitine is represented by V₁₆, while its synthesis and excretion are represented by V₅. V₁₆ is dependent on the variables Pool₄ and Salt through the kinetic orders g₁₆₁₀ (null value) and g_OS16 (−0.6), respectively. On its own V₅ is dependent on the variables Pool₄, Pool₃, Cro and Salt through the kinetic orders 1, g₅₉ (0.5), g₅₃ (1.15) and g_OS17 (0.6), respectively. Our results show that the magnitudes of these fluxes are reduced in osmotic conditions (see Figure 4B). In the case of V₁₆, the determinant (negative) factor is the osmotic stress response since the g₁₆₁₀ value is null. But in the case of V₅, the observed decrease in the flux seems to be due to the combined effects of the decrease in Pool₄ and Pool₃ in spite of the counteracting influence of the osmotic stress. This indicates that the carnitine metabolism is down regulated by an osmotic stress response mechanism, leading to the accumulation of the osmoprotectant L-carnitine, while its excretion is not affected by the osmotic stress.

Another effect revealed by our model refers to the metabolism of peptone, which is present in the reactor medium. Peptone is made up of peptides and amino acids, among them proline (46 mg/g peptone, MC24 bacteriological peptone from LAB M laboratory). It is known that proline uptake from the extracellular medium plays a role as osmoprotectant by eliciting the (rapid) excretion of K⁺ and contributing to the depletion of trehalose [11]. Some of our model observations clearly correlate with these observations. First, it can be seen that flux V₂, which in our model represents peptone uptake, increases (27%) when in osmotic conditions, suggesting increased proline uptake. At the same time V₁₂, which also represents trehalose catabolism, increases more than two-fold. The values of the related osmotic kinetic orders, g_OS2 and g_OS12, related with V₂ and V₁₂, respectively, have positive values (1.1 and 0.5, respectively). These results suggest that the input of peptone (V₂) and trehalose catabolism (V₁₂) are affected by the osmotic stress.

Concluding remarks

In analyzing the influence of osmotic stress on flux redistribution in the osmotic stressed steady state, not only the regulatory effects inherently associated with the osmotic stress response mechanisms should be considered, but also the simultaneous influence of the changes that occur in other variables in the system. The model approach used to represent the central metabolism and L-carnitine biosynthesis subjected to long term adaptation to osmotic stress conditions allows the influence of the osmotic stress condition on fluxes to be quantified.

The model analysis shows that, after salt up-shift, the energy and fermentation pathways in the central metabolism undergo substantial rearrangement as they move towards an enhanced energy production. This is the case of the increase observed in the fermentative (V₁, V₂, V₁₀, V₁₁), anaplerotic (V₁₂ and V₁₃) and succinate (V₄ and V₆; see [10]) fluxes. This is further illustrated by the observation that the increase in the fermentation flux, V₁₁ (from Pool₂ to Pool₃), is not connected with fluxes towards Pool₄, representing the tricaboxylic acid intermediates and the synthesis of biomass. The values of the osmotic stress associated with these fluxes reflect these changes.

Pyruvate kinase (V₁₀) and Pyruvate dehydrogenase (V₁₁), which render pyruvate and acetyl-CoA, respectively, control energy yields during growth [10]. In fact, the increase in Pyruvate kinase activity is in good agreement with the observed increased glycerol consumption (V₁; g_OS1), suggesting that glycolytic rates increased as a consequence of stress towards fermentation (g_OS2, g_OS8, g_OS9, g_OS10, and g_OS14). On the other hand, under anaerobiosis, acetyl-CoA is transformed to acetate (forming ATP) by phosphotransacetylase-acetate kinase (Pta-Ack) pathway (V₈ in our model, which increases, see [27])

This would permit for increased energy synthesis to withstand the osmotic stress and would explain the increased rates of generation of fermentation products.

Furthermore, under anaerobic conditions, the TCA cycle (Pool₁ and Pool₄) provides biosynthetic precursors. In osmotic stress conditions, the activities of the controlling anaplerosis and gluconeogenesis enzymes isocytrate lyase, phosphoenol pyruvate carboxylase and phosphoenol pyruvate carboxykinase are altered [10]. This demonstrates the effect of long-term salt stress as regards cellular needs for anaplerotic intermediaries and energy (Pool₁ and Pool₄, reversibly connected with Pool₂). These pathways allow the oxalacetate pool needed for biosynthesis to be replenished (Pool₁ node). Taken together, the model results presented demonstrate the involvement of the biosynthetic pathways in the adaptation to osmotic conditions, since they are required for the production of cellular structural components. Greater fluxes in the central energy-producing and anaplerotic pathways have also been found in C. glutamicum when exposed to increased osmolarity [28]. Interestingly, the model outcome confirms the importance of acetate metabolism during long-term exposure to salt and during stress adaptation.

Further, in the transition phase, osmotic adaptations of E. coli metabolism translates into monotonic increases and decreases, with the exception of peptone and fumarate uptake into the cell which initially showed decreased concentrations.

Regarding the role of the osmoprotectant L-carnitine, we conclude that its catabolism is negatively influenced by the osmotic stress, while its synthesis and excretion is unaffected by any osmotic stress response mechanism.

Supporting Information

Table S1

Mean parameters and SD values of the selected solutions.

(DOCX)

Table S2

System parameters value for six solutions.

(DOCX)