Skip to main content
PMC home page
Medical Physics logoLink to Medical Physics
. 2012 Mar 28;39(4):2163–2169. doi: 10.1118/1.3697529

Feasibility of low-dose single-view 3D fiducial tracking concurrent with external beam delivery

Michael A Speidel 1,a), Brian P Wilfley 2, Annie Hsu 3, Dimitre Hristov 3
PMCID: PMC3326074  PMID: 22482637

Abstract

Purpose: In external-beam radiation therapy, existing on-board x-ray imaging chains orthogonal to the delivery beam cannot recover 3D target trajectories from a single view in real-time. This limits their utility for real-time motion management concurrent with beam delivery. To address this limitation, the authors propose a novel concept for on-board imaging based on the inverse-geometry Scanning-Beam Digital X-ray (SBDX) system and evaluate its feasibility for single-view 3D intradelivery fiducial tracking.

Methods: A chest phantom comprising a posterior wall, a central lung volume, and an anterior wall was constructed. Two fiducials were placed along the mediastinal ridge between the lung cavities: a 1.5 mm diameter steel sphere superiorly and a gold cylinder (2.6 mm length × 0.9 mm diameter) inferiorly. The phantom was placed on a linear motion stage that moved sinusoidally. Fiducial motion was along the source-detector (z) axis of the SBDX system with ±10 mm amplitude and a programmed period of either 3.5 s or 5 s. The SBDX system was operated at 15 frames per second, 100 kVp, providing good apparent conspicuity of the fiducials. With the stage moving, detector data were acquired and subsequently reconstructed into 15 planes with a 12 mm plane-to-plane spacing using digital tomosynthesis. A tracking algorithm was applied to the image planes for each temporal frame to determine the position of each fiducial in (x,y,z)-space versus time. A 3D time-sinusoidal motion model was fit to the measured 3D coordinates and root mean square (RMS) deviations about the fitted trajectory were calculated.

Results: Tracked motion was sinusoidal and primarily along the source-detector (z) axis. The RMS deviation of the tracked z-coordinate ranged from 0.53 to 0.71 mm. The motion amplitude derived from the model fit agreed with the programmed amplitude to within 0.28 mm for the steel sphere and within −0.77 mm for the gold seed. The model fit periods agreed with the programmed periods to within 7%.

Conclusions: Three dimensional fiducial tracking with approximately 1 mm or better accuracy and precision appears to be feasible with SBDX, supporting its use to guide radiotherapy.

INTRODUCTION

The curative potential of external beam radiotherapy is critically dependent on having the ability to accurately aim radiation beams at intended targets while sparing surrounding healthy tissues. This requirement is particularly challenging for abdominal and thoracic tumors, because of random or quasiperiodic motion occurring during beam delivery. Such motion exhibits high level of spatial and temporal complexity with significant interpatient as well as inter- and intrafraction variability in magnitude and patterns.1, 2, 3 For instance, a study of 70 218 respiratory cycles for 143 treatment fractions in 42 stereotactic body radiotherapy patients reported that while inferior-superior displacements constituted a significant component of respiratory-induced motion, in 40% of these fractions, motion was predominantly in anterior-posterior or left-right direction.3 Furthermore, even though the trajectories were predominantly linear, large variations in magnitude, direction, and linearity were observed from patient to patient, fraction to fraction, and, importantly, cycle to cycle.3 Thus, a capability for real-time three-dimensional (3D) target localization concurrent with beam delivery would be ideal in monitoring and managing random and quasiperiodic motion.

Currently, however, due to concerns with respect to excessive imaging dose, 3D target localization and tracking is synchronized with an external respiratory signal subsequently used to guide the delivery. This approach would still benefit from real-time 3D localization as correlations between external surrogates and target positions are nonstationary and can become poor if not reestablished promptly.4, 5 Furthermore, for certain breathing maneuvers, such correlations appear to be lacking.6 This is also the case for random physiological prostate motion, which is mostly influenced by transient changes in rectal filling rather than breathing. In some clinical settings, two x-ray imaging systems mounted in fixed positions in the treatment room are used for real-time (1–30 samples/s) stereoscopic three-dimensional localization of implanted fiducials that serve as target surrogates.7, 8, 9, 10 More recently, electromagnetic localization of implanted transponders was introduced clinically for prostate treatments.11 A shortcoming of both approaches is the need for additional hardware despite the availability of both kilovoltage (kV) and megavoltage (MV) on-board imaging integrated with the gantry of modern C-arm medical linear accelerators.

On the other hand, robust real-time 3D target localization during beam delivery is challenging with existing on-board imaging systems. Stereoscopic localization of implanted fiducials by simultaneous data acquisition with mutually orthogonal kV and MV imaging chains is possible12, 13, 14 as long as the fiducials are visible in the MV images. However, during the delivery of intensity modulated beams, this may not always be the case as fiducials are often hidden behind the leaves of multileaf collimators in the beam’s eye view. Furthermore, depending on the imaging view and patient build, small fiducials may not be discernible in MV images at all.15 On its own, single view (monoscopic) kV x-ray imaging along an axis orthogonal to the treatment beam is insufficient for 3D fiducial localization as fiducial displacements along the rays from the x-ray source to the detector cannot be accurately determined. More importantly, since the localization uncertainty is predominantly along a plane orthogonal to the treatment beam axis, it can be significant in terms of dosimetric impact to targets and organs at-risk.16

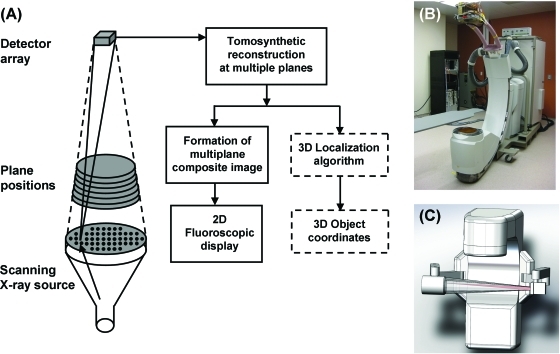
In order to estimate the undetected components of fiducial displacements in monoscopic imaging, investigators have proposed to parameterize fiducial coordinates as functions of one or two independent variables that serve as parameters for models describing the imaging process.17, 18, 19, 20, 21, 22 A model fit to data extracted from monoscopic image(s) results in parameter estimates, which are subsequently transformed to actual fiducial coordinates. These approaches rely heavily on model validity during the imaging process, and thus they are prone to potentially significant errors with physiologically induced changes in putative correlations between fiducial coordinates. Thus, it would be preferable to directly measure 3D fiducial coordinates in real-time with an on-board imaging system. In this paper, we propose a novel on-board imaging concept for single-view, real-time 3D tracking concurrent with external beam radiation therapy (EBRT) delivery based on Scanning-Beam Digital X-ray (SBDX, NovaRay Medical, Inc.) technology (Fig. 1). The feasibility of tracking implanted fiducials is investigated in a phantom using an SBDX prototype system.

Figure 1.

Figure 1

Open in a new tab

(a) The SBDX system uses a raster scanned focal spot, transmission target, multihole collimator, high speed detector, and hardware image reconstructor. The 3D localization algorithm (dashed boxes) utilizes the multiple image planes reconstructed for each temporal frame. (b) SBDX prototype system on C-arm. (c) Concept drawing of an on-board SBDX system integrated with a Linac.

METHODS

Imaging system and tracking algorithm

SBDX is an inverse geometry x-ray fluoroscopy technology with high dose efficiency and real-time tomosynthesis capability.23, 24 The x-ray source has a focal spot that is raster-scanned over an array of positions on a transmission-style target [Fig. 1a]. A multihole collimator positioned beyond the target surface defines a series of narrow overlapping x-ray beams, each of which is directed toward a small, high speed, photon-counting detector array. The prototype system used in this study had 100 × 100 focal spot positions on a 2.3 mm pitch, and a 5.5 × 5.5 cm detector with 48 × 48 elements positioned 150 cm from the target plane. A detector image is acquired from a new focal spot position every 1.28 μs. An area up to 16 cm wide at isocenter can be scanned at up to 30 frame/s, depending on the number of focal spot positions employed. As scanning proceeds, the detector images are transmitted to a set of digital tomosynthesis reconstruction channels operating in parallel (up to 16), each of which generates a full field-of-view image in real time at the rate of scanning (e.g., 30 frame/s). The image planes are oriented perpendicular to the source-detector (z) axis and typically programmed with 12 mm plane-to-plane spacing. As one views each image plane in turn, an object will appear blurred for planes distal to the z-position of the object, appear sharp at the plane nearest to the object in z, and then appear blurred again for proximal planes. The effect is entirely like the depth-of-field effect in a conventional visible-light camera.

The tomosynthesis capability of SBDX offers the possibility of resolving the three-dimensional location of fiducials in view, as opposed to the two-dimensional localization available with conventional projection x-ray fluoroscopy. A technique for extracting the 3D positions of small, high contrast objects from the image planes reconstructed for each frame period has been developed and evaluated in phantoms.25 The method localizes objects along the source-detector axis by treating object sharpness versus plane position as a distribution function whose center-of-mass represents the true object position. Thus, z-coordinates can be calculated with higher precision than the plane-to-plane spacing. The essential aspects of the technique are summarized below.

First, image planes are reconstructed at fixed positions surrounding the object(s) of interest using the shift-and-add tomosynthesis method employed in the SBDX hardware.23 Next, a rectangular 2D filtering kernel (K1) is applied for noise suppression, and gradient filtering is applied to each image plane to determine the degree of local sharpness and contrast in the images. These gradient-filtered images, termed a score stack, are scaled in units of contrast (0% to 100%). To assist in the subsequent segmentation of the stack into object regions, another rectangular 2D filter kernel (K2) is applied to each plane to spread edge gradients over the object area. The score stack provides a measure of object focus versus z-plane position at each (x,y) position in the field-of-view.

Last, the score stack is segmented into distinct object regions, and a 3D coordinate is calculated for each region. A maximum intensity projection (MIP) of the score stack along the z-direction is generated. Object regions are detected by applying a specified contrast threshold (T1) to this MIP. The z-coordinate of an object is determined by extracting the scores versus z-plane within the object region, subtracting a specified baseline contrast (T2), and then calculating the center-of-mass of the baseline-subtracted z-distribution. The (x,y) coordinates are derived from the center-of-mass of the object region in the two-dimensional score MIP. The end result is a set of (x,y,z) coordinates corresponding to objects detected in the frame period. Further detail with regard to the image analysis technique can be found in Ref. 25. Selection of filter kernels and thresholds is described in Sec. 2C.

Experimental setup

An IMRT Dose Verification Phantom (Acrylic IMRT Dose Verification Phantom, Standard Imaging, Inc., Middleton, WI) was assembled from six 3-cm thick slab components. The phantom comprised two solid acrylic slabs in each of the lowest and highest (posterior and anterior) positions and two lung slabs between the solid slabs. As shown in Fig. 2, each lung slab had two cavities separated by an acrylic mediastinal ridge along the midline. In one such slab, two fiducials were placed on the right side of this ridge. The superior fiducial was a steel sphere of diameter 1.5 mm. The inferior fiducial was a gold cylinder of length 2.6 mm and diameter 0.9 mm. Lung-equivalent inserts were placed in the cavities of this slab. The lung space contralateral to the gold fiducial included a 3.7 cm diameter water-equivalent (1.04 g/cm3) insert.

Figure 2.

Figure 2

Open in a new tab

Lung phantom slab showing locations of the gold seed fiducial (right) and steel sphere fiducial (left) on the mediastinal ridge.

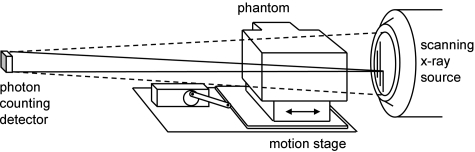
The phantom assembly was placed on a linear motion stage and the C-arm of the SBDX system was placed in a lateral view (Fig. 3). For imaging, the stage was oriented to move in a patient’s right-left direction in order to produce fiducial motion primarily along the source-detector axis (z-axis) of the imaging system, the direction that would be most challenging to track with conventional monoscopic x-ray imaging. The trajectory was sinusoidal and adjustable for both amplitude and period. The amplitude was set to ±10 mm, and the period was set at either 5 s or 3.5 s (nominal). The uncertainty of set nominal values as assessed by independent optical tracking measurements with the RPM 1.7 system (Varian Medical Systems, Palo Alto, CA) was ±1 mm in amplitude and ±0.1–0.2 s in period. The motion stage was operated asynchronously with respect to the imaging system; there was no explicit respiratory gating.

Figure 3.

Figure 3

Open in a new tab

Experimental setup. The imaging orientation was designed to test the most challenging geometry where phantom and fiducial motion is aligned with the source-detector (z) axis.

The SBDX system was operated at 15 frame/s, 100 kVp, with a fluoroscopic dose rate. A 71 × 71 hole scan mode yielding 11.4 cm field-of-view at isocenter was used. The images yielded good apparent conspicuity of the fiducials. Two imaging runs were acquired with the motion period set to 3.5 and 5 s. A third run was acquired in an electronically collimated scan mode where the x-ray beam was turned on for only a circular region (8 hole radius) within the 71 × 71 pattern, positioned such that only the gold fiducial and its immediate surroundings were illuminated.

Raw SBDX detector images generated during each imaging run were recorded to a memory board in the SBDX prototype hardware reconstructor. After the experiment, the data were transferred to a computer for offline image reconstruction and fiducial tracking. This method was used because the tracking algorithm was not part of the real time hardware reconstructor.

Image reconstruction and tracking analysis

Tomosynthetic image reconstruction was performed for each frame period at 15 fixed image planes with 12 mm plane-to-plane spacing. Figure 4 shows example image planes from a single frame period. The position of the plane stack along the source-detector axis was selected so that it included the entire trajectory of the fiducials. The plane spacing and number of planes were selected to match typical values that would be employed for fluoroscopic imaging.

Figure 4.

Figure 4

Open in a new tab

(a) Example x-y image reconstructed at a z-plane near the gold seed. (b) Gold seed region-of-interest in all 15 z-planes of the same temporal frame, demonstrating depth resolution. (c) A y-z image generated from a single image column passing through the gold seed in part b. The calculated z-coordinate is the center-of-mass of the distribution of object scores versus z-plane (shown with bars) after thresholding. (d) Example image plane acquired with electronic scan collimation around the gold seed.

The tracking algorithm was run on the reconstructed images frame-by-frame yielding the position of each fiducial as a function of time. The filter kernels (K1, K2) and contrast thresholds (T1, T2) in the tracking algorithm are adjustable parameters. The values used for the gold fiducial were K1 = 3 × 3 pixels (0.5 mm), K2 = 6 × 6 pixels (1.0 mm), T1 = 35% contrast, T2 = 20% contrast. The values for the steel sphere were K1 = 5 × 5 (0.8 mm), K2 = 10 × 10 (1.6 mm), T1 = 30%, and T2 = 20%. Tracking parameters were determined by testing a range of filter sizes and thresholds within a manually defined object region and background region of the first image frame, as described in Ref. 25. The filter kernel combination yielding the highest peak object score relative to background score and the widest range of valid object detection thresholds was selected. For object detection, the midpoint of the valid threshold range was used.

The measured 3D coordinates of an object versus time were compared to a model of the programmed motion trajectory, r(t) = ro + v sin ((2π/τ)(t − to)), where r(t) is the 3D coordinate at time t, the 3D vector v describes the direction of motion and maximum object displacement, τ is the period of sinusoidal motion, and ro and to are position and time offsets, respectively. The model was fit to the data using a nonlinear least squares method, and then the RMS deviation (RMSD) between the measured and model positions was calculated in the x, y, and z directions. For model fitting, ro, v, to, and τ were free parameters.

Tracking performance depends on object contrast, object size, and the photon fluence in the images. Peak object contrast was calculated as one minus the ratio of the minimum image value inside the object divided by the value in the surrounding background, in a plane where the object was in focus. Background image fluence was calculated as the mean pixel value within a background region-of-interest divided by the pixel area, at the same plane. Peak pixel signal-difference-to-noise-ratio (SDNR) was calculated as the peak signal difference generated by the object divided by the standard deviation in the surrounding background pixels. Pixel standard deviation was measured from adjacent-frame subtraction images and then divided by √2 to minimize the influence of spatial nonuniformity over the measurement ROI. All image pixel values were scaled linearly with respect to photon counts.

RESULTS

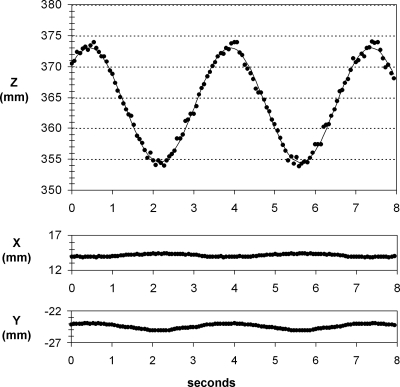
Figure 5 shows the tracked x, y, and z coordinates of the gold seed over 120 frames of 15 frame/s imaging, as the phantom underwent 3.5 s nominal periodic sinusoidal motion with ±10 mm amplitude. Tracked motion was sinusoidal and primarily along the source-detector axis (z-axis). The 3D motion model fit to the tracked 3D coordinates had a 3.47 s period and ±9.28 mm amplitude (coefficient of determination R2 = 0.95). The RMSD between the tracked z-coordinate and the model fit z-coordinate was 0.56 mm. RMSD in the x and y directions was 0.04 mm.

Figure 5.

Figure 5

Open in a new tab

Tracked x, y, and z coordinates of the gold seed versus time, with the phantom undergoing 3.5 s sinusoidal motion (symbols: data; solid line: model fit).

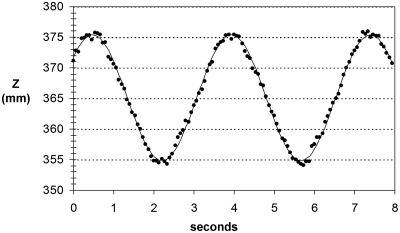
Figure 6 shows the tracked z-coordinate of the steel sphere in the same imaging run. For this fiducial, the motion model fit had a 3.46 s period and ±10.28 mm amplitude (R2 = 0.96). The z-coordinate RMSD was 0.53 mm. For both fiducials, the difference between the programmed amplitude and the model fit amplitude was similar to the z-coordinate RMS deviations about the model fit trajectory.

Figure 6.

Figure 6

Open in a new tab

Tracked z-coordinate of the steel sphere versus time for 3.5 s sinusoidal motion (symbols: data; solid line: model fit).

Similar 3D tracking results were obtained in the second imaging run, using 5 s nominal periodic motion, and in the third imaging run, which used electronic collimation around the gold seed [see Fig. 4d] and a 3.5 s period. Table TABLE I. lists model fit parameters, z-coordinate RMSD, and SDNR measurements for all cases examined. The difference between the programmed and model fit parameters ranged from −0.77 to 0.28 mm for motion amplitude (−7.7% to 2.8% difference) and from −0.33 s to 0.04 s for the motion period (−6.5% to 1.1%). The z-coordinate RMS deviations ranged from 0.53 to 0.71 mm.

TABLE I.

Programmed motion, motion parameters derived from fits to 3D tracking data, and Z-coordinate deviations.

Image run Fiducial Field-of-view Nominal perioda (s) Nominal amplitudea (mm) Model fit period (s) Model fit amplitude (mm) Z-coordinate RMSD (mm) Peak pixel SDNR
1 Gold Full 3.5 ±10 3.47 ±9.28 0.56 21.3
1 Steel Full 3.5 ±10 3.46 ±10.28 0.53 25.7
2 Gold Full 5.0 ±10 4.67 ±9.32 0.57 21.3
2 Steel Full 5.0 ±10 4.68 ±10.12 0.64 25.8
3 Gold Collimated 3.5 ±10 3.54 ±9.23 0.71 19.9
Open in a new tab
a

Programmed value.

Peak pixel SDNR was 21% higher for the steel sphere compared to the gold seed, due to a combination of higher local background fluence (5067 versus 4277 photons/mm2 per frame) and higher peak object contrast (0.94 versus 0.86). Previous studies have shown that frame-to-frame tracking precision along the z-axis is improved for higher background fluence and higher contrast objects.25 Differences in image fluence, contrast, and object dimensions may be responsible for the slightly different model fit amplitudes derived for the two fiducials in this study.

DISCUSSION AND CONCLUSION

This study reports on the feasibility of single-view 3D fiducial tracking during external beam radiation therapy based on SBDX fluoroscopic imaging capabilities. This technology performs high speed tomosynthesis at multiple image planes per frame period. By applying a recently developed 3D tracking technique to the data acquired during SBDX imaging, it was found that small, high contrast fiducials (e.g., a gold seed) undergoing simulated respiratory motion could be tracked along the source-detector axis versus time using a single gantry view. Tracking accuracy and precision were each found to be better than 1 mm. These results are similar to those reported for tracking of cardiac catheters in phantoms.25

A notable feature of the inverse geometry scanning method employed in SBDX is its capability to provide 3D localization in a dose efficient manner. Narrow beam scanning drastically reduces image scatter levels relative to conventional fluoroscopy, which in turn allows a desired image quality to be obtained with fewer primary x-rays and lower patient dose.24 Entrance dose is further reduced because x-rays are spread over a larger area at the patient entrance, compared to conventional cone beam imaging. This study also indicates that significant integral dose reduction could be obtained in the case of single object tracking, by modifying the active portion of the scan pattern so that only the area around the object is illuminated. This electronic collimation technique only requires that a sufficiently large region of the collimator remain active (e.g., ten hole diameter for an isocenter object) so that the object is imaged over the full tomographic angle of the system. Further, this technique can be extended to multiple tracked objects by prescribing individual illumination regions per object: the x-ray source has the capability of turning on or off for any or many regions in the field of view. Other existing strategies for minimizing fluoroscopic dose such as the use of surrogate signal monitoring combined with “on demand” real-time imaging can also be used with the SBDX system.

While low-dose radiographic and fluoroscopic imaging with 3D fiducial localization capability is an attractive feature of the on-board SBDX concept, in view of potential implementation its potential for volumetric imaging needs to be considered. Volumetric inverse-geometry computed tomography (IGCT) has been previously demonstrated with tabletop setups employing the SBDX system.26, 27 Schmidt et al. demonstrated IGCT images with submillimeter in-plane resolution, which are free from cone-beam artifacts. Acquisition times with the prototype were on the order of tens of seconds,26 within the industry-limited maximum linac gantry rotation speed of 1 revolution per minute. For IGCT purposes, the field-of-view (FOV) is limited by the extent of the source array in the transverse (in-plane) direction and the smaller of the detector and source dimensions in the axial (cranial-caudal) direction. The SBDX prototype in this study would provide a 16 cm transverse × 5 cm axial IGCT FOV using all 100 source columns. More recently, a 5.3 × 10.6 cm detector has been constructed that would enable a 16 × 10 cm cone-beam artifact free IGCT FOV. (The increased tomographic angle afforded by this detector is also expected to improve z-axis tracking precision.28) The transverse CT FOV can be doubled through full gantry rotation and a source-detector offset, an approach used with current on-board systems. This extended FOV is expected to be suitable for 3D soft tissue target localization as evidenced by reports on the clinical use of a relatively small transverse FOV CBCT for body imaging.29, 30 This is done in order to reduce the integral imaging dose despite the introduction of image artifacts. Other potential approaches that are being researched to significantly increase the transverse FOV include the use of multiple SBDX detectors27 or noncircular acquisition trajectories.31

In summary, the results of the present study clearly demonstrate the feasibility of using Scanning-Beam Digital X-ray imaging for 3D localization and tracking of fiducials. This capability in combination with real-time implementation of the tracking and collimation techniques can potentially enable simple yet robust approach to image-based intrafractional motion management. This possibility warrants further explorations with regard to the potential of SBDX as an on-board imaging system for image-guided radiation therapy.

ACKNOWLEDGMENTS

Dr. Speidel acknowledges financial support provided by NIH Grant No. R01 HL084022. Technical support for this work was provided by Triple Ring Technologies, Inc., and NovaRay, Inc. Dr. Wilfley has a financial interest in NovaRay, Inc.

References

  1. Keall P. J. et al. , “The management of respiratory motion in radiation oncology report of AAPM Task Group 76,” Med. Phys. 33(10), 3874–3900 (2006). 10.1118/1.2349696 [DOI] [PubMed]
  2. von Siebenthal M., Szekely G., Lomax A. J., and Cattin P. C., “Systematic errors in respiratory gating due to intrafraction deformations of the liver,” Med. Phys. 34(9), 3620–3629 (2007). 10.1118/1.2767053 [DOI] [PubMed]
  3. Suh Y., Dieterich S., Cho B., and Keall P. J., “An analysis of thoracic and abdominal tumour motion for stereotactic body radiotherapy patients,” Phys. Med. Biol. 53(13), 3623–3640 (2008). 10.1088/0031-9155/53/13/016 [DOI] [PubMed]
  4. Nishioka S., Nishioka T., Kawahara M., Tanaka S., Hiromura T., Tomita K., and Shirato H., “Exhale fluctuation in respiratory-gated radiotherapy of the lung: A pitfall of respiratory gating shown in a synchronized internal/external marker recording study,” Radiother. Oncol. 86(1), 69–76 (2008). 10.1016/j.radonc.2007.11.014 [DOI] [PubMed]
  5. Feng M., Balter J. M., Normolle D., Adusumilli S., Cao Y., Chenevert T. L., and Ben-Josef E., “Characterization of pancreatic tumor motion using cine MRI: Surrogates for tumor position should be used with caution,” Int. J. Radiat. Oncol., Biol., Phys. 74(3), 884–891 (2009). 10.1016/j.ijrobp.2009.02.003 [DOI] [PMC free article] [PubMed]
  6. Hunjan S., Starkschall G., Prado K., Dong L., and Balter P., “Lack of correlation between external fiducial positions and internal tumor positions during breath-hold CT,” Int. J. Radiat. Oncol., Biol., Phys. 76(5), 1586–1591 (2010). 10.1016/j.ijrobp.2009.08.008 [DOI] [PubMed]
  7. Schweikard A., Glosser G., Bodduluri M., Murphy M. J., and Adler J. R., “Robotic motion compensation for respiratory movement during radiosurgery,” Comput. Aided Surg. 5(4), 263–277 (2000). 10.3109/10929080009148894 [DOI] [PubMed]
  8. Shirato H., Shimizu S., Kitamura K., Nishioka T., Kagei K., Hashimoto S., Aoyama H., Kunieda T., Shinohara N., Dosaka-Akita H., and Miyasaka K., “Four-dimensional treatment planning and fluoroscopic real-time tumor tracking radiotherapy for moving tumor,” Int. J. Radiat. Oncol., Biol., Phys. 48(2), 435–442 (2000). 10.1016/S0360-3016(00)00625-8 [DOI] [PubMed]
  9. Shimizu S., Shirato H., Kitamura K., Shinohara N., Harabayashi T., Tsukamoto T., Koyanagi T., and Miyasaka K., “Use of an implanted marker and real-time tracking of the marker for the positioning of prostate and bladder cancers,” Int. J. Radiat. Oncol., Biol., Phys. 48(5), 1591–1597 (2000). 10.1016/S0360-3016(00)00809-9 [DOI] [PubMed]
  10. Shirato H., Shimizu S., Shimizu T., Nishioka T., and Miyasaka K., “Real-time tumour-tracking radiotherapy,” Lancet 353(9161), 1331–1332 (1999). 10.1016/S0140-6736(99)00700-X [DOI] [PubMed]
  11. Kupelian P., Willoughby T., Mahadevan A., Djemil T., Weinstein G., Jani S., Enke C., Solberg T., Flores N., Liu D., Beyer D., and Levine L., “Multi-institutional clinical experience with the Calypso System in localization and continuous, real-time monitoring of the prostate gland during external radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 67(4), 1088–1098 (2007). 10.1016/j.ijrobp.2006.10.026 [DOI] [PubMed]
  12. Wiersma R. D., Mao W., and Xing L., “Combined kV and MV imaging for real-time tracking of implanted fiducial markers,” Med. Phys. 35(4), 1191–1198 (2008). 10.1118/1.2842072 [DOI] [PMC free article] [PubMed]
  13. Wiersma R. D., Riaz N., Dieterich S., Suh Y., and Xing L., “Use of MV and kV imager correlation for maintaining continuous real-time 3D internal marker tracking during beam interruptions,” Phys. Med. Biol. 54(1), 89–103 (2009). 10.1088/0031-9155/54/1/006 [DOI] [PubMed]
  14. Cho B., Poulsen P. R., Sloutsky A., Sawant A., and Keall P. J., “First demonstration of combined kV/MV image-guided real-time dynamic multileaf-collimator target tracking,” Int. J. Radiat. Oncol., Biol., Phys. 74(3), 859–867 (2009). 10.1016/j.ijrobp.2009.02.012 [DOI] [PMC free article] [PubMed]
  15. Adamson J. and Wu Q., “Prostate intrafraction motion evaluation using kV fluoroscopy during treatment delivery: A feasibility and accuracy study,” Med. Phys. 35(5), 1793–1806 (2008). 10.1118/1.2899998 [DOI] [PMC free article] [PubMed]
  16. Nill S., Unkelbach J., Dietrich L., and Oelfke U., “Online correction for respiratory motion: Evaluation of two different imaging geometries,” Phys. Med. Biol. 50(17), 4087–4096 (2005). 10.1088/0031-9155/50/17/012 [DOI] [PubMed]
  17. Cho B., Poulsen P. R., and Keall P. J., “Real-time tumor tracking using sequential kV imaging combined with respiratory monitoring: A general framework applicable to commonly used IGRT systems,” Phys. Med. Biol. 55(12), 3299–3316 (2010). 10.1088/0031-9155/55/12/003 [DOI] [PMC free article] [PubMed]
  18. Cho B., Poulsen P. R., Sawant A., Ruan D., and Keall P. J., “Real-time target position estimation using stereoscopic kilovoltage/megavoltage imaging and external respiratory monitoring for dynamic multileaf collimator tracking,” Int. J. Radiat. Oncol., Biol., Phys. 79, 269–278 (2011). 10.1016/j.ijrobp.2010.02.052 [DOI] [PMC free article] [PubMed]
  19. Poulsen P. R., Cho B., and Keall P. J., “Real-time prostate trajectory estimation with a single imager in arc radiotherapy: A simulation study,” Phys. Med. Biol. 54(13), 4019–4035 (2009). 10.1088/0031-9155/54/13/005 [DOI] [PubMed]
  20. Poulsen P. R., Cho B., Langen K., Kupelian P., and Keall P. J., “Three-dimensional prostate position estimation with a single x-ray imager utilizing the spatial probability density,” Phys. Med. Biol. 53(16), 4331–4353 (2008). 10.1088/0031-9155/53/16/008 [DOI] [PubMed]
  21. Poulsen P. R., Cho B., Ruan D., Sawant A., and Keall P. J., “Dynamic multileaf collimator tracking of respiratory target motion based on a single kilovoltage imager during arc radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 77(2), 600–607 (2010). 10.1016/j.ijrobp.2009.08.030 [DOI] [PubMed]
  22. Poulsen P. R., Cho B., Sawant A., and Keall P. J., “Implementation of a new method for dynamic multileaf collimator tracking of prostate motion in arc radiotherapy using a single kV imager,” Int. J. Radiat. Oncol., Biol., Phys. 76(3), 914–923 (2010). 10.1016/j.ijrobp.2009.06.073 [DOI] [PubMed]
  23. Speidel M. A., Wilfley B. P., Star-Lack J. M., Heanue J. A., and Van Lysel M. S., “Scanning-beam digital x-ray (SBDX) technology for interventional and diagnostic cardiac angiography,” Med. Phys. 33, 2714–2727 (2006). 10.1118/1.2208736 [DOI] [PubMed]
  24. Speidel M. A., Wilfley B. P., Star-Lack J. M., Heanue J. A., Betts T. D., and Van Lysel M. S., “Comparison of entrance exposure and signal-to-noise ratio between an SBDX prototype and a wide-beam cardiac angiographic system,” Med. Phys. 33, 2728–2743 (2006). 10.1118/1.2198198 [DOI] [PubMed]
  25. Speidel M. A., Tomkowiak M. T., Raval A. N., and Van Lysel M. S., “Three-dimensional tracking of cardiac catheters using an inverse geometry x-ray fluoroscopy system,” Med. Phys. 37(12), 6377–6389 (2010). 10.1118/1.3515463 [DOI] [PMC free article] [PubMed]
  26. Schmidt T. G., Star-Lack J., Bennett N. R., Mazin S. R., Solomon E. G., Fahrig R., and Pelc N. J., “A prototype table-top inverse-geometry volumetric CT system,” Med. Phys. 33(6), 1867–1878 (2006). 10.1118/1.2192887 [DOI] [PubMed]
  27. Mazin S. R., Star-Lack J., Bennett N. R., and Pelc N. J., “Inverse-geometry volumetric CT system with multiple detector arrays for wide field-of-view imaging,” Med. Phys. 34(6), 2133–2142 (2007). 10.1118/1.2737168 [DOI] [PubMed]
  28. Speidel M. A., Lowell A. P., Heanue J. A., and Van Lysel M. S., “Frame-by-frame 3D catheter tracking methods for an inverse geometry cardiac interventional system,” Proc. SPIE 6913, 69131I (2008). 10.1117/12.772745 [DOI]
  29. McBain C. A., Henry A. M., Sykes J., Amer A., Marchant T., Moore C. M., Davies J., Stratford J., McCarthy C., Porritt B., Williams P., Khoo V. S., and Price P., “X-ray volumetric imaging in image-guided radiotherapy: The new standard in on-treatment imaging,” Int. J. Radiat. Oncol., Biol., Phys. 64(2), 625–634 (2006). 10.1016/j.ijrobp.2005.09.018 [DOI] [PubMed]
  30. Oldham M., Letourneau D., Watt L., Hugo G., Yan D., Lockman D., Kim L. H., Chen P. Y., Martinez A., and Wong J. W., “Cone-beam-CT guided radiation therapy: A model for on-line application,” Radiother. Oncol. 75(3), 271–278 (2005). 10.1016/j.radonc.2005.03.026 [DOI] [PubMed]
  31. Li T., Li X., Yang Y., Heron D. E., and Hug M. S., “A novel off-axis scanning method for an enlarged ellipse cone-beam computed tomography field of view,” Med. Phys. 37(12), 6233–6239 (2010). 10.1118/1.3514130 [DOI] [PubMed]

Articles from Medical Physics are provided here courtesy of American Association of Physicists in Medicine

RESOURCES