Abstract
Quantitative estimations of first-in-human (FIH) doses are critical for phase I clinical trials in drug development. Human pharmacokinetic (PK) prediction methods have been developed to project the human clearance (CL) and bioavailability with reasonable accuracy, which facilitates estimation of a safe yet efficacious FIH dose. However, the FIH dose estimation is still very challenging and complex. The aim of this article is to review the common approaches for FIH dose estimation with an emphasis on PK-guided estimation. We discuss 5 methods for FIH dose estimation, 17 approaches for the prediction of human CL, 6 methods for the prediction of bioavailability, and 3 tools for the prediction of PK profiles. This review may serve as a practical protocol for PK- or pharmacokinetic/pharmacodynamic-guided estimation of the FIH dose.
KEY WORDS: allometric scaling, FIH dose, in vitro–in vivo correlations, pharmacokinetics, prediction
INTRODUCTION
Estimation of a first-in-human (FIH) dose is an essential element in clinical development of a drug molecule for approval by the Food and Drug Administration (FDA). Selection of the starting dose in humans is a complex process, as it must fall within an optimal window. The starting dose must be low enough to be safe but high enough to avoid excessive dose escalations, which are costly and time-consuming. The most widely used method for FIH dose estimation is based on no observable adverse effect levels (NOAELs) in multiple species (1,2). NOAELs are determined in relevant animal studies and normalized to body surface area (in milligrams per square meter), and then extrapolated to human equivalent doses (HEDs). The HED from the most appropriate species is then divided by a safety factor to generate the maximum recommended starting dose (MRSD) in humans. However, the NOAEL-based approach relies on a somewhat arbitrary safety factor to estimate the starting dose, and the method is very conservative for FIH dose estimation (3). In contrast, pharmacokinetic-guided approaches provide a more mechanistic rationale and are becoming more common with many pharmaceutical companies and institutes. Accurate predictions of human pharmacokinetics (PK) prior to phase I studies have resulted in significant time savings, ranging from 1 to 6 months, during dose escalations (4).
Clearance (CL) and bioavailability (F) are two important pharmacokinetic parameters which are related directly to FIH dose estimation. Using the lowest area under the curve (AUC) observed at NOAEL in one animal species and the predicted human CL and F, one can estimate the FIH dose (5). Over the past few decades, many empirical and physiological approaches have been developed for quantitative prediction of human CL (3,6–13) and F. These predictive approaches typically require in vivo preclinical data, in vitro metabolism and disposition data obtained from animal and human tissues, and/or physicochemical parameters of the drug compounds. Each approach has its advantages and disadvantages. Although several excellent review articles have discussed and compared some predictive approaches (3,14–23), to our knowledge, a comprehensive and practical summary of all the prediction approaches is still not available. Therefore, this review introduces commonly used methods for FIH dose estimation and summarizes 17 approaches to predict human CL, 6 methods to predict bioavailability, and 3 tools to generate PK profiles. For each approach, we discuss the assumptions, equations, required data and parameters, accuracy of prediction, advantages, and limitations. This review article may be used as a practical manual to predict FIH doses.
ESTIMATION OF FIRST-IN-HUMAN DOSE
Many methods have been used for FIH dose estimation and no consensus has been reached for which method is most accurate (5). Currently available approaches are based on NOAELs (2,5,24), minimal anticipated biological effect levels (MABELs) (25), pharmacokinetic prediction (5,24,26,27), pharmacokinetic/pharmacodynamic (PK/PD) simulation (16,28,29), and similar drug comparison (5,24). Advances in PK and PK/PD modeling and simulation have increased the use of these approaches (5). Unlike the empirical estimation methods, these model-guided approaches have a mechanistic rationale to understand the effect of physiological variables or disease status on pharmacokinetic parameters (16).
NOAEL-Based Approach
In July 2005, the US FDA issued the Guidance on Estimating the Maximum Safe Starting Dose in Initial Clinical Trials for Therapeutics in Adult Healthy Volunteers (2). The suggested process for selecting MRSD involves the following: (1) determine the NOAEL in each animal species tested, (2) convert the NOAEL to an HED using appropriate scaling factors, (3) apply a safety factor to the HED to define the human MRSD. For mice, rats, and dogs, HED scaling based on body weight rather than surface area will increase the HED by 12, 6, and 2 times, respectively. To generate a conservative HED, the conversion is based on dose normalization by body surface area for most systemically administered low molecular weight therapeutics. The body surface area conversion factor is a unitless number that converts milligrams per kilogram doses for each animal species to the milligrams per kilogram dose in humans (HED). The species that generates the lowest HED is deemed the most appropriate one. When preclinical toxicity data indicate that a particular species is more relevant for assessing human risk, the HED for that species may be used in subsequent calculations regardless of whether it is the most sensitive (4). To define the MRSD in humans, the safety factor applied to the HED from the most appropriate species is generally at least 10 (5). Finally, the MRSD may need to be adjusted based on the pharmacologically active dose.
For small molecule chemical entities, the conservative NOAEL-based approach has a good safety record and is simple and practical. However, consideration of the pharmacologically active dose may be overlooked. The importance of adjusting the MRSD to prevent toxicity was illustrated in the 2006 FIH clinical trial for TGN1412, a monoclonal antibody directed against T lymphocytes. TGN1412 produced multiorgan failure in six healthy volunteers (30). The NOAEL was 50 mg/kg, and interspecies scaling (from cynomolgus monkeys) based on body weight gave an HED of 16 mg/kg. Although a very conservative safety factor of 160 was applied to generate an MRSD of 0.1 mg/kg, adverse effects were still observed in humans (31).
MABEL-Based Approach
The tragic incident of TGN1412 led to the introduction of the MABEL by European Medicines Agency (EMEA) (25), which issued a guideline in 2007 containing strategies to identify and mitigate risks in FIH trials with investigational medicinal products. The MABEL is the lowest dose that is associated with any biological effect, whether it be toxicity or a desired pharmacological effect (16). MABEL is calculated using the following PK/PD data: (1) in vitro target binding and receptor occupancy in target human and animal cells, (2) in vitro concentration–response curves in target human and animal cells, (3) in vivo dose–exposure–response profiles in relevant animal species, and (4) exposures at pharmacological active doses in relevant animal species. To minimize the potential risks of adverse effects in humans, a safety factor is applied in the calculation of the FIH dose from the MABEL. The value of the safety factor depends on the novelty of the active substance, the biological potency, the mode of action, the degree of species specificity, and the shape of the dose–response curve and the degree of uncertainty in the calculation of the MABEL. Per the EMEA guideline, the FIH doses are calculated from the NOAEL and MABEL and the lowest value is recommended for the clinical trial (25). For biotherapeutics with potentially agonistic modes of action on key body systems, no more than 10% occupancy is proposed for the first-in-man trial (16). In the case of TGN1412, the estimated FIH dose is 0.001 mg/kg using the MABEL-based approach (31). In contrast, the 0.1 mg/kg FIH dose of TGN1412 estimated by the NOAEL-based approach leads to a receptor occupancy greater than 90%, which is very likely to cause adverse effects.
Similar Drug Comparison Approach
The similar drug comparison approach may be used when human PK/PD data are available for a drug similar to the one under investigation (5,24). The dose of the investigated drug can be calculated from the dose of the reference drug: 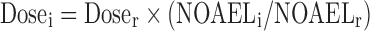 . The dose obtained is usually corrected by an arbitrary safety factor to accommodate uncertainty (5).
. The dose obtained is usually corrected by an arbitrary safety factor to accommodate uncertainty (5).
Pharmacokinetic-Guided Approach
As discussed above, the advances in CL, steady-state volume of distribution (Vdss), and plasma concentration–time profile predictions have made it possible to approximate human pharmacokinetics with reasonable accuracy, which facilitates estimation of the FIH dose.
In a pharmacokinetic-guided approach, the NOAEL and corresponding AUC in several animal species are determined. The species that results the lowest NOAEL is used as the index species for scaling. The starting oral dose is the product of the AUC of the drug in the index species and the predicted human CL, corrected by oral bioavailability (F): 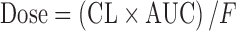 (5,16,24). Besides AUC, the steady-state concentration (Css) or maximum concentration (Cmax) may also be used as the systematic exposure (5,27). The starting dose can be calculated as follows:
(5,16,24). Besides AUC, the steady-state concentration (Css) or maximum concentration (Cmax) may also be used as the systematic exposure (5,27). The starting dose can be calculated as follows: 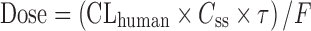 ; where τ is the dosing interval.
; where τ is the dosing interval.
Mahmood et al. (26) proposed dose calculations using the AUC in a species whose clearance (per kilogram of body weight) is nearest to that predicted in humans. A correction factor is then obtained by dividing the clearance of the chosen species by the predicted human clearance. Thus, the starting dose is defined by the following equation: 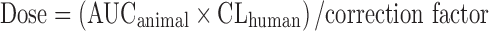 .
.
Collins et al. (32) applied the pharmacokinetic-guided approach to three anticancer drugs, which reduced the phase I clinical trials for each drug by 12–24 months. However, a few assumptions are made with pharmacokinetic-guided approaches: (1) only the parent compound is active, and (2) given equal plasma concentrations, the drug shows equal pharmacological activity or toxicity in human and nonhuman animal species. This results in the inability to account for interspecies differences in pharmacodynamics, which are extremely important to identify prior to phase I trials considering the TGN1412 incident. Preclinical predictions of both human PK and PD parameters are necessary to accurately estimate a nontoxic yet efficacious FIH dose (4,27).
PK/PD Model-Guided Approach
To avoid inaccuracy caused by interspecies differences in exposure–response relationships, PK/PD modeling has been utilized to estimate the FIH dose (4,16,27,33). Lowe et al. (16) reported the estimation of human doses using a four-step approach requiring multiple sources of information. In the first step, by using in vitro and in vivo pharmacological experiments, they set up the concentration–effect relationships to identify biomarkers, determined PD parameters such as EC50, and developed the PD models. The second step identified the interspecies differences in the concentration–response profiles, for both desired and adverse effects. This included differences in tissue distribution, tissue and plasma protein binding, blood cell binding, and target receptor occupancy. In the third step, human pharmacokinetic parameters, such as CL, bioavailability, and plasma concentration–time profiles, were predicted as described in “Prediction of Human Clearance”, “Prediction of Bioavailability”, and “Prediction of Human Plasma Concentration–Time Profiles” sections. The final step was integrating human PK and PD models to predict human dose–response relationships, which involved two approaches. The simple one is the threshold model, which assumed no response delay in the PD model. Based on the predicted human PK profile, a dosing regimen was designed to keep drug concentrations above the threshold of efficacy (e.g., EC50) but below the threshold of adverse effects. The other approach used a PK/PD model to simulate the dose–exposure–response–time profiles, which could incorporate the complex PD models.
Heimbach et al.(29) further improved the four-step approach by incorporating formulation and biopharmaceutical parameters (e.g., Biopharmaceutics Classification System), which made it possible to project the PK/PD profiles of drugs with various dosage forms and properties. They also demonstrated that the human PK/PD profile could be projected using animal data from a single species. It is worth mentioning that the PK/PD model-based approach is especially successful for a well-studied class of biotherapeutics such as monoclonal antibodies, whose PK properties are usually uniform based on their isotype. The receptor occupancy (RO), which can be measured by in vitro experiments, may be used as the biomarker for the human PK/PD model. When estimating the starting dose, due to the downstream biological effect, the RO value is recommended to be low for an agonist and high for an antagonist (28).
Summary of FIH Dose Estimation
An accurate estimation of human starting doses is critical for phase I trials. The assumptions, applicability, advantages, and disadvantages of the above five approaches are summarized in Table I. Although PK- and PK/PD-guided approaches are increasingly used, it is strongly recommended that the NOAEL, MABEL, PK, and PK/PD modeling and similar drug comparison approaches also be utilized to obtain several estimated doses (5). Subsequently, all toxicological, pharmacological, pharmacokinetic, and biopharmaceutical information should be evaluated to determine the optimal FIH dose.
Table I.
Assumptions, Applicability, Advantages, and Disadvantages of Five Approaches for FIH Dose Estimation
| Method | Assumptions | Applicability | Advantages | Disadvantages |
|---|---|---|---|---|
| Simple allometry | Doses scale 1:1 between species when normalized to body surface area or body weight (2) | Scaling based on body surface area: for most small molecules. Scaling based on body weight: The therapeutic is administered orally, intranasally, subcutaneously, or intramuscularly and the dose is limited by local toxicities. Proteins administered intravascularly with Mr >100 kDa (2) | Good safety record for small molecule drugs; easy to use | Arbitrary safety factor makes the approach very conservative. Neglect the interspecies differences in pharmacology, such as binding affinity and potency |
| MABEL | Starting with lowest active dose is safer that the starting with NOAEL | Applicable to both biotherapeutics and small molecule chemical entities; pharmacological mechanisms and knowledge are required, for example, the binding affinity to molecular targets | Based on pharmacologic knowledge rather than an empirical factor | Requires extensive mechanistic data |
| Similar drug comparison | Drug candidates with similar chemical structures have similar PK and PD properties and the ratio of the starting dose to the NOAEL will be the same for both compounds | Human PK data are available for a drug similar to the one under investigation | Easy to use; very limited data are required | Only applicable to very limited drug candidates |
| PK-guided approach | Dose-limiting toxicities are correlated with PK parameters such as plasma drug concentrations and AUC (32) | Human PK parameters such as CL and bioavailability are predicted from preclinical data with a reasonable accuracy. In vitro data show no dramatic differences in pharmacology between animals and human | Based on pharmacokinetic properties rather than an empirical factor | Neglect interspecies differences in pharmacodynamics; depends on the prediction accuracy of human PK parameters |
| PK/PD modeling-guided approach | PK/PD models developed using preclinical data can provide a reasonable simulation of human PK/PD–time profile | This approach can be used when human dose–exposure–response relationships are simulated by a mathematic model | Interspecies differences in both PK and PD are considered; reduce the reliance on empirical safety factors | A lot of efforts are required to establish and validate PK/PD models |
In order to use PK- and PK/PD-guided FIH dose selection, human pharmacokinetic parameters (CL, bioavailability, and AUC) need to be predicted. The following sections summarize the available methods for human CL, bioavailability, and PK profile prediction.
PREDICTION OF HUMAN CLEARANCE
The 17 approaches for human clearance prediction discussed in this review are from three categories: interspecies scaling, physiologically based in vitro–in vivo extrapolation (IVIVE), and computational (in silico) approaches.
The interspecies scaling includes simple allometry (SA), allometric scaling of CL of unbound drug, rule of exponents (RoE), allometric scaling of drugs with renal and biliary excretion, allometric scaling after normalization by in vitro CL, multi-exponential allometry, the two term power equation, the fu corrected intercept method (FCIM), and the liver blood flow method (LBF). Most interspecies scaling predictions were empirical approaches and based on in vivo animal data. However, additional animal and human in vitro metabolism data have been introduced to allometric scaling to improve the accuracy of prediction (8).
IVIVE predictions are physiologically based approaches. Human clearance is extrapolated from in vitro metabolism in human liver microsomes, hepatocytes, or human cDNA recombinant CYP450 isoenzymes by using a physiologically based scaling factor (PB-SF). The IVIVE is further improved by incorporating correction factors such as a drug-specific factor (SF) derived from the animal CL, an empirical factor determined by a regression between human in vivo intrinsic CL (CLint, in vivo) and human in vitro intrinsic CL (CLint, in vitro) or protein binding in plasma and/or microsomes. For renally excreted drugs, a physiologically based IVIVE approach (20,34) was developed to predict human renal clearance (CLR).
Computational approaches and statistical tools such as multivariate linear regression (MLR), principle component analysis (PCA), partial least squares (PLS), and backpropagation neural and artificial neural network (ANN) can be employed to establish correlations between human CL and animal CL or physiochemical properties of the compounds.
Interspecies Scaling
Simple Allometry
As shown in Table II, simple allometric scaling is based on a power function CL = a × Yb, where Y may be the body weight (W) or body surface area and a and b are the coefficient and exponent of the allometric equation, respectively. For the compounds with high hepatic extraction ratios, the hepatic clearance (CLH) is limited by LBF. Since LBF is correlated with body weight across species, SA is expected to be more predictive for compounds with high CLH (14). This is supported by Tang’s global examination of SA for CL prediction (10). Among 57 hepatically eliminated compounds, prediction accuracy depended upon the value of CL: high CL (n = 11) > moderate CL (n = 17) > low CL (n = 29). The study also revealed that CL prediction by SA was more accurate for proteins (n = 10) than nonprotein chemicals (n = 102). Consistently, Wang and Prueksaritanont (35) reported that human CL of therapeutic proteins can be predicted reasonably well by simple allometric scaling with a fixed exponent of 0.8. On the other hand, as with tubular and intestinal secretion, reabsorption, and metabolism, the accurate prediction of renal (CLR) and bile clearance (CLbile) using SA is difficult (19,20). A coefficient of determination (r2), which is obtained from a linear regression of log-transformed animal body weights and the corresponding CL, has been reported in most allometric scaling studies. Tang and Mayersohn (36) proved there is no correlation between r2 and prediction accuracy of human CL by using a mathematical model and literature data.
Table II.
Approaches for Human Clearance Prediction
| Method | Equation | Data required | Dataset | AFE or APE | <twofold |
|---|---|---|---|---|---|
| Simple allometry (SA) (3,6,11) |
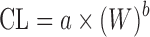 where a and b are the coefficient and exponent of the allometric equation and W is body weight where a and b are the coefficient and exponent of the allometric equation and W is body weight |
CL and body weight in at least two animal species | n = 60 (10) | 3.23 | 81% |
| n = 102 (11) | 2.65 | 54% | |||
| n = 26 (11) | N.A. | 46% | |||
| n = 50 (9) | 1.41 | 53% | |||
| n = 102 (9) | 1.28 | 54% | |||
| n = 103 (42) | N.A. | 53% | |||
| n = 24 (37) | N.A. | 17% | |||
| n = 22 (63) | 2.03 | 68% | |||
| n = 45 (40) | N.A. | 71% | |||
| Allometric scaling of unbound CL (38) | Unbound CL = CL/f u, p | CL, body weight, and plasma unbound (f u, p) in at least two animal species | n = 24 (37) | N.A. | 62% |
| Unbound CL = a × (W)b | n = 12 (12) | 1.79 | 69% | ||
| where f u, p is the unbound fraction in plasma | n = 20 (38) | 2.7 | 55% | ||
| Two term power equation (39) |
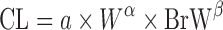 or or 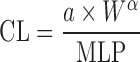
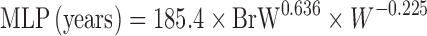 where a is the coefficient and α and β are the exponents of the allometric equation. W and BrW are body weight and brain weight where a is the coefficient and α and β are the exponents of the allometric equation. W and BrW are body weight and brain weight |
CL and body weight in at least three animal species | N.A. | N.A | N.A. |
| Rule of exponents (RoE) (3) | If 0.55 < b <0.70, CL = a × (W)b | CL, body weight, and brain weight in at least two animal species | All categories | ||
| If 0.71 < b < 0.99, CLhuman = a × (MLPanimal × CLanimal)b / MLPhuman | n = 60 (10) | 1.85 | 81% | ||
| If b ≥ 1, CLhuman = a × (BrWanimal × CLanimal)b / 1.53 | n = 102 (11) | 2.25 | 54% | ||
| If b > 1.3, CL will be overpredicted | n = 103 (42) | N.A. | 49% | ||
| If b < 0.55, CL will be underpredicted | n = 24 (37) | N.A. | 37% | ||
| n = 45 (40) | N.A. | 93% | |||
| Allometric scaling for renally and biliarily excreted drugs (7,44) | For renal secreted drugs: 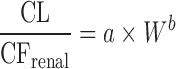
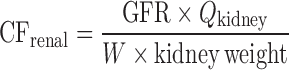
|
CL, body weight, GFR, kidney blood flow, kidney weight, bile flow, and UDPGT activity in at least two animal species | Renal-secreted drugs | ||
For biliary excreted drugs: 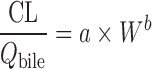 or or 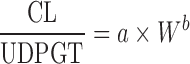
|
n = 10 (43) | N.A. | 70% | ||
| Biliary excreted drugs, n = 8 (44) | N.A. | 50% | |||
| Allometric scaling after normalization by CLint, in vitro (8,45) |
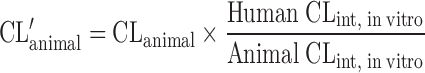
|
CL and body weight in at least two animal species, human and animal microsomal or hepatocyte K m, V max, or concentrations | Extensively metabolized compounds | ||
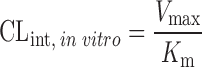 or or 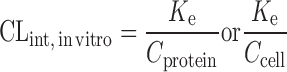
|
n = 10 (8) | N.A. | 80% | ||
| n = 11 (14) | 1.6 | 82% | |||
| Multi-exponential Allometry (MA) (9,48) |
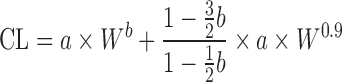 where a and b are the coefficient and exponent of SA where a and b are the coefficient and exponent of SA |
CL and body weight in at least two animal species | All categories | ||
| n = 50 (9) | 1.19 | 76% | |||
| n = 102 (9) | 1.39 | 54% | |||
| n = 45 (48) | N.A. | 89% | |||
| Liver blood flow method (LBF) (11,49) |
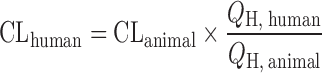
|
Human and animal liver blood flow, animal CL | All categories | Rat 2.57 | Rat, 45% |
| n = 102 (11) | Dog 2.79 | Dog, 50% | |||
| Monkey 1.89 | Monkey, 70% | ||||
| n = 103 (49) | N.A. | Rat, dog, 66% | |||
| N.A. | Monkey, 72% | ||||
| n = 103 (42) | N.A. | Rat, 40% | |||
| N.A. | Dog, 44% | ||||
| N.A | Monkey, 68% | ||||
| Scaling from one or two animal species (11) |
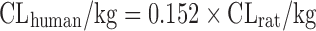
|
CL in at least one species of rat, dog, or monkey | All categories | Rat, 58% | |
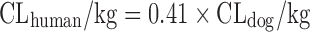
|
Dog, 33% | ||||
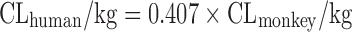
|
n = 26 (11) | N.A. | Monkey, 44% | ||
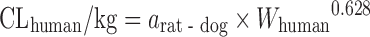
|
Rat–dog, 55% | ||||
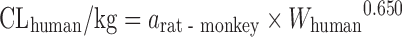
|
Rat–monkey, 78% | ||||
| Vertical allometry (3,6) and f u corrected intercept method (FCIM) (10,40) | Vertical allometry (VA) criteria: ClogP > 2; f u, rat/f u, human > 5; metabolic elimination | ClogP, elimination route, CL, and body weight in at least two animal species, plasma unbound fraction in rats and humans | All categories | ||
FCIM approach: 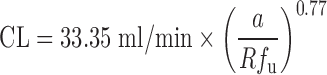 where a is the coefficient of SA and Rf
u is the ratio of unbound fraction in plasma between rats and human where a is the coefficient of SA and Rf
u is the ratio of unbound fraction in plasma between rats and human |
n = 60 (10) | 78 | 90% | ||
| n = 24 (37) | N.A. | 50% | |||
| n = 40 (40) | N.A. | 89% | |||
| In vitro–in vivo extrapolation (IVIVE) using physiological scaling factors (12,23,60) |

|
Drug disappearance rate in human microsomes or hepatocytes | All categories | ||
Well-stirred model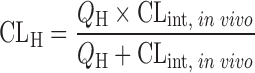
|
n = 33 (13) | 6.17 | 15% | ||
Parallel tube model 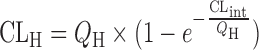
|
n = 22 (63) | 2.01 | 64% | ||
Dispersion model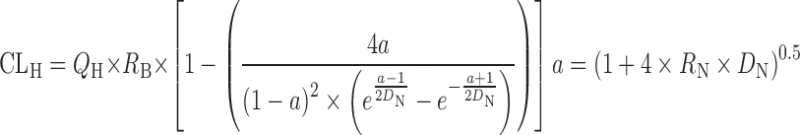
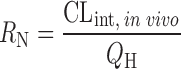 D
N is the dispersion number
D
N is the dispersion number |
n = 7 (12) | 1.95 | 86% | ||
| n = 29 (65) | 2.28 | 79% | |||
| IVIVE using a drug-specific scaling factor (13,60,61) |
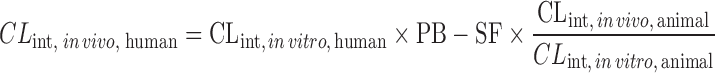
|
Drug disappearance rate in human and animal microsomes or hepatocytes, animal hepatic clearance, the fraction unbound in animal plasma, the animal blood-to-plasma concentration ratio | All categories | ||
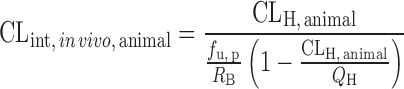
|
n = 33 (13) | 2.33 | 39% | ||
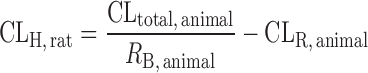
|
n = 13 (60) | 1.57 | 69% | ||
| where PB-SF is the physiologically based scaling factor. The ratio of animal in vivo and in vitro CLint is the drug-specific scaling factor | 1.68 | 77% | |||
| IVIVE using an empirical scaling factor (13,62–64) |
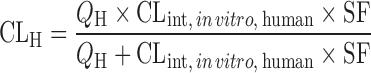 , where SF is the empirical scaling factor, determined by the nonlinear iterative least squares regression between CLint, in vivo and CLint, in vitro
, where SF is the empirical scaling factor, determined by the nonlinear iterative least squares regression between CLint, in vivo and CLint, in vitro
|
Drug disappearance rate in human and rat microsomes or hepatocytes, a dataset of human CLint, in vivo and CLint, in vitro | All categories | ||
| n = 33 (13) | 1.00 | 46% | |||
| n = 22 (63) | 1.64 | 64% | |||
| n = 52 (64) | 1.8–2.2 | 62–76% | |||
| IVIVE with protein binding correction or at the presence of human plasma (67,70) | Well-stirred model 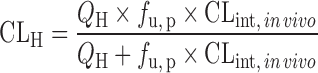
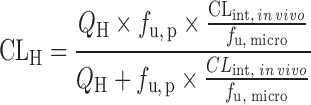
|
Drug disappearance rate in human microsomes or hepatocytes, the fraction unbound in human plasma (f u, p), and liver microsomes (f u, micro), or hepatocytes (f u, hepa) | All categories | ||
Hallifax equation: 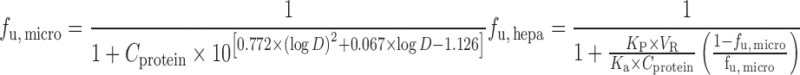
|
n = 7 (12) | 9.28 | 57% | ||
| n = 29 (65) | f u, p 4.39 | 45% | |||
| f u, p, f u, m 2.31 | 62% | ||||
| n = 8 (97) | N.A. | 50% | |||
| n = 7 (67) | N.A. | 86% | |||
| n = 10 (70) | N.A. | 80% | |||
| IVIVE using recombinant P450 enzymes (68) | Relative abundance approach Relative activity approach Relative activity approach |
Intrinsic activity of each recombinant CYP enzymes for each test compound, relative abundance, or activity of CYP enzymes | Benzodiazepines | ||
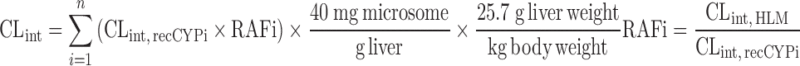
|
n = 5 (69) | N.A. | 80% | ||
| n = 72 (68) | N.A. | 44% | |||
| n = 15 (98) | N.A. | 93% | |||
| Physiologically based approach for renal clearance prediction (34) |
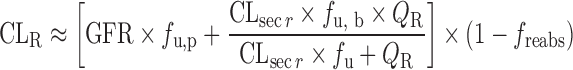
|
GFR, f u, p, CLsecr, and P e | N.A. | N.A. | N.A. |
| Computational approaches: multiple linear regression (MLR) (72), partial least squares (PLS) (73), artificial neural network (ANN) (63,97), and k-nearest neighbors approach (kNN) (74) | Multivariate linear regression analysis 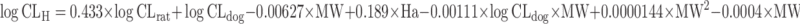
|
Molecular weight and hydrogen bond acceptor number of the test compound, CL in dogs and rats | All categories | ||
| n = 68 (72) | N.A. | 74% | |||
| n = 50 (71) | 1.28 | 78% | |||
| Extensively metabolized compounds n = 22 (63) | 1.81 | 68% |
Allometric Scaling of Unbound CL
The rationale for predicting unbound CL (CLu) is that plasma protein binding of many drugs varies from one species to another and only unbound drug can be eliminated. Obach et al. conducted a comprehensive retrospective analysis (Table II) to compare the allometric scaling of total CL (n = 14) and CLu (n = 13) (12). Based on average fold errors (AFEs) (1.91-fold for CL prediction and 1.79-fold for CLu prediction) and the percentages of compounds falling within twofold error (64% for CL prediction and 69% for CLu prediction), prediction of CLu was slightly improved. This was supported by a recent study, which compared the prediction performance of allometric scaling for CL and CLu by evaluating 24 compounds (37). Whereas only 17% of predicted CL by SA fell within twofold error, 62% of the CL values predicted by unbound CL approach showed less than twofold error. In another study, Mahmood compared allometric scaling of total CL and CLu by analyzing the data of 20 drugs from literature (38). Defining success as a difference between predicted and observed CL of 30% or less, allometric scaling of CLu did not show advantages. However, allometric scaling of CLu is superior to allometric scaling of CL if the success cutoff is set as twofold error (45% for total CL approach and 55% for unbound CL approach). Thus, the cutoff selection is critical for assessing the predictability of various approaches.
Two Term Power Equation
Since the CL of compounds with low hepatic extraction is not correlated with body weight, Boxenbaum and Fertig (39) related CL of compounds with low hepatic extraction in humans to two other physiological parameters: brain weight (BrW) and maximum lifespan potential (MLP) (Table II). In another proposed equation, the product of CL and MLP was allometrically scaled with body weight. CL prediction studies using this approach are limited.
Rule of Exponents
To improve the prediction of human CL by SA, based on a comprehensive analysis of data of 50 drugs from at least three animal species, Mahmood and Balian (3) developed the rule of exponents. They introduced two correction factors (BrW and MLP) into SA and proposed guidelines for the selection of correction factors based on the exponents of the simple allometry approach (Table II). In terms of accuracy of RoE for human CL prediction, 42 out of 45 drugs fell within twofold error compared to 35 out of 45 for the SA approach (40). A recent comparative study of 68 compounds consistently showed that RoE provided better predictions than other allometric scaling methods and similar accuracies to IVIVE, especially for low lipophilic and intermediate/high clearance compounds (41). However, the performance of RoE was controversial. Nagilla and Ward (42) comprehensively evaluated the roles of correction factors, such as BrW, MLP, glomerular filtration rate (GFR), uridine diphosphate glucuronyltransferase (UDPGT) activity, and bile flow rate, by using a dataset of 103 compounds. The results showed that none of the correction factors resulted in improved predictability. This was supported by the predicted oral CL of 24 compounds in Sinha's report (37). The RoE approach resulted in only 37% of predicted human oral CL falling within twofold error, suggesting that the predictability of RoE somehow depends on the selection of datasets.
Allometric Scaling for Renally and Biliarily Excreted Drugs
Considering the complicated mechanisms of renal excretion (filtration, reabsorption, and active secretion), SA may not be used to predict human CL of drugs with high renal CL. Mahmood (3,43) proposed a modified scaling approach (Table II) to improve the predictability of drugs eliminated renally by using GFR, kidney blood flow (Qkidney), body weight (W), or kidney weight as the correction factor. Similarly, bile flow rate or UDPGT activity was used as the correction factor to predict CL of drugs with biliary excretion (44). Both corrected approaches showed improved predictability compared with SA and RoE, although the sizes of the datasets were small (n = 8 and n = 10). For drugs undergoing enterohepatic recirculation, prediction of CL is difficult because less is known about the interspecies differences in hepatobiliary transporter expression (16).
Allometric Scaling After Normalization by In Vitro Intrinsic CL
The clearance of compounds with low or intermediate hepatic extraction ratios is strongly dependent on both liver blood flow and intrinsic CL (8). SA usually fails to predict the CL of such compounds. Lave et al. (8,45) used the human and animal in vitro intrinsic CL (CLint, in vitro) to correct the in vivo animal CL (Table II). CLint, in vitro was derived from in vitro incubation with liver microsomes or hepatocytes (CLint, in vitro = Vmax/Km). In order to measure the Vmax (enzyme's maximum metabolic rate) and Km (the substrate concentration at which the reaction rate is half of the Vmax), an assay for the metabolite is required. However, in the early drug development stage, a standard of the metabolite is usually not available. Hence, the CLint, in vitro is derived from the in vitro half-life (T1/2) of the drug in liver microsomes or hepatocytes (46) as described by the following equations. For the liver microsomal assay, CLint, in vitro ≈ 0.693 / (T1/2 × Cprotein) = Ke / Cprotein, where Ke and Cprotein are the rate constant of drug metabolism and the concentration of the liver microsomes, respectively. For the hepatocyte assay, CLint, in vitro ≈ Ke / Ccell, where Ccell is the hepatocyte concentration. Lave et al. (14) used this approach to predict human CL of 11 hepatically eliminated drugs. The results showed that 82% of the predictions (9 out of 11) fell within a twofold factor of the actual human CL values, with an AFE of 1.6-fold. This was consistent with their earlier study, for which eight out of ten drugs fell within twofold error (8).
Multi-Exponential Allometry
To eliminate uncertainty in selecting the preferred correction factor used with SA, Goteti et al. (9) developed a new multi-exponential allometric approach (MA) (Table II). The assumption of MA is that CL is correlated with both body weight and volumes of eliminating organs (liver and kidneys). The proposed MA function is CL = a × Wb + c × Wd, where a and b are the coefficient and slope from SA, respectively; c and d are the coefficient and slope from MA, respectively; and W is body weight. When the organ volumes of the liver or kidney of preclinical species were plotted against body weight, the slopes were approximately equal to 0.9 (47). Hence, the MA slope d was selected as 0.9. By analyzing training datasets (n = 102 and n = 50), a correlation between c and a was established: c = a × (1–1.5b) / (1–0.5b). The new approach improved predictability compared with SA (AFE = 1.19% and 76% of predictions with <twofold error for training set, and AFE = 1.39% and 54% of predictions with <twofold error for test set). In another study, Goteti et al. (48) compared MA, SA, and RoE approaches by analyzing 45 drugs with data from at least three species. The results showed that the performance of MA was superior to SA but inferior to RoE. However, the prediction accuracy of SA was superior to that of MA when the exponent of SA was less than 0.7.
Liver Blood Flow Approach
For hepatically eliminated drugs, the human CL can be extrapolated by using the hepatic blood flow ratio between humans and animals (Table II). In a comprehensive evaluation of allometric scaling and LBF approaches using data for 103 drugs, Ward and Smith (49) found that the monkey LBF was the most accurate approach for human CL estimation. This method was superior to three-species and two-species allometric scaling with or without correction factors, where the correct predictions were 72% for monkey LBF versus 62–66% for various allometric scaling. It was also superior to rat and dog LBF (66% for both rat and dog LBF). These findings were supported by Nagilla et al. (42) and Tang et al. (11). A recent study showed similar results, concluding that the prediction accuracy by mouse and monkey LBF methods was better than that by rat and dog LBF methods (41).
Scaling from One or Two Animal Species
Based on the intravenous CL of 102 drugs in rats, dogs, monkeys, and humans in a training dataset, Tang et al. (11) developed one- and two-species scaling methods for human CL prediction. The optimized equations are listed in Table II. A test dataset of 26 compounds was used to examine the methods. The results showed that the one- or two-species approaches generally were at least as predictive as RoE or SA. Controversially, Mahmood (50) tested the one- and two-species approaches using another dataset of 45 drugs and found that the prediction accuracy of RoE was superior to that of one- and two-species approaches. Recently, Deguchi et al. compared the prediction accuracy of RoE and single-species scaling (fixed exponent = 0.75) for 12 drugs metabolized by UDP-glucuronosyltransferases (UGTs) and found that one-species scaling from monkeys was superior to RoE (51).
Vertical Allometry and fu Corrected Intercept Method
A compound exhibiting a large overprediction of human clearance by allometric scaling is considered to follow vertical allometry (52). The allometric scaling approaches corrected by various factors and RoE are not able to accurately predict CL of compounds following vertical allometry (10). Empirical criteria (Table II) have been proposed by Tang and Mayersohn (6) to identify vertical allometry: compounds with ClogP (calculated octanol–water partition coefficient) > 2, a ratio of unbound fraction in plasma between rats and humans Rfu > 5, and elimination by metabolism. The criteria can identify the compounds following vertical allometry (VA) but cannot improve the quantitative prediction of CL alone. Based on empirical criteria, Tang and Mayersohn (10) hypothesized that Rfu, ClogP, coefficient a, and exponent b from SA could be potentially useful to quantitatively predict human CL and reduce the inaccuracy of VA predictions. Using a dataset from literature and a backward stepwise procedure, they established a relationship between human CL, a, b, Rfu, and eClogP, which resulted in a simplified equation:
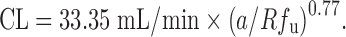 |
1 |
The new approach was named the FCIM. The performance of FCIM was compared with those of SA and RoE. The average absolute percentage errors by FCIM, RoE, and SA were 78%, 185%, and 323%, respectively. In another study, Sinha et al. (37) showed that 17%, 37%, 50%, and 62% of CL predictions (n = 24) fell within twofold error by using SA, RoE, FCIM, and unbound CL approaches. Depending upon the SA exponent (b) value and the method used, the percentage of predictions that fell within twofold error increased. They were 79% when applying FCIM for b < 0.5 or b > 1.2 and applying the unbound CL approach for 0.5 < b < 1.2. Mahmood (40) also compared the performances of RoE and FCIM by using a dataset containing 40 drugs. Eighty-nine percent of predictions by FCIM had percentage errors less than 200%, which was superior to SA (78% of predictions) but inferior to RoE (93% of predictions). The predictions of FCIM were more accurate when 0.9 < Rfu < 2 or b > 1.3.
In Vitro–In Vivo Extrapolation
With the progress of in vitro techniques in drug development, especially the determination of in vitro intrinsic clearance (CLint, in vitro) from human liver microsomes, hepatocytes, and recombinant CYP450 isoenzymes, IVIVE is attracting more attention from the pharmaceutical industry. Different from the empirical allometric scaling approaches, IVIVE is a physiologically based prediction approach and can be validated by using human and animal tissues. Although the predictive performances of early IVIVE approaches were not satisfactory, this has recently improved with corrected IVIVE approaches (14). Two excellent review articles have summarized the advances in human hepatic CL prediction using IVIVE (14,23).
IVIVE Using Physiologically Based Scaling Factors
The prediction of hepatic clearance from in vitro metabolic data was proposed by Houston in 1994 (43). The first step of this approach was to determine the intrinsic in vitro CL (CLint, in vitro) from human liver microsome or hepatocyte data as described in “Allometric Scaling After Normalization by In Vitro Intrinsic CL”. CLint, in vitro was then converted into CLint, in vivo using a PB-SF (Table II), which was 3.1 × 109 hepatocytes per kilogram of human body weight (120 × 106 cell/g liver × 25.7 g liver/kg body weight) (47) or 1,028 mg microsomes per kilogram human body weight (40 mg microsome/g liver × 25.7 g liver/kg body weight) (12,53). The relation between hepatic clearance (CLH) and CLint, in vivo depends on three mathematical models used for describing the disposition of drug in the liver (23). For the well-stirred model, the drug is assumed to be mixed instantly in the liver. In contrast, for the parallel tube model, the drug is only mixed in the small sections along the blood flow path from the input to the output of the liver. In addition to these two extreme cases, the dispersion model is used to describe the flow dynamics of the drug based on analysis of the biodistribution of hepatic residence time of solutes after a bolus injection into the liver. CLH prediction accuracies of the parallel tube and dispersion models were similar and both were superior to the well-stirred model (54), although the latter was widely used due to the calculation simplicity. For drugs with high CLH, the dispersion model provided the most reliable predictions (55).
Underprediction of human CLH was observed when the PB-SF was used to scale the CLint, in vitro to CLint, in vivo. Ito and Houston (13) predicted the CLH of 55 compounds from human liver microsomal data and observed a ninefold underprediction of the CLint, in vivo. The CLH scaled from hepatocyte incubation, which offers a complete set of clearance pathways, is expected to be more accurate than scaling from liver microsomes and liver slices. For example, in liver microsome incubation, inhibitory metabolites may accumulate due to the lack of subsequent conjugation and slow down the metabolism of parent drugs (56). Also, UDPGT activity in liver microsome preparations is much lower than that in isolated hepatocytes (57). Brown et al. (58) predicted the CLint, in vivo of 37 compounds using human hepatocyte data. As expected, a significant reduction in prediction bias was obtained. However, on average, a 4.5-fold underprediction of CLint, in vivo was still observed. Chiba et al. (23) offered a few explanations for these results. First, the preparation process and storage condition of the liver tissues are likely responsible for the potential loss of metabolic activity. Second, the extrahepatic metabolism (e.g., in the intestine and kidneys) of drugs in humans can significantly contribute to the total clearance, resulting in CLH underprediction from in vitro data. Third, the underprediction may also be caused by the lack of appropriate correction of nonspecific binding of the drug with microsomal lipids and cellular components. Finally, clearance is more often underpredicted for substrates of hepatic uptake transporters than other compounds, suggesting that the transporter-mediated hepatic uptake can increase CLH and contribute to the underprediction from in vitro data. Although liver microsome and hepatocyte systems caused similar underprediction of CLH (9-fold versus 4.5-fold), the average P450 enzyme maximal activity (Vmax) of human hepatocytes has been found to be between 2- and 20-fold less than that of microsomes (59). To minimize the underprediction of human CLH, the IVIVE approach was modified by introducing some correction factors as discussed in the following sections.
IVIVE Corrected by Drug-Specific Scaling Factors
This approach requires human microsomal or hepatocyte data, PB-SF, and a drug-specific scaling factor (the ratio of CLint, in vivo and CLint, in vitro obtained from an animal species) (13,60,61). The animal CLint, in vitro is obtained from animal microsomal or hepatocyte incubation and the animal CLint, in vivo is calculated from CLH, animal, which is derived from the animal total CL. Ito and Houston determined the drug-specific scaling factors of 33 compounds in rats and found that the drug-specific factors improved the predictive accuracy of human CLH. The AFE decreased from 6.17 to 2.33 and the percentage within twofold error increased from 15.2% to 39.4%. In another study, Naritomi et al. (60) used the drug-specific factors obtained from rats and dogs to predict human CLint, in vivo of eight drugs. The results showed that the rat and dog drug-specific factors reduced the AFE from 4.02 to 1.57 and 1.68, respectively, and increased the percentage within twofold error from 25% to 69% and 77%, respectively.
IVIVE Corrected by an Empirical Scaling Factor
Lave et al. (62) conducted a nonlinear iterative least squares regression analysis on a training dataset to obtain the best fit of human CLint, in vivo and human CLint, in vitro. The average coefficient was determined as an empirical SF. The SF was utilized to convert the human CLint, in vitro of drugs in the test dataset into CLint, in vivo. The incorporation of the empirical SF into IVIVE increased the percentage within twofold error from 15.2% to 45.5% (n = 33) (13). Using the empirical SF, Zuegge et al. (63) found the AFE decreased from 2.01 to 1.64 and the percentage within threefold error increased from 77.3% to 95.5%. To further improve the predictions, Fagerholm (64) used drug class scaling factors (CD-SFs) to replace the single empirical SF. Based on CLint, in vivo (low and high) and drug class (acid, neutral, and base), the drugs were divided into six subgroups and the CD-SF for each subgroup was estimated by least squares regression analysis. Compared with the IVIVE using a single SF, CD-SFs improved predictions: AFE = 1.3 and percentage within twofold error = 76% (n = 29).
IVIVE with Protein Binding Correction
Since only unbound compound is subjected to metabolism, lack of protein binding correction may cause underprediction of CLH. To reduce the prediction bias, IVIVE models were developed to incorporate factors such as the fraction of unbound drug in plasma (fu, p), in liver microsomes (fu, micro), or in hepatocytes (fu, hepa) (Table II). The unbound fractions can be measured using in vitro assays (65) or calculated using Hallifax equations (66). Obach (65) examined the effect of protein binding corrections on CL predictions for 29 basic, neutral, and acidic compounds. For basic and neutral compounds, human CL was well predicted with or without both plasma and microsomal protein binding corrections but including only fu, p resulted in poor predictions. For the acidic compounds, IVIVE without protein binding correction yielded poor predictions of human CL and inclusion of both protein binding corrections improved predictions. Hence, both plasma binding and microsomal binding corrections are recommended. An alternative strategy for protein binding correction is to add human plasma to the incubation solution. Skaggs et al. (67) showed that correction with fu, micro and fu, p resulted in 57% of CL predictions within twofold error (n = 7), but liver microsome incubation in the presence of human plasma increased predictions within twofold error to 71% (n = 7).
IVIVE of Clearance from Individual Metabolic Enzymes
Recombinant enzymes represent an alternative in vitro metabolic system to hepatic microsomes or hepatocytes for human CLH predictions (Table II) (68). This approach can account for interindividual variation of P450 expression. Furthermore, it avoids the batch-to-batch variation in the metabolic activities of human hepatocytes and liver microsomes.
To estimate CLint, in vitro from intrinsic CL in individual recombinant P450 enzymes (CLint, CYPi), two approaches have been proposed. In the relative abundance approach, recombinant P450 enzyme activities are adjusted according to levels of immunoquantified protein (61). The relative activity approach utilizes a relative activity factor (RAF) (69). RAF is the ratio of the metabolic rate of a specific marker in human liver microsomes to that of a specific recombinant P450 enzyme. The equations for both approaches are listed in Table II. Stringer et al. (68) predicted the CLint, in vivo of 72 drugs using the relative abundance or relative activity approach, with or without protein binding correction. The results showed that IVIVE predictive accuracy from recombinant P450 enzymes (AFE = 1.53, n = 72) was superior to accuracy from liver microsome (AFE = 2.32, n = 41) and hepatocytes (AFE = 5.21, n = 57). The most accurate CLint, in vivo predictions, in terms of lowest bias and highest precision, were obtained by using the parallel tube model, protein binding correction, and the RAF approach.
IVIVE can predict CL of compounds metabolized by non-P450 enzymes. Kilford et al. demonstrated the use of IVIVE of glucuronidation-mediated CL from human liver microsome incubation in the presence of both P450 and UGT cofactors (70). Recently, Zientek et al. proposed an IVIVE method to predict human aldehyde oxidase-mediated CL using pooled human liver cytosol and liver S-9 fractions (71).
Physiologically Based Approach for Renal Clearance Prediction
The IVIVE approaches discussed above are not applicable for renally excreted drugs. Allometric scaling corrected with GFR and kidney blood flow was proposed to predict CLR. However, the performance of the empirical approach may not be satisfactory considering the interspecies differences in unbound fraction, urine pH, active transport, and fraction of reabsorption (freabs) (20). Based on in vitro passive permeability (Pe), Fagerholm (20,34) proposed a permeability-based classification system and established the relationship between in vitro Pe and freabs. CLR was calculated using the following equation, although the method was not validated using data sets.
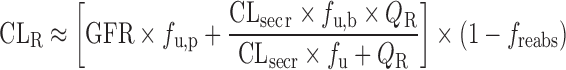 |
2 |
If there is no active transport (CLsecr = 0) and Pe is less than that of atenolol (freabs = 0):
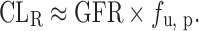 |
If there is no active transport (CLsecr = 0): 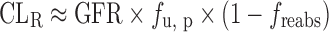 .
.
If Pe is higher than that of carbamazepine (freabs = 1), CLR = 0
Computational (In Silico) Approaches
Besides the interspecies scaling and physiologically based IVIVE, computational (in silico) approaches were also developed for human CL prediction (Table II). Statistical methods such as MLR (72), PLS (73), and ANN (63) have been employed to quantitatively relate observed human CL to in vitro animal data, in vivo animal data, in vitro human data, or molecular descriptors.
Wajima et al. (72) selected rat and dog CL, molecular weight, ClogP, and the number of hydrogen bond acceptors as the descriptors for MLR analysis to establish a quantitative relationship with observed human CL. The regression equation is listed in Table II. The authors claimed that the performance of this approach is superior to allometric scaling. However, it was criticized by Mahmood (3) because the same dataset was used for regression analysis and performance evaluation.
Recently, Yu created a fully in silico model to predict total clearance of compounds in humans by using a k-nearest neighbors technique (74). The model was developed by utilizing a training set of 370 compounds and examined by a test set of 92 compounds. The average prediction accuracy of the test set was within twofold error. When the model was applied to a collection of 20 drugs from literature, the prediction accuracy was inferior to RoE but better than SA. Since in silico models only rely on one- and two-dimensional molecular descriptors, they are capable of rapidly screening virtual compounds before chemical synthesis in early drug discovery stages.
Summary of Human CL Prediction
To assist pharmacokineticists in method selection, we summarize the assumptions, applicability, advantages, and disadvantages of each approach in Table III. Most interspecies scaling and IVIVE approaches are applicable to compounds eliminated by hepatic metabolism, and reasonable prediction accuracy has been achieved for compounds with intermediate to high hepatic extraction. In contrast, accurate prediction of human renal and biliary excretion is still difficult, although this has improved with the incorporation of correction factors such as GFR and bile flow into allometric scaling. Physiologically based approaches have been proposed to predict human renal and biliary CL. However, their performances have not been widely examined using comprehensive datasets.
Table III.
Assumptions, Applicability, Advantages, and Disadvantages of 17 Approaches for Human CL Prediction
| Method | Assumptions | Applicability | Advantages | Disadvantages |
|---|---|---|---|---|
| Simple allometry (SA) | Relationships between anatomy and physiologic functions are similar among mammalian species | Compounds with high hepatic clearance; therapeutic proteins | Simple and widely used | Empirical method, requires in vivo data from multiple species, neglect interspecies differences |
| Allometric scaling of unbound CL | Interspecies differences in protein binding decrease the accuracy of prediction | Compounds with interspecies differences in protein binding | Minimizes interspecies differences in protein binding | Accuracy and reliability of the published unbound fraction in plasma (f u, p) |
| Two term power equation | For compounds with low hepatic extraction, the product of CL and MLP, or brain was allometrically scaled with body weight | Compounds with low hepatic extraction | Simple and only require in vivo preclinical CL | Based on an empirical assumption; not commonly used |
| Rule of exponents (RoE) | The prediction accuracy of allometric scaling depends on the exponents | Low lipophilic and intermediate or high clearance compounds (41) | Provides a guideline for selection of correction factors | Its prediction accuracy superior to that of SA is still controversial |
| Allometric scaling for renally and biliary excreted drugs | For renal and biliary excreted drugs, total CL is correlated with not only body weight but also renal or biliary physiological parameters | Renal and biliary excreted drugs | Minimizes interspecies differences in renal or biliary physiological parameters | Active transport and enterohepatic recirculation are neglected |
| Allometric scaling after normalization by CLint, in vitro | Interspecies differences in CLint,in vitro affect prediction accuracy | Compounds with low or intermediate hepatic extraction ratios | Minimizes interspecies differences in CLint,in vitro | Its predictability is controversial; not suitable for compounds eliminated by active secretory processes (10) |
| Multi-exponential allometry (MA) | CL is correlated with both body weight and volumes of eliminating organs (liver and kidneys) | Compounds with an exponent of SA b > 0.7 | Eliminates the uncertainty around the choice of the preferred correction factor used with SA | Prediction accuracy is superior to SA but inferior to RoE |
| Liver blood flow method | Hepatic extraction ratios (EH) and blood–plasma ratios keep constant in monkey and human | Hepatically metabolized compounds | Only requires CL from monkey | Neglect interspecies differences in BP ratios and protein binding |
| Scaling from one or two animal species | A data-driven empirical one-species method is more predictive than empirical LBF method | Hepatically metabolized compounds | Only requires CL from one or two species | Its predictability is controversial; neglect interspecies differences in metabolism and protein binding |
| f u corrected intercept method (FCIM) | Rfu and ClogP, as well as coefficient a and exponent b from simple allometry, could quantitatively predict human CL; Rf u < 10 | Compounds with an exponent of SA b < 0.5 or b > 1.2 | Simple; can be applied to compounds following vertical allometry | No solid physiological or biochemical basis; neglect interspecies differences in metabolism |
| In vitro–in vivo extrapolation (IVIVE) using physiologically based scaling factors | Drug metabolic enzymes have comparable activities under in vitro and in vivo situations | Hepatically metabolized compounds | Has a firmer physiological basis than SA; requires only in vitro data | CL is always underpredicted; extrahepatic metabolism is neglected |
| IVIVE corrected by a drug-specific scaling factor | Underprediction of CLH by IVIVE keeps constant across species | Hepatically metabolized compounds | Partially corrects the underprediction caused by decreased in vitro enzyme activities and extrahepatic metabolism | Neglects interspecies differences in extrahepatic metabolism, protein binding, and active transport |
| IVIVE corrected by an empirical scaling factor | Underprediction of CLH by IVIVE keeps constant among different drugs | Hepatically metabolized compounds | Partially corrects the underprediction caused by decreased in vitro enzyme activities | Neglects drug-specific differences in extrahepatic metabolism, protein binding, and active transport |
| IVIVE with protein binding correction or in the presence of human plasma | Underprediction is caused by the nonspecific binding of the drug with microsomal lipids and cellular components | Hepatically metabolized compounds | Corrects the underprediction caused by protein binding | Neglects extrahepatic metabolism, active transport, and different in vitro and in vivo enzyme activities |
| IVIVE using recombinant enzymes | Recombinant enzymes have constant intrinsic CL under in vitro and in vivo situations | Hepatically metabolized compounds | Incorporates interindividual variation of P450 expression; can predict CL of compounds metabolized by non-P450 enzymes | Underprediction was observed |
| Physiologically based approach for renal clearance prediction (34) | In vivo fraction of reabsorption can be predicted from in vitro passive permeability | Renal excretion drugs | Interspecies differences in unbound fraction, urine pH, active transport, and fraction of reabsorption | Not validated using comprehensive data sets |
| Computational approaches: multiple linear regression (MLR), partial least squares (PLS), artificial neural network (ANN), and k-nearest neighbors approach (kNN) | Correlations can be established between in vitro, in vivo animal data, in vitro human data, or molecular descriptors and observed human CL using statistical models | Rapid screening of virtual compounds before chemical synthesis in early drug discovery stages | High-throughput, low costs, in vivo data, and experimental are not always required | Black box model; predictive performance is not acceptable for some drugs |
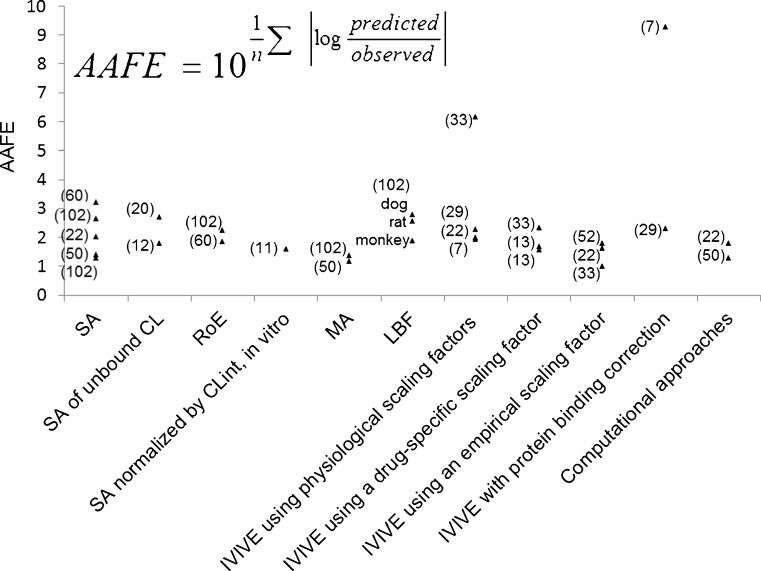
The reported prediction accuracies of various approaches were assessed by the percentage of predictions that fell within twofold error (Fig. 1) and absolute average fold error (AAFE) (Fig. 2). Generally, interspecies scaling and IVIVE approaches exhibit comparable prediction accuracies but the AAFEs of IVIVE approaches show higher variation than those of interspecies scaling (Fig. 2), which is likely due to the smaller datasets in IVIVE studies. In addition, both Figs. 1 and 2 show that RoE and MA are superior to SA while LBF is comparable to SA in terms of twofold errors and AAFEs. Similarly, the incorporation of drug-specific or empirical scaling factors decreases the AAFEs of IVIVE by correcting the underprediction of IVIVE. However, it is difficult to conclude which approach is most accurate due to variations among datasets, including dataset sizes (n ranges from 5 to 103), properties of compounds (base, neutral, acid, and zwitterion), and elimination mechanisms (hepatic metabolism, renal excretion, and biliary excretion). Hence, a comprehensive comparison of various approaches using a large and exhaustive dataset is warranted to address the controversies in human CL prediction. Obach et al. (75) have presented a dataset including human intravenous PK data of 670 drugs which might shed light on the assessment of various approaches.
Fig. 1.
Percentages of human CL predictions fell within twofold error (the size of each data set is labeled in brackets)
Fig. 2.
Absolute average fold errors of human CL predicted by various approaches (the size of each data set is labeled in brackets)
PREDICTION OF BIOAVAILABILITY
Oral administration is the most favorable route for drug delivery due to convenience and patient compliance. However, one key issue for oral drug development is the drug candidates' bioavailability. Many lead compounds fail in the developmental stages due to their poor bioavailability. The definition of bioavailability is “the rate and extent to which the active ingredient or active moiety is absorbed from a drug product and becomes available at the site of action.” Bioavailability is mainly determined by absorption and first-pass metabolism (both intestinal and hepatic metabolism). As a result, bioavailability (F) can be mathematically represented by the following equation:
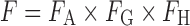 |
3 |
where FA is the fraction of drug absorbed, FG is the fraction of drug that escapes intestinal metabolism, and FH is the fraction of drug that escapes liver metabolism.
FH can be expressed as 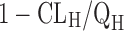 . As discussed above, human CLH can be predicted quite accurately using interspecies scaling or IVIVE methods. Compared to hepatic clearance, intestinal metabolism is rather limited due to the low occurrence of CYP enzymes and low blood flow. Therefore, in general, the intestinal metabolism can be neglected. However, it could greatly decrease the bioavailability of compounds that are subjected to conjugation (such as sulfation and glucuronidation) or CYP3A4 metabolism. Similar to hepatic metabolism prediction, intestinal metabolism can be estimated using IVIVE from human intestinal microsome or enterocyte systems. Several physiologically based models have also been developed to estimate intestinal metabolism. Badhan et al. developed a physiologically based model incorporating geometric variations, pH alterations, and heterogeneous expression and distribution of CYP3A and PgP which predicted the FG of ten compounds with considerable accuracy (76). Recently, Kadono et al. (77) established a simplified method to predict human FG of highly permeable CYP3A4 substrates by incorporating an empirical scaling factor. Intrinsic CLs of nine model compounds in enterocytes were normalized with midazolam intrinsic CL to obtain CLm, index. A correlation between FG and CLm. index of model compounds was then established to estimate the empirical scaling factor.
. As discussed above, human CLH can be predicted quite accurately using interspecies scaling or IVIVE methods. Compared to hepatic clearance, intestinal metabolism is rather limited due to the low occurrence of CYP enzymes and low blood flow. Therefore, in general, the intestinal metabolism can be neglected. However, it could greatly decrease the bioavailability of compounds that are subjected to conjugation (such as sulfation and glucuronidation) or CYP3A4 metabolism. Similar to hepatic metabolism prediction, intestinal metabolism can be estimated using IVIVE from human intestinal microsome or enterocyte systems. Several physiologically based models have also been developed to estimate intestinal metabolism. Badhan et al. developed a physiologically based model incorporating geometric variations, pH alterations, and heterogeneous expression and distribution of CYP3A and PgP which predicted the FG of ten compounds with considerable accuracy (76). Recently, Kadono et al. (77) established a simplified method to predict human FG of highly permeable CYP3A4 substrates by incorporating an empirical scaling factor. Intrinsic CLs of nine model compounds in enterocytes were normalized with midazolam intrinsic CL to obtain CLm, index. A correlation between FG and CLm. index of model compounds was then established to estimate the empirical scaling factor.
Various in vitro, in vivo, and in silico computational approaches have been developed to predict human intestinal absorption and oral bioavailability. The in vitro methods include the Caco-2 monolayer permeability assay (78), the parallel artificial membrane permeability assay (PAMPA) (79) and the immobilized artificial membrane (IAM) chromatographic assay (80). In silico models are divided into two classes: quantitative structure–activity relationship (QSAR) models and physiologically based pharmacokinetic models (PBPK).
In Vitro Methods
Caco-2 Monolayer Permeability Assay
In this assay, Caco-2 cells derived from human adenocarcinoma colon cells are allowed to form a monolayer on a polycarbonate membrane in a transwell device. The apparent permeability coefficient (Papp) can be derived from the following equation (78):
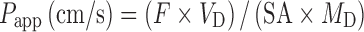 |
4 |
where F is the flux rate (mass/time), VD is the donor volume, SA is the surface area for transport, and MD is the donor amount at t = 0.
A strong correlation was observed between in vivo human absorption and Papp obtained from the Caco-2 assay (n = 35 and r = 0.95) (78). The relationship was expressed as follows:
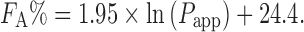 |
5 |
The limitation of the Caco-2 permeability assay is that it cannot accurately predict active drug transport due to the under- or overexpression of the active transporters in Caco-2 cells (81).
PAMPA
PAMPA is a filter-supported artificial lipid membrane system which is designed to evaluate the passive transcellular permeability. The membrane was constructed using a lipid composition (PC/PE/PS/PI/CHO/1,7-octadiene) which is similar to that of the intestinal brush border membrane (79). Papp can be calculated using following equation:
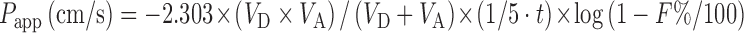 |
6 |
where VD is the donor volume, VA is the acceptor volume, S is the membrane area, t is the incubation time, F is the flux, and F% = ODA/ODR × 100. ODA is the optical density of the solution of the acceptor compartment, and ODR is the optical density of the reference solution.
FA can be estimated from Papp by the following equation:
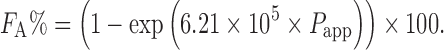 |
7 |
A study of the PAMPA and Caco-2 permeability assays revealed that they show comparable FA prediction accuracies (82). The PAMPA assay is advantageous over the Caco-2 assay in terms of high-throughput screening and costs. However, it would be difficult to predict drug absorption potential of paracellularly or actively transported compounds using PAMPA.
IAM
The IAM chromatographic assay is based on the partitioning of drug molecules into artificial membranes. IAMs are chromatographic surfaces composed of silica particles, each containing a covalently conjugated monolayer of phospholipids (such as phosphotidylcholine) (80). As a result, this chromatographic surface resembles half of the cell membrane bilayer and is used to mimic the lipid environment of a fluid cell membrane. The solute capacity factor K'IAM obtained from the IAM chromatographic assay was found to predict drug absorption. K'IAM can be calculated by the following equation:
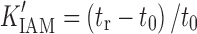 |
8 |
where tr is the solute retention time and t0 is the column dead time, which can be determined by a non-retained compound such as citric acid.
Ketecha et al. (83) established a relationship between logK'IAM and FA:
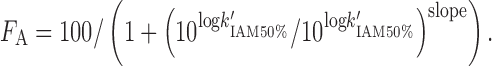 |
9 |
Similar to the PAMPA assay, the IAM chromatographic assay is used to estimate passive transcellular permeation but cannot accurately predict paracellular or active drug transport.
In Vivo Methods
Although certain animal species may be used to predict human oral absorption, it is challenging to predict oral bioavailability using animal models when incorporating first-pass metabolism. For instance, Cao et al. observed a correlation (r2 = 0.8) between human and rat drug permeability in the small intestine, whereas no correlation (r2 = 0.29) was found in oral bioavailability between rat and human due to the interspecies differences in the expression of metabolic enzymes in the intestine (84). In addition, Akabane et al. demonstrated that monkeys had significantly lower bioavailability than humans for 8 of 13 tested compounds due to higher intestinal metabolism in monkeys (85). Therefore, in general, animal models might not be a reliable way to predict human bioavailability due to the highly varied first-pass metabolism between species.
In Silico Computational Models
Compared to in vitro and in vivo models, in silico computational models are faster, simpler, more cost-effective, and more suitable for high-throughput screening. During the last two decades, a variety of in silico models have been developed with different levels of complexity for the evaluation of human intestinal absorption and oral bioavailability, selection of lead drug candidates, and guidance of formulation optimization. Generally, in silico models can be divided into two classes: QSAR models and PBPK models.
QSAR Models
Lipinski’s rule of five is the first in silico model to predict oral absorption and permeability qualitatively (86). It sets boundaries for acceptable absorption or permeability based on drug properties such as molecular weight, number of hydrogen bond donors, number of hydrogen bond acceptors, and ClogP. Andrews et al. developed a quantitative structure–bioavailability relationship (QSBR) which employed a stepwise regression procedure to link human oral bioavailability with the 82 substructural descriptors of 591 drug molecules (87). The QSBR model demonstrated greater accuracy than Lipinski’s rule of five in predicting human oral bioavailability, and the identified substructural fragments crucial for bioavailability could serve to guide drug design and synthesis. Yoshida and colleagues used the ordered multicategorical classification method using the simplex technique method to determine physicochemical and structural factors that contribute to oral bioavailability (88). By using those identified physicochemical parameters relating to absorption and 15 structural descriptors relating to metabolism, they established QSAR for the oral bioavailability of 232 drugs, with a correct classification rate of 71%. In addition, the model predicted the oral bioavailability of a separate test set of 40 compounds with 60% accuracy.
PBPK Models
A variety of PBPK models have been developed and validated, including the dispersion model, the compartmental absorption and transit model, the advanced compartmental absorption and transit (ACAT) model, the advanced dissolution, absorption, and metabolism model, the GI transit absorption model, and the Grass model. Huang et al. have recently published a review of such models and several commercially available software programs such as GastroPlus™, PKSim®, IDEA™, and Simcyp®.
PREDICTION OF HUMAN PLASMA CONCENTRATION–TIME PROFILES
When predicting the first-in-human dosing, special attention is paid to the AUC after oral dosing, elimination half-life, and peak-to-trough plasma concentration ratio. This is because an estimate of exposure (AUC) is required to ensure efficacy and safety. Accurate assessment of the drug’s maximum concentration (Cmax) and trough concentration (Cmin) is useful to avoid unwanted toxicity and maintain efficacious concentrations. Hence, early prediction of the concentration–time profiles for humans is of great importance. Currently, several methods have already been used to predict concentration–time profiles in humans based on preclinical data, such as the species-invariant time method (Dedrick plots), the Css–mean residence time (MRT) method, and the PBPK model.
Species-Invariant Time Method (Dedrick Plots)
The general idea behind the species-invariant time method originates from the allometric approach, and the prediction performance depends on the allometric relationships of the pharmacokinetic parameters across species. The species-invariant time method is based on the assumption that by normalizing the concentrations by body weights and transforming the chronological time to the physiological time, which is defined by the number of heartbeats or the number of respirations an animal will have in its lifespan, the plasma concentration–time curves should be superimposable in all species. Dedrick first transformed chronological time to the equivalent time (89) and Boxenbaum (89) later introduced new units of pharmacokinetic time: kallynochrons, apolysichrons, and dienetichrons. The transformation equations are listed in Table IV. In the Dedrick plot using equivalent time, the intravenous plasma concentration–time curve was transformed by dividing the concentrations and time scales of various species by dose (per kilogram of body weight) or W0.25, respectively. In the Dedrick plot using kallynochrons, apolysichrons, and dienetichrons as time units, b, c, and d are the allometric scaling exponents of CL, Vdss, and CL × MLP, respectively (90). The transformed concentration–time curves of various species are superimposed and then back-transformed to estimate human i.v. plasma concentration–time profiles. The predicted human i.v. profile, in combination with the estimated mean absorption rate constants and bioavailability, was then used to simulate the oral pharmacokinetic profile in humans. Mahmood and Yuan (90) compared the accuracies of transformations via equivalent time, kallynochrons, and apolysichrons for predicting human CL, Vdss, and T1/2. They observed that equivalent time was inferior to kallynochrons and apolysichrons, which might be due to the fixed exponent of 0.25. Since the correction factors for Dedrick plot transformations were derived from allometric scaling exponents, it is not surprising that they observed comparable prediction accuracy between allometric scaling and Dedrick plots.
Table IV.
Predictive Approaches of Human Plasma Concentration–Time Profile
| Method | Equation | Data required | Dataset | <twofold |
|---|---|---|---|---|
| Species-invariant time method (90) |
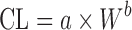
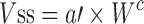
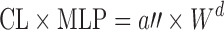
|
Plasma concentration–time profiles, dose, CL, and Vdss in at least two animal species | All categories | |
Equivalent time: 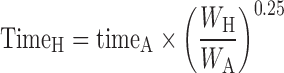
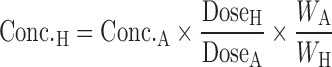
|
n = 2 (100) | 100% (AUC) | ||
Kallynochrons: 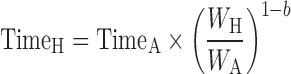
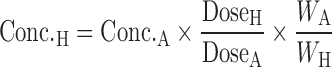
|
n = 3 (90) | 67% (CL) | ||
Apolysichrons: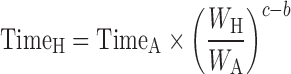
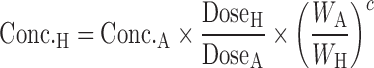
|
||||
Dienetichrons: 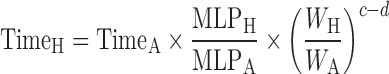
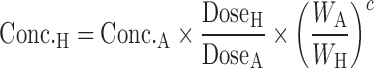
|
||||
| C ss–MRT method (91,92) |
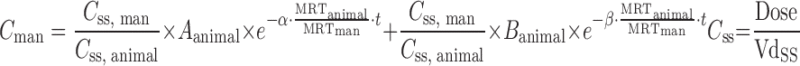
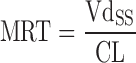
|
Plasma concentration–time profiles, dose, CL, and Vdss in at least two animal species | n = 4 (92) | 75% (AUC) |
| 75% (C max) | ||||
| 50% (C min) | ||||
| 100% (t 1/2) | ||||
| n = 4 (91) | 100% (CL) | |||
| 50% (CL) | ||||
| 75% (Vdss) | ||||
| Human PK prediction using PBPK model (95,96) | Predict K
p (tissue composition-based method) or experimentally measure in rats and assume K
p, u, rat = K
p, u, human. For hepatically eliminated compounds: CLH is scaled from microsome or hepatocyte data. For renally eliminated compounds: 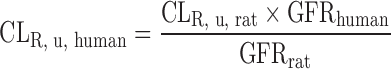 . Oral absorption: GastroPlusTM
. Oral absorption: GastroPlusTM
|
Blood flow, in vitro intrinsic clearance, tissue-to-plasma ratios, B/P ratio, fraction unbound in plasma, solubility and permeability information | n = 19 (96) | 83% (CL) |
| 50% (Vdss) | ||||
| 75% (t 1/2) | ||||
| 92% (AUC) | ||||
| 67% (C max) | ||||
| 100% (t max) |
Css–MRT Method
Wajima et al. (91) developed a method to predict human plasma concentration–time profiles based on the assumption that profiles are similar among species, and therefore, the curves normalized by Css and MRT from a variety of animal species can be superimposed. In the first step, they demonstrated superposition of normalized i.v. pharmacokinetic profiles of preclinical species (Table IV). As such, they normalized the time axis with the MRT and the concentration axis with Css (Css = dose/Vdss). The superimposed curves were then back-transformed to estimate human i.v. plasma concentration–time profiles using human Css and MRT values, which were estimated from projected human Vdss and CL values. The human i.v. plasma concentration–time profiles, the projected mean absorption rate constants, and bioavailability were utilized to simulate human oral plasma concentration–time profiles (92). Wajima et al. (91) assessed the Css–MRT and Dedrick plot methods on four drugs. Although the curves transformed by the Dedrick plot were not superimposed among species, the plasma concentration–time curves normalized by Css and MRT agreed well among species. This confirmed the assumption that concentration–time profiles are similar between human and animal species. Fura et al. (92) applied the Css–MRT method to four proprietary compounds. They observed that the predicted values of AUC, Cmax, Cmin, and T1/2 of each compound were within twofold error when using CL projected from the FCIM method.
PBPK Model
Wide use of the PBPK model in drug discovery and development has been limited by its mathematical complexity and the labor intensive input parameters required. However, recent advances in the prediction of hepatic CL and tissue–plasma partition coefficient (Kp) and the availability of simulation software have greatly improved the application of the PBPK model in human pharmacokinetics prediction. A PBPK model is usually composed of multiple tissue compartments (e.g., lung, spleen, liver, gut, adipose tissue, muscle, heart, brain, kidney, skin, testes, red marrow, yellow marrow, and the rest of the body), which are linked together by blood circulation. For most PBPK models, it is assumed that the drug distributes instantaneously and homogenously within each compartment, and drug uptake within each tissue compartment is limited by blood flow. But some exploration of diffusion-limited tissue models was also reported (24,25). The physiological parameters required for the human PBPK model are obtained from literature. The required drug-specific input parameters include CLH, CLR, and Kp for each tissue and absorption rate. For drugs eliminated by hepatic metabolism, CLH is predicted by IVIVE or allometric scaling as discussed above. For renally eliminated drugs, CLR is obtained by using either allometric scaling or the GFR ratio approach as described by Lin (93). The Kp for each tissue is predicted by using the tissue composition-based models (Poulin–Theil's equations, Berezhkovskiy's equations, Rodgers' equations, or Arundel's method). For compounds that are poorly predicted by the tissue composition models, the experimentally determined animal in vivo Kp is used to calculate animal unbound tissue–plasma partition coefficient (Ku, p). Humans and animals are assumed to share equal Ku, p. Usually, commercial software such as GastroPlus™ (Simulations Plus Inc., Lancaster, CA), PKSim™ (Bayer Technologies, Leverkusen, Germany), or SimCyp™ (Sheffield, UK) are used to predict the rate and extent of oral drug absorption. The mechanism of GastroPlus™ is known as the ACAT model (30,94), which is a physiologically based model consisting of nine compartments corresponding to different segments of the gastrointestinal tract. The ACAT model can describe the release, dissolution, degradation, metabolism, uptake, and absorption of a compound as it transits through the different segments of the digestive tract. It is also used to predict the human plasma concentration profiles after oral dosing. Then, noncompartmental analysis is performed using WinNonLin (Pharsight, Mountain View, CA) to calculate the pharmacokinetic parameters (95). Jones et al. (96) compared the prediction performance of the PBPK model and the kallynochrons Dedrick plot by analyzing 19 compounds. The prediction accuracy of the PBPK model was much higher than that of the Dedrick plot. In addition, the PBPK approach accurately predicted the multiphasic shape of the pharmacokinetic profiles for many compounds. Furthermore, De Buck et al. (95) developed a PBPK model to predict human pharmacokinetics using 26 compounds. The prediction accuracies of AUC, apparent volume of distribution after oral dosing (Vd/F), and Cmax after oral dosing were 74%, 70%, and 65% within twofold error, respectively.
PERSPECTIVES
Physiologically based approaches have been widely utilized to predict human hepatic clearance based on in vitro metabolism data. However, physiologically based prediction of nonhepatic elimination such as renal, biliary, and intestinal clearance is still limited. In most PBPK models, renal clearance is determined by using either allometric scaling or GFR ratio approach. Tubular secretion and reabsorption as well as tubular metabolism of drugs are very difficult to predict. More effort is required to establish the in vitro/in vivo relationship for active secretion and to scale in vitro kidney microsomal data to in vivo metabolic clearance. Similarly, challenges posed by active transport, enterohepatic circulation, and metabolism have resulted in very few attempts to use physiologically based approaches to predict biliary and intestinal clearance, and the predictability is poor (19). One step to improve the prediction of biliary and intestinal clearance is to identify the interspecies differences in expression and activity of hepatic/bile and intestinal transporters and metabolizing enzymes.
Currently, most PK/PD models assume only the parent drug is responsible for the pharmacological activity and/or adverse effects and the metabolites are inactive. However, this is not true in most cases. To project more accurate human dose–exposure–response–time profiles, the pharmacological activity and toxicity of the drug metabolites should be determined and integrated into the PK/PD modeling. Software such as Simcyp™ and GastroPlus™ have facilitated PK/PD modeling and FIH dose estimation. Further software refinement, such as integration of population PK/PD covariates, will make individual projection and dosing possible. For example, preclinical PK/PD data can be used to identify important covariates such as biochemical measurements (e.g., GFR, albumin, urea, and creatinine), organ functionality, genotype/phenotype, and drug–drug interactions. Incorporation of these significant covariates into the PK/PD models will facilitate the accurate prediction of individual FIH doses.
It is well known that drug transporters play important roles in the processes of absorption, distribution, and excretion. However, active drug transport has been neglected in most predictive approaches for human CL, Vdss, F, and plasma concentration–time profiles and is one of the factors responsible for prediction bias. For example, in addition to elimination by metabolic degradation, transporter-mediated hepatic uptake and canalicular excretion have been increasingly recognized as potential rate-determining steps in hepatic clearance. The in vitro assessment should account for clearance from both transporter-mediated uptake/excretion and metabolic degradation (23). With knowledge of the location and function of drug transporters and the substrates for these transporters becoming more available, active drug transport is expected to be increasingly incorporated into prediction models.
CONCLUSION
In summary, accurate prediction of human CL and bioavailability of drug candidates and estimation of FIH doses are critical for a successful phase I clinical trial. We have summarized and compared 5 approaches for FIH dose estimation, 17 approaches to estimate human clearance, 6 approaches to predict bioavailability, and 3 tools to predict PK profiles. The advantages, limitations, assumptions, and predictability of these approaches were discussed. For CL prediction, although allometric scaling is simple and practical, it should be used with caution due to its empirical nature. On the other hand, physiologically based prediction methods are increasingly utilized because of their mechanistic rationale. Although PK- and PK/PD-guided approaches are gaining popularity, both mechanistic and empirical techniques should be integrated to support the FIH dose selection. Dose estimation always requires careful consideration of all of the available information. There is no universal approach that will work in every case.
ACKNOWLEDGMENTS
This work was partially supported by the National Institutes of Health (RO1 CA120023); University of Michigan Cancer Center Research Grant (Munn); and University of Michigan Cancer Center Core Grant to DS.
Contributor Information
Lawrence X. Yu, Phone: +1-301-8275246, FAX: +1-301-5946289, Email: Lawrence.Yu@fda.hhs.gov
Duxin Sun, Phone: +1-734-6158740, FAX: +1-734-6156162, Email: duxins@umich.edu.
REFERENCES
- 1.Contrera JF, Matthews EJ, Kruhlak NL, Benz RD. Estimating the safe starting dose in phase I clinical trials and no observed effect level based on QSAR modeling of the human maximum recommended daily dose. Regul Toxicol Pharmacol. 2004;40(3):185–206. doi: 10.1016/j.yrtph.2004.08.004. [DOI] [PubMed] [Google Scholar]
- 2.FDA. Guidance for industry-Estimating the maximum safe dose in initial clinical trials for therapeutics in adult healthy volunteers. Rockville. 2005.
- 3.Mahmood I. Application of allometric principles for the prediction of pharmacokinetics in human and veterinary drug development. Adv Drug Deliv Rev. 2007;59(11):1177–92. doi: 10.1016/j.addr.2007.05.015. [DOI] [PubMed] [Google Scholar]
- 4.Reigner BG, Williams PE, Patel IH, Steimer JL, Peck C, van Brummelen P. An evaluation of the integration of pharmacokinetic and pharmacodynamic principles in clinical drug development. Experience within Hoffmann La Roche. Clin Pharmacokinet. 1997;33(2):142–52. doi: 10.2165/00003088-199733020-00005. [DOI] [PubMed] [Google Scholar]
- 5.Reigner BG, Blesch KS. Estimating the starting dose for entry into humans: principles and practice. Eur J Clin Pharmacol. 2002;57(12):835–45. doi: 10.1007/s00228-001-0405-6. [DOI] [PubMed] [Google Scholar]
- 6.Tang H, Mayersohn M. A global examination of allometric scaling for predicting human drug clearance and the prediction of large vertical allometry. J Pharm Sci. 2006;95(8):1783–99. doi: 10.1002/jps.20481. [DOI] [PubMed] [Google Scholar]
- 7.Mahmood I. Response to the comments on the commentary ‘Prediction of absolute bioavailability for drugs using oral and renal clearance following a single oral dose: a critical view’. Biopharm Drug Dispos. 1998;19(7):483–4. doi: 10.1002/(SICI)1099-081X(199810)19:7<483::AID-BDD140>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 8.Lave T, Dupin S, Schmitt C, Chou RC, Jaeck D, Coassolo P. Integration of in vitro data into allometric scaling to predict hepatic metabolic clearance in man: application to 10 extensively metabolized drugs. J Pharm Sci. 1997;86(5):584–90. doi: 10.1021/js960440h. [DOI] [PubMed] [Google Scholar]
- 9.Goteti K, Brassil PJ, Good SS, Garner CE. Estimation of human drug clearance using multiexponential techniques. J Clin Pharmacol. 2008;48(10):1226–36. doi: 10.1177/0091270008320369. [DOI] [PubMed] [Google Scholar]
- 10.Tang H, Mayersohn M. A novel model for prediction of human drug clearance by allometric scaling. Drug Metab Dispos. 2005;33(9):1297–303. doi: 10.1124/dmd.105.004143. [DOI] [PubMed] [Google Scholar]
- 11.Tang H, Hussain A, Leal M, Mayersohn M, Fluhler E. Interspecies prediction of human drug clearance based on scaling data from one or two animal species. Drug Metab Dispos. 2007;35(10):1886–93. doi: 10.1124/dmd.107.016188. [DOI] [PubMed] [Google Scholar]
- 12.Obach RS, Baxter JG, Liston TE, Silber BM, Jones BC, MacIntyre F, et al. The prediction of human pharmacokinetic parameters from preclinical and in vitro metabolism data. J Pharmacol Exp Ther. 1997;283(1):46–58. [PubMed] [Google Scholar]
- 13.Ito K, Houston JB. Prediction of human drug clearance from in vitro and preclinical data using physiologically based and empirical approaches. Pharm Res. 2005;22(1):103–12. doi: 10.1007/s11095-004-9015-1. [DOI] [PubMed] [Google Scholar]
- 14.Lave T, Coassolo P, Reigner B. Prediction of hepatic metabolic clearance based on interspecies allometric scaling techniques and in vitro-in vivo correlations. Clin Pharmacokinet. 1999;36(3):211–31. doi: 10.2165/00003088-199936030-00003. [DOI] [PubMed] [Google Scholar]
- 15.Hosea NA, Collard WT, Cole S, Maurer TS, Fang RX, Jones H, et al. Prediction of human pharmacokinetics from preclinical information: comparative accuracy of quantitative prediction approaches. J Clin Pharmacol. 2009;49(5):513–33. doi: 10.1177/0091270009333209. [DOI] [PubMed] [Google Scholar]
- 16.Lowe PJ, Hijazi Y, Luttringer O, Yin H, Sarangapani R, Howard D. On the anticipation of the human dose in first-in-man trials from preclinical and prior clinical information in early drug development. Xenobiotica. 2007;37(10–11):1331–54. doi: 10.1080/00498250701648008. [DOI] [PubMed] [Google Scholar]
- 17.Fagerholm U. Prediction of human pharmacokinetics—evaluation of methods for prediction of volume of distribution. J Pharm Pharmacol. 2007;59(9):1181–90. doi: 10.1211/jpp.59.9.0001. [DOI] [PubMed] [Google Scholar]
- 18.Fagerholm U. Prediction of human pharmacokinetics—evaluation of methods for prediction of hepatic metabolic clearance. J Pharm Pharmacol. 2007;59(6):803–28. doi: 10.1211/jpp.59.6.0007. [DOI] [PubMed] [Google Scholar]
- 19.Fagerholm U. Prediction of human pharmacokinetics-biliary and intestinal clearance and enterohepatic circulation. J Pharm Pharmacol. 2008;60(5):535–42. doi: 10.1211/jpp.60.5.0001. [DOI] [PubMed] [Google Scholar]
- 20.Fagerholm U. Prediction of human pharmacokinetics—renal metabolic and excretion clearance. J Pharm Pharmacol. 2007;59(11):1463–71. doi: 10.1211/jpp.59.11.0002. [DOI] [PubMed] [Google Scholar]
- 21.Ghibellini G, Leslie EM, Brouwer KL. Methods to evaluate biliary excretion of drugs in humans: an updated review. Mol Pharm. 2006;3(3):198–211. doi: 10.1021/mp060011k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Houston JB, Galetin A. Progress towards prediction of human pharmacokinetic parameters from in vitro technologies. Drug Metab Rev. 2003;35(4):393–415. doi: 10.1081/DMR-120026870. [DOI] [PubMed] [Google Scholar]
- 23.Chiba M, Ishii Y, Sugiyama Y. Prediction of hepatic clearance in human from in vitro data for successful drug development. AAPS J. 2009;11(2):262–76. doi: 10.1208/s12248-009-9103-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sharma V, McNeill JH. To scale or not to scale: the principles of dose extrapolation. Br J Pharmacol. 2009;157(6):907–21. doi: 10.1111/j.1476-5381.2009.00267.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.European Medicines Agency. Guideline on strategies to identify and mitigate risks for first-in-human clinical trials with investigational medicinal products. 2007. [DOI] [PMC free article] [PubMed]
- 26.Mahmood I, Green MD, Fisher JE. Selection of the first-time dose in humans: comparison of different approaches based on interspecies scaling of clearance. J Clin Pharmacol. 2003;43(7):692–7. [PubMed] [Google Scholar]
- 27.Iavarone L, Hoke JF, Bottacini M, Barnaby R, Preston GC. First time in human for GV196771: interspecies scaling applied on dose selection. J Clin Pharmacol. 1999;39(6):560–6. doi: 10.1177/00912709922008164. [DOI] [PubMed] [Google Scholar]
- 28.Agoram BM. Use of pharmacokinetic/pharmacodynamic modelling for starting dose selection in first-in-human trials of high-risk biologics. Br J Clin Pharmacol. 2009;67(2):153–60. doi: 10.1111/j.1365-2125.2008.03297.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Heimbach T, Lakshminarayana SB, Hu W, He H. Practical anticipation of human efficacious doses and pharmacokinetics using in vitro and preclinical in vivo data. AAPS J. 2009;11(3):602–14. doi: 10.1208/s12248-009-9136-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Suntharalingam G, Perry MR, Ward S, Brett SJ, Castello-Cortes A, Brunner MD, et al. Cytokine storm in a phase 1 trial of the anti-CD28 monoclonal antibody TGN1412. N Engl J Med. 2006;355(10):1018–28. doi: 10.1056/NEJMoa063842. [DOI] [PubMed] [Google Scholar]
- 31.Artursson P, Karlsson J. Correlation between oral drug absorption in humans and apparent drug permeability coefficients in human intestinal epithelial (Caco-2) cells. Biochem Biophys Res Commun. 1991;175(3):880–5. doi: 10.1016/0006-291X(91)91647-U. [DOI] [PubMed] [Google Scholar]
- 32.Rubas W, Cromwell ME, Shahrokh Z, Villagran J, Nguyen TN, Wellton M, et al. Flux measurements across Caco-2 monolayers may predict transport in human large intestinal tissue. J Pharm Sci. 1996;85(2):165–9. doi: 10.1021/js950267+. [DOI] [PubMed] [Google Scholar]
- 33.Muller PY, Brennan FR. Safety assessment and dose selection for first-in-human clinical trials with immunomodulatory monoclonal antibodies. Clin Pharmacol Ther. 2009;85(3):247–58. doi: 10.1038/clpt.2008.273. [DOI] [PubMed] [Google Scholar]
- 34.Fagerholm U. The role of permeability in drug ADME/PK, interactions and toxicity—presentation of a permeability-based classification system (PCS) for prediction of ADME/PK in humans. Pharm Res. 2008;25(3):625–38. doi: 10.1007/s11095-007-9397-y. [DOI] [PubMed] [Google Scholar]
- 35.Dokoumetzidis A, Kosmidis K, Argyrakis P, Macheras P. Modeling and Monte Carlo simulations in oral drug absorption. Basic Clin Pharmacol Toxicol. 2005;96(3):200–5. doi: 10.1111/j.1742-7843.2005.pto960309.x. [DOI] [PubMed] [Google Scholar]
- 36.Tang H, Mayersohn M. Utility of the coefficient of determination (r2) in assessing the accuracy of interspecies allometric predictions: illumination or illusion? Drug Metab Dispos. 2007;35(12):2139–42. doi: 10.1124/dmd.107.016444. [DOI] [PubMed] [Google Scholar]
- 37.Sinha VK, De Buck SS, Fenu LA, Smit JW, Nijsen M, Gilissen RA, et al. Predicting oral clearance in humans: how close can we get with allometry? Clin Pharmacokinet. 2008;47(1):35–45. doi: 10.2165/00003088-200847010-00004. [DOI] [PubMed] [Google Scholar]
- 38.Mahmood I. Interspecies scaling: role of protein binding in the prediction of clearance from animals to humans. J Clin Pharmacol. 2000;40(12 Pt 2):1439–46. [PubMed] [Google Scholar]
- 39.Boxenbaum H, Fertig JB. Scaling of antipyrine intrinsic clearance of unbound drug in 15 mammalian species. Eur J Drug Metab Pharmacokinet. 1984;9(2):177–83. doi: 10.1007/BF03189622. [DOI] [PubMed] [Google Scholar]
- 40.Mahmood I. Prediction of human drug clearance from animal data: application of the rule of exponents and ‘fu Corrected Intercept Method’ (FCIM) J Pharm Sci. 2006;95(8):1810–21. doi: 10.1002/jps.20650. [DOI] [PubMed] [Google Scholar]
- 41.Stoner CL, Cleton A, Johnson K, Oh DM, Hallak H, Brodfuehrer J, et al. Integrated oral bioavailability projection using in vitro screening data as a selection tool in drug discovery. Int J Pharm. 2004;269(1):241–9. doi: 10.1016/j.ijpharm.2003.09.006. [DOI] [PubMed] [Google Scholar]
- 42.Nagilla R, Ward KW. A comprehensive analysis of the role of correction factors in the allometric predictivity of clearance from rat, dog, and monkey to humans. J Pharm Sci. 2004;93(10):2522–34. doi: 10.1002/jps.20169. [DOI] [PubMed] [Google Scholar]
- 43.Houston JB. Utility of in vitro drug metabolism data in predicting in vivo metabolic clearance. Biochem Pharmacol. 1994;47(9):1469–79. doi: 10.1016/0006-2952(94)90520-7. [DOI] [PubMed] [Google Scholar]
- 44.Mahmood I. Interspecies scaling of biliary excreted drugs: a comparison of several methods. J Pharm Sci. 2005;94(4):883–92. doi: 10.1002/jps.20313. [DOI] [PubMed] [Google Scholar]
- 45.Lave T, Coassolo P, Ubeaud G, Brandt R, Schmitt C, Dupin S, et al. Interspecies scaling of bosentan, a new endothelin receptor antagonist and integration of in vitro data into allometric scaling. Pharm Res. 1996;13(1):97–101. doi: 10.1023/A:1016037519116. [DOI] [PubMed] [Google Scholar]
- 46.Obach RS. The prediction of human clearance from hepatic microsomal metabolism data. Curr Opin Drug Discov Devel. 2001;4(1):36–44. [PubMed] [Google Scholar]
- 47.Shibata Y, Takahashi H, Chiba M, Ishii Y. Prediction of hepatic clearance and availability by cryopreserved human hepatocytes: an application of serum incubation method. Drug Metab Dispos. 2002;30(8):892–6. doi: 10.1124/dmd.30.8.892. [DOI] [PubMed] [Google Scholar]
- 48.Goteti K, Garner CE, Mahmood I. Prediction of human drug clearance from two species: a comparison of several allometric methods. J Pharm Sci. 2010;99(3):1601–13. doi: 10.1002/jps.21926. [DOI] [PubMed] [Google Scholar]
- 49.Ward KW, Smith BR. A comprehensive quantitative and qualitative evaluation of extrapolation of intravenous pharmacokinetic parameters from rat, dog, and monkey to humans. II. Volume of distribution and mean residence time. Drug Metab Dispos. 2004;32(6):612–9. doi: 10.1124/dmd.32.6.612. [DOI] [PubMed] [Google Scholar]
- 50.Mahmood I. Role of fixed coefficients and exponents in the prediction of human drug clearance: how accurate are the predictions from one or two species? J Pharm Sci. 2009;98(7):2472–93. doi: 10.1002/jps.21597. [DOI] [PubMed] [Google Scholar]
- 51.Charman WN, Porter CJ, Mithani S, Dressman JB. Physiochemical and physiological mechanisms for the effects of food on drug absorption: the role of lipids and pH. J Pharm Sci. 1997;86(3):269–82. doi: 10.1021/js960085v. [DOI] [PubMed] [Google Scholar]
- 52.Tang H, Mayersohn M. On the observed large interspecies overprediction of human clearance (“vertical allometry”) of UCN-01: further support for a proposed model based on plasma protein binding. J Clin Pharmacol. 2006;46(4):398–400. doi: 10.1177/0091270005285457. [DOI] [PubMed] [Google Scholar]
- 53.Hakooz N, Ito K, Rawden H, Gill H, Lemmers L, Boobis AR, et al. Determination of a human hepatic microsomal scaling factor for predicting in vivo drug clearance. Pharm Res. 2006;23(3):533–9. doi: 10.1007/s11095-006-9531-2. [DOI] [PubMed] [Google Scholar]
- 54.Ito K, Houston JB. Comparison of the use of liver models for predicting drug clearance using in vitro kinetic data from hepatic microsomes and isolated hepatocytes. Pharm Res. 2004;21(5):785–92. doi: 10.1023/B:PHAM.0000026429.12114.7d. [DOI] [PubMed] [Google Scholar]
- 55.Niro R, Byers JP, Fournier RL, Bachmann K. Application of a convective-dispersion model to predict in vivo hepatic clearance from in vitro measurements utilizing cryopreserved human hepatocytes. Curr Drug Metab. 2003;4(5):357–69. doi: 10.2174/1389200033489334. [DOI] [PubMed] [Google Scholar]
- 56.Ashforth EI, Carlile DJ, Chenery R, Houston JB. Prediction of in vivo disposition from in vitro systems: clearance of phenytoin and tolbutamide using rat hepatic microsomal and hepatocyte data. J Pharmacol Exp Ther. 1995;274(2):761–6. [PubMed] [Google Scholar]
- 57.Soars MG, Burchell B, Riley RJ. In vitro analysis of human drug glucuronidation and prediction of in vivo metabolic clearance. J Pharmacol Exp Ther. 2002;301(1):382–90. doi: 10.1124/jpet.301.1.382. [DOI] [PubMed] [Google Scholar]
- 58.Brown HS, Griffin M, Houston JB. Evaluation of cryopreserved human hepatocytes as an alternative in vitro system to microsomes for the prediction of metabolic clearance. Drug Metab Dispos. 2007;35(2):293–301. doi: 10.1124/dmd.106.011569. [DOI] [PubMed] [Google Scholar]
- 59.Sun D, Yu LX, Hussain MA, Wall DA, Smith RL, Amidon GL. In vitro testing of drug absorption for drug ‘developability’ assessment: forming an interface between in vitro preclinical data and clinical outcome. Curr Opin Drug Discov Devel. 2004;7(1):75–85. [PubMed] [Google Scholar]
- 60.Naritomi Y, Terashita S, Kimura S, Suzuki A, Kagayama A, Sugiyama Y. Prediction of human hepatic clearance from in vivo animal experiments and in vitro metabolic studies with liver microsomes from animals and humans. Drug Metab Dispos. 2001;29(10):1316–24. [PubMed] [Google Scholar]
- 61.Naritomi Y, Terashita S, Kagayama A, Sugiyama Y. Utility of hepatocytes in predicting drug metabolism: comparison of hepatic intrinsic clearance in rats and humans in vivo and in vitro. Drug Metab Dispos. 2003;31(5):580–8. doi: 10.1124/dmd.31.5.580. [DOI] [PubMed] [Google Scholar]
- 62.Lave T, Dupin S, Schmitt C, Valles B, Ubeaud G, Chou RC, et al. The use of human hepatocytes to select compounds based on their expected hepatic extraction ratios in humans. Pharm Res. 1997;14(2):152–5. doi: 10.1023/A:1012036324237. [DOI] [PubMed] [Google Scholar]
- 63.Zuegge J, Schneider G, Coassolo P, Lave T. Prediction of hepatic metabolic clearance: comparison and assessment of prediction models. Clin Pharmacokinet. 2001;40(7):553–63. doi: 10.2165/00003088-200140070-00006. [DOI] [PubMed] [Google Scholar]
- 64.Fagerholm U. Prediction of human pharmacokinetics—improving microsome-based predictions of hepatic metabolic clearance. J Pharm Pharmacol. 2007;59(10):1427–31. doi: 10.1211/jpp.59.10.0014. [DOI] [PubMed] [Google Scholar]
- 65.Obach RS. Prediction of human clearance of twenty-nine drugs from hepatic microsomal intrinsic clearance data: an examination of in vitro half-life approach and nonspecific binding to microsomes. Drug Metab Dispos. 1999;27(11):1350–9. [PubMed] [Google Scholar]
- 66.Stringer R, Nicklin PL, Houston JB. Reliability of human cryopreserved hepatocytes and liver microsomes as in vitro systems to predict metabolic clearance. Xenobiotica. 2008;38(10):1313–29. doi: 10.1080/00498250802446286. [DOI] [PubMed] [Google Scholar]
- 67.Skaggs SM, Foti RS, Fisher MB. A streamlined method to predict hepatic clearance using human liver microsomes in the presence of human plasma. J Pharmacol Toxicol Methods. 2006;53(3):284–90. doi: 10.1016/j.vascn.2005.10.002. [DOI] [PubMed] [Google Scholar]
- 68.Stringer RA, Strain-Damerell C, Nicklin P, Houston JB. Evaluation of recombinant cytochrome P450 enzymes as an in vitro system for metabolic clearance predictions. Drug Metab Dispos. 2009;37(5):1025–34. doi: 10.1124/dmd.108.024810. [DOI] [PubMed] [Google Scholar]
- 69.Galetin A, Brown C, Hallifax D, Ito K, Houston JB. Utility of recombinant enzyme kinetics in prediction of human clearance: impact of variability, CYP3A5, and CYP2C19 on CYP3A4 probe substrates. Drug Metab Dispos. 2004;32(12):1411–20. doi: 10.1124/dmd.104.000844. [DOI] [PubMed] [Google Scholar]
- 70.Kilford PJ, Stringer R, Sohal B, Houston JB, Galetin A. Prediction of drug clearance by glucuronidation from in vitro data: use of combined cytochrome P450 and UDP-glucuronosyltransferase cofactors in alamethicin-activated human liver microsomes. Drug Metab Dispos. 2009;37(1):82–9. doi: 10.1124/dmd.108.023853. [DOI] [PubMed] [Google Scholar]
- 71.Yang J, Jamei M, Yeo KR, Tucker GT, Rostami-Hodjegan A. Prediction of intestinal first-pass drug metabolism. Curr Drug Metab. 2007;8(7):676–84. doi: 10.2174/138920007782109733. [DOI] [PubMed] [Google Scholar]
- 72.Wajima T, Fukumura K, Yano Y, Oguma T. Prediction of human clearance from animal data and molecular structural parameters using multivariate regression analysis. J Pharm Sci. 2002;91(12):2489–99. doi: 10.1002/jps.10242. [DOI] [PubMed] [Google Scholar]
- 73.Nikolic K, Agababa D. Prediction of hepatic microsomal intrinsic clearance and human clearance values for drugs. J Mol Graph Model. 2009;28(3):245–52. doi: 10.1016/j.jmgm.2009.08.002. [DOI] [PubMed] [Google Scholar]
- 74.Dokoumetzidis A, Kalantzi L, Fotaki N. Predictive models for oral drug absorption: from in silico methods to integrated dynamical models. Expert Opin Drug Metab Toxicol. 2007;3(4):491–505. doi: 10.1517/17425255.3.4.491. [DOI] [PubMed] [Google Scholar]
- 75.Obach RS, Lombardo F, Waters NJ. Trend analysis of a database of intravenous pharmacokinetic parameters in humans for 670 drug compounds. Drug Metab Dispos. 2008;36(7):1385–405. doi: 10.1124/dmd.108.020479. [DOI] [PubMed] [Google Scholar]
- 76.Badhan R, Penny J, Galetin A, Houston JB. Methodology for development of a physiological model incorporating CYP3A and P-glycoprotein for the prediction of intestinal drug absorption. J Pharm Sci. 2009;98(6):2180–97. doi: 10.1002/jps.21572. [DOI] [PubMed] [Google Scholar]
- 77.Kesisoglou F, Wu Y. Understanding the effect of API properties on bioavailability through absorption modeling. AAPS J. 2008;10(4):516–25. doi: 10.1208/s12248-008-9061-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Yee S. In vitro permeability across Caco-2 cells (colonic) can predict in vivo (small intestinal) absorption in man—fact or myth. Pharm Res. 1997;14(6):763–6. doi: 10.1023/A:1012102522787. [DOI] [PubMed] [Google Scholar]
- 79.Sugano K, Hamada H, Machida M, Ushio H, Saitoh K, Terada K. Optimized conditions of bio-mimetic artificial membrane permeation assay. Int J Pharm. 2001;228(1–2):181–8. doi: 10.1016/S0378-5173(01)00845-6. [DOI] [PubMed] [Google Scholar]
- 80.Pidgeon C, Ong S, Liu H, Qiu X, Pidgeon M, Dantzig AH, et al. IAM chromatography: an in vitro screen for predicting drug membrane permeability. J Med Chem. 1995;38(4):590–4. doi: 10.1021/jm00004a004. [DOI] [PubMed] [Google Scholar]
- 81.Kansy M, Senner F, Gubernator K. Physicochemical high throughput screening: parallel artificial membrane permeation assay in the description of passive absorption processes. J Med Chem. 1998;41(7):1007–10. doi: 10.1021/jm970530e. [DOI] [PubMed] [Google Scholar]
- 82.Zhu C, Jiang L, Chen TM, Hwang KK. A comparative study of artificial membrane permeability assay for high throughput profiling of drug absorption potential. Eur J Med Chem. 2002;37(5):399–407. doi: 10.1016/S0223-5234(02)01360-0. [DOI] [PubMed] [Google Scholar]
- 83.Kotecha J, Shah S, Rathod I, Subbaiah G. Relationship between immobilized artificial membrane chromatographic retention and human oral absorption of structurally diverse drugs. Int J Pharm. 2007;333(1–2):127–35. doi: 10.1016/j.ijpharm.2006.10.010. [DOI] [PubMed] [Google Scholar]
- 84.Cao X, Gibbs ST, Fang L, Miller HA, Landowski CP, Shin HC, et al. Why is it challenging to predict intestinal drug absorption and oral bioavailability in human using rat model. Pharm Res. 2006;23(8):1675–86. doi: 10.1007/s11095-006-9041-2. [DOI] [PubMed] [Google Scholar]
- 85.Akabane T, Tabata K, Kadono K, Sakuda S, Terashita S, Teramura T. A comparison of pharmacokinetics between humans and monkeys. Drug Metab Dispos. 2010;38(2):308–16. doi: 10.1124/dmd.109.028829. [DOI] [PubMed] [Google Scholar]
- 86.Lipinski CA, Lombardo F, Dominy BW, Feeney PJ. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv Drug Deliv Rev. 1997;23(1–3):3–25. doi: 10.1016/S0169-409X(96)00423-1. [DOI] [PubMed] [Google Scholar]
- 87.Andrews CW, Bennett L, Yu LX. Predicting human oral bioavailability of a compound: development of a novel quantitative structure-bioavailability relationship. Pharm Res. 2000;17(6):639–44. doi: 10.1023/A:1007556711109. [DOI] [PubMed] [Google Scholar]
- 88.Yoshida F, Topliss JG. QSAR model for drug human oral bioavailability. J Med Chem. 2000;43(13):2575–85. doi: 10.1021/jm0000564. [DOI] [PubMed] [Google Scholar]
- 89.Dedrick R, Bischoff KB, Zaharko DS. Interspecies correlation of plasma concentration history of methotrexate (NSC-740) Cancer Chemother Rep. 1970;54(2):95–101. [PubMed] [Google Scholar]
- 90.Mahmood I, Yuan R. A comparative study of allometric scaling with plasma concentrations predicted by species-invariant time methods. Biopharm Drug Dispos. 1999;20(3):137–44. doi: 10.1002/(SICI)1099-081X(199904)20:3<137::AID-BDD165>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
- 91.Wajima T, Yano Y, Fukumura K, Oguma T. Prediction of human pharmacokinetic profile in animal scale up based on normalizing time course profiles. J Pharm Sci. 2004;93(7):1890–900. doi: 10.1002/jps.20099. [DOI] [PubMed] [Google Scholar]
- 92.Fura A, Vyas V, Humphreys W, Chimalokonda A, Rodrigues D. Prediction of human oral pharmacokinetics using nonclinical data: examples involving four proprietary compounds. Biopharm Drug Dispos. 2008;29(8):455–68. doi: 10.1002/bdd.632. [DOI] [PubMed] [Google Scholar]
- 93.Gibson CR, Bergman A, Lu P, Kesisoglou F, Denney WS, Mulrooney E. Prediction of phase I single-dose pharmacokinetics using recombinant cytochromes P450 and physiologically based modelling. Xenobiotica. 2009;39(9):637–48. doi: 10.1080/00498250902954296. [DOI] [PubMed] [Google Scholar]
- 94.Lowe PJ, Tannenbaum S, Wu K, Lloyd P, Sims J. On setting the first dose in man: quantitating biotherapeutic drug-target binding through pharmacokinetic and pharmacodynamic models. Basic Clin Pharmacol Toxicol. 2010;106(3):195–209. doi: 10.1111/j.1742-7843.2009.00513.x. [DOI] [PubMed] [Google Scholar]
- 95.De Buck SS, Sinha VK, Fenu LA, Nijsen MJ, Mackie CE, Gilissen RA. Prediction of human pharmacokinetics using physiologically based modeling: a retrospective analysis of 26 clinically tested drugs. Drug Metab Dispos. 2007;35(10):1766–80. doi: 10.1124/dmd.107.015644. [DOI] [PubMed] [Google Scholar]
- 96.Jones HM, Parrott N, Jorga K, Lave T. A novel strategy for physiologically based predictions of human pharmacokinetics. Clin Pharmacokinet. 2006;45(5):511–42. doi: 10.2165/00003088-200645050-00006. [DOI] [PubMed] [Google Scholar]
- 97.Schneider G, Coassolo P, Lave T. Combining in vitro and in vivo pharmacokinetic data for prediction of hepatic drug clearance in humans by artificial neural networks and multivariate statistical techniques. J Med Chem. 1999;42(25):5072–6. doi: 10.1021/jm991030j. [DOI] [PubMed] [Google Scholar]
- 98.Mohutsky MA, Chien JY, Ring BJ, Wrighton SA. Predictions of the in vivo clearance of drugs from rate of loss using human liver microsomes for phase I and phase II biotransformations. Pharm Res. 2006;23(4):654–62. doi: 10.1007/s11095-006-9663-4. [DOI] [PubMed] [Google Scholar]
- 99.Huang C, Zheng M, Yang Z, Rodrigues AD, Marathe P. Projection of exposure and efficacious dose prior to first-in-human studies: how successful have we been? Pharm Res. 2008;25(4):713–26. doi: 10.1007/s11095-007-9411-4. [DOI] [PubMed] [Google Scholar]