A highly efficient and effective motif discovery method for ChIP-seq/ChIP-chip data using positional information

Abstract

Identification of DNA motifs from ChIP-seq/ChIP-chip [chromatin immunoprecipitation (ChIP)] data is a powerful method for understanding the transcriptional regulatory network. However, most established methods are designed for small sample sizes and are inefficient for ChIP data. Here we propose a new k-mer occurrence model to reflect the fact that functional DNA k-mers often cluster around ChIP peak summits. With this model, we introduced a new measure to discover functional k-mers. Using simulation, we demonstrated that our method is more robust against noises in ChIP data than available methods. A novel word clustering method is also implemented to group similar k-mers into position weight matrices (PWMs). Our method was applied to a diverse set of ChIP experiments to demonstrate its high sensitivity and specificity. Importantly, our method is much faster than several other methods for large sample sizes. Thus, we have developed an efficient and effective motif discovery method for ChIP experiments.

INTRODUCTION

Decoding the transcriptional regulatory network is a challenging task in molecular biology (1,2). In human, despite the estimated 1391 sequence-specific DNA-binding transcription factors, only ∼60 of them have been experimentally verified for both DNA-binding and regulatory functions (3). As of January, 2011, there were only 75 matrix models describing the binding motifs of human transcription factors in the JASPAR database (4). With the rapid development of high-throughput DNA sequencing technology, it is now popular to experimentally map the genome-wide binding regions of transcription factors using chromatin immunoprecipitation (ChIP) coupled with massively parallel sequencing technology (ChIP-seq) or microarray (ChIP-chip) (1,2). For example, binding regions of 23 worm transcription factors (5) and 103 fly transcription factors (6) have been studied in single projects. Identification of functional DNA-motifs from such data may provide valuable resources for modeling the transcription regulatory networks. Although the resolution of binding regions identified from ChIP-seq can be a few hundred base pairs (2), it has been found (7) that existing iterative motif discovery methods, e.g. MEME (8), do not have the computational efficiency required to process the huge amount of data from ChIP-seq/ChIP-chip experiments.

On the other hand, modeling and discovery of DNA motifs from a set of DNA sequences have been a major research focus in computational biology (1,2,9). In the earlier works (8–18), it is generally assumed that the underlying DNA motifs to be discovered are enriched in certain regions (e.g. promoters of co-expressed genes) without any positional preference. Since some transcription factors are known to bind DNA regions close to 5′ transcription start site (TSS) of their target genes (19), Linhart et al. (20) introduced a binomial test to determine if a given DNA motif tends to appear in certain bins of the 5′TSS regions of genes. Kim et al. (21) introduced a Bayesian model to incorporate positional bias of transcription factor binding sites (TFBSs) in promoter regions to discover DNA motifs. Narang et al. (22) introduced a spatial confinement score combined with an overrepresentation score and relative entropy score to discover DNA motifs. Using positional preference for DNA motif discovery was most recently revisited by Keilwagen et al. (23).

With the ChIP-seq/ChIP-chip technique, positional information is more evident in such data sets. For example, peak intensity profiles were used a priori (24) to accelerate the optimization process. Such intensity profiles were also used to score PWMs (25). Although the above-mentioned motif discovery tools have achieved success in many scenarios, positional information has not been fully exploited for motif discovery. For example, it was found that the underlying DNA motifs are distributed more frequently around the summits of peaks than in the flanking regions of the peaks (26). While the intensity profiles used by Hu et al. (24) and Kulakovskiy et al. (25) contain positional information, estimation accuracy of the intensity profiles at peaks with low-read coverage was error prone. In addition, both fragment length and distribution of the underlying DNA motif may affect the peak intensity profile (27) that often renders the determination of ‘peak segments’ for motif discovery ad hoc. Also, it is unknown how to optimally specify the start and end points of the detected ChIP peaks for most currently available motif discovery software. As a result, ‘foreground’ sequences are often determined using arbitrary thresholds. For example, in Jothi et al. (7) and Hu et al. (24), a 200-bp region centered on the peak summit is used, while a region having a 1000-bp length is used in Corbo et al. (28). It is thus interesting to ask how the positional information can be best utilized for DNA motif discovery.

In this work, we first noticed that in a typical ChIP experiment for a sequence-specific transcription factor, the functional DNA motif interacting with the studied protein tends to cluster around the peak summit (26). Based on this observation, we propose a Gaussian-uniform mixture model to describe the positional patterns of k-mers relative to the peak summit. A scoring method is also proposed to quickly rank and discover k-mers from ChIP data. A positional information guided motif discovery software, termed POSMO, is then implemented. In the following, using both simulated and real data sets, we will demonstrate the higher effectiveness and efficiency of POSMO than available software tools.

MATERIALS AND METHODS

In the following, we assume that the ChIP-seq/ChIP-chip experiments are for sequence-specific DNA-binding transcription factors. It may not be suitable for ChIP-seq/ChIP-chip experiments for non-specific DNA binding proteins, such as histones.

Data sets used in this work

To demonstrate the practical use of our method, we obtained ChIP-seq data for STAT1 (29), CRX (28), CTCF (30), NRSF (31) and FOXA2 (32). To validate the performance of our method for ChIP-chip data, we obtained data for CTCF in human (33). To validate the performance of our method on other species, we obtained ChIP-seq data for CAD, KNI, KR1, KR2, BCD, HB1 and HB2 of Drosophila melanogaster (34). We also demonstrated the usefulness of our method on a large cohort of core transcription factors involved in mouse embryonic stem cells (35). Binding motifs of the above transcription factors are either documented in the JASPAR database (4) or in the original publications, facilitating the comparison between our method and other available methods.

Model for motif discovery

Naturally, after peak calling on ChIP-seq/ChIP-chip data, we have a set of chromosomal positions about the potential binding events of a given transcription factor. Typically, peak calling software also reports a ‘summit’ for each peak [e.g. MACS (36), SISSRs (7), for a recent comparison see (37)]. Therefore, these peaks can be uniquely aligned according to the location (µ₀) of their respective summits. Next, based on the nature of the ChIP-seq/ChIP-chip experiment (7,29,36), we assume that a functional DNA motif exists in the vicinity of peak summits. The DNA motif is a k-mer with unknown k. In practice, many such k-mers may exist as a result of degeneracy and a word-clustering algorithm is employed to group them together. Location (X) of such motifs is assumed to follow a Gaussian distribution: X∼N(µ₀, σ²), where µ₀ is the peak summit and σ is an unknown parameter related to the binding nature of the transcription factor being studied, the noise level (e.g. antibody specificity) of the ChIP experiment as well as the noise in the sequencing step. In addition, σ is small compared to the flanking regions of each candidate peak. This assumption is quite reasonable since the underlying functional DNA motifs are generally enriched in peak summit regions with length of a few hundred base pairs or less (7,29,36), and we can freely increase the length (e.g. ±5000 bp was used in this work; denoted as m) of flanking sequences of each peak. Finally, as a background model, the given k-mer is assumed to be uniformly distributed in the flanking regions of the identified peaks. With these assumptions, we have

(1)

where α is an unknown enrichment parameter between 0 and 1 and is specific to the k-mer. Inferences on α and σ for a given k-mer can be made when there is a sufficient number of observations. In principle, a maximum likelihood estimation of α and σ can be obtained by optimization methods (38). However, since a majority of k-mers are usually unrelated to the transcription factor, directly solving the above mixture model is not computationally efficient. In fact, we introduced a novel statistic to score and rank each k-mer as follows.

Since the peak sequences with exactly the same lengths are aligned by the summit (Supplementary Figure S1A), we can count the appearance frequency of each k-mer at a particular position relative to the peak summit across all aligned peak sequences. In other words, we have an appearance frequency profile (A₁, A₂, … , A_2m) for each k-mer (Supplementary Figure S1B), where A_i is the total times of observing a given k-mer at position i of all peaks. According to the above mixture model, the appearance frequency profile will be relatively higher when the position index i is close to peak summit µ₀, provided that the corresponding k-mer is the binding motif of the investigated transcription factor. Clearly, a significant jump must be observed around the summit region (Supplementary Figure S1C) when the appearance frequency profile of a k-mer related to the studied transcription factor is converted into a cumulative appearance frequency profile (CAFP). We thus adopted scoring such a jump. Since a higher jump corresponds to larger area between the observed CAFP and the diagonal line (corresponding to α = 0), we used the area (R) between the CAFP and the diagonal (see Supplementary Text 1 for detailed definition) to score each k-mer, and the obtained score is hereinafter referred to as POSMO R score. We allow this area (R) to have a negative value, which corresponds to cases where a given k-mer is depleted around the summit region, but enriched in flanking regions. As shown in Supplementary Text 1, we proved that the POSMO R score asymptotically follows a normal distribution 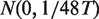for large T (say >60), where T represents total occurrences of a given k-mer. With this distribution, we can evaluate the statistical significance of each k-mer by POSMO R score. Such significance scores, termed POSMO Z scores, are then used to rank k-mers (Supplementary Figure S1D).

Although the above POSMO Z score is highly effective in ranking the true k-mers on top, it obviously does not efficiently account for σ in Equation (1). Thus, for the purpose of efficiency, we proposed an approximate solution to estimate σ using linear models. As can be seen in Supplementary Figure S1C, the CAFP has two linear components of the same slope in the flanking regions. In other words, we can model the linear components in the flanking regions by:

Estimators 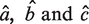can be derived using least square methods for the above model. We then approximately estimate σ of the Gaussian component by checking the residual of the linear fitting of the two flanking regions. Since the profile in Supplementary Figure S1C is monotonic, we can calculate the residual at each position using the linear model on left flanking region and right flanking region. The start (s) and end (e) positions where the residual first exceeds 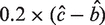are estimated by:

The distance between these two positions (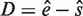; hereinafter termed D score) is a second filter in addition to the above POSMO Z score. A true k-mer will have a relatively smaller positive D score than other k-mers. Clearly, the complexity to calculate the above POSMO R score and D score is linear with the length of the flanking regions.

Thresholds

Obviously, a majority of the 4 ^k k-mers are unrelated to the transcription factor being studied. With the above POSMO Z score and D score for each k-mer, we next want to detect ‘significant k-mers’ for further analysis. For this purpose, we only consider positive D scores that correspond to k-mers enriched in peak summit regions. A k-mer will be retained if its D score is small, but non-negative:

where t_D is set to 1.645 (corresponding to one-sided P-value of 0.05) in this work.

Next, we checked the population mean (µ_Z) and standard deviation (σ_Z) of the POSMO Z scores of each k-mer. A k-mer will be filtered out if its POSMO Z score is small:

where t_Z is set to 2.33 (corresponding to one-sided P-value of 0.01) in this work. k-mers satisfying the above two filters are called ‘significant k-mers’ and will be subject to word clustering, as described in the next section. We note that the above thresholds (t_D and t_Z) are quite arbitrary and could be fine-tuned for specific data sets. However, in the present work, we found that our method is robust to these parameters (Supplementary Table S3).

Word clustering

Although the desired k-mers are generally within the significant k-mer list, it is difficult to manually inspect the whole list of significant k-mers. In addition, different variations of the same binding motif exist in the list of significant k-mers due to degeneracy. Thus, a traditional PWM representation may be more informative. This raised a question of k-mer clustering, which is still an open problem in bioinformatics. Different methods for clustering k-mers have been proposed. For example, Schones et al. (39) found that the chi-square statistics and Fisher-Irwin test are good measurements of PWM similarity. Mahony et al. (40) studied the effectiveness of different similarity metrics and tree-building methods on grouping k-mers from an analysis of variance (ANOVA) perspective. They found that the Pearson correlation coefficient is a good similarity measure between PWMs. However, we found that their metric on automatic determination of the number of clusters is generally not satisfactory for our PWMs, i.e. the CH_log statistic by Mahony et al. (40) does not always generate reasonable global minima to determine optimal cluster numbers (data not shown). Thus, we developed a simpler, yet effective, method to group the significant k-mers by considering context, as described below.

Specifically, with the significant k-mers, we rescan the whole data set of peak sequences, e.g. (−5, 5 kb) flanking region of the peak summits. Each significant k-mer as defined in section ‘Thresholds’ is assigned its POSMO Z score, while insignificant k-mers are set to zero. For each continuous sequence segment with score >0, we extract its flanking regions (e.g. ±20 bp) surrounding the k-mer (w₀) with highest score and label this sequence segment using corresponding k-mer (w₀). This step is particularly useful when our k is smaller than the optimal k₀, in which case several k-mers are highly significant because they are simple shifts of the same DNA motif. DNA segments are then grouped according to their labeling k-mers, respectively. For each of these labeling k-mers, a position specific frequency matrix (PWM) is obtained. Next, each PWM is converted into a 4 × w vector where w (>k) is a predetermined length (here we used w = k + 2). Different PWMs are compared using Pearson's correlation coefficient over its region with maximum information content, where the information content is defined as:

where p_i,k is the frequency of observing nucleotide k at position I = 1,2, … w. Different offsets are tried to best match a pair of PWMs. At each step of our hierarchical clustering, the pair of PWMs with highest similarity score is joined, and a new PWM is constructed in the clustering tree. We iterate this process until only one node is left. We found that the similarity score between joined nodes in each step decreases when the tree level is close to the root node. With this observation, we determine the final number of clusters by the tree level which is closest to the root node and which has similarity score over a predefined threshold T₀. We found that setting T₀ between (0.8, 0.9) generally gives reasonably good results. A sequence logo was, in turn, generated using the seqLogo package in the BioConductor open source software package, as was done in Hu et al. (24).

Comparison with other algorithms on ranking k-mers by POSMO Z score

We first set out to compare our algorithm with other motif-discovery methods. For this purpose, we compared our algorithm with DME (41), as a representative of enumerative methods, and MEME (8), as a representative of iterative optimization methods. The comparison was carried out with simulated data using the following procedure:

1. simulate 2000 sequences each with length L (e.g. 10 000 bp);

2. half (here 1000) of the sequences are randomly chosen as foreground data and another half (1000) as control data;

3. a k-mer w₀ is generated to be planted into 50 sequences [corresponding to α = 0.24 in Equation (1), as the expected number of a given 8-mer in background will be 1000 × 10 000/4⁸≈ 153 and 50/(153 + 50) = 0.24], foreground sequences in step 4;

4. for each of the 50 sequences (see above) selected as foreground, a random integer x (>0 and <10 000-k) is sampled from Gaussian distribution N(µ, σ²), where µ (here 5000) controls the location of the real peaks (to be discovered by ChIP experiments), and σ controls the spread of the peaks. The k-mer at position x is replaced by the k-mer in step 3);

5. all the foreground sequences are processed by POSMO;

6. for each foreground and background sequence, the substrings from position 5000 − l to 5000 + l are extracted to compile a new foreground data set and a new background data set, where l is set as 100 bp. These two data sets are input to DME and MEME as foreground and background, respectively;

7. the rank of the known k-mer in step (3) by POSMO, DME and MEME is recorded; and

8. steps (1) through (6) are repeated many (e.g. 500) times to summarize the rank distribution of the known k-mers. A lower rank of the target k-mer is better.

Implementation

We have implemented our algorithm using C++. The POSMO program can be freely downloaded from http://cb.utdallas.edu/Posmo/index.html.

RESULTS

Simulation study

We first used simulation to compare our POSMO algorithm with established methods, such as exhaustive enumeration [e.g. YMF (42), DWE (43) and DME (41)] and iterative optimization [e.g. MEME (8)]. We decided to compare our algorithm with DME and MEME as representatives of the above two categories. As it turned out, our method performs in a manner similar to DME and MEME in ranking the target k-mers on top when the underlying distribution of the target motif is well correlated with the ChIP peak (Supplementary Figure S2A). In a typical ChIP experiment, the cross-linked DNA sequences are sheared into desired length, and these smaller DNA segments are then sequenced. However, some transcription factors may interact with co-factors, which, in turn, lead to sharper or flatter peaks. These unknown parameters will affect the spread of the motif distribution under the ChIP peaks, as modeled by σ in Equation (1). As can be seen from Supplementary Figure S2B, performance of POSMO is more robust to larger σ as compared to that of MEME and DME. In addition, the ChIP peaks may have systematic shift from the true binding site (36,44). As can be seen from Supplementary Figure S2C, POSMO is much more robust against such a systematic error than either MEME or DME. This is not surprising since the performance of both MEME and DME is dependent on the accuracy of the foreground sequences. In this sense our simulation method is in favor of our POSMO methods, since MEME and DME do not consider the positional preferences at all. On the other hand, POSMO is able to find the target motif without the need of explicitly specifying foreground and background sequences since it implicitly contrasts the ‘peak center’ with the flanking region. Based on the above simulation results, we proceeded to apply our method to real ChIP data sets in the next sections.

Application on real data

ChIP-seq on STAT1, NRSF, CTCF, CRX and FOXA2

We first applied our POSMO algorithm on ChIP peaks identified by Jothi et al. (7) on STAT1 (29). A refined motif of STAT1 was recently reported by Hu et al. (24). We therefore studied the performance of POSMO in ranking k-mers for STAT1-binding motif, using the PWM of STAT1 by Hu et al. (24) as the gold standard. By focusing on the 4741 top peaks of STAT1 ChIP data [NumTags >50 in Jothi et al. (7); see Table 4 for robustness of our method against the number of top peaks used], we found that 8-mers directly related to STAT1 binding are indeed ranked on top (Table 1 and Supplementary Table S1).

Table 4.

POSMO is robust to large sample sizes

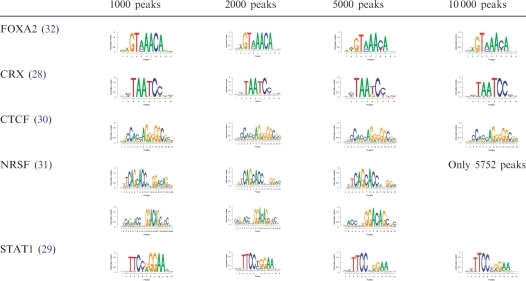Table 1.

Top five k-mers ranked by POSMO are related to the underlying transcription factor-DNA interaction

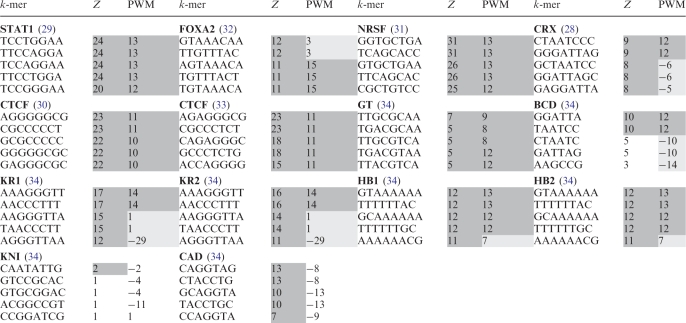Dark shaded cells represent either significant k-mers called by our POSMO algorithm (Z columns), or a k-mer with a significant PWM score (PWM columns; >µ + 3σ criterion over all 4 ^k k-mers). Light-gray shaded cells represent k-mers which are shifts of the genuine motif, thus having an insignificant PWM score. POSMO Z score is the average POSMO Z score of a k-mer and its reverse complementary k-mer. k-mers for each transcription factor are sorted according to POSMO Z score (Z columns).

We next asked whether POSMO could generally rank k-mers related to studied transcription factors on top. To accomplish this, we collected ChIP-seq data for CRX (28), CTCF (30), NRSF (31) and FOXA2 (32). As can be seen from Table 1 and Supplementary Table S1, POSMO successfully ranked the desired k-mers on top for all studied factors, indicating the effectiveness of our method in ranking functional k-mers for ChIP-seq data.

ChIP-chip on CTCF

We also asked if POSMO could process ChIP-chip data, which has less resolution than that of ChIP-seq data (2). For this purpose, we obtained the 13 720 peaks of CTCF binding determined using ChIP-chip (33). As shown in Table 1 and Supplementary Table S1, the top five 8-mers found by POSMO are all related to the CTCF binding motif. This result suggested that our method is applicable to ChIP-chip data.

ChIP-seq data from D

melanogaster. We next asked if our method could process ChIP-seq data from species other than human. To address this question, we obtained ChIP peaks for transcription factors BCD, HB1, HB2, CAD, KNI, GT, KR1 and KR2 of D. melanogaster (34). Table 1 and Supplementary S1 clearly show that POSMO is able to rank the target k-mers on top for GT, KR1, KR2, BCD, HB1 and HB2. POSMO failed to rank the known motif of CAD and KNI on top. However, we found that both MEME and DME also failed to discover the correct DNA motifs for CAD and KNI (Table 5 and Supplementary Table S2), indicating that the underlying nature of this data set may not permit us to find the desired motifs.

Table 5.

Performance comparison of POSMO, MEME, DME, ChIPMunk, HMS and DREME on ChIP data

Transcription factor	Rank by POSMO	Rank by MEME	Rank by DME	Rank by ChIPMunk	Rank by HMS	Rank by DREME
STAT1 (29)	1	1	1	1a	1	1
NRSF (31)	1, 2	1, 2	1, 2	1	1	1
CTCF (30)	1	1	1	1	1	1
CTCF (33)	1	3	1	1b	NA	1
FOXA2 (32)	1	1	1	1	1	1
CRX (28)	1	1	1	1	No match	1
BCD (34)	1	4	4	1	No match	2
CAD (34)	No match	No match	No match	No match	No match	No match
HB1 (34)	1	1	1	1	No match	2
HB2 (34)	1	1	1	1	No match	3
KR1 (34)	1	1	1	1	No match	3
KR2 (34)	1	1	1	1	No match	3
KNI (34)	No match	No match	No match	No match	No match	No match
GT (34)	1	3	7	1	No match	No match
c-MYC (35)	1	1	1	1	1	1
n-MYC (35)	1	1	1	1	1	1
CTCF (35)	1	1	1	1	No match	1
ESRRB (35)	1	1	1	1	1	1
STAT3 (35)	1	1	2	1	No match	1
OCT4 (35)	1	1	1	1	1	1
SOX2 (35)	1	1	1	1	1	3
KLF4 (35)	1	1	2	1	1	1
E2F1 (35)	No match	No match	No match	No match	No match	No match
TCFCP2L1 (35)	1	1	1	1	1	1
ZFX (35)	1	1	1	1	No match	1
NANOG (35)	1	1	1	1c	No match	1
SMAD1 (35)	1d	No match	No match	1	1	1
Total successes	24/27	23/27	23/27	24/27	12/26	23/27
Average rank	1	1.30	1.47	1	1	1.43

Among the Top 5 motifs found by MEME, DREME and DME, the rank (per P-values) of the known binding motif is listed. For NRSF, there are two known motifs and their ranks are counted separately. No match: the software did not report any motif similar to the known motif.

^aTop 3 peaks removed to get the correct motif.

^bTriangle intensity profile used.

^cMotif length of 20 used.

^d±200 bases flanking peak summit.

ChIP-seq data from core transcriptional networks in mouse ES cells

We also investigated the performance of our algorithm on the 13 sequence-specific transcription factors involved in the core transcriptional networks in mouse ES cells (35). As shown in Supplementary Table S1, POSMO successfully ranked the desired k-mers on top for 9 of the 13 factors (c-MYC, n-MYC, CTCF, ESRRB, KLF4, OCT4, SOX2, STAT3, ZFX and E2F1). Although the k-mer with highest PWM score is ranked 34th for TCFCP2L1, most of the top-ranked k-mers are just shift of the known motif (light gray cells in Supplementary Table S1). For E2F1, no motifs were found in the original work by Chen et al. (35). In Bailey (45), the top two motifs found for E2F1 are in the form of GGAA and ATGGCG. On the other hand, the top k-mers found by POSMO contain the sequence TTCCGG, which is partly similar to the in vitro E2F1 motif documented in JASPAR. As a confirmation, we found that our top k-mers, especially motif TTCCGG (Supplementary Table S1), also appeared in independent E2F1 ChIP-seq data (46). Interestingly, in this independent E2F1 ChIP-seq data (46), a motif TTGGCGC with rank 14 is partly similar to the E2F1 motif documented in JASPAR. For SMAD1, our algorithm did not find any significant motifs. However, POSMO identified a motif (Supplementary Table S2) weakly similar to the known SMAD1 motif when using ±200 bp flanking region of the peak summits, indicating that the length of flanking regions may be further optimized for POSMO.

In summary, the above results clearly indicated that POSMO is highly effective for both ChIP-chip and ChIP-seq data from human, mouse and other species, such as fly. In the next section, we will try to group these significant k-mers into PWM representation.

Word clustering on real data

Even though our POSMO software is generally able to rank the desired DNA k-mers on top, it is difficult to manually inspect them. Consequently, we next applied our novel word clustering algorithm on the sequence contexts of significant k-mers in the genome to obtain PWM representations (see ‘Materials and Methods’ section). As can be seen in Table 2, motifs reported for CTCF, STAT1, NRSF, CRX and FOXA2 by our word clustering method are highly similar to those reported in the literature.

Table 2.

Sequence motifs discovered by POSMO

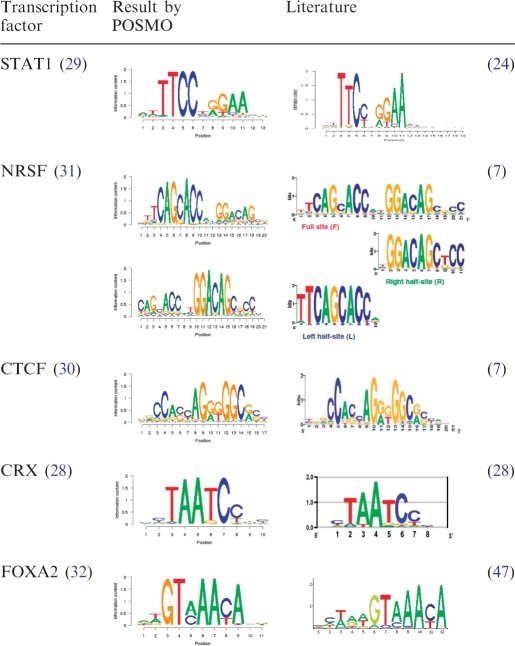The DNA motifs after word clustering are listed. As a comparison, the DNA motifs from the literature are also listed. For NRSF, two motifs are reported by POSMO, which correspond to the left and right half-sites reported by Hu et al. (24).

In the case of D. melanogaster, the motifs found by our method for BCD, HB1, HB2, KR1, KR2 and GT (Supplementary Table S2) are highly similar to the motifs cataloged in JASPAR. For transcription factor CAD and KNI, the known motif was not found by either our algorithm or other algorithms (Supplementary Table S2). Interestingly, for CAD, our algorithm reported a motif with consensus CAGGTA, which is implicated in the regulation of early transcribed genes during Drosophila development (48).

For the core transcription factors involved in mouse ES cells, motifs reported by POSMO are also highly similar to the known motifs for CTCF, n-MYC, c-MYC, STAT3, KLF4, SOX2, OCT4, ZFX, TCFCP2L1 and ESRRB (Supplementary Table S2). Similar to a recent study using an improved version of MEME by Bailey (45), our algorithm did not report any motif for SMAD1. However, POSMO identified a motif (Supplementary Table S2) weakly similar to the known SMAD1 motif when using ±1000 bp flanking region of the peak summits, indicating that the length of flanking regions may be further optimized for POSMO. The motif for E2F1 was not found by either Chen et al. (35) or other methods including POSMO. However, our algorithm found a motif with the pattern CCGGAAG (reverse complement is CTTCCGG; see Supplementary Table S5), which is partly similar to the known motif TTT[G/C][G/C]CGC documented in JASPAR. Interestingly, we note that CCGGAAG is highly similar to the binding motifs of ETS transcription factors (49), which might indicate the interaction between E2F1 and ETS transcription factors. Notably, this motif is also found in an independent E2F1 ChIP-seq data (46) (data now shown).

POSMO is robust to input parameters

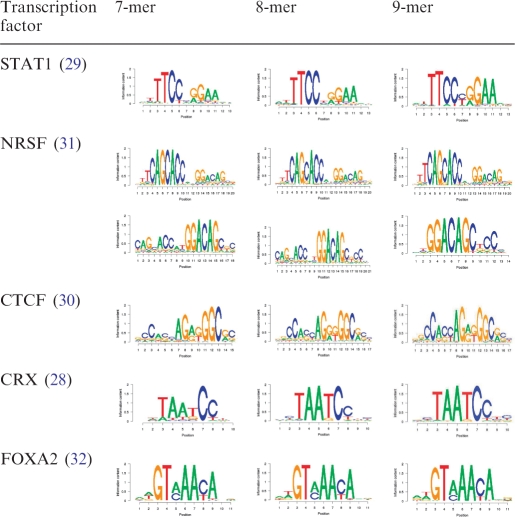
One general concern for motif finders using the k-mer enumeration method is the determination of k. We thus asked how k affects the performance of POSMO. For this purpose, we ran our POSMO algorithm for 7-, 8- and 9-mer on STAT1, NRSF, CTCF, CRX and FoxA2 data. As can be seen from Table 3, different k values do not greatly affect the obtained DNA motifs. Apparently, the closer the specified word pattern is to the truth, the better the results will be. Since it is difficult to know this parameter a priori, it may be helpful to try several parameters in real applications. However our results on long motifs of CTCF and NRSF suggest that in general we do not need very large k to discover long motifs. This is due to our heuristic word clustering method by considering context, as described in ‘Materials and Methods’ section.

Table 3.

Input pattern lengths of 7, 8 and 9 are compared (POSMO is robust to input parameter k)

We also asked how input parameters t_D and t_Z (see ‘Materials and Methods’ section) of POSMO could affect the performance of POSMO. We tried a series of parameters on t_D and t_Z and found that our method is not sensitive to them (Supplementary Table S3). Thus, this fact renders our method easy to use in practice.

POSMO performs well for large sample sizes

As discussed in Schmid and Bucher (26), the percentage of top peak sequences containing the known motif generally decreases as the threshold relaxes. Therefore, we asked how the total number of peak sequences would affect our motif finding results. We ranked the identified peaks for STAT1, CTCF, NRSF and FOXA2 according to the peak height, and we used the top 1000, 2000, 5000 and 10 000 peaks as input for POSMO. As can be seen in Table 4, POSMO is effective for all tested parameters. In particular, POSMO was found to be effective for input data sets containing 10 000 peaks for all studied transcription factors, suggesting the superior performance of POSMO for large sample sizes. Since ChIP-seq experiments typically produce thousands of peak sequences, we conclude that POSMO has broad applicability for ChIP experiments.

POSMO is more effective than available methods for ChIP data

We next compared the overall performance of POSMO with that of DME (41), MEME (8), ChIPMunk (25), HMS (24) and DREME (45) on motif discovery. For this purpose, we checked the rank of the known motifs among all discoveries in DME (5 motifs to be reported), MEME (only top 500 peaks are used as a result of running speed constraint and 5 motifs to be reported), ChIPMunk (1 motif to be reported), HMS (ChIP-seq intensity profile under the peaks were also compiled for applicable transcription factors), DREME and POSMO (details on the motifs found by each method can be found in Supplementary Table S2). For POSMO, our algorithm reported the total number of occurrences of each motif in the ChIP-seq/ChIP-chip data, which could be used to rank all the discovered motifs. As can be seen in Table 5, POSMO performs in a manner similar to DME, MEME and DREME, though with better average rank of the discovered motifs. Motifs discovered by POSMO are similar to that discovered by ChIPMunk. However, the top 3 extremely high scoring peaks must be removed for ChIPMunk to discover the correct motif for STAT1 (Table 5 and Supplementary Table S2). In addition, POSMO is better than HMS for fly transcription factors and several mammal transcription factors including CRX, STAT3 and ZFX, suggesting the high effectiveness of our method. POSMO did not find motif for SMAD1 using our default settings; however, we noted that POSMO correctly identified the motif for SMAD1 when shorter flanking regions (±200 bp) are used (Table 5 and Supplementary Table S2). This result suggests that flanking length may be further optimized for motif finding. Interestingly, the true motif found by POSMO is always ranked in first place, again indicating that PSOMO is more effective than other tools. This property is particularly useful to assign DNA motifs to a newly investigated transcription factor for which no prior motif information is available.

POSMO is more efficient than available methods

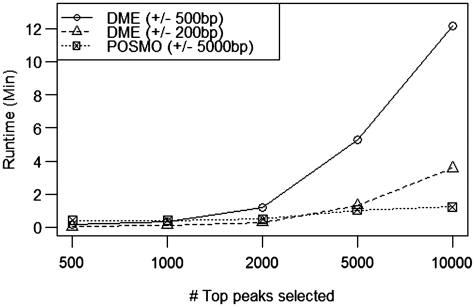
We also compared the running time of POSMO with other established methods. As established in Keilwagen et al. (23), DME by Smith et al. (41) is one of the fastest algorithms for large sample sizes. We therefore compared the running time of our method with that of DME using various numbers of peaks ranging from 500 to 10 000. As can be seen in Figure 1, our method is significantly faster than DME for large sample sizes, where the running time of our method scales linearly with the number of peak sequences, with a typical running time of only a few minutes. In addition, a comparison on the real ChIP data sets revealed that POSMO is significantly more efficient than ChIPMunk, HMS and DREME (Supplementary Table S4). Thus, we conclude that our method is highly efficient for motif discovery from large sample sizes of ChIP experiments. Clearly, the efficiency of our method will quickly decrease with large k. However, as was demonstrated in (50), 77% of the transcription factor binding motifs have <11 informative positions. Most importantly, as can be seen in Table 3, our method is robust to different ks for tested transcription factors. In particular, our method works well for CTCF and NRSF motif, which have a long motif >13 bp. This result indicates that we do not need a very large k to find a long motif, partly due to our heuristic word clustering method. Thus, the efficiency of our algorithm is generally guaranteed.

Figure 1.

POSMO is more efficient than DME for large sample sizes. Shown in the y-axis is the time spent for a given number of top peaks shown in the x-axis. Results for POSMO (dashed line with boxes) and DME (dashed line with triangles for a smaller peak window and solid line with circles for a larger peak window) are shown. Here k = 8 for both POSMO and MEME.

Co-motif finding

In principle, different DNA motifs may co-localize to perform regulatory functions by forming protein complexes. Therefore, it will be very interesting to see if we can discover co-motifs from such high-throughput ChIP-seq data. In fact, sophisticated method targeting this question is already proposed in SpaMo by Bailey and colleagues (51). Though our POSMO is not specifically designed for the purpose of finding co-motifs, we still asked if it can find some of the known co-motifs. For a few transcription factors such as STAT1, CRX, E2F1 and n-Myc (see Supplementary Table S5 for details), POSMO reported some of the known co-motifs as identified by Bailey and colleagues (51). Interestingly, POSMO found co-motif CAGGTA for many fly transcription factors. However, we note that our POSMO is not purposely designed to find co-motifs; therefore, POSMO reported much less co-motifs than SpaMo did. An extension of POSMO specifically designed to detect co-motifs is under development.

DISCUSSION

ChIP-seq/ChIP-chip is a popular experimental method to map in vivo binding sites of transcription factors. DNA motif discovery from such data is a necessary step toward understanding gene regulation. However, available motif finding tools are mostly designed to find DNA motifs in sequence segments by optimizing alignments, which renders the optimization process inefficient for large sample sizes. Recently, a few methods have been developed to utilize signal intensity to accelerate the discovery process. In this work, we have introduced a new k-mer enumeration method, POSMO, to predict transcription factor binding motifs. Using simulation, we found that our method is more robust against the information spread and systematic errors in peak locations than available methods in terms of ranking the target k-mer. The high prediction accuracy is further confirmed using a diverse set of real ChIP-seq/ChIP-chip data sets on human, mouse and fly. We also developed a novel word clustering algorithm by checking the sequence context of each significant k-mer. We found that our word clustering method can generate motif representation consistent with reports found in the literature. We found that motifs discovered by POSMO is consistent with that discovered by DME and MEME, though our method always gives the true motif highest rank in all tested data sets. This property could be very important when there is no prior knowledge on the binding motifs of a newly investigated transcription factor. Thus, our method is more effective for motif discovery.

On the other hand, since estimation of peak summits is more accurate than estimation of the exact ‘peak regions’ from ChIP-chip/ChIP-seq data, our method provides better usability. In addition, since POSMO essentially contrasts far flanking sequences with sequences under the peak summit, our method does not require explicit ‘background’ to normalize the k-mer appearance frequency, which is generally recommended for many motif discovery methods (i.e. to also construct background data set). This property also better mimics the biology of transcription factor-DNA interactions: instead of optimizing the binding affinity between the target DNA motif and many other genome-wide ‘background’ sequences, a transcription factor is actually searching the target DNA motifs from the pool of surrounding local DNA sequences. Our results suggested that these local sequences can be better approximated by flanking sequences of ChIP-peak regions than by other ‘control’ sequences.

Most importantly, since our method is essentially a k-mer enumeration method where hypothesis testing procedures are extensively used, it is very efficient, with a typical running time of only a few minutes for thousands, or even more, ChIP-seq peaks for word length <10. This is in clear contrast to most established methods, such as MEME, which utilize extensive optimization techniques that can take up to hours for a few hundred ChIP-seq peaks (7). Thus, we believe our method will be a useful alternative to quickly study the binding sites of transcription factors.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online: Supplementary Text 1, Supplementary Figures 1 and 2, Supplementary Tables 1–5.

FUNDING

National Institute of Health (HG001696 to M.Q.Z.); National Basic Research Program of China (2012CB316503 to M.Q.Z.); National Natural Science Foundation of China (91019016, 31061160497 to M.Q.Z.); National Science Foundation (DMS-1106091 to R.S.) and UTD Startup Fund (to Z.X.). Funding for open access charge: NIH.

Conflict of interest statement. None declared.