Predicting the strength of UP-elements and full-length E. coli σ^E promoters

Abstract

Predicting the location and strength of promoters from genomic sequence requires accurate sequenced-based promoter models. We present the first model of a full-length bacterial promoter, encompassing both upstream sequences (UP-elements) and core promoter modules, based on a set of 60 promoters dependent on σ^E, an alternative ECF-type σ factor. UP-element contribution, best described by the length and frequency of A- and T-tracts, in combination with a PWM-based core promoter model, accurately predicted promoter strength both in vivo and in vitro. This model also distinguished active from weak/inactive promoters. Systematic examination of promoter strength as a function of RNA polymerase (RNAP) concentration revealed that UP-element contribution varied with RNAP availability and that the σ^E regulon is comprised of two promoter types, one of which is active only at high concentrations of RNAP. Distinct promoter types may be a general mechanism for increasing the regulatory capacity of the ECF group of alternative σ's. Our findings provide important insights into the sequence requirements for the strength and function of full-length promoters and establish guidelines for promoter prediction and for forward engineering promoters of specific strengths.

INTRODUCTION

Bacterial genome sequences are being completed at an exponentially increasing rate but the ability to use these sequences as genomic blueprints requires accurate prediction of promoters and of their strength. Detecting the existence and elements of a promoter is a challenge because promoters are constructed of multiple poorly conserved motifs separated by variable length spacers. Moreover, once promoters are identified, it is challenging to predict their maximal initiation rates because transcription initiation is comprised of multiple kinetic steps including initial binding of RNA polymerase (RNAP) and subsequent ‘melting’ (strand-opening) of the DNA. Here, we develop the first sequence-based model of a full-length bacterial promoter, identify the key determinants of promoter sequence that correlate with promoter strength and use these features to establish a predictive model for promoter strength.

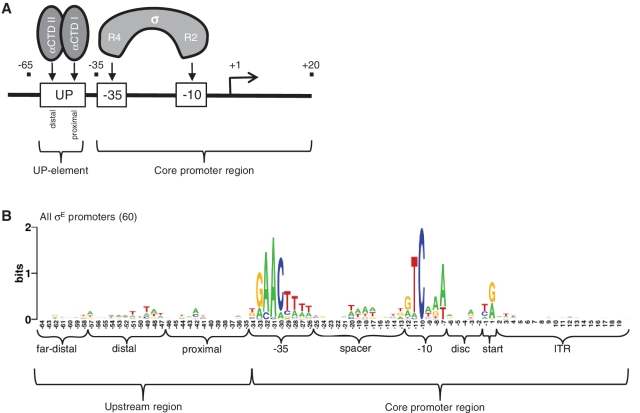
Bacterial promoters are comprised of a core promoter region recognized by σ, and an upstream region, termed the UP-element, recognized by the α subunits of RNAP (Figure 1A). With the exception of σ⁵⁴-dependent promoters, the core promoter region is comprised of the −35 and −10 motifs, located, respectively, at these distances upstream of the transcription start point. Each σ factor recognizes core promoter motifs with distinct sequences. Thus, specific promoter recognition is determined by the σ factor, which binds to RNAP to form holoenzyme and directs the complex to its target promoter sequences. The σ70 family of σ factors is comprised of four phylogenetically related groups (1). Group 1 is the housekeeping σs; these are essential and recognize thousands of promoters. Groups 2–4 are the alternative σs, which recognize discrete sets of promoters enabling specialized responses to environmental stresses and developmental cues. σs are modular proteins, comprised of a variable number of domains. The Group 4 or Extracytoplasmic function (ECF) σs have only 2-domains, one recognizing the −10 motif and the other recognizing the −35 motif (1). Importantly, these σs are the most abundant alternative σs and are involved in regulating a diverse repertoire of stress and developmental responses (2–4). Their promoters provide an ideal test-bed for constructing and improving promoter models, as they are simple and relatively well-conserved.

Figure 1.

Structure of bacterial promoters. (A) Schematic of RNA polymerase subunit interactions with promoter DNA indicating the promoter-specific interactions between the C-terminal domains of the 2 α subunits (αCTD I and II) with the proximal and distal subsites, respectively, of the UP-element (UP), and between Region 2 (R2) and Region 4 (R4) of the σ subunit with the −10 and −35 promoter motifs, respectively. Promoter is indicated by the solid line, motifs indicated by boxes, transcription start point by bent arrow and (+1). Distances upstream (−ve) and downstream (+ve) of the transcription start site in nt are indicated. The core promoter (−35 to +20) and UP-regions (−65 to −35) are indicated. (B) Sequence logo of library of 60 E. coli and Salmonella σ^E promoters used in this study. The different promoter regions used to construct the sequence models are indicated. Disc is discriminator; start includes the −1 and +1 position; ITR is initial transcribed region. The Far-distal site represents an upstream site transiently occupied by αCTD II at some promoters.

The UP-element increases promoter strength (5–8). It is composed of alternating A- and T-tracts (6,9–11) and has two subsites, each recognized by the C-terminal domain of one of the two α subunits of RNAP (αCTDs: αCTD I and αCTD II) (see Figure 1A) (6,9,10,12). Each αCTD binds the DNA minor groove via a helix-hairpin-helix motif; however, there are no direct sequence-specific contacts. Instead, the preference for A- and T-tract DNA reflects a structural property of these sequences: the narrower minor grooves of A-tract DNA facilitate optimal insertion of the R265 side chain of αCTD (13–15). The αCTDs are mobile, being connected to their N-terminal domain and hence the main body of RNAP via a flexible linker (16). While αCTD I is primarily located on the promoter-proximal subsite, which is centered near −43 and adjacent to the −35 motif enabling interaction with select σs (17–19), αCTD II is mobile. αCTD II not only binds predominantly to the promoter distal subsite centered near −53 (9), but can also transiently occupy multiple minor groove sites on the same face of the helix further upstream centered at positions −63, −73, −83 and/or −93 (20–22).

Position weight matrices (PWMs) are typically used to model and predict transcription factor binding sites and promoters; however, their predictions can suffer from many false positives (23,24). Previously, we tested the utility of PWMs to predict the strength of core promoter sequences (from −35 to +20) using a library of 60 promoters recognized by σ^E, an Escherichia coli ECF σ (25) and separate PWMs for each core promoter motif [−35 motif, spacer, −10 motif, discriminator, start and initial transcribed region (ITR); Figure 1B]. Our best model summed the PWM scores of select motifs that positively correlated with promoter strength (−35, −10, discriminator and start) and included a penalty term applied for non-optimal spacer and discriminator lengths. This demonstrates the utility of PWMs to predict the strength of core promoter sequences. In addition, applying minimal scores for each motif enabled successful discrimination between active and weak/inactive promoters, which is critical for accurate promoter prediction. In contrast, the contribution of UP-element sequences to promoter strength is not expected to be well-described by PWMs. Natural UP-elements display little position-specific sequence conservation (Figure 1B), and the known requirement of narrowed minor grooves for optimal α-binding, suggests a dependency between adjacent nucleotides. This state is not captured by PWMs, which assume that the binding energy contribution of each nucleotide position is independent and additive.

In this work, we successfully model UP-element contributions to promoter strength, developing a sequence-based model that captures both the structural features of the DNA subsites and the multiple binding locations of α. We demonstrate that the UP-element model can be combined with our core promoter model (25) to generate the first model that accurately identifies full-length promoters and estimates their strength. We also find that the contribution of the UP-elements to promoter strength depends both on RNAP levels and properties of the core promoter. Since ECF σ promoters are predominantly regulated by the availability of their active cognate σ, and hence by the availability of σ-specific RNAP holoenzyme, this finding has significant implications for understanding the regulation of ECF σ promoters in vivo. Our work suggests strategies for improving the accuracy of full-length promoter prediction and for forward engineering promoters of specific strengths for use in synthetic biology.

MATERIALS AND METHODS

Strains, plasmids and growth conditions

All strains were grown in M9 complete minimal medium supplemented with appropriate antibiotics at 30°C with shaking. M9 complete minimal medium was prepared as described (26) supplemented with 0.2% glucose, 1 mM MgSO₄, vitamins and all amino acids (40 μg/ml). Media was supplemented with 30 μg/ml kanamycin and/or 100 μg/ml ampicillin as required. All assay strains are derivatives of E. coli K−12 strain MG1655 (27) and MC1061 (28) and are listed in Supplementary Supplementary Table S1. Assays with basal levels of σ^E were performed in derivatives of CAG45113 (MG1655) transformed with derivatives of the GFP expression vector, pUA66 (29), carrying the long and short σ^E promoter libraries (8) (Supplementary Table S1). Assays with over-expression of σ^E were performed in derivatives of CAG58200 (MG1655 ΔlacX74 [ΦλrpoHP3::lacZ]) carrying the plasmid pLC245 (23) expressing rpoE from the IPTG inducible Ptrc promoter, and pUA66 carrying the long and short σ^E promoter libraries (8) (Supplementary Table S1). σ^E-independent promoter activities were determined in derivatives of CAG22216 (MC1061 ΔlacX74 [ΦλrpoHP3::lacZ] rpoE::ΩCm (30) carrying the long and short σ^E promoter libraries (8) (Supplementary Table S1).

All σ^E promoter constructs were carried on the low copy vector, pUA66, driving the expression of GFP from the reporter gene gfpmut2, and were constructed as described in (8). Briefly, full-length (long) promoter sequences from −65 to +20 with respect to the transcription start site were cloned into the XhoI–BamHI sites of pUA66, creating derivatives pUA66 E1-E60 (Supplementary Table S1). The core (short) promoter library contained sequences from the −35 motif to +20 cloned in XhoI–BamHI of pUA66, creating derivatives pUA66 Et1-Et60 (Supplementary Table S1). Note that due to variable spacer lengths between the promoter motifs, the cloned upstream position was always taken as the first G of the GGAACTT −35 motif, thereby all core promoter sequences contain a full-length −35 motif with no additional upstream sequences.

In vivo promoter assays

All in vivo promoter assays were performed as described in ref. (8) with the exception that strains were grown in M9 complete minimal medium instead of LB. The lower autofluorescence of M9 medium compared to LB permits more accurate quantification of GFP and hence promoter activity under basal σ^E levels. Strain derivatives of CAG45113 and CAG22216 were grown at 30°C for measurements of promoter strength when σ^E is expressed at the basal level or in the absence of σ^E (these latter strains have a suppressor of σ^E essentiality to permit their growth); CAG58200 derivatives were supplemented with 100 µM IPTG to induce rpoE expression for measurements of promoter strength under high (over-expression) levels of σ^E. Briefly, overnight cultures of the strains in 96-well microplates were diluted 200-fold to an OD₄₅₀ ∼0.03 in fresh medium ±100 µM IPTG for CAG58200 derivatives. Strains in the covered 96-well microplates were incubated in a multimode microplate reader-incubater shaker (Varioskan; Thermo Fisher Scientific), and measurement of optical density (OD_{450 nm}) and fluorescence (relative fluorescence units or RFU; excitation = 481 nm; emission = 507 nm) was performed every 15 min. Promoter strength was taken as the slope of the change in GFP fluorescence as a function of cell growth during exponential growth phase (OD₄₅₀ = 0.2−0.45) as described in ref. (8).

Promoter templates for in vitro transcription

Linear promoter fragments for in vitro transcription assays were generated by PCR from the pUA66 E1-E60 and pUA66 Et1-Et60 plasmid templates (Supplementary Table S1) as described in (25) (primer sequences available on request). Briefly, promoter fragments were generated from the plasmid templates using upstream primers and a downstream primer that incorporates the highly efficient rpoC terminator sequence (31). This generated promoter fragments from −203 to +145 containing vector sequence upstream and vector sequence + rpoC terminator sequence downstream of promoter sequences −65 to +20 for full-length promoters and −35 to +20 for core promoters (Supplementary Figure S1A, B). Both promoter libraries generate a 118 nt mRNA transcript. The competitor promoter fragment contained PrpoH core promoter and generates a 149 nt mRNA transcript (Supplementary Figure S1C) (25).

Purification of RNA polymerase core enzyme and σ^E

RNA polymerase core enzyme was purified as described in ref. (32). N-terminally His₆-tagged σ^E was purified as described in ref. (33) from soluble cell lysates of strain BL21λDE3 (pLysS, pRER76) with the following modifications: A 500 ml culture of BL21λDE3 (pLysS, pRER76) was grown at 25°C in LB + 100 µg/ml ampicillin and 50 µg/ml chloramphenicol until OD₆₀₀ = 0.5. The culture was supplemented with an additional 100 µg/ml ampicillin and induced with 1 mM IPTG for 2 h with shaking at 25°C. Cells were harvested by centrifugation and resuspended in 10 ml Lysis Buffer (50 mM NaH₂PO₄(H₂O) pH 8.0, 500 mM NaCl, 10% w/v glycerol, 10 mM imidazole). Cells were lysed by sonication and the lysate centrifuged at 10 000g for 10 min at 4°C. The majority of σ^E was present in the soluble fraction and was purified using a QIAGEN Ni²⁺ affinity column under native conditions as per manufacturer's instructions (Valencia, CA, USA). Our modified lysis buffer was used in the loading and wash steps (+20 mM Imidazole), and σ^E was eluted using modified elution buffer [50 mM NaH₂PO₄(H₂O) pH 8.0, 500 mM NaCl, 10% w/v glycerol] with a stepwise imidazole gradient from 20 to 200 mM in 20 mM increments. σ^E eluted between 60 and 100 mM imidazole and was essentially pure. The σ^E containing fractions were pooled and dialyzed into storage buffer [20 mM Tris–HCl (pH 7.9 at 4°C), 500 mM NaCl, 1 mM EDTA, 50% w/v glycerol, 1 mM DTT] and then stored at −80°C.

In vitro transcription assays

Multi-round transcription assays were used to measure promoter strength (rate of mRNA production) and were performed in triplicate with 10 and 50 nM RNAP. To facilitate accurate determination of promoter strength, the assays were modified in four ways: (i) Inclusion of the highly efficient rpoC terminator at the end of the promoter templates ensured specific transcript termination, rather than termination by RNA polymerase ‘running’ off the end of the template. This gave a 5-fold increase in specific transcript signal strength (25). (ii) With test promoters, transcript generation during incubation with RNA polymerase was carefully evaluated to ensure proper ‘multi-rounds’ and that there was no depletion of NTPs (data not shown). (iii) To facilitate rapid analysis of large numbers of promoters, assays were performed ‘high-throughput’ in 96-well plates and loaded on a standard S2 sequencing gel poured with 32-well combs using a standard 12-channel multichannel pipette. (iv) Inclusion of a control promoter in each assay enabled the test promoter transcript to be normalized against the control promoter to account for variations in RNA polymerase activity and gel loading, enabling comparison of test promoter activities. The transcription reactions (6 µl) contained 0.5 nM test promoter and 0.5 nM competitor promoter DNA, 5–50 nM core RNA polymerase with 2-fold excess σ^E in 1× Binding Buffer (5% glycerol, 20 mM Tris pH 8.0, 300 mM KAc, 5 mM MgAc, 0.1 mM EDTA, 1 mM DTT, 50 µg/ml BSA, 0.05% Tween), 150 µM GTP/ATP/UTP, 10 µM CTP, 0.5 µCi α³²P-CTP (3000 Ci/mmol; 110 TBq/mmol) and incubated at 37°C for 10 min. Reactions were terminated by addition of 4.5 µl Stop Solution (20 mM EDTA, 80% deionized formamide and 0.1% [w/v] bromophenol blue and xylene cyanol). Transcripts were resolved on a 6% denaturing polyacrylamide sequencing gel (see example in Supplementary Figure S1D), visualized using a Molecular Dynamics Storm 560 Phosphorimager scanning system (Sunnyvale, CA, USA), and quantified using the software ImageQuant v5.2 (G.E. Healthcare Life Sciences). For each assay, promoter strength = (test promoter–background)/(control promoter–background).

Promoter strengths and UP-effects used for modeling

All σ^E-dependent and independent promoter strengths (background subtracted) determined in vivo and in vitro together with their calculated UP-effects are presented in Supplementary Table S2. UP-effects were calculated as log₂([full-length promoter activity]/[core promoter activity]). To prevent extreme UP-effect ratios generated from very weak promoter activities, promoter strengths <2-fold of the background were reset to 2-fold above background. For example, all in vivo promoter activities less than 2 were reset to 2; all in vitro promoter activities less than 0.05 were reset to 0.05. Full-length promoter models were constructed using active full-length promoters defined as 2-fold above background, with the exception of in vivo basal promoter activities. Here, a lower cutoff was used (>1.5) to increase the number of active promoters in the model from 15 to 18. The active in vivo basal full-length promoter set excluded three promoters that exhibited significant σ^E-independent activity (plsB, yfjO, yecI; Supplementary Table S2). YbcR was also excluded from the basal in vivo active dataset since it was unusually active in this and no other condition (in vitro or in vivo; Supplementary Table S2). Although ybcR exhibited negligible σ^E-independent activity in M9 medium, significant independent activity was observed in LB (8), suggesting additional or spurious regulation of this promoter.

Scoring promoter sequences

Sequence logos of aligned promoter motifs were generated using WebLogo v2.8 [http://weblogo.berkeley.edu//; (34)]. Position weight matrices were constructed using the method of (35) with aligned sequences for each motif. Core promoter motifs (−35, spacer, −10, discriminator, start and initial transcribed region; see Figure 1B and sequences listed in Supplementary Table S3) were defined and scored using PWMs as described in (25). A combined spacer and discriminator length penalty score (S + D pen) was applied to promoters with suboptimal spacing between the +1, −10 and −35 motifs based on the observed spacing frequency for σ^E promoters (Figure S3) as described in (25). A core promoter score, C, was derived by summing select motif PWMs and S + D pen scores. Upstream sequences (listed in Supplementary Table S3) were scored as described in Supplementary Figure S2 to derive an upstream score, U.

Total promoter score was taken as the sum of the core and upstream scores: S_p = U + C. This assumes that upstream and core promoter scores have equal weight to total promoter score. However, given that the core scores (C) are based on PWMs and that the upstream scores (U) are A- and T-tract counts of length or frequency, this may not be the case. Accordingly, Partial Least Squares Regression (PLSR) (36) was used to solve for the upstream and core model coefficients as described in (25) using the model: S_p = x_U.U + x_C.C; where x_U and x_C are x-value coefficients applied to promoter model scores, U and C. The model was solved using a matrix of y-values (S_p) and x-variables (U and C) with the software package ‘The Unscrambler v9.8’ (CAMO Software AS, Norway; http://www.camo.no).

Promoter score, S_p, was taken to be proportional to the log of promoter strength, 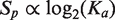, where K_a is occupancy or promoter strength (37). The fit of S_p with log₂(K_a) was assessed by Pearson's correlation coefficient (R) and significance (p) determined using a two-tailed test (http://www.danielsoper.com/statcalc3). Similar assumptions were applied to the correlation of upstream scores (U) with UP-effect, E, (E = (log₂([full-length promoter activity]/[core promoter activity])) to give 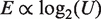. Outliers in the correlation of promoter score (S_p) with strength (K_a) were identified as having both high residual y-variance and high leverage values using the software ‘The Unscrambler v9.8’. Promoter models were tested for over-fitting using 10-fold cross-validation as described in ref. (25).

RESULTS

Quantifying the effects of upstream sequences on promoter strength

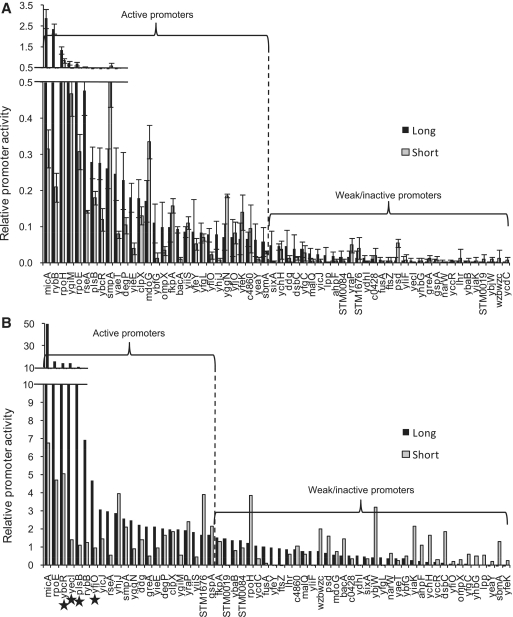
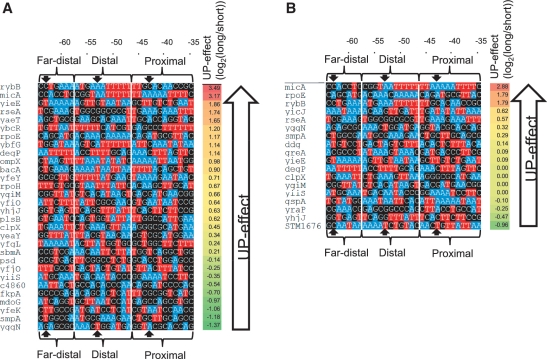
We determined the contribution of upstream sequences to promoter strength (UP-effect) using our previously characterized library of 60 natural σ^E-dependent promoters from E. coli and Salmonella enterica (Figure 2, Supplementary Table S1) (8,25). The UP-effect is calculated as the log₂ ratio of the activity of the full-length promoter, containing sequences from −65 to +20, as compared to its core promoter derivative, containing sequences from −35 to +20 and an upstream sequence derived from a common vector sequence (Supplementary Figure S1A and B). Promoter strength was measured both in vitro (Figure 2A) and in vivo (Figure 2B) under limiting σ^E-RNAP, which mimics the basal expression levels of the σ^E system. In vitro measurements utilized competitive multi-round transcription assays with limiting amounts of RNAP. Each reaction contained two promoter templates on separate linear fragments: a strong competitor promoter and a test promoter (Figure S1; also see Materials and Methods). In vivo assays used promoters expressing a GFP reporter in cells expressing basal levels of σ^E, performed as described previously (8), except that cells were grown in M9-glucose medium to reduce autofluorescence and enable more accurate measurement of low σ^E activity. We define active promoters as those with activity ≥ 2-fold above background. Under our stringent assay conditions with low σ^E levels, 30 out of the 60 promoters tested were active in vitro, and a largely overlapping set of 22 promoters were active in vivo. Four of the promoters active in vivo were excluded from subsequent analysis because they exhibited σ^E independent activity, limiting the in vivo set to 18 promoters (see ‘Materials and Methods’ section; Supplementary Table S2). Promoter models were constructed from the active promoters. Calculation of the UP-effect (log₂[full-length promoter activity / core promoter activity]) revealed a range of positive and negative effects on activity of the core promoter in vitro (Figure 3A) and in vivo (Figure 3B). Positive UP-effects were associated with A- and T-tracts indicative of UP-elements, and UP-effects were usually greater in vitro than in vivo.

Figure 2.

Relative activities of the full-length and core promoter libraries in vitro and in vivo. Promoter activities as determined by in vitro multi-round transcriptions with 10 nM RNAP (A) or in vivo gfp fluorescent assays in strains expressing basal levels of σ^E during exponential growth (B). Activities of both full-length (long; −65 to +20) and core (short; −35 to +20) promoter derivatives are indicated. Relative promoter activities represent promoter strength: in (A) quantified transcripts in vitro from the test promoter normalized against transcripts from the control rpoHP3 promoter; in (B), arbitrary fluorescence of promoter::gfp fusion measured in vivo (see ‘Materials and Methods’ section). Active promoters are indicated for both data sets (defined as long promoter activities >2-fold above background). Promoters marked with a star have high σ^E-independent activities in vivo and were excluded from the in vivo active promoter set. Each bar indicates the average of three independent experiments (A); error bars represent 1 SD.

Figure 3.

Upstream sequences of active in vitro and in vivo promoters. Color-coded sequence map to illustrate A- and T-tracts of upstream regions (−64 to −35) of 30 promoters active in vitro with 10 nM RNAP (A) and 18 promoters active in vivo with basal levels of σ^E during exponential growth (B): Nucleotides adenosine are colored blue, thymine red and guanine/cytosine black. Far-distal, distal and proximal α-subsites are indicated; block arrows mark the center of α binding sites at −43, −53 and −63. Promoters are ordered by magnitude of UP-effect; ranked strongest to weakest UP-effect from top to bottom within each group. UP-effect of each promoter is indicated (UP-effect = log₂([full-length promoter activity]/[core promoter activity])).

Modeling the UP-effect

We divided the upstream regions of promoters into three putative α-binding subsites: proximal (−46 to −35), distal (−57 to −47) and far−distal (−58 to −64) (illustrated in Figures 1 and 3). We tested whether various models were successful, based on the correlation (R) of subsite scores predicted by the model with UP-effect (Table 1). Using aligned upstream sequences, we first tested PWM models (Table 1). As expected, PWMs performed poorly, even with over-represented motifs identified within each subsite using MEME or WCONSENSUS, or by incorporating adjacent nucleotide dependencies using dinucleotide PWMs (data not shown). The promoter library is too small for statistically meaningful analysis of trinucleotide models. Together these results suggest higher order dependencies are required for UP-element function.

Table 1.

Correlation of subsite scores with UP-effect

Promoter model	Correlation (R) of model score with UP-effecta
	Subsite score correlations			Combined subsite score correlations
	Far-distal	Distal	Proximal	FD + Db	D + Pc	All 3d
In vitro multi-rounds at 10 nM RNAP (30 promoters)
PWM	−0.02	0.43*	0.16		0.48**	0.33
Percentage AT content	0.18	0.32	0.51**	0.37	0.55**	0.54**
A-tract/T-tract counts (3 nt)	0.23	0.57**	0.43*	0.68****	0.66****	0.74****
A-tract/T-tract length	−0.19	0.56**	0.17	0.34	0.55**	0.38*
A-tract/T-tract length ± 1 nt	−0.01	0.56**	0.28	0.42	0.57**	0.48**
In vivo at basal levels of σE (18 promoters)e
PWM	−0.47*	0.25	0.16		0.26	−0.08
Percentage AT content	−0.29	0.24	0.10	0.01	0.19	0.07
A-tract/T-tract counts (3 nt)	−0.08	0.62*	0.44	0.38	0.78***	0.66*
A-tract/T-tract length	−0.06	0.49*	0.36	0.36	0.55*	0.46
A-tract/T-tract length ± 1 nt	−0.27	0.47*	0.34	0.17	0.53*	0.29
Cluster 1 at 10 nM RNAP (20 promoters)
PWM	−0.46*	0.26	−0.16		0.12	−0.25
Percentage AT content	−0.24	0.31	0.33	0.14	0.42	0.29
A-tract/T-tract counts (3 nt)	0.12	0.64**	0.49*	0.57**	0.78****	0.74***
A-tract/T-tract length	−0.27	0.62**	0.32	0.34	0.66**	0.46*
A-tract/T-tract length ± 1 nt	−0.28	0.60**	0.38	0.33	0.65**	0.43
Cluster 2 at 50 nM RNAP (9 promoters)
PWM	−0.05	−0.23	0.03		−0.13	−0.17
Percentage AT content	0.47	0.49	0.23	0.71*	0.49	0.57
A-tract/T-tract counts (3 nt)	0.84**	0.03	0.29	0.34	0.26	0.46
A-tract/T-tract length	0.13	−0.32	−0.35	−0.21	−0.38	−0.30
A-tract/T-tract length ± 1 nt	0.49	−0.27	−0.13	0.18	−0.26	0.09

^aThe highest subsite or combined subsite model correlation for each promoter group is indicated in bold. Significant correlations (R) by two-tailed test are indicated: p < 0.05*; p < 0.01**; p < 0.001***; p < 0.0001****. ^bCombined Far-Distal + Distal model subsites. ^cCombined Distal + Proximal model subsites. ^dCombined Far-Distal + Distal + Proximal model subsites. ^eActive basal promoters in cluster 1: degP, ddg, rpoE, rseA, ygiM, yraP, rybB, STM1676, micA; and in cluster 2: yicJ.

We then built models for each subset based on known features of UP-elements (A/T content, A- and T-tract length/frequency) (Table 1; see Figure S2 for model descriptions). Our best model counted the number of overlapping A- and T-tracts 3 nt in length. This model is based on the finding that near maximal narrowing of the minor groove is achieved after a run of three A residues (15). The highest correlation with in vitro UP-effects counted the number of overlapping 3 nt A- and T-tracts (e.g. 1,2 or 3) across all three subsites (R = 0.74; p = 3×10⁻⁶), while the highest correlation in vivo was achieved by combining counts of overlapping 3 nt A- and T-tracts in just the distal and proximal subsites (R = 0.78; p = 1×10⁻⁴). A more complex model mimicked the features of A- and T-tract distribution observed at strong UP-elements (9,10). Here, the far-distal and distal subsites were scored by the length of contiguous A-tract followed by T-tract that overlapped the center of the α-binding sites (i.e. the number of nucleotides), and the proximal subsite was scored by the length of A- or T-tract that overlapped the center of the proximal α-binding site (Supplementary Figure S2). Overall, this model performed slightly less well than the simpler overlapping 3 nt A- and T-tract counts (Table 1). To test the importance of exact placement of the A- and T-tracts, a variation of the A- and T-tract length model was used in which the tracts only had to be within 1 nt of the center of the α-binding sites. This gave little difference in score correlations, suggesting that close proximity of A- and T-tracts to the binding sites is sufficient to capture UP-effects (Table 1). We also tested the correlation of A/T content with UP-effect (Table 1). This yielded only slightly weaker correlations in vitro, but for the in vivo promoters this approach performed poorly, suggesting that both A- and T-tract length and number provide more information than simple A/T content. In summary, the success of overlapping 3 nt A- and T-tract counts strongly indicates the importance of minor groove width for UP-effect. Interestingly, the distal and proximal subsites scores generated the strongest correlations across all models, suggesting that these subsites are the main contributors to the UP-effect.

Modeling full-length promoters

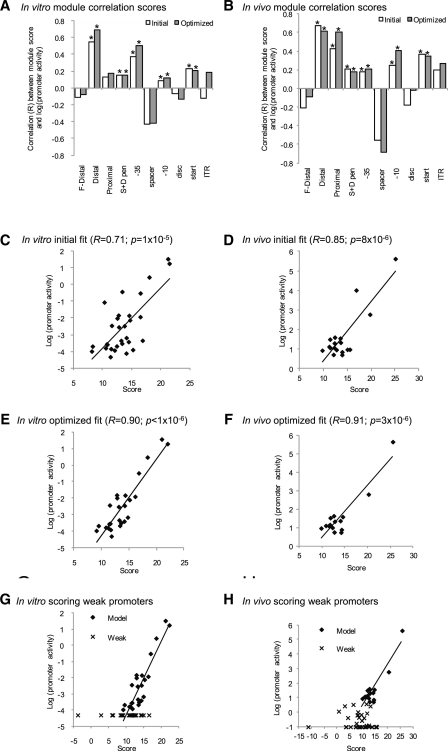
We derived a model describing the strength of full-length promoters by first determining which UP-effect model provided the best correlation with full-length promoter strength and then combining this model with the core promoter model. In the in vivo case, the UP effect model that correlated best with full length promoter strength in vivo was the same model that best described UP-effects alone (proximal and distal overlapping 3 nt A- and T-tract counts, Table 1). For in vitro measurements, the distal site A-tract/T-tract length (±1 nt) model correlated best with full length promoter strength; we note that this was one of the top subsite models that best described the UP-effects (Table 1). The core promoter model (25) (see ‘Materials and Methods’ section) was based on PWMs constructed for each core promoter motif (Figure 1B) and a penalty term applied for non-optimal spacer and discriminator lengths (S + D penalty, see Supplementary Figure S3). Figure 4A and B illustrates the initial correlation of each UP and core promoter module with full-length promoter strength for both in vitro and in vivo data. Most module scores positively correlate with promoter strength, except the far-distal UP-subsite, and the spacer and discriminator motifs. The best full-length promoter models were constructed by summing the scores of select modules that positively correlated with promoter strength (indicated with asterisks in Figure 4A and B). This generated good correlation of promoter score with promoter strength both in vitro, R = 0.71 (p = 1×10⁻⁵; Figure 4C) and in vivo, R = 0.85 (p = 8×10⁻⁶; Figure 4D) (summarized in Table 2). All other module combinations and models resulted in lower correlations (data not shown). These initial models were optimized based on the assumption that a small number of promoters may have unusual sequence properties that detract from the model and therefore present as outliers in the correlation of score with promoter strength. Five outliers from the in vitro promoter model and three from the in vivo model were detected and removed based on their high residuals and leverage properties on the general fit of the model. Subsequent analysis revealed that outliers generally have at least one unusually low scoring module, validating the idea that their properties differ from the other promoters (see Discussion). The remaining promoters were used to construct optimized models using the same selection of modules as in the initial models (see optimized modules, Figure 4A and B), resulting in an improved fit of R = 0.90 (p < 1×10⁻⁶) (in vitro) and a slightly improved fit of R = 0.91 (p = 3×10⁻⁶) in vivo (Table 2; Figure 4E and F). Each optimized full-length model was tested for over-fitting using 10-fold cross-validation. The validated promoter scores still correlated well with promoter strength (R = 0.81 and 0.86 for in vitro and in vivo, respectively; Table 2; Figure S4), demonstrating that each model has good predictive utility. As the full-length in vitro and in vivo promoter models combine different scoring systems for the UP and core models, we explored whether using partial least squares regression (PLSR; see ‘Materials and Methods’ section) (36) to calculate optimal coefficients to scale their contributions improved fit. Although this procedure increased fit, cross-validation of these models resulted in lower validation scores compared to models with no coefficients, suggestive of over-fitting (data not shown). Therefore, our final models do not have coefficients to scale contributions of UP and core promoter modules.

Figure 4.

Promoter models of active in vitro and in vivo promoters. (A and B) Correlation (R) of promoter module scores with promoter strength: (A) in vitro 30 active promoters; (B) in vivo 18 active promoters. Each bar graph illustrates module correlations for initial and optimized promoter models. Promoter modules are indicated below the horizontal axis. F-Distal, Distal and Proximal are the three UP-element subsites scored using the UP-element models; −35, −10, disc [discriminator], start [+1] and ITR [initial transcribed region] are the core promoter motifs scored using PWMs; S + D pen is the spacer + discriminator penalty term for suboptimal spacing between the −35,−10 and start motifs (see ‘Materials and Methods’ section). Bars with an asterisk above indicate modules summed to generate full-length promoter score for both the initial and optimized promoter models. (C–H) Fits of full-length promoter scores with promoter strength either in vitro (C, E and G) or in vivo (D, F and H). R denotes correlation coefficient; p denotes significance as determined by two-tailed test. (C and D) Initial model fits. (E and F) Optimized model fits after removal of outliers and models rebuilt. (G and H) Fit of optimized model scores against strength of all 60 promoters, active (Model; diamonds) and weak/inactive (Weak, crosses) promoters. The trend line for each model is based on fits with the active (Model) promoters.

Table 2.

Correlation (R) and significance (p) of full-length promoter strength with promoter model score

Data set	Correlation (R) between promoter strength and total promoter scorea			Correlation (R) between promoter strength and optimized sub-model score		Outliers
	Initb	Optc	Vald	UP model	Core modele
MR 10 nM RNAPf	0.71 (p = 1×10−5)	0.90 (p < 1×10−8)	0.81 (p = 9×10−7)	0.69g (p = 1×10−4)	0.64 (p = 6×10−4)	ygiM, rseA, ompX, yfeK, sbmA
In vivo basalh	0.85 (p = 8×10−6)	0.91 (p = 3×10−6)	0.86 (p = 4×10−5)	0.88i (p = 2×10−5)	0.74 (p = 2×10−3)	degP, clpX, rpoE

^aCorrelation between promoter strength and total promoter score generated by summing UP and core model scores. ^bInitial fit. ^cOptimized fit after removal of outliers and rebuilding model. ^dValidated promoter scores fit, ^eCore model: S + D pen + PWM₋₃₅ + PWM₋₁₀ + PWM_start. ^fIn vitro promoter activities using 30 active promoters (Figure 2A). ^gUP model: distal subsite A-tract/T-tract length (±1 nt) scores. ^hIn vivo promoter activities using 18 active promoters (Figure 2B). ⁱUP model: distal + proximal A-tract/T-tract counts (3 nt).

^hIn vivo promoter activities using 18 active promoters (Figure 2B),

Accurate promoter prediction requires correct identification of functional promoters with few false positives from similar, but non-functional sequences. Our datasets of active and inactive promoters (Figure 2) are ideal to identify features that distinguish active promoters. We previously showed that effective discrimination between active and inactive core promoters required a minimum threshold score for each motif based on the lowest score of that motif in the active promoter set (25). This rule also distinguishes active and inactive full-length promoters. Active and inactive full-length promoters have similar sequence logos (Supplementary Figure S5), and applying our full-length models to score the inactive promoters poorly distinguished between active and inactive promoters (Figure 4G and H). This demonstrates that overall sequence conservation is a poor indicator of promoter function. However, applying minimum module score thresholds for each motif based on the lowest score of that motif in the active promoter set successfully identified 77% of all inactive promoters in vitro and 95% of inactive promoters in vivo (Table 3; Supplementary Figure S6). The combined −10/−35 PWM scores identified the largest number of inactive promoters with 57% in vitro and 78% in vivo scoring below threshold, and in addition the discriminator and ITR motifs scored below threshold in many inactive promoters (Table 3; Supplementary Figure S6). These results show that individual core motif cutoff thresholds are required to accurately distinguish inactive full-length promoters, demonstrating the essentiality of these modules for promoter function. In contrast, the UP models did not distinguish any inactive promoters. This is because several active promoters had no score for their upstream sequences, demonstrating that UP-elements are not essential for promoter function.

Table 3.

Inactive promoters scoring below module cut-off thresholds

Data set	Number of inactive promoters	Percentage of inactive promoters scoring below module cut-off thresholds
		S + D pen	−35	Spacer	−10	Disc	Start	ITR	−10/−35a	Full-length scoreb	All modulesc
MR 10 nM RNAP	30	3	33	7	10	13	7	27	57	33	77
In vivo basal	37	3	54	3	22	24	0	51	78	59	95

^aCombined −10 and −35 PWM score threshold. ^bFull-length model score threshold comprised of core and UP models. ^cCumulative effect of applying all module cut-off thresholds.

Promoter strength at different concentrations of RNAP

Strong UP-elements contribute to promoter strength predominantly by enhancing the binding of RNAP (7,38), suggesting that their relative contribution will decrease as RNAP availability increases. This is a particularly important consideration for ECF σs, where regulation is based on increasing the free pool of σ by releasing this σ from its inhibitory interaction with its cognate anti-σ, enabling formation of the transcriptionally active σ-specific RNAP holoenzyme (2,3). However, there has been no systematic analysis of the behavior of ECF σ regulon promoters as a function of σ-specific RNAP levels. Here, we used our σ^E promoter library and promoter models to examine the effects of σ^E-RNAP levels on promoter activity and also to determine how the UP-effect alters as a function of RNAP concentration.

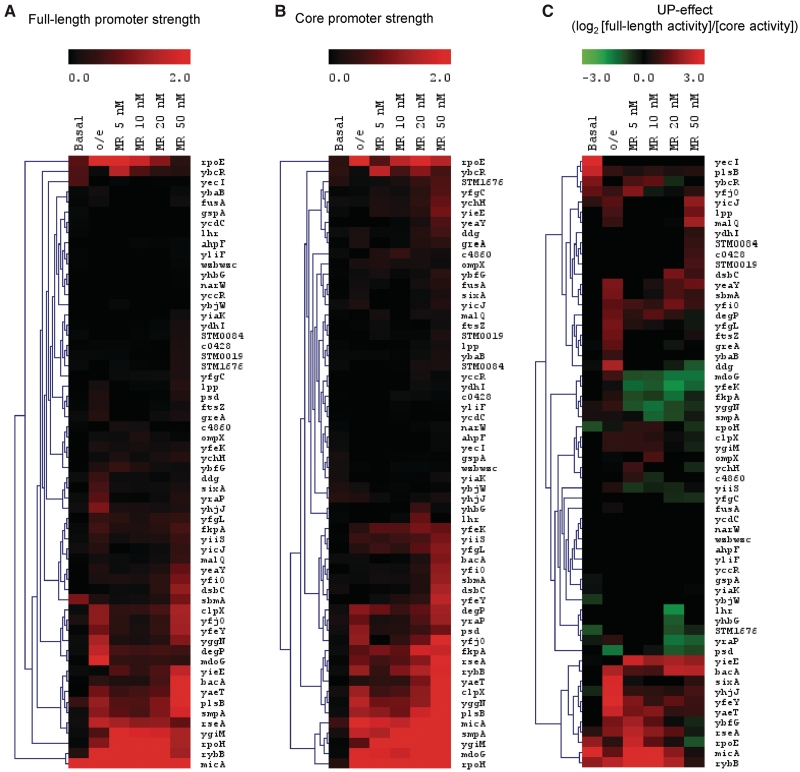
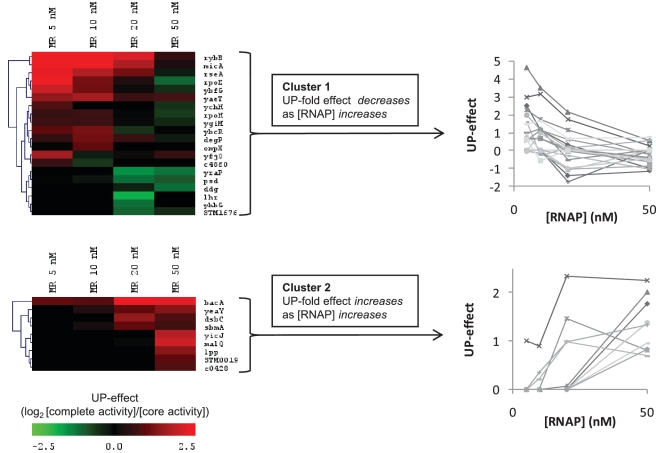
The activity of full-length and core promoters across a range of σ^E-RNAP levels is displayed as a heat map (Figure 5A and B). The first two columns indicate promoter behavior in vivo for cells expressing basal (low) σ^E as compared to those overexpressing σ^E. The other columns indicate effects in vitro using a multi-round assay with a competitor promoter template (PrpoH) across a range of RNAP concentrations (5–50 nM; see ‘Materials and Methods’ section) to mimic promoter competition in vivo. The data are clustered across the different conditions to identify promoters that respond similarly to increasing concentrations of holoenzyme. As expected, the number of active promoters increased with σ^E-RNAP levels. The UP-effects of the promoters across the different conditions are similarly displayed in Figure 5C. Notably, the UP-effects were highly variable across the different conditions, suggesting a complex response to RNAP levels. Because the in vitro assays are more controlled than those performed in vivo, they may enable us to identify the origin of these variable effects. We performed hierarchical clustering (see ‘Materials and Methods’ section) to identify groups of promoters with similar patterns of activity based on the in vitro competitive multi-round data. Two discrete clusters were identified: Cluster 1, in which the UP-effect decreased as RNAP concentration increased (20 promoters); and Cluster 2, in which the UP-effect increased as RNAP concentration increased (9 promoters) (Figure 6). These opposing UP-effects suggest that additional factors, such as properties of the core promoter, may also influence the UP-effect.

Figure 5.

Heat maps of full-length and core promoters and their UP-effects under different RNAP levels. Heat maps of promoter strengths of all 60 full-length (A) and core (B) promoters. Promoter strength is indicated by a sliding black-red color scale from low to high activity promoters. (C) Heat map of the UP-effect of all 60 promoters (UP-effect = log₂([full-length promoter activity]/[core promoter activity])). The UP-effect for each promoter is indicated by a sliding color scale: red indicates a positive UP-effect; green indicates a negative UP-effect; black indicates no UP-effect. Both heat maps are horizontally clustered using Euclidean clustering to indicate the similarity of relative promoter activities or UP-effects across the different conditions. Promoter activities were determined in different conditions with varying levels of RNAP either in vivo from exponentially growing cultures in M9 complete minimal medium with basal σ^E levels (Basal) or over-expressing σ^E (o/e), or from in vitro competitive multi-rounds transcription assays with either 5, 10, 20 or 50 nM σ^E-holoenzyme (MR 5 nM to MR 50 nM). The following promoters have high σ^E-independent basal activity in vivo (see ‘Materials and Methods’ section) and were eliminated from further analysis in the basal σ^E datasets: plsB, rpoH, ybcR, yecI and yfjO.

Figure 6.

UP-effect varies according to the concentration of RNA polymerase. Cluster analysis of the change in UP-effect across different RNAP concentrations [RNAP] in multi-round in vitro transcription assays. The heat map illustrates two main clusters identified from the top 50% most variable UP-effect promoters with [RNAP] (5, 10, 20, 50 nM RNAP). The line charts illustrate the UP-effect profiles with [RNAP] for each promoter in each clusters 1 and 2.

Contribution of the UP-element depends on the competitiveness of the core promoter

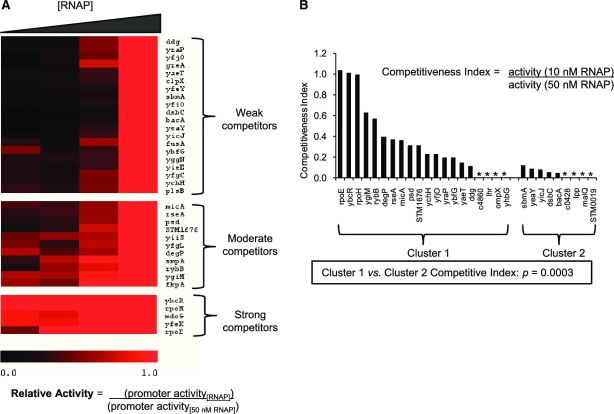
The contribution of the UP-element is likely to depend on the binding strength of the core promoter: strong binding core promoters would be expected to relieve the requirements for UP-elements under high levels of RNAP. We therefore examined whether the Cluster 1 and Cluster 2 promoters differed in the binding strengths of their core promoters. The competitive multi-round assays provide a crude measure of relative promoter binding strength. Because the activity of the test promoter is displayed relative to that of the competitor, at low RNA polymerase concentrations test promoters with tight binding will compete well with the strong competitor control promoter and appear more active (e.g. micA and rybB, see Figure 5B). Accordingly, promoters with similar or higher levels of activity relative to the control promoter at low RNAP concentrations were termed strong competitors, whereas those that showed little activity at low RNAP concentration and increased their relative activity only at high RNAP concentrations were termed weak competitors. A competitive index (CI) was derived to describe promoter competitiveness based on their activity under low and high RNAP levels (CI = (activity [low RNAP])/(activity [high [RNAP]) (Figure 7A). Using the CI, promoters from Cluster 1 were found to be significantly enriched for strong competitor core promoters compared to Cluster 2 (Figure 7B; p = 0.0003 using t-test). Thus, Cluster 1 promoters are likely to become saturated as RNAP levels increase, explaining why their upstream sequences have little effect on promoter strength at high RNAP. Conversely, as Cluster 2 promoters contained weak competitor core promoters that were active only at high RNAP, their UP-effect was only apparent at high levels of RNAP (Figure 7B).

Figure 7.

Cluster 1 and Cluster 2 core promoters differ in their competitiveness for RNAP. (A) Competitive in vitro multi-round transcriptions with different concentrations of RNAP identifies strong and weak competitive core promoters. The heat map displays core promoter activities across different RNAP concentrations ([RNAP]; 5, 10, 20, 50 nM RNAP) relative to their activity with 50 nM RNAP. Each assay contains a test and a competitor (PrpoH) promoter template: promoter activity was calculated as (test activity)/(competitor activity). Relative promoter activity was calculated by normalizing promoter activities at different [RNAP] to their activity with 50 nM RNAP: relative activity = (promoter activity_[RNAP])/(promoter activity_{[50 nM RNAP]}). Consequently, all promoters have a relative activity of 1 (indicated by red color) with 50 nM RNAP. Promoters were clustered into three groups based on their relative activity across different [RNAP]. Promoters with low activities with 50 nM RNAP were eliminated from this analysis to prevent artificially high relative activity ratios. (B) Cluster 1 promoters are enriched for strong competitive core promoter sequences. The bar chart illustrates ‘competitiveness index’ ((promoter activity_{[10 nM RNAP]})/(promoter activity_{[50 nM RNAP]})) of each core promoter for Cluster 1 and Cluster 2 core promoters. Promoters marked with * have no competitiveness index data due to no measurable activity with 50 nM RNAP. Significance in difference between competitive index values of Cluster 1 and Cluster 2 promoters, P = 0.0003 (t-test).

Cluster 1 and Cluster 2 upstream sequences differ in their composition

We applied the different UP models to the upstream sequences of the Cluster 1 and 2 promoters, using conditions of maximal UP-effect (Cluster 1: 10 nM RNAP; Cluster 2: 50 nM RNAP), to determine if they differed in their composition or function (Table 1; Figures S7 and S8). The best models of UP-effect for Cluster 1 promoters were the same as those identified for all 30 active promoters at 10 nM RNAP (overlapping 3 nt A- and T-tract counts; compare first and second third row of Table 1). In contrast, the best UP-element models for Cluster 2 promoters differed from those derived for all 30 promoters. For Cluster 2 promoters, the far-distal A- and T-tract counts generated the highest correlation with UP effects (R = 0.84; p = 5×10⁻³), while the proximal and distal subsite A- and T-tract models performed poorly (Table 1). Also, the percentage AT content generated moderate correlations with UP-effect. Interestingly, the Cluster 2 upstream regions are more AT-rich than the Cluster 1 regions (70% versus 61%, respectively). These results suggest that the α-subunits have different requirements for activity at Cluster 2 promoters.

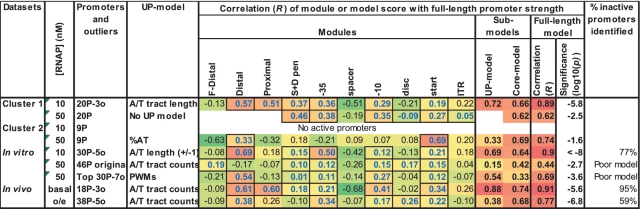
Modeling the strength of promoters at different RNAP concentrations

Up to this point, our models were constructed from the promoter subset active at low RNAP concentration and the activity of the full-length promoter was modeled at low RNAP. However, we have identified two distinct clusters of promoters with differential UP-effects depending on RNAP concentration. We therefore expanded our modeling to examine the properties of full-length promoters at high concentrations of RNAP. For each dataset we applied our full-length promoter modeling approach, constructing models only from the active promoters and testing their ability to predict promoter strength and to accurately distinguish inactive from active promoters under each condition (Figure 8). As expected, models constructed on datasets with low RNAP levels (in vitro, 10 nM RNAP; in vivo, basal σ^E levels) performed better at predicting full-length promoter strength and distinguishing inactive promoters than models using datasets with high RNAP levels (in vitro, 50 nM RNAP; in vivo, over-expression of σ^E). Indeed, models constructed from all 46 promoters active at 50 nM RNAP could not be optimized and correlated only poorly with full-length promoter strength (R = 0.44) [constructing models from the top 30 active promoters yielded an improved correlation (R = 0.69)]. Also, models based on in vivo over-expression of σ^E identified only 59% of inactive promoters.

Figure 8.

Summaries of full-length promoter models for promoter strength measured under different conditions. Datasets: Groups of active promoters used to construct models. [RNAP]: RNAP concentrations (nM) for in vitro assays or levels of σ^E expression (basal or o/e [over-expression]) for in vivo assays. Promoters and outliers: The first number denotes the number of active promoters (P) in the dataset; the second number denotes the number of outliers (o) removed to optimize the model. Top denotes the number of strongest active promoters. UP-model: Lists the type of UP-model used in the full-promoter model. Correlation (R): Correlation of module scores, sub-models and full-length models with promoter strength. F-Distal, distal and proximal modules comprise the UP-model, the other remaining modules form the core-model. Cells with a black border and blue text denote modules that were summed for each dataset to calculate sub-model scores and full-length model scores. Significance (log₁₀(p)) of the full-model correlation values are indicated.

Significantly, all models based on datasets obtained at low RNAP levels are comprised of similar modules, suggesting a similarity of promoter function across these conditions. In contrast, models derived from datasets at high RNAP levels tended to have different solutions, suggesting altered motif requirements under these conditions. For example, under these conditions, there is no UP model for Cluster 1 promoters since none of the UP models improved overall model performance and the UP-effect is minimal at high RNAP levels; for Cluster 2 promoters the model is comprised both of different core modules, and an UP-model solution that differs from the best UP-effect models for the same set of promoters (compare with Table 1). The different solutions at high RNAP levels are likely due to the active promoters being comprised of a mixed population of weak or strong UP-effects and also weak or strong competitive core regions. In contrast, at low RNAP levels only promoters that have high binding affinities (high K_B) and therefore are strong competitors for RNAP are active. These differences are likely to reduce the efficacy of a single predictive model of the type described here to capture promoter strength at higher RNAP levels.

DISCUSSION

This work presents the quantitative sequence requirements and descriptive promoter strength models of full-length promoters for the first time. By comparing the strength of core and full-length σ^E-dependent promoter sequences, we have been able to quantify the contribution of upstream sequences to promoter strength. We find a large range of UP-effects across active promoters. Significantly, their effects can be successfully modeled using descriptions of A- and T-tract frequency and length, which are consistent with the known binding requirements of the α subunits. We also find that full-length promoters can be modeled by combining the UP-element models with core models comprised of PWMs of key motifs and penalties for suboptimal motif positions. These models provide important metrics with which to dissect the requirements of promoter structure and function. In addition, we have identified important properties of UP-element and core promoters that modify the behavior of promoters across a range of RNAP concentrations. These findings impact both the design of models for promoter prediction and the design of promoters for applications in synthetic biology.

UP-element structure

Our understanding of UP-element structure was previously based on SELEX studies, which found that long continuous runs of A- and T-tract had strong UP-element function (9,10). This finding is consistent with the fact that optimal α-DNA interactions require a narrowed minor groove (13–15). However, naturally occurring UP-elements, which consist of shorter A- and T-tracts that differ both in length and frequency, had not been modeled (Figure 3). Our modeling of natural UP-elements showed that models based on frequency and length of A- and T-tracts capture important properties of natural UP-elements. Our best overall UP-element model consisted of the frequency of overlapping 3 nt A- and T-tracts. The 3 nt tract is the minimum A-tract length for maximal minor groove narrowing (15), and is most likely to capture the contribution of these more ‘broken’ A- and T-tracts in natural promoters. In addition, our models show that the distal and proximal subsites are the most significant contributors to the UP-effect at most promoters. This likely reflects the optimal binding location of the α subunits at activator-independent promoters (6,9,10,12). Finally, the best subsite models were for the distal subsite: measuring the frequency of overlapping 3 nt A- and T-tracts, and also the length of A-tract followed by T-tract, a feature characteristic of optimized distal subsites (9). It is likely that this combination of A- followed by T-tract provides a stable region of narrowed minor groove, since the flanking A- and T-tracts will generate minor groove narrowing from both directions of the DNA. The key remaining questions are the effects of different tract length and locations of tracts, single nucleotide interruptions and the composition of flanking sequences. Answering such questions requires much larger sequence libraries to provide the fine resolution necessary for addressing these issues.

Full-length promoter models

Combining the UP-element model with our previously described core promoter model enabled us to evaluate the contributions of all promoter motifs to promoter strength (Figures 4A and B and 8). This analysis revealed that although distal and proximal UP-elements are major contributors to promoter strength, the motifs important for strength of the core promoter [PWMs of the −35, −10 and start motifs, and spacer penalties; (25)] are also important for strength of the full promoter. Thus, UP-elements strongly contribute to promoter strength, but they do not mask the requirement for core promoter motifs. Indeed, similar modules distinguish inactive from active promoters in both core and full promoters (25) (Table 3; Supplementary Figure S6). Therefore, it is the properties of the core promoter that determine promoter functionality in ECF σ-type promoters as UP-elements are not required for promoter function and do not compensate for the poor functional characteristics of core promoters.

Our results suggest that too many strong interactions between RNAP and the promoter hinder escape of RNAP from σ^E-dependent promoters, as was previously found for near consensus σ⁷⁰ promoters (39–41). The strongest σ^E-dependent promoters were composed of combinations of high and low scoring motifs and the strengths of the −10 and −35 motifs are negatively correlated (Supplementary Figure S6; data not shown), as expected if strong interactions are carefully calibrated for maximal activity. Intriguingly, although there is very little sequence conservation in the sequence of the spacer between the −10 and −35 motifs, except for a minor enrichment of A/T residues in its central portion, the spacer sequence is exceptionally strongly negatively correlated with promoter strength (Figure 8 and Supplementary Figure S6). We suggest that the spacer sequence affects promoter strength by altering DNA flexibility since this region undergoes large conformational changes during the formation of the initiation complex (reviewed in (42)). Suboptimal spacer sequences, likely to lack enriched A/T residues, may destabilize the bound RNAP initiation complex. At the strongest promoters, the non-conserved spacer may balance the requirement for strong interactions that promote RNAP binding with unstable interactions to facilitate promoter escape.

Promoter strength across different levels of RNAP

We report the first systematic analysis of promoter strength as a function of RNAP concentration. Our models for both the core promoter and the UP-element capture parameters related to binding, rather than subsequent steps of transcription initiation. The fact that these models performed very well only at low RNAP concentration indicates that such parameters dominate promoter strength under these conditions. Thus, we suggest that binding affinity (K_B) governs the activity of σ^E promoters at low concentrations of RNAP. In accord with this conclusion, most promoters active at low RNAP fall into our ‘competitive’ Cluster 1 promoter class (Figure 7). Moreover, these promoters show decreasing UP-element stimulation at higher RNAP concentration, consistent with expectations for core promoters having tight binding. As RNAP increases, binding of the core promoter to RNAP will saturate, limiting the effect of additional binding conferred by the UP-element.

Importantly, systematic modeling across RNAP concentrations revealed that the σ^E regulon has a second distinct promoter type, which differs in both properties and sequence from the predominant Cluster 1 promoters. Cluster 2 promoters are likely to be weaker binding: their core sequences compete poorly at low RNAP concentration; however, they show increasing stimulation by UP-elements with increasing RNAP concentration. Consequently, most Cluster 2 promoters were only active at high RNAP concentrations. Cluster 1 and Cluster 2 promoters differ in their −35 sequences. Although both contain the consensus core element of the −35 element (GAAC) (43), their flanking sequences differ (Supplementary Figure S7). In particular, the downstream T-tract is present only in Cluster 1. T-tracts provide a rigid structural unit and the first T is involved in non-specific contacts with σ^E R149 (43). Thus, Cluster 1 and 2 promoters could have an altered trajectory of DNA, possibly explaining why the most important descriptor of UP-effect in Cluster 2 promoters is the far-distal UP-site. Interestingly, the presence of sequences in the far upstream UP-element region has been shown to be important for increasing the rate of isomerization of the open complex (38,44), suggesting that UP sites at Cluster 2 promoters may facilitate a step subsequent to initial promoter binding.

Our initial σ^E promoter identification efforts were directed at identifying all sequences able to function as σ^E promoters, so that we could examine different categories of promoters. Thus, in vivo detection used the sensitive 5′ RACE technique following σ^E overexpression, and in vitro detection employed high levels of RNA polymerase with no competitor template (8,23). This important decision allowed us to dissect the promoter properties of diverse sequences and enabled us to classify promoters as Cluster 1-type, Cluster 2-type and weak/inactive. Although Cluster 1-type promoters are generally active at low RNAP concentration, a subset (7/20) are active only at high RNAP concentration. These promoters typically have weak or medium strength competitive core promoters and low scoring UP-elements, suggesting that these promoters also have weak overall binding strengths. Cluster 2 promoters are active only at high RNAP concentration and most (6/9) have weakly competitive core promoters and relatively strong UP-elements. Finally, promoters classified as inactive even under high RNAP have a very low scoring core motif and often weak UP-elements, suggestive of function in vivo only when levels of free σ^E are extremely high (8).

The discovery of the distinct Cluster 1 and Cluster 2 promoter types is important for our general understanding of ECF σ responses. The activity of most ECF σ promoters is primarily regulated by changes in the concentration of its active σ. Our studies suggest that only select promoters will be active at low to moderate levels of the ECFσ and that regulons may have additional promoter types designed to be active only under extreme conditions. A tiered response increases the regulatory capacity of ECF σ's.

Distinct properties of alternative σ promoters

Although we were able to model the strength of near-consensus UP-elements at σ⁷⁰ promoters (9,10) using overlapping A- and T-tract 3 nt counts and length (Supplementary Figure S9; Supplementary Table S4), there are important differences between the UP-element performance at housekeeping (σ⁷⁰) promoters and at σ^E promoters. UP-elements recruit σ⁷⁰ holoenzyme to weak promoters, thereby dramatically increasing promoter strength (6,11,45). In contrast, our data indicate that the presence of UP-elements at σ^E promoters does not significantly relieve the requirement for well-conserved core promoter sequences. Moreover, the behavior of Cluster 2 promoters indicates that there is a minimum RNAP concentration requirement for UP-element function: below this concentration there is insufficient promoter occupancy to enable isomerization. Thus, at σ^E promoters, UP-elements are subsidiary to the core promoter elements whereas at σ⁷⁰ promoters, they may be able to substitute, in part, for core promoter elements.

These findings are consistent with an emerging view of the differences between the housekeeping σs and the diverged alternative σs (ECF, Group 4 σs and Group 3 σs). Whereas housekeeping σs recognize thousands of promoters genome-wide that are comprised of partially redundant, poorly conserved −35, −10 and extended −10 motifs (42), the diverged alternative promoters recognize 10 to 100-fold fewer promoters and are comprised of more highly conserved core promoters that require every promoter motif for function. Recent studies indicate that a major contributing factor to this differential promoter usage is that housekeeping σs contain key aromatic residues that facilitate promoter melting (46,47); whereas most alternative σs lack some of these key residues, resulting in a suboptimal melting capacity (48). Consequently, the strong melting capacity of housekeeping σs enable their tolerance of poorly conserved promoters, since only transient occupancy of the promoter is sufficient to enable melting. In contrast, the weak melting ability of alternative σs results in slow isomerization to open complex: consequently, only near consensus promoters provide a sufficiently slow dissociation rate to enable melting to occur (48,49). The difference in promoter melting ability between the housekeeping and alternative σs has important implications for the effect of UP-elements on promoter strength. The strong melting capacity of housekeeping σs enables weak promoters to be strongly activated by UP-elements that ‘recruit’ RNAP to these sequences. In contrast, the weak melting capacity of alternative σs confines UP-element function to well-conserved promoters capable of supporting open complex formation.

Constructing models for promoter prediction

Our modeling efforts suggest a pathway for predicting the biological circuits of newly discovered ECF σs. First, promoters should be identified using high-throughput experiments performed at low concentrations of the σ (e.g. basal or near basal conditions) as the tools currently available are best suited to model promoters under binding limited conditions. Second, outliers to general trends should be removed as they detract from the general predictive value of our models. Importantly, 7/8 promoters identified as outliers in our experiments contained at least one very low scoring module (five different modules in total; Supplementary Figure S6). These promoters are likely to contain sequences that functionally compensate for the particular low scoring module in that promoter. The fact that there are different low scoring modules suggests that there may be several solutions to compensate for suboptimal modules. As the lowest z-score for each module varies in active promoters (see Supplementary Figure S6), the best approach for optimizing new models would be to remove promoters containing modules with discrepantly low z-scores. Third, all core promoter motifs should be used to discriminate functional (e.g. active) from inactive or very weak promoters. Finally, only select motifs (including UP-elements) should be used to estimate promoter strength. Our results make it clear that there is a need for new approaches that model additional facets of the transcription process beyond the initial binding step. We envision that DNA structure and flexibility will provide additional readouts to help model such steps.

Designing promoters for synthetic biology

Synthetic biology designs genetic circuits for particular outputs, including transplantation of metabolic pathways into suitable hosts (50–52). These systems require careful engineering such that the expression levels of the genetic components are tuned to an appropriate input level for the next section of the circuit. This ensures desired circuit behavior and reduces toxicity of pathway intermediates (53). An example of such ‘tunability’ has been achieved by altering ribosome binding site (rbs) sequences to adjust rbs strength and hence protein translation using an ‘rbs calculator’ based on thermodynamic principles (54). This and our previous work (25) provide the foundation for developing an analogous ‘promoter calculator’ for engineering promoters of specific strengths for genetic circuits. We suggest that a minimum predictable promoter unit should extend from −65 to +20. This will include the UP-elements that dramatically affect promoter strength even of alternative sigmas, and also the downstream +1 and initial transcribed region (ITR) that can affect promoter function by modifying open complex stability and promoter escape (25,55).

SUMMARY

Many of our findings on modeling σ^E promoters will be applicable as other alternative σs. Their core promoter motifs are well conserved, making them tractable to modeling, and the sequence requirements of the UP-elements are conserved across bacteria. The rapid application of next generation sequencing to RNA-seq is now providing a wealth of high-resolution information of transcript start sites at a genomic level (56–58). This dramatically simplifies identifying promoter sequences, which are located directly upstream of start sites, enabling construction of descriptive promoter models for entire genomes. RNA-seq also provides quantitative information on transcript abundance and hence promoter strength, which would enable optimization of promoter models with strength. This will enable the construction of promoter strength models that can then be used for promoter predictions in closely related genomes that share orthologous σs, thereby rapidly expanding the characterization of transcriptional networks across bacteria.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Figures 1–9, Supplementary Tables 1–4, and Supplementary References [9,10].

FUNDING

Funding for open access charge: National Institutes of Health (GM57755 to C.A.G.).

Conflict of interest statement. None declared.