Linear and nonlinear elasticity imaging of soft tissue in vivo: demonstration of feasibility

Abstract

We establish the feasibility of imaging the linear and nonlinear elastic properties of soft tissue using ultrasound. We report results for breast tissue where it is conjectured that these properties may be used to discern malignant tumors from benign tumors. We consider and compare three different quantities that describe nonlinear behavior, including the variation of strain distribution with overall strain, the variation of the secant modulus with overall applied strain and finally the distribution of the nonlinear parameter in a fully nonlinear hyperelastic model of the breast tissue.

1. Introduction

Elasticity imaging or elastography encompasses a collection of techniques that are used to image the mechanical properties of tissue in vivo. All these techniques involve imaging the tissue using a standard modality, such as ultrasound or MRI, while it deforms due to a prescribed external load or due to internal motion (motion during the cardiac cycle, for example). The sequence of deformation images thus obtained are used to determine the displacement field in the interior of the tissue typically using cross-correlation based techniques. The interior displacements are then utilized to infer the mechanical properties of tissue.

Broadly speaking the excitation and the accompanying deformation can either be dynamic or static (see Parker et al (2005) for a nice unified discussion). In dynamic elasticity imaging shear waves are set up and imaged in the tissue, and the local wave speed is used to estimate the elastic modulus (see Kruse et al 2000, Sinkus et al 2000, Oliphant et al 2001, Bercoff et al 2003, McLaughlin and Renzi 2006, Greenleaf et al 2003 for a review). The excitation is either applied to the surface or as in the case of radiation force elastography in the interior of tissue (Nightingale et al 2002). Recently, dynamic excitation has also been used to determine the viscous properties (Sinkus et al 2005) of tissue.

In static, or more appropriately quasi-static elasticity imaging, the excitation is on a slower time scale such that the inertia of the tissue does not play a role in its motion. In this case the tissue is typically slowly compressed and imaged using ultrasound, and successive ultrasound images are registered to determine the displacement field. The displacement field is then used to calculate the component of strain along the axis of the transducer (axial strain) and imaged. This strain image is then interpreted as an image of the reciprocal of the shear or Young’s modulus for the tissue (Ophir et al 1991, Garra et al 1997, Kallel and Ophir 1998) (see Ophir et al (2002) for a review). In some instances the displacement field is used to solve an inverse elasticity problem to explicitly determine the spatial distribution of the elastic modulus of interest. This involves selecting an appropriate mathematical description of tissue deformation and then determining the spatial distribution of material parameters in this description (Kallel and Bertrand 1996, Doyley et al 2000, Oberai et al 2003). While several techniques have been proposed for solving this inverse problem, most applications to date have been limited to synthetic displacement data or displacement data obtained from tissue-mimicking phantoms.

One of the motivations for imaging the elastic properties of tissue is that diseased tissue tends to be stiffer than its surroundings. This is certainly true of tumors found in the breast and the prostate. Motivated by this observation several clinical trials have been conducted (some are on-going) with the aim of assessing the utility of elasticity imaging in the detection and diagnosis of breast and prostate cancer (Garra et al 1997, Hiltawsky et al 2001, Hall et al 2003, Itoh et al 2006, Regner et al 2006, Burnside et al 2007). Most of these, as indeed most elasticity imaging studies to date, have focused on the linear elastic properties of tissue. However, recent data from ex vivo measurements of breast and prostate tissue indicate that in addition to the linear properties, nonlinear elastic properties may be useful in differentiating benign and malignant tumors (Krouskop et al 1998, Wellman et al 1999). For example, in Wellman et al (1999) it is reported that while fibroadenoma (a benign tumor in the breast) and invasive ductal carcinoma (IDC) have similar elastic moduli at small strain, their moduli at large strain differ by a factor of about 2.5, with IDC being stiffer. Thus while it might not be possible to distinguish a fibroadenoma from an IDC at small strain alone, it may be possible to do this by considering data at larger strain (about 10% strain as shown in this paper). Similarly, it has been reported that at small strains the shear modulus of ductal carcinoma in situ (DCIS) is close to that of glandular tissue, while at large strains DCIS is stiffer by a factor of about 8. Once again this points to the possibility of directly imaging DCIS by mapping the variation of the elastic properties of tissue as a function of strain. In other words these applications require imaging the nonlinear elastic properties of tissue.

While there is a large collection of work in linear elasticity imaging, there have been few attempts at imaging the nonlinear properties of tissue. Skovoroda and coworkers recognized the potential of nonlinear elasticity imaging (Erkamp et al 2004a, 2004b) and in Skovoroda et al (1999) account for the effect large strains in their inversions, however they assume linear stress–strain behavior. In Erkamp et al (2004a) they evaluate nonlinear elastic parameters of tissue using force-displacement data, however they assume homogeneous material properties of the tissue. Sinkus and coworkers (Sinkus et al 2006) have employed dynamic ultrasound elastography to determine the nonlinear parameters of tissue by imaging the second harmonics of a time-dependent shear displacement. However these estimates of nonlinear properties are determined at small values of applied strain (less than 1%) where differences among tissue types might be difficult to discern.

In order to image nonlinear elastic properties using quasi-static, ultrasound based elastography it is likely that overall compressive strains that are greater than 10% are required. This estimate is based on ex vivo tests conducted by Krouskop et al that indicate that at smaller strains the departure from linearity for most tissue types is minimal (Krouskop et al 1998). Once the displacements at these large strains have been measured, an inverse problem must be solved in order to determine the nonlinear elastic parameters of tissue. Both these problems, that is displacement estimation at large strain, and the inverse nonlinear elasticity problem, are challenging problems in their own right. In Hall et al (2002) we reported the initial observation of deformation-dependent strain image contrast using our first motion tracking algorithm for real-time elasticity imaging (Zhu and Hall 2002). A more recent motion tracking algorithm significantly improves the displacement estimate accuracy for large deformations (Jiang and Hall 2007). The key to accumulating relatively small deformations (i.e., 1–2% axial strain) over large total deformations (<10% axial strain) is the need to limit tissue motion out of the image plane. Accurately tracking motion for large deformations is assisted with real-time feedback of strain images that help to demonstrate (nearly) uniaxial motion from frame to frame. With real-time feedback it is common to accurately track motion for at least 10% accumulated axial strain. In Gokhale et al (2008) we have developed a new, efficient algorithm for solving the inverse nonlinear elasticity problem. This involves posing the inverse problem as a minimization problem and then utilizing the adjoint elasticity equations and a novel continuation strategy in material parameters to solve this problem in reasonable time. In this manuscript we combine these developments to reconstruct the nonlinear elastic images of tissue. We report the first set of clinical images displaying the linear and nonlinear elastic properties of tissue derived from ultrasound measurements of quasi-static deformation. We also describe how these images may play an important role in the diagnosis of breast cancer.

For completeness, we consider three descriptors of nonlinear behavior of tissue. First, we create an incremental axial strain image about an overall strain state and observe how this image changes with increasing overall strain. We note that if the ratio of strain in a region A versus another region B is reducing with increasing strain then A is stiffening faster relative to B. Second, for a given value of overall strain we evaluate the shear modulus assuming linear elasticity and infinitesimal strains and observe how this modulus image varies with overall strain. We term this image the secant modulus image. By this measure if the ratio of the modulus in a region A relative to B is increasing with strain, then A is stiffening with respect to B. Finally, we reconstruct the linear and nonlinear elastic parameters for the tissue in a fully nonlinear tissue constitutive model, while fully accounting for finite strains. This gives us the most direct measure of nonlinear behavior in tissue.

The organization of the remainder of the manuscript is as follows. In section 2 we describe the methods for acquiring ultrasound images, estimating tissue displacement, and linear and nonlinear properties of tissue. Thereafter in section 3 we present results on two sets of breast data. For each set these include a B-mode ultrasound image, incremental strain images, secant modulus images and images of the linear and nonlinear elastic parameters. In section 4, we discuss these results and explain the relative merits of incremental strain, secant modulus and nonlinear elasticity images. We end with conclusions in section 5.

2. Methods

2.1. Acquisition of ultrasound images

Radiofrequency (RF) echo data were recorded during in vivo breast imaging at three institutions: the University of Kansas Medical Center in Kansas City, KS (approved by the KUMC Human Subjects Committee), Mayo Clinic in Rochester, MN (approved by the Mayo Foundation institutional review board), and the Charing Cross Hospital, London, UK (approved by the Riverside research ethics committee, Chelsea & Westminster Hospital (NHS Trust)). Informed consent was obtained from all enrolled patients. Our study was also compliant with the Health Insurance Portability and Accountability Act (data acquired at KUMC and Mayo Clinic). The protocol was approved by the appropriate Institutional Review Boards. All sites used equivalent Siemens SONOLINE Elegra (Siemens Medical Solutions, Ultrasound Division, Issaquah WA) with VFX13-5multi-rowlinear array operating at 10 MHz. The Elegra samples the RF echo data at 40 MHz and we used a 200 µm spacing between adjacent acoustic beams. A free-hand compression technique (Hall et al 2002) was used by clinicians who were trained to begin with the transducer ‘just barely in contact’ with the skin surface and then apply increasing pressure in a cyclic manner over an approximately 10–20% strain range. A real-time strain imaging algorithm (Zhu and Hall 2002) was implemented on the Elegra and used during RF echo signal acquisition (Hall et al 2002) to provide visual feedback of strain image quality during scanning to assist in the acquisition of high quality data.

2.2. Estimates of tissue displacement and incremental strain images

The motion tracking method for displacement and strain estimation is reported in Jiang and Hall (2007). Basically the motion tracking method uses a guided search block-matching algorithm that employs a relatively large motion tracking kernel (approximately 0.5 mm × 1 mm) and 2D search region to establish a good estimate of displacement in the center of the region of interest. That set of displacement estimates is used to guide the location of the search region in laterally adjacent RF echo segments while reducing the size of the required search region to 3 × 3 RF samples. A smaller (0.2 mm × 1 mm) kernel is used for this guided search. Displacement estimates are made on a 200 µm × 200 µm sample grid with RF-sample precision. Sub-sample displacement estimates (necessary for strain imaging) are obtained with quadratic interpolation of the block-matching results (Ignacio et al 1995). The linear regression with a 1.6 mm window is used on the axial component of the displacement field to obtain axial strain fields and strain images.

An automated algorithm (Jiang et al 2006) was used to select the ‘best’ sequence of displacement data for further processing. The algorithm computes a ‘displacement quality measure’ (DQM) for the entire displacement and strain field as a single quantity that is based on the product of the cross-correlation coefficient of the reference and motion-compensated RF echo fields and the cross-correlation coefficient of the consecutive strain fields. This measure correlates highly with the subjective ranking of strain images (Jiang et al 2006). Sequences with at least 10% accumulated strain also having individual DQM values exceeding 0.8 were selected for further analysis. One example of the most common benign solid breast tumor (fibroadenoma) and malignant tumor (invasive ductal carcinoma) were selected from the accumulated data set for this proof of concept modulus reconstruction study.

2.3. Modulus reconstruction

The core of our modulus reconstruction approach is built around an iterative optimization strategy. This involves iteratively improving estimates of material property distributions so that they yield predicted displacements that best match the measured displacements.

Secant modulus images

For the linear elasticity case (reconstruction of secant shear modulus) the quantity to be minimized is (Oberai et al 2003, 2004)

$$\pi =\frac{1}{2}{\displaystyle {\int }_{\mathrm{\Omega }}{(U-U_{\text{meas}})}^2\mathrm{d}\mathrm{\Omega }+\frac{{\alpha }_{\mu }}{2}ℛ(\mu ).}$$ (1)

In the equation above U_meas is the axial component of the measured displacement field at a given value of overall applied strain. The field U is the axial component of the corresponding predicted displacement. We constrain the predicted displacement vector to satisfy the equations of equilibrium for an incompressible linear elastic solid in a state of plane stress. Through these equations the displacement field is related to the shear modulus of the material, which is denoted by μ. In our objective function (1), the first term is the data matching term and the second term is a regularization term. In this term ℛ is the total variation diminishing (TVD) regularization functional that penalizes large changes in μ, without penalizing their steepness. Finally, α_μ is the regularization parameter that determines the importance of the regularization relative to the data matching term. For details on the formulation of this problem and the algorithm, the reader is referred to Oberai et al (2003, 2004). Since the measured data contains no force measurements we only recover the relative value of the shear modulus μ. The actual shear modulus distribution is related to the reconstructed value through an unknown multiplicative constant, which may be determined from a single force measurement, but such a measurement is unavailable for the data used here.

Nonlinear elasticity images

For the nonlinear elasticity case (reconstruction of shear modulus at zero strain and the nonlinear parameter) the function to be minimized is given by

$$\pi =\frac{1}{2}{\displaystyle {\int }_{\mathrm{\Omega }}(w_1{(U^1-U_{\text{meas}}^1)}^2+w_2{(U^2-U_{\text{meas}}^2)}^2)\mathrm{d}\mathrm{\Omega }+\frac{{\alpha }_{\mu }}{2}ℛ({\mu }_0)+\frac{{\alpha }_{\gamma }}{2}ℛ(\gamma ).}$$ (2)

In the nonlinear case we have two measured displacements, one at a small value of overall strain, denoted by $U_{\text{meas}}^1$ and another at a large value of overall strain denoted $U_{\text{meas}}^2$. Correspondingly we also have two predicted displacement fields whose axial components are denoted by U¹ and U² in the equation above. The predicted displacement fields are required to satisfy the equations of equilibrium for an incompressible, hyperelastic solid undergoing finite deformations in a state of plane stress. The stress–strain relation is exponential and is determined by the Veronda–Westman strain energy density function (Veronda and Westman 1970). This function involves two material parameters. These are the shear modulus of the material at zero strain, denoted by μ₀, and the nonlinear parameter γ, which denotes degree of nonlinearity in the material. The strain energy density function is given by

$$W={\mu }_0\left(\frac{{\mathrm{e}}^{\gamma (I_1-3)}-1}{\gamma }-\frac{I_2-3}{2}\right),$$ (3)

where I₁ and I₂ are the first and second invariants, respectively, of the Cauchy–Green strain tensor. The details of this formulation are presented in Gokhale et al (2008).

The other terms that appear in (2) are:

1. The weighting factors w₁ and w₂. These parameters are used to scale the data matching term and are selected to ensure that both the large deformation data and the small deformation contribute to it in (roughly) equal measures. In our examples, the large deformation displacements are about ten times larger than the small deformation displacements. Thus to ensure equal contributions we set w₁ = 10² and w₂ = 1. If these weighting factors were not used, the contribution from the smaller deformation would be insignificant compared to the contribution from the large deformation. Indeed, the contribution from the smaller deformation would be only slightly larger in magnitude than the contribution of the noise in the larger deformation. Without the weighting factors, we would essentially be trying to recover two material parameters from a single deformation field. This problem is severely underdetermined in that there are an infinite combinations of μ₀ and γ that could match the single measured displacement field.

2. There are two regularization terms ℛ(μ₀) and ℛ(γ) that regularize the shear modulus at zero strain and the nonlinear parameter, respectively. The parameters α_μ and α_γ determine the extent of this regularization.

We remark that similar to the linear case, in the nonlinear case also we reconstruct the relative distribution of μ₀ which is related to the actual distribution through a multiplicative constant. This constant may in principal be determined through a single overall force measurement during compression.

Computational Algorithm

For both linear and nonlinear elastic cases we minimize π using a quasi-Newton method (BFGS). We represent the displacement fields and the material properties using standard bilinear finite element functions. Thus we seek the values of the material properties at the nodes of the mesh that will minimize π. In order to converge to these values, at every iteration the quasi-Newton algorithm requires the gradient vector, which represents the change in π due to a small change in the material properties at each node. For the linear elasticity case, we evaluate this vector efficiently by utilizing the adjoint elasticity equations. The major computational costs associated with using this approach for solving the inverse problem are ≈2n_iterC, where C is the cost of solving a single linear forward elasticity problem and n_iter is the total number of iterations of the optimization algorithm. Note that these costs are independent of the number of parameters used to represent the material properties and since this number can be very large (≈10⁴) this is a significant advantage.

For the nonlinear case the use of adjoint equations alone does not yield acceptable computational costs. In order to further lower these costs we utilize a continuation strategy in material parameters in addition to the adjoint elasticity equations. This approach is described in detail in Gokhale et al (2008). Within this approach we recognize that the optimization algorithm converges to the final distribution of material properties in increments of properties that are typically small. As a result, for solving the forward problem associated with the current state of material properties, the displacement field corresponding to the previous iteration provides a very good starting guess. Using this approach the major computational costs for solving the inverse nonlinear elasticity problem are ≈2(n_iter + n_load)n_NewtonC, where n_load is the number of load steps needed to converge to the final large deformation state starting from an undeformed state and n_Newton is the number of Newton iterations per load step. The cost of solving the forward nonlinear elasticity problem is ≈2n_loadn_NewtonC. In our examples we have found n_load ≈ n_iter and as a result the cost of solving the inverse nonlinear elasticity problem is roughly only two times that of solving the corresponding forward problem. In order to compare the cost of solving the inverse nonlinear problem with that of solving the linear problem, we recognize that n_Newton ≈ 6, so the cost of solving the nonlinear inverse problem is about 2n_Newton ≈ 12 times that of solving the linear inverse problem.

The Veronda–Westman Constitutive Law (Veronda and Westman 1970)

The Veronda–Westman model provides an exponential dependence of stress on the strain. It was originally developed to model skin, which exhibits such behavior. Similar behavior has been reported in ex vivo experimental data for breast tissue (Krouskop et al 1998), and so motivates our choice of the Veronda–Westman model in this study. We illustrate the important aspects of the Veronda–Westman material model by considering a simple example. For an incompressible Veronda–Westman material in uniaxial tension the axial component of the Cauchy stress is given by

$$\sigma =2{\mu }_0({\mathrm{\lambda }}^2-{\mathrm{\lambda }}^{-1})\left({\mathrm{e}}^{\gamma ({\mathrm{\lambda }}^2+2{\mathrm{\lambda }}^{-1}-3)}-\frac{1}{2\mathrm{\lambda }}\right),$$ (4)

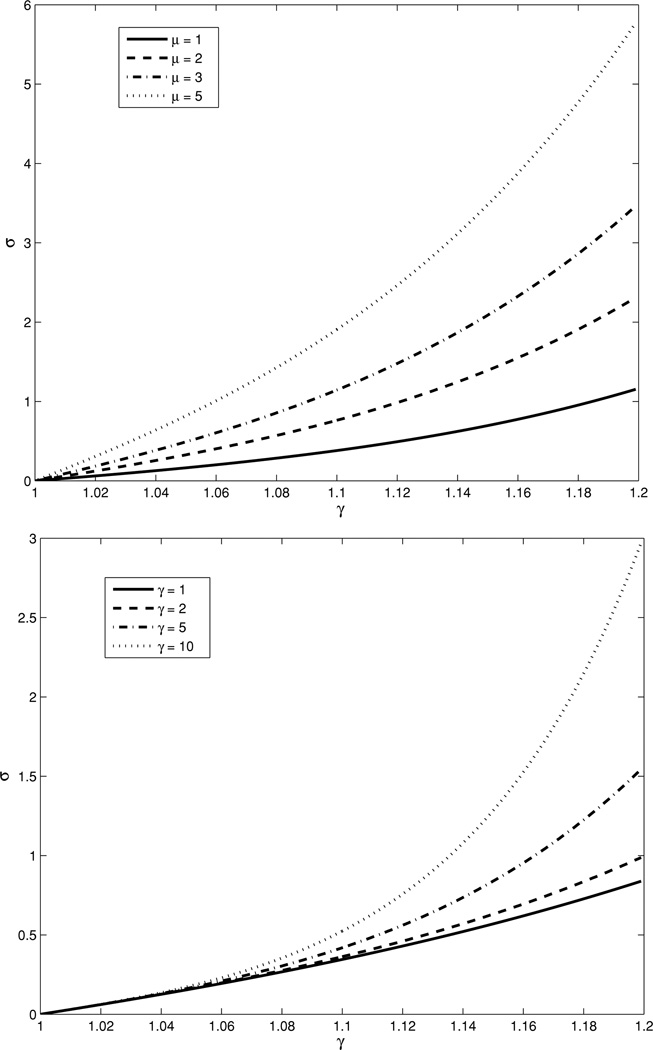
where λ = 1 + ε, is the stretch and ε is the strain. In figure 1 we have plotted σ as a function of λ for different values of μ₀ and γ. In these figures we observe an exponential stress–strain response. We also observe that the parameter μ₀ determines the slope of the stress–strain curve at zero strain (λ = 1), while γ determines the rate at which the curve departs from linear behavior.

Figure 1.

Stress (σ) versus stretch (λ) curves for Veronda–Westman constitutive model. Top: effect of varying μ₀ with γ = 3, constant. Bottom: effect of varying γ with μ₀ = 1, constant.

The roles of μ₀ and γ become clearer if we evaluate the slope of the stress–strain curve which is equal to the (tangent) Young’s modulus at a given value of strain. That is

$$E(\mathrm{\lambda })=\frac{\mathrm{d}\sigma }{\mathrm{d}\epsilon }=2{\mu }_0\left({\mathrm{e}}^{\gamma ({\mathrm{\lambda }}^2+2{\mathrm{\lambda }}^{-1}-3)}[2\mathrm{\lambda }+{\mathrm{\lambda }}^{-2}+2\gamma ({\mathrm{\lambda }}^3-2+{\mathrm{\lambda }}^{-3})]-\frac{1}{2}-{\mathrm{\lambda }}^{-3}\right)$$ (5)

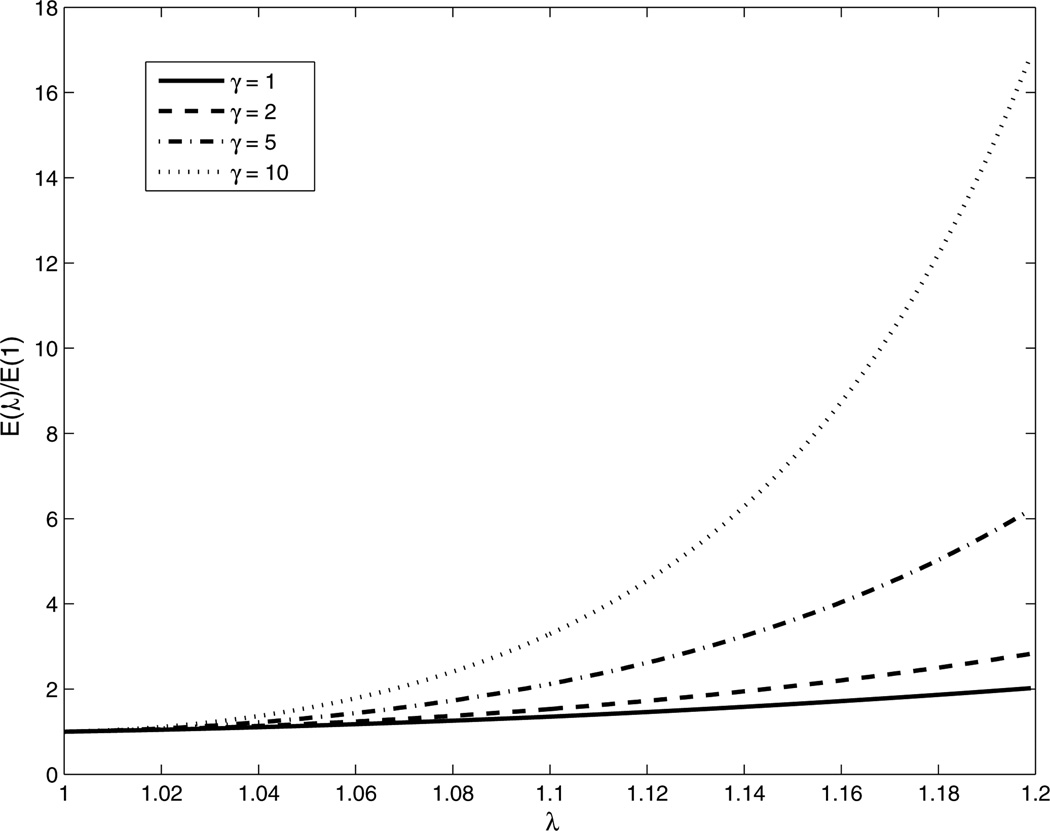
At zero strain (λ = 1) from the above expression we have E(1) = 3μ₀ implying that the Young’s modulus at zero strain is completely determined by the parameter μ₀ which is equivalent to the shear modulus at zero strain. Also using this expression we conclude that the ratio of the Young’s modulus at finite strain to the Young’s modulus at zero strain, that is E(λ)/E(1), is entirely determined by the parameter γ. Thus any change in the modulus as a function of strain is solely determined by γ, which is appropriately labeled as the nonlinear parameter for the material. In figure 2 we have plotted the ratio E(λ)/E(1) as a function of the stretch for different values of γ. We observe that the Young’s modulus increases exponentially with strain, and the rate of increase is determined by γ.

Figure 2.

Young’s modulus (E) versus stretch (λ) curves for the Veronda–Westman constitutive model: effect of varying the nonlinear parameter γ.

3. Results

3.1. Secant modulus images

Using the displacement estimates at two distinct levels of overall strain in the linear elastic modulus reconstruction algorithms described in section 2, the shear modulus for each tumor type was reconstructed. The assumption of linear elasticity was invoked even for the large-strain data set. As a result the recovered modulus was interpreted as a secant modulus for the tissue. Further since no force measurements were made, it was recognized that the resulting modulus distribution was recovered up to a multiplicative factor. The axial component of the displacement was down sampled by a factor of 4 from the displacement estimates on to a grid (h_x = 0.682 mm, h_y = 0.599 mm for fibroadenoma and h_x = 0.750 mm, h_y = 0.599 mm for IDC) and represented using standard bilinear finite element shape functions. Here the x- and y- axes are coincident with lateral and axial directions, respectively. The shear modulus was reconstructed on the same grid and was also represented using bilinear finite element shape functions. On every edge of the sample the axial (y) displacement was imposed, while it was assumed that there was no traction in the lateral (x) direction. This meant that shear traction on the top and bottom edges and normal traction on the left and right edges were assumed to be zero. It is reasonable to expect that the shear traction on the top edge would be small due to the lubrication between the transducer and skin. Further, since the predominant stress state is compressive, it may be assumed that shear stress on the bottom edge is also small. For the left and right edges normal tractions were assumed to be small because during the examination the breast was allowed to strain freely in the lateral direction. The value of the regularization parameter was set to 10⁻⁴ and the solution was considered converged after 100 iterations of the BFGS algorithm. At this iterate, the cumulative drop in the objective function over the final five iterations was smaller than 0.1% of its starting value for all reconstructions. The initial guess for the shear modulus was set to 2 and was constrained to lie in the interval (1, 100).

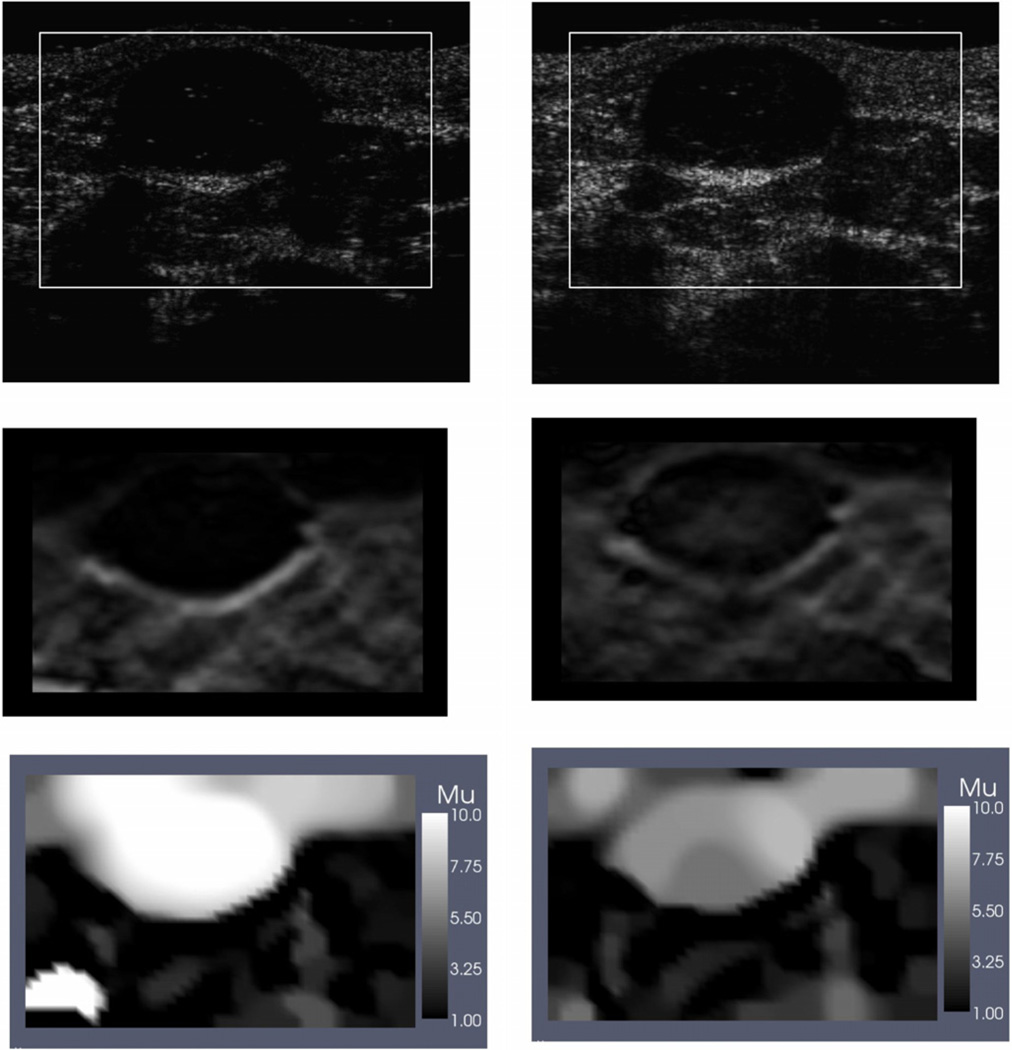
In figure 3 we have displayed relative shear modulus images for the fibroadenoma at minimal strain and at about 12% axial strain beyond minimal strain. (In this and all images that follow, the images have all been mapped back to the reference (minimal strain) configuration for easy comparison; this includes B-mode, strain and reconstructed modulus images.) We have also included B-mode ultrasound and axial strain images for comparison. We observe that the tumor is clearly seen in the shear modulus images at both levels of overall strain. In the large-strain shear modulus image the modulus contrast in the tumor has reduced from 10:1 to 7:1.

Figure 3.

Images for fibroadenoma. Left column: images at small strain; right column: images at large strain. Top row: B-mode ultrasound images; middle row: axial strain image; bottom row: relative shear modulus (secant) images.

In figure 4 we have shown the B-mode ultrasound, axial strain and relative shear modulus images for the IDC at minimal strain and at about 12% axial strain beyond minimal strain. We observe that the tumor is clearly seen in bothmodulus images. In the large-strain shear modulus image the tumor appears to have retained its stiffness in comparison with the background. In fact it has stiffened slightly toward the right edge. However, this stiffening is too small to be discerned in the image.

Figure 4.

Images for infiltrating ductal carcinoma (IDC). Left column: images at small strain; right column: images at large strain. Top row: B-mode ultrasound images; middle row: axial strain image; bottom row: relative shear modulus (secant) images.

3.2. Linear modulus and nonlinear parameter images

The two axial displacement estimates at minimal and large values of overall strain for each tumor were used in the nonlinear inverse elasticity algorithm in order to estimate the shear modulus at zero strain and the degree of nonlinearity. The boundary conditions, the shape functions and the grid size were the same as those for the secant modulus reconstructions and are described above. The regularization parameters for the shear modulus and the nonlinear parameter were set to 2 × 10⁻³. The weighting parameter for the small strain was set to w₁ = 100 and that for the large strain was set to w₂ = 1. The initial value of the infinitesimal strain shear modulus, μ, was set to 2 and it was constrained to lie in the interval (1, 20), while the initial value of the nonlinear parameter was set at γ = 1 and it too was confined to the interval (1, 20). The optimization iterations were stopped when the cumulative drop in the objective function over the final five iterations became smaller than 0.5% of its starting value. This took about 20 iterations for each case.

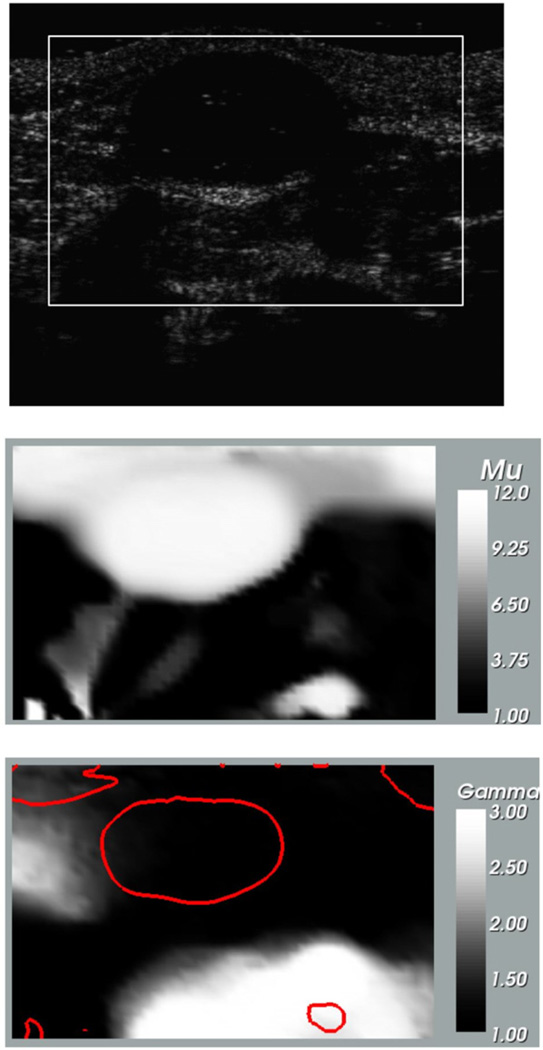
In figure 5 we have displayed the B-mode ultrasound, the infinitesimal strain relative shear modulus and the nonlinear parameter images for the fibroadenoma. We observe that tumor is clearly seen in the shear modulus image whereas it is absent from the nonlinear image. In order to locate the tumor in the nonlinear image we have plotted the iso-contour of μ = 10 in this image with a dark curve.

Figure 5.

Images for fibroadenoma. Top: B-mode ultrasound image at small strain; middle: relative shear modulus at zero strain (μ₀); bottom: nonlinear parameter (γ). The dark curve represents the iso-contour of μ = 10 and is plotted to locate the tumor in the nonlinear parameter image.

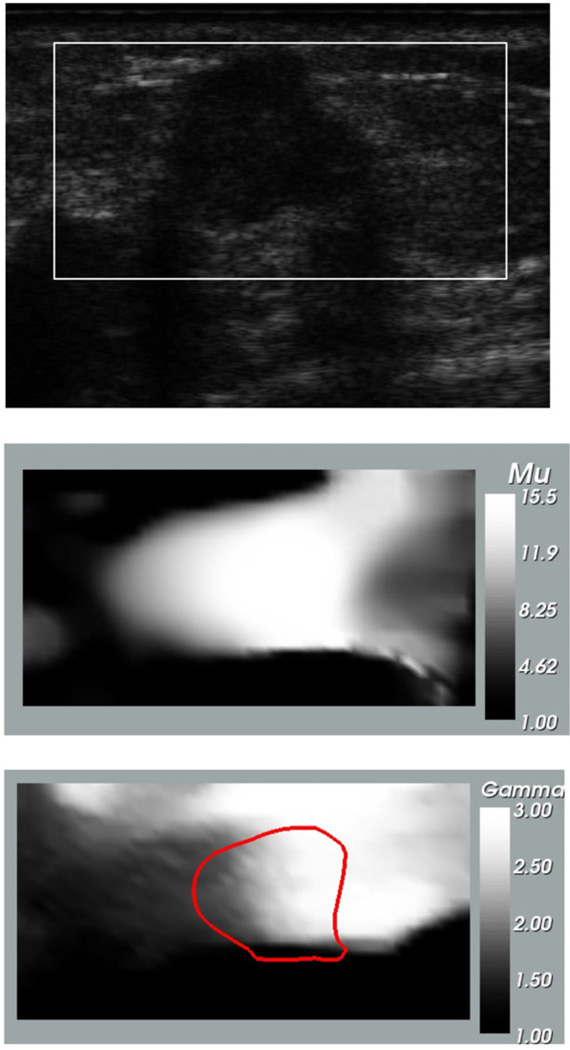
In figure 6 we have displayed the B-mode ultrasound, the infinitesimal strain relative shear modulus and the nonlinear parameter images for the IDC. We observe that tumor is clearly seen in the shear modulus image and a portion of the tumor and surrounding tissue also stand out in the nonlinear parameter image. This indicates that some tissue within the tumor and adjacent to it is stiffening in comparison with the background. The dark curve in the nonlinear image corresponds to the iso-contour of μ = 13.

Figure 6.

Images for infiltrating ductal carcinoma. Top: B-mode ultrasound image at small strain; middle: relative shear modulus at zero strain (μ₀); bottom: nonlinear parameter (γ). The dark curve represents the iso-contour of μ = 13 and is plotted to locate the tumor in the nonlinear parameter image.

4. Discussion

4.1. Fibroadenoma

By comparing the incremental strain image at minimal preloading with the strain image at 12% overall strain (figure 3) we observe that the region within the tumor is lighter in the latter. This indicates that in relation with the background the strain within the tumor has increased pointing to a relative softening of the tumor with respect to the surrounding tissue. This is seen more clearly in the relative secant modulus images at the two strain levels (figure 3). The ratio of the shear modulus of the tumor to the background is seen to decrease from about 10:1 to 7:1. In theory, we should expect the secant modulus at small strains to be a good approximation to the zero-strain shear modulus. Indeed, in figure 5 we see the image for the shear modulus at zero strain, is very similar (both quantitatively and qualitatively) to the secant modulus image at low strain (figure 3). This agreement between the two results provides a stringent test of the procedures used here, and of both reconstruction codes.

We observe in the nonlinear parameter image that the region within the tumor has about the same value as the background. On the other hand, the incremental strain images and the secant modulus images appear to indicate otherwise; that is, they imply the ratio of the tumor to background stiffness is slightly decreasing with increasing overall strain. These two observations may appear contradictory at first, however they may be reconciled once it is recognized that the strain and secant modulus images represent the nonlinear behavior of tissue about a local strain state and that the strain state within the tissue is inhomogeneous. In particular, the average strain within the tumor is less than the strain in the background, and therefore in these regions these images describe changes in modulus about two different strain states. The nonlinear parameter image, on the other hand, represents the nonlinear behavior of tissue that is unbiased by the local value of strain. This effect is explained in detail below with the help of a hypothetical tissue phantom.

We consider a simple phantom material comprised of three horizontal layers of incompressible materials that follow the Veronda–Westman constitutive law. The top and bottom layers, which we refer to as the background layers, are thick and made of the same material while the center layer is thin. All layers have the same nonlinear parameter γ_inclusion = γ_background = 3, while the shear modulus of the center layer is five times that of the background (μ_{0 inclusion} = 5, μ_{0 background} = 1). This specimen is a simplified model of the fibroadenoma we have studied above, in that the nonlinear parameter of the inclusion is the same as the background while its shear modulus is higher. This specimen is subjected to a uniaxial test with loading in the vertical direction. First we load to a small level of overall strain, say 1%. Since the center layer is thin, the overall strain of the entire specimen is approximately equal to the strain in the background, so the background strains by about 1%. Given this strain we evaluate the stress in the background using (4) and recognizing that the same stress must be transmitted to the inclusion, we once again use (4) to evaluate the strain in the inclusion to be 0.202%. Once we know the stress and strain in the background and the inclusion we can evaluate the secant modulus for these layers. The ratio of the secant modulus of the inclusion to the background turns out to be 4.95, which is very close to the ratio of their shear moduli at zero strain as might be expected. Next we load the specimen to 15% overall strain and once again assume that this is the strain in the background. Using the same approach as for the 1% case we then evaluate the stress in both layers and consequently the strain in the inclusion which is 4.32%. Note that this is much smaller than the strain in the background which is 15%. With this in hand we evaluate that the contrast in the secant modulus is equal to 3.47. Thus in going from 1% strain to 15% strain the contrast in the secant modulus has dropped from 4.95 to 3.47. A naive interpretation of this result might be that the inclusion has hardened less than the background and is therefore ‘less’ nonlinear, which we know to be incorrect. What has happened can be attributed to the fact that in both strain states the inclusion strains less than the background. In the small strain state the strain everywhere is too small to elicit a nonlinear response and in evaluating the secant modulus we end up measuring the unstrained tangent modulus in both the inclusion and the background. However for the large-strain state, the strain in the background is large enough so that it hardens with strain, while the strain in the inclusion is not large enough for this effect to be prominent. As a result, it appears that the background has become more stiff in the large-strain case.

4.2. Invasive ductal carcinoma

In the incremental strain images for the IDC the variation of strain contrast between the tumor and its surroundings from minimal preloading to 11% overall strain is not clearly seen (see figure 4). Even in the secant modulus images (figure 4) we observe that the modulus contrast does not change very much. Actually it appears to drop somewhat everywhere in the tumor except near the right edge where it increases very slightly. As for the nonlinear reconstructions, once again we observe that the shear modulus at zero strain (figure 6) is similar to the shear modulus at minimal preloading. In the nonlinear parameter image we observe that the parameter is elevated near the right edge of the tumor, indicating that it has a greater tendency to harden with strain.

As was the case with the fibroadenoma, the incremental strain images and the secant modulus images for the IDC initially appear to contradict the nonlinear parameter result. For the IDC the strain and secant images indicate that the stiffness contrast within the tumor does not change with increasing strain, whereas the nonlinear parameter image indicates that with increasing strain it stiffens at greater rate than the background. Once again this discrepancy can be attributed to smaller strain within the tumor and is explained below using a simple model for the IDC.

Like the fibroadenoma we model the IDC as a three-layer phantom. However in this case the inclusion (center layer) is more stiff (μ_{0 inclusion} = 5) and more nonlinear (γ_inclusion = 3) than the background (μ_{0 background} = 1, γ_background = 1). When we strain this sample to 1% strain in the background, the strain in the inclusion is 0.202%, which yields a contrast in the secant modulus of 4.96. When we strain the background to 15%, the strain in the inclusion is 3.6%. Thus the contrast in the secant modulus is 4.2. Based on the secant modulus results it would appear as though the inclusion is not hardening with strain (in fact it is softening slightly), while we know that its nonlinear parameter is much larger than the background. Once again the reason for this erroneous interpretation is that strain within the inclusion is smaller compared to the background. In the large overall strain state this causes the inclusion to harden less than it would have if it were strained to the same level as the background.

4.3. Measures of nonlinear behavior

In this study we have considered three measures of elastic tissue behavior: incremental strain images, secant modulus images and nonlinear elasticity images. It is useful to point out their relative merits.

1. Incremental strain images: strain images provide best resolution and require least computational effort. However they suffer from artifacts in that they can only be considered the reciprocal of stiffness images if the stress state is one dimensional. This is clearly not the case for the examples considered in this study. In addition these images reveal the nonlinear response of tissue at a given location about the local value of strain and since different regions may be subject to differing levels of strain, care must be exercised in interpreting them as images of nonlinear behavior.

2. Secant modulus images: secant modulus images require more computational effort than strain images because they involve the solution of a linear inverse elasticity problem. In order to keep these costs under check they are solved on a grid that is four times coarser than the strain images. As a result these images are at a lower resolution. However, the tumors clearly stand out in these images and their interpretation does not depend on the validity of the uniaxial stress assumption. For nonlinear elastic behavior these images suffer from the same drawback as strain images, as they too reveal the nonlinear behavior about the local strain state, which varies within the tissue.

3. Nonlinear elasticity images: nonlinear elasticity images (images of the shear modulus at zero strain and the nonlinear parameter) are computationally challenging and are evaluated at the same coarse resolution as the secant modulus images. Like the secant modulus images, they do not assume a one-dimensional stress state. In addition the nonlinear parameter image describes the nonlinear behavior of tissue independent of the local strain state. Hence it is independent of the type and magnitude of the load, and to that extent it provides the most objective assessment of nonlinear behavior of tissue. These images are, however, based on a specific form of the nonlinear stress–strain relation. As such, they incur errors if the tissue behavior is significantly different from this relation.

Finally, we close the discussion by noting that for the examples considered in this study, the nonlinear images are consistent with ex vivo results that indicate that with increasing strain, IDCs harden to a greater extent than fibroadenomas (Krouskop et al 1998, Wellman et al 1999). This points to the possibility of using nonlinear elasticity images in diagnosing malignant breast tumors. We also note that in the present study the strain within the tumor is modest even when the overall strain is close to 12%. A conservative estimate of this strain is the product of the overall strain and the ratio of shear modulus of the background to the tumor, that is $\approx 12\%\times \frac{1}{10}=1.2\%$. At this level of strain, the nonlinear behavior of the tumor may still be small and could be overwhelmed by measurement noise. Thus, for future studies we recommend that even higher values of overall strain, perhaps closer to 25% be employed.

5. Conclusions

The feasibility of imaging the linear and nonlinear elastic properties of breast tissue in vivo was established. The nonlinear behavior of tissue was measured in terms of three different metrics, namely, the variation of strain distribution with overall strain, the variation of the secant modulus distribution with overall strain and the distribution of linear and nonlinear elastic parameters. It was argued that of the three the last, that is distribution of nonlinear elastic parameters, most accurately represents the mechanical properties of the tissue. It was also demonstrated that it has the potential of improving the differential diagnosis of cancerous tumors.