Trimmed-likelihood estimation for focal lesions and tissue segmentation in multisequence MRI for multiple sclerosis.

Abstract

We present a new automatic method for segmentation of multiple sclerosis (MS) lesions in magnetic resonance images. The method performs tissue classification using a model of intensities of the normal appearing brain tissues. In order to estimate the model, a trimmed likelihood estimator is initialized with a hierarchical random approach in order to be robust to MS lesions and other outliers present in real images. The algorithm is first evaluated with simulated images to assess the importance of the robust estimator in presence of outliers. The method is then validated using clinical data in which MS lesions were delineated manually by several experts. Our method obtains an average Dice similarity coefficient (DSC) of 0.65, which is close to the average DSC obtained by raters (0.66).

I. Introduction

Multiple sclerosis (MS) is a chronic inflammatory-demyelinating disease of the central nervous system. Magnetic resonance imaging (MRI) detects lesions in MS patients with high sensitivity but low specificity, and is used for diagnosis, prognosis and as a surrogate marker in MS trials [1]. In these trials, the number of MS lesions and the total lesion load (TLL) have been used as markers [2].

Conventional MRI in MS usually consists in T2-weighted (T2-w), proton density (PD), fluid-attenuated inversion recovery (FLAIR), and T1-weighted (T1-w) with and without gadolinium enhancement [3]. MS lesions can occur in any tissue of the central nervous system but on conventional MRI, MS lesions in the gray matter (GM) have a signal intensity similar to the intensity of the surrounding normal appearing GM and therefore other specialized sequences are necessary to detect GM lesions [4]. On the contrary, white matter (WM) lesions are described as hyper-intense compared to the surrounding normal appearing WM on T2-w, FLAIR and PD sequences [5]. Depending on the intensity on the other sequences, lesions are classified as: T2-w lesions (iso-intense lesions on T1-w), black holes (hypo-intense lesions on T1-w) and active lesions (lesions enhanced by gadolinium). In this manuscript, the term MS lesions refers to all three types of lesions and no distinction is made among the three types. In order to avoid positive false lesion detections, MS lesions have to be present on more than one MRI sequence [6], which implies the use of multi-sequence approaches.

Manual segmentation of MS lesions has been used for the segmentation of MS lesions but it shows high intra- and inter-rater variability, and is very time consuming [7]. To reduce this variability, semi-automatic segmentation methods have been proposed [8], [9], [10]. In large clinical trials, semi-automatic segmentation methods need human raters to segment hundreds of images. The use of an automatic segmentation method should reduce the human interaction and improve reproducibility but the variability of MR protocols and the heterogeneity of the disease make it difficult to develop such automatic segmentation methods.

Several automatic segmentation methods for MS lesions have been presented that can be classified in two categories: supervised or data-driven. Supervised methods employ a test database of previously segmented images to learn the characteristics of MS lesions [11], [12], [13], [14]. The results of the supervised methods depend on the way the test database has been segmented and on the MR protocol of the database which may limit the interest of these approaches in multi-center trials.

Data-driven methods avoid the use of any sample database, extracting all the necessary information directly from the images [15], [16], [17], [18]. The majority of these data-driven methods models the distribution of the image intensities using a Gaussian mixture model (GMM), where each Gaussian law represents a tissue: e.g. cerebrospinal fluid (CSF), gray matter (GM) or white matter (WM). The GMM enables characterization of the image intensities with a reduced number of parameters. In healthy subjects [19], these parameters have been estimated using a maximum likelihood estimator (MLE) with an optimization method such as the Expectation-Maximization (EM) algorithm [20]. The EM algorithm has been widely used in this context because it is very easy to implement and always converges to a local maximum (or saddle point) of the data likelihood.

This approach has been extended to segment the normal appearing brain tissues (NABT) and the MS lesions in different ways. Some authors proposed a more complex model to include an extra class for MS lesions using an extra Gaussian [21] or a uniform probability density function [22]. However, MS lesions are heterogeneous thus it is difficult to model their intensities distribution. Another option is to treat the MS lesions as outliers to the standard 3-class model and modify the estimation method to account for these outliers. Following this idea, a modified EM algorithm [23] was presented where, in each iteration, voxels whose intensities are not well accounted for by the model were down-weighted to reduce their influence in the estimation process and an atlas was used to include the information about the expected location of the major tissue types. However, no proof of convergence of the algorithm was given.

In a similar way, the trimmed likelihood estimator (TLE) [24] was employed for the segmentation of MS lesions [25]. The main difference with the previous method is that the h percent of the points considered as outliers are completely rejected from the estimation, not only down-weighted. The parameter h, which has to be set manually, is a trade-off between the accuracy and the robustness of the estimation. The TLE can be computed using the FAST-TLE algorithm that has the same convergence properties as the EM algorithm for the MLE when h is constant. The TLE was combined with an atlas and a hidden Markov chain in the segmentation of lesions [26]. The authors proposed an adaptive h but no proof of convergence of the approach was given. In addition, the initialization of the FAST-TLE was performed using the MLE that reduces the robustness of the global approach.

In this paper, we propose a new automatic multi-sequence segmentation method for MS lesions and normal appearing brain tissues that does not require a training database or atlas information. A previous version of this method was presented in [27] and an extension using the mean shift algorithm was proposed in [28]. In this paper, we explain the method in greater detail and include significantly more validation when compared to the previous conference papers. We use the FAST-TLE to estimate the NABT tissues with a fixed h [24] and we propose a hierarchical initialization based on random initializations [29] to avoid its convergence to a local maximum and to provide an accurate initialization. The method segments all MS lesions in one class; a classification into the different lesion subtypes could be done afterwards using other algorithms [30], [25].

We validate our method using both simulated [31] and clinical data. On clinical images, our method is compared with five raters and another automatic segmentation method [23].

The paper is organized as follows. Section II explains the segmentation method. Results on simulated and clinical data are described in Sections III and IV respectively. We discuss our results in Section V.

II. Methods

The proposed method classifies each voxel of the brain as one of four classes: MS lesions, WM, GM, or CSF. We consider a typical MR protocol for MS (T1-w, T2-w and PD images) as input of our method. However, other sequences can be added with minimal modifications; for example, FLAIR images can be exchanged for PD images. Figure 1 illustrates the workflow proposed for the segmentation of MS lesions and NABT. MR images go through a preprocessing stage composed of three steps: correction of intensity inhomogeneities [32], and rigid registration of the T1-w image onto the T2-w image [33]. The T1-w image is used for skull stripping in order to focus the segmentation on the brain voxels [34]. Our segmentation method is composed of three steps: estimation of the NABT model, detection of candidate lesions, and application of a priori heuristic rules to extract the MS lesions from these outliers.

Fig. 1.

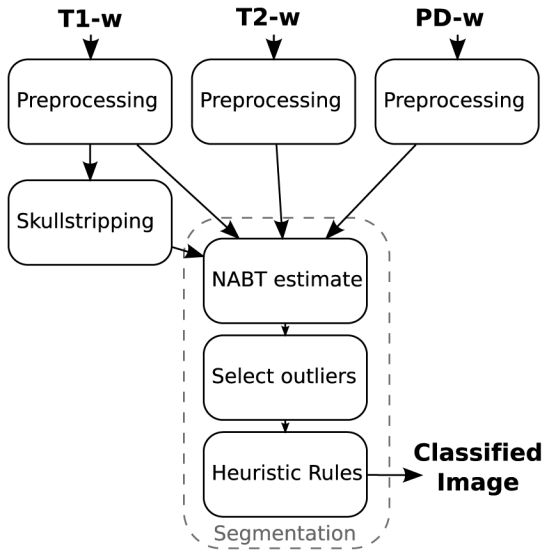
Workflow for the proposed automatic MS lesions segmentation

A. Estimation of NABT Model

In conventional MRI, the noise follows a Rician distribution [35], which can be approximated by a Gaussian distribution for high SNR [36]. The distribution of intensities within each brain structure is usually also approximated by a Gaussian distribution. We then model the image intensities of a healthy brain with a 3-class GMM, where each Gaussian represents one of the brain tissues WM, GM and CSF. We consider the m MR sequences as a multi-sequence image with n voxels. The intensity vector y_i = [y_i1 … y_im] of the voxel i can be modeled as follows,

$$f({\mathbf{y}}_i\mid \theta )=\sum _{j=1}^3{\alpha }_j·N({\mathit{\mu }}_j,{\mathbf{\sum }}_j)$$ (1)

where the mean μ_j and the covariance matrix Σ_j define the parameters of each Gaussian N(μ_j, Σ_j). These parameters and the mixing parameter α_j are merged in the parameter vector θ.

These parameters can be estimated using the MLE

$$\widehat{\theta }=\underset{\theta }{argmax}L(\theta )=\underset{\theta }{argmax}\prod _{i=1}^{n}f({\mathbf{y}}_i\mid \theta )$$ (2)

if we consider y_i as independent and identically distributed random variables, and L is the likelihood function.

In order to obtain the MLE, we can employ the EM algorithm [20], a technique which is used to iteratively estimate θ̂. From a given θ_l, the EM algorithm obtains another θ_l+1 where L(θ_l+1) ≥ L(θ_l). The algorithm is generally considered to have converged when θ_l+1 and θ_l are “sufficiently” close to each other.

This method is usually chosen because it is easy to implement and there is a proof of convergence, but it has two main drawbacks. The first drawback is that the EM algorithm does not ensure to reach the global maximum; different initial parameters θ₀ may lead to different solutions, which makes the choice of θ₀ an important issue. The second drawback is the sensitivity of the MLE to outliers. In statistics, this sensitivity is measured by the breakdown point (BP), which can be defined as the smallest number of outliers that can cause the estimator to take arbitrarily large values [37], and, in the case of the MLE, BP=0. In other words, a single outlier can cause at least one of the parameters to become arbitrarily large.

We propose two solutions to minimize the effect of these two drawbacks: employing a hierarchical initialization scheme in order to increase the chances of reaching the global maximum, and replacing the likelihood with the trimmed likelihood (TL) computed using a FAST-TLE algorithm [24].

1. Hierarchical Initialization

When using MLE, the initialization of the EM can be given by a probabilistic atlas, where each voxel contains the probabilities of belonging to the WM, GM or CSF. In [23], the atlas was linearly registered to the patient images and the initial tissue parameters (mean and variance) were computed using the probabilities given by the atlas. Such an atlas-based initialization method has two drawbacks; the registration is a time-consuming task, and may provide improper initializations in MS patients having considerable brain atrophy or lesion load.

In other clustering applications, a general approach uses the EM algorithm with different random initial parameters θ₀ and then selects the solution with maximum L; to gain more chances of reaching the global maximum, more starting parameters are needed, which increases the computational time.

Biernacki et al. [29] proposed to reduce the computational cost of the above-mentioned random technique with a four-step method. First, they chose multiple starting parameters at random. Second, they ran the EM algorithm for each set of starting parameters but, instead of waiting until the convergence of the algorithm, they provided intermediary parameters only after 50 iterations of the EM algorithm. Third, they selected the intermediate parameters providing the best likelihood and fourth, they ran the EM algorithm again until the convergence was reached, starting with the best intermediate parameters. In practice, the number of initial set of starting parameters needs to be high to cover the large range of possible solutions, and this number greatly increases in multidimensional spaces.

We propose a new method to initialize our multi-sequence NABT estimation which includes a priori information in order to reduce the computational cost. First, we perform a NABT estimation on the T1-w only, applying the initialization scheme proposed by Biernacki et al. [29] using 100 initial random parameters obtaining the mean and the variance for each tissue in T1-w. For the random initial parameters, the mean of each class is randomly drawn using a uniform distribution between the minimum and maximum of the image and the standard deviation of each class is set to a third of the standard deviation of intensities of the whole image. The advantage of using this random initialization only on one sequence is that the number of initializations can be reduced significantly compared to the multi-sequence approach and the T1-w is chosen because it has the best contrast between NABT.

By using the NABT parameters computed in the T1-w image, we compute an initial classification image of each tissue. One option would be to apply the same technique as in [23] considering this initial T1-w classification as our atlas, but that would lead to masks containing errors that can affect the estimation of the NABT parameters on the other sequences. In practice on T1-w, lesions are either classified as GM or WM depending on their intensity and errors in the extraction of the brain are typically classified as CSF. For this reason, a 256-bin histogram is computed for each tissue t ∈ CSF, GM, WM and sequence s ∈ T2, PD using the T1-w classification. The histogram is then smoothed using a Gaussian kernel with standard deviation of 5 bins and all modes of the histogram are found. For WM and GM where outliers are less important than in CSF, we set the initial μ_t,s as the absolute mode of the histogram, but for CSF, we set μ_CSF,s as the brightest mode. If this method is employed on FLAIR images, the μ_t,FLAIR of all tissues are set to the absolute mode because the outliers have less effect on the estimation of the CSF than on T2-w (skull-stripping errors and CSF are dark in FLAIR images).

We then compute the variance of each tissue and sequence using a robust variance estimator [38]

$${\sigma }_{s,t}^2={(1.4918·\mathit{med}(\mid y_i-{\mu }_{t,s}\mid ))}^2.$$ (3)

where med( ) is the median operator. The final covariance matrix for each tissue t that is used in the initialization of the FAST-TLE is given by

$$\left(\begin{array}{ccc}{\sigma }_{T1,t}^2& 0& 0\\ 0& {\sigma }_{T2,t}^2& 0\\ 0& 0& {\sigma }_{PD,t}^2\end{array}\right).$$ (4)

2. Trimmed Likelihood

Neykov et al. [24] proposed a modification of the MLE in order to make it more robust to outliers. The basic idea consists in maximizing the trimmed likelihood (TL) instead of the likelihood,

$$TL(\theta )=\prod _{i=1}^{k}f({\mathbf{y}}_{\nu (i)}\mid \theta )$$ (5)

where the trimming parameter k (n/2 < k ≤ n) determines how many voxels are rejected from the estimation and the function ν(i) sorts all voxels according to their probability f(y_ν(i)|θ). In other words, the likelihood is only computed with the k voxels that are the most likely to belong to the model. In the rest of the document, we employ the fraction $h=\frac{n-k}{n}$ where 0 ≤ h < 0.5. For h = 0, the TLE is equivalent to the MLE.

The TLE can be computed using the FAST-TLE algorithm [24]. First, a subset of k points is selected using ν(i) according to the initial parameters θ⁰. Second, the EM algorithm is employed to compute the MLE of these k points and obtain θ¹. These two steps are iterated until convergence. We can prove that FAST-TLE has the same convergence properties as the EM algorithm and that the breakdown point is h [37], which means that the TLE can obtain a good estimation of the data even if the data are contaminated with up to h outliers.

B. Detection of Candidate Lesions

A high value should be chosen for the trimming parameter h in order to ensure all MS lesions voxels and other artifacts are rejected from the estimation of the NABT model. In practice, the h rejected voxels contain some voxels that actually fit the NABT model reasonably well. Thus, we define the distance d_i as the minimal Mahalanobis distance of the voxel i from one of the Gaussians in the NABT model.

$$d_i=\underset{\forall j}{min}\left\{\sqrt{{({\mathbf{y}}_i-{\mathit{\mu }}_j)}^T{\mathrm{\sum }}_j^{-1}({\mathbf{y}}_i-{\mathit{\mu }}_j)}\right\}.$$ (6)

If we consider that the voxel intensities of each tissue follow a Gaussian law, the Mahalanobis distance follows a ${\chi }_m^2$ law with m degrees of freedom [25], [39], where m is the number of MR sequences. The voxel i is considered a candidate lesion when the distance d_i is greater than a threshold that is defined by the ${\chi }_m^2$ law for a given p-value p_maha.

C. A Priori Heuristic Rules

Candidate lesions detected with the Mahalanobis distance include MS lesions, vessels, registration errors, flow artifacts, noise, etc. We define three rules in order to discriminate MS lesion voxels from the other voxels: intensity rule, size rule and neighbor information rule.

1. Intensity Rule

MS lesions are known to be hyper-intense compared to the WM intensity on T2-w and PD-w and FLAIR sequences. We use the information given by the NABT model to define hyper-intensity.

A voxel is considered to be hyper-intense for a given sequence (e.g. T2-w) if its intensity y is greater than a threshold y_th that is defined by the probability of the Gaussian distribution

$$p_{\text{hyper}}={\int }_{y_{\text{th}}}^{\infty }N({\mu }_{\text{WM}}^{\text{T}2},{\sigma }_{\text{WM}}^{\text{T}2})dy.$$ (7)

If the voxel is not considered hyper-intense on T2-w and PD (and FLAIR, if this sequence is available), it is discarded as a lesion. Other intensity rules can also be defined for other subtypes of MS lesions [25].

2. Size Rule

In order to avoid false positives, candidate lesions smaller than 9 mm³ in size are rejected. These small candidate lesions are usually produced by noise or flow artifacts. In clinical practice, lesions must have a radius of 3 mm on one image slice to be considered as such [40].

3. Neighbor Information Rule

In MRI, external CSF may contain artifacts due to fluid flow. These effects can cause voxels in the cortex or external CSF to have intensities similar to MS lesions. In order to reduce the number of false positives due to these effects, we remove all candidate lesions that are not contiguous to WM voxels, as classified by the TLE, or that are contiguous to the brain mask border.

III. Validation Using Simulated Data

The McConnell Brain Imaging Center (Montréal, Qc, Canada) developed a realistic simulated brain image database freely available online¹ called BrainWeb [31]. This database was based on a realistic anatomic phantom and a MR simulator. The phantom was based on high-SNR MRI images of a healthy subject in order to obtain a realistic anatomy. To the original healthy phantom, they added MS lesions so as to obtain three MS phantoms with different lesion loads: mild (0.4 cm³), moderate (3.5 cm³) and severe (10.1 cm³). The MR simulator allowed the configuration of the MR acquisition parameters and the addition of image artifacts (noise and intensity inhomogeneity).

The advantage of BrainWeb is the existence of a ground truth that can be used in the evaluation of our automatic segmentation method. For this paper, we downloaded MR images (T1-w, T2-w and PD) obtained from the three MS phantoms with several levels of noise (n= 1%, 3%, 5%, 7% and 9% of the intensity of the brightest tissue) and intensity inhomogeneity (rf= 0%, 20% and 40%) with a resolution of 1 mm² in plane and 1 mm and 3 mm slice-thickness.

To compare the results of the segmentation with the ground truth, we employ the Dice similarity coefficient (DSC)

$$\text{DSC}=\frac{2\mid S\cap R\mid }{\mid S\mid +\mid R\mid }$$ (8)

where R is the reference segmentation and S is the segmentation. DSC ranges from 0.0 to 1.0 (perfect segmentation), with a value of 0.7 generally considered to be a good segmentation [41].

In this section, we describe three experiments on the BrainWeb images. The first experiment assesses the ability of the TLE to estimate the NABT model adequately. The second experiment studies the Mahalanobis distance and the a priori heuristic rules for the detection of lesions. The third experiment evaluates the segmentation results of our automatic method in presence of noise and intensity inhomogeneity. In order to focus in the segmentation method, no preprocessing (denoising or intensity inhomogeneity correction) is employed in this section.

A. Estimation of the NABT Model

We evaluated the accuracy and robustness of TLE with different h values when varying the slice thickness and the number of outliers. Typical outliers, other than MS lesions, come from errors occurring in the brain extraction step. Using BrainWeb images, we have simulated the two types of outliers.

The T1-w, T2-w and PD images from BrainWeb with 3% of noise and 20% of inhomogeneities and moderate lesion load were employed. In order to evaluate the influence of the resolution and partial volumes, both 3 mm slice-thickness and 1 mm slice-thickness were employed. Errors from the brain extraction step were simulated by dilating the perfect brain mask mask_gt from the phantom with spherical structuring elements of different sizes: 1, mask_r1 (4% of outliers); 2, mask_r2 (8% of outliers); and 3, mask_r3 (12% of outliers). Using the voxels already labelled as lesion in the original images, more lesions voxels were added to the original images, creating additional sets of three images with: 5% of outliers, 10% of outliers and 15% of outliers. The position of these new lesion voxels is not relevant in this experiment as no spatial information is used in the estimation of the NABT.

The NABT model was estimated for each simulated image with h varying from 0 (MLE) to 0.49 (limit of convergence). Each voxel was classified using the NABT model and the DSC was computed for each tissue (CSF, GM and WM). In this section, lesion detection was not performed because the focus was on the estimation of the NABT model only.

For brain extraction errors in 1 mm slice-thickness images (Figure 2), the DSC for MLE (h = 0) decreased when outliers were added to the image. This was more visible in CSF because there were less CSF voxels than GM or WM voxels, and the DSC is sensitive to the size of the segmentation target. Once h > outliers, the DSC was stable and similar to the value obtained when no outliers were present. Finally, when h ≫ outliers, the DSC dropped because too many points were rejected and the TLE failed to estimate the NABT model properly.

Fig. 2.

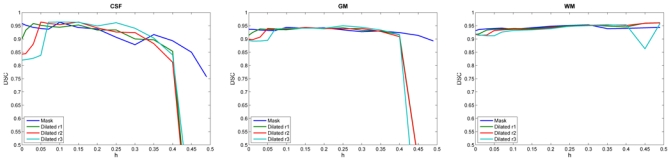
DSC for each brain tissue with variation of h on BrainWeb images (1mm slice-thickness) with errors in the brain extraction step. TLE algorithm shows a good stability when we increase the number of outliers compared to the MLE (h = 0.0).

For brain extraction errors in 3 mm slice-thickness images (Figure 3), the behavior of the TLE was similar to the one observed for 1 mm slice-thickness images. Due to the reduction in the number of brain voxels, the DSC values were lower and the instability happened for lower h when compared to the 1 mm slice-thickness images.

Fig. 3.

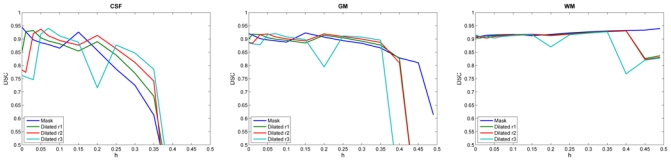
DSC for each brain tissue with variation of h on BrainWeb images (3mm slice-thickness) with errors in the brain extraction step. The same response as for 1mm slice-thickness is observed but enhanced by the reduced voxel resolution in the image, especially for high values of h.

When including lesions voxels as outliers, we observed the same behavior as for brain extraction errors (results only for 3 mm slice-thickness, Figure 4). The classification of WM was very affected by the inclusion of the outliers when h < outliers. Once h > outliers, the TLE obtained similar DSC values to those obtained with MLE with no outliers.

Fig. 4.

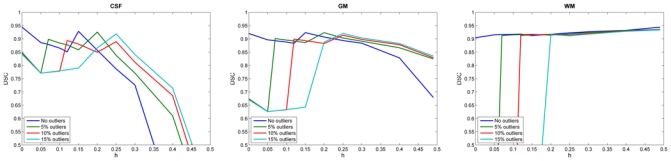
DSC for each brain tissue with variation of h on BrainWeb (3mm slice-thickness) images with an increased number of lesion voxels. The influence of outliers is reduced when h is larger than the number of outliers but when too many points are rejected the estimation is no longer accurate.

In our method, we set h = 0.25 for the segmentation of real images, which was high enough to cope with a high number of outliers but out of the instability range. Although when the perfect mask is employed for the BrainWeb images, we use h = 0.05 (Sections III-B and III-C).

B. Detection of Lesions

In our method, lesion detection consists of two steps: the detection of candidate lesions and the use of a priori heuristic rules to discriminate the true lesions from the other outliers. The detection of candidate lesions depends on the p_maha and the use of heuristic rules depends on p_hyper.

In this experiment, we employed the images T1-w, T2-w and PD with 1mm slice-thickness from BrainWeb with 3% noise and 20% inhomogeneity with the three available lesion loads (mild, moderate and severe). Segmentation was performed using the perfect brain mask extracted from the ground truth and with different values of p_maha and p_hyper. Our segmentation was compared to the ground truth using the DSC.

The results are displayed in Figure 5. The best DSC value varied for each lesion load, increasing with lesion load: mild (> 0.7), moderate (> 0.8) and severe (> 0.85). The DSC is sensitive to the size of the segmentation, which may explain the lower results of the mild lesion load compared to the severe lesion load [41].

Fig. 5.

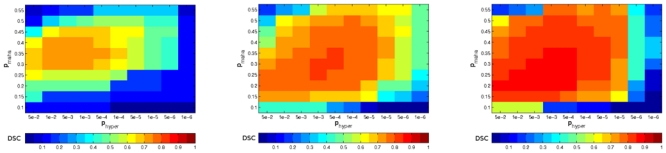
DSC values for the automatic segmentation varying the Mahalanobis threshold (p_maha) and the hyper-intensity definition (p_hyper) on the BrainWeb images. From left to right: mild, moderate and severe lesion loads. The optimal set of parameters on average is p_maha = 0.3 and p_hyper = 1 · 10⁻³.

Using these results, we obtained the optimal parameters of our method for the segmentation of lesions intersecting the zones of the graph using the best results of each lesion load, we obtained p_maha = 0.3 and p_hyper = 1 · 10⁻³ that we use as the optimal parameter for running our algorithm.

C. Noise and Intensity Inhomogeneity

Our algorithm was applied to segment the MS lesions in BrainWeb images with 1mm slice-thickness for all levels of noise, inhomogeneity and lesion load to give a complete evaluation of our algorithm. The brain mask was extracted from the ground truth and no other preprocessing was performed (no denoising, nor intensity inhomogeneity correction). The parameters found in the last section were used: h = 0.05, p_maha = 0.3 and p_hyper = 1 · 10⁻³. Our automatic segmentation was compared to the ground truth using the DSC.

Regarding the effect of noise on the segmentation (Figure 6), high levels of noise (n ≥ 7%) resulted in low DSC (< 0.5) and, for 1% of noise, the DSC was lower than for 3% of noise. Regarding the effect of inhomogeneity (Figure 6), the DSC scores of images with 40% of intensity inhomogeneity were lower than those of images with no inhomogeneity while images 0% and 20% of inhomogeneity obtained similar scores for 3% and 5% of noise. The DSC was higher when the lesion load increases, which can be explained by the above mentioned sensitivity of the DSC to the volume of lesions.

Fig. 6.

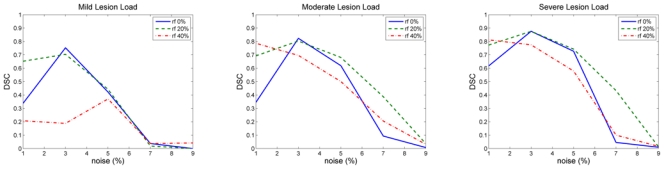
BrainWeb results: DSC values for the automatic segmentation performed by our algorithm for the three MS phantoms and all levels of noise and inhomogeneity.

The problems obtained for 1% of noise can be due to the instability of the EM algorithm for small covariances [42]. For 1% of noise, the results were improved when the inhomogeneity increased as the variance of each tissue also increased, reducing the problems of instability. For high levels of noise, our method failed to segment the image because it is based only on intensity. In presence of high levels of noise, we consider that the use of a denoising technique may be necessary [43].

The accuracy of our algorithm was reduced for high levels of inhomogeneity. Our approach assumes that the intensity of each tissue is constant and the inhomogeneity biases our estimation of the NABT model, reducing accuracy. In our setting, we propose to correct these intensity inhomogeneities in order to avoid this bias.

The relation between the DSC and the total lesion load can be associated with the dependency of the DSC on the target volume: for mild lesion loads, an error of one voxel causes the DSC to decrease more than for higher lesion loads because the measure is normalized by the size of the segmentation target [41].

IV. Validation Using Clinical Data

Ten MRI were acquired on a 1.5T Philips Gyroscan (Philips Medical Systems, Best, The Netherlands) scanner and MR protocol including FFE T1-w acquisition (TE=10 ms, TR=35 ms, angle=40°, FOV=250 mm, in-plane voxel size 0.97 × 0.97 mm²) and TSE dual echo (T2-w and PD) acquisition (TE1/TE2=30/90 ms, TR=2 s, angle=90°, FOV=250 mm, in-plane voxel size 0.97 × 0.97 mm²) with 3-mm axial slice thickness.

Five raters manually segmented MS lesions on every patient using the display² software developed at the McConnell Brain Imaging Center. In addition, all the raters segmented the same images again 8 months later. To sum up, each patient has 10 manual segmentations of the MS lesions, two times per rater.

Although manual segmentation performed by a unique rater is often used as a gold standard of the comparison between automatic methods, large intra-rater and inter-rater variability has been demonstrated in manual segmentation [7]. To reduce the influence of these variabilities, we built a consensus silver standard with manual segmentations, where a voxel was considered to be a part of a lesion if the majority of the manual segmentations considered it as a lesion. In the resulting consensus, isolated voxels were removed from the lesion class. The patients were ordered according to their total lesion load (TLL) (Table I).

TABLE I.

Total lesion load (TLL) in cm³ for the patients computed using the consensus silver standard.

Patient	1	2	3	4	5	6	7	8	9	10
TLL (cm3)	1.0	1.2	1.4	2.7	2.8	6.0	6.2	20.0	33.9	47.7

A. Evaluation of the hierarchical initialization

We performed an experiment to compare the two approaches of initialization described in Section II-A1: the atlas-based initialization and the hierarchical initialization. For the atlas-based initialization, the anatomical atlas [44] was linearly registered [33] to the patient image and the mean intensity and variance for each tissue using the probability of each tissue type given by the atlas. For the ten patients, we computed the initialization parameters with both methods and measured the time employed in the initialization. The log-likelihood was then computed with the initialization parameters (TL⁰) and with the solution of the FAST-TLE algorithm with h = 0.25 (TL^final).

The time employed by the atlas-based initialization was around 170 seconds while the hierarchical initialization took around 5 seconds in an Intel(R) Core(TM)2 Quad CPU 2.40GHz. with 4Gb. of memory. The log-likelihood using the atlas initialization ${TL}_{\mathit{atlas}}^0$ was always lower than the one obtained by the hierarchical initialization ${TL}_{\mathit{hier}}^0$ for every patient (average difference: ${TL}_{\mathit{hier}}^0-{TL}_{\mathit{atlas}}^0=71,705$), which is a good improvement compared to the difference between log-likelihood using the atlas initialization and the log-likelihood after convergence (average difference: ${TL}_{\mathit{atlas}}^{\mathit{final}}-{TL}_{\mathit{atlas}}^0=141,280$). The number of iterations required using the hierarchical initialization (494.3 ± 212.1) was smaller than the number of iterations using the atlas-based initialization (740.5 ± 252.4) and the final log-likelihood was larger using the hierarchical initialization than the atlas-based initialization for 6 patients (average difference: ${TL}_{\mathit{hier}}^{\mathit{final}}-{TL}_{\mathit{atlas}}^{\mathit{final}}=14,461$) and the same for the other 4 patients.

We conclude that the proposed hierarchical initialization is faster, providing a better initialization than the atlas initialization and resulting in less number of iterations until convergence and in a slightly better final log-likelihood.

B. Parameter h

We are unable to perform the same analysis of the TLE that the one performed with the simulated data because of the lack of information on the NABT in clinical images. Instead, the consensus silver standard was used to study the effects of h on the segmentation of MS lesions. The parameters of the lesion detection step were fixed as for simulated data (p_maha = 0.3 and p_hyper = 1e − 3) and the segmentations were performed for 0 ≤ h < 0.5. The segmentations were compared with the consensus silver standard using DSC.

The MLE (h = 0) obtained DSC values near or equal to zero (Figure 7). The MLE failed to obtain a good segmentation because the presence of outliers such as lesions, vessels and errors in the extraction of the brain, caused a sub-optimal estimation of the NABT model.

Fig. 7.

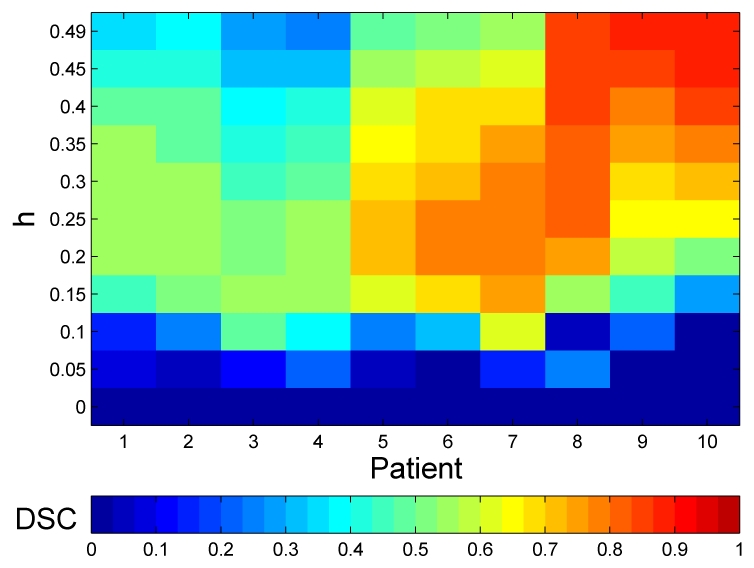
DSC values for the automatic segmentation on the clinical data when varying h.

Two different behaviors were observed according to the TLL of the patients for the TLE. The patients with low TLL (Patients 1 to 7) obtained their best scores when 0.15 < h < 0.35. These patients had a TLL similar to the simulated images and therefore had a similar behavior although they require a higher h because there are probably more outliers in real images than in the simulated images from BrainWeb.

On the contrary, the patients with the highest TLL (Patients 8,9 and 10) obtained their best DSC values when h = 0.49. The TLL of these patients was higher than 20cm³, which was more than twice the size of lesions in the BrainWeb database. The increase in the h for these patients was not proportional to the increase of TLL. Their lesions were less conspicuous and bright, and they were mixed with dirty white matter (Figure 10). For these patients, experts also segmented part of the dirty white matter as lesions and therefore h was required to be high for this patients to consider the dirty white matter as outliers and not only the lesions.

Fig. 10.

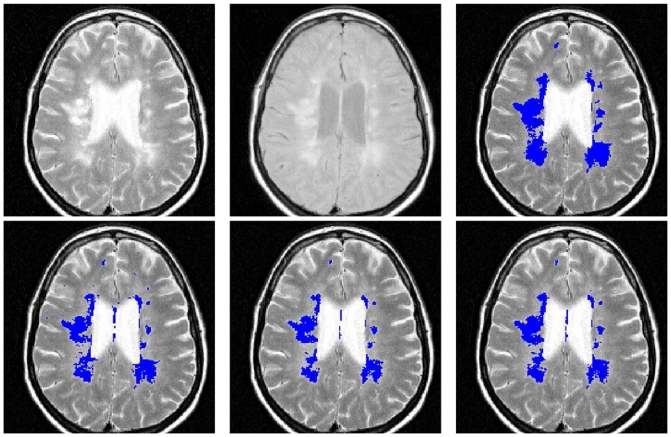
Slice from patient 9. Top, from left to right: T2-w, PD-w and consensus silver standard. Bottom, from left to right: EMS, TLEMS_h25 and TLEMS_h35 segmentations.

C. Comparison using DSC

We compared our method TLEMS (TLE for MS Segmentation) to the agreement between experts and to a publicly available method called EMS [23]³. EMS is an automatic segmentation method also based on the estimation of a GMM for the NABT. It uses a modified EM algorithm where voxels are down-weighted in the estimation according to the probability they have to be outliers. This method has one main parameter κ that adjusts the sensibility of the method to outliers. The modified EM algorithm also includes information from a brain atlas and corrects intensity inhomogeneity. It includes Markov random fields to avoid small lesion detection and intensity rules to select lesions from other outliers. The output of EMS is a probabilistic image of the MS lesions and a threshold of 0.5 was used to obtain the final binary segmentation. In order to obtain the optimal κ for our data, we employed EMS on our images varying κ from 2.6 to 3.6. We obtained the best results using κ = 3, which is the default value of EMS.

The similarity of every pair of manual segmentations was computed using DSC for each patient. The mean and the variance of these DSC values gave us a measure of the inter-rater agreement, we called these values the inter-rater DSC (IRDSC). For each automatic segmentation method, we computed the DSC with the consensus silver standard. For TLEMS, two different h values were selected: h = 0.25 (TLEMS_h25) and h = 0.35 (TLEMS_h35). Our method takes around 2 minutes to segment one image in an Intel(R) Core(TM)2 Quad CPU 2.40GHz. with 4Gb. of memory.

The IRDSC increased with the lesion load (Figure 8), which might be explained by the bias of DSC towards the lesion size. While the first four patients had values lower than 0.65, the last three patients were over 0.75. When we compared the automatic methods with the IRDSC, we observed that DSC values of TLEMS_h25 and TLEMS_h35 were within a standard deviation of the IRDSC or better in 8 out of 10 patients and EMS in 7 out of 10 patients only. TLEMS_h35 obtained the best results for the three last patients and was always better or similar than EMS for all patients. On the contrary, TLEMS_h25 obtained the best results for the first seven patients.

Fig. 8.

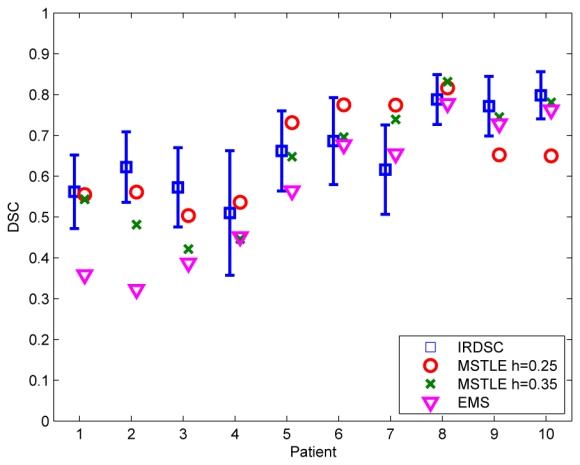
DSC values for the two automatic methods TLEMS and EMS and the mean ± one standard deviation of the agreement between raters (IRDSC).

The average DSC of TLEMS_h25 was 0.65, higher than the average of TLEMS_h35 (0.63) or EMS (0.56) and very close to the average of the IRDSC that was 0.66. Paired t-tests were performed on the DSC values of each segmentation method (p < 0.05). The DSC of EMS was significantly lower than those of IRDSC, TLEMS_h25 and TLEMS_h35, but the DSC TLEMS_h25 and TLEMS_h35 were not significantly different than IRDSC. Visual examples of the differences are shown for two patients with different TLL in Figures 9 and 10.

Fig. 9.

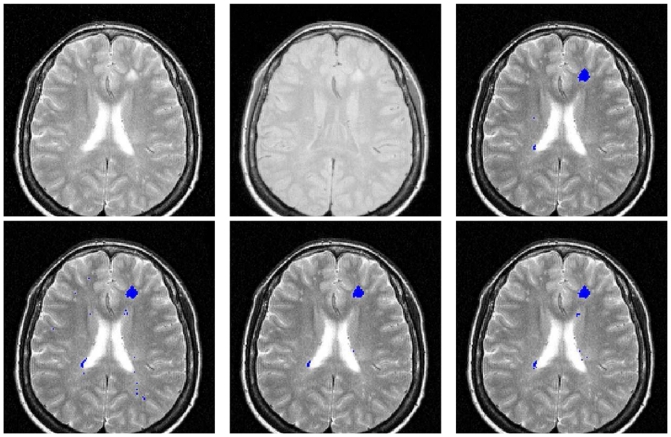
Slice from patient 5. Top, from left to right: T2-w, PD-w and consensus silver standard. Bottom, from left to right: EMS, TLEMS_h25 and TLEMS_h35 segmentations.

D. Comparison using STAPLE

The STAPLE (Simultaneous Truth And Performance Level Estimation) algorithm was designed to study the performance of different experts when the ground truth is not available [45]. This algorithm takes into account that all segmentation methods or experts are somehow imperfect and that their sensitivity and specificity can be measured. The sensitivity and specificity of each method is estimated using an EM approach that computes at the same time the STAPLE silver standard (SSS).

Once the SSS is created, we can compute the sensitivity Se and specificity Sp of other methods as follows

$$Se=\frac{{\sum }_{i=1}^n{D}_i·W_i}{{\sum }_{i=1}^n{W}_i}$$ (9)

$$Sp=\frac{{\sum }_{i=1}^n{\overline{D}}_i·(1-W_i)}{{\sum }_{i=1}^n(1-W_i)}$$ (10)

where D_i is the voxel i of the binary segmentation and W_i is the probability of the voxel i to be a lesion on the SSS and n is the number of voxels of the image. Our specificity measures are computed in the whole brain. Considering that the volume of lesions is small compared to the brain volume, specificity values are always close to one.

The first manual segmentation of every expert was employed for the computation of the SSS. Sensitivity and specificity were then computed for all automatic segmentations and the second manual segmentations using equations (9) and (10). This option provided a fair comparison of the experts and automatic methods because the manual segmentations for the evaluation were not the same as the ones employed in the creation of the SSS.

The results of the STAPLE evaluation are shown in Figure 11. Experts showed low sensitivity in the segmentation with the median for each patient going from 0.42 to 0.79. The variability among experts was large. The specificity of experts was higher for patients with lower sensitivity.

Fig. 11.

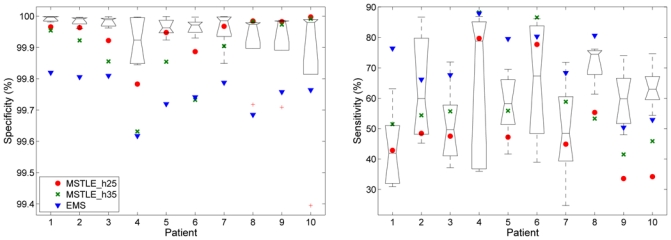
The boxplot shows the median and the quartiles of the specificity (left) and sensitivity (right) of the raters using the STAPLE algorithm using clinical data and the points show the results for the automatic methods: TLEMS_h25 and TLEMS_h35 and EMS. Experts segmented twice each image, the first manual segmentations were employed to create the STAPLE silver standard and the second ones were employed to evaluate the specificity and sensitivity of the experts.

EMS obtained a higher sensitivity than the experts in the majority of the images but a lower specificity. TLEMS_h25 and TLEMS_h35 showed a higher specificity than EMS and in the range of the experts in half of the patients. The sensitivity of both TLEMS_h25 and TLEMS_h35 was within the range of the experts in the first seven patients and was lower in the patients with the highest lesion load, which agreed with the results of the evaluation using the consensus silver standard.

E. Comparison using total lesion load

We studied the correlation between the TLL computed manually by the experts and the automatic methods using the Pearson’s correlation and the intraclass correlation coefficient (ICC) [46].

We computed the Pearson’s correlation coefficient between each pair of experts to obtain the inter-rater variability. We also employed the two manual segmentations performed by the same expert to obtain the intra-rater variability. Finally, we computed the correlation coefficient for the automatic methods compared to each rater. The average inter-rater correlation varied between 0.97 and 0.98 (Table III), similar to the intra-rater correlation. The automatic methods showed similar performance and very good correlations of 0.97 for EMS and TLEMS_h35, and 0.96 for TLEMS_h25.

TABLE III.

Pearson’s correlation coefficient between raters (inter- and intra-rater) and automatic methods

Rater	1	2	3	4	5	Average
1	-	-	-	-	-	0.97 ± 0.01
2	0.97	-	-	-	-	0.97 ± 0.01
3	0.98	0.96	-	-	-	0.98 ± 0.01
4	0.96	0.98	0.99	-	-	0.98 ± 0.01
5	0.98	0,98	0.99	0.99	-	0.98 ± 0.01
Intra-rater	0.97	0.98	0.98	0.98	0,98	0.98 ± 0.00
TLEMS_h25	0.97	0.94	0.97	0.95	0.97	0.96 ± 0.01
TLEMS_h35	0.95	0.97	0.97	0.97	0.98	0.97 ± 0.01
EMS	0.99	0.95	0.97	0.95	0.98	0.97 ± 0.01

The ICC gives measures the agreement all raters simultaneously contrary to the Pearson’s correlation that can only be used to compare two raters. According to the notation of [46], we used the third case of study proposed with one single measure (ICC(3,1)). We observed a very good agreement among the raters (ICC(3,1)=0.94). To evaluate the automatic methods, we computed the ICC using the five raters and each automatic method independently. The results were: EMS (ICC(3,1)=0.93), TLEMS_35 (ICC(3,1)=0.91) and TLEMS_h25 (ICC(3,1)=0.89). The ICC in all cases is large, which showed a good agreement between the volumes obtained by manual segmentation and the volumes computed by the automatic methods.

F. Segmentation using FLAIR images

During the 2008 Medical Imaging Computing and Computer Assisted Intervention conference (MICCAI 2008), a challenge on automatic segmentation of MS lesions was organized⁴. The organizers performed a comparison of the different methods proposed in an objective way.

Images from MS patients were separated into two groups: testing and training, and only the manual segmentation of the training data was available to tune the segmentation methods. Organizers kept the manual segmentation of the testing data making the participants blind to the final evaluation of the segmentation. Four metrics were employed: volume difference, average distance, true positives and false negatives. The comparison included data from two different sites and T1-w, T2-w, FLAIR and DWI images were available and lesions were segmented by two experts. Metrics were normalized between 0 and 100 considering 90 to be the experts’ agreement [47], where the experts’ agreement was computed as: 68% of volume difference, 75% of overlap error, 68% of true positive rate in lesion detection and 32% of false negative rate.

A preliminary version of our method [27], participated in the MICCAI challenge using T1-w, T2-w and FLAIR images. The images were already registered and upsampled by the organizers to isotropic 0.5 mm. Our pipeline included the intensity inhomogeneity correction of the three sequences [48] and skull-stripping [34] prior to using our automatic segmentation method. In this challenge, our method obtained the fourth place out of nine participants with a final score of 71 out of 100, not far from the winner score, which was 77.

V. Discussion

In this paper, we proposed a new algorithm for the segmentation of MS lesions, based on a TLE [24] which provides a good estimation of the intensity parameters of the NABT. In our experiments, we demonstrated how the trimmed likelihood estimator allows a better estimation compared to the maximum likelihood estimator when there are outliers. In our validation, the MLE was not able to correctly estimate the NABT model, which makes us think that a robust estimation is critical for any kind of model estimation in MR brain images.

Outliers include MS lesions but also other voxels that do not follow the NABT model such as skull-stripping errors, vessels or acquisition artifacts. As shown in the BrainWeb experiments, our method does not require a perfect brain mask in order to perform a accurate segmentation; errors in the skull-stripping process are correctly detected as outliers by the TLE without affecting the NABT model estimation. It suggests that the TLE could be used in order to reduce the skull-stripping errors and obtain a more accurate brain mask for atrophy studies.

We have proposed a new hierarchical method to initialize the estimation of the NABT without the use of an atlas. Similarly to the EM, k-means or the fuzzy c-means, the initialization of the TLE is important in order to avoid local maxima and get rid of the outliers but there is little information in the literature about how the methods are initialized. Our method takes into account the a priori information about the tissue intensity on each sequence and uses random initializations to reduce the risk of convergence to a local maximum of the trimmed likelihood.

Our method can work both with and without FLAIR images. FLAIR is a very sensitive sequence specially for periventricular lesions but it is known to be less sensitive than T2-w and PD in the posterior fossa and it is more prone to false positives. The use of both T2-w and FLAIR at the same time should give complementary information to improve the segmentation and we believe it should be the standard protocol for lesion segmentation. In clinical practice, FLAIR is not always employed and thus the development of methods without FLAIR images is still necessary.

Evaluation of segmentation algorithms in medical images is complicated because of the absence of a ground truth. We employed a simulated realistic phantom in order to evaluate our algorithm with different acquisition parameters, but these images are not as complex as real images and this first validation has to be seen only as a preliminary step before the real validation on clinical images. In the literature, most algorithms are compared to a manual gold standard, often defined by only a single rater. Manual segmentation is subject to high intra- and inter-rater variability [7]. We compared our algorithm with five raters in order to evaluate our algorithm, taking into account the variability among raters, thus enabling a more accurate evaluation of our algorithm. We also compared our method with a similar segmentation approach, EMS, showing that our method performs better than EMS specially for low lesion loads.

The relation between the volume of lesions and the number of rejected outliers cannot explain the necessity of h = 0.49 for patients high TLL shown in our experiments. Lesions on patients with high lesion loads seem less bright than in other patients because they are surrounded by dirty white matter and the definition of the lesion boundary is less obvious (Figure 10). The distinction of dirty white matter and lesions in some cases is very subtle and both definitions should be clarified in order to have more information to differentiate them. In addition, we employed BrainWeb images with different TLL to choose the optimal parameters for our method and therefore we obtained high DSC scores for patients with similar TLL compared with images from BrainWeb (≤10 cm³) but the patients with the highest TLL required an adaptation of the parameters. An extension of the BrainWeb database will be interesting in order to cover a wider range of TLL for MS patients to better evaluate the segmentation methods.

The TLE for the estimation of the NABT needs a fixed parameter h in order to guarantee convergence and there is no method to estimate the optimal value of h for a given image. We have proven that our algorithm can have a stable behavior once h is larger than the number of outliers but high values of h will result in a more robust but less accurate estimation. In the field of robust estimation in regression, several methods have been proposed in order to obtain high breakdown point while maintaining a good accuracy. The basic idea is to first perform a robust estimation with a method with a high breakdown point followed by a step to improve the accuracy of the estimation [38]. These methods could be adapted to the estimation of GMM in order to improve the estimation of the NABT parameters.

However, the results on clinical data show similar agreement of our method with the silver standard to the agreement between raters. The comparison of our method with other methods of the literature is complicated as few methods are freely available and each method is usually optimized for a specific MR protocol which make the comparison difficult. As shown in Table IV, the results of TLEMS are comparable with other results reported in the literature. Our method does not require registration of an atlas for the segmentation [23], [11], [49], [17] nor the use of a training database [49], [11]. In an effort to make the comparison with other methods possible, our application can be used online (http://www.irisa.fr/visages/benchmarks/).

TABLE IV.

Comparison of DSC for automatic segmentation methods from the literature with clinical and BrainWeb images (3% noise and 20% inhomogeneity). Each method uses different clinical images in its evaluation.

Method	Clinical Images	BrainWeb
TLEMS_ 25	0.65	0.72
[17]	0.63	0.81
[11]	0.60	0.79
[23]	0.51	0.80*
[16]	0.75	NA
[49]	0.61	NA
[50]	NA	0.63
[18]	NA	0.79*
[26]	NA	0.77

^*DSC was only computed on slices from 60 to 120

TABLE II.

DSC values for the raters agreement, EMS and TLEMS on clinical data using the consensus silver standard.

	Mean IRDSC	EMS	TLEMS_h25	TLEMS_h35
1	0.56	0.35	0.55	0.54
2	0.62	0.31	0.56	0.48
3	0.57	0.38	0.50	0.42
4	0.51	0.43	0.54	0.45
5	0.66	0.54	0.73	0.65
6	0.69	0.68	0.77	0.70
7	0.62	0.64	0.77	0.74
8	0.79	0.77	0.82	0.83
9	0.77	0.73	0.65	0.74
10	0.80	0.76	0.65	0.78
Average	0.66	0.56	0.65	0.63