DETECTING COPY NUMBER VARIATIONS FROM ARRAY CGH DATA BASED ON A CONDITIONAL RANDOM FIELD MODEL

Abstract

Array comparative genomic hybridization (aCGH) allows identification of copy number alterations across genomes. The key computational challenge in analyzing copy number variations (CNVs) using aCGH data or other similar data generated by a variety of array technologies is the detection of segment boundaries of copy number changes and inference of the copy number state for each segment. We have developed a novel statistical model based on the framework of conditional random fields (CRFs) that can effectively combine data smoothing, segmentation and copy number state decoding into one unified framework. Our approach (termed CRF-CNV) provides great flexibilities in defining meaningful feature functions. Therefore, it can effectively integrate local spatial information of arbitrary sizes into the model. For model parameter estimations, we have adopted the conjugate gradient (CG) method for likelihood optimization and developed efficient forward/backward algorithms within the CG framework. The method is evaluated using real data with known copy numbers as well as simulated data with realistic assumptions, and compared with two popular publicly available programs. Experimental results have demonstrated that CRF-CNV outperforms a Bayesian Hidden Markov Model-based approach on both datasets in terms of copy number assignments. Comparing to a non-parametric approach, CRF-CNV has achieved much greater precision while maintaining the same level of recall on the real data, and their performance on the simulated data is comparable.

1. Introduction

Structure variations in DNA sequences such as inheritable copy number alterations have been reported to be associated with numerous diseases. It has also been observed that somatic chromosomal aberrations (i.e. amplifications and deletions) in tumor samples have shown different clinical or pathological features in different cancer types or subtypes.^1–3 With remarkable capacity from current technologies in assessing copy number variants (CNVs), there is a great wave of interest recently from the research community to investigate inheritable as well as somatic CNVs.^1–8 Broadly speaking, there are essentially three technological platforms for copy number variation detections: array-based technology (including array comparative genomic hybridization (aCGH), as well as many other variants such as oligonucleotide array or bacterial artificial chromosome array), SNP genotyping technology,^3,4 and next-generation sequencing technology.⁹

Not surprisingly, various algorithms have been proposed for different data in recent years. The primary goal of all such studies is to identify and localize the copy number changes. One important commonality in data from different platforms is the spatial correlation among clones/probes/sequences. Many existing approaches have taken advantage of such a property by utilizing the same methodology, Hidden Markov Models (HMMs), which can conveniently model spatial dependence using a chain structure. Results have shown initial success^4,5,7,8 of HMMs. However, there is an inherited limitation for all these HMMs, i.e. they are all first-order HMMs and cannot take into consideration long-range dependence. We propose to develop and apply a novel undirected graphical model based on Conditional Random Fields (CRFs)¹⁰ for the segmentation of CNVs. It has been shown that CRFs consistently outperform HMMs in a variety of applications, mainly because CRFs can potentially integrate all information from data.¹⁰ This property makes CRFs particularly appealing for modeling CNV data since one can define feature functions using data from a region rather than a single or two data points for emissions and transitions, respectively, in HMMs.

Our major analytical contributions include the construction of the CRF model, the definition of effective feature functions using robust statistics, and the development of efficient computation algorithms for parameter estimations. As an illustration of our proposed model, we have applied our approach on real and simulated data based on array technology, and compared its performance with two popular segmentation algorithms. Experimental results have demonstrated that CRF-CNV outperforms a Bayesian Hidden Markov Model-based approach on both datasets in terms of copy number assignments, with little sacrifice of accuracy in breakpoint identification due to smoothing. Compared to a non-parametric approach, CRF-CNV has achieved much greater precision while maintaining the same level of recall on the real data. On the simulated data, CRF-CNV has obtained better accuracy in identifying breakpoints with comparable performance in copy number assignments.

The remainder of this article is organized as follows. In Sec. 2, we give a brief overview of aCGH data and existing approaches for detecting CNVs from aCGH data. We also briefly mention the differences between HMMs and CRFs. Details about model developments and implementations are provided in Sec. 3. Our experimental results on two datasets and comparisons with other two programs are presented in Sec. 4. We conclude the paper with a few discussions in Sec. 5.

2. Preliminary

2.1. ACGH data and analysis

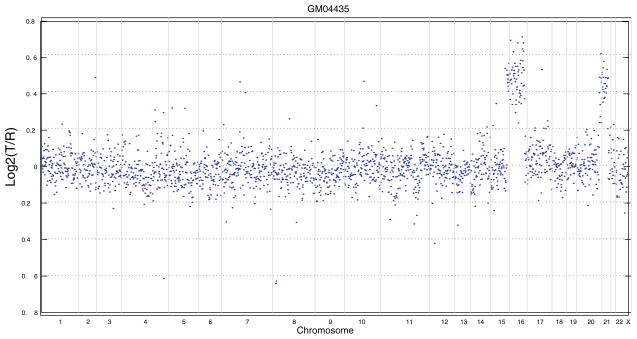
Though theoretically, our approach can be applied to data from different experimental platforms, we focus primarily on aCGH data in this analysis. Mathematically, aCGH data usually consist of an array of log₂ intensity ratios for a set of clones, as well as the physical position information of each clone along a genome. Fig. 1 plots the normalized log₂ ratio of one cell line (GM04435) analyzed by Snijders et al.¹¹ Each data point represents one clone and the y-axis represents normalized log₂ intensity ratio. The primary goal in CNV detection based on aCGH is to segment a genome into discrete regions that share the same mean log₂ ratio pattern (i.e. have the same copy numbers). Ideally, the log₂ ratio of a clone should be 0 if the cancer sample/cell line has a normal number (i.e. 2) copies of DNA, and the value should be around 0.585 (or −1) if it has one copy of gain (or loss). However, as shown in Fig. 1, aCGH data can be quite noisy with vague boundaries between different segments. It may also have complex local spatial dependence structure. These properties make the segmentation problem intrinsically difficult. Approaches using a global threshold generally do not work in practice.

Fig. 1.

Array CGH profile of a Corriel cell line (GM04435). The borders between chromosomes are indicated by vertical bars.

2.2. Existing algorithms

In general, a number of steps are needed to detect copy number changes from aCGH data. First, raw log₂ ratio data usually needs some pre-processing, including normalization and smoothing. Normalization is an absolute necessary step to alleviate systemic errors due to experimental factors. Usually the input data is normalized by making the median or mean log₂ ratio of a selected median set from normal copy number regions to be zero. Smoothing is used to reduce noises that are due to random errors or abrupt changes. Smoothing methods generally filter the data using a sliding window, attempting to fit a curve to the data while handling abrupt changes and reducing random errors.

The second step in analyzing aCGH data is referred to as segmentation and aims to identify contiguous sets of clones (segments) that share the same mean log₂ ratio. Broadly, there are two related estimation problems. One is to infer the number and statistical significance of the alterations, the other is to locate their boundaries accurately. A few different algorithms have been proposed to solve these two estimation problems. Olshen et al.¹² have proposed a non-parametric approach based on the recursive circular binary segmentation (CBS) algorithm. Hupe et al.¹³ have proposed an approach called GLAD, which is based on a median absolute deviation model to separate outliers from their surrounding segments. Willenbrock and Fridlyand¹⁴ have compared the performance of CBS (implemented in DNA-Copy) and GLAD using a realistic simulation model, and they have concluded that CBS in general is better than GLAD. After obtaining the segmentation outcomes, a post-processing step is needed to combine segmentations with similar mean levels and to classify them as single-copy gain, single-copy loss, normal, multiple gains, etc. Methods such as GLADMerge¹³ and MergeLevels¹⁴ can take the segmentation results and label them accordingly.

As noted by Willenbrock and Fridlyand,¹⁴ it is more desirable to perform segmentation and classification simultaneously. An easy way to merge these two steps is to use a linear chain HMM. A few variants of HMMs have been proposed for aCGH data in recent years.^7,15 Guha et al.¹⁵ have proposed a Bayesian HMM which can impose biological meaningful priors on the parameters. Shah et al.⁷ have extended this Bayesian HMM by adding robustness to outliers and location-specific priors, which can be used to model inheritable copy number polymorphisms. Note that all these models are first-order HMMs which cannot capture long-range dependence. Intuitively, it makes sense to consider high-order HMMs to capture informative local correlation, which is an important property observed from aCGH data. However, considering higher orders will make HMMs more complex and computationally intensive.

2.3. Conditional random fields

To overcome the limitations of HMMs, we propose a new model based on the theory of Conditional Random Fields (CRFs). CRFs are undirected graphical models designed for calculating the conditional distribution of output random variables Y given input variables X.¹⁰ It has been extensively applied to language processing, computer vision, and bioinformatics with remarkable performance when compared with directed graphical models including HMMs. The key difference between CRFs and HMMs is that one can define meaningful feature functions that can effectively capture local spatial dependence among observations.

In general, a linear-chain CRF (Fig. 2) is defined as the conditional distribution

Fig. 2.

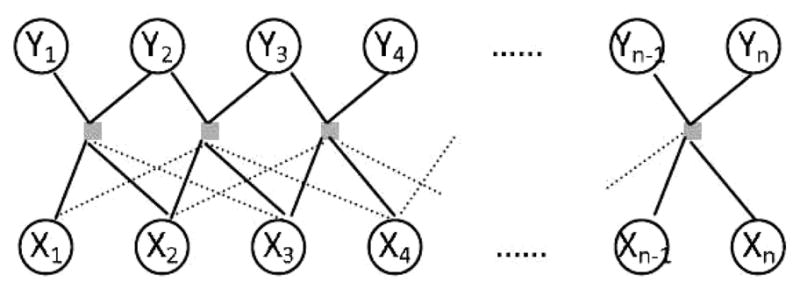
A linear chain conditional random field model for array CGH data.

$$P(Y\mid X)=\frac{1}{Z_{\theta }(X)}exp\left\{\sum _{i=2}^n\sum _{j=1}^{S(i)}{\theta }_{ij}{f}_{ij}(Y_{i-1},Y_i,{\stackrel{\sim }{X}}_i)\right\},$$

where the partition function

$$Z_{\theta }(X)=\sum _{Y}exp\left\{\sum _{i=2}^n\sum _{j=1}^{S(i)}{\theta }_{ij}{f}_{ij}(Y_{i-1},Y_i,{\stackrel{\sim }{X}}_i)\right\}.$$

Here θ = {θ_ij} are parameters. Functions {f_ij} are feature functions. X̃_i is a neighbor set of X_i that are needed for computing features related clone i and i + 1. S(i) is the total number of feature functions related to clone i and i + 1.

We will use a linear-chain CRF model for CNV detection. Our feature functions to be defined can use observed data from a region. Therefore, it can capture abundant local spatial dependence. In addition, by using a linear-chain CRF, we can effectively combine smoothing, segmentation and classification into one unified framework.

3. Methods

3.1. Linear-chain CRF model for aCGH data

Our model is based on the linear-chain CRF Model in Fig. 2. Let X = (X₁,…, X_n) denote the normalized log₂ ratio intensities along one chromosome for an individual, where X_i is the log₂ ratio for clone i. One can assume that these n clones are sequentially positioned on a chromosome. Let Y = (Y₁, …, Y_n) denote the corresponding hidden copy number state, where Y_i ∈{1, …, s} and s the total number of copy number states. These states usually indicate deletion, single-copy loss, neutral, single-copy gain, two-copy gain or multiple-copy gain. The exact number of states and their meaning need to be specified based on specific input data. X̃_i(u) is defined as a neighbor set of X_i around clone i, i.e. X̃_i(u) = {X_i−u,…, X_i−1, X_i, X_i+1, …, X_i+u}, where u is a hyper-parameter to define the dependence length. Similarly, we define X̃_i,i+1(u) = {X_i−u,…, X_i, X_i+1,…, X_i+1+u}, ${\stackrel{\sim }{X}}_{i,i+1}^{-}(u)=\{X_{i-u},\dots ,X_{i-1},X_i\}$ and ${\stackrel{\sim }{X}}_{i,i+1}^{+}(u)=\{X_{i+1},X_{i+2},\dots ,X_{i+1+u}\}$. The dependence length u plays a similar role like the width of a sliding window in smoothing methods. The conditional probability of Y given observed log₂ ratio X based on our linear-chain CRF structure can be defined as

$$P(Y\mid X)=\frac{1}{Z_{\theta }(X)}exp\left\{\sum _{i=1}^n\sum _{j=1}^s[{\lambda }_j{f}_j(Y_i,{\stackrel{\sim }{X}}_i(u))+{\mu }_j{g}_j(Y_i,{\stackrel{\sim }{X}}_i(u))]+\sum _{j=1}^s{\omega }_j{l}_j(Y_1,{\stackrel{\sim }{X}}_1(u))+\sum _{i=1}^{n-1}\sum _{j=1}^s\sum _{k=1}^s{\nu }_{jk}{h}_{jk}(Y_i,Y_{i+1},{\stackrel{\sim }{X}}_{i,i+1}(u))\right\},$$ (1)

where the partition function

$$Z_{\theta }(X)=\sum _{Y}exp\left\{\sum _{i=1}^n\sum _{j=1}^s[{\lambda }_j{f}_j(Y_i,{\stackrel{\sim }{X}}_i(u))+{\mu }_j{g}_j(Y_i,{\stackrel{\sim }{X}}_i(u))]+\sum _{j=1}^s{\omega }_j{l}_j(Y_1,{\stackrel{\sim }{X}}_1(u))+\sum _{i=1}^{n-1}\sum _{j=1}^s\sum _{k=1}^s{\nu }_{jk}{h}_{jk}(Y_i,Y_{i+1},{\stackrel{\sim }{X}}_{i,i+1}(u))\right\}.$$

Here θ = {λ_j, μ_j, ω_j, ν_jk} are parameters that need to be estimated. Functions f_j, g_j, l_j and h_jk are feature functions that need to be defined. For notational simplification, we drop the parameter u in our subsequent discussions and write X̃_i(u) as X̃_i and etc. Parameters, feature functions and main variables in our model are summarized in Table 1.

Table 1.

Notation for key elements in our CRF-CNV model.

n	Number of clone
s	Number of copy number state
Xi	log2 ratio for clone i
Yi	Hidden copy number state for clone i
u	Dependent length
σ2	Penalization coefficient
aj	Mean log2 ratios with copy number state j
λj, μj	Emission parameters
fj, gj	Emission feature functions
ωj, νjk	Transition parameters
lj, hjk	Transition feature functions
X̃i(u)	Neighbor set of Xi
X̃i,i+1(u)	Neighbor set of Xi and Xi+1

3.2. Feature functions

One important step to build our model is to define meaningful feature functions that can capture critical information from input data. Essentially, we define two types of feature functions, analogous to the emission and transition probabilities in HMMs. However, our feature functions can be of any form. Therefore, our model can provide much more flexibility and be able to capture long-range dependence. The emission feature functions f_j (Y_i, X̃_i) and g_j (Y_i, X̃_i) are defined as follows

$$f_j(Y_i,{\stackrel{\sim }{X}}_i)=\{\begin{array}{ll}\mathit{med}{\stackrel{\sim }{X}}_i\hfill & \text{if}{Y}_i=j\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}{g}_j(Y_i,{\stackrel{\sim }{X}}_i)=\{\begin{array}{ll}{(\mathit{med}{\stackrel{\sim }{X}}_i)}^2\hfill & \text{if}{Y}_i=j\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$

where med X̃_i is defined as the median value of set X̃_i. Our emission features serve two purposes. First, they are used as a median filter that will automatically smooth the input data. More importantly, the feature functions based on the first-order and second-order median statistics are robust sufficient statistics one can derive from a normal distribution, which resemble the emission pattern of log₂ ratio intensities for a given hidden copy number state.

The transition feature function h_jk(Y_i, Y_i+1, X̃_i,i+1) and the initial feature function l_j (Y₁, X̃₁) are defined as follows

$$\begin{array}{c}{h}_{jk}(Y_i,Y_{i+1},{\stackrel{\sim }{X}}_{i,i+1})=\{\begin{array}{ll}\frac{(a_{j+1}-a_j)/2+(a_{k+1}-a_k)/2}{(a_{j+1}-a_j)/2+(a_{k+1}-a_k)/2+\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{-}-a_j+\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{+}-a_k}\hfill & \text{if}{Y}_i=j,\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{-}\ge a_j,Y_{i+1}=k,\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{+}\ge a_k\hfill \\ \frac{(a_{j+1}-a_j)/2+(a_k-a_{k-1})/2}{(a_{j+1}-a_j)/2+(a_k-a_{k-1})/2+\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{-}-a_j+a_k-\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{+}}\hfill & \text{if}{Y}_i=j,\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{-}\ge a_j,Y_{i+1}=k,\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{+}<a_k\hfill \\ \frac{(a_j-a_{j-1})/2+(a_{k+1}-a_k)/2}{(a_j-a_{j-1})/2+(a_{k+1}-a_k)/2+a_j-\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{-}+\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{+}-a_k}\hfill & \text{if}{Y}_i=j,\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{-}<a_j,Y_{i+1}=k,\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{+}\ge a_k\hfill \\ \frac{(a_j-a_{j-1})/2+(a_k-a_{k-1})/2}{(a_j-a_{j-1})/2+(a_k-a_{k-1})/2+a_j-\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{-}+a_k-\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{+}}\hfill & \text{if}{Y}_i=j,\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{-}<a_j,Y_{i+1}=k,\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{+}<a_k\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}\\ l_j(Y_1,{\stackrel{\sim }{X}}_1)=\{\begin{array}{ll}\frac{(a_{j+1}-a_j)/2}{(a_{j+1}-a_j)/2+\mathit{med}{\stackrel{\sim }{X}}_1-a_j}\hfill & \text{if}{Y}_1=j,\mathit{med}{\stackrel{\sim }{X}}_1\ge a_j\hfill \\ \frac{(a_j-a_{j-1})/2}{(a_j-a_{j-1})/2+a_j-\mathit{med}{\stackrel{\sim }{X}}_1}\hfill & \text{if}{Y}_1=j,\mathit{med}{\stackrel{\sim }{X}}_1<a_j\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\end{array}$$

Here a_j denotes the mean log₂ ratio for clones with copy number state j (j = 1, …, s). a₀ and a_s+1 denote the greatest lower bound of log₂ ratio for clones with copy number state 1 and the least upper bound of log₂ ratio for clones with copy number state s, respectively. Without loss of generality, we assume a₀ < a₁ < ··· <a_s+1. We define the initial feature function l_j (Y₁, X̃₁) such that data from the clone set X̃₁ will only provide information to its own labelled state. Furthermore, when Y₁ = j, the closer the med X̃₁ to a_j, the higher value for l_j (Y₁, X̃₁), the more information data will provide and contribution to parameter ω_j is higher. It will achieve the highest value of 1 when med X̃₁ = a_j. The transition feature function h_jk (Y_i, Y_i+1, X̃_i,i+1) is similarly defined using the clone set X̃_i,i+1. When Y_i = j and Y_i+1 = k, the closer the $\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{-}$ to a_j and the $\mathit{med}{\stackrel{\sim }{X}}_{i,i+1}^{+}$ is to a_k, the higher the value for h_jk(Y_i, Y_i+1, X̃_i,i+1), and the data will contribute more information to ν_jk. Clearly, both types of our feature functions can capture the local spatial dependence over a set of adjacent clones, thus potentially providing more robust inference about hidden copy number states.

The feature functions in our CRF-CNV model can be regarded as a generalization of feature functions in HMMs. (see Appendix A). The transition feature functions of HMMs are index functions. They do not depend on observations. However, our transition feature functions can capture the local spatial dependence over a set of adjacent clones. The way we define feature functions embodies the core idea of CRFs, which make our CRF-CNV model more promising.

3.3. Parameter estimation

Unlike the standard algorithms for HMM training, there are significant computational challenges to efficiently and accurately estimate parameters for CRFs. Implementation of the training algorithms for our proposed CRF model requires sophisticated statistical and numerical algorithms. To our best knowledge, no existing implementations can be trivially used to solve our problem. We propose the following algorithm for the parameter estimation.

In general, given a set of training data 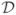= {(X^(d), Y^(d)), d = 1, …, D}, to estimate parameter θ in model (1), one needs to maximize a penalized conditional log likelihood which is defined as follows

$$\begin{array}{l}{L}_{\theta }=\sum _{d=1}^D\mathit{logP}(Y^{(d)}\mid X^{(d)})-\frac{{\left|\right|\theta \left|\right|}^2}{2{\sigma }^2}\\ =\sum _{j=1}^s{\lambda }_j\sum _{d=1}^D\sum _{i=1}^n{f}_j(Y_i^{(d)},{\stackrel{\sim }{X}}_i^{(d)})+\sum _{j=1}^s{\mu }_j\sum _{d=1}^D\sum _{i=1}^n{g}_j(Y_i^{(d)},{\stackrel{\sim }{X}}_i^{(d)})+\sum _{j=1}^s{\omega }_j\sum _{d=1}^D{l}_j(Y_1^{(d)},{\stackrel{\sim }{X}}_1^{(d)})+\sum _{j=1}^s\sum _{k=1}^s{\nu }_{jk}\sum _{d=1}^D\sum _{i=1}^{n-1}{h}_{jk}(Y_i^{(d)},Y_{i+1}^{(d)},{\stackrel{\sim }{X}}_{i,i+1}^{(d)})-\sum _{d=1}^D{\mathit{logZ}}_{\theta }(X^{(d)})-\frac{{\left|\right|\theta \left|\right|}^2}{2{\sigma }^2}.\end{array}$$ (2)

Here D is the number of training samples, ||θ|| is the L² norm of θ, σ² is the penalization coefficient. The penalization term ||θ||²/2σ² is added for regularization purpose. Before one can solve the optimization problem, one has to first specify an additional set of hyper-parameters that include the dependence length u, the mean log₂ ratios {a_j, j = 0, …, s + 1} and the penalization coefficient σ². The set of {a_j} can be directly estimated given the training data set 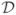, i.e. the maximum likelihood estimate of a_j is just the mean value log₂ ratios of all clones with copy number state j in 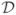for j = 1, …, s. While a₀ and a_s+1 can be imputed using the minimum log₂ ratio of all clones with copy number state 1, and the maximum value from all clones with copy number state s, respectively. For the dependent length u and the penalization coefficient σ², we rely on a grid search approach through cross-validation. More specifically, the original training set 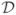will first be partitioned into two sets 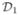and 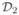. We call 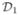the new training set and 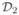the validation set. For a given range of (discrete) parameter values of u and σ², we train the model on 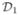and get estimates of θ for each fixed pair of (u₀, ${\sigma }_0^2$). The exact procedure to estimate θ given (u₀, ${\sigma }_0^2$) will be discussed shortly. We then apply the trained model with estimated parameters on the validation set 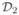and record the prediction errors under the current model. The model with the smallest prediction error as well as their associated parameters (u, σ², θ) will be chosen as the final model. The prediction error is defined as the mean absolute error (MAE) for all samples in the validation set 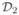. The absolute error for a clone i is defined as |Y_i − Ŷ_i|, where Y_i is the known copy number and Ŷ_i is the predicted copy number for clone i. This measure not only captures whether a prediction is exactly the same as the real copy number, but also reflects how close these two numbers are.

For a given set of hyper-parameters {a_j}, u and σ², the optimization of L_θ in Eq. (2) can be solved using gradient-based numerical optimization methods.¹⁶ We choose the non-linear Conjugate Gradient (CG) method in our implementation, which only requires the computation of the first derivatives of L_θ. The partition function Z_θ(X) in the log likelihood and the marginal distributions in gradient functions can be computed using forward-backward algorithms. Due to page limitation, we provide the technical details of the CG method and the efficient computation of the derivatives of L_θ in Appendix B.

For graphical model based approaches such as HMMs, many researchers group both individuals and chromosomes in the analysis of aCGH data, which can dramatically reduce the number of parameters needed without sacrificing much inference accuracy. We also take a similar approach. This is reflected by our homogeneous CRF structure.

3.4. Evaluation methods

We have implemented the above proposed approach as a Matlab package termed CRF-CNV and evaluated its performance using a publicly available real dataset with known copy numbers¹¹ and a synthetic dataset from Willenbrock and Fridlyand.¹⁴ Notice that many clones have normal (2) copies of DNAs, therefore the number of correctly predicted state labels is not a good measure of performance of an algorithm. Instead, we compare the performance of CRF-CNV with two popular programs in terms of the number of predicted segments and the accuracy of segment boundaries, referred to as breakpoints. To summarize the performance of an algorithm over multiple chromosomes and individuals, we use a single value called F–measure, which is a combination of precision and recall. Recall that given the true copy number state labels and predicted labels, precision (P) is defined as $\frac{\mathit{ntp}}{np}$ and recall (R) is defined as $\frac{\mathit{ntp}}{nt}$, where ntp is the number of true positive (correctly predicted breakpoints), np is the number of predicted breakpoints, and nt is the number of true breakpoints. F -measure is defined as F = 2P R/(P + R), which intends to find a balance between precision and recall. The two programs we chose are CBS¹² and CNA-HMMer,⁷ both of which have been implemented as Matlab tools. As mentioned earlier, CBS is one of the most popular segmentation algorithms and different groups have shown that it generally performs better than many other algorithms. CNA-HMMer is chosen because we want to compare the performance of our CRF model with HMMs, and CNA-HMMer is an implementation of Bayesian HMM model with high accuracy.⁷

4. Experimental Results

4.1. A real example

The Coriell data is regarded as a well-known “gold standard” dataset which was originally analyzed by Snijders et al.¹¹ The data is publicly available and has been widely used in testing new algorithms and in comparing different algorithms. The CBS algorithm has been applied on this dataset in the original paper. We redo the analysis using the Matlab code to obtain a complete picture. The Coriell data consists of 15 cell lines, named GM03563, GM00143, …, GM01524. We simply use number 1, 2, …, 15 to represent these cell lines. For this particular dataset, there are only three states (s = 3), i.e. loss, neutral and gain. Notice that unlike CBS, CRF-CNV requires training data to obtain parameters. It is unfair to directly compare the prediction results of CRF-CNV on training data with results from CBS. We take a simple approach which divides the 15 samples into three groups, with each group having 5 samples. In the first run, we use Group 1 as training data and Group 2 as validation data to obtain model parameters (as discussed in Sec. 3.3). We then use the model to predict data in Group 3 (testing data), and record the prediction results. In the second and third run, we alternate the roles of Groups 1–3 and obtain prediction results of samples in Group 1 and Group 2, respectively. Finally we summarize our results over all 15 samples. For example, for the first run, we first obtain {a_j, j = 0, …, 4} directly based on samples in Group 1. The estimates of {a_j } is (−1.348, −0.682, −0.001, 0.497, 0.810). To search the penalization coefficient σ² and the dependent length u, we define the search space as A × B = {0, 1, 2, …, 30} × {0, 1, …, 5}. For each data point (m, u₀) ∈ A × B, we let σ² = 400 × 0.8^m and u = u₀. Essentially, to search σ² in a broad range, we use a geometric decay. The upper bound on u is set to be 5 because for aCGH data such as the Coriell dataset, each clone can cover a quite long range of DNA. The optimal σ² and u will be chosen by minimizing the prediction errors on samples in Group 2 (the validation set). Our results indicate that the model with u = 1 and m = 21 achieves the lowest prediction error. Note that u = 1 implies feature functions are defined based on a window size of 3. The values of θs can be estimated simultaneously. We then apply Viterbi’s algorithm to find the most possible hidden copy number states for samples in Group 3, as well as the number and boundaries of segments. Run 2 and Run 3 will obtain results on Group 1 and Group 2. For the CNA-HMMer, one can either use its default priors or use training data to obtain informative priors. We have tested the performance of CNA-HMMer both with and without informative priors.

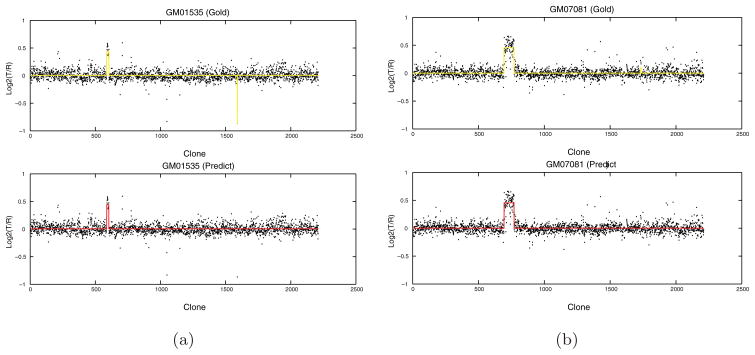
Table 2 shows the segment numbers of each sample from the Gold Standard, and from the predicted outcomes of the three algorithms CRF-CNV, CBS and CNA-HMMer. The segment number detected by CRF-CNV is exactly the same as the Gold Standard for almost all samples (except for samples 9 and 10). Further examination of samples 9 and 10 (see Fig. 3) reveals that the segment that we missed in sample 9 only has one clone, which has been smoothed out by our algorithm. The segment missed in sample 10 is also very short and the signal is very weak. Our results have shown that CBS has generated many more segments comparing to the ground truth, which is consistent with the results in the original paper. The overall number of segments reported by CNA-HMMer with default priors is even greater than the total number from CBS. On the other hand, once we have used training data to properly assign informative priors for CNA-HMMer, it almost returns the same number of segments as CRF-CNV. The only exception is that CNA-HMMer missed one breakpoint in sample 1. This illustrates that by using correctly labeled training data, both CRF-CNV and CNA-HMMer can effectively eliminate all false positives in this dataset. For the subsequent experiments, we only report the results of CNA-HMMer with proper training.

Table 2.

Comparison of segment numbers returned by three algorithms.

Method \Sample	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	Sum
Gold	5	3	5	3	5	3	5	5	5	5	3	5	2	3	3	60
CRF-CNV	5	3	5	3	5	3	5	5	3	3	3	5	2	3	3	56
CBS	17	42	7	6	9	5	5	6	5	5	13	7	17	3	9	156
CNA-HMMer(default)	9	83	9	7	11	3	7	5	11	11	21	5	16	10	16	224
CNA-HMMer (trained)	3	3	5	3	5	3	5	5	3	3	3	5	2	3	3	54

Fig. 3.

Predicted breakpoints by CRF-CNV (bottom) vs. true breakpoints (up) on two cell lines GM01535 (a) and GM07081 (b).

As a comparison measure, the number of segments is a very rough index because it does not contain information about breakpoints. To further examine how accurate the predicted breakpoints by each approach, we pool all the breakpoints from all the samples and use the F measure defined earlier to compare the performance of the three algorithms. Note that even though exact matches are possible, shifting by a few clones around boundaries is also likely given noisy input data. Therefore we use a match extent index D to allow some flexibility in defining matches of predicted breakpoints to those given by the gold standard. Table 3 shows F measures given different match extent values for the three methods. Clearly, CBS has the worst performance, regardless of the match extent values. This partially reflects that it has many false positives. The results from CNA-HMMer are very accurate when no match extent is allowed and then shows modest increase when we increase the value of D from 0 to 1. The results of CRF-CNV lie in between when the match index D = 0. However, the performance of CRF-CNV is greatly enhanced when D = 1 and finally it outperforms CNA-HMMer when D ≥ 2. The primary reason CRF-CNV has shifted one or a few positions for many breakpoints is because of the automatic median smoothing step. In contrast, CNA-HMMer directly models outliers using prior distributions.

Table 3.

Comparison of F measure with different match extent values for three algorithms.

Method \Match extent	CRF-CNV	CNA-HMMer	CBS
0	0.638	0.877	0.333
1	0.914	0.947	0.500
2	0.948	0.947	0.519
3	0.967	0.947	0.519
4	0.967	0.947	0.519

4.2. Simulated data

Though results on the real data have shown that CRF-CNV has a better performance than CBS and CNA-HMMer, the experiment is limited because the sample size is very small. To further evaluate the performance of CRF-CNV, we test the three algorithms using a simulated dataset obtained from Willenbrock and Fridlyand.¹⁴ The dataset consists of 500 samples, each with 20 chromosomes. Each chromosome contains 100 clones. Each clone belongs to one of six possible copy number states. The authors generated these samples by sampling segments from a primary breast tumor dataset of 145 samples and used several mechanisms (e.g. the fraction of cancer cells in a sample, the variation of intensity values given a copy number state) to control the noise level. By using simulated data from the literature, we can obtain an unbiased picture about CRF-CNV’s performance. The original paper also compared three algorithms and concluded that CBS has the best performance.

To train CRF-CNV, we divide the 500 samples into three groups as usual. This time, the training set Group 1 contains sample 1–50, the validation set Group 2 contains sample 51–100 and the test set Group 3 contains sample 101–500. We use the same grid search approach as discussed earlier to obtain hyper-parameters {a_j}, u and σ². For each fixed set of hyper-parameters, we use the conjugate gradient method to obtain parameter θ. Finally, we use Viterbi’s algorithm to decode the most possible hidden copy number state labels for samples in Group 3 and compare the results with the other two algorithms. In addition, we also compare the predictions by CRF-CNV on Group 2 and Group 3 to see, using new testing data, how much deterioration our model might incur based on sub-optimal parameters inferred from a small number of samples. Results from CBS and CNA-HMMer are also presented separately for these two groups for easy comparison. We also use Group 1 as training data to assign proper priors for CNA-HMMer.

Table 4 shows the total number of segments in Group 2 and Group 3 predicted by CRF-CNV, CBS and CNA-HMMer, and in comparison with the known segment number. Interestingly, on this simulated data, both CBS and CNA-HMMer have predicted smaller number of segments. CRF-CNV has predicted smaller number of segments on Group 2 and greater number of segments in Group 3. However, the number of segments does not provide a whole picture. We therefore examine the accuracy of boundary prediction by each method using the F measure for both Group 2 and Group 3. Table 5 shows the F measures for different methods, different groups and different match extents. As expected, the F measure increases as D increases from 0 to 4 for all methods and for both data groups. It is also not surprising to see that the results of CBS and CNA-HMMer on Group 2 and Group 3 are consistent. Interestingly, the performance of CRF-CNV on Group 3 is also very close to its own performance on Group 2. This property is desirable because it illustrates the robustness of CRF-CNV. The performance on new testing data is almost the same as the performance on validation data, which is used to select optimal hyper-parameters. This observation alleviates the need of training samples by our approach and makes it more practical. Note that the sizes of training data and validation data are also very small. One can expect that with a small number of training data, our approach can be used to reliably predict new data generated under the same experimental conditions. In terms of the performance of the three approaches, CNA-HMMer is more accurate then CRF-CNV, and CBS is the worst for the case of exact match. However, when we relax the matching criteria by increasing the value of D, both CBS and CRF-CNV achieve better performance than CNA-HMMer. The results of CNA-HMMer and CRF-CNV are consistent with those from the real data. While CBS has much better performance compared to those from the real data, this might be attributed to the simulation process because CBS was used to segment the 145 samples from the primary breast tumor dataset.¹⁴

Table 4.

Comparison of number of segments predicted by three different approaches.

Method\Data	Group 2	Group 3
Gold	997	8299
CRF-CNV	966	8868
CNA-HMMer	784	6692
CBS	867	7430

Table 5.

Comparison of F measure of different methods with different match extent.

Method\Match extent	0	1	2	3	4
CRF-CNV(Group2)	0.590	0.792	0.875	0.900	0.906
CNA-HMMer(Group2)	0.702	0.801	0.832	0.852	0.855
CBS(Group2)	0.436	0.850	0.885	0.900	0.909
CRF-CNV(Group3)	0.568	0.786	0.864	0.889	0.896
CNA-HMMer(Group3)	0.697	0.805	0.840	0.858	0.869
CBS(Group3)	0.436	0.847	0.893	0.911	0.918

5. Conclusion and Discussions

The problem of detecting copy number variations has drawn much attention in recent years and many approaches have been proposed to solve the problem. Among these computational developments, CBS has gained much popularity and it has been shown that it generally performs better than other algorithms on simulated data.¹⁴ However, as shown in the original paper (as well as rediscovered by our experiments), CBS has reported many more false positives on copy number changes in the standard Coriell dataset identified by spectral karyotyping.¹¹ Another commonly used technique for segmentation is HMMs. HMM approaches have the advantage of performing parameter estimation and copy number decoding within one framework and its performance is expected to improve with more observations. Furthermore, Lai et al.¹⁷ have shown that HMMs performed the best for small aberrations given a sufficient signal/noise ratio. However, almost all HMMs for aCGH are first-order Markov models and thus cannot incorporate long region spatial correlations within data.

We have presented a novel computational model based on the theory of conditional random fields. We have also developed effective forward/backward algorithms within the conjugate gradient method for efficient computation of model parameters. We evaluated our approach using real data as well as simulated data, and results have shown our approach performed better than a Bayesian HMM on both datasets when a small shift is allowed while mapping breakpoints. Comparing with CBS, our approach has much less false positives on the real dataset. On the simulated data set, the performance of our approach is comparable to CBS, which has been shown to be the best among three popular segmentation approaches.

Like with any other CRF, in order to train our model, one has to rely on some training data. To be practically useful, Bayesian HMMs such as CNA-HMMer also need training data for proper assignments of informative priors. We argue that the problem is not that serious as it appears to be, primarily for two reasons. First, as illustrated in our experiments, our algorithm is indeed very robust and performs consistently even when one may not find the optimal estimates of model parameters. For example, we used a simplified procedure in the analysis of the simulated dataset by randomly picking one subset for training. Theoretically, parameters estimated from such a procedure might heavily depend on this particular subset and might not be necessarily globally optimal. However, the results in Table 5 have shown that the performance on new testing data is almost the same as the results in the verification data which has been used to tune the parameters. Furthermore, the training size required by our algorithm is very small, as illustrated by both the real and the simulated data. Our algorithm requires the number of hidden states to be known. It suggests that we train our algorithm for a specific platform. The parameters can then be used for future data to be generated on the same platform. Our algorithm can be applied in real application that the set of hidden states for predicted data is a subset of the platform we train. If the predicted data contains the state we never learnt from training data, the accuracy of our algorithm will be reduced.

In terms of computation costs, CNV-CRF has two separate portions: time for training and time for prediction. The training requires intensive computations to optimize the log-likelihood and to determine the hyper-parameters. In addition, one can also perform k-fold cross-validations, which will require much more computational time. On the contrary, once the parameters have been estimated, the prediction phase is rather efficient. Fortunately, the training phase of our algorithm only requires a small number of samples, which makes the algorithm still practically useful. For our proposed method, we focus primarily on aCGH data. More recently, new algorithms have been proposed to identify CNVs from new SNP-genotyping platforms by integrating information from both SNP probes and CNV probes.¹⁸ Next-generation sequencing is on the horizon, i.e. one can use massively parallel sequencing technique to identify CNVs with finer resolutions. For our future work, we will investigate possible extensions and applications of our algorithm on other high-throughput technologies (such as SNP-genotyping and next-generation sequencing) in detecting copy number alterations.

Biographies

Xiao-Lin Yin is currently a senior research associate at the Electrical Engineering and Computer Science Department at Case Western Reserve University, Cleveland, OH. He received his Ph.D. at the School of Mathematics and Statistics at Northeast Normal University, Changchun, P. R. China, in 2006. His research interests cover haplotype association, copy number variation detection, population genetics and modernization of Chinese Herbal medicine.

Jing Li is currently an Assistant Professor in the Department of Electrical Engineering and Computer Science at Case Western Reserve University. He received a B.Sc. in Statistics from Peking University, Beijing, China in July 1995, a M.Sc. in Statistical Genetics from Creighton University in Aug. 2000, and Ph.D. in Computer Science from University of California–Riverside in June 2004. He was a winner of the ACM Student Research Competition in 2003. Jing Li’s recent research interests include bioinformatics, computational molecular biology, algorithms and statistical genetics.

Appendix A. Relationship of CRFs and HMMs

A special case of our linear-chain CRF model defined in Subsec. 3.1 corresponds to a familiar HMM. For example, let ${\lambda }_j=c_j/d_j^2,{\mu }_j=-1/(2d_j^2)$, ω_j = log P(Y₁ = j), ν_jk = log P(Y_i+1 = k|Y_i = j), f_j (Y_i, X_i(u)) = I_{Yi=j}medX̃_i, g_j (Y_i, X̃_i(u)) = I_{Yi=j}(med X̃_i)² l_j (Y₁, X̃₁(u)) = I_{Y1=j}, h_jk(Y_i, Y_i+1, X̃_i,i+1(u)) = I_{{Yi=j,Yi+1=k}}, let med X̃_i = T_i, then Model (1) becomes

$$P(Y\mid X)=\frac{1}{Z_{\theta }(X)}P(Y_1)\prod _{i=1}^{n}P(T_i\mid Y_i)\prod _{i=1}^{n-1}P(T_{i+1}\mid Y_i),$$ (3)

where $P(T_i\mid Y_i=j)={\prod }_{i=1}^n\frac{1}{\sqrt{2\pi }{d}_i}exp\{-\frac{{(T_i-b_j)}^2}{2d_j^2}\},Z_{\theta }(X)={\sum }_{Y}P(Y_1){\prod }_{i=1}^{n}P(T_i\mid Y_i){\prod }_{i=1}^{n-1}P(Y_{i+1}\mid Y_i)$. Model 3 is equivalent to an HMM with normal emission distribution. In this regard, if Model 1 is built based on median smoothed data {med X̃_i}, the model parameters and feature functions are selected as above, then Model 1 reduces to Model 3. However, we notice that in our Model 1, neither the initial function l_j (Y₁, X̃₁(u)) nor the transition function h_jk(Y_i, Y_i+1, X̃_i,i+1(u))} is a simple index function. They depend on the observation X. Moreover, the parameters θ of Model 1 are with more freedom than that of Model 3. These properties make our Model 1 more promising.

Appendix B. Outline of the CG Algorithm and Efficient Computation of the Derivatives of L_θ

The nonlinear CG method only requires the computation of the first derivatives. The outline is as follows

$$\begin{array}{l}{d}^{(0)}={\gamma }^{(0)}=L^{\prime }({\theta }^{(0)}),\\ \text{Find}{\alpha }^{(i)}\text{that}\text{maximize}L({\theta }^{(i)}+{\alpha }^{(i)}{d}^{(i)}),\\ {\theta }^{(i+1)}={\theta }^{(i)}+{\alpha }^{(i)}{d}^{(i)},\\ {\gamma }^{(i+1)}=\frac{\partial L}{\partial \theta }{\mid }_{\theta ={\theta }^{(i+1)}},\\ {\beta }^{(i+1)}=\frac{{({\gamma }^{(i+1)})}^{\prime }{\gamma }^{(i+1)}}{{({\gamma }^{(i)})}^{\prime }{\gamma }^{(i)}},\\ d^{(i+1)}={\gamma }^{(i+1)}+{\beta }^{(i+1)}{d}^{(i)},\end{array}$$

where θ⁽⁰⁾ is the initial value of θ, $\frac{\partial L}{\partial \theta }$ is the first derivative function of L. The first order derivatives of L_θ with respect to {λ_j}, {μ_j}, {ω_j} and {ν_jk} are given by

$$\begin{array}{l}\frac{\partial L_{\theta }}{\partial {\lambda }_j}=\sum _{d=1}^D\sum _{i=1}^n{f}_j(Y_i^{(d)},{\stackrel{\sim }{X}}_i^{(d)})-\sum _{d=1}^D\sum _{i=1}^n\sum _{y}P(Y_i=y\mid X^{(d)})f_j(y,{\stackrel{\sim }{X}}_i^{(d)})-\frac{{\lambda }_j}{{\sigma }^2},j=1,\dots ,s,\\ \frac{\partial L_{\theta }}{\partial {\mu }_j}=\sum _{d=1}^D\sum _{i=1}^n{g}_j(Y_i^{(d)},{\stackrel{\sim }{X}}_i^{(d)})-\sum _{d=1}^D\sum _{i=1}^n\sum _{y}P(Y_i=y\mid X^{(d)})g_j(y,{\stackrel{\sim }{X}}_i^{(d)})-\frac{{\mu }_j}{{\sigma }^2},j=1,\dots ,s,\\ \frac{\partial L_{\theta }}{\partial {\omega }_j}=\sum _{d=1}^D{l}_j(Y_1^{(d)},{\stackrel{\sim }{X}}_1^{(d)})-\sum _{d=1}^D\sum _{y}P(Y_1=y\mid X^{(d)})l_j(y,{\stackrel{\sim }{X}}_1^{(d)})-\frac{{\omega }_j}{{\sigma }^2},j=1,\dots ,s,\\ \frac{\partial L_{\theta }}{\partial {\nu }_{jk}}=\sum _{d=1}^D\sum _{i=1}^n{h}_{jk}(Y_i^{(d)},Y_{i+1}^{(d)},{\stackrel{\sim }{X}}_{i,i+1}^{(d)})-\sum _{d=1}^D\sum _{i=1}^{n-1}\sum _{y,y^{\prime }}P(Y_i=y,Y_{i+1}=y^{\prime }\mid X^{(d)})h_{jk}(y,y^{\prime },{\stackrel{\sim }{X}}_{i,i+1}^{(d)})-\frac{{\nu }_{jk}}{{\sigma }^2},j,k=1,\dots ,s.\end{array}$$

We have noticed the computational cost of training. The partition function Z_θ(X) in the likelihood and the marginal distributions P (Y_i = y|X^(d)), P (Y_i = y, Y_i+1 = y′|X^(d)) in the gradient can be efficiently computed by forward-backward algorithms, both of which have an O(ns²) complexity, where n is the clone number, s is the hidden state number. However, each training data will have a different partition function and marginal distributions, so we need to run forward-backward for each training data for each gradient computation. The cost for all training is O(ns²DG), where D is the number of training examples, G is the number of gradient computations required by the optimization procedure.

We define forward variables γ_i and backward variables η_i as follows

$$\begin{array}{l}{\gamma }_1(y,d)=F(Y_1=y,{\stackrel{\sim }{X}}_1^{(d)})G(Y_1=y,{\stackrel{\sim }{X}}_1^{(d)})L(Y_1=y,{\stackrel{\sim }{X}}_1^{(d)}),y=1,\dots ,s,\\ {\gamma }_i(y^{\prime },d)=F(Y_i=y^{\prime },{\stackrel{\sim }{X}}_i^{(d)})G(Y_i=y^{\prime },{\stackrel{\sim }{X}}_1^{(d)})\sum _{y=1}^s{\gamma }_{i-1}(y,d)H(Y_{i-1}=y,Y_i=y^{\prime },{\stackrel{\sim }{X}}_{i-1,i}^{(d)}),i=2,\dots ,n;y^{\prime }=1,\dots ,s,\\ {\eta }_n(y,d)=1,y=1,\dots ,s,\\ {\eta }_i(y^{\prime },d)=\sum _{y=1}^s{\eta }_{i+1}(y)F(Y_{i+1}=y,{\stackrel{\sim }{X}}_{i+1}^{(d)})G(Y_{i+1}=y,{\stackrel{\sim }{X}}_{i+1}^{(d)})H(Y_i=y^{\prime },Y_{i+1}=y,{\stackrel{\sim }{X}}_{i,i+1}^{(d)}),i=1,\dots ,n-1;y^{\prime }=1,\dots ,s.\end{array}$$

Here,

$$\begin{array}{c}F(Y_i,{\stackrel{\sim }{X}}_i)=exp\left\{\sum _{j=1}^s{\lambda }_j{f}_j(Y_i,{\stackrel{\sim }{X}}_i)\right\},G(Y_i,{\stackrel{\sim }{X}}_i)=exp\left\{\sum _{j=1}^s{\mu }_j{g}_j(Y_i,{\stackrel{\sim }{X}}_i)\right\},\\ L(Y_1,{\stackrel{\sim }{X}}_1)=exp\left\{\sum _{j=1}^s{\omega }_j{f}_j(Y_1,{\stackrel{\sim }{X}}_1)\right\},\\ H(Y_{i-1},Y_i,{\stackrel{\sim }{X}}_{i-1,i})=exp\left\{\sum _{j=1}^s\sum _{k=1}^s{\nu }_{jk}{h}_{jk}(Y_{i-1},Y_i,{\stackrel{\sim }{X}}_{i-1,i})\right\}.\end{array}$$

Combining forward and backward recursions, we see that

$$\begin{array}{l}P(Y_i=y\mid X^{(d)})={\gamma }_i(y,d){\eta }_i(y,d)/Z_{\theta }(X^{(d)}),y=1,\dots ,s;i=1,\dots ,n,\\ P(Y_i=y,Y_{i+1}=y^{\prime }\mid X^{(d)})={\gamma }_i(y,d)F(Y_{i+1}=y^{\prime },{\stackrel{\sim }{X}}_{i+1}^{(d)})G(Y_{i+1}=y^{\prime },{\stackrel{\sim }{X}}_{i+1}^{(d)})H(Y_i=y,Y_{i+1}=y^{\prime },{\stackrel{\sim }{X}}_{i,i+1}^{(d)}){\eta }_{i+1}(y^{\prime },d)/Z_{\theta }(X^{(d)}),y,y^{\prime }=1,\dots ,s;i=1,\dots ,n-1.\end{array}$$

Z_θ(X^(d)) can also be efficiently computed using forward variables $Z_{\theta }(X^{(d)})={\sum }_{y=1}^s{\gamma }_n(y,d)$.

We notice that the forward variables γ_i and backward variables η_i are unstable. They may suffer from overflow or underflow due to numerous times of exponential product calculations. Stable modification is to derive recursive relationship of the forward variables γ_i and backward variables η_i in the log type. It is easy to show that log γ_i(y′, d) obeys the recursive relationship

$$\begin{array}{l}log{\gamma }_i(y^{\prime },d)=log{\gamma }_{i-1}(y_0,d)+log(F(Y_i=y^{\prime },{\stackrel{\sim }{X}}_i^{(d)})G(Y_i=y^{\prime },{\stackrel{\sim }{X}}_i^{(d)})H(Y_{i-1}=y_0,\\ Y_i=y^{\prime },{\stackrel{\sim }{X}}_{i-1,i}^{(d)})+log\{1+\sum _{y\ne y_0}exp[log{\gamma }_{i-1}(y,d)+log(F(Y_i=y^{\prime },{\stackrel{\sim }{X}}_i^{(d)})G(Y_i=y^{\prime },{\stackrel{\sim }{X}}_i^{(d)})H(Y_{i-1}=y,Y_i=y^{\prime },{\stackrel{\sim }{X}}_{i-1,i}^{(d)}))-log{\gamma }_{i-1}(y_0,d)-log(F(Y_i=y^{\prime },{\stackrel{\sim }{X}}_i^{(d)})G(Y_i=y^{\prime },{\stackrel{\sim }{X}}_i^{(d)})H(Y_{i-1}=y_0,Y_i=y^{\prime },{\stackrel{\sim }{X}}_{i-1,i}^{(d)})]\},i=2,\dots ,n;y^{\prime }=1,\dots ,s,\end{array}$$

where y₀ = arg max_y log γ_i−1(y, d). The backward variables η_i(y′, d) has a similar log-type recursive relationship; we omit it for brevity.

The marginal distributions P (Y_i = y|X^(d)) and P (Y_i = y, Y_i+1 = y′|X^(d)) can be calculated using stable log γ_i and log η_i, for example, P (Y_i = y|X^(d)) = exp{log γ_i(y, d) + log η_i(y, d) − log Z_θ(X^(d))}, y = 1, …, s; i = 1, …, n, where log Z_θ(X^(d)) = log γ_n(y₀, d) + log(1 + Σ_y≠y0 exp[log γ_n(y, d) − log γ_n(y₀ d)]), y₀ = arg max_y log γ_n(y, d).