Geometric constraints explain much of the species richness pattern in African birds

Abstract

The world contains boundaries (e.g., continental edge for terrestrial taxa) that impose geometric constraints on the distribution of species ranges. Thus, contrary to traditional thinking, the expected species richness pattern in absence of ecological or physiographical factors is unlikely to be uniform. Species richness has been shown to peak in the middle of a bounded one-dimensional domain, even in the absence of ecological or physiographical factors. Because species ranges are not linear, an extension of the approach to two dimensions is necessary. Here we present a two-dimensional null model accounting for effects of geometric constraints. We use the model to examine the effects of continental edge on the distribution of terrestrial animals in Africa and compare the predictions with the observed pattern of species richness in birds endemic to the continent. Latitudinal, longitudinal, and two-dimensional patterns of species richness are predicted well from the modeled null effects alone. As expected, null effects are of high significance for wide ranging species only. Our results highlight the conceptual significance of an until recently neglected constraint from continental shape alone and support a more cautious analysis of species richness patterns at this scale.

It has been recognized for centuries that species are not evenly distributed on the Earth's surface (1). The search for patterns of species richness and their cause has been a central focus for decades in ecology and biogeography (2–6). A plethora of hypotheses have been suggested to account for regional patterns of species richness, including energy-related variables (7, 8), topographic heterogeneity (9, 10), area (4, 11), and evolutionary time (12, 13).

The usual analytical approach taken to evaluate geographical species richness patterns uses absolute species numbers, assuming that in the absence of whatever ecological and evolutionary mechanisms that led to today's pattern, species richness would be even across space. However, recent work suggests that only under very specific assumptions is this the case. The real world contains boundaries that influence the geometry of species' ranges to an extent that can significantly affect the pattern of species richness (14, 15). When considering the latitudinal gradient in species richness for a terrestrial taxon, obviously the northern and southern edge of the great continental landmasses present hard boundaries to the latitudinal extent of range (16, 17). It has been demonstrated both with analytical null models (18, 19) and with simulations (14, 20–22) that without the existence of environmental or other gradients, a mid-domain peak of species numbers can be expected by chance when ranges are placed randomly within such a bounded domain. In fact, this expectation proves true for any set of theoretical or empirical ranges placed within a bounded domain. Depending on the exact distribution of the species' ranges, the models predict a symmetrical pattern of parabolic or quasiparabolic form. Recognition of the role of geometric constraints has also influenced our perception of what shapes one-dimensional (1-D) patterns along elevational (23) and bathymetric richness gradients (22).

Considering these new realizations, an inappropriate null model (of even distribution of species across space) may have been in place for 150 years (15). To understand and disentangle the deterministic effects of environmental, ecological, evolutionary, and historical factors on patterns of species richness across space, it is important to consider and control for confounding stochastic effects. However, by using 1-D geometric null models to enhance the understanding of, for example, the latitudinal gradient is only the first important step. Firstly, if interpreted too simplistically the results can be misleading, because species' ranges are not purely linear in the real world (24). Secondly, the usual measure of species richness used in 1-D studies is “band sum” (i.e., the sum of species whose ranges extend into a given latitudinal or longitudinal band). Unfortunately, this procedure confounds observed or simulated pattern with area effects. If the attempt to evaluate the mid-domain effect of geometric constraints on the geography of species is to be consistent, expansion of the 1-D geometric null model to a two-dimensional (2-D) perspective is required (15). Here we present a general 2-D null model for spatial patterns in species richness and exemplify the significance of geometric constraints on a continental scale pattern by applying it to the species richness of all 1,596 bird species endemic to Africa.

The effects of 2-D geometric constraints can be pictured as follows: because species tend to have continuous distributions when viewed at regional scales, their pattern of occurrence inherently includes positive spatial autocorrelation—that is, a species is more likely to be present at a place close to one where it is known to occur than at one distant from that place. In addition, on an insular continent overlaid by a grid of quadrats, a quadrat near to a hard boundary (e.g., the continental coastline) is on average surrounded by fewer quadrats than one far away from it. Thus, the likelihood that a quadrat contains part of a given species' range that is randomly placed on the continent is a function not only of the range size, but also of its geographic position. It tends to increase with average distance from hard boundaries. Considering the whole species pool this means that, by chance alone, more species are expected to occur in regions away from boundaries (e.g., centers of continents). The exact probability of a quadrat containing one species' range or the full species pool is a function of a quadrat's distance to all boundaries and the range-size values. Here we use a Monte Carlo simulation solution for this problem.

The outlined effect on the spatial distribution of a species pool only applies when the boundary really is a true border for all species in the analysis. Of course, the argument is not limited to the land–sea boundary, but could be extended to include regional and local boundary effects, for example, for habitat specialists. However, an objective, noncircular rationale for the selection of subgroups is likely to prove difficult. If the goal is to examine a continental community as a whole, a simple distinction between regions that are habitable and nonhabitable for the whole community appears to be justifiable, relevant, and simple.

Methods

In the search for an appropriate null model for species richness in bounded regions, we accept certain parameters as clearly given from empirical data: the overall number of species, their geographic range sizes, and the geographic location of taxon-wide boundaries.

The “Area Model.”

This is our basic model, in which species ranges are scattered randomly across the continent and constraining hard boundaries exist. On a gridded plane the edges of the fully habitable continent delimit a hard boundary, beyond which the plane is fully uninhabitable (e.g., ocean for terrestrial animals). Allocation of a species' range (defined as number of quadrats occupied) by random sampling of quadrats without replacement is analogous to throwing rice grains onto a bounded checkerboard, whereby all grains end up somewhere on the board. This model has similarities with the passive sampling hypothesis (25, 26), where the probability of a species' occurrence is proportional to the area considered.

The “Geometric Constraints Model.”

In this model we introduce range continuity as an assumption. Several different techniques for describing and simulating species distributions have been used for detecting species associations (27). Here we apply a very simple process of range allocation, akin to dropping a certain volume of dye onto a bounded shape, which then spreads within the bounded surface. For each species with a predetermined range size, a “starting” quadrat is chosen randomly among all habitable quadrats. A species' range is then produced by repeated “expansion” in steps of one quadrat added per time in random direction from a randomly chosen edge of all already occupied quadrats until the final range size is reached. Quadrats qualifying for “expansion” must be adjacent in horizontal or vertical (i.e., cardinal) direction, not yet occupied by the species, and habitable. This process is repeated for all species. It is similar to a flow of liquid through an unstructured bounded lattice according to a nearest neighbor rule, which results in maximum spatial contagion of ranges. We believe that this range expansion algorithm is the most parsimonious one with a process that is stripped of any underlying ecological and physiographical factors except hard boundaries. When actual geographic ranges of species are mapped onto a coarse-resolution grid on regional and continental scale, cells indicating presence tend to show a clumped distribution and are usually connected (28). We calculate species richness by summing the number of overlapping ranges in each quadrat.

Empirical Data.

We use species richness data on African breeding birds to compare the model outcomes with real-world patterns. African birds are suitable for this test, because of their large geographic ranges, well known large-scale distribution, and the well defined biogeographical boundaries of the African landmass. We used the distribution data of all 1,905 African breeding birds compiled by the Zoological Museum, University of Copenhagen on a 1° longitude–latitude grid with 2,605 quadrats (quadrats containing less than 50% dry land had been excluded). Quadrat size varies slightly with latitude, ranging from 10,190 km² to 12,364 km². Maps were compiled from standard reference works and dozens of other published references (including recent atlases and unpublished research) and, for difficult regions and taxa, experts' opinions were sought (the full list of sources is available at http://www.zmuc.dk/commonweb/research/biodata.htm; for mapping methodology see refs. 29 and 30). The distribution of 1,596 of these species is confined to the African, almost exclusively sub-Saharan mainland.

Empirical Richness Patterns.

We derived a map of empirical species richness by calculating the sum of species at any one quadrat. Acknowledging the significant change in habitat and barrier that the Sahara constitutes for birds, we drew a line along the southern edge of the World Wildlife Fund ecoregions “South Saharan Steppe” and “Woodland and North Saharan Steppe and Woodland” (31) and defined this as the northern boundary of the focal region for analysis. Just four of the 1,596 species endemic to Africa extend (only marginally) into regions north of this boundary. All other boundaries were simply defined by the edges of continental Africa. This led to a map of sub-Saharan Africa with 1,742 1° quadrats with 372,792 positive quadrat records of 1,596 species. On a quadrat-by-quadrat basis, the species richness of these endemic birds is highly correlated with overall breeding bird species richness (r² = 0.984, n = 1,742).

Modeled Richness Patterns.

We modeled the patterns of species richness in this region expected from our “area model” and “geometric constraints model” by using the observed number of species and the statistical distribution of geographic range sizes as given parameters. Means of 100 runs were used for analysis. For both observed and modeled data latitudinal and longitudinal gradients of species richness were calculated as band sums (sum of species whose ranges extend into a band of 1° width) and band means (mean number of species per quadrat in a given latitudinal or longitudinal band). The program geospod, developed for this analysis, can be downloaded from http://evolve.zoo.ox.ac.uk/software/.

Statistics.

Biogeographical data, such as geographical ranges, are spatially autocorrelated, which reduces P values by overestimating degrees of freedom. Acknowledging this problem, no actual levels of significance are presented.

Results and Discussion

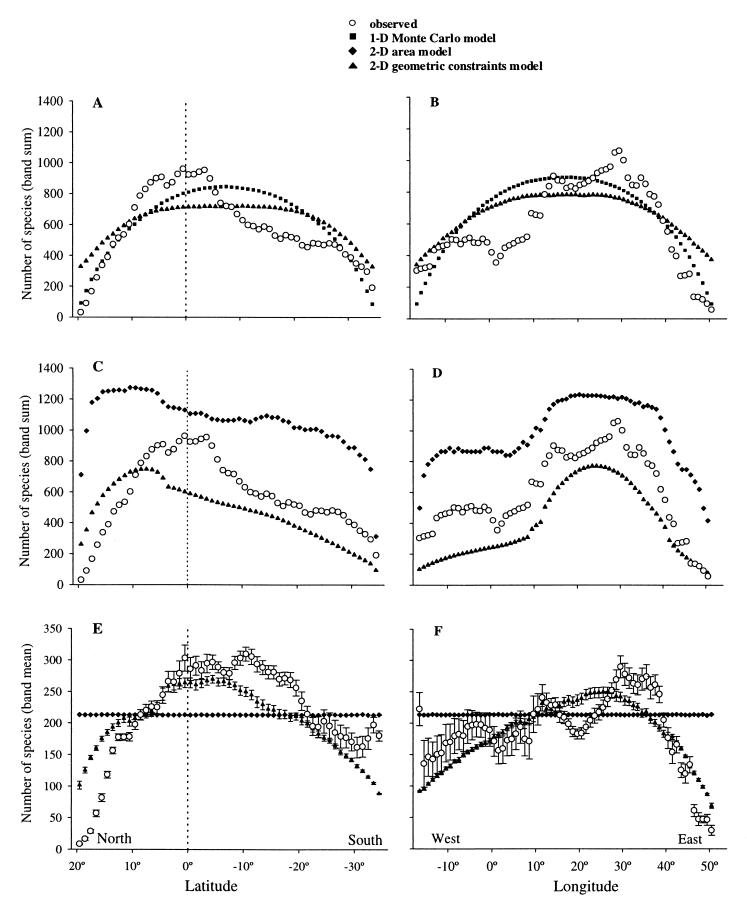
Traditionally, species richness data on this scale have been examined from a 1-D perspective, in particular in the form of band sums, usually with reference to latitude. Fig. 1 A and B (open circles) present the observed species richness patterns in Africa by using a traditional band sum perspective. Species richness of latitudinal bands increases steeply from the Sahara to the equator and then decreases gradually toward the south (Fig. 1A). Examined from west to east, species numbers show a plateau in Western Africa, then reach much higher numbers in the central longitudes, and decrease steeply in the eastern parts toward the edge (Fig. 1B).

Figure 1.

Latitudinal (Left) and longitudinal (Right) gradients in observed and simulated species richness of breeding birds endemic to Africa. (A and B) Observed and simulated band sums (means from 100 runs, error bars too small for display) using observed 1-D range extents. (C and D) Observed and simulated band sums (means from 100 runs, error bars too small for display) using observed 2-D range sizes. (E and F) Mean species richness per quadrat (±SE) of observed and 2-D simulation data (means from 100 runs).

We compare the observed pattern with the predictions of the 1-D null model proposed by Colwell & Hurtt (14), which randomizes the empirical latitudinal and longitudinal range extents and predicts an approximately parabolic pattern. To directly compare this 1-D model with our 2-D geometric constraints model we retrieved for all species the longitudinal and latitudinal range extents from the distribution database. With these extents as observed range sizes, we run both models for a “condensed African continent” of observed length, but with just one quadrat width along the focal domain. The results of the 1-D version of our 2-D model exhibit a less marked peak and less steep drop-off in species sums toward the edges (triangles in Fig. 1 A and B) than the 1-D model (squares in Fig. 1 A and B). This inconsistency is due to the fact that the algorithm of the 2-D geometric constraints model allows ranges to “build” toward or away from the edges by permitting the initial midpoint to move. In contrast, the 1-D model discards any range midpoint that, with the given range size, would extend beyond the boundary and chooses a new midpoint until the range is fully contained in the domain. Therefore, in the 1-D model more species accumulate in the middle and fewer near the edges. Both models show reasonably good agreement with the observed patterns of band sums (Table 1).

Table 1.

1-D and 2-D fits of null model predictions on observed species richness of breeding birds endemic to Africa

Perspective	n	1-D model			2-D GC model used as 1-D			2-D models used as 2-D
								A			GC
		r2	ta=0	tb=1	r2	ta=0	tb=1	r2	ta=0	tb=1	r2	ta=0	tb1
1-D band sum
Latitude	55	0.66	0.84	−1.59	0.66	−4.17	3.88	0.26	−0.97	−1.71	0.44	2.46	−0.86
Longitude	68	0.61	0.38	−1.59	0.62	−4.14	3.62	0.92	−13.53	4.71	0.88	8.22	1.00
1-D band mean
Latitude	55	—	—	—	—	—	—	0.01	0.87	−0.87	0.63	−1.05	1.60
Longitude	68	—	—	—	—	—	—	0.02	1.30	−1.30	0.57	1.69	−1.50
2-D	1,742	—	—	—	—	—	—	0.00	2.50	−2.61	0.21	3.83	−6.19

Different perspectives, measures, and models. 1-D model refers to the one-dimensional Monte Carlo model that uses observed range extents (15); GC and A refer to the geometric constraints and area model, respectively. n is the number of observations for each test; t_a=0 is the t test statistic that indicates the deviation of intercept a from zero for the regression of observed versus predicted data (a measure of fit in magnitude); t_b=1 indicates the deviation of slope b of the regression from unity (a measure of fit in shape). t values in italics indicate a rejection of the tested hypothesis at the P = 0.05 level (two-tailed). Note that in this test as few as ten truly independent observations are sufficient to reject the null hypothesis for any t > 2.3 and not even over 10,000 observations can reject it for any t < 1.96. 

When the actual 2-D range sizes are used for simulation and the traditional band sum perspective is taken, both the 2-D geometric constraints model and area model (a model accounting for the effects of area per se, but ignoring the effects of geometric constraints) partly show a good fit with the observed pattern along the latitudinal and longitudinal gradient (Fig. 1 C and D). The species richness predictions from the area model are consistently higher and the predictions from the geometric constraints model (assuming continuous ranges) are consistently lower than the observed species richness, forming an envelope about the observed values. Both 1-D and 2-D simulations of these two models show a much better fit along the longitudinal than the latitudinal gradient. For latitude they both predict highest species richness between 15° and 5° north, whereas the observed richness peaks around the equator.

Because band sums do not control for area effects, the appropriate 1-D measure to use is band means (average number of species per quadrat within each band). Band means of species richness are smaller in magnitude and in pattern in some places different to band sums (Fig. 1 E and F). The results of the geometric constraints model fit both magnitude and shape of the latitudinal and longitudinal pattern very well. This model closely mimics the relatively steep increase from north to south and decrease in species richness from east to west. Unsurprisingly, the band means of the area model predictions are constant and show no correlation with the real data (29).

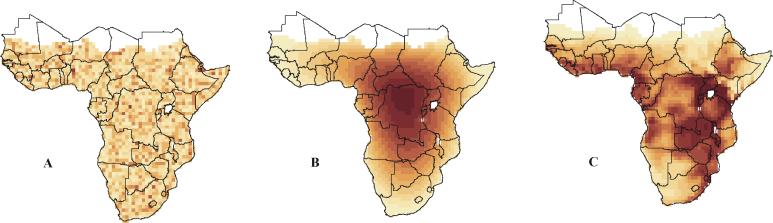
A look at the 2-D pattern (Fig. 2) reveals that the species richness predictions under the geometric constraints model are highest in the central Africa/Congo region, with a gradual decrease toward the continental edges. This is somewhat in contrast with the observed centers of highest species richness, which are in the Albertine Rift and Eastern Arc Mountains of East Africa and the Cameroon highlands. However, large parts of West and Southern Africa come out as particularly species-poor in both simulated and observed data and the model fit is good overall. A split of the data into passerine (1,064 species) and nonpasserine (532 species) birds reveals that species richness in both groups is similarly well predicted by the null model (Table 2).

Figure 2.

Simulated and observed species richness patterns of all 1,596 breeding birds endemic to Africa. (A) Means of 100 runs of the area model: randomly scattered ranges for 1,596 species with range sizes drawn from observed data; values range from 209 (light) to 217 (dark) species. (B) Means of 100 runs of the geometric constraints model: continuous ranges with range sizes drawn from observed data; values range from 60 (light) to 312 (dark) species. (C) Observed data; values range from 3 (light) to 546 (dark) species. All values are shown in quantile classification.

Table 2.

1-D and 2-D fits of geometric constraints model predictions for different categories

Perspective	n	Passerines (1,064)			Nonpasserines (532)			Range size
								≤100 (756)			>100 (840)
		r2	ta=0	tb=1	r2	ta=0	tb=1	r2	ta=0	tb=1	r2	ta=0	tb1
1-D band mean
Latitude	55	0.58	−1.94	2.48	0.65	0.12	0.23	0.05	3.28	−3.03	0.68	−1.35	1.84
Longitude	68	0.60	0.01	−0.08	0.49	3.66	−3.25	0.00	1.71	−1.71	0.60	1.86	−1.71
2-D	1,742	0.18	2.32	−2.91	0.22	11.43	−11.90	0.02	12.57	−12.59	0.26	6.53	−6.69

Regression results from the geometric constraints model for different categories. Numbers in parentheses refer to numbers of species in the category. n is the number of observations for each test; t_a=0 is the t test statistic that indicates the deviation of intercept a from zero for the regression of observed versus predicted data (a measure of fit in magnitude); t_b=1 indicates the deviation of slope b of the regression from unity (a measure of fit in shape). t values in italics indicate a rejection of the tested hypothesis at the P = 0.05 level (two-tailed). Note that in this test as few as ten truly independent observations are sufficient to reject the null hypothesis for any t > 2.3 and not even over 10,000 observations can reject it for any t < 1.96. 

We note that, although band sum is the measure most commonly used in species richness gradient analyses and null model simulations, it can give a misleading picture when applied to real-world continents and regions. Unless the geographic extent of the other dimension is constant along the domain, mid-domain or other peaks can occur simply because of variation in the width of that domain (32). The importance of area in shaping species richness patterns has long been recognized, and its impact on shaping species richness patterns has recently received new attention (21, 33). In the band-sum perspective, the effect of area alone, as demonstrated with our model using randomly scattered ranges, can account for much of the pattern of observed richness, while matching very poorly the actual 2-D pattern. This commands caution toward purely 1-D analyses or null model simulations using band sums, unless the effect of width of the other dimension is modeled explicitly (19).

One-dimensional analyses may oversimplify the issue of which mechanisms determine species richness, because biological processes act in at least two dimensions. An extension of the null-model analysis to two dimensions is thus needed and reveals that although the predictive power of geometric constraints is still indisputably strong, it is weaker than in the 1-D view of the same pattern. This may reflect that ecological and physiographical factors manifest themselves more in 2-D than simply in latitude and longitude. Our results suggest that a null model accounting for geometric constraints on species distribution cannot serve as a sole general explanation for the spatial variation in species richness. However, this is not what a null model sets out to do (34, 35). The aim of our study was to enhance the principles of geometric constraints from one to two dimensions by formulating an appropriate model, and to visualize its significant consequences with reference to real-world, large-scale geographic boundaries and observed patterns.

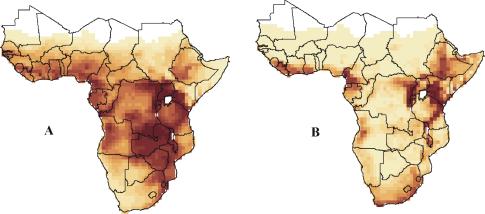
Will geometric constraints help us to understand the distribution of birds of conservation concern? Most often, threat of extinction coincides with small range size (36), which itself affects the impact of geometric constraints. Under a random placement of range origins (geometric constraints model), small-ranging species are less likely to experience hard boundaries than wide-ranging species—the impact of boundaries on their species richness pattern should be smaller. When restricting simulation and analysis to species with ranges up to 100 1° quadrats (756 species), the expected pattern from geometric constraints alone is almost uniform with a drop toward the edges. Thus, null-model predictions here do not offer new insights. Small-ranging species are in fact distributed markedly nonuniformly, with over 100 species in the Eastern Arc, Albertine Rift, and Cameroon mountain regions (Fig. 3B), and the null-model fit is close to zero in both 1-D domains and both perspectives. It is species with large ranges for which the continental geometry has highest impact (19); they are very likely to also occupy the center of the bounded area, which therefore hosts more species. The map for the 840 species with ranges above 100 quadrats (Fig. 3A) clearly confirms this notion, because the model fits are very good. Certainly, for wide-ranging species, and more generally all assemblies including them, large-scale species richness patterns are affected by boundaries and their effect can be modeled. However, the challenge of explaining the variation above and beyond null-model expectations remains.

Figure 3.

Species richness of breeding birds endemic to Africa for species with large (>100 quadrats, 840 species, A) and small (≤100 quadrats, 756 species, B) range size. Quantile classification. Values range from 2 (light) to 440 (dark) in A and from 0 (light) to 120 (dark) in B.

Abbreviations

1-D

one-dimensional

2-D

two-dimensional