Isolation and two-step classification of normal white blood cells in peripheral blood smears

Abstract

Introduction:

An automated system for differential white blood cell (WBC) counting based on morphology can make manual differential leukocyte counts faster and less tedious for pathologists and laboratory professionals. We present an automated system for isolation and classification of WBCs in manually prepared, Wright stained, peripheral blood smears from whole slide images (WSI).

Methods:

A simple, classification scheme using color information and morphology is proposed. The performance of the algorithm was evaluated by comparing our proposed method with a hematopathologist's visual classification. The isolation algorithm was applied to 1938 subimages of WBCs, 1804 of them were accurately isolated. Then, as the first step of a two-step classification process, WBCs were broadly classified into cells with segmented nuclei and cells with nonsegmented nuclei. The nucleus shape is one of the key factors in deciding how to classify WBCs. Ambiguities associated with connected nuclear lobes are resolved by detecting maximum curvature points and partitioning them using geometric rules. The second step is to define a set of features using the information from the cytoplasm and nuclear regions to classify WBCs using linear discriminant analysis. This two-step classification approach stratifies normal WBC types accurately from a whole slide image.

Results:

System evaluation is performed using a 10-fold cross-validation technique. Confusion matrix of the classifier is presented to evaluate the accuracy for each type of WBC detection. Experiments show that the two-step classification implemented achieves a 93.9% overall accuracy in the five subtype classification.

Conclusion:

Our methodology achieves a semiautomated system for the detection and classification of normal WBCs from scanned WSI. Further studies will be focused on detecting and segmenting abnormal WBCs, comparison of 20× and 40× data, and expanding the applications for bone marrow aspirates.

INTRODUCTION

The principal types of cells present in the blood are red blood cells (RBC), WBCs, and platelets. The percentage of WBC subtypes observed in human blood normally ranges between the following values: neutrophils 50-70%, eosinophils 1-5%, basophils 0-1%, monocytes 2-10%, lymphocytes 20-45%. Their specific proportions can help determine the presence of various pathologic conditions.[1]

The observation of whole blood smears under a microscope provides important qualitative and quantitative information regarding the diagnosis of various diseases including leukemia. Figure 1 shows examples of the main subtypes of normal WBCs. WBC identification and classification into these subtypes is frequently manually performed by experienced technicians or pathologists and involves two main elements. The first is the qualitative study of the morphology of the WBCs which gives information about the adequacy of the smear among other parameters including morphologic features of the cells. The second is quantitative and it consists of differential counting of at least 100 WBCs. Figure 2 shows the distribution of WBC subtypes. The accuracy of cell classification and counting is markedly affected by individual operator's abilities and experience. In addition, the identification and differential count of blood cells is a time-consuming, repetitive task. Substituting automatic detection of WBCs for the manual process of locating, identifying, and counting different classes of cells is an important challenge in the domain of clinical diagnostic laboratories.

Figure 1.

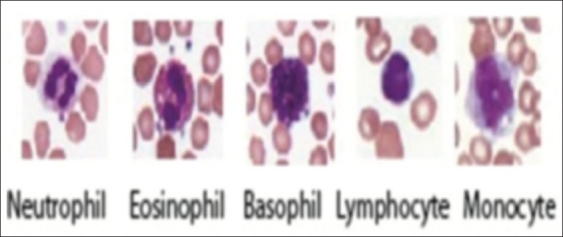
Examples of WBC subtypes

Figure 2.

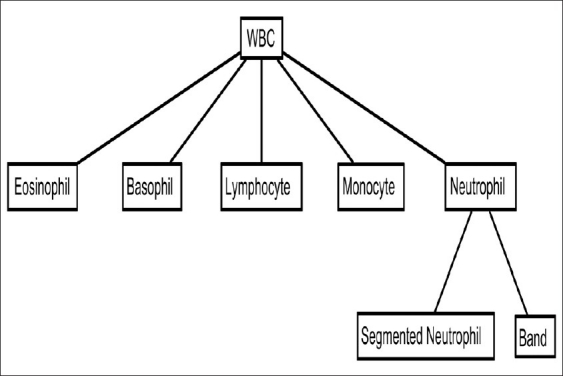
Distribution of WBC subtypes

While other technologies such as automated blood analyzers can perform a rapid and inexpensive five part differential, there is no morphologic correlate with these methods which is frequently an important factor in diagnosis. Even samples which have normal differential counts may have morphologic clues to underlying conditions such as myelodysplasia, infection, or B12 or folate deficiency. Our proposed method is best viewed as a complement to the traditional laboratory analysis (such as a CBC) rather than a replacement. Other technologies such as flow cytometry can also perform accurate differential cell counts, but the cost using this technology for a differential count far outweighs the benefit unless phenotypic analysis is also needed. Amnis Image Stream offers a rather unique technology which merges flow cytometery and imaging technologies. However, in addition to the costs associated with standard flow cytometry it is also uncertain how cellular and subcellular details in this setting which uses fluorescent antibody labeled cells would compare to those of Wright staining. Cellavision is probably the most comparable technology for performing differential counts based on morphology. Cellavision can perform differential counts on glass slides of blood and body fluids. However, our technique is the first known implementation of these techniques on whole slide images. The advantages of using whole slide imaging for this study include leveraging existing hardware, enhancing the software to facilitate development of other applications, and annotating the WSI so that the cells may be classified and identified in the context of the original image. Our proposed method has been applied successfully to a large dataset and achieves good classification accuracy for all of the WBC subtypes considered. The software is in the development stage and our initial data only evaluated normal WBCs from manually selected regions of the WSI. Further development may include classification of abnormal cells and additional automation. Our method has been implemented using MATLAB 2009a, a high level technical computing language on a system with Intel Dual-Core T4200 Processor, 2GHz, 4GB RAM. The functions from the Image Processing Toolbox and Statistics Toolbox have been used to develop our algorithm. The source code for the algorithm is available here. (http://www.sci.utah.edu/~tolga/Programs.zip).

Background

WBC Segmentation

Image segmentation is a critical step in many image analysis problems. The segmentation step is crucial because the accuracy of the subsequent feature extraction and classification step depends on correct segmentation of WBCs. It is also a difficult and challenging problem due to the complex appearance of these cells, uncertainty and inconsistencies in the microscopic image with variations in illumination. Improvement of cell segmentation has been a common direction in many research efforts. Many automatic segmentation methods have been proposed, most of them based on local image information such as histogram of regions, pixel intensity, discontinuity, and clustering techniques.

Many of the segmentation algorithms introduced are based on the edge information present in images. We discuss several of these approaches next. As proposed by Ongun,[2] WBCs were segmented using active contour models (snakes and balloons)[3] which were initialized using morphological operators. This method works well only if the WBCs have dark cytoplasm and are distinctly separate from adjacent RBCs. Kumar defined a new edge operator, the teager energy operator, to highlight the nucleus boundary which is very effective for segmenting the nuclei in cell images.[4] They also used a simple morphological method to segment the cytoplasm from the background and the RBCs. The cytoplasm segmentation works well when the RBCs and WBCs are not close to each other. In contrast, our method works well even with a complicated background. Jiang and colleagues,[5] introduced a novel WBC segmentation scheme by combining scale-space filtering and watershed clustering. Scale space filtering is used to obtain the nucleus from the subimage. Watershed clustering in 3-D HSV (Hue, saturation, value) histogram is processed to extract the cytoplasm. This method may not be sufficient in the case of high density of cells, where the RBCs are clustered close to the WBCs.[6] To overcome the difficulty associated with the high density of cells, Dorini[6] introduced the use of some simple morphological operators and explored the scale-space properties of a toggle operator to improve the segmentation accuracy in the WBCs. To avoid leaking, a common problem in cell images due to the low contrast between nucleus, cytoplasm and background, they used a scale-space toggle operator for contour regularization. In this method, cytoplasm segmentation presents a few limitations: The RBCs touching the WBC are also detected as part of the cytoplasm. In our method, we eliminate the RBCs before detecting the WBCs.

The above-mentioned algorithms are based on edge information. Edge detection methods do not work very well when not all cell details are sharp. But these methods work well if the contrast between the background and the gray internal membrane of the cell is stretched using a contrast stretching filter as stated by Piuri and Scotti.[7] However, the problem of touching RBCs and WBCs remain unresolved. Sadeghian's method[8] used Zack's simple thresholding method[9] for cytoplasm segmentation, which is based on the fact that the color intensity of RBC in a blood image is quite different from that of cytoplasm. Nuclear segmentation was performed using a GVF (gradient vector flow) snake. A few approaches that were introduced recently dealt only with the segmentation of the nucleus of the WBC. For instance, Hamghalam and Ayatollahi[10] used histogram analysis and measurement of distance among nuclei. The thresholding point was chosen based on the histogram analysis. Nuclei whose distances are less than the diameter of the WBC were merged. Rezatofighi introduced a novel method based on orthogonality theory and Gram-Schmidt process for segmenting the WBC nuclei.[11] To apply Gram-Schmidt orthogonalization for the segmentation of nucleus of WBC, a 3D feature vector was defined for each pixel using the RGB components of the images. Then, according to the Gram-Schmidt method, a weighting vector w was calculated for amplifying the desired color vectors and weakening the undesired color vectors. They chose the threshold appropriately based on the histogram information. In these two approaches, cytoplasm segmentation was not addressed. We address cytoplasm segmentation in addition to nuclei segmentation. The successful segmentation of the cytoplasm along with the nucleus segmentation aids in the automatic classification of the WBCs.

WBC Classification

WBCs are classified according to the characteristics of their cytoplasm and nucleus. Pathologists traditionally report normal WBCs as classified into five classes, i.e., monocytes, lymphocytes, neutrophils, eosinophils, and basophils. Since the chosen features affect the classifier performance, deciding which features must be used in a specific data classification problem is as important as the classifier itself. Hematology experts examine the cell shape, size, color, and texture in combination with the nuclear features. It is important to reflect the rules and heuristics used by the hematology experts in selection of the features. Several researchers have previously proposed features to differentiate WBCs.

As proposed by Ongun,[2] several types of features such as intensity- and color-based features, texture-based features, and shape-based features are utilized for a robust representation of WBCs. Classification methods used in this work include k-Nearest Neighbors, Learning Vector Quantization, MultiLayer Perceptron, and Support Vector Machine. Scotti and Piuri[7] evaluated the binary images of the cytoplasm and nucleus to characterize the feature set. The standard set of features like area, perimeter, convex areas, solidity, major axis length, orientation, filled area, eccentricity were separately evaluated for the nucleus and the cytoplasm. In addition features like the ratio between the nucleus and the cell areas, the nuclear “rectangularity” (ratio between the perimeter of the tightest bounding rectangle and the nuclear perimeter), the cell “circularity” (ratio between the perimeter of the tightest bounding circle and the cell perimeter), number of lobes in nucleus, area, and mean gray-level intensity of the cytoplasm were computed. Their system was evaluated using 10-fold cross-validation. The performance was compared using different classifiers like nearest neighbor classifiers, feed-forward neural network, radial basis function neural network, parallel classifier built with feed-forward neural network. In our method, we suggest a preliminary classification of the WBC based on the number of lobes (single or multi-lobed) in the nucleus along with the feature set to achieve better classification rate for each of the WBC subtypes.

Our approach aims at achieving a method to identify WBCs from manually prepared, Wright-stained WSI. The manually prepared Wright-stained peripheral smear is easily and routinely performed at low cost. A manual differential count is routinely performed in many laboratories when a standard CBC has an abnormal value or when requested by a clinician. The manual differential is performed by a lab technician or a hematopathologist. The personnel time associated with performing a 100 cell count can range from 1-2 minutes per slide. However, considering the volume of peripheral smears reviewed in a day, the time dedicated to cell counting can be considerable. In addition, the technologist time per slide can be considerably greater when the white cell count is very low. By utilizing our existing whole slide imaging technology, we sought to investigate the feasibility of automating the identification of WBCs from digital images. This is a preliminary investigation in which we sought to determine if these techniques were flexible enough to use without performing additional stains or cell preparations, adding additional steps, or interrupting the current procedures or workflow. We propose a simple segmentation scheme based on the difference in color channels and morphological operations to segment the WBCs. The algorithm has low computational cost but good accuracy. Two-step classification with the aid of a comprehensive feature set is helpful in realizing better accuracy rates in the classification of WBCs. In this initial work, our slide data was aggregated and analyzed as a group. We validate our approach on 320 images with 1938 cells. For comparison we implemented the segmentation algorithm proposed by Dorini[6] and the features selected for classification were based on the features implemented by Scotti and Piuri.[7]

METHOD

Slide Preparation and Scanning

An Aperio CS scanner (Aperio Technologies, Vista, CA) outfitted with an Olympus UPlanSApo 20×, 0.75 Numerical Aperture Objective Lens and Basler L301kc trilinear-array CCD line scan camera was used to create the whole slide images. Ten sequential, Wright-stained peripheral blood slides submitted for hematopathologist review were scanned at 20×. Slides were prepared manually according to the lab protocol and our current workflow. A drop of blood was pulled between two slides at roughly 45 angle to create a blood film slide which was allowed to air dry. Slides were briefly fixed in methanol prior to staining with Harelco Wright's stain. Slides were then cover slipped prior to scanning at 20×. The use 20× vs. 40× is frequently an issue of discussion in digital pathology. While 20× provides faster scan times and smaller files, the image quality is better with a 40× scan. We chose 20× as a starting point to demonstrate proof of concept with a secondary goal of comparing the performance of the algorithms on 40×. Scan times ranged from 5-10 minutes per slide. Whole slide imaging captured a technician selected area of the blood film (ranging from 17 mm - 22 mm in height by 15 mm - 25 mm in length) using automated focus. Images were compressed at a quality setting of 70% during the capture process with resulting file sizes averaging between 20 and 60 megabytes.

Detection and Segmentation of White Blood Cells from Peripheral Blood Smear

WBC counting is performed by pathologists only in thin areas of the blood smear. Similarly, we manually selected optimal regions adjacent to feathered edge and stored the images corresponding to the thin sections of the blood smear. While regions were manually selected in this preliminary study, additional work is being done to automate this process. Each of these images has 2-15 WBCs.

For easy identification of the WBCs, the whole blood slides are stained with Wright's stain, which produces a dark intensity in nuclei of WBCs. We convert the images from RGB (red, green, blue) to HSV (hue, saturation, value) space. First, using the saturation image, we threshold it to approximately identify the nuclei. A threshold value of 0.55 is used in our experiment (saturation range = 0-1). We eliminate extremely small regions based on their area. The advantage of using the saturation image for thresholding is to eliminate variations in illumination that occur. Finally, we crop the part around the nucleus making sure that the whole WBC is captured. If the distance between two nuclei is less than 5.52 μm, then they belong to the same WBC. The advantage of using only the cropped image is that the regions containing mostly RBCs (which lack nuclei) are eliminated. We process all the images and record the detected WBCs. The advantage of this method is that we do not have any false negatives in the detection of the WBCs. We do capture some redundant cells (false positives) which have been stained, but we eliminate them in further processing by manually assigning them to a noise class. Figure 3 depicts the flowchart for WBC detection.

Figure 3.

Flowchart for WBC detection

We have implemented a novel, simple, and robust segmentation scheme for segmenting WBCs. Information is present in all color channels of the images. RBCs are mostly pink/red in color and the WBCs have a dark stained nucleus. We take advantage of the information present in the blue and red channels. The intensity range of images is 0–255. First we threshold (threshold value = 0.9 ^*255) the given subimage based on intensity and eliminate small regions to obtain a binary image. This eliminates the background pixels, leaving only the RBCs and the WBC. Thresholding and smoothing the difference in the red and blue channels helps in identifying the RBCs (threshold value = 0.1 ^*255). Subtracting the RBCs and the background from the original image results mostly in an image of WBCs. Hence, we are left with WBCs which may have small parts of RBCs attached to them. We fill in details lost due to our thresholding operation using a standard hole filling algorithm. Using a disk-shaped structuring element we get rid of the thin parts (morphological opening) of the RBCs which are attached to the WBC. This procedure helps in detecting the boundary of the WBC. Once the WBC boundary has been extracted we concentrate on separating the WBC region into cytoplasm and nucleus. We use the saturation image again to threshold the detected WBC. This thresholding (threshold value = 0.55) operation yields a binary image of the nucleus. By taking the difference between the WBC image and the nucleus image we get the cytoplasm region. Hence this simple, extremely fast method can be used to segment the blood image to get the desired results. Figure 4 depicts the flowchart for the WBC segmentation. Figure 5 shows examples of the segmented WBC.

Figure 4.

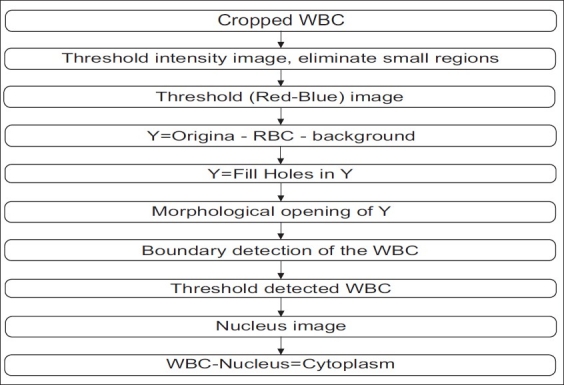
Flowchart for WBC segmentation

Figure 5.

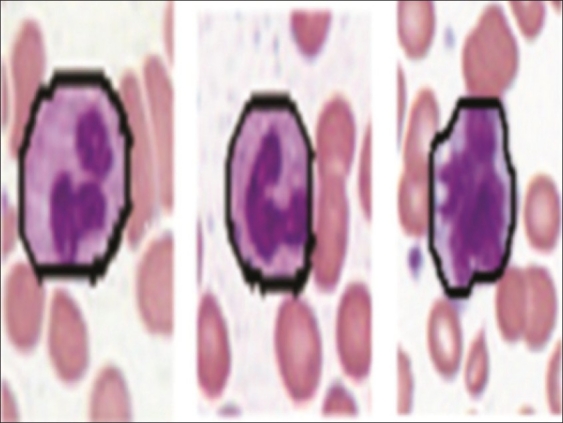
Segmented WBC

Segmented vs. Nonsegmented Nucleus Classification

WBCs can be broadly classified into cells with segmented nuclei and cells with nonsegmented nuclei as shown in Figure 6. The nucleus shape is the key factor in deciding the class to which the WBC belongs. We have found that deciding whether the nucleus is segmented or nonsegmented first gives a significant advantage to the final classification process. Ambiguities associated with connected nuclear lobes are resolved by detecting local maximum curvature points, detecting concavities, and partitioning them through geometric rules. The flowchart in Figure 7 gives the steps for the classification of WBC into segmented and nonsegmented WBCs. Figure 8 gives a visual interpretation of the goals of each step. Figure 8a shows a white blood cell image. Figure 8b shows the boundary of the nucleus superimposed on the white blood cell. The process of classification of the WBC into these two broad classes can be described in the following steps:

Figure 6.

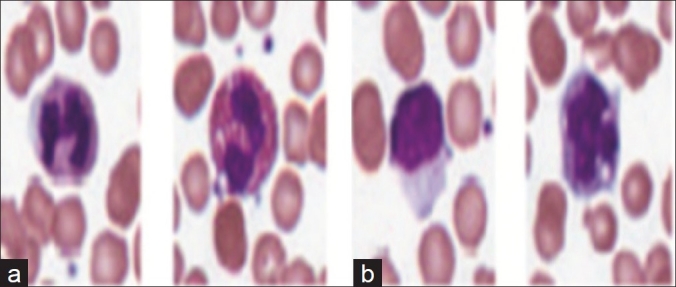
Examples of WBC with (a) segmented and (b) nonsegmented nucleus

Figure 7.

Step 1 of classification

Figure 8.

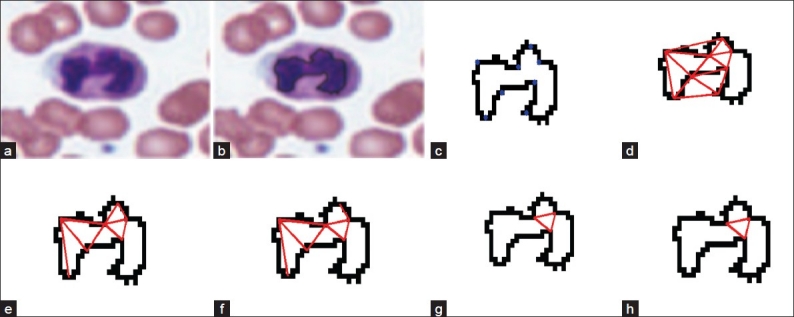
Steps representing segmented vs. nonsegmented nucleus classification, (a) White blood cell image; (b) Nucleus boundary superimposed on the white blood cell image; (c) Maximum curvature points; (d) Triangulation of maximum curvature points; (e) Removal of background edges; (f) Retaining edges if the tangents are in opposite directions; (g) Retaining edges if the edge vector and tangent vector are perpendicular; (h) Retains edges if the end points have curvatures in the same direction

Detection of maximum curvature points: The goal of this step is to identify local curvature maxima corresponding to sharp bends (corners). We utilize global and local curvature properties in extracting the maximum curvature points. After contour extraction we compute the curvature using Equation and retain the local curvature maxima points.[12,13]

where x(s) and y(s) represent the x-coordinates and y-coordinates of the boundary points respectively. x’ and y’ represent the first derivatives with respect to s. x” and y” represent the second derivatives with respect to s.

Elimination of low curvature maxima is done by calculating an adaptive threshold according to the mean curvature within a region of interest.[12] The region of interest (ROI) of a maximum curvature point is defined as the segment of the contour between the two nearest curvature minima points surrounding it denoted by L1 and L2. The ROI of each maximum curvature point is used to calculate a local threshold adaptively where P is the position of the maximum curvature point on the contour, and R is a coefficient:

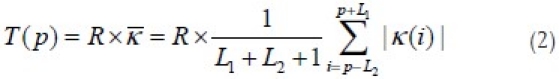
where 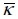is the mean curvature of the ROI and i is the index of the point on the nucleus boundary. The absolute value of the curvature is used to distinguish between low curvature maxima points against high curvature maxima points. A round corner (low curvature maxima) tends to have absolute curvature smaller than T(p), while a sharp corner (high curvature maxima) tends to have an absolute curvature larger than T(p). The reasoning for choosing an appropriate value of R can be found in reference 12. A value of 1.5 is used for R in our experiment. Figure 8c shows high curvature maxima detected from a contour.

Delaunay triangulation of points of maximum curvature: The goal of this step is to construct the set of all potential edges that might correspond to the boundaries between the different lobes of a segmented nucleus. The high curvature maxima found in the previous step are used as the candidate vertices for these edges. A triangle S from T satisfies the Delaunay criterion if the interior of the circumcircle through the vertices of S does not contain any points. If all triangles satisfy the Delaunay criterion, then the triangulation T is called Delaunay triangulation.[14] We apply the Delaunay triangulation (DT) to all points of maximum curvature to find candidate edges which potentially separate different segments of the nuclei.[15] The results for an example contour are shown in Figure 8d.

Rules to Retain Necessary Edges

Shape and Color-Based Rules

A set of conditions based on observations are first checked to see if a WBC has segmented nuclei.

We eliminate all edges if the nucleus has a roundness ratio >λ₁ and classify the cell as nonsegmented nucleus type. The roundness ratio is calculated as the ratio of the area and the square of the perimeter of the contour as shown in Equation (3).[16] A circle has the value “1” and for structures with increasing irregularity, the value tends to “0.”

Eliminate all edges if the ratio of the original area of nucleus to the convex hull of nucleus >λ₁ and classify the cell as of nonsegmented nucleus type. A set A is said to be convex if the straight line segment joining any two points in A lies entirely within A. The convex hull H of an arbitrary set >λ is the smallest convex set containing S.[17]

Find the ratio of the area of the red/pink regions to the area of the entire of WBC. The red/pink regions are found by taking the difference between the red and blue image (red - blue) and thresholding it to obtain a binary image. If the ratio is >λ₃, then the nucleus is classified directly without further processing as a segmented nucleus.

We use λ₁ = 0.75, λ₂ = 0.85, λ₃ = 0.3.

If there are two or more nuclei present in one cell, the nucleus is directly classified as a segmented nucleus;

Geometric Rules

If the above reasons are not satisfied, a series of geometric rules helps us in separating the cells with segmented nucleus from the cells with nonsegmented nucleus. Let S_ij be the edge connecting two points of maximum curvature maxima p_i and p_j. T_i and T_j are the unit vectors representing the tangent directions at p_i and S_ij. The following set of rules is used:

We need to retain edges that are inside the nucleus only. Hence, we eliminate edges that pass through the background and edges that intersect the boundary [Figure 8e].

For a valid edge separating two lobes, the tangent vectors at the endpoints are in opposite directions. We use the dot product of the tangents to check this condition.

The edge S_ij is eliminated if T_i T_j T_i > Th1; observe here that the dot product of these two tangents will be negative always if these tangents are oppositely directed [Figure 8f].

The tangents need to be orthogonal to the edge vector.[15]

We eliminate edges if 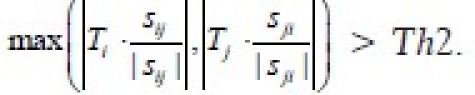If the edges and the tangents are orthogonal, the dot product of vectors along these vectors will be approximately 0 [Figure 8g].

We need to ensure that the endpoints of the edges have curvatures in the same direction as in Figure 9a. To check this condition, we calculate the product of the curvature values at the endpoints of the edge. The edge S_ij is eliminated if κ_i κ_j < 0. The product is negative if the points have curvatures in different directions as shown in Figure 9b. This condition eliminates edges if the end points of the edge have opposite curvatures [Figure 8h].

Figure 9.

Examples to illustrate the curvature of convex and concave regions

We used Th2 = 0 and Th2 = 0.4.

We check the above conditions for each edge in the Delaunay triangulation. After the above conditioning, we label as segmented nucleus if the number of detected edges is larger than zero. Otherwise, the WBC is classified as a cell with nonsegmented nucleus.

An example of this classification is shown in Figure 8. Figure 8a shows a white blood cell image. Figure 8b shows the boundary of the nucleus superimposed on the white blood cell. Figure 8c shows the local curvature maxima points on the nucleus boundary. Figure 8d shows the triangulation of the points of maximum curvature to find the candidate edges. In Figure 8e the background edges have been eliminated. Figure 8f retains edges if the angle between tangents is close to π radians. Figure 8g retains edges if the edge vector and tangent vector are close to perpendicular. Figure 8h retains edges if end points have curvatures in the same direction. Finally, three edges are present in the end indicating that the nucleus has three segments that are interconnected.

Automated Classification of WBC to its Subtype

To classify the WBC to its respective subtype, we use features that describe the characteristics of the cytoplasm and the nucleus. We choose 19 features such as area, perimeter, convex area, solidity, orientation, eccentricity, separately evaluated for the nucleus and the WBC. The result obtained from the previous step gives us information about the broad nucleus type (segmented or nonsegmented). This result is a novel binary feature added to our classifier. In addition features like “circularity” (ratio between the perimeter of the tightest bounding circle and the nuclear perimeter) of the nucleus, nucleus to cytoplasm ratio, ratio of nucleus area to area of WBC, entropy of the cytoplasm, and mean gray-level intensity of the cytoplasm (all three color channels) are computed.[7] Fishers linear discriminant is used to reduce our multidimensional dataset to six dimensions. We use a linear discriminant in this six-dimensional space to classify the data to their respective type. Linear discriminant analysis (LDA) is used to find a linear combination of the features which characterizes or separates these five classes of WBCs. The classifier is biased using the number of samples in each class. The system is evaluated using 10-fold cross-validation. Cross-validation is a technique for assessing how the results of a statistical analysis will generalize to an independent dataset. It is mainly used in settings where the goal is prediction, and one wants to estimate how accurately a predictive model will perform in practice. One round of cross-validation involves partitioning a sample of data into complementary subsets, performing the analysis on one subset (called the training set), and validating the analysis on the other subset (called the validation set or testing set). To reduce variability, multiple rounds of cross-validation are performed using different partitions, and the validation results are averaged over the rounds. The functions from the Statistics Toolbox in MATLAB have been used to analyze the data.

RESULTS AND DISCUSSION

Segmentation Results

This system has been tested using images obtained from the ARUP Laboratory, University of Utah. Our dataset consists of 320 images at 20× magnification that contain 1938 expert labeled WBCs. The input images have been processed to detect the WBCs. We obtained 1938 subimages with single correctly positioned WBCs. We did not have any false negatives in the detection of WBCs. The false positive rate was 10.25%. The false positives consist of regions of artifact or debris that have stain and color characteristics which fall within the thresholding parameters. We eliminated the false positives by manually assigning them to a noise class. The performance of the segmentation algorithm was evaluated by comparing our proposed method with a hematologist's visual segmentation. The segmentation algorithm was applied to 1938 subimages of WBCs; 1804 of them were accurately segmented. The accuracy rate for segmentation was 93.08 %. Figure 10 shows some segmentation results. The main advantage is the elimination of the RBCs using the difference image. Some of the examples present segmentation results for more complex images, with a complicated background and containing several RBCs close to the WBC. There are also cells with multiple nuclei. We obtained good segmentation results for both cases. The examples shown reflect the performance of the algorithm for all the WBC types.

Classification Results

A vector of 19 features was extracted for every WBC. The experts assigned the correct classification of each extracted WBC. The resulting dataset (1938(number of cells)×19 (features)) has been used to determine the subtype of the WBC segmented using linear discriminants as described in the Methods section. The system was evaluated using a 10-fold cross-validation technique.

We observed that there is a lot of misclassification between various classes as seen in Table 1.[6,7] The rows in the confusion matrix represent the real subtype and the columns represented the detected subtype. An initial classification of the WBCs into cells with a segmented nucleus (neutrophils, eosinophils, basophils) and cells without nuclear segmentation (lymphocyte, monocyte) improves the performance of the classification. The accuracy of classification is improved for all the classes, see Table 2.

Table 1.

Confusion matrix for the comparison method (five subtypes)[6,7] Rows represent the correct classification by experts. For each row, the columns represent the classification made by the approach used in the comparison method. The classification percentages made by the algorithm is enclosed in brackets. Diagonal entries indicate correct classification and are indicated in bold

Table 2.

Confusion matrix using our novel two-step classification (five subtypes). Rows represent the correct classification by experts. For each row, the columns represent the classification made by our algorithm. The classification percentages made by the algorithm is enclosed in brackets. Diagonal entries indicate correct classification and are indicated in bold

This five subtype classification is generally performed by pathologists. We obtain very good classification results for the given dataset as seen in Table 2. Experiments show that the two-step classification implemented achieves a 93.9% overall accuracy in the five subtype classification. Results indicate that the morphological analysis of white blood cells is achievable and it offers good classification accuracy. The individual classification rate needs to be improved for eosinophils and monocytes. A higher segmentation accuracy would result in lowering the error rate in the classification process.

CONCLUSION

There are currently WBC classification systems based on morphology in clinical use such as the Cellavision system. However, the classification performed by Cellavision utilizes small snap shot images obtained directly from a glass slide. In contrast the techniques described in this paper allow identification of WBCs from a whole slide image. The use of WSI technology allows some advantages over the Cellavision system including leveraging of capital equipment, expansion of software to include other applications involving WSI, and identifying and localizing the WBCs in the context of the original WSI. While the localization functions were not part of the current study, further work is currently being pursued to implement some of these benefits. Viewing the classified cells in their original context on Wright stained WSI allows the pathologist to also evaluate red blood cells, platelets, and smear adequacy data in addition to the WBCs. This technique may facilitate work flow by replacing tedious and monotonous work with automation while maintaining all of the digitized data in the original smear. Even though the time to scan and analyze the slide may is longer than a manual differential count, the time associated with pathologist review may actually be decreased by completing the automated analysis prior to the pathologist spending any time on the case. In addition, scanning and classifying the cells is mostly machine driven and requires very little hands on time, thus allowing personnel to perform other duties.

This is a report of a developmental step to assess the viability of a larger scale automated solution. The methodology achieves a semiautomated system for the detection and classification of normal WBCs from scanned WSI. Experiments show that the two-step classification implemented achieves good overall accuracy in the five subtype classification. Results indicate that the morphological analysis of white blood cells is achievable and it offers good classification accuracy. Further studies will be focused on detecting and segmenting abnormal WBCs, comparison of 20× and 40× data, and expanding the applications for bone marrow aspirates. In the future, we will also perform the elimination of false positives in WBC detection in an automated manner using linear discriminants on the same feature set used for classification.