Abstract
Enormous progress has been achieved understanding the molecular mechanisms regulating endoreduplication. By contrast, how this process is coordinated with the cell cycle or cell expansion and contributes to overall growth in multicellular systems remains unclear. A holistic approach was used here to give insight into the functional links between endoreduplication, cell division, cell expansion, and whole growth in the Arabidopsis (Arabidopsis thaliana) leaf. Correlative analyses, quantitative genetics, and structural equation modeling were applied to a large data set issued from the multiscale phenotyping of 200 genotypes, including both genetically modified lines and recombinant inbred lines. All results support the conclusion that endoreduplication in leaf cells could be controlled by leaf growth itself. More generally, leaf growth could act as a “hub” that drives cell division, cell expansion, and endoreduplication in parallel. In many cases, this strategy allows compensations that stabilize leaf area even when one of the underlying cellular processes is limiting.
In multicellular systems, growth is achieved by an increase in cell number, cell size, or both. A cellular process, endoreduplication, also called endopolyploidization or endoreplication, is described as also interacting with the growth of various tissues in plants, animals, and humans (Gandarillas et al., 2000; Edgar and Orr-Weaver, 2001; Lee et al., 2009), but how it interacts with cell division and cell expansion is still unclear. Endoreduplication consists in doubling chromosomal DNA without mitosis, so successive rounds of endoreduplication result in the doubling of nuclear DNA content each time. The transition from the cell cycle to endoreduplication is a finite event regulated by well-identified genetic mechanisms (Vlieghe et al., 2005; Nieuwland et al., 2009). A beneficial role of endoreduplication in plant development is supposed because this cellular process was selected during evolution and is widespread in higher plants, but its precise role in organ development is still unknown. Because endoreduplication often covaries with cell and/or organ size, it is often stated that it could trigger cellular and/or organ growth (Kondorosi et al., 2000; Castellano et al., 2001; Larkins et al., 2001; Lee et al., 2009). In addition, because cells entering the endocycle program cannot resume mitotic divisions, endoreduplication and cell division have been described as alternative processes that coexist in a tissue, leading to a large range of cell sizes (Roeder et al., 2010). However, variations in endoreduplication do not always reflect variation in cell size and/or cell number (for review, see John and Qi, 2008; Lee et al., 2009). As a consequence, many studies have been devoted to understanding the relationships between endoreduplication, cell division, and cell or organ growth in various multicellular systems such as Drosophila (Edgar and Nijhout, 2004; Pierce et al., 2004), Caenorhabditis elegans (Flemming et al., 2000; Lozano et al., 2006), and plant organs (Kondorosi et al., 2000; Chevalier et al., 2011). However, all these studies do not converge toward a clear consensus about the functional links between cellular processes and organ size. Whether cellular processes drive organ growth or whether organ growth drives cellular processes is still under debate in many organisms (Nijhout, 2003; Fleming, 2007; Tsukaya, 2008; Harashima and Schnittger, 2010).
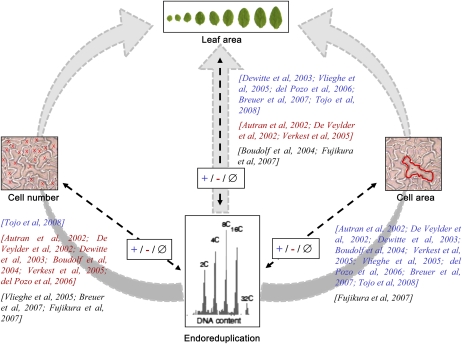
A large effort to address this question was also started in the multicellular leaf system in the model plant Arabidopsis (Arabidopsis thaliana), resulting into a number of discrepancies, as illustrated by the results of 10 nonexhaustive papers presented in Figure 1. In the large majority of these papers, a decrease or increase in endoreduplication is accompanied by a respective decrease or increase in cell area, although this is not always the case in one study among the 10 (Fujikura et al., 2007). In other plant organs, final ploidy levels are also sometimes uncoupled from final cell sizes (Gendreau et al., 1998; Beemster et al., 2002). By contrast, covariations between endoreduplication and either cell number or leaf area are not consistent between studies. Positive covariations, negative covariations, and the absence of covariation were described between these variables depending on the study. At least two reasons can explain such discrepancies. First, the authors analyzed the phenotypic consequences of the modification of a specific molecular mechanism regulating cell division or endoreduplication. In this context, it is not possible to ensure that genetic disruptions of one or the other process may reflect the “normal” mechanisms that interact with growth in intact complex systems (Nijhout, 2003). Second, these studies have been performed by different laboratories in different growing conditions, and because (1) the reproduction of the same phenotype between laboratories is difficult and (2) changes in environmental conditions such as light intensity or soil humidity differently affect endoreduplication, cell expansion, and cell division in a leaf, this could contribute to the difficulty of finding agreement between the observations (Cookson et al., 2006; Massonnet et al., 2010).
Figure 1.
Published covariations between endoreduplication and cell number, cell area, or organ area in Arabidopsis leaves. Covariations were established from a nonexhaustive list of 10 selected references that are indicated on each arrow in square brackets. The references are noted in blue when a positive covariation (+) was described between endoreduplication and another variable (i.e. when an increase or decrease in endoreduplication was accompanied by a respective increase or decrease in the other variable), in red when a negative covariation (−) was described between endoreduplication and another variable (i.e. when an increase or decrease in endoreduplication was accompanied by a respective decrease or increase in the other variable), and in black in the case of an absence of covariation (∅; i.e. when a variation in endoreduplication was not accompanied by a change in the other variable). The three gray arrows represent putative functional links frequently described in the literature between endoreduplication and leaf area, either via a control of cell number (left) and cell area (right) or a direct link (middle).
In this context, the aim of our work was to gain insight into the potential contribution of endoreduplication to the control of organ growth and its interaction with cell division and cell expansion. To this end, we selected the Arabidopsis leaf as a multicellular model system. A quantitative multiscale phenotypic analysis of leaf growth was performed from the cell level (ploidy level, cell number, and cell size) to the leaf level (individual leaf area) and the whole plant level (rosette area and rosette expansion rate). Papers have reported that a delay in flowering date, and consequently a change in whole plant leaf number, affected cell number and/or size in individual leaves (Cookson et al., 2007; Tisné et al., 2008). In many cases, lines with high numbers of leaves have large epidermal cell area but low epidermal cell number in their leaves, whereas lines with low numbers of leaves have the opposite phenotype (Tisné et al., 2008). To test an eventual role of endoreduplication in the functional relationships between leaf number and cell size and/or number, rosette leaf number was also considered in our study. All these variables were scored in a set of 200 genotypes grown under similar environmental conditions. The set of genotypes included genetically modified plants with a gain or a loss of function in genes encoding proteins known to control endoreduplication level, leaf area, leaf shape, cell area, or cell number (Table I). A population of recombinant inbred lines issued from the cross of two natural variants, Landsberg erecta (Ler) and Antwerp (An-1), was also selected. A large range in cell area and cell number was described in this population, mainly due to the erecta mutation that is carried by the Ler line and segregates in the recombinant lines (Tisné et al., 2008). First, correlation and quantitative genetic analyses were combined to analyze the covariations between these variables. However, a bivariate correlation does not give insight into which variable regulates the other and can also result from a regulation of the two variables via common pathways. Then, in order to gain insight into the functional relationships between endoreduplication and other growth variables, we used a structural equation modeling (SEM) approach. This multivariate statistical technique allows one to test the fit of data to causal hypotheses about the functioning of a system (Shipley, 2000; Pugesek et al., 2003). In the papers reported in Figure 1, endoreduplication, cell division, and cell expansion are mainly discussed as driving leaf growth by a cascade effect (i.e. endoreduplication would affect cell number and/or cell area and both cell number and cell area would be combined to control leaf area; Fig. 1, gray arrows on the left and right, respectively). Alternatively, endoreduplication could control leaf growth without intermediate cellular links (Fig. 1, gray arrow in the middle) or leaf growth could control cellular processes, as is sometimes debated in many organisms without, to our knowledge, clear experimental evidence (Nijhout, 2003; Fleming, 2007; Tsukaya, 2008; Harashima and Schnittger, 2010). Here, the use of SEM allowed us to distinguish between these alternatives and suggested that leaf growth itself would be the major force driving endoreduplication.
Table I. Correlation between endoreduplication and other leaf growth variables.
Pearson’s correlations between EF and six leaf growth variables (epidermal cell area in leaf 6 [CA], epidermal cell number in leaf 6 [CN], leaf 6 area [AL6], rosette leaf number [LN], relative rosette expansion rate [RER], and rosette leaf area [RA]) in the 88 mutants, the wild-type Col-0, the 109 lines from the Ler × An-1 RIL population, and the two corresponding parental lines are shown. Significance values are as follows: *** P < 0.001. When correlations were significant in both sets of genotypes, the differences of slopes and intercepts between the two sets were tested by an analysis of covariance. *** P < 0.001.
| Sample | CA | CN | AL6 | LN | RER | RA |
| EF mutants | 0.29 | 0.49*** | 0.67*** | 0.18 | 0.55*** | 0.58*** |
| EF RILs | 0.57*** | 0.16 | 0.61*** | 0.019 | 0.69*** | 0.45*** |
| Analysis of covariance | ||||||
| Slopes mutant/RILs | – | – | 0.63/0.47 | – | 494/503 | 0.04/0.009*** |
| Intercepts mutant/RILs | – | – | 0.95/1.28*** | – | 0.3/0.24 | 1.22/1.48 |
RESULTS
Variation in Endoreduplication in Arabidopsis Mutants and Recombinant Inbred Lines
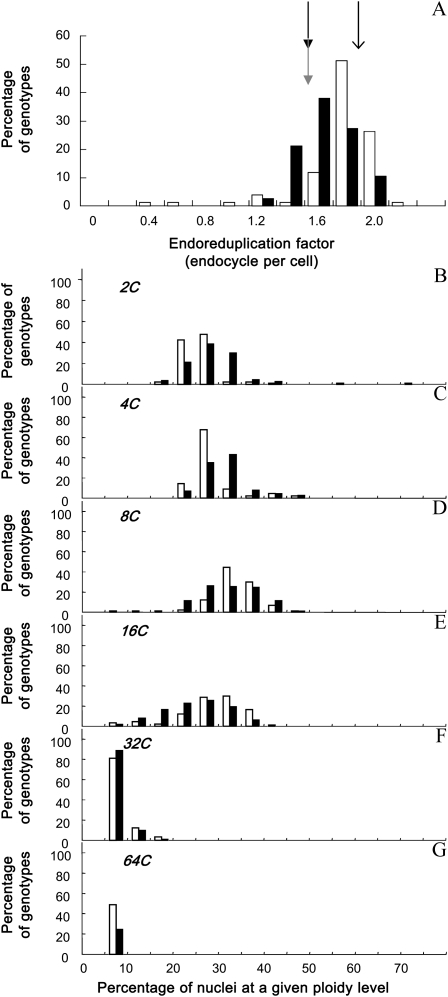
The endoreduplication factor (EF; i.e. the mean number of endocycles per cell) varied by 7-fold from 0.33 to 2.17 endocycles per leaf cell across the 200 genotypes (Fig. 2A; Supplemental Figs. S1A and S2A). It did not differ significantly between the two parents of the recombinant inbred line (RIL) population, Ler and An-1 (1.5 endocycles per cell), and was higher in Columbia (Col-0; 1.8 endocycles per cell; Fig. 2A; Supplemental Figs. S1 and S2). The RIL population tended to have lower EF than the mutant collection (Fig. 2, A [due to a larger proportion of nuclei in 2C and 4C], B, and C), but three genotypes had very low EF compared with all other genotypes, namely KRP1OE, cycd5.1, and KRP2OE (Fig. 2A; Supplemental Fig. S1A).
Figure 2.
Variation of endoreduplication in the two sets of genotypes. Frequency distribution of EF (A) and the percentage of nuclei in 2C (B), 4C (C), 8C (D), 16C (E), 32C (F), and 64C (G) are shown. Genotypes are divided into two groups: the mutant collection (white bars) and the Ler × An-1 RIL population (black bars). In A, mean values of EF are shown by an arrow for Col-0 and by gray and black arrows for An-1 and Ler, respectively.
In all genotypes, leaves contained a mix of cells with 2C, 4C, 8C, and 16C nuclei (i.e. corresponding to zero, one, two, and three endocycles, respectively). In most genotypes, the proportions of 2C, 4C, and 8C nuclei varied in a range from 15% to 50% of their cells (Fig. 2, B–D). A lower but significant proportion of nuclei (between 5% and 40%) progressed through one additional round of endocycling, allowing them to reach 16C (Fig. 2E). Most genotypes (96% in the mutant collection and 99% in the RIL population) also displayed 32C nuclei (four endocycles), but only for a low proportion of cells (between 5% and 20%; Fig. 2F). In some genotypes (49% in the mutant collection and 25% in the RIL population), cells with 64C nuclei were also measured (Fig. 2G).
Endoreduplication Is Robustly Correlated to Leaf Area and Rosette Expansion Rate But Neither to Cell Area nor to Cell Number
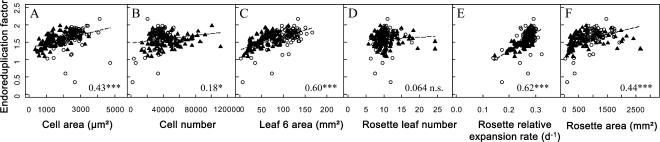
We analyzed the bivariate relationships between EF and growth-related traits, namely cell area, cell number, leaf 6 area, rosette leaf number, rosette relative expansion rate, and rosette area (Fig. 3). A large phenotypic variation was observed for all these traits in the two sets of genotypes (Fig. 2A; Supplemental Fig. S3). As shown for EF, the distributions of rosette area, leaf 6 area, and cell area were shifted toward lower values in the RIL population compared with the mutant collection (Supplemental Fig. S3). By contrast, the distribution of cell number was shifted toward higher values (Supplemental Fig. S3). When all 200 genotypes were considered together, EF was significantly and positively correlated to rosette area, rosette relative expansion rate, leaf 6 area, cell number, and cell area (Fig. 3), although the relationship with cell number was weaker (Fig. 3B). By contrast, EF was not correlated to rosette leaf number (Fig. 3D).
Figure 3.
Correlation between the EF and the other leaf growth variables. Correlation is shown between the EF and epidermal cell area (μm2; A), epidermal cell number (B), leaf 6 area (mm2; C), rosette leaf number (D), rosette relative leaf expansion rate (d−1; E), and rosette leaf area (mm2; F). White circles and black triangles represent mean values of the considered growth variable for each genotype of the mutant collection and the RIL population, respectively. The linear relationship (dotted line) and the Pearson’s coefficient noted inside each graph (bottom right corner) correspond to the relation and the coefficient when all 200 genotypes are considered together. Asterisks indicate significant correlations, with values as follows: * P < 0.05, *** P < 0.001; ns indicates a nonsignificant correlation. Correlations were also tested by dividing the 200 genotypes in two subgroups: the mutant collection and the RIL population (Table I).
When the mutant collection and RIL population data sets were considered separately, the absence of correlation between EF and rosette leaf number was confirmed in both sets of genotypes. In addition, robust positive correlations were still found between EF and leaf 6 area, rosette relative expansion rate, and rosette area (Table I). The relationship between EF and rosette relative expansion rate was common to both sets of genotypes (i.e. same slopes and same intercepts; Fig. 3E; Table I). However, for the two other relationships, despite a similar trend, the intercepts of the relationships between EF and leaf 6 area differed significantly and the slope of the relationships between EF and rosette area was significantly higher in the mutant collection than in the RIL population (Fig. 3, C and F; Table I). Correlations between endoreduplication and growth variables at the cellular scale differed between the two sets of genotypes. A significant positive correlation between EF and epidermal cell area was found in the RIL population but not in the mutant collection (Fig. 3A; Table I). In contrast, EF was positively correlated to epidermal cell number in the mutant collection but not in the RIL population (Fig. 3B; Table I). In summary, similar trends were observed between EF and growth traits at the leaf or rosette level but not at the cellular level.
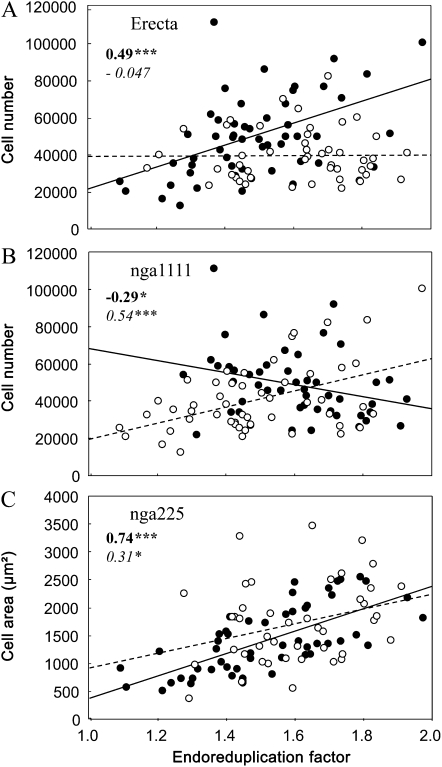
In the RIL population, as reported previously by Tisné et al. (2008), correlations could be altered by the genetic identity of the individuals, specifically by the effect of the alleles at one of the loci. Therefore, we tested whether the slopes of the relationships between EF and the other six leaf growth variables were affected by allelic segregation at each locus. On all 486 possible pairs of relationships (six correlations at 81 markers), three had significantly different slopes when subsets of the RIL population were considered separately (RILs with Ler alleles against RILs with An-1 alleles). Alleles at both Erecta (ER) and nga1111 markers affected the slope of the regression between EF and cell number (Fig. 4, A and B). EF was positively correlated to cell number in lines with Ler alleles at the ER marker but not for others (Fig. 4A). In addition, EF was positively correlated to cell number in lines with An-1 alleles at nga111 but negatively for others (Fig. 4B). So, the absence of correlation between EF and cell number when all lines of the RIL population were considered together (Table I) masked different trends (i.e. positive, negative, or no relationships), depending on allelic identity at two markers (Table I; Fig. 4, A and B). Alleles at nga225 slightly affected the slope of the relationship between EF and cell area but with similar trends (i.e. a positive correlation; Fig. 4C). The relationships between EF and leaf 6 area, rosette area, or rosette relative expansion rate were not affected by the alleles at each marker, confirming the robustness of these relationships.
Figure 4.
Allelic segregation affects the slope of linear regression between EF and leaf growth variables. Relationships are shown between EF and cell number (A and B) or cell area (C) in subpopulations from the Ler × An-1 population. In each panel, the population is divided into two subpopulations, depending on the alleles at ER (A), nga1111 (B), or nga225 (C) markers. At each marker, RILs with the Ler and An-1 alleles are shown by black and white circles, respectively, with linear regressions in solid or dotted lines, respectively. Pearson correlation coefficients are noted in boldface or italics for RILs with Ler or An-1 alleles, respectively. Asterisks indicate significant correlations, with values as follows: * P < 0.05, *** P < 0.001.
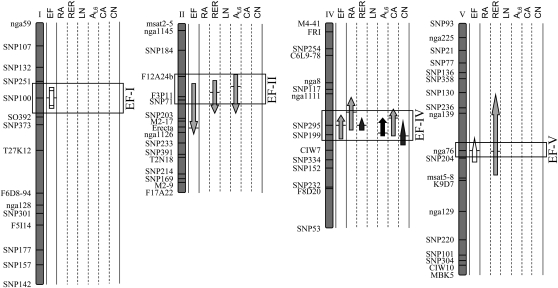
Quantitative Trait Loci for Endoreduplication Colocalize with Quantitative Trait Loci for Leaf Growth Traits
A quantitative trait locus (QTL) analysis was carried out in the RIL population to investigate the genetic bases of EF variation and covariation with the leaf growth variables. Both main effect and epistatic QTLs were mapped for EF (Fig. 5). Four QTLs that controlled EF, EF-I, EF-II, EF-IV, and EF-V, were detected on chromosomes I, II, IV, and V, respectively. The QTL model explained 37% of the phenotypic variance of EF, with two main effect QTLs (EF-II and EF-IV) and one epistatic interaction (EF-I × EF-V). Main effect and epistatic QTLs were also mapped for the growth variables (Supplemental Fig. S4), but only those that colocalized with EF QTLs were reported in Figure 5. Main effect QTLs mapped for endoreduplication systematically colocalized with QTLs for rosette relative expansion rate. In addition, EF-II and EF-IV colocalized with QTLs for leaf 6 area and EF-IV colocalized with QTLs for rosette area, cell area, and cell number. In all groups of colocalizations, EF QTLs had the same allelic effects as other QTLs, and the positive effect on all variables was due either to Ler (EF-IV and EF-V) or An-1 (EF-II) alleles. Colocalizations of EF QTLs with QTLs controlling rosette area, rosette relative expansion rate, leaf 6 area, and cell area were in agreement with the positive correlations reported above (Table I). In addition, the EF QTL at SNP295 (EF-IV) colocalizes with a QTL controlling cell number, despite an absence of correlation between both variables (Table I).
Figure 5.
Ler × An-1 linkage map showing QTLs for EF and other leaf growth variables. For each variable (EF, rosette area [RA], rosette relative expansion rate [RER], number of rosette leaves [LN], leaf 6 area [AL6], epidermal cell area [CA], and number [CN]), QTLs are represented by arrows along the chromosomes. The locations of all QTLs identified are shown as 95% Bayes credible intervals, with the positions of horizontal bars corresponding to the maximum LOD score values. The direction of the arrows indicates the sign of the additive effect: arrows pointing upward indicate that Ler alleles have a positive effect (i.e. they increase the values of the trait). The shape of the arrows indicates the nature of the QTL: main effects (headed arrows), in epistatic interaction (nonheaded arrows), and epistatic QTLs with no main effect (rectangle). The gray scale of the arrows indicates the percentage of phenotypic variance explained by the QTL: 0% to 10%, 10% to 20%, 20% to 30%, and 30% to 100% from lightest to darkest.
Functional Relationships between Leaf Growth and Endoreduplication Are Consistent across the Sets of Genotypes
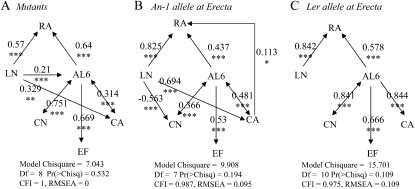
We further used SEM to investigate the functional links among our set of leaf growth traits. First, direct and indirect relationships between EF and growth traits were tested on the 200 genotypes by specifying different models based on the empirical relationships reported in this study, the models previously described by Tisné et al. (2008), and the hypotheses from the literature (Fig. 1). No model provided an acceptable fit to the whole data set from these 200 genotypes (data not shown). This was in accordance with the results showing that covariations between EF and cell number or cell area depended on the set of genotypes. Therefore, the models were tested separately for the mutant collection and the two RIL subpopulations split by the allelic value at the ER marker (as suggested by Tisné et al., 2008). The models described by Tisné et al. (2008) were used as a basis since they included the same variables except EF.
First, we considered that EF was responsible for (1) the variation of cell area and covaried with cell number, as commonly stated in the literature (Fig. 1), or (2) the variation of leaf area. However, the models including such links were all rejected in all three sets of genotypes (P < 0.05; Supplemental Fig. S5). Second, we tested the alternative hypothesis that leaf growth itself would control the occurrence of endoreduplication, by adding a direct link from leaf area to EF. The models including this path were not rejected, either in the two RIL subpopulations or in the mutant collection (Fig. 6; P > 0.05). As indicated by the standardized path coefficients higher than 0.5, the strength of the causal relationship between leaf area and EF was high in the three sets of genotypes.
Figure 6.
Functional relationships between leaf growth variables in the three sets of genotypes. Path diagrams were tested in each set of genotypes: the mutant collection (A), RILs from the Ler × An-1 population with the An-1 alleles at the ER marker (B), and RILs with the Ler alleles at the ER marker (C). Arrows represent linear functional relations between leaf growth variables: rosette area (RA), rosette leaf number (LN), leaf 6 area (AL6), epidermal cell number (CN), mean epidermal cell area (CA), and EF. Single-headed arrows represent causal relationships, and double-headed arrows represent free correlations. Standardized path coefficients are indicated on each arrow with the level of significance (*** P < 0.001, ** P < 0.01, * P < 0.05). All models were tested against our data, and statistical significance values are given below each diagram. CFI, Comparative fit index; Df, degrees of freedom; RMSEA, root mean square error of approximation.
Even if a common functional model was not found for the whole set of genotypes and we were forced to split the genotypes into three subsets to reveal the functional relationships between EF and other variables, many functional links were conserved (Fig. 6). As expected, both leaf 6 area and leaf number contributed to rosette area. More interestingly, leaf 6 area independently controlled cell area, cell number, and the extent of endoreduplication, and cell number also exerted a control on leaf area (Fig. 6). The main differences among the three sets of genotypes were due to the presence or absence of functional links between leaf number and leaf 6 area, cell number, or cell area. Leaf number exerted a control on (1) cell area both in the mutant collection and the RIL subpopulation carrying the An-1 allele at the ER marker, (2) cell number in the RIL subpopulation carrying the An-1 allele at the ER marker, and (3) leaf 6 area in the mutant collection. By contrast, it did not control any underlying variables in the RIL subpopulation carrying the Ler allele at ER (Fig. 6).
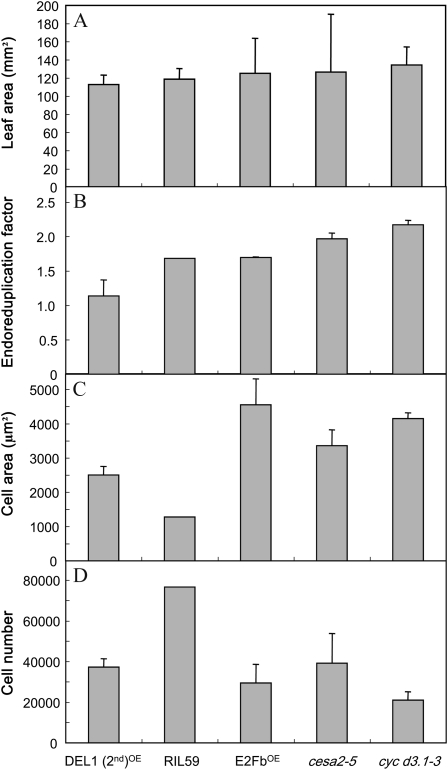
Leaf Growth Controls Underlying Cellular Processes in Parallel
As explained above, a common feature of the three models presented in Figure 6 was that leaf growth exerts a parallel control on cell division, cell expansion, and endoreduplication. Such functional relationships would allow the development of a leaf with the same final area but with completely different underlying cellular components. This is illustrated in Figure 7 for five genotypes extracted from the whole set of 200 genotypes. Final leaf 6 area did not vary significantly among these five genotypes (Fig. 7A). By contrast, the EF varied from 1.14 to 2.17 endocycles per cell, cell area varied from 1,276 to 4,555 μm2, and epidermal cell number varied from 21,063 to 76,637 (Fig. 7, B–D).
Figure 7.
The same leaf area can be reached with different cell area, cell number, and EF. Five genotypes with the same final leaf 6 area were extracted among the 200 genotypes studied. Four issued from the mutant collection, and the last one is a RIL from the Ler × An-1 population. These genotypes reached a similar leaf area (A) but with different cellular components (EF [B], mean epidermal cell area [C], and epidermal cell number [D]).
DISCUSSION
Variability of Endoreduplication and Other Leaf Growth Traits in Arabidopsis Leaves
Endoreduplication is a widespread process among plants that depends on species, genotypes, environmental conditions, organs, and cell types (Traas et al., 1998; Joubès and Chevalier, 2000; Kinoshita et al., 2008; Radziejwoski et al., 2010). For example, 16C or 32C cells are often reported in leaves, roots, and hypocotyls of Arabidopsis (Gendreau et al., 1998; Cookson et al., 2006), whereas in tomato (Solanum lycopersicum) fruits, DNA content can reach up to 256C (Bertin et al., 2007). Here, the ploidy could reach up to 64C in leaves of a large number of genotypes among the 200 studied.
In the RIL population derived from the cross between Ler and An-1, a large phenotypic variation was observed for all traits, including those for which parental values hardly differed, such as EF. More than 50 recombinant inbred lines issued from the cross between Ler and An-1 increased their individual leaf area compared with both parents, and five others decreased it. For most variables, including EF, the “natural” variability found in the RIL population was equivalent to or even larger than the “artificial” variability found in the mutant collection. The variability of endoreduplication and other growth variables reported here suggests that the Arabidopsis leaf is a good system in which to disentangle the role of endoreduplication in the control of organ growth. In addition, our results highlight that populations of recombinant inbred lines can be a powerful solution to create variability in growth variables.
The Extent of Endoreduplication in a Leaf Covaries with Leaf Area Independently of Cell Number and Cell Area
Endoreduplication is often viewed as an alternative cell cycle in plants that would support growth even in the absence of mitosis-promoting cyclin-dependent kinase activity (Nieuwland et al., 2009). Consistently, plants exhibiting a reduced activity of M-phase-specific B-type cyclin-dependent kinase exit the mitotic cell cycle and enter the endocycle prematurely (Boudolf et al., 2004). This implies that the number of endocycles and cell number covary negatively, as reported in many studies (see corresponding refs. in Fig. 1). In addition, because tight relationships were often reported between cell size and endopolyploidy, it was suggested that endoreduplication would favor bigger cells (see corresponding refs. in Fig. 1). Intriguingly, our holistic approach combining data sets issued from both a natural RIL population and an artificial mutant collection showed that endoreduplication relates with leaf growth, whereas the relationships with cellular variables were not always consistent according to the set of genotypes. In addition, the relationships between EF and cellular variables were also affected by the allelic identity at different markers in the RIL population. By contrast, the stable covariation between leaf area and the extent of endoreduplication observed in leaves that have reached their final area was also verified over leaf development (Supplemental Fig. S6; Supplemental Protocol S1). Changes in endoreduplication over time strictly follow leaf area dynamics both in optimal conditions and when leaf growth dynamics is affected by a water deficit treatment (Supplemental Fig. S6; Supplemental Protocol S1).
The robustness of the relationships between endoreduplication and leaf growth is also supported by genetic analyses showing that the two main effect QTLs that control endoreduplication also map with QTLs for leaf area or rosette expansion rate. Only one of them, identified at the SNP295 marker, colocalizes with QTLs for cell area and cell number, but this QTL was already described as a QTL directly controlling leaf growth and indirectly controlling cell division and cell expansion in a cascade (Tisné et al., 2008). This QTL is also likely to control endoreduplication by a cascade effect.
In summary, both correlation and genetics analyses do not support the model based on most published data in which endoreduplication is linked to leaf growth via the cellular processes (cell division and cell expansion; Fig. 1). However, our data support the idea of a direct link between leaf growth and endoreduplication.
The Covariation between Leaf Area and Endoreduplication Underlies a Control of Endoreduplication by Leaf Growth Itself
The absence of direct links between endoreduplication, cell division, and cell expansion, and the presence of a functional link between leaf growth and endoreduplication, were confirmed by the structural equation models. In addition, these models suggested that leaf growth per se exerts a control on the extent of endoreduplication and not the reverse. As suggested by John and Qi (2008), endoreduplication itself would not drive growth via cell expansion, but growth would be necessary to drive endoreduplication. This result casts light on some discrepancies in the literature and explains why correlations between endoreduplication and cell size or cell number were not always consistent across studies (Fig. 1). These variables are not directly related, but they covary with organ growth. This result also helps one to understand a few strange phenotypes. For example, it was difficult to explain until now how shading treatments could have opposite effects on endoreduplication in leaves and hypocotyls in the same species (i.e. a reduction in leaves [Cookson et al., 2006] and an increase in hypocotyl [Gendreau et al., 1998]). Cell size was increased in response to shading in both organs. However, this is in accordance with the functional model established here, as leaf size is decreased with shading whereas hypocotyl length is increased (Gendreau et al., 1998; Cookson et al., 2006). In both organs, endoreduplication follows growth that is differently affected by shading, without any link with cell expansion.
Leaf Growth: A Hub Driving Cellular Processes
Many works have provided evidence that changes in cell number or cell size due to abiotic constraints or genetic modifications impact leaf growth (Francis, 1992; Granier et al., 2000). However, others revealed that this is not always the case, showing that the two cellular variables present some degree of compensation (Cockcroft et al., 2000; Cookson et al., 2006). One hypothesis to explain the compensation phenomenon is that leaf expansion has its own control and controls underlying cellular variables, according to the organismal theory of development (Fleming, 2007). However, this would lead to complete compensation when one of the two cellular processes is affected, which is rarely the case. For example, leaf area is reduced by shading, and this is accompanied by an increase in cell area, which is not sufficient to compensate for the decrease in cell number (Cookson et al., 2006). Because compensations between cell number and cell size are partial, it was proposed that leaf expansion was controlled both at the cellular level and at the organ level, with a compensatory system linking the two processes (Tsukaya, 2003, 2006). Our model here supports this theory, suggesting that cell division and cell expansion contribute independently to leaf expansion and that the link between the two cellular processes is due to whole leaf expansion that has its own control but also exerts a retrocontrol on both cellular processes.
This model also suggests that endoreduplication is also under the control of whole leaf growth. Cell division, cell expansion, and endoreduplication could then be viewed as alternative strategies to follow (in the case of endoreduplication) or ensure (in the cases of cell division and cell expansion) leaf growth when spatial or temporal molecular patterns are restricted for one of them but favorable for others. Whole leaf growth would be controlled by carbon availability, wall extensibility, and hydraulic properties that would promote in a cascade cell division, cell expansion, or endoreduplication. Because relative leaf expansion rate is strongly and positively correlated to the extent of endoreduplication, it is possible to hypothesize that in the case of rapid leaf growth, cell division cannot follow the cadence and therefore the cell cycle is shunted toward the endoreduplicated cycle. The idea that cellular processes are alternative strategies to allow leaf growth is well illustrated across the genotypes studied here, since the same final leaf area could be achieved with different cellular strategies (cell number, cell size, and extent of endoreduplication; Fig. 7). For example, when cell division is limited by molecular constraints, such as the inactivation of genes encoding for D-type cyclins, in cycD3.1-3 (Fig. 7), cell area and the extent of endoreduplication are increased. Similarly, the very low cell area in RIL59 is totally compensated for by a high cell number (Fig. 7). There are also environmental contexts in which reducing leaf growth is advantageous, such as in drought conditions to limit their transpiring area. In this precise case, it is interesting that all three cellular processes, cell division, cell expansion, and endoreduplication, are reduced (Cookson et al., 2006).
CONCLUSION
The results presented here clearly show the usefulness of comparative studies with high numbers of genotypes grown in common environmental conditions to identify stable emerging properties of plant development. Three years after the polemical review from John and Qi (2008) that cast doubt on the putative role of cell division and endoreduplication in growth control, our results bring experimental evidence of a noncellular control of growth. Our data support a robust statistical model, common to different subsets of genotypes of Arabidopsis, in which endoreduplication, cell expansion, and cell division could be controlled by whole leaf growth. This control is unidirectional for endoreduplication but not for cell division and cell expansion, which, in addition, have a control on leaf area.
One hypothesis to explain the functional relationships between leaf expansion, cell division, cell expansion, and endoreduplication could be that the high leaf expansion rate of large leaves would cause a strong demand of cell production, which is possible until a certain step, after which the cell cycle cannot follow the cadence because of molecular, biochemical, or energetic limitations and endoreduplication takes place (Kondorosi et al., 2000). One way to test this hypothesis should be to mechanically force leaf expansion and test how this impacts in a cascade the extent of endoreduplication. However, this should be done on another species than Arabidopsis, because of the difficulty of carrying out such experiments in such small leaves.
MATERIALS AND METHODS
Plant Material
Two hundred genotypes of Arabidopsis (Arabidopsis thaliana) were selected with an expected variability in endoreduplication. In this context, a collection of 88 mutants and transgenic lines were selected according to a gain or loss of function of genes involved in endoreduplication or cell cycle progression or with suspected impact on leaf area, leaf shape, and/or epidermal cell size (Supplemental Table S1). All these mutants and transgenics were selected in the Col-0 ecotype. Two accessions, Ler and An-1, and a population of 109 RILs (in F8; el-Lithy et al., 2006) issued from their cross, were also selected.
Growth Conditions
Three experiments were performed in a growth chamber equipped with the automated phenotyping platform PHENOPSIS (Granier et al., 2006). Nine repetitions of the 88 modified genotypes (named “mutant collection”) were grown in identical environmental conditions in two successive experiments (experiments 1 and 2; Table II). Five repetitions of the 109 RILs with eight repetitions of their parental lines (named “RIL population”) were grown in a third experiment (experiment 3). Mean micrometeorological conditions supposed to be optimal for Arabidopsis development are presented in Table II for each experiment. Light, provided by HQi lamps with additional cool-white fluorescent tubes, was maintained for 16 h in experiments 1 and 2 (mutant collection) and for 12 h in experiment 3 (RIL population) to limit the differences in both flowering date and leaf number between the mutant collection and the RIL population.
Table II. Environmental conditions during the three experiments.
The photosynthetic active radiation (PAR) is the mean calculated during the period with lights on in the chamber. Plants were watered daily to reach target soil water content (SWC). Mean air temperature and air humidity were calculated during the period with the lights on (D) and the lights off (N), respectively.
| Experiment | Daylength | PAR | Temperature D/N | Air Humidity D/N | SWC |
| h | μmol m−2 s−1 | °C | % | g water g−1 dry soil | |
| 1 | 16 | 120 | 21.5/21.2 | 74.4/78.8 | 0.40 |
| 2 | 16 | 120 | 21.3/21.2 | 76.8/71.2 | 0.40 |
| 3 | 12 | 250 | 20.6/20.5 | 67/70 | 0.40 |
Leaf Growth Analyses
Rosette leaf number was counted at stage 5.00 (bolting; Boyes et al., 2001) on six plants for the mutant collection and four plants for the RIL population. Whole rosette area was estimated from images of all individual pot surfaces taken on a daily basis by the PHENOPSIS automaton (Granier et al., 2006), using a semiautomated procedure developed on ImageJ (1.38X; http://rsb.info.nih.gov/ij/). Rosette relative expansion rate (RER; d−1) was calculated as follows: RER í d(ln RA)/dt, where RA is rosette area and t is time from stage 1.02 to stage 5.00.
Each plant was harvested at stage 6.00, and individual leaves, ranked in the order of their emergence on the rosette, were scanned. Rosette area (mm2) was determined as the sum of the individual leaf blade areas as measured on scanned images with image-analysis software (Bioscan-Optimas version 4.10). Leaf 6 area (mm2) was determined with the same method. An imprint of the leaf 6 upper surface was also taken with nail varnish. It was analyzed with a microscope (Leitz DM RB; Leica) to determine mean epidermal cell area (μm2) by measuring 25 epidermal cell areas at four different zones on each leaf with image-analysis software (Bioscan-Optimas version 4.10). Epidermal cell number was estimated from mean epidermal cell density determined in three different zones on the same imprint, multiplying this value by leaf area.
Flow Cytometry Analysis
In experiments 1 and 2, the fifth leaf was harvested on three plants per genotype at stage 6.00. In experiment 3, one rosette per genotype was harvested at stage 5.00. Samples were immediately frozen in liquid nitrogen, and flow cytometry analyses were done as described by Cookson et al. (2006). For each sample, 3,000 nuclei were counted and the percentage of cells at 2C, 4C, 8C, 16C, 32C, and 64C was calculated. The EF was calculated from these percentage values as follows (Cookson et al., 2006): EF í (0 × %2C) + (1 × %4C) + (2 × %8C) + (3 × %16C) + (4 × %32C)/100.
QTL Mapping
QTLs were first identified using single interval mapping with the software package MapQTL5 (Kyazma). Cofactors were then selected using the automatic cofactor selection chromosome per chromosome. The selected cofactors were used in multiple QTL mapping. The cofactors for which no QTLs were detected (log of the odds [LOD] under a 95% LOD threshold < 2.4, estimated by performing permutation tests implemented in MapQTL5 using at least 1,000 permutations of the original data set) were removed successively. Detection and testing of epistatic interactions between loci were performed using the software Epistat (Chase et al., 1997). Both epistatic interactions and QTLs in main effects were statistically tested using the general linear model module of the statistical package SPSS 11.0.1 for Windows (SPSS). QTL models were composed of all statistically significant (P < 0.05) main and interaction effects. The estimated additive genetic effect, the percentage of variance explained by each QTL, and the total variance explained by the models were obtained using the statistical package SPSS.
Statistical Analyses
All statistical analyses were done using R 2.9.0 (R_Development_Core_Team, 2008; http://www.r-project.org/). Correlations between leaf growth traits were tested using mean values of each genotype for the whole data set or separately for the mutant collection and the subpopulations of RILs carrying either the An-1 alleles or the Ler alleles at the ER marker, because it has previously been shown that allelic identity at this marker led to strong modifications of the relationships between leaf growth variables (Tisné et al., 2008). The slopes and ordinates of the linear regression were compared by ANOVA. Two genotypes (35SE2Fb and RIL56) were excluded from the analyses due to their high number of leaves, which strongly modified the correlations (Supplemental Figs. S1 and S2).
The effect of each marker on the correlation between EF and other growth variables was determined by analysis of covariance with the generalized linear model. The marker was considered to affect the slope of the linear regression between two variables only when the P value given by the generalized linear model was below a threshold of 0.001 (Tisné et al., 2008).
SEM
SEM is a multivariate statistical technique currently used to examine hypothetical causal relationships between variables in three steps (Shipley, 2000; Pugesek et al., 2003). First, assumptions on the relationships functionally relating variables are formulated and represented by a set of equations constituting a theoretically plausible model. Second, the SEM analysis compares the covariance matrix issued from the hypothetic model against the covariance matrix issued from the observations by a χ2 test. Third, the P value for the proposed model is examined, and a not significant P value means that the proposed model is then a plausible representation of the functional relationships among variables, since the model is not statistically different from the data. Otherwise, the model has to be modified and tested again. Once a model has not been rejected and is considered biologically plausible, parameter estimates can be used to study direct as well as indirect effects of the variables. In particular, standardized path coefficients quantify the strength of a relationship while the effects of the other variables are held constant. Parameter estimates are tested for significance using z statistics. Two other indices, root mean square error of approximation and comparative fit index, were also used to assess the closeness of fit. Good models have a root mean square error of approximation of less than 0.05 and a comparative fit index of greater than 0.95. Hypothetical models relating EF to other plant growth-related variables were tested in R using the SEM package (Fox, 2006), which uses the standard maximum likelihood estimator. Rosette area and leaf number were log transformed in the RIL population to satisfy conditions for the SEM procedure (i.e. linearity of the bivariate relationships and normal distribution of the residuals).
Data will be publicly available in the PHENOPSIS database (http://bioweb.supagro.inra.fr/phenopsis/; Fabre et al., 2011).
Supplemental Data
The following materials are available in the online version of this article.
Supplemental Figure S1. Variation of leaf growth variables within the collection of mutants.
Supplemental Figure S2. Variation of leaf growth variables within the Ler x An-1 RIL population.
Supplemental Figure S3. Frequency distribution of six leaf growth variables in the mutant collection and the RIL population.
Supplemental Figure S4. Ler x An-1 linkage map showing QTLs for endoreduplication factor and other leaf growth variables.
Supplemental Figure S5. Path diagrams tested and rejected in each set of genotypes.
Supplemental Figure S6. Changes in leaf area and endoreduplication over time.
Supplemental Table S1. List of genotypes in the mutant collection.
Supplemental Protocol S1. Protocol for Supplemental Figure S6.
Acknowledgments
We thank Alexis Bediee for technical assistance. We are grateful to all people who have shared their genotypes for this study: C. Gutierrez for CDC6a(40-4)OE, CDC6a(64-1)OE, and CDC6a(87-5)OE; J. Murray for CYCD2.1OE, CYCD3.1OE, DPaOE, E2Fa(2nd)OE, E2FB, KRP1, cycd2.1, cycd2.1 × cycd4.1, cycd3.1-3, cycd4.1, cycd5.1, cycd6.1, cycd7.1gabikat, cycd7.1inra, e2fb, krp1, and krp2; P. Doerner for cycA1.2, cycA2.1, cycA2.2, cycA2.2 × cycA2.3, cycA2.3, cycA2.4, cycA2.4 × cycA2.2, cycA2.4 × cycA2.3, cycB1.1, cycB1.2, cycB3.1, tcp20-1, and tcp20-2; C. Meyer and J.D. Faure for dpl1, lac1-like, lag1-like, lcb3, sphk1, sphk2, sur2a, sur2b, tor35-7, tor65-1, TORG166, and TORG548; J.L. Micol for ave1, re2-1, re-6, ret2-1, ret3-1, rug2-2, rug3, ven1-2, ven4-2, and ucu2-3; G. Mouille for cesa2, cesa2/5, cesa2/6, cesa5, cesa6, pom1-2, and qua2-1; D. Weigel for JAW-D and MIR156OX; W. Gruissem for era 1, nap1.1, and NAP1; D. Szymanski for brk1-1, ric4, and spk; M. Jakoby for nok-gb; C.L. Torregrossa for Athb13; and D. Vreugdenhil for the RILs.
References
- Autran D, Jonak C, Belcram K, Beemster GTS, Kronenberger J, Grandjean O, Inzé D, Traas J. (2002) Cell numbers and leaf development in Arabidopsis: a functional analysis of the STRUWWELPETER gene. EMBO J 21: 6036–6049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beemster GTS, De Vusser K, De Tavernier E, De Bock K, Inzé D. (2002) Variation in growth rate between Arabidopsis ecotypes is correlated with cell division and A-type cyclin-dependent kinase activity. Plant Physiol 129: 854–864 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertin N, Lecomte A, Brunel B, Fishman S, Génard M. (2007) A model describing cell polyploidization in tissues of growing fruit as related to cessation of cell proliferation. J Exp Bot 58: 1903–1913 [DOI] [PubMed] [Google Scholar]
- Boudolf V, Vlieghe K, Beemster GTS, Magyar Z, Torres Acosta JA, Maes S, Van Der Schueren E, Inzé D, De Veylder L. (2004) The plant-specific cyclin-dependent kinase CDKB1;1 and transcription factor E2Fa-DPa control the balance of mitotically dividing and endoreduplicating cells in Arabidopsis. Plant Cell 16: 2683–2692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyes DC, Zayed AM, Ascenzi R, McCaskill AJ, Hoffman NE, Davis KR, Görlach J. (2001) Growth stage-based phenotypic analysis of Arabidopsis: a model for high throughput functional genomics in plants. Plant Cell 13: 1499–1510 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breuer C, Stacey NJ, West CE, Zhao Y, Chory J, Tsukaya H, Azumi Y, Maxwell A, Roberts K, Sugimoto-Shirasu K. (2007) BIN4, a novel component of the plant DNA topoisomerase VI complex, is required for endoreduplication in Arabidopsis. Plant Cell 19: 3655–3668 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castellano MM, del Pozo JC, Ramirez-Parra E, Brown S, Gutierrez C. (2001) Expression and stability of Arabidopsis CDC6 are associated with endoreplication. Plant Cell 13: 2671–2686 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chase K, Adler FR, Lark KG. (1997) Epistat: a computer program for identifying and testing interactions between pairs of quantitative trait loci. Theor Appl Genet 94: 724–730 [Google Scholar]
- Chevalier C, Nafati N, Mathieu-Rivet E, Bourdon M, Frangne N, Cheniclet C, Renaudin JP, Gévaudant F, Hernould M. (2011) Elucidating the functional role of endoreduplication in tomato fruit development. Ann Bot 107: 1159–1169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cockcroft CE, den boer BG, Healy JM, Murray JA. (2000) Cyclin D control of growth rate in plants. Nature 405: 575–579 [DOI] [PubMed] [Google Scholar]
- Cookson SJ, Chenu K, Granier C. (2007) Day-length affects the dynamics of leaf expansion and cellular development in Arabidopsis thaliana partially through floral transition timing. Ann Bot 99: 703–711 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cookson SJ, Radziejwoski A, Granier C. (2006) Cell and leaf size plasticity in Arabidopsis: what is the role of endoreduplication? Ann Bot 29: 1273–1283 [DOI] [PubMed] [Google Scholar]
- del Pozo JC, Diaz-Trivino S, Cisneros N, Gutierrez C. (2006) The balance between cell division and endoreplication depends on E2FC-DPB, transcription factors regulated by the ubiquitin-SCFSKP2A pathway in Arabidopsis. Plant Cell 18: 2224–2235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Veylder L, Beeckman T, Beemster GTS, de Almeida Engler J, Ormenese S, Maes S, Naudts M, Van Der Schueren E, Jacqmard A, Engler G, et al. (2002) Control of proliferation, endoreduplication and differentiation by the Arabidopsis E2Fa-DPa transcription factor. EMBO J 21: 1360–1368 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dewitte W, Riou-Khamlichi C, Scofield S, Healy JM, Jacqmard A, Kilby NJ, Murray JAH. (2003) Altered cell cycle distribution, hyperplasia, and inhibited differentiation in Arabidopsis caused by the D-type cyclin CYCD3. Plant Cell 15: 79–92 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar BA, Nijhout HF. (2004) Growth and cell cycle control in Drosophila. Hall MN, Raff M, Thomas G, , Cell Growth: Control of Cell Size Monographs 42. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY, pp 23–84 [Google Scholar]
- Edgar BA, Orr-Weaver TL. (2001) Endoreplication cell cycles: more for less. Cell 105: 297–306 [DOI] [PubMed] [Google Scholar]
- el-Lithy ME, Bentsink L, Hanhart CJ, Ruys GJ, Rovito D, Broekhof JLM, van der Poel HJA, van Eijk MJ, Vreugdenhil D, Koornneef M. (2006) New Arabidopsis recombinant inbred line populations genotyped using SNPWave and their use for mapping flowering-time quantitative trait loci. Genetics 172: 1867–1876 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fabre J, Dauzat M, Nègre V, Wuyts N, Tireau A, Gennari E, Neveu P, Tisné S, Massonnet C, Hummel I, et al. (2011) PHENOPSIS DB: an information system for Arabidopsis thaliana phenotypic data in an environmental context. BMC Plant Biol 11: 77–84 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming AJ. (2007) Cell cycle control during leaf development. Inzé D, , Cell Cycle Control and Plant Development. Annual Plant Reviews, Vol 32. Blackwell Publishing, Oxford, pp 203–226 [Google Scholar]
- Flemming AJ, Shen ZZ, Cunha A, Emmons SW, Leroi AM. (2000) Somatic polyploidization and cellular proliferation drive body size evolution in nematodes. Proc Natl Acad Sci USA 97: 5285–5290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox J. (2006) Structural equation modelling with the sem package in R. Structural Equation Modelling 13: 465–486 [Google Scholar]
- Francis D. (1992) The cell cycle in plant development. New Phytol 122: 1–20 [DOI] [PubMed] [Google Scholar]
- Fujikura U, Horiguchi G, Tsukaya H. (2007) Dissection of enhanced cell expansion processes in leaves triggered by a defect in cell proliferation, with reference to roles of endoreduplication. Plant Cell Physiol 48: 278–286 [DOI] [PubMed] [Google Scholar]
- Gandarillas A, Davies D, Blanchard JM. (2000) Normal and c-Myc-promoted human keratinocyte differentiation both occur via a novel cell cycle involving cellular growth and endoreplication. Oncogene 19: 3278–3289 [DOI] [PubMed] [Google Scholar]
- Gendreau E, Höfte H, Grandjean O, Brown S, Traas J. (1998) Phytochrome controls the number of endoreduplication cycles in the Arabidopsis thaliana hypocotyl. Plant J 13: 221–230 [DOI] [PubMed] [Google Scholar]
- Granier C, Aguirrezabal L, Chenu K, Cookson SJ, Dauzat M, Hamard P, Thioux JJ, Rolland G, Bouchier-Combaud S, Lebaudy A, et al. (2006) PHENOPSIS, an automated platform for reproducible phenotyping of plant responses to soil water deficit in Arabidopsis thaliana permitted the identification of an accession with low sensitivity to soil water deficit. New Phytol 169: 623–635 [DOI] [PubMed] [Google Scholar]
- Granier C, Turc O, Tardieu F. (2000) Co-ordination of cell division and tissue expansion in sunflower, tobacco and pea leaves: dependence or independence of both processes? J Plant Growth Regul 19: 45–54 [DOI] [PubMed] [Google Scholar]
- Harashima H, Schnittger A. (2010) The integration of cell division, growth and differentiation. Curr Opin Plant Biol 13: 66–74 [DOI] [PubMed] [Google Scholar]
- John PCL, Qi R. (2008) Cell division and endoreduplication: doubtful engines of vegetative growth. Trends Plant Sci 13: 121–127 [DOI] [PubMed] [Google Scholar]
- Joubès J, Chevalier C. (2000) Endoreduplication in higher plants. Plant Mol Biol 43: 735–745 [DOI] [PubMed] [Google Scholar]
- Kinoshita T, Fujita M, Maeda Y. (2008) Biosynthesis, remodelling and functions of mammalian GPI-anchored proteins: recent progress. J Biochem 144: 287–294 [DOI] [PubMed] [Google Scholar]
- Kondorosi E, Roudier F, Gendreau E. (2000) Plant cell-size control: growing by ploidy? Curr Opin Plant Biol 3: 488–492 [DOI] [PubMed] [Google Scholar]
- Larkins BA, Dilkes BP, Dante RA, Coelho CM, Woo YM, Liu Y. (2001) Investigating the hows and whys of DNA endoreduplication. J Exp Bot 52: 183–192 [PubMed] [Google Scholar]
- Lee HO, Davidson JM, Duronio RJ. (2009) Endoreplication: polyploidy with purpose. Genes Dev 23: 2461–2477 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lozano E, Sáez AG, Flemming AJ, Cunha A, Leroi AM. (2006) Regulation of growth by ploidy in Caenorhabditis elegans. Curr Biol 16: 493–498 [DOI] [PubMed] [Google Scholar]
- Massonnet C, Vile D, Fabre J, Hannah MA, Caldana C, Lisec J, Beemster GTS, Meyer RC, Messerli G, Gronlund JT, et al. (2010) Probing the reproducibility of leaf growth and molecular phenotypes: a comparison of three Arabidopsis accessions cultivated in ten laboratories. Plant Physiol 152: 2142–2157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieuwland J, Scofield S, Murray JAH. (2009) Control of division and differentiation of plant stem cells and their derivatives. Semin Cell Dev Biol 20: 1134–1142 [DOI] [PubMed] [Google Scholar]
- Nijhout HF. (2003) The control of growth. Development 130: 5863–5867 [DOI] [PubMed] [Google Scholar]
- Pierce SB, Yost C, Britton JS, Loo LWM, Flynn EM, Edgar BA, Eisenman RN. (2004) dMyc is required for larval growth and endoreplication in Drosophila. Development 131: 2317–2327 [DOI] [PubMed] [Google Scholar]
- Pugesek BH, Tomer A, von Eye A. (2003) Structural Equation Modelling: Applications in Ecological and Evolutionary Biology. Cambridge University Press, Cambridge, UK [Google Scholar]
- Radziejwoski A, Vlieghe K, Lammens T, Berckmans B, Maes S, Jansen MAK, Knappe C, Albert A, Seidlitz HK, Bahnweg G, et al. (2010) Atypical E2F activity coordinates PHR1 photolyase gene transcription with endoreduplication onset. EMBO J 30: 355–363 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R_Development_Core_Team (2008) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria: http://www.R-project.org (February 8, 2008) [Google Scholar]
- Roeder AHK, Chickarmane V, Cunha A, Obara B, Manjunath BS, Meyerowitz EM. (2010) Variability in the control of cell division underlies sepal epidermal patterning in Arabidopsis thaliana. PLoS Biol 8: e1000367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shipley B. (2000) Cause and Correlation in Biology: A User’s Guide to Path Analysis, Structural Equations, and Causal Inference. Cambridge University Press, Cambridge, UK [Google Scholar]
- Tisné S, Reymond M, Vile D, Fabre J, Dauzat M, Koornneef M, Granier C. (2008) Combined genetic and modeling approaches reveal that epidermal cell area and number in leaves are controlled by leaf and plant developmental processes in Arabidopsis. Plant Physiol 148: 1117–1127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tojo T, Tsuda K, Yoshizumi T, Ikeda A, Yamaguchi J, Matsui M, Yamazaki K. (2008) Arabidopsis MBF1s control leaf cell cycle and its expansion. Plant Cell Physiol 50: 254–264 [DOI] [PubMed] [Google Scholar]
- Traas J, Hülskamp M, Gendreau E, Höfte H. (1998) Endoreduplication and development: rule without dividing? Curr Opin Plant Biol 1: 498–503 [DOI] [PubMed] [Google Scholar]
- Tsukaya H. (2003) Organ shape and size: a lesson from studies of leaf morphogenesis. Curr Opin Plant Biol 6: 57–62 [DOI] [PubMed] [Google Scholar]
- Tsukaya H. (2006) Mechanism of leaf-shape determination. Annu Rev Plant Biol 57: 477–496 [DOI] [PubMed] [Google Scholar]
- Tsukaya H. (2008) Controlling size in multicellular organs: focus on the leaf. PLoS Biol 6: e174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verkest A, Manes CL, Vercruysse S, Maes S, Van Der Schueren E, Beeckman T, Genschik P, Kuiper M, Inzé D, De Veylder L. (2005) The cyclin-dependent kinase inhibitor KRP2 controls the onset of the endoreduplication cycle during Arabidopsis leaf development through inhibition of mitotic CDKA;1 kinase complexes. Plant Cell 17: 1723–1736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlieghe K, Boudolf V, Beemster GTS, Maes S, Magyar Z, Atanassova A, de Almeida Engler J, De Groodt R, Inzé D, De Veylder L. (2005) The DP-E2F-like gene DEL1 controls the endocycle in Arabidopsis thaliana. Curr Biol 15: 59–63 [DOI] [PubMed] [Google Scholar]