Abstract
Extensive natural variation has been described for the timing of flowering initiation in many annual plants, including the model wild species Arabidopsis (Arabidopsis thaliana), which is presumed to be involved in adaptation to different climates. However, the environmental factors that might shape this genetic variation, as well as the molecular bases of climatic adaptation by modifications of flowering time, remain mostly unknown. To approach both goals, we characterized the flowering behavior in relation to vernalization of 182 Arabidopsis wild genotypes collected in a native region spanning a broad climatic range. Phenotype-environment association analyses identified strong altitudinal clines (0–2600 m) in seven out of nine flowering-related traits. Altitudinal clines were dissected in terms of minimum winter temperature and precipitation, indicating that these are the main climatic factors that might act as selective pressures on flowering traits. In addition, we used an association analysis approach with four candidate genes, FRIGIDA (FRI), FLOWERING LOCUS C (FLC), PHYTOCHROME C (PHYC), and CRYPTOCHROME2, to decipher the genetic bases of this variation. Eleven different loss-of-function FRI alleles of low frequency accounted for up to 16% of the variation for most traits. Furthermore, an FLC allelic series of six novel putative loss- and change-of-function alleles, with low to moderate frequency, revealed that a broader FLC functional diversification might contribute to flowering variation. Finally, environment-genotype association analyses showed that the spatial patterns of FRI, FLC, and PHYC polymorphisms are significantly associated with winter temperatures and spring and winter precipitations, respectively. These results support that allelic variation in these genes is involved in climatic adaptation.
The timing of flowering initiation is an important adaptive trait because it synchronizes reproduction with the most favorable season of the year for seed development. Furthermore, it determines the time invested for vegetative growth and the resources available for reproduction. Large amounts of intraspecific variation have been found for flowering initiation in most annual plants, which has been shown to be involved in adaptation mainly by the identification of genetically based clines along geographic and/or environmental gradients (Stebbins, 1950; Briggs and Walters, 1997). This is illustrated with the classical garden experiments carried out in Prunella vulgaris, a species showing annual and biennial growth habits, flowering the first or the second year, respectively (Böcher, 1949). Such studies detected latitudinal, altitudinal, and climatic clines across Europe for the distribution of growth habits, hence supporting the role of the underlying genetic variation in adaptive evolution.
Plant adaptation to different climates has recently become a major topic, due to the potential effects of present global climate changes on agriculture and biodiversity (Schlenker and Roberts, 2009; Ibáñez et al., 2010; Manel et al., 2010). It has been shown that flowering time is a very sensitive life history trait that is strongly affected by increasing temperature, especially in annual crops and wild plants (Fitter and Fitter, 2002; Craufurd and Wheeler, 2009; Schlenker and Roberts, 2009; Ibáñez et al., 2010; Wilczek et al., 2010). In addition, a very rapid evolution of flowering time, measured as genetic change in response to climate fluctuation, has been demonstrated in Brassica rapa (Franks et al., 2007). Currently, identification of the flowering genes and the nucleotide polymorphisms affecting the functions of those genes (referred to as functional polymorphisms) that underlie climatic adaptation is a challenging goal in plant biology (Jung and Müller, 2009; Semenov and Halford, 2009; Manel et al., 2010).
More than 60 genes have been shown to be involved in the regulation of flowering initiation, mainly by genetic and molecular studies in the model, annual, and wild plant Arabidopsis (Arabidopsis thaliana; Koornneef et al., 1998; Kobayashi and Weigel, 2007). Detailed characterization of these genes has revealed several flowering pathways that integrate different environmental and endogenous signals, including the vernalization, photoperiod, and autonomous pathways (Kobayashi and Weigel, 2007; Kim et al., 2009). In addition, extensive natural variation has also been described for flowering time in Arabidopsis (for review, see Koornneef et al., 1998; Lempe et al., 2005; Shindo et al., 2005), whose molecular bases are being elucidated by different approaches. Ten genes have been demonstrated to contribute to this variation by combining quantitative trait locus mapping and functional analyses (for review, see Alonso-Blanco et al., 2009; Schwartz et al., 2009). Moreover, candidate gene and genome-wide association mapping strategies applied on global (world-wide) collections of wild genotypes have recently identified additional potential alleles of those genes and new loci that await further characterization (Caicedo et al., 2004; Olsen et al., 2004; Stinchcombe et al., 2004; Balasubramanian et al., 2006; Ehrenreich et al., 2009; Atwell et al., 2010; Li et al., 2010).
The existent natural variation for flowering initiation in Arabidopsis is probably involved in adaptation, since latitudinal clines have been found across Europe for some flowering-related traits analyzed in different environments (Caicedo et al., 2004; Stinchcombe et al., 2004, 2005; Lempe et al., 2005; Shindo et al., 2005). In addition, analyses of the spatial distribution of common functional polymorphisms have detected latitudinal clines in two flowering genes, FLOWERING LOCUS C (FLC) and PHYTOCHROME C (PHYC), suggesting their contribution to such geographic clines (Stinchcombe et al., 2004; Balasubramanian et al., 2006; Samis et al., 2008). However, until now, topoclines of flowering gene polymorphisms have not been resolved into ecoclines related to climatic or other ecological gradients, either in Arabidopsis or in other plant species (Izawa, 2007; Ducrocq et al., 2008; Xue et al., 2008). Therefore, the precise environmental factors that might drive the evolution and distribution of flowering variation in annual plants remain unknown.
It is expected that the phenotypic and genotypic flowering variation involved in climatic adaptation will show spatial patterns correlated with the climatic factors driving natural selection. These causal genotype-environment relationships are often referred to as spatial dependence (Legendre et al., 2002; Manel et al., 2010). However, genotypes can also show significant association with environmental variables as a consequence of nonadaptive processes involved in the dispersal and demographic history of the species. Such biotic processes, as well as aggregated sampling designs, lead to spatial autocorrelation of genetic data (i.e. correlation between values of a variable at neighboring locations) and to a lack of independence of observations (Sokal and Oden, 1978). This is especially relevant in organisms like Arabidopsis, showing strong geographic structure for presumably neutral markers, at global and regional scales (Nordborg et al., 2005; François et al., 2008; Picó et al., 2008; Platt et al., 2010). To facilitate the detection of genotypic spatial patterns caused by climate, statistical methods are being developed that take into account spatial autocorrelation in the analysis of spatial genetic data (Dormann, 2007; Manel et al., 2010). In particular, several studies have recently proposed to correct for different levels of genetic structure when testing for correlation between genotypic and environmental variables (Hancock et al., 2008; Eckert et al., 2010). Thus, as widely described for phenotype-genotype associations (Zhao et al., 2007; Myles et al., 2009), correcting for genetic relatedness reduces the detection of false positives in geographically structured populations when testing environmental associations.
In this work, we specifically address two major questions. First, we aim to identify climatic factors that might act as natural selective forces shaping the spatial distribution of genetic variation for flowering initiation in Arabidopsis. Second, we intend to identify flowering genes and polymorphisms involved in climatic adaptation. To approach both goals, we characterized Arabidopsis variation for nine flowering-related traits in 182 wild genotypes collected in the Iberian Peninsula. This geographic region provides an ideal scenario to evaluate Arabidopsis climatic adaptation because it is part of the species native range (Hoffmann, 2002), it spans a large diversity of climates and ecological habitats (Myers et al., 2000; Ninyerola et al., 2000), and it has been shown to contain a large amount of genetic variation for Arabidopsis (Picó et al., 2008). Furthermore, given the prevalence of very-low-frequency alleles with strong geographic structure found in Arabidopsis global studies (Nordborg et al., 2005; Kim et al., 2007; François et al., 2008), it is expected that intensive regional collections might increase the frequency of such rare alleles, enabling the detection of their effects on flowering traits. This is illustrated by means of association analyses with four genes previously involved in natural variation, which identified novel allelic series of six to 11 putative loss- and change-of-function FLC and FRIGIDA (FRI) alleles associated with several flowering traits. In addition, the spatial patterns of flowering traits and of FRI, FLC, and PHYC polymorphisms appear associated with temperature or precipitation, hence supporting their roles in climatic adaptation. These results show the power of environmentally documented regional collections to uncover new clues on the molecular mechanisms of adaptation that cannot be inferred from current global analyses.
RESULTS
Geographical Distribution of Flowering Traits
A collection of 182 accessions sampled in different Arabidopsis populations that cover the distribution area as well as the different ecological habitats and climates of the Iberian Peninsula (Supplemental Fig. S1) were analyzed for nine flowering traits in two experimental environments: with and without a vernalization treatment. Twenty-two genotypes (12%) completely failed to flower without vernalization but flowered when vernalized, which indicates that these genotypes have an obligate requirement for vernalization (Supplemental Fig. S2). As expected, vernalization produced an overall acceleration of flowering, measured either as leaf number (LN) or flowering time (FT), although there was a 10-fold variation for the vernalization sensitivity estimated for both flowering parameters (SLN and SFT; Supplemental Fig. S2). In addition, vernalization also led to an overall reduction of the mean rate of leaf production as estimated by LN/FT and VLN/VFT ratios (0.79 ± 0.01 and 0.64 ± 0.01, respectively).
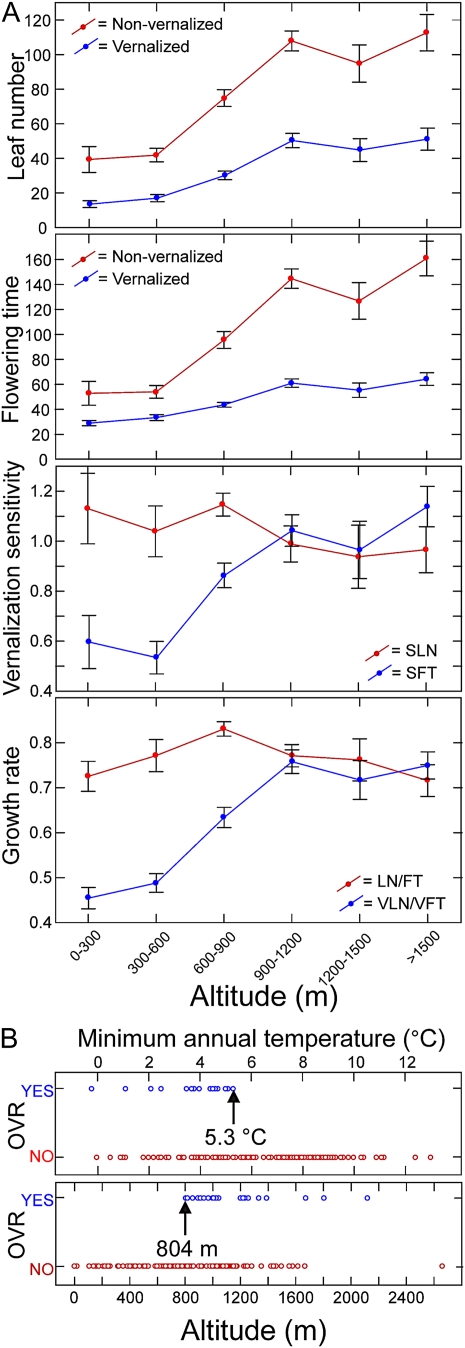
Multiple regression analyses of flowering traits on the three geographical variables (latitude, longitude, and altitude) showed that all traits except SLN and LN/FT are strongly associated with altitude (0.55 > β > 0.32; P < 0.001; Supplemental Table S1). As shown in Figure 1, variation for LN and FT display strong altitudinal clines: the higher the altitude of origin, the later the flowering initiation. In particular, accessions collected below 600 m flowered significantly earlier than the rest, while accessions above 900 m flowered substantially later. In addition, the obligate vernalization requirement (OVR) was exclusively observed at altitudes above 800 m (Fig. 1B). In contrast, clinal variation was not found for SLN and LN/FT but was detected for SFT and VLN/VFT. This result suggests that vernalization reduces the rate of leaf production of accessions from low altitudes as a consequence of their reduced vernalization sensitivity for flowering time but not for leaf number (Fig. 1).
Figure 1.
Altitudinal clines of flowering-related traits in Arabidopsis. A, Leaf number, flowering time, vernalization sensitivity, and growth rate of Iberian accessions classified in six altitudinal ranges given in meters above sea level. Each panel shows the corresponding trait with or without vernalization treatment, except for vernalization sensitivity, which is shown for leaf number and flowering time. Data points are means ± se. B, Distribution of accessions with or without OVR in relation to altitude (bottom panel) and minimum annual temperature (top panel).
On the other hand, most traits show weaker but significant association with latitude and/or longitude (0.32 > β > 0.23; P < 0.001). In addition, the spatial distribution of the 182 genotypes exhibited an aggregated pattern (Kolmogorov-Smirnov test = 0.249; P < 0.0001; Supplemental Fig. S1). Since latitudinal/longitudinal associations and aggregated samplings may increase the spatial autocorrelation, we quantified the autocorrelation patterns of the flowering traits by means of correlograms. These analyses showed significant autocorrelations extending up to 200 to 250 km for OVR, LN, FT, VLN, VFT, and VLN/VFT (P < 0.05). However, Moran’s I values were rather low, with averages ranging between 0.14 and 0.21. Lower autocorrelation was observed for vernalization sensitivity (SLN and SFT) and for LN/FT, with Moran’s I values ranging from 0.12 to 0.18 and extending up to 30 to 140 km. Therefore, values of flowering traits appear not fully independent from each other, making it necessary to consider their autocorrelation when comparing with other spatially correlated variables such as weather records.
Climatic Distribution of Flowering Traits
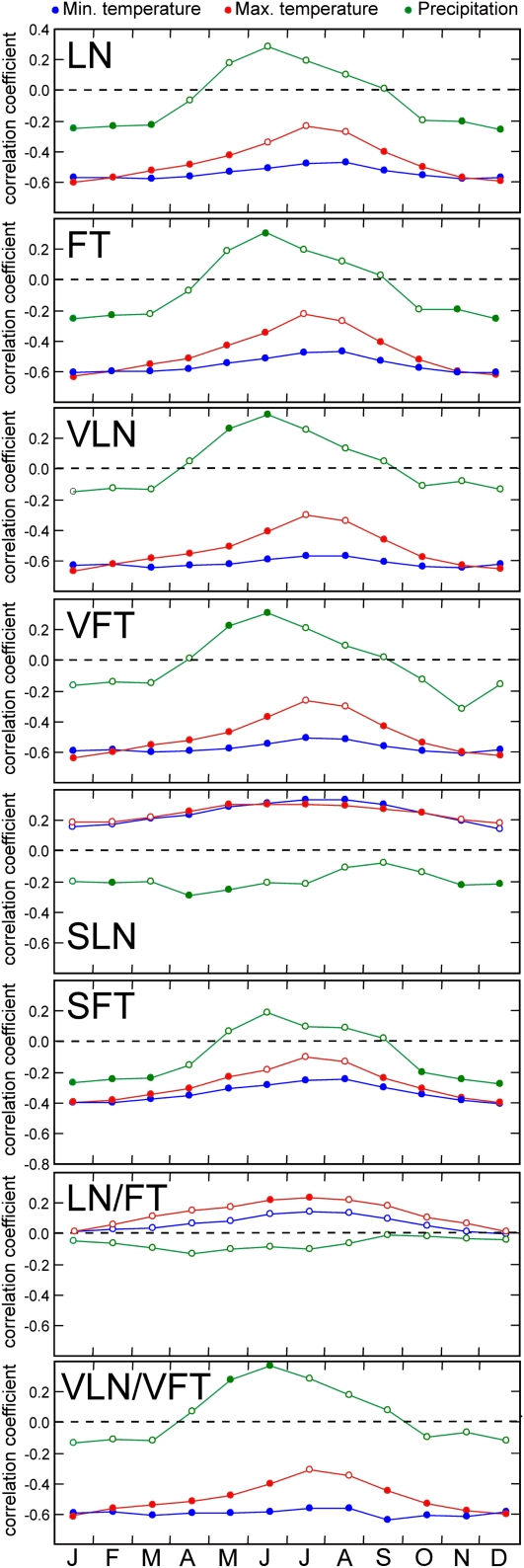
To dissect the altitudinal patterns observed for flowering traits in terms of environmental variables, we analyzed their correlation with annual climatic factors and with the vegetation type of the local populations of origin (Supplemental Table S2). Most traits (all but LN/FT and SLN) showed similar or stronger correlation with minimum annual temperature than with altitude (−0.34 > r > −0.67; P < 0.0001, based on Dutilleul’s modified t test), late flowering initiation appearing associated with low minimum temperature. Similar analyses using monthly climatic variables (Fig. 2) showed that most traits negatively correlate with minimum and maximum temperatures throughout the year, although the strongest correlations were found with winter variables (−0.41 > r > −0.64; P < 0.0001). In contrast, more complex relationships were found with monthly precipitations, since winter values correlated negatively with LN, FT, SLN, and SFT, while summer precipitations correlated positively with all flowering traits recorded after vernalization (VLN, VFT, and VLN/VFT). In addition, autologistic regressions of the qualitative trait OVR showed the strongest associations also with minimum annual and monthly temperatures (R2 = 0.24–0.27; P < 0.0001), the OVR appearing distributed only in populations with annual minimum temperatures below 5.3°C (Fig. 1B). On the other hand, weaker but significant correlations were also detected between most flowering traits and the type of vegetation cover in the local populations (−0.22 > r > −0.34; P < 0.05), early flowering correlating with high proportion of anthropic vegetation.
Figure 2.
Relationship between flowering traits and monthly climatic variables throughout the year. Each panel shows the correlation coefficients between the flowering trait indicated and monthly minimum temperature (blue line), maximum temperature (red line), and total precipitation (green line). Months on the abscissa are indicated at the bottom with the first letter of the month. Colored circles depict significant correlations (P < 0.05), while white circles are nonsignificant coefficients tested with Dutilleul’s modified t test accounting for the spatial autocorrelation of data.
Simultaneous autoregressive (SAR) analyses of flowering traits on the various geographical and environmental factors confirmed that minimum annual temperature and total precipitation are the main climatic factors accounting for phenotypic variation (R2 of the models varying from 13.6% to 43.5%; Table I). In contrast, the proportion of anthropic vegetation of the local populations only contributed marginally to the variation for flowering time and its vernalization response, while altitude did not show a significant effect on any trait. Thus, the altitudinal clines observed for flowering traits appeared strongly determined by climatic factors.
Table I. SAR analyses testing the effects of altitude and environmental factors on flowering traits of Arabidopsis.
For each trait, the following data are given: the number of genotypes (N); the regression coefficient and significance of altitude, of the mean minimum annual temperature, of the total annual precipitation, and of the proportion of anthropic vegetation cover; and the r2 and the F value of the full model. Significance is as follows: *** P < 0.0001; ** P < 0.01; * P < 0.05; ns, nonsignificant.
| Trait | N | Altitude | Minimum Temperature | Total Precipitation | Anthropic Vegetation | R2 | F |
| % | |||||||
| LN | 182 | 0.10 ns | −0.48*** | −0.27*** | −0.11 ns | 39.7 | 29.8*** |
| FT | 182 | 0.18 ns | −0.41*** | −0.28*** | −0.16* | 43.5 | 37.8*** |
| VLN | 181 | 0.06 ns | −0.56*** | −0.18** | −0.11 ns | 42.9 | 33.5*** |
| VFT | 181 | 0.07 ns | −0.51*** | −0.21*** | −0.14* | 40.1 | 29.4*** |
| SLN | 180 | 0.26 ns | 0.44** | −0.19* | −0.06 ns | 13.6 | 6.2** |
| SFT | 180 | 0.21 ns | −0.17 ns | −0.29*** | −0.17* | 24.6 | 13.8** |
| LN/FT | 157 | 0.23 ns | 0.21 ns | 0.01 ns | 0.16 ns | 4.4 | 1.4 ns |
| VLN/VFT | 179 | 0.03 ns | −0.59*** | −0.12 ns | −0.03 ns | 38.7 | 28.9*** |
Nucleotide Diversity of Flowering Initiation Genes
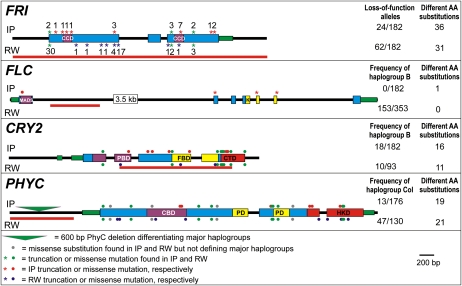
To identify gene polymorphisms that may contribute to the extensive variation described for flowering-related traits, we sequenced FRI, FLC, CRYPTOCHROME2 (CRY2), and PHYC as candidate genes previously involved in Arabidopsis natural variation. Analysis of 3.4 to 6.0 kb per gene containing the complete coding region, in 18 to 182 accessions, showed the following three distinct patterns of nucleotide diversity (Fig. 3).
Figure 3.
Comparison of flowering gene sequences between the Iberian Peninsula (IP) and the rest of the world (RW). Each panel shows gene structure, truncation mutations, and missense substitutions found in FRI, FLC, CRY2, and PHYC. The total frequency of loss-of-function alleles or of major haplogroups described previously, as well as the number of different amino acid (AA) substitutions, are given at the right of each panel. In the FRI panel, asterisks indicate protein truncations and numbers close to them correspond to their frequencies. Black lines, blue boxes, and green rectangles depict intron or promoter regions, exons, and untranslated regions, respectively. Boxes in purple, yellow, or red depict the following functional domains described previously: CCD, coiled-coil domain; MADS, MADS domain; K, K box; PBD, pterin-binding domain; FBD, flavin-binding domain; CTD, C-terminal domain; CBD, chromophore-binding domain; PD, PAS domain; HKD, His kinase domain. Sequence data of accessions from the rest of the world were obtained from Shindo et al. (2005; FRI), Caicedo et al. (2004; FLC), Olsen et al. (2004; CRY2), and Balasubramanian et al. (2006; PHYC). Red lines indicate gene segments sequenced in all 182 accessions.
FRI appeared characterized by an overall low diversity (πsilent = 0.00224), but it displayed a large amount of nonsynonymous diversity (Supplemental Table S3). In total, 36 different amino acid substitutions were found, mainly in the first half of FRI protein, 24 of them appearing as Iberian specific when comparing with previously available sequences from the rest of the world distribution (Fig. 3; Supplemental Fig. S3; Shindo et al., 2005). In addition, 11 different insertions/deletions (indels) and nonsense mutations generating truncated FRI proteins were found in a total of 24 out of 182 Iberian accessions. This result indicates that presumed FRI loss-of-function alleles are found in Iberia at a significantly lower frequency than the average reported in the rest of the world distribution (13.2% and 34.0%, respectively). Eight of these alleles appear as Iberian specific, while the two commonest deletions found in the rest of the world distribution are absent or at very low frequency in this region (Fig. 3). Furthermore, network analysis of FRI protein haplotypes indicates that most loss-of-function mutations have originated independently in different ancestral haplotypes (Supplemental Fig. S4).
FLC also displayed an overall low nucleotide diversity (πsilent = 0.00271), but it is characterized by a very low nonsynonymous diversity, since only one amino acid substitution was found in a single Iberian accession (Supplemental Table S3). A 1.6-kb deletion, a donor splice site substitution, and a nonsense mutation were found exclusively in three early-flowering accessions, Svi-0, Alb-1, and Vad-0, which are predicted to generate truncated proteins of 61, 135, and 163 amino acids, respectively (Fig. 3). Haplotype network analysis reveals that in the Iberian Peninsula there is only one haplogroup, FLC-A, out of the two highly differentiated haplogroups (FLC-A and FLC-B) previously detected in the rest of the world distribution (Caicedo et al., 2004; Supplemental Fig. S4). Furthermore, the four commonest FLC Iberian haplotypes, which appeared differentiated by two to eight polymorphisms located mainly in the first intron, were not found outside this region.
CRY2 and PHYC displayed 5- to 8-fold higher nucleotide diversity than FRI or FLC (πsilent = 0.012–0.018) as well as a higher linkage disequilibrium proportion among informative polymorphisms (Supplemental Table S3). Consistently, variation in these genes was organized in two haplogroups differentiated by eight and nine amino acid substitutions (Fig. 3), which have been described before as CRY2-A/CRY2-B and PHYC-Ler/PHYC-Col (Olsen et al., 2004; Balasubramanian et al., 2006). Comparison with previously available sequences from other world regions showed that CRY2 haplogroups are present at similar frequencies in Iberia than in the rest of the world (CRY2-B frequency of 9.9% and 10.8%, respectively). In contrast, the PHYC-Col haplogroup was found at much lower frequency in Iberia (7.4%) than in world distribution samples (36.2%). Thus, a similar pattern of nucleotide diversity is found in the four genes across the distribution range of Arabidopsis. However, the Iberian Peninsula appears significantly differentiated in the frequency of potentially functional polymorphisms (Fig. 3).
Association Analysis between Flowering Traits and Genes
The effect of FRI, FLC, CRY2, and PHYC on flowering traits was evaluated from the 182 Iberian sequences obtained for a 0.7- to 3.5-kb fragment per gene, selected on the basis of their nucleotide diversity pattern (Fig. 3; see “Materials and Methods”). A total of 35 flowering gene polymorphisms showing minor allele frequency (MAF) greater than 5% and absence of linkage disequilibrium (Supplemental Table S3) were tested by association analysis using the Q+K mixed-model approach for structured populations. Five genetic clusters were detected from 101 presumed neutral single nucleotide polymorphisms (SNPs) with STRUCTURE and were used to account for population structure (Fig. 4A; Supplemental Fig. S5). In addition, a kinship matrix K was derived from the same SNPs and included in the model to reduce false associations due to genetic relatedness (Supplemental Fig. S6A). As shown in Table II, two of the commonest FRI truncations showed significant association with several traits. Since FRI truncations are expected to cause a similar FRI loss of function, the total effect of the 11 truncations was estimated simultaneously in a joint diallelic test (see “Materials and Methods”). Thus, all FRI truncations together accounted for 4.1% to 15.5% of the phenotypic variation for most traits (Supplemental Table S4).
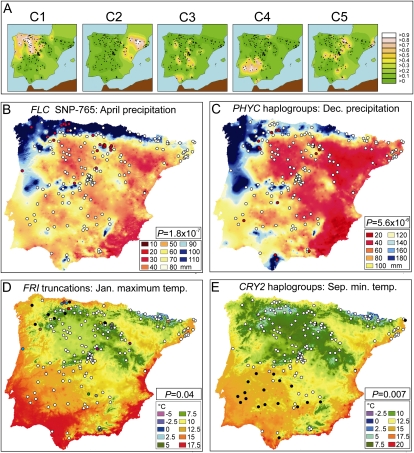
Figure 4.
Geographic and climatic distribution of flowering gene polymorphisms. A, Geographic distribution of the five genetic clusters (C1–C5) identified in the Iberian Peninsula. Each map shows the Kriging-based quantitative distribution of one genetic cluster, and the legend to the right indicates the range of cluster membership proportions corresponding to each color. Black dots depict the location of the 182 populations. B, Distribution of FLC SNP-765 in relation to April precipitation. C, Distribution of PHYC haplogroups in relation to December precipitation. D, Distribution of FRI truncations in relation to January maximum temperature. E, Distribution of CRY2 haplogroups in relation to September minimum temperature. The two alleles are represented by white and red dots (B and C) or white and black dots (E). In D, white dots depict presumed functional FRI alleles, while the 11 different FRI truncation alleles are represented in different colors. The statistical significance of the corresponding climate-genotype association is indicated inside each panel.
Table II. Association analyses between flowering traits and genes.
The table includes the statistical significance and R2 of polymorphisms showing significant effects on some traits (P < 0.001). Statistical parameters of the commonest FRI truncations (the only polymorphisms with MAF of less than 5% tested) and the major PHYC and CRY2 haplogroups are also shown. Polymorphisms are named according to the type of mutation and the nucleotide position, the first coding nucleotide corresponding to position 1. nc, Nucleotide.
| Gene | Polymorphism | Gene Effect | MAF | Traitsa | P | R2 |
| % | % | |||||
| FRI | Indel-1,688 | Truncation FRI-401 | 1.6 | LN, FT, SFT | 2.9 × 10−4–0.004 | 5.3–3.6 |
| Del-1,767 | Truncation FRI-428 | 3.8 | LN, FT, VLN, VLN/VFT,VFT | 8.6 × 10−4–0.008 | 4.5–2.5 | |
| fri-jointb | FRI truncations | 13.2 | LN, FT, VFT, SFT, VLN, LN/FT, VLN/VFT, OVR | 5.1 × 10−11–0.002 | 15.5–4.1 | |
| FLC | SNP-765 | First intron substitution | 13.2 | LN, SLN, LN/FT, FT | 3.3 × 10−4–0.003 | 6.4–3.3 |
| Indel-621 | First intron indel (1 nc) | 5.5 | VFT, VLN | 0.001–0.006 | 3.6–2.9 | |
| Indel-1,075 | First intron indel (2 nc) | 7.7 | VLN/VFT, VLN, SLN, VFT | 6.9 × 10−4–0.002 | 4.6–3.3 | |
| FLC-multiallelic | First intron mutations | 5.5 | SLN, VFT, LN, VLN/VFT, VLN, FT, LN/FT | 1.3 × 10−5–0.004 | 11.9–5.4 | |
| PHYC | Haplogroup SNPs | Nine amino acid substitutions | 7.1 | – | >0.09 | – |
| CRY2 | Haplogroup SNPs | Eight amino acid substitutions | 9.9 | – | >0.29 | – |
Traits are arranged according to decreasing statistical significance.
Joint analysis as a diallelic polymorphism (i.e. the 11 FRI truncation alleles versus the remaining FRI alleles).
Simultaneous analysis of the three FLC polymorphisms showing significant effects on flowering traits as a multiallelic polymorphism (for details, see text).
Three FLC polymorphisms also affected differently several flowering traits (Table II). The rare allele of SNP-765, which is one of the eight mutations defining the most frequent Iberian-specific haplotype, accelerated flowering when plants were not vernalized and reduced vernalization sensitivity (Supplemental Table S4). In contrast, two indels affected flowering and growth rate mostly after vernalization treatment, the rare alleles of these indels showing opposite effects on various traits (Supplemental Table S4). Together, this FLC variation accounted for 5.4% to 11.9% of the variation for most flowering traits, as estimated from a multiallelic FLC analysis including these three FLC alleles versus the remaining alleles (see “Materials and Methods”). Furthermore, SNP-765 of FLC mainly showed association in a FRI loss-of-function background (Supplemental Fig. S7), suggesting a novel genetic interaction between FLC and FRI. On the contrary, none of the CRY2 and PHYC polymorphisms showed significant association with any flowering trait.
Geographic and Climatic Distribution of Flowering Gene Polymorphisms
Genetic variation of presumably neutral markers is spatially structured in the Iberian Peninsula, as shown by the significant isolation by distance found among the 182 genotypes (r = 0.30; P = 0.001) and by the discrete geographic distribution of some genetic clusters detected with STRUCTURE (Fig. 4A). Consequently, several of these genetic clusters showed significant associations with various geographic and climatic variables (Supplemental Fig. S8). Cluster 1 was mainly associated with low summer temperatures. However, cluster 2 was associated with high altitude, high summer precipitation, and low annual temperatures, while cluster 4 showed the opposite patterns and appeared associated with low altitude, low summer precipitation, and high annual temperatures. These genetic cluster-climate relationships accounted only for part of the climatic clines described for flowering traits (Supplemental Table S5). However, such genetic structure-environment covariance should be taken into account when searching for spatial patterns of allele frequency that result from adaptations to climate and not from the genetic relatedness and demographic history. Thus, associations between the 35 flowering gene polymorphisms and environmental variables were tested using a mixed-model approach similar to that described for phenotype-genotype analyses, where genetic relatedness was included to reduce the proportion of false positives (Supplemental Fig. S6B).
SNP-765, defining the commonest FLC haplotype, and the polymorphisms differentiating the major PHYC haplogroups were significantly associated with annual precipitation as well as with spring and winter precipitations, respectively (P < 5.6 × 10−6; Supplemental Table S6). As shown in Figure 4, rare alleles of both polymorphisms appeared associated with high precipitation. To evaluate the significance of these associations, we carried out similar environmental tests with 68 presumed neutral SNP markers used to determine the genetic structure and showing comparable allele frequencies (Supplemental Fig. S6B). Among all tests performed, FLC and PHYC polymorphism displayed the strongest statistical significances, which supports that these environmental associations result from climatic adaptation.
On the other hand, FRI truncations displayed a certain geographic structure (Fig. 4D), but no significant association was detected between FRI polymorphisms or haplotypes and the environmental variables when analyzing the 182 Iberian accessions. However, since several independent FRI truncations are present mainly within genetic cluster 1, we also analyzed climatic associations in the 50 accessions with a cluster 1 membership coefficient larger than 0.5. These analyses showed that FRI truncations are significantly associated with high winter maximum temperature (P < 8.6 × 10−5; Supplemental Table S6) and to a lesser extent with low altitude and high minimum winter temperature (P < 0.001). Finally, polymorphisms characterizing CRY2 haplogroups showed strong geographical structure, but this closely overlapped with the distribution of genetic cluster 4 (Fig. 4E). Accordingly, CRY2 climatic associations could not be separated from the overall climatic associations of the genetic structure.
DISCUSSION
Altitudinal Variation of Flowering-Related Traits Reflects Climatic Adaptation
Clinal variation of quantitative traits has been classically interpreted as evidence of evolutionary adaptation or adaptive evolution (Stebbins, 1950), and its detection has been the aim of multiple flowering initiation studies in Arabidopsis. However, analyses using global collections of wild genotypes have only found latitudinal clines for some flowering initiation traits (Caicedo et al., 2004; Stinchcombe et al., 2004, 2005; Lempe et al., 2005; Shindo et al., 2005). Our study conducted on a collection of 182 Iberian genotypes collected in a small latitudinal range (36°N–43°N) reveals previously undetected altitudinal clines of multiple flowering-related traits spanning a 0- to 2,600-m range. In addition, altitudinal clines have been dissected in terms of two main climatic factors, minimum winter temperature and precipitation, in agreement with clines recently reported for a sample of 17 populations restricted to northeastern Spain (Montesinos-Navarro et al., 2011). These climatic clines account for about 40% of the phenotypic variation for flowering time and leaf number, with and without vernalization treatment. Moreover, correlation analyses show an opposite climatic clinal behavior for the vernalization sensitivity measured as SFT or as SLN. In agreement with the observed positive regional correlation between SLN and minimum temperature, the negative latitudinal cline previously described for SLN might be determined by the same climatic factor (Lempe et al., 2005; Stinchcombe et al., 2005). Furthermore, the significant altitudinal and climatic clines observed for the rate of leaf production after vernalization suggest that vernalization effects on vegetative growth may play a role in climatic adaptation. In agreement, it has been recently shown that most natural genetic variation affecting flowering initiation also affects the rate of leaf production (Méndez-Vigo et al., 2010).
Interestingly, the OVR observed in 12% of Iberian accessions appears restricted to altitudes above 800 m and to locations with annual minimum temperatures below 5.3°C. A similar OVR phenotype has been previously described in a global analysis as specific of northern European accessions collected exclusively above 45°N (Shindo et al., 2005). Thus, our study points out the ecological bias existing in current world-wide Arabidopsis collections and highlights the subsequent difficulties for resolving geographic clines into ecoclines. More importantly, this analysis demonstrates the relevance of climatic factors as forces driving the evolution and geographic distribution of genetically based variation for Arabidopsis flowering traits. We do not know whether the identified climatic factors operate directly on these traits and/or indirectly through other unknown environmental factors that could correlate with climate. As a matter of fact, the weak correlation observed with the type of vegetation of local populations suggests that adaptations by genetic modification of flowering traits are also partly influenced by other environmental factors.
Global and Regional Association Analyses Are Complementary for the Identification of Functional Allelic Series at FRI and FLC
Using phenotype-genotype association analysis of well-known candidate genes, we identified new functional allelic series of FRI and FLC as major components accounting for the variation for flowering initiation and vernalization sensitivity. Previous studies have demonstrated the relevance of these vernalization pathway genes in Arabidopsis global variation (Caicedo et al., 2004; Stinchcombe et al., 2004; Aranzana et al., 2005; Lempe et al., 2005; Shindo et al., 2005, 2006; Zhao et al., 2007; Atwell et al., 2010; Li et al., 2010). However, the regional diversity of FLC alleles found in this work reveals a broad FLC functional diversification with differential contributions at different spatial scales. On the one hand, the absence in this region of the globally common haplogroup FLC-B supports the FLC latitudinal differentiation previously described in Europe (Caicedo et al., 2004). On the other hand, the six new Iberian FLC alleles showing different effects on gene function indicate that regional polymorphisms with low or moderate frequency also account for a substantial proportion of flowering variation. Three of these alleles are predicted to generate truncated proteins and show very low frequency exclusively in early accessions. In agreement with FLC function as a floral repressor (Michaels and Amasino, 1999), these alleles probably cause a severe or complete loss of function. In contrast, the three haplotypes identified in association analyses seem to cause different changes of FLC function because they show distinct effects on the flowering traits with and without vernalization. These haplotypes are differentiated by two to eight polymorphisms located mainly in intron 1, suggesting that such mutations affect the epigenetic regulation of FLC expression (Bastow et al., 2004; Kim et al., 2009). Interestingly, various FLC polymorphisms involve microsatellite-like sequences, suggesting that some repeated sequences in intron 1 might affect the regulation of FLC expression. However, further functional studies are required to demonstrate the distinct functions and genetic mechanisms of these haplotypes. In addition, all these potentially functional alleles of FLC show a restricted subregional geographic distribution; therefore, they have been previously undetected in world-wide analyses due to their consequent low global frequency.
In agreement with earlier studies, the 11 Iberian FRI loss-of-function alleles showed the strongest associations with most flowering traits (Stinchcombe et al., 2004; Aranzana et al., 2005; Lempe et al., 2005; Shindo et al., 2005; Zhao et al., 2007). As described for FLC, FRI truncation alleles also display significant geographic structure at the Iberian regional level, and most of them were not detected in global analyses. However, three of them are also found in the rest of Europe, providing additional information on the demographic history of Arabidopsis. Two FRI truncations present only in accessions of genetic cluster 1 and distributed in northwestern Iberia (shown in red and light blue in Fig. 4D), are also found in Great Britain, Belgium, and France (Le Corre et al., 2002; Shindo et al., 2005). This geographic pattern is in agreement with the hypothesis that the Iberian genetic cluster 1 contributed mainly to the colonization of northern and western Europe (Picó et al., 2008). In contrast, the Landsberg erecta FRI deletion showing the widest global geographic distribution (Johanson et al., 2000; Shindo et al., 2005; Toomajian et al., 2006) appears only in a 7-km area in southeastern Spain. Therefore, a recent Arabidopsis migration event has probably introduced this allele in Iberia.
In contrast to FRI and FLC, the lack of significant phenotypic associations for the major haplogroups of photoreceptor genes CRY2 and PHYC suggests that they do not contribute to the variation of the flowering traits analyzed here. This agrees with a previous CRY2 global study where the effect of population structure could not be separated from that of CRY2 (Zhao et al., 2007). On the contrary, PHYC has been previously associated with flowering initiation under a short-day photoperiod (Balasubramanian et al., 2006; Samis et al., 2008). This association has been shown to be latitude dependent, the PHYC-Col haplogroup appearing mainly distributed in northern Europe, in agreement with the lower PHYC-Col frequency observed in the Iberian Peninsula.
Overall, our results show the complement between regional and global association mapping studies to detect functional alleles with different frequency, age, and adaptive/demographic history. Frequent world-wide haplogroups differentiated by a large amount of genetic variation, such as those of CRY2 and PHYC, may suggest that strong purifying and/or balancing selection is acting on them since a long time ago on a global scale. The phenotypic effects of these alleles can be independently tested in both kinds of analyses to support the outcome at different spatial scales. In contrast, in genes like FRI and FLC, the detection of multiple dysfunctional alleles with different levels of geographic structure suggests that natural selection is recurrently maintaining newly generated alleles. Such differential patterns of nucleotide variation suggest that the environmental cues acting on the photoperiod and vernalization pathway genes could have different patterns of temporal and spatial variation, as can be hypothesized, for instance, for long-term changes in light and temperature, respectively. Widely distributed haplotypes are probably relatively old alleles (Toomajian et al., 2006) that can be evaluated in global analyses but not necessarily in regional studies. This is illustrated by some frequent FLC haplogroups and FRI truncations whose detection at the regional level is hampered by the low regional frequency derived from the strong global geographic structure (Nordborg et al., 2005; François et al., 2008; Platt et al., 2010). In contrast, subregionally distributed alleles can be interpreted as more recent and/or locally adapted alleles that will only be detected at a regional scale. Nevertheless, the effect of such subregional alleles will not be detected even at a regional scale when they occur at low frequency (less than 5%). The large amount of such low-frequency alleles observed in this work (most loss-of-function FRI and FLC alleles and missense FRI mutations) point to two general limitations that need to be addressed in future association studies to fully uncover the diversity of natural functional alleles. First, as shown in this work, estimation of the contribution of such alleles and genes requires the development and implementation of multiallelic tests. Second, analyses at subregional and local scales should complement current studies, since low-frequency alleles of genes like FRI and FLC will probably account for a significant proportion of the unexplained phenotypic variation.
Integration of Environmental Information Detects Signals of Plant Climatic Adaptation in the FLC, PHYC, and FRI
Although association analysis identifies potential flowering gene polymorphisms that might be involved in adaptation, demonstrating their adaptive role requires environmental evaluation. The significant climate-genotype associations found for FLC and PHYC alleles provide an independent argument supporting that both genes underlie Arabidopsis climatic adaptation. In particular, the early-flowering FLC-765 haplotype appears distributed mainly in a subregion with high annual and spring precipitation. This phenotypic and spatioclimatic pattern is in agreement with the general negative relationship observed between flowering initiation and precipitation, which suggests that FLC is one of the genes contributing to such a genetically based cline. It remains unknown how precipitation may affect the FLC spatial pattern. However, since the observed FLC-765 flowering phenotype involves a genetic interaction with FRI and the latter is not associated with precipitation, it is likely that spring precipitation operates through other FLC-765 pleiotropic effects. These include the effect detected here on the rate of leaf production as well as the previously reported pleiotropy on water use efficiency (McKay et al., 2003) and germination (Chiang et al., 2009). Therefore, further functional and population biology studies describing the demographic behavior of wild populations segregating for this haplotype are necessary to prove the direct or indirect role of precipitation as a selective force shaping FLC genetic and spatial variation (Montesinos et al., 2009). Similarly, the PHYC-Col haplogroup also appears preferentially distributed in subregions with high winter precipitation. However, unlike FLC-765, the PHYC-Col haplogroup has been associated with late flowering under short-day photoperiods (Balasubramanian et al., 2006; Samis et al., 2008), which further increases the complex relationships found in this work between precipitation and flowering. Nevertheless, this climatic factor might also account for the spatial pattern of PHYC-Col by its pleiotropic effects on other traits, like hypocotyl length, previously described for PHYC (Balasubramanian et al., 2006).
Altitudinal and climatic patterns suggest that FRI also contributes to climatic adaptation, but it involves more complex environmental relationships. The associations of early-flowering FRI truncations with low altitude and high winter temperatures suggest that FRI is one of the genes contributing to the major geographical and climatic clines described for the flowering traits. In addition, the genetic background and geographic dependencies of the detected climatic associations suggest that selection operates on FRI through unknown genetic interactions present only in genetic cluster 1. Alternatively, this dependency might be explained because different environmental factors act on FRI in different subregions or because a specific combination of climatic factors and other unknown environmental cues might operate specifically in the cluster 1 subregion.
In contrast to the preceding three genes, no significant signal of climatic adaptation was found for CRY2 alleles. However, several factors might limit the detection of genotype-environment associations resulting from adaptation to climate. First, gene polymorphisms showing a spatial pattern largely overlapping with the overall genetic structure of the populations under study (e.g. those defining CRY2 haplogroups) cannot be evaluated. As in association mapping (Zhao et al., 2007; Ehrenreich et al., 2009), genotype-environment associations can only be tested for polymorphisms showing different history and/or age than the genetic backgrounds of studied populations. In addition, (1) polymorphisms of genes showing multiple independent mutations with similar phenotypic effects, (2) polymorphisms whose spatial distributions are determined by several environmental cues, and (3) polymorphisms involved in genetic or genotype-by-environment interactions will also show weaker correlations with environmental variables.
Previous studies have combined genetic association analysis with geographic correlations to identify flowering genes and functional polymorphisms involved in plant adaptation in several annual plants (Caicedo et al., 2004; Stinchcombe et al., 2004; Balasubramanian et al., 2006; Izawa, 2007; Ducrocq et al., 2008; Samis et al., 2008; Xue et al., 2008). However, our analysis integrates the three sources of variation underlying adaptive evolution (i.e. phenotypic, genotypic, and environmental variation). Thus, we have dissected geographic clines of flowering phenotypes and gene polymorphisms into climatic patterns, hence extending previous and ongoing studies at a global scale. These analyses illustrate the usefulness of Arabidopsis regional dense collections that are ecologically unbiased and environmentally documented to identify major genes involved in climatic adaptation. As recently reported for genome-wide association studies (Atwell et al., 2010; Li et al., 2010), it can be expected that the expansion of environmental analyses to genomic data generated by current high-throughput genotyping techniques will strongly accelerate the identification of genes that might, directly or indirectly, participate in adaptation to future climate changes.
MATERIALS AND METHODS
Sampling Design, Plant Material, and Environmental Data
A total of 182 wild local populations of Arabidopsis (Arabidopsis thaliana) were surveyed in a region of around 800 × 700 km of the Iberian Peninsula (Supplemental Fig. S1). Populations were in situ geo-referenced for their latitude, longitude, and altitude with a global positioning system receiver (Garmin International; Supplemental Table S7). They were spaced at an average distance of 357 ± 202 km, with a minimum and maximum of 1 and 1,042 km respectively. Altitudes ranged from 0 to 2,600 m above sea level. Ninety-nine populations have been described previously (Picó et al., 2008), but the remaining 83 were specifically sampled for this work. Seeds from a single random individual per population (accession) were collected and analyzed in this study. The collection of 182 accessions is available through the Nottingham Arabidopsis Stock Centre (http://arabidopsis.info).
Climatic data of each population location were obtained from the Digital Climatic Atlas of the Iberian Peninsula (http://www.opengis.uab.es/wms/iberia/index.htm), which was developed at a 200-m resolution following the climatic models described by Ninyerola et al. (2000). Models were based on meteorological records of 15 to 50 years, for the period 1950 to 1999, from 2,285 meteorological stations located across the Iberian Peninsula. The following 65 climatic variables were obtained for each location: mean monthly and mean annual temperature, mean minimum and maximum monthly and annual temperature, total monthly and total annual precipitation, and mean monthly and mean annual solar radiation. Population habitats were quantified as the proportions of anthropic and natural types of vegetation cover in each location, which were estimated from the CORINE Land Cover Map (http://www.idee.es). The land cover in a 78-ha circular area around the global positioning system coordinates of each location was classified as the proportion of the following categories: urban, crops, bushes, and woods. Anthropic and natural land cover was estimated by summing the proportional cover of urban and crops, and bushes and woods, respectively.
Growth Conditions and Measurements of Flowering-Related Traits
All accessions were grown simultaneously in two environmental conditions, with and without 6 weeks of vernalization treatment (V and NV, respectively). Seeds were sown in petri dishes containing a filter paper soaked with demineralized water and then stored during 4 d at 4°C to break seed dormancy. Thereafter, seeds were transferred to a growth chamber at 21°C with a short-day photoperiod (8 h of light/16 h of darkness), where they remained during 4 d for germination. Germinated seedlings were then planted in 0.9-L pots with soil:vermiculite mix at 3:1 proportion. For the vernalization treatment, pots were placed in a cold chamber at 4°C with a short-day photoperiod during 6 weeks. Subsequently, pots were moved to an air-conditioned greenhouse supplemented with additional light to provide a daylength of 16 h. For the environment without vernalization, pots were moved directly to the same greenhouse. To reduce differences between the two conditions due to environmental factors other than the low-temperature treatment, seeds for NV were sown 6 weeks later than seeds for V environment. The vernalization treatment was then finished right after planting the NV samples. Thus, plants grown in both conditions were developmentally synchronized to share environmental conditions for most of their vegetative development. Fifteen plants were grown per genotype and treatment in a three-block design. Five plants per accession were grown in one pot per block, pots being completely randomized within blocks. The experiment was finished 200 d after planting the NV treatment.
Flowering initiation was measured as leaf number (LN and VLN for NV and V treatments, respectively) and as flowering time (FT and VFT for NV and V treatments, respectively). LN and VLN were calculated as the total number of rosette and cauline leaves in the main inflorescence developed by a plant. FT and VFT were estimated as the number of days from the planting date of the NV treatment until the opening of the first flower. A substantial proportion of plants did not flower at the end of the experiment but remained at the vegetative phase (26.1% and 3.3% for NV and V conditions, respectively). To avoid underestimation of flowering initiation parameters due to the removal of nonflowering individuals, values of 200 or 112 d, and 150 or 125 leaves, were given to such individuals for the NV or V conditions, respectively. These flowering time values correspond to maximum scores observed in flowering plants, while leaf numbers were calculated from regression lines of LN (or VLN) onto FT (or VFT) using flowering data of all accessions. The percentage of NV individuals per accession that remained in the vegetative phase at the end of the experiment was used as a quantitative measurement of the OVR. Accessions that completely failed to flower in NV conditions were considered to have a qualitative obligate requirement of vernalization. The ratios LN/FT and VLN/VFT of the flowering individuals were estimated as measurements of the average rate of leaf production, a major component of vegetative growth. Mean phenotypic values of seven to 15 individuals per accession (average of 13.6 and 10.7 plants for the NV and V conditions, respectively) were used for the analysis of these traits.
Vernalization sensitivity (SLN and SFT) was estimated as described by Lempe et al. (2005). Basically, SLN was calculated as [log(LN) − log(VLN)]/[log(meanLN) − log(meanVLN)], with LN and VLN being the mean values of each accession and meanLN and meanVLN corresponding to the means of all accessions. Similarly, SFT was calculated as [log(FT) − log(VFT)]/[log(meanFT) − log(meanVFT)].
LN, VLN, FT, and VFT variables were log transformed, while OVR was transformed with angular transformation (arcsinÖ) to improve normality. Statistical analyses of these traits were carried out using transformed variables. Phenotypic values of all accessions and traits are shown in Supplemental Table S8.
Flowering Gene Sequencing and Analysis
DNA was isolated for sequencing and genotyping from single plant tissues using the Bernartzky and Tanksley (1986) protocol without mercaptoethanol.
Four flowering time genes previously analyzed in world-wide collections of wild genotypes of Arabidopsis were selected for sequencing: FRI and FLC are involved in the vernalization pathway, while CRY2 and PHYC affect the photoperiod pathway. To determine the amount and pattern of nucleotide variation of these genes, we sequenced the complete coding region, the 5′ and 3′ untranslated regions, and part of the promoter regions in 18 to 34 Iberian accessions (Supplemental Table S3). To sequence each gene, seven to 10 overlapping fragments of 0.5 to 1 kb were PCR amplified (Supplemental Table S9). PCR products were then sequenced using an ABI PRISM 3700 DNA analyzer. Additional specific primers were developed to sequence polymorphic regions containing poly(A), poly(T), or poly(AT) repeats located in introns 1 and 6 of FLC or particular deletions of FRI. In addition, specific markers were developed to genotype FLC loss-of-function alleles in the 182 accessions (Supplemental Table S9).
For association analyses, due to the prevalent linkage disequilibrium found in CRY2 and PHYC (see “Results” and Supplemental Table S3), only a segment of 0.9 kb of the promoter region of PHYC and 1.5 kb of the coding region of CRY2 were sequenced in all accessions. Given the low nonsynonymous nucleotide diversity observed in 34 complete coding sequences of FLC (see “Results”), only a highly polymorphic 0.7-kb segment of FLC intron 1 was sequenced in the complete set. In contrast, since FRI showed a very high frequency of missense substitutions (Supplemental Fig. S3), the complete FRI gene was sequenced in all accessions.
DNA sequences were aligned using DNASTAR version 8.0 (Lasergene), and alignments were inspected and edited by hand with GeneDoc (Nicholas et al., 1997). Nucleotide diversity, recombination, and linkage disequilibrium were estimated with DnaSP version 5 (Librado and Rozas, 2009). For linkage disequilibrium, Fisher’s exact tests were applied to all pair combinations of informative segregating sites, and the percentage of significant pairwise comparisons was calculated.
Haplotype networks of flowering genes were constructed using the software NETWORK version 4.5 (http://www.fluxus-engineering.com) with the median-joining method.
SNP Genotyping and Population Genetic Analyses
The 83 new accessions included in this study were genotyped for 143 SNPs evenly distributed throughout the genome and described previously in the remaining 99 accessions (Picó et al., 2008). SNPs were analyzed in three mixes of 47 to 48 loci using the SNPlex technique (Applied Biosystems) through the CEGEN genotyping service (http://www.cegen.org). A total of 101 SNPs showed a frequency of missing data lower than 31% (average of 5.5%) and were used for the assessment of genetic structure. On average, 5.6% of the SNPs appeared as missing data per accession. Only five SNPs segregated as singletons, the average MAF being 0.18 ± 0.15. All accessions showed different multilocus genotypes, and all pairs of accessions but one differed in at least three SNP markers. The average proportion of allelic differences between pairs of accessions was 0.26 ± 0.05. Genotypic data of all accessions are given in Supplemental Table S10.
The population structure of the 182 accessions was assessed using the model-based clustering algorithm implemented in STRUCTURE version 2.2 (Pritchard et al., 2000; Falush et al., 2003) as described previously (Picó et al., 2008). The algorithm was run 10 times for each K value from K = 2 to K = 15, and differences between the data likelihood of successive K values were tested using the nonparametric Wilcoxon test for two related samples. A final K = 5 was estimated as the largest K value with significantly higher likelihood than that from K-1 runs (two-sided P < 0.005). A similarity coefficient between runs of 0.99 was estimated using the symmetric similarity coefficient (Nordborg et al., 2005). This parameter and the average matrix of ancestry membership proportions of the 10 runs (Q matrix) were computed using CLUMPP version 1.1 (Jakobsson and Rosenberg, 2007). Previous population structure analyses of a subset of 100 accessions genotyped with the same SNP markers identified a maximum K = 4 (Picó et al., 2008). Comparison of current and previous structures for K = 4 shows very similar genetic and geographical patterns (Supplemental Fig. S9). In addition, comparison between K = 4 and K = 5 of the current population analysis indicates that genetic cluster 5, which appears when increasing population size, derives mainly from clusters 2 and 4 (Supplemental Fig. S5). All subsequent analyses involving genetic structure were performed using K = 4 and K = 5 matrices, and very similar results were obtained in both cases.
Estimated average matrices of membership proportions were graphically represented using DISTRUCT software (Rosenberg et al., 2002). The geographical distribution of ancestry matrices was represented with Kriging methods using the R script available at http://www-timc.imag.fr/Olivier.Francois/admix_display.html (O. François, unpublished data).
The relationship between genetic distance and Euclidean geographical distance among accession pairs was determined by Mantel correlation test using the Isolation by Distance Web service version 3.13 (Jensen et al., 2005). Genetic distance was estimated as the proportion of allelic differences over the total number of alleles in the set of 101 SNPs. Genetic and geographical distances were log transformed prior to analysis, and the significance of correlations was calculated with 1,000 randomizations.
Genetic Association Analyses
Phenotype-genotype associations were tested using the mixed-model approach for structured populations (Yu et al., 2006) as implemented in TASSEL version 2.1 (Bradbury et al., 2007). Two levels of genetic relatedness, the population structure (Q matrix) and the relative kinship (K matrix), were included in the model (Zhao et al., 2007; Myles et al., 2009; Supplemental Fig. S6A). Population structure was estimated with STRUCTURE (see above) as the Q matrix containing the membership proportions of all genotypes to the K = 5 ancestral populations. To ensure independence, only K-1 clusters of the Q matrix were used as covariates in the model. The kinship matrix was estimated as twice the proportion of shared alleles from the 96 nonsingleton SNPs genotyped, as proposed by Zhao et al. (2007) and in the TASSEL manual (Bradbury et al., 2007). Association analyses were also carried out using the STRUCTURE Q matrix derived for K = 4 and using the K matrix generated from TASSEL with the 101 genome-wide SNP markers. Similar results were obtained in all Q+K combinations; therefore, only the most conservative results obtained for K = 5 are reported.
The association of each polymorphism with the nine quantitative traits was evaluated using the mixed linear model (MLM) and the Expectation-Maximization algorithm of TASSEL. Polymorphisms with MAF lower than 5% or in complete linkage disequilibrium were not tested, while polymorphisms with more than two alleles were simplified to diallelic markers by removing the alleles with a lower than 5% frequency.
The joint effect of the different independent FRI alleles that generate protein truncations was analyzed as a diallelic polymorphism. For that, FRI alleles were grouped in two functional classes: truncation alleles versus presumably full-length protein alleles. This polymorphism is referred to as fri-joint, and it was tested as described for the rest of the diallelic polymorphisms with the MLM method. Given the large effect of these FRI loss-of function alleles (see “Results”), association analyses of all sequence polymorphisms were also tested using only the subset of 158 accessions with full-length protein FRI alleles. In addition, the effect of the three FLC alleles showing significant phenotypic association, and originating independently from each other (Supplemental Fig. S4), was analyzed simultaneously as a multiallelic polymorphism. This was tested using the MLM method with four FLC alleles and is referred to as FLC-multiallelic. Such a multiallelic approach was not used for the joint analysis of the multiple FRI truncation alleles to avoid the overestimation of effects as a consequence of low allelic frequencies. Interactions between FRI and FLC polymorphisms were analyzed using the general linear models (GLM) module of STATISTICA version 8.
Analyses of Geographic and Environmental Data
The spatial distribution pattern of the 182 genotypes was analyzed from the geographical coordinates of population locations with the Kolmogorov-Smirnov test, as implemented in the R package Spatstat (Baddeley and Turner, 2005).
Spatial autocorrelation patterns of the flowering variables were analyzed using correlograms (Sokal and Oden, 1978) generated with the software PASSaGE version 2 (Rosenberg and Anderson, 2011). For each variable, Moran’s I autocorrelation coefficients (Moran, 1950) were calculated and plotted for 50 successive spatial intervals, with coefficients ranging between 1 (positive spatial autocorrelation) and −1 (negative spatial autocorrelation). The significance of Moran’s I values was calculated from 1,000 permutations.
Correlations between flowering variables and environmental or geographical variables were tested with Dutilleul’s modified t test, which corrects the variance of the test statistic and the degrees of freedom according to the extent of spatial autocorrelation of each variable of the correlation (Dutilleul et al., 1993, Legendre et al., 2002). The relationships between OVR trait (response variable) and environmental variables (explanatory variable) were analyzed by autologistic regression (Dormann, 2007) using the logistic regression module of the software SAM version 3.1 (Rangel et al., 2010).
The multivariate effects of geographic, climatic, and vegetation variables, as well as the effect of the genetic structure groups, on phenotypic traits were analyzed with SAR models (Kissling and Carl, 2008). SAR analysis is a multiple regression technique explicitly developed for spatial data that uses generalized least squares (GLS) to estimate regression parameters, and it includes in the model an additional term for the autocorrelation matrix of the errors (Beale et al., 2010). Associations between climatic variables and genetic groups (quantified as the membership proportions estimated in the Q matrix from STRUCTURE) were also analyzed with SAR models. Dutilleul’s modified t tests and SAR analyses were carried out using the correlation and generalized least squares spatial autoregression modules of the software SAM version 3.1 (Rangel et al., 2010).
Environment-genotype associations were tested using a mixed-model approach including environmental variables as response variables and nucleotide polymorphisms as explanatory variables. Two levels of genetic relatedness (population structure [Q matrix] and relative kinship [K matrix]) were included in MLM models with TASSEL (Bradbury et al., 2007). Q and K matrices were estimated as described for genetic association analysis. We carried out similar environmental analyses without controlling for genetic structure or controlling only for the population structure (Q model) using GLM in TASSEL (Bradbury et al., 2007). As shown in Supplemental Figure S6B, analyses with no control for genetic structure produced larger P values, while GLM and MLM methods including one or two levels of genetic structure reduced the proportion of false-positive associations derived from genotype-environment covariance. Since the MLM method with two levels of genetic relatedness (Q+K) produced the most conservative results, only these outcomes are reported.
GenBank accession numbers of the DNA sequences generated in this work are JF318221 to JF318956.
Supplemental Data
The following materials are available in the online version of this article.
Supplemental Figure S1. Geographical distribution of Arabidopsis populations surveyed in this work.
Supplemental Figure S2. Frequency distribution of flowering-related traits in the 182 Iberian accessions.
Supplemental Figure S3. Polymorphisms affecting FRI protein structure.
Supplemental Figure S4. Haplotype networks of FRI and FLC genes.
Supplemental Figure S5. Population structure of the 182 Arabidopsis accessions.
Supplemental Figure S6. Cumulative distributions of P values obtained in analyses of the association between nucleotide polymorphisms and flowering traits or environmental variables.
Supplemental Figure S7. Genetic interaction between FRI and FLC polymorphisms.
Supplemental Figure S8. Relationship between genetic structure and climatic variables throughout the year.
Supplemental Figure S9. Comparison of Arabidopsis geographical structure in the Iberian Peninsula using different numbers of accessions and genetic groups.
Supplemental Table S1. Multiple linear regressions testing the effects of geographic variables on flowering traits.
Supplemental Table S2. Correlations between geographical and environmental variables and flowering traits.
Supplemental Table S3. Summary of nucleotide polymorphisms and diversities in candidate flowering genes.
Supplemental Table S4. Allelic effects of polymorphisms associated with flowering traits.
Supplemental Table S5. SAR analyses testing the effect of genetic structure and climatic factors on flowering traits.
Supplemental Table S6. Association analyses between climatic variables and flowering gene polymorphisms.
Supplemental Table S7. Geographical and ecological description of Arabidopsis Iberian populations surveyed in this work.
Supplemental Table S8. Phenotypic values of all traits and accessions.
Supplemental Table S9. Oligonucleotides used for the sequencing of flowering genes.
Supplemental Table S10. Genotypic data of 101 SNP markers used for population structure assessment.
Acknowledgments
We thank Joan Pino (Centre de Recerca Ecologica i Aplicacions Forestals) for kindly collecting the environmental data, Oscar Gavira for providing the Bea sample, and Jenifer Pozas (Centro Nacional de Biotecnología, Consejo Superior de Investigaciones Científicas) for excellent technical assistance.
References
- Alonso-Blanco C, Aarts MG, Bentsink L, Keurentjes JJ, Reymond M, Vreugdenhil D, Koornneef M. (2009) What has natural variation taught us about plant development, physiology, and adaptation? Plant Cell 21: 1877–1896 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aranzana MJ, Kim S, Zhao K, Bakker E, Horton M, Jakob K, Lister C, Molitor J, Shindo C, Tang C, et al. (2005) Genome-wide association mapping in Arabidopsis identifies previously known flowering time and pathogen resistance genes. PLoS Genet 1: e60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atwell S, Huang YS, Vilhjálmsson BJ, Willems G, Horton M, Li Y, Meng D, Platt A, Tarone AM, Hu TT, et al. (2010) Genome-wide association study of 107 phenotypes in Arabidopsis thaliana inbred lines. Nature 465: 627–631 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baddeley A, Turner R. (2005) Spatstat: an R package for analyzing spatial point patterns. J Stat Softw 12: 1–42 [Google Scholar]
- Balasubramanian S, Sureshkumar S, Agrawal M, Michael TP, Wessinger C, Maloof JN, Clark R, Warthmann N, Chory J, Weigel D. (2006) The PHYTOCHROME C photoreceptor gene mediates natural variation in flowering and growth responses of Arabidopsis thaliana. Nat Genet 38: 711–715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastow R, Mylne JS, Lister C, Lippman Z, Martienssen RA, Dean C. (2004) Vernalization requires epigenetic silencing of FLC by histone methylation. Nature 427: 164–167 [DOI] [PubMed] [Google Scholar]
- Beale CM, Lennon JJ, Yearsley JM, Brewer MJ, Elston DA. (2010) Regression analysis of spatial data. Ecol Lett 13: 246–264 [DOI] [PubMed] [Google Scholar]
- Bernartzky R, Tanksley S. (1986) Genetics of acting-related sequences in tomato. Theor Appl Genet 72: 314–324 [DOI] [PubMed] [Google Scholar]
- Böcher TW. (1949) Racial divergences in Prunella vulgaris in relation to habitat and climate. New Phytol 48: 289–314 [Google Scholar]
- Bradbury PJ, Zhang Z, Kroon DE, Casstevens TM, Ramdoss Y, Buckler ES. (2007) TASSEL: software for association mapping of complex traits in diverse samples. Bioinformatics 23: 2633–2635 [DOI] [PubMed] [Google Scholar]
- Briggs D, Walters SM. (1997) Plant Variation and Evolution. Cambridge University Press, Cambridge, UK [Google Scholar]
- Caicedo AL, Stinchcombe JR, Olsen KM, Schmitt J, Purugganan MD. (2004) Epistatic interaction between Arabidopsis FRI and FLC flowering time genes generates a latitudinal cline in a life history trait. Proc Natl Acad Sci USA 101: 15670–15675 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiang GC, Barua D, Kramer EM, Amasino RM, Donohue K. (2009) Major flowering time gene, FLOWERING LOCUS C, regulates seed germination in Arabidopsis thaliana. Proc Natl Acad Sci USA 106: 11661–11666 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craufurd PQ, Wheeler TR. (2009) Climate change and the flowering time of annual crops. J Exp Bot 60: 2529–2539 [DOI] [PubMed] [Google Scholar]
- Dormann C. (2007) Assessing the validity of autologistic regression. Ecol Modell 207: 234–242 [Google Scholar]
- Ducrocq S, Madur D, Veyrieras JB, Camus-Kulandaivelu L, Kloiber-Maitz M, Presterl T, Ouzunova M, Manicacci D, Charcosset A. (2008) Key impact of Vgt1 on flowering time adaptation in maize: evidence from association mapping and ecogeographical information. Genetics 178: 2433–2437 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dutilleul P, Clifford P, Richardson S, Hemon D. (1993) Modifying the t test for assessing the correlation between two spatial processes. Biometrics 49: 305–314 [PubMed] [Google Scholar]
- Eckert AJ, van Heerwaarden J, Wegrzyn JL, Nelson CD, Ross-Ibarra J, González-Martínez SC, Neale DB. (2010) Patterns of population structure and environmental associations to aridity across the range of loblolly pine (Pinus taeda L., Pinaceae). Genetics 185: 969–982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehrenreich IM, Hanzawa Y, Chou L, Roe JL, Kover PX, Purugganan MD. (2009) Candidate gene association mapping of Arabidopsis flowering time. Genetics 183: 325–335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falush D, Stephens M, Pritchard JK. (2003) Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164: 1567–1587 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitter AH, Fitter RS. (2002) Rapid changes in flowering time in British plants. Science 296: 1689–1691 [DOI] [PubMed] [Google Scholar]
- François O, Blum MG, Jakobsson M, Rosenberg NA. (2008) Demographic history of European populations of Arabidopsis thaliana. PLoS Genet 4: e1000075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franks SJ, Sim S, Weis AE. (2007) Rapid evolution of flowering time by an annual plant in response to a climate fluctuation. Proc Natl Acad Sci USA 104: 1278–1282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock AM, Witonsky DB, Gordon AS, Eshel G, Pritchard JK, Coop G, Di Rienzo A. (2008) Adaptations to climate in candidate genes for common metabolic disorders. PLoS Genet 4: e32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann MH. (2002) Biogeography of Arabidopsis thaliana (L.) Heynh. (Brassicaceae). J Biogeogr 29: 125–134 [Google Scholar]
- Ibáñez I, Primack RB, Miller-Rushing AJ, Ellwood E, Higuchi H, Lee SD, Kobori H, Silander JA. (2010) Forecasting phenology under global warming. Philos Trans R Soc Lond B Biol Sci 365: 3247–3260 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izawa T. (2007) Adaptation of flowering-time by natural and artificial selection in Arabidopsis and rice. J Exp Bot 58: 3091–3097 [DOI] [PubMed] [Google Scholar]
- Jakobsson M, Rosenberg NA. (2007) CLUMPP: a cluster matching and permutation program for dealing with label switching and multimodality in analysis of population structure. Bioinformatics 23: 1801–1806 [DOI] [PubMed] [Google Scholar]
- Jensen JL, Bohonak AJ, Kelley ST. (2005) Isolation by Distance, Web service. BMC Genet 6: 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johanson U, West J, Lister C, Michaels S, Amasino R, Dean C. (2000) Molecular analysis of FRIGIDA, a major determinant of natural variation in Arabidopsis flowering time. Science 290: 344–347 [DOI] [PubMed] [Google Scholar]
- Jung C, Müller AE. (2009) Flowering time control and applications in plant breeding. Trends Plant Sci 14: 563–573 [DOI] [PubMed] [Google Scholar]
- Kim DH, Doyle MR, Sung S, Amasino RM. (2009) Vernalization: winter and the timing of flowering in plants. Annu Rev Cell Dev Biol 25: 277–299 [DOI] [PubMed] [Google Scholar]
- Kim S, Plagnol V, Hu TT, Toomajian C, Clark RM, Ossowski S, Ecker JR, Weigel D, Nordborg M. (2007) Recombination and linkage disequilibrium in Arabidopsis thaliana. Nat Genet 39: 1151–1155 [DOI] [PubMed] [Google Scholar]
- Kissling WD, Carl G. (2008) Spatial autocorrelation and the selection of simultaneous autoregressive models. Glob Ecol Biogeogr 17: 59–71 [Google Scholar]
- Kobayashi Y, Weigel D. (2007) Move on up, it’s time for change: mobile signals controlling photoperiod-dependent flowering. Genes Dev 21: 2371–2384 [DOI] [PubMed] [Google Scholar]
- Koornneef M, Alonso-Blanco C, Peeters AJ, Soppe W. (1998) Genetic control of flowering time in Arabidopsis. Annu Rev Plant Physiol Plant Mol Biol 49: 345–370 [DOI] [PubMed] [Google Scholar]
- Le Corre V, Roux F, Reboud X. (2002) DNA polymorphism at the FRIGIDA gene in Arabidopsis thaliana: extensive nonsynonymous variation is consistent with local selection for flowering time. Mol Biol Evol 19: 1261–1271 [DOI] [PubMed] [Google Scholar]
- Legendre P, Dale MRT, Fortin M-J, Gurevitch J, Hohn M, Myers D. (2002) The consequences of spatial structure for the design and analysis of ecological field surveys. Ecography 25: 601–615 [Google Scholar]
- Lempe J, Balasubramanian S, Sureshkumar S, Singh A, Schmid M, Weigel D. (2005) Diversity of flowering responses in wild Arabidopsis thaliana strains. PLoS Genet 1: e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Huang Y, Bergelson J, Nordborg M, Borevitz JO. (2010) Association mapping of local climate-sensitive quantitative trait loci in Arabidopsis thaliana. Proc Natl Acad Sci USA 107: 21199–21204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Librado P, Rozas J. (2009) DnaSP v5: a software for comprehensive analysis of DNA polymorphism data. Bioinformatics 25: 1451–1452 [DOI] [PubMed] [Google Scholar]
- Manel S, Joost S, Epperson BK, Holderegger R, Storfer A, Rosenberg MS, Scribner KT, Bonin A, Fortin MJ. (2010) Perspectives on the use of landscape genetics to detect genetic adaptive variation in the field. Mol Ecol 19: 3760–3772 [DOI] [PubMed] [Google Scholar]
- McKay JK, Richards JH, Mitchell-Olds T. (2003) Genetics of drought adaptation in Arabidopsis thaliana. I. Pleiotropy contributes to genetic correlations among ecological traits. Mol Ecol 12: 1137–1151 [DOI] [PubMed] [Google Scholar]
- Méndez-Vigo B, de Andrés MT, Ramiro M, Martínez-Zapater JM, Alonso-Blanco C. (2010) Temporal analysis of natural variation for the rate of leaf production and its relationship with flowering initiation in Arabidopsis thaliana. J Exp Bot 61: 1611–1623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michaels SD, Amasino RM. (1999) FLOWERING LOCUS C encodes a novel MADS domain protein that acts as a repressor of flowering. Plant Cell 11: 949–956 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montesinos A, Tonsor SJ, Alonso-Blanco C, Picó FX. (2009) Demographic and genetic patterns of variation among populations of Arabidopsis thaliana from contrasting native environments. PLoS ONE 4: e7213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montesinos-Navarro A, Wig J, Pico FX, Tonsor SJ. (2011) Arabidopsis thaliana populations show clinal variation in a climatic gradient associated with altitude. New Phytol 189: 282–294 [DOI] [PubMed] [Google Scholar]
- Moran PAP. (1950) Notes on continuous stochastic phenomena. Biometrika 37: 17–23 [PubMed] [Google Scholar]
- Myers N, Mittermeier RA, Mittermeier CG, da Fonseca GA, Kent J. (2000) Biodiversity hotspots for conservation priorities. Nature 403: 853–858 [DOI] [PubMed] [Google Scholar]
- Myles S, Peiffer J, Brown PJ, Ersoz ES, Zhang Z, Costich DE, Buckler ES. (2009) Association mapping: critical considerations shift from genotyping to experimental design. Plant Cell 21: 2194–2202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholas KB, Nicholas HBJ, Deerfield DW. (1997) GeneDoc: analysis and visualization of genetic variation. EMBNEW.NEWS 4: 1–4 [Google Scholar]
- Ninyerola M, Pons X, Roure JM. (2000) A methodological approach of climatological modelling of air temperature and precipitation through GIS techniques. J Climatol 20: 1823–1841 [Google Scholar]
- Nordborg M, Hu TT, Ishino Y, Jhaveri J, Toomajian C, Zheng H, Bakker E, Calabrese P, Gladstone J, Goyal R, et al. (2005) The pattern of polymorphism in Arabidopsis thaliana. PLoS Biol 3: e196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olsen KM, Halldorsdottir SS, Stinchcombe JR, Weinig C, Schmitt J, Purugganan MD. (2004) Linkage disequilibrium mapping of Arabidopsis CRY2 flowering time alleles. Genetics 167: 1361–1369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Picó FX, Méndez-Vigo B, Martínez-Zapater JM, Alonso-Blanco C. (2008) Natural genetic variation of Arabidopsis thaliana is geographically structured in the Iberian peninsula. Genetics 180: 1009–1021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Platt A, Horton M, Huang YS, Li Y, Anastasio AE, Mulyati NW, Agren J, Bossdorf O, Byers D, Donohue K, et al. (2010) The scale of population structure in Arabidopsis thaliana. PLoS Genet 6: e1000843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. (2000) Inference of population structure using multilocus genotype data. Genetics 155: 945–959 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rangel TF, Diniz-Filho JAF, Bini LM. (2010) SAM: a comprehensive application for spatial analysis in macroecology. Ecography 33: 46–50 [Google Scholar]
- Rosenberg MS, Anderson CD. (2011) PASSaGE: Pattern Analysis, Spatial Statistics and Geographic Exegesis. Version 2. Methods Ecol Evol 2: 229–232 [Google Scholar]
- Rosenberg NA, Pritchard JK, Weber JL, Cann HM, Kidd KK, Zhivotovsky LA, Feldman MW. (2002) Genetic structure of human populations. Science 298: 2381–2385 [DOI] [PubMed] [Google Scholar]
- Samis KE, Heath KD, Stinchcombe JR. (2008) Discordant longitudinal clines in flowering time and phytochrome C in Arabidopsis thaliana. Evolution 62: 2971–2983 [DOI] [PubMed] [Google Scholar]
- Schlenker W, Roberts MJ. (2009) Nonlinear temperature effects indicate severe damages to U.S. crop yields under climate change. Proc Natl Acad Sci USA 106: 15594–15598 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz C, Balasubramanian S, Warthmann N, Michael TP, Lempe J, Sureshkumar S, Kobayashi Y, Maloof JN, Borevitz JO, Chory J, et al. (2009) Cis-regulatory changes at FLOWERING LOCUS T mediate natural variation in flowering responses of Arabidopsis thaliana. Genetics 183: 723–732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semenov MA, Halford NG. (2009) Identifying target traits and molecular mechanisms for wheat breeding under a changing climate. J Exp Bot 60: 2791–2804 [DOI] [PubMed] [Google Scholar]
- Shindo C, Aranzana MJ, Lister C, Baxter C, Nicholls C, Nordborg M, Dean C. (2005) Role of FRIGIDA and FLOWERING LOCUS C in determining variation in flowering time of Arabidopsis. Plant Physiol 138: 1163–1173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shindo C, Lister C, Crevillen P, Nordborg M, Dean C. (2006) Variation in the epigenetic silencing of FLC contributes to natural variation in Arabidopsis vernalization response. Genes Dev 20: 3079–3083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokal RR, Oden NL. (1978) Spatial autocorrelation in biology. 1. Methodology. Biol J Linn Soc Lond 10: 199–228 [Google Scholar]
- Stebbins GL. (1950) Variation and Evolution in Plants. Columbia University Press, New York [Google Scholar]
- Stinchcombe JR, Caicedo AL, Hopkins R, Mays C, Boyd EW, Purugganan MD, Schmitt J. (2005) Vernalization sensitivity in Arabidopsis thaliana (Brassicaceae): the effects of latitude and FLC variation. Am J Bot 92: 1701–1707 [DOI] [PubMed] [Google Scholar]
- Stinchcombe JR, Weinig C, Ungerer M, Olsen KM, Mays C, Halldorsdottir SS, Purugganan MD, Schmitt J. (2004) A latitudinal cline in flowering time in Arabidopsis thaliana modulated by the flowering time gene FRIGIDA. Proc Natl Acad Sci USA 101: 4712–4717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toomajian C, Hu TT, Aranzana MJ, Lister C, Tang C, Zheng H, Zhao K, Calabrese P, Dean C, Nordborg M. (2006) A nonparametric test reveals selection for rapid flowering in the Arabidopsis genome. PLoS Biol 4: e137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilczek AM, Burghardt LT, Cobb AR, Cooper MD, Welch SM, Schmitt J. (2010) Genetic and physiological bases for phenological responses to current and predicted climates. Philos Trans R Soc Lond B Biol Sci 365: 3129–3147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue W, Xing Y, Weng X, Zhao Y, Tang W, Wang L, Zhou H, Yu S, Xu C, Li X, et al. (2008) Natural variation in Ghd7 is an important regulator of heading date and yield potential in rice. Nat Genet 40: 761–767 [DOI] [PubMed] [Google Scholar]
- Yu J, Pressoir G, Briggs WH, Vroh Bi I, Yamasaki M, Doebley JF, McMullen MD, Gaut BS, Nielsen DM, Holland JB, et al. (2006) A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet 38: 203–208 [DOI] [PubMed] [Google Scholar]
- Zhao K, Aranzana MJ, Kim S, Lister C, Shindo C, Tang C, Toomajian C, Zheng H, Dean C, Marjoram P, et al. (2007) An Arabidopsis example of association mapping in structured samples. PLoS Genet 3: e4 [DOI] [PMC free article] [PubMed] [Google Scholar]