A power law for cells

Abstract

Darwin observed that multiple, lowly organized, rudimentary, or exaggerated structures show increased relative variability. However, the cellular basis for these laws has never been investigated. Some animals, such as the nematode Caenorhabditis elegans, are famous for having organs that possess the same number of cells in all individuals, a property known as eutely. But for most multicellular creatures, the extent of cell number variability is unknown. Here we estimate variability in organ cell number for a variety of animals, plants, slime moulds, and volvocine algae. We find that the mean and variance in cell number obey a power law with an exponent of 2, comparable to Taylor's law in ecological processes. Relative cell number variability, as measured by the coefficient of variation, differs widely across taxa and tissues, but is generally independent of mean cell number among homologous tissues of closely related species. We show that the power law for cell number variability can be explained by stochastic branching process models based on the properties of cell lineages. We also identify taxa in which the precision of developmental control appears to have evolved. We propose that the scale independence of relative cell number variability is maintained by natural selection.

How variable is organismal development? More than a century of comparative morphology has shown that nearly all morphological structures show at least some intraspecific phenotypic variation (1–7). Darwin identified four repeatable comparative patterns of intraspecific variability in morphological traits (2). First, “when any part or organ is repeated many times in the structure of the same individual (as the vertebrae in snakes, and the stamens in polyandrous flowers) the number is variable: whereas the number of the same part or organ, when it occurs in lesser numbers is constant.” Second, “beings low in the scale of nature are more variable than those that are higher.” Third, “rudimentary parts, …  are apt to be highly variable.” Fourth, “a part developed …  in an extraordinary degree or manner, …  tends to be highly variable.” Although Darwin did not formulate or test these “laws of variation” quantitatively (2), they seem to refer to the relative variability of different structures, rather than to their absolute variability (see Materials and Methods). Over the following century, biologists have accumulated more data on comparative patterns of morphological variability and developed the quantitative tools to describe them. For example, the increased relative variability of secondary sexual characters (a special case of Darwin's fourth law), has attracted great interest (8–10). Furthermore, new patterns of morphological variation have been described. For example, the evolution of extremely small adult body size (miniaturization), a common phenomenon in animals, tends to be associated with increased relative variability (11). However, our understanding of the mechanistic basis of such patterns of variability has not progressed substantially. One reason for this is that developmental biologists traditionally have shown little interest in variation (12). Despite the fact that most properties of individual cells—patterns of gene expression, cell-cycle times, fates, and migrations—show considerable stochasticity (7, 13–18), modern developmental biology is overwhelmingly deterministic (19, 20).

Why is this? We suspect that it is because although the variability of cellular properties is widely recognized, it has not been the subject of systematic study. Little is known about the levels of relative cellular variability shown by different species, organs, or ontogenetic stages. It is generally recognized that some small metazoans, such as the nematode Caenorhabditis elegans, appear to have unusually invariant cell lineages and hence adult cell numbers—a property known as eutely (21–24). But recent studies suggest that most nematodes show considerable amounts of variation for cell number in at least some somatic tissues (25–27). More generally, if we view cells as “multiple parts” of an organ, does their relative variability scale with their number as Darwin's first law of variation suggests? To address these questions we begin by surveying the literature for estimates of relative cell number variability and investigate whether this trait is related to organ size and varies among particular taxa. Finally, we test whether the observed patterns of cell number variability can be explained by simple stochastic models of cell lineages based on the theory of branching processes.

Materials and Methods

Cell Number Variability.

We collected 2,177 estimates of the mean (M) and variance (V) in cell number from 138 published studies. Several estimates were not independent as they were obtained on the same sample. A total of 178 species are included in this survey but the majority of estimates come from only four species: fruitfly (25%), mouse (11%), rat (13%), and human (11%).

Darwin admitted that it was difficult to compare “relative degrees of variability” (2). Here we use the coefficient of variation, CV = 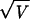/M, which standardizes the variance with respect to the mean (7, 28), as a measure of relative variability. For example, if three individuals of one species show 10, 12, and 14 cells in a given organ, and three individuals of a bigger species show 100, 120, and 140 cells in the same organ, then the first species has a lower absolute variability than the second (V = 4 and 400, respectively), but both species have the same relative cell number variability (CV = 16.7%).

The data were summarized by calculating the median CV of different estimates for each species and organ. The summarized data and references for this survey are given in Table 1, which is published as supplemental data on the PNAS web site, www.pnas.org. Unless otherwise stated, all ranges of CVs presented in the text are interquartile ranges.

Power Law.

We tested whether M and V in cell number followed a power law relationship of the form:

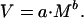1

In practice we used the logarithmic form of this equation, which is linear:

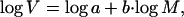2

where b is the slope and log a is the intercept.

For each of 16 data sets extracted from 12 published studies we estimated M and V from untransformed cell number data, and then applied a log₁₀ transformation to these estimates. Other data sets were extracted from the literature and analyzed, but we excluded data sets that yielded estimates of b with a 95% confidence interval greater than 4 (see below). We estimated the exponent b of the power law by using the structural relationship model (29):

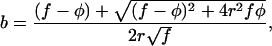where r is the product-moment correlation between log M and log V, f the ratio of the sample variances in log V and log M, and φ the ratio of the error variances in log V and log M. Linear regression assumes φ = ∞ and, therefore, would tend to underestimate the true value of b because estimates of log M and log V are both subject to error. For each data set, r and f were calculated from the observations weighted by the degrees of freedom of each V estimate, and φ was calculated from 10⁵ simulated samples from a normal distribution with CV equal to the geometric mean of the CVs of the samples in the data set. The estimates of φ ranged from 4 to 2,109 in different data sets. The 95% confidence interval of b was estimated by bootstrapping 10⁴ data sets and calculating b by using the original value of φ. For the different data sets the coefficient of determination (r²) of the structural relationship model varied between 0.32 and 0.99 (median = 0.76). Adding a quadratic term to a regression model of the form of Eq. 2 produced nonsignificant reductions of the residual sum of squares in all data sets (P > 0.05).

Results

Cell Number Variability Follows a Power Law.

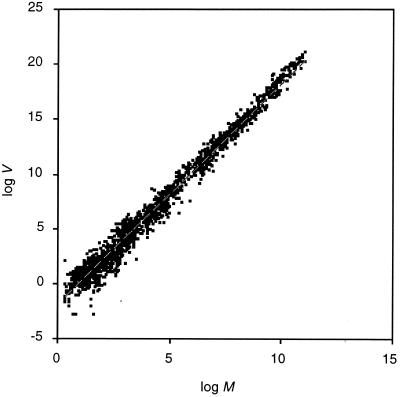
Fig. 1 shows the relationship between log M and log V for 2,122 estimates from the literature (the 51 estimates with V = 0 could not be included). V in cell number increases with the M and the relationship follows a power law of the form of Eq. 1. The least-squares estimates of the coefficients, using a regression model of the form of Eq. 2 are b = 2.03 and a = 0.0119 (this model explains 98.2% of the variance in log V; we did not attempt to test the significance of the relationship because several estimates were not independent).

Figure 1.

Power law relationship between M and V in cell number for 2,126 estimates in the literature. The dashed line shows the best fitting discrete cell lineage model with P₀ = P₁ = P₃ = 0.612% for 1–37 generations. This model explains 98.2% of the variance in log V.

Do cell numbers follow Darwin's first law? If b = 2, then relative variability in cell number, as measured by the CV, is independent of M:

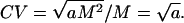Values of b higher or lower than 2 would imply a positive or negative relationship between CV and M, respectively. The exponent of the power law is slightly greater than 2, as predicted by Darwin's first law. However, the linear relationship between CV and log M explains only 0.2% of the variance in cell number CV.

Relative Cell Number Variability Differs Among Taxa and Tissues.

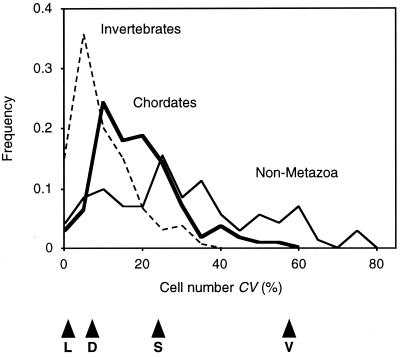
Does the above pattern mean that the cell number CV is constant among higher taxa over 12 orders of magnitude? Our data suggests that this is not the case (Fig. 2). Simple organisms such as slime molds (CV interquartile range: 20–35%, n = 9) and volvocine algae (23–50%, n = 45) show higher relative variability than metazoans (6.6–19%, n = 246) or angiosperms (4.0–18%, n = 18), which seems to support Darwin's second law. On the other hand, chordates are arguably more complex than invertebrates, yet the former show higher levels of relative cell number variability (11–24%, n = 112) than the latter (4.5–13%, n = 134).

Figure 2.

Frequency distribution of relative cell number variability in different multicellular groups. The 318 estimates were grouped into: nonmetazoa (plain line; median = 26.1%, n = 72), invertebrates (dashed line; median = 7.5%, n = 134), and chordates (bold line; median = 17.3%, n = 112). Arrowheads indicate median CVs for some organs: (L) leech H. medicinalis segmental ganglia; (D) fruit fly D. melanogaster wing; (S) slime mould Dictyostelium discoideum fruiting body; (V) volvocine alga V. carteri soma.

The above generalizations must be treated with caution because there is considerable variation in CV among tissues within these broad groupings and our sampling of tissues is uneven. For example, Drosophila larvae show lower relative cell number variability in the eye, antenna, wing, haltere, and leg imaginal discs (5.9–13%, n = 40) than in abdominal histoblasts (9.4–20%, n = 266) (30, 31). Even so, the pattern of relative cell number variability of chordates versus other metazoans is unchanged if we consider only the data on nervous systems (chordates, 10–23%, n = 62; other metazoa, 2.2–15%, n = 30).

The Exponent of the Power Law Is Conserved Among Closely Related Species.

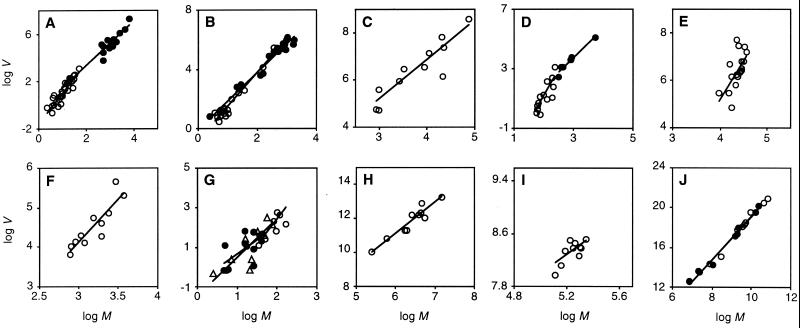
How did the power law in cell number variability arise? Organ size has evolved repeatedly in multicellular creatures, and larger organs will, in general, have more cells and more complex cell lineages than smaller ones (26, 27, 32–37). Do particular taxa have characteristic levels of cell number variation independent of organ size? Fig. 3 shows the relationship between M and V for several homologous tissues among 16 groups of closely related species (or strains of the same species) across a wide range of taxa (comprising ≈10% of the data in Fig. 1). We fitted a structural relationship of the form of Eq. 2 to each of the 16 data sets and the mean of the distribution of the resulting estimates of b does not differ significantly from 2 (mean b and 95% confidence interval: 2.21 ± 0.32; t test, P = 0.2). This result shows that, in general, cell number CVs are independent of organ size among homologous tissues of closely related species, contrary to the expectation of Darwin's first law. This pattern is evident from a closer examination of the data. The volvocine algae Pleodorina californica, Volvox obversus, and Volvox barberi all show CV = 60% for somatic cell number despite showing very different M (21, 867, and 6,884, respectively) (35).

Figure 3.

Power law relationship between M and V in cell number of a given tissue among strains or species. The axes are displayed such that the range of log M is half that of log V. A linear structural relationship model of the form of Eq. 2 was fitted to each data set and is represented by a line. (A) Volvocine algae (35): germ (○), structural relationship exponent b = 2.62 (95% bootstrap CI: 2.13–3.10), geometric mean of the CV = 28%; soma (●), b = 1.89 (1.68–2.48), CV = 37%. (B) Strains of V. carteri (75): germ (○), b = 2.30 (1.97–2.64), CV = 52%; soma (●), b = 1.93 (1.73–2.34), CV = 74%. (C) Slime mold fruiting body (76): b = 1.68 (1.05–2.10), CV = 29%. (D) Epidermis of free living nematodes (25, 26): terrestrial (○), b = 3.65 (1.94–4.89), CV = 3.4%; marine (●), b = 1.96 (1.73–2.95), CV = 7.0%. (E) Hawaiian Drosophila wings (36): b = 3.36 (1.93–5.82), CV = 6.6%. (F) Drosophila sperm (77): b = 2.19 (1.39–2.90), CV = 12%. (G) Insect γ-aminobutyric acid-like immunoreactive neurons (78): T2 segment “K” cluster (○), b = 2.55 (1.08–3.65), CV = 16%; T2 segment “X” cluster (●), b = 1.43 (−0.14–2.50), CV = 19%; T3 segment “X” cluster (▴), b = 1.97 (1.07–3.80), CV = 17%. (H) Mammalian cerebellum Purkinje cells (79): b = 1.83 (1.59–2.42), CV = 31%. (I) Mouse retinal ganglion (46): b = 1.83 (1.59–2.42), CV = 31%. (J) Mammalian heart (80): connective tissue (○), b = 2.23 (2.10–2.52), CV = 28%; muscle (●), b = 2.21 (2.08–2.50), CV = 26%.

Two tissues do not show this scale independence of relative cell number variability: germ of volvocine algae and mammalian heart, both of which show exponents significantly greater than 2 (Fig. 3 A and J). In addition, the epidermis of terrestrial nematodes (26) shows an exponent not significantly greater than 2, but this estimate is a significant outlier in our survey (Dixon's test, P < 0.05). In all three tissues there is a positive correlation between CV and M, as suggested by Darwin's first law.

There Is No Clear Distinction Between Eutelic and Noneutelic Taxa.

We find that the range of relative cell number variability shown by multicellular organs is large, ranging between 0 and 75%. Organs usually considered to be eutelic have CVs under 5%. These include the epidermis of the nematode C. elegans (2%), the yolk and gastric glands of the rotifer Hydatina senta (median 4.5%), and the segmental ganglia of the leech Hirudo medicinalis (1%) (26, 38–40). More surprisingly, the primary roots of Arabidopsis thaliana also show relatively constant cell numbers (median of four cell types 2%) (41). However, there is no clear separation between eutelic and noneutelic taxa. Our data set includes estimates for the epidermis of 20 species of free-living nematodes; of these, nine have CVs between 5% and 15%, implying levels of relative cellular variability far higher than those of classically eutelic organisms (25, 26, 42), and comparable to those of Drosophila melanogaster wings (CV interquartile range: 6.3–7.5%, n = 120 estimates) and mouse retinal ganglia (5.5–8.8%, n = 73) (43–48). Finally, we note that the larval tissues of the sea urchin Clypeaster japonicus (6.6–13%, n = 9) are no more eutelic than Drosophila wings (49). There is, then, no evidence that species with “type I embryos” are especially eutelic (50).

Cell Lineage Models

The observation that the M and V in cell number are related by a power law is analogous to a well established empirical relationship in ecology: Taylor's law for the M and V of population abundance, where values of b typically vary between 1 and 2 (51–55). Perhaps this is not surprising because, after all, we are dealing with “populations” of cells. Anderson and others (54, 55) have shown that Taylor's power law can arise from stochasticity in demographic processes that determine population size, such as birth, death, and migration. Can a similar explanation account for the power law for cell numbers? We decided to explore this idea by developing a general model of cell number variability.

Discrete Generation Times.

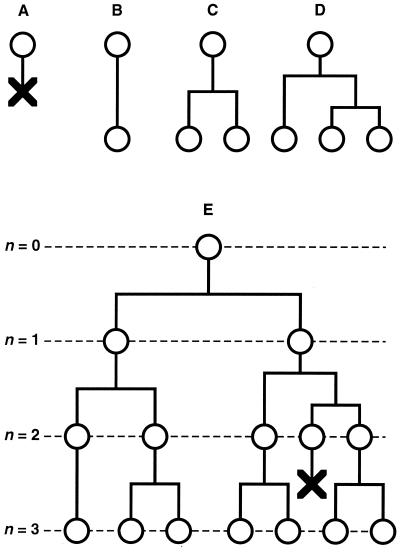
A cell lineage with one cell type can be described by a discrete-time branching process—the Galton-Watson process (56). Imagine a cell lineage starting from a single cell. At the end of a fixed generation time, the cell produces two daughter cells and these undergo another generation, and so on. In such a process, after n generations there would be 2ⁿ cells in the population. Now suppose that for a given cell the canonical fate of dividing during the fixed generation time occurs with probability P₂ < 1. By chance, the cell may die with probability P₀ (producing zero descendants), or may survive but fail to divide with probability P₁ (one descendant), or may divide and one of its daughters may divide as well with probability P₃ (three descendants), and so on (Fig. 4). For a given generation, this process is described by the following probability generating function (pgf):

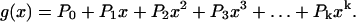3

The mean and variance in the number of offspring from a single cell after one fixed generation time are given by the following equations:

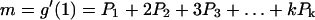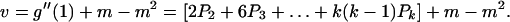If m > 1 and all of the daughter cells independently follow the same offspring number pgf as the initial cell, then the cell population grows exponentially and, after n generations, the M and V in cell number are given by (56):

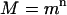4

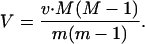5

Figure 4.

Cell lineage model. (A–D) Main types of cellular behavior incorporated in the cell lineage model, illustrated for the descendants of one cell during a single generation. (A) The cell dies. (B) The cell survives but does not divide. (C) The cell divides. (D) The cell divides and one of its daughters divides. (E) Example of an hypothetical cell lineage with three cell generations displaying all of the cellular behaviors in the model.

Variable Generation Times.

If we incorporate variable generation times into the above model we obtain an age-dependent branching process (56). If every cell independently undergoes a generation time of random duration according to a given probability distribution with mean μ and variance ϖ, after which it will have produced a number of daughters according to the pgf given in Eq. 3 (with mean m > 1 and variance v given above), then the cell population grows exponentially. As t becomes large, the age structure of the cell population stabilizes and the M and V in cell number are given by (13, 57):

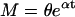6

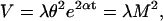7

where the constants α, θ, and λ can be approximated by (13):

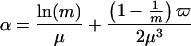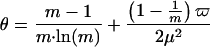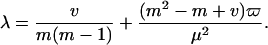Cell Lineage Stochasticity Can Predict the Power Law.

Eqs. 4 and 5 (or 6 and 7) imply that, as n becomes large (or as t increases), the cell number CV will tend to a constant value and, therefore, the relationship between V and M will tend to be described by a power law of the form of Eq. 1 with b = 2 and a = CV². Note that this expectation is true whatever the precise values of P₀, P₁, P₂., . . P_k provided these are constant among the species being compared.

Can our models provide any insights on the levels of cell lineage stochasticity expected to occur in real organisms? We can use Eqs. 3–5 for the discrete-time cell lineage model to predict the observed values of M and V. If we constrain the pgf to have P₀ = P₁ = P₃ = (1 − P₂)/3 then the best fit would be for P₀ = P₁ = P₃ = 0.612%, which predicts a power law of the form of Eq. 1 with b = 2.01 and a = 0.0150 (Fig. 1). This finding suggests that the level of relative cell number variability observed in typical multicellular organisms (CV = 12%), can be explained by relatively low levels of cell lineage stochasticity (≈2% deviations from a canonical lineage), which suggests that multicellular development is remarkably well regulated. This result depends on two assumptions on how cell populations grow. First, cell populations are expected to undergo fixed numbers of generations. Second, cells are supposed to behave independently of each other. In other words, our models assume that final cell number is regulated in a strictly density-independent manner. It is likely that real cell populations violate both assumptions to different extents. If the first assumption is violated, then we will tend to overestimate the degree of cell lineage stochasticity. For example, simple nonmetazoa like volvocine algae show variation in the number of cell generations (V. Koufopanou, personal communication), and this variation is likely to contribute substantially to their high relative cell number variability. If, on the other hand, the second assumption is violated, then we will tend to underestimate the degree of cell lineage stochasticity. For example, during development of the nervous system cell survival is often contingent on competition for neurotropic factors produced by target cells (58, 59).

Discussion

Our models, simple though they are, accurately and parsimoniously predict the power law observed for a given tissue within a closely related group of species or strains (Fig. 3). But we have identified three taxa of related species—volvocine algae, nematodes, and mammals—which show values of b higher than 2. These deviations from the power law suggest that larger species tend to show greater CVs, in agreement with Darwin's first law of variation. For example, where muscle cells of mouse and rat hearts show CVs of ≈20%, ox and horse hearts, which have ≈3 orders of magnitude more muscle cells, show CVs of 31% and 47%, respectively (Fig. 3J). Similarly, where the epidermis of the nematodes C. elegans and Panagrolaimus rigidus have CVs of 2%, the larger nematodes Rhabditoides regina and Panagrellus redivivus show CVs of 7% and 14%, respectively (Fig. 3D).

Why might homologous tissues in related species differ in CV? The amount of variation in cell number in a population of adult creatures depends on three factors (27). First, the form of the canonical cell lineage, that is, the number, types, and historical relationships of the cells that make up a tissue (the pgf in our model). Second, the amount of stochastic variation in cellular behavior generated by cell-autonomous mechanisms (the probabilities P₀, P₁, and P₃ in our model). Third, the mode and extent of cell number regulation. We propose that taxa that deviate from the power law relation with an exponent of 2 differ in one or more of these factors. Our data do not permit us to distinguish between competing explanations for divergent CVs, but the recent finding that expression of regulatory switch molecules in eukaryote cells is frequently stochastic (17), and can result in random cell fate assignments (18), suggests one way by which evolutionary changes in the precision of developmental control might be explored.

Is the widespread occurrence of the power law for cell number variability caused by adaptation or developmental constraint? Although power laws with exponents of 2 tend to obtain within any given tissue and taxon, different tissues and taxa clearly vary in cell number CV, suggesting the existence of genetic variation for relative cell number variability. This variation notwithstanding, perhaps the best reason for believing that cell number CVs generally are maintained by selection is their very constancy. Although power law exponents higher or lower than 2 may occasionally occur, they cannot exist over species that differ in cell number by several orders of magnitude. To see this consider the human parasitic nematode Ascaris lumbricoides. This worm is ≈3,000 larger by area than C. elegans; if we assume that it has 3,000 times as many epidermal cells and extrapolate its CV from the high exponent of terrestrial nematode epidermis (b = 3.65), we obtain a CV of over 1,000%, which would imply that epidermal cell numbers could vary over several orders of magnitude within the species. Because variation in cell number is the principal determinant of variation in overall organ size (32–36, 48, 60), and the masses of most organs and tissues typically scale linearly with body mass within species (61, 62), drastic changes in the size of any structure will upset the proper balance of parts and functions and result in unfit organisms. So even if high exponents are occasionally found, they cannot exist across species that differ in cell number by several orders of magnitude without leading to species with increased cell number having absurdly high CVs. Conversely, exponents lower than 2 will, over several orders of magnitude in cell number, lead to species with increased cell number having CVs far lower than are seen in even the most eutelic creatures. We conclude that, as organisms evolve in body size and cell number, CVs are maintained by selection within a very narrow range, thus giving rise to the scale independence of relative cell number variability.

Here the similarity between the power laws for populations of individuals and cell number in complex organisms breaks down. It is not clear that the relative variability in the size of populations of individuals is a target of group selection. Also, population size tends to show much greater CVs than cell number, typically over 100% (51, 53). This could explain the relatively high cell number variability shown by the simplest multicellular organisms. Because volvocine algae and slime molds are intermediate in organization between colonies of cells and individuals, they may not be subject to the same selective pressures that act on more complex organisms.

Our approach for analyzing cell number variability should be applicable to other developmental processes as well. Many serially homologous organs such as vertebral number in fish, and segment number in centipedes show considerable variation in number, both within and among species (3, 63–67). Intraspecific variation in the number of such structures also may obey power laws because, like cells, they have their origin in a branching process, albeit of tissue blocks. Somite formation in vertebrates, and segmentation in short-germ arthropods, for example, are the result of asymmetrical branching processes in which somites and segments bud off from a band of undivided mesoderm (68, 69). Because branching tissues are, themselves, made up of branching cell lineages, any theory considering the variability of organ primordia will need to consider the influence of variation in the number of constituent cells. One possible basis for such a theory comes from the observation that the final cell number achieved by a growing organ can be viewed as the result of mechanisms that stochastically generate variability in cell fate and those which selectively restrict such variation (58, 70). Growing organs may, then, resemble other self-organizing systems whose dynamics are based on variation-selection processes (71–73). An adequate account of the origins of stochastic variation in development may, therefore, need to consider the production and restriction of variation at several levels in development, analogous to hierarchical selection in evolution (74).

Abbreviations

CV

coefficient of variation

M

mean

V

variance

pgf

probability generating function