Abstract
Structural connectivity between cortical regions of the human brain can be characterized non-invasively with diffusion tensor imaging (DTI) based fiber tractography. In this paper, a novel fiber tractography technique, globally optimized fiber tracking and hierarchical fiber clustering, is presented. The proposed technique uses k-means clustering in conjunction with modified Hubert statistic to partition fiber pathways, which are evaluated with simultaneous consideration of consistency with underlying DTI data and smoothness of fiber courses in the sense of global optimality, into individual anatomically coherent fiber bundles. In each resulting bundle, fibers are sampled, perturbed and clustered iteratively to approach the optimal solution. The global optimality allows the proposed technique to resist local image artifacts, and to possess inherent capabilities of handling complex fiber structures and tracking fibers between gray matter regions. The embedded hierarchical clustering allows multiple fiber bundles between a pair of seed regions to be naturally reconstructed and partitioned. The integration of globally optimized tracking and hierarchical clustering greatly benefits applications of DTI based fiber tractography to clinical studies, particularly to studies of structure-function relations of the complex neural network of the human. Experiments with synthetic and in vivo human DTI data have demonstrated the effectiveness of the proposed technique in tracking complex fiber structures, thus proving its significant advantages over traditionally used streamline fiber tractography.
Keywords: Diffusion Tensor Imaging, Fiber Tracking, Fiber Clustering, Global Optimization
I. Introduction
Diffusion tensor magnetic resonance imaging (DT-MRI or DTI) is a unique technique that measures diffusive motion of water molecules in living tissue [1]. Since water molecules in the human brain diffuse faster along the major axis of fiber tracts than across their membranes, characterizing water diffusion in each voxel provides a certain indication of the local orientation of the neural fibers in that voxel. The directional dependence of water diffusion and hence the local tissue orientation in each voxel can be represented by a matrix, called a diffusion tensor, diagonalization of which yields three pairs of eigenvalues-eigenvectors that give the diffusivity along three principle directions.
The notion that diffusion tensors contain the information of local tissue orientation can be exploited to infer neuronal fiber structures in vivo with DTI. In fact, this idea has been extensively pursued during the past decade, leading to abundant fiber tractography algorithms in the literature that reconstruct neuronal fiber pathways based on integrating local orientation information [2–9]. Nevertheless, reliable reconstruction of neural fibers with DTI, particularly with the goal of routine laboratory use, remains an open problem. The commonly used streamline methods, which “grow” fibers from pre-defined seed points sequentially to generate entire fiber pathways, suffer from several major limitations, most notably cumulative errors along the tracking pathways and ambiguities in defining the fiber orientation at fiber crossings with the tensor model. Although probabilistic streamline tracking may potentially be able to address these problems, in essence it still tracks fibers step-wise without considerations of global optimality of the fiber pathways reconstructed.
To ameliorate the problems associated with streamline-like methods, efforts have been made to develop tracking techniques based on the concept of global optimization, so that the effects of local imaging artifacts can be minimized. For instance, Tuch et al proposed a simulated annealing method to find most probable pathways between cortical regions [10]. Jbabdi et al developed a global Bayesian framework for simultaneous inference of structural and functional connectivity, with model parameters optimized by using a Markov Chain Monte Carlo algorithm [11]. There are also a variety of other globally optimized tracking techniques that have been proposed more recently, which include graph search [12], shortest path finding [13], Gibbs and Bayesian tracking [14], spin glass modeling [15], and stochastic optimization of structural connectivity and microstructural properties with differential evolution [16].
It should also be noted that, although instrumental to visualization, most of the fiber tractography techniques alone offer little anatomical interpretations or quantitative characterizations of connectivity. Thus, reconstructed fiber pathways are typically further bundled to allow for meaningful anatomical interpretations and/or quantifications of structural connectivity. Toward this end, a plethora of manual [17, 18], automated [19–21] and knowledge guided [22–24] bundling techniques have been proposed during the past decade, to further classify fiber pathways reconstructed by tractgraphy.
Motivated by the needs for fiber tracking that is robust to imaging artifacts and fiber bundling that divides fibers into distinct anatomical bundles, we have proposed a novel technique that integrates globally optimized fiber tracking with hierarchical fiber clustering. Specific features of the proposed framework include:
Given a pair of regions of interests (ROIs), fiber tracts that connect them are reconstructed and clustered into anatomically distinct bundles simultaneously.
Reconstructed fiber pathways are globally optimal in the sense that fiber tracts are consistent with the direction map provided by DTI and the fiber tracts are reasonably smooth.
A hierarchical clustering process successively divides fiber pathways between a pair of ROIs into multiple natural anatomical bundles.
Except for the ROIs that are designated a priori, the proposed framework works in a fully automated fashion. It yields globally optimal fiber pathways that are immune to the effects of local imaging artifacts, and simultaneously organizes the fibers into distinct anatomical bundles to facilitate further interpretations and characterizations. To the best of our knowledge, this is the first technique that solves the problems of fiber tracking and bundling with a single “one shot” approach.
The remainder of the paper is organized as follows. First, the framework of the proposed technique is described in detail in Section II. Then tracking experiments using synthetic and in vivo human DTI data are presented in Section III, with experimental results demonstrating the capabilities and advantages of the technique proposed. Finally, main contributions of this work are summarized and relevant technical issues are discussed in Section IV.
II. Methods
Typical practice of fiber tracking involves finding connection pathways that connect certain designated ROIs. Very often we are given a pair (or more) of ROIs, and are expected to find plausible fiber pathways connecting them. This scenario in fact bears particular relevance to studies of the complex neural network of the human brain, in which certain ROIs are determined a priori from other sources such as anatomical or functional MRI.
Tracking fiber pathways that connect designated ROIs can be treated as a path finding problem. To approach this problem, we propose a framework that takes a volume of DTI data and designated ROIs as inputs and generates optimal fiber bundles connecting the ROIs. The framework involves multiple steps including random fiber generation, selection, iterative fiber clustering, and sampling and perturbation, which are graphically illustrated in Fig. 1. First we parametrically represent the fibers connecting a pair of ROIs (Fig. 1b). By evaluating the consistency of the fibers with DTI data and the smoothness of their courses, a subset of best candidate fibers are selected (Fig. 1c). The subset is then divided into two distinct bundles by using fiber clustering (Fig. 1d). After statistical evaluation of divisibility, each of the resulting bundles is further divided into two until no divisions should be undertaken (Fig. 1f). Finally, each resulting bundle of fibers are sampled and randomly perturbed repeatedly until convergence, yielding globally optimal fiber bundles that connect the given ROIs (Fig. 1g).
Figure 1.
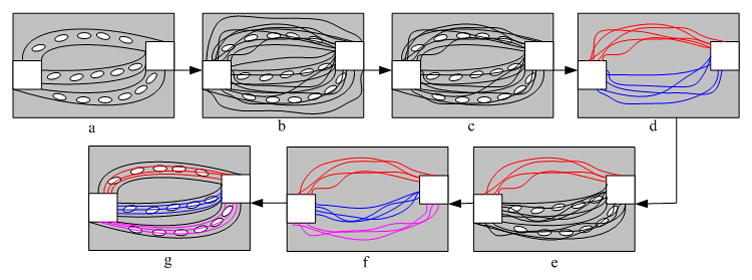
Flowchart of the proposed framework. The white squares denote the ROIs, the gray bundles contain designated fiber pathways, and the white ellipses denote diffusion tensors along the bundle. Fibers clustered into different bundles are shown in different colors.
A. Parametric representation of fibers
A fiber pathway between a pair of ROIs can be regarded as a curve f in the 3-D space, and represented as continuously-valued Fourier series, i.e.,
| (1) |
In the equation above, the superscript d denotes the x, y, or z direction, t is the index to the point along the curve f, n is the order of Fourier series, an and bn are respectively coefficients for the cosine and sine components, and N is the maximum order of Fourier series for approximation with reasonable accuracy (N =10 in this work).
According to Eq. 1, any fiber curve can be represented by 6N Fourier coefficients (N coefficients for an and bn in each of the three directions respectively) since the Fourier series are complete orthonormal basis. The 6N coefficients can be used to compose fiber pathways that connect the ROI pair. Solutions to these coefficients are found through an optimization procedure that will be described in detail below. Prior to the optimization, random values of a reasonable range are initially assigned to them. Note that in this work, the end points of the curve are not initialized entirely randomly, but are confined within the specific ROIs given.
B. Evaluation of fiber pathways
Randomly initialized fiber pathways are selected on the basis of objective criteria: they should best fit the DTI field, and should be reasonably smooth along the fiber. Fiber pathways simultaneously possessing these properties (with certain trade-offs) are regarded as globally optimal.
Mathematically, globally optimal fiber pathways may be constructed with the framework of classical Bayesian theory [25]. Let T denote a DTI field and C denote the set of 3D curves that cover all possible fiber pathways connecting a pair of designated ROIs. According to the Bayes decision rule, the fiber curve with a maximum probability is an optimal curve Copt:
| (2) |
The term p(C) is a prior probability of curve C, i.e., the probability of the existence of curve C without any information from the measurement data; the term p(T|C) is a conditional probability of T given a curve C. The term p(C|T) is a conditional probability of solution C given the tensor field T; maximizing this term amounts to maximizing the product of p(C) and p(T|C) since p(T) is independent of C.
In our design, p(C) and p(T|C) are modeled to find the optimal solution. The models take into account the criteria that curves are reasonably smooth and consistent with the tensor field. Firstly, let unit vector vt denote the local tangential direction at the tth uniformly sampled point of a curve C, and assume the field of such vectors to be a Markovian random field (MRF). According to the MRF theory, vt is a random realization of the vector field in the neighborhood of t. Therefore, p(C) observes a Gibbs distribution [26]:
| (3) |
where Z1 is a normalization constant. With the only consideration of the immediate preceding point along the curve, P(vt) can be simply defined as:
| (4) |
The prior probability defined as such gives higher probability p(C) to the curves with lower curvature, thus constraining the curve to be smooth.
Secondly, we assume that the tensor measurement at position t depends only on the local fascicle direction vt, and thus may express the conditional probability p(T|C) as another Gibbs distribution:
| (5) |
where Z2 is a normalization constant.
To constrain the local fascicle direction vt to be consistent with the tensor field, we model the probability p(Tt|vt) such that it increases with the angular difference between the local fiber direction vt and the major eigenvector of the local diffusion tensor et:
| (6) |
Note that using the angular difference between vt and et to model the conditional probability is a common choice. It is reasonable if the angular difference is solely caused by random noise. We recognize that in degenerative cases such as fiber crossing or branching, this model is inadequate. This limitation, however, may be overcome by using high angular resolution diffusion imaging (HARDi) [27–30] and extending the above model to accommodate fiber orientation density distributions derived from HARDi.
Combining the prior probability model in Eq. 3 and the conditional probability model in Eq. 5 gives an expression for p(C| T), which turns out to be a new Gibbs distribution:
| (7) |
where Z3 = Z1 • Z2. The parameter α will be explained shortly below.
With the Gibbs distribution above, we can reach an optimal solution by minimizing the following cost function:
| (8) |
The first term in the above cost function constrains the curve to be smooth, and the second term maintains a consistency between the local fiber direction and the tensor dominant direction. The weighting parameter α (chosen to be between 0.1 and 10 in this work) regulates a trade-off between the smoothness of the fiber and consistency with the data.
C. Fiber bundle clustering
From a set of candidate solutions to the fiber pathways, a subset of fibers are selected according to the cost function in Eq. 8. This subset is successively clustered into anatomically distinct fiber bundles using the classical k-means clustering algorithm [31]. In each clustering process, the fibers are divided into maximally two bundles based on the modified Hubert (MH) statistic [32]. Each of the resulting bundles is then further divided into two until no divisions should be performed. Details of the k-means clustering and MH statistic are given below.
The k-means clustering is a method that aims to divide n observations into k clusters in which each observation belongs to the cluster with the nearest mean. In this work, fibers are clustered into two distinct bundles in each iteration using the mean Euclidean distance δ between a pair of fibers as follows:
| (9) |
where p and q denote a pair of fibers, m is the index to the point along the fiber and M is the number of sampled points (M=50 in this work).
The k-means clustering itself is also an iterative process. In our implementation, the mean Euclidean distances between all fiber pairs in a given set are first computed, with the pair of fibers having the largest mean Euclidean distance chosen to be the prototypes (i.e., cluster centers). All other fibers are then grouped into either of the two clusters on the basis of the mean Euclidean distance to the prototypes. Finally, new prototypes are calculated by point-wise averaging the coordinates of all the fibers in each group. This process is repeated until clustering convergence (Changes in fiber grouping <5% in this work)
After the clustering process, the modified Hubert statistic, which is a measure of correlation between the matrix of inter-cluster distances and the distances recovered from the clustering solution, is used to evaluate the validity of fiber set division. Specifically, let L denote a label function established by the k-means clustering process that maps a set of n fibers to two clusters:
| (10) |
Let x denote a fiber and m denote a cluster prototype, the MH statistic is computed as follows:
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
All the sums above are over the set:
| (16) |
And N = n(n − 1)/2.
The MH measure for the clustering {C1, C2} is:
| (17) |
As pointed out by Dubes [32], if |1 − MH(kmax)| ≥ 0.3, there exists only one cluster in the fiber set. In this situation, fibers will not be divided into two bundles and the clustering process terminates for this set of fibers. Otherwise, the fibers are divided into two bundles and each of them goes through the same clustering process successively, thus achieving hierarchical fiber bundling.
D. Sampling and perturbation of fibers
For each of the fiber bundles obtained from the clustering procedure, or the entire set of fibers if it is not dividable according to the MH statistic, a new set of fibers are generated by using a sampling technique called importance sampling [33]. Specifically, we first compute the probability density function (PDF) of the cost function of all fibers within a bundle, and then sample the fibers such that fibers with higher probability densities are sampled at higher probabilities.
After the importance sampling, the fibers are randomly perturbed by adding small variances to their Fourier coefficients. In this work, the amount of perturbation for each coefficient is at the order of one standard deviation of the coefficients of all the fibers in the bundle. This offers an opportunity to generate new fibers with better cost function values and meanwhile maintains the stability of the solutions.
The importance sampling and random perturbation are iteratively performed. At the end of each iteration, a subset of optimal fibers based on the cost function in Eq. 8 are selected for the next iteration. The iterative process will be terminated when change of the mean cost function value is smaller than 5%, in which circumstance we regard the process to have converged.
III. Tracking Experiments and Results
The algorithm proposed was evaluated with a series of fiber tracking experiments on synthetic as well as in vivo human DTI datasets. Section III-A below presents tracking results from synthetic datasets. We first examine the results from five synthetic phantoms each with a different geometric configuration. Then the capability of the proposed algorithm to reconstruct globally optimal fiber pathways in the presence of complex fiber configurations such as fiber crossing and kissing is demonstrated. Finally one of the synthetic datasets from above is used to statistically evaluate the optimization process and demonstrate the validity of fiber tracking results. Section III-B shows results of fiber tracking by the proposed technique from several real human brain datasets, followed by a comparison of the proposed technique with the “shortest paths” global fiber tracking [13] in terms of in vivo performance. Finally, Section III-C presents computational efficiency of the proposed algorithm.
A. Fiber tracking with synthetic datasets
Assessment of performance on tracking curves
To evaluate the performance of the proposed algorithm to track curves, five tensor fields were synthesized, with each containing a different geometric configuration. Synthetic tensors in these curves were constructed to have a trace of 2.1×10−5 cm2/s and a fractional anisotropy (FA) of 0.8, thus closely mimicking physiological conditions in the human brain. The first one, shown in Fig. 2a, was a sinusoidal curve with two extremas. Each tensor was represented by an ellipsoid whose principal axes were parallel to the three eigenvectors of the tensor and the radii of the ellipsoid along the axes were proportional to their corresponding eigenvalues. Diffusion weighted imaging was simulated along 32 non-collinear directions with a b value of 1000 s/mm2, and the resulting signals were further corrupted with zero mean Gaussian noise at a standard deviation of 0.05. Fig. 2b to 2e contained the following geometrical configurations: two bundles connecting two ROIs, three bundles connecting two ROIs, two bundles connecting three ROIs, and three bundles connecting four ROIs.
Figure 2.
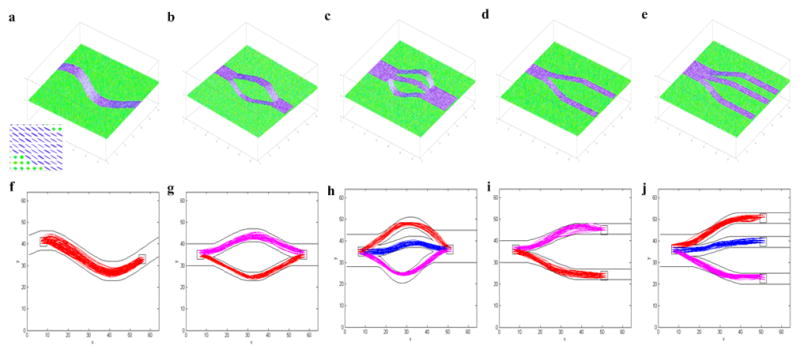
Tests of tracking curves with synthetic tensor data. Upper panel (a–e): synthetic phantoms with different geometric structures. Lower panel (f–j): tracking results. The ROIs for the tracking experiments are denoted in white squares, and fibers clustered into different bundles are shown in different colors. Inset in the first column is an enlarged view of a part of the tensor field.
For each of the synthetic tensor fields, two or more ROIs were defined (denoted as a square in Fig. 2f to 2j), between which “fibers” were tracked using the proposed algorithm. First, a total of 1000 random curves connecting the designated ROIs were generated. Among them, 100 curves with best cost function values were selected, which were subsequently divided into different “fiber” bundles. If there existed only one bundle based on the MH statistic, these curves were sampled using importance sampling and then perturbed to generated 1000 new curves. A subset of 100 best curves were selected from these new curves to repeat the sampling and perturbation processes until the termination criterion was met. On the other hand, if the 100 selected curves could be divided into two bundles, each bundle was then processed individually as above.
The tracking results obtained are shown in Fig. 2f to 2j respectively, in which 100 randomly selected “fibers” were demonstrated in each figure. As can be seen, these “fibers” grossly follow the synthetic curves for all the combinations of different bundles and ROI numbers. Close inspections reveal that the proposed algorithm produces “fibers” that exhibit good convergence along the entire path.
Assessment of tracking performance in the presence of complex fiber configurations
The capability to reconstruct globally optimal fibers in the presence of complex fiber configurations, such as “kissing” and “crossing”, is an inherent feature of the proposed algorithm. This capability was examined with synthetic phantoms containing “fibers” with each of the above structures, as shown in Fig. 3a (“kissing”), 3c (“crossing”) respectively. The parameter settings used were the same as before and ROI pair was denoted by square in Fig. 3b and 3d.
Figure 3.
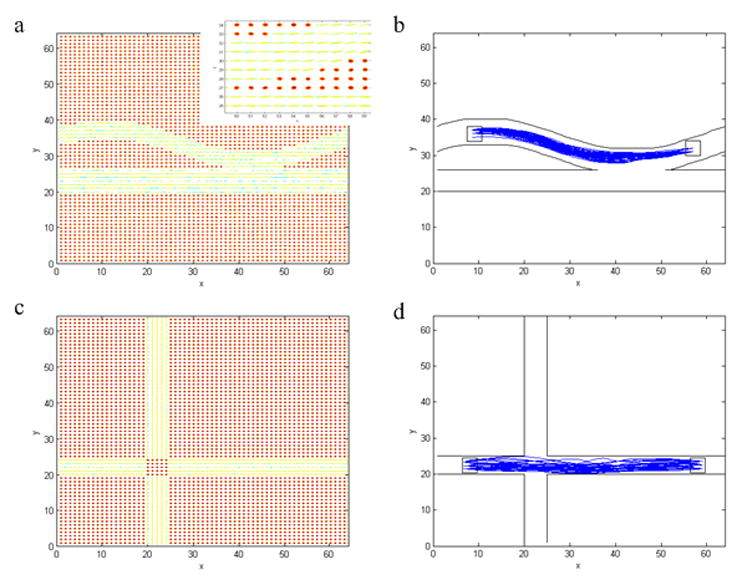
Tests of tracking performance in the presence of complex fiber configurations with synthetic tensor data. The first column shows the synthetic structure of “fiber kissing” (a) and “fiber crossing” (c). The second column (b, d) shows the “fibers” tracked by proposed technique. The ROIs for the tracking experiments are denoted in white squares.
Tracking results are shown in the right column of Fig. 3. As expected, the proposed method had no problems tracking “fibers” in the presence of the “crossing” or “kissing”. Moreover, it can be observed that it produced “fibers” with good convergence to the desired pathways.
Statistical analysis of reconstructed fiber tracts
Mean values of the cost function of the tracked “fibers” in Fig. 2a and their variations with the number of iterations are shown in Fig. 4. It is shown that mean values of the cost functions are high at the beginning, but decrease rapidly during the first a few iterations. They tend to stabilize to low values around 5 iterations, beyond which further declines are quite small. This indicates that the algorithms start to converge around the 5thiteration, at which the tracked “fibers” are close to the final optimal pathways. Meanwhile, variations of the PDF of the cost function with the number of iterations are demonstrated in Fig. 4b. It can be seen that at the first a few iterations, the PDF spreads over a wide range. As the number of iterations increases, mean value of the cost function becomes small and the range of PDF becomes narrower. Eventually, the PDF is stabilized, again indicating that convergent results have been reached.
Figure 4.
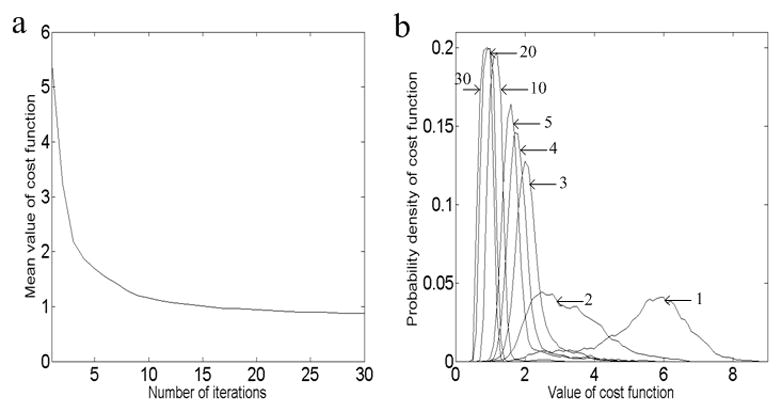
Variations of mean value of cost function (a) and probability density of cost function (b) with the number of iterations.
The synthetic experiments in the preceding sections, and the in vivo experiments to be presented next as well, demonstrate the capability of the proposed algorithm to track known fiber tracts. While these experiments provide certain intuitive validations of the algorithm proposed, an issue of equal importance still remains, i.e., the validity of the fiber pathways tracked by the algorithm. In fact, this issue is critical since the proposed algorithm always generates connection pathways for a given pair of ROIs, whether or not there exist genuine underlying fiber tracts is unknown.
To address this issue, a principled validity test with the same phantom as shown in Fig. 2a was undertaken. First, “fiber” pathways between the two ROIs were tracked with the proposed algorithm as above. The mean of the 10% tracked “fibers” with lowest cost function values was then derived and treated as a standard “fiber”, for which the value of the cost function was calculated. The diffusion tensors along the mean “fiber tract” were subsequently perturbed randomly, followed by recalculation of the value of the cost function. The process of tensor perturbation was repeated 10,000 times, each resulting in a new value of the cost function. We found that the value of the cost function for the standard “fiber” is 1.21. This is far smaller than the values of the cost function after tensor perturbations along the “fiber tract”, which range from 7.67 to 8.41 (two tail t-test, p=0). This certainly proves that the tracked “fiber” has a genuine structure rather than random patterns underlying it.
B. Fiber tracking with in vivo human DTI data
To assess in vivo performance of the algorithm proposed, diffusion weighted images (DWI) of nine healthy human volunteers were acquired. Prior to the imaging, informed consent was obtained from each subject according to a protocol approved by Vanderbilt University Institutional Review Board.
All imaging was carried out on a 3T Philips Intera Achieva MR scanner (Best, The Netherlands), using an eight-element SENSE coil and a single shot, echo-planar pulsed gradient spin-echo imaging sequence. Diffusion weighting was performed along 32 non-collinear directions with a b value of 1000 s/mm2 (matrix size=128×128, FOV=256×256 mm2, TE=60 ms, TR=10 s, thickness=2 mm, gap=0, SENSE factor=2). To improve the signal-to-noise ratio of the images, three repeated scans were obtained from each subject; after motion and distortion correction the three sets of images were averaged using Philips diffusion registration PRIDE tool (Release 0.4). From the averaged DWI data, diffusion tensors and subsequently FA maps were computed [1]. To aid defining ROIs for fiber tracking, T1-weighted images were also acquired during the same imaging session, along with functional MRI signals that were obtained by using designated tasks to activate the cortical language regions [34].
Three ROIs for the in vivo experiments were the left Broca’s area, the pre-motor region and the left Wernicke’s area, defined using the method reported earlier [34]. With these ROIs, fiber tracking was performed using the proposed technique and the parameter settings used were the same as in the synthetic experiments. As it is not possible to measure quantitatively the accuracy of in vivo fiber tracking due to a lack of “gold standard”, performance evaluation of the proposed technique was based on qualitative judgment of consistency of the reconstructed fiber tracts with their known neuro-anatomy.
Figure 5 shows fibers tracked of the pathways between the left Broca’s area and the pre-motor region, and the left Broca’s and Wernicke’s area, from in vivo datasets respectively. For each bundle, a set of randomly selected 30 fibers were drawn for visualization. It is clearly demonstrated that the reconstructed fiber pathways exhibit good agreement with their known neuro-anatomy for all the datasets studied. Although there are certain differences among the subjects, which are partly due to inter-subject anatomical variations, the pathways reconstructed are largely consistent across them. Of particular notes, there can be two connecting routes between the Broca’s area and Wernicke’s area – the dorsal route and the ventral route. Among the nine datasets studied in this work, the algorithm reconstructed fiber pathways of the dorsal route (red curves) for all of them and tracked the pathways of the ventral route (blue curves) for three of them (shown from left to right of Fig. 5 are one typical case of only dorsal route and all three cases of both dorsal and ventral routes respectively). These findings are consistent with the neuroanatomy of the language circuitry documented from Frieerici [35] and agree well with the proportion of the ventral routes that can be tracked with DTI [36], in which four out of eleven subjects showed the ventral route.
Figure 5.
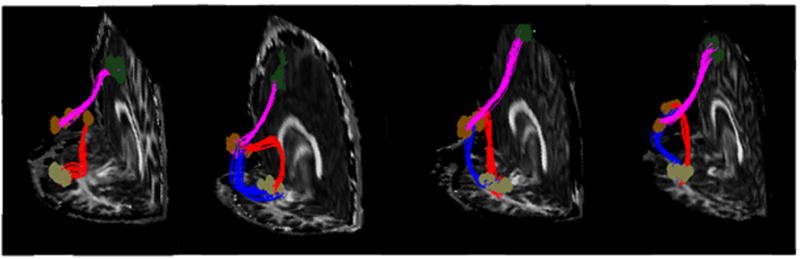
Fibers tracked between the Broca’s area, the pre-motor region and the Wernicke area using the proposed technique. Tracts shown are the results from four different in vivo datasets. Note the pre-motor region is denoted by dark green dots, the Broca’s area is denoted by brown dots and the Wernicke area is denoted by gray dots. Pathways connecting the Broca’s area and the premotor region are shown in magenta and pathways connecting the Broca’s area and the Wernicke area are shown in red (dorsal route) and blue (ventral route).
To compare the performance of our algorithm with other global fiber tracking, we tracked fibers on the same in vivo datasets with the “shortest paths” global tractography [13]. This global tractography was selected because, in essence, all global tracking algorithms are finding some “shortest paths” as the optimal solution. In this comparison, the ROIs for both algorithms are the left Broca’s area and the pre-motor region. For our method, the parameter settings used were the same as in the synthetic experiments, and for the “shortest paths” method, the parameter settings were the same as in the literature [13].
An example comparison is given in Fig. 6, which shows randomly selected 30 trajectories of each bundle reconstructed using our method (6a) and using the “shortest paths” method (6b). As can be seen clearly, while the proposed method found both dorsal (red curves) and ventral routes (blue curves), the “shortest paths” method was only able to reconstruct the dorsal one (red curves). This is due to the fact that the shortest paths method does not possess the functionality of fiber clustering, so that only one bundle could be found if there are large disparities in the cost function between two bundles. By contrast, our method explicitly cluster fibers to different bundles, and then reconstruct optimal fibers for each bundle hierarchically. This feature ensures the capability of constructing all possible bundles connecting a given ROI pair. It should be noted that, the dorsal route reconstructed by both methods are grossly similar, which in fact serves as a mutual validation of the two methods.
Figure 6.
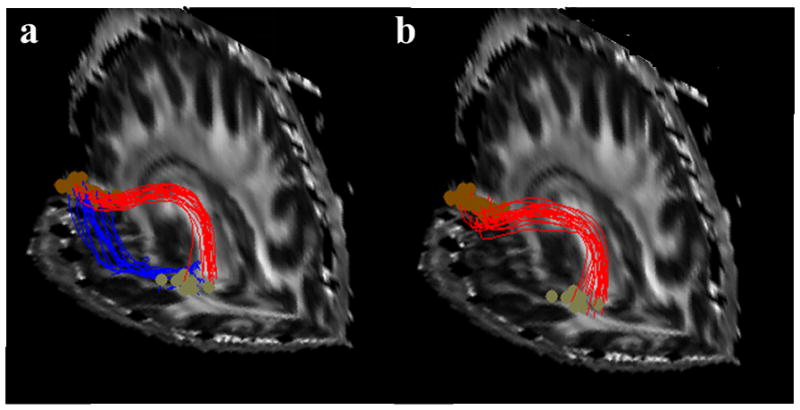
Fibers tracked between the Broca’s area and the pre-motor region using the proposed technique (a) and the “shortest paths” global tractography (b).
C. Computational efficiency
Computational efficiency of the proposed algorithm depends heavily on the number of fiber bundles to be reconstructed. For a single fiber bundle, it takes about 2 minutes to complete 30 iterations of tracking and bundling on a notebook computer with an Intel Core(TM) i7 CPU and 4GB RAM. Actual computational time can be several times shorter since the algorithm often converges within first 10 iterations.
IV. Discussion and Conclusion
In this work, a novel DTI based technique for fiber tractography – unified tracking and bundling – has been proposed. Given a pair of ROIs, the fibers connecting them are clustered into anatomically distinct bundles on the basis of modified Hubert statistic, each of which further goes through importance sampling and random perturbation to reconstruct the globally optimal fibers using the Bayes decision rule. One of the most salient features of the technique is the reconstruction of anatomically consistent fiber bundles in a single framework, which is certainly beneficial to clinical applications of DTI based fiber tractography. The technique proposed has been examined and validated with a series of fiber tracking experiments on synthetic DTI data, which have been demonstrated to be effective in fiber tracking and bundling. Experiments with in vivo human brain DTI data have also indicated that the fiber bundles reconstructed are consistent with neuroanatomy.
DTI based fiber tracking as a new technique for non-invasive mapping of brain structural connectivity has been the research interest of many studies. To date a whole variety of fiber tracking algorithms have been proposed [37], the vast majority of which are streamline based methods. As recognized by many investigators, deterministic streamline tracking suffers from the problems of cumulative noise and limited capability of handling complex fiber structures such as fiber crossing, kissing or branching. While probabilistic streamline methods were proposed later to address these issues, they tend to have the problem of low efficiency and difficulty in further interpretation of tracking results. Technically, instead of step-wise integration of local fiber directions as with streamline methods, our method seeks optimal solutions at the scale of entire fiber pathways connecting a designated ROI pair. This brings the proposed technique a number of intrinsic advantages over streamline based fiber tracking. First, as mentioned earlier, it obviously has a great immunity to random image noise and other local image artifacts. Second, the outcome of fiber tracking is independent of tracking directions. In contrast to the streamline based methods which may produce different results when launched from different ROIs, the direction independency of the proposed technique allows a more objective and thus more reliable characterization of structural connectivity between two regions. Third, the bundling procedure embedded in the unified framework greatly facilitates interpretation and further processing of fiber tracking results.
More importantly, the hierarchical bundling procedure embedded in the proposed technique has a significant advantage of reconstructing multiple connecting routes between a pair of ROIs. This is important to exploratory studies since very often the number of connecting routes is not known a priori. Reconstructing multiple fiber bundles particularly when both major and minor connecting routes exist is quite problematic for streamline based methods and many of the global optimization methods. Although probabilistic streamline methods may be able to track minor pathways, it certainly comes at the cost of computational complexity – they typically require a substantially larger number of trials, especially when the ROIs are distant to each other, which lead to a drastic increase of the computational burden. Meanwhile, in most globally optimized fiber tracking, the state of optimum tends to have large disparities between different bundles and thus cannot be simultaneously achieved by using a single optimization procedure which is typically implemented. In contrast, by explicitly grouping fibers to distinct bundles, our technique reconstructs not only major fiber bundles, but also all possible fiber bundles or even those significantly affected by pathology. This capability renders the proposed technique to have a much wider domain of applications. For instance, in many clinical scenarios, alterations in fiber connectivity may take the form of impaired structural integrity or disruption of connecting route [38, 39]. Depending on the nature and severity of these alterations, it may be difficult for the streamline based methods to reconstruct the impaired fiber pathways successfully. These alterations, however, do not hinder our method from finding optimal fiber pathways since it is insensitive to the local changes of fiber structures.
Finally, it should be pointed out that, in spite of the great potential, the proposed technique does not come without limitations. Most notably, the technique needs an ROI pair as the prior and generates optimal fiber pathways connecting them but provides no information about distribution patterns of the fibers emanating from any of the ROIs. The information however is readily available from probabilistic fiber tracking. This limits the proposed technique to applications in which both ROIs are predetermined. Second, since in principle the technique proposed always yields some fiber pathways between a given ROI pair, the validity of these pathways needs to be assessed statistically or in reference with neuroanatomical knowledge prior to making inferences about the structural connectivity.
In summary, we have proposed a novel fiber tracking technique that integrates globally optimized fiber tracking and hierarchical fiber clustering. Given designated ROIs, the proposed technique generates globally optimal fiber pathways in the form of distinct anatomical bundles. Notwithstanding the existence of some limitations, experiments with synthetic and in vivo human DTI data have demonstrated the effectiveness and advantages of the technique, thus offering the potential of using it as a useful tool in clinical studies of DTI based fiber connectivity.
Acknowledgments
This study was supported by NIH grants R01NS058639 (A.W. Anderson), S10RR023047 (J.C. Gore) and Scientific Research Fund of SiChuan Provincial Education Department (09ZZ004, 10ZA130).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Basser PJ, Matiello J, Le Bihan D. Estimation of the effective selfdiffusion tensor from the NMR spin echo. J Magn Reson. 1994;103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- 2.Mori S, Crain BJ, Chacko VP, van Zijl PCM. Three dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol. 1999;45:265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- 3.Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo fiber tractography using DT-MRI data. Magn Reson Med. 2000;44:625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 4.Poupon C, Clark CA, Frouin V, Regis J, Bloch I, Le Bihan D, Mangin JF. Regularization of diffusion-based direction maps for the tracking of brain white matter fascicles. NeuroImage. 2000;12:184–195. doi: 10.1006/nimg.2000.0607. [DOI] [PubMed] [Google Scholar]
- 5.Lazar M, Alexander AL. Bootstrap white matter tractography (BOOTTRAC) NeuroImage. 2005;24:524–532. doi: 10.1016/j.neuroimage.2004.08.050. [DOI] [PubMed] [Google Scholar]
- 6.Friman O, Farneback G, Westin C. A bayesian approach for stochastic white matter tractography. IEEE Trans Med Imag. 2006;25(8):965–978. doi: 10.1109/tmi.2006.877093. [DOI] [PubMed] [Google Scholar]
- 7.Lu Y, Aldroubi A, Gore JC, Anderson AW, Ding Z. Improved fiber tractography with Bayesion tensor regularization. NeuroImage. 2006;31:1061–1074. doi: 10.1016/j.neuroimage.2006.01.043. [DOI] [PubMed] [Google Scholar]
- 8.Behrens T, Berg HJ, Jbabdi S, Rushworth M, Woolrich M. Probabilistic diffusion tractography with multiple fibre orientations: what can we gain? NeuroImage. 2007;34:144–155. doi: 10.1016/j.neuroimage.2006.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mishra A, Anderson AW, Wu X, Gore JC, Ding Z. An improved Bayesian tensor regularization and sampling algorithm to track neuronal fiber pathways in the language circuit. Medical Physics. 2010;37(8):4274–87. doi: 10.1118/1.3456113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tuch DS, Wiegell MR, Reesel TG, Belliveau LW, Wedeen VJ. Measuring Cortico-Cortical Connectivity Matrices with Diffusion Spectrum Imaging. Proc. Intl. Soc. Mag. Reson. Med; Glasgow, Scotland, UK. 2001. p. 502. [Google Scholar]
- 11.Jbabdi S, Woolrich MW, Andersson JL, Behrens TE. A Bayesian framework for global tractography. Neuroimage. 2007;37:116–29. doi: 10.1016/j.neuroimage.2007.04.039. [DOI] [PubMed] [Google Scholar]
- 12.Iturria-Medina Y, Canales-Rodríguez EJ, Melie-García L, Valdés-Hernández PA, Martínez-Montes E, Alemán-Gómez Y, Sánchez-Bornot JM. Characterizing brain anatomical connections using diffusion weighted MRI and graph theory. Neuroimage. 2007;36:645–60. doi: 10.1016/j.neuroimage.2007.02.012. [DOI] [PubMed] [Google Scholar]
- 13.Zalesky A. DT-MRI fiber tracking: A shortest paths approach. IEEE Trans Med Imag. 2008;27(10):1458–1471. doi: 10.1109/TMI.2008.923644. [DOI] [PubMed] [Google Scholar]
- 14.Reisert M, Mader I, Anastosoulus C, Weigel M, Schnell S, Kiselev V. Global Fiber Reconstruction Becomes Practical. Neuroimage. 2011;54(2):955–962. doi: 10.1016/j.neuroimage.2010.09.016. [DOI] [PubMed] [Google Scholar]
- 15.Fillard P, Poupon C, Mangin J. A novel global tractography algorithm based on an adaptive spin glass model. Lecture Notes in Computer Science. 2009;5761:927–934. doi: 10.1007/978-3-642-04268-3_114. [DOI] [PubMed] [Google Scholar]
- 16.Sherbondy A, Rowe MC, Alexander DC. MicroTrack: An Algorithm for Concurrent Projectome and Microstructure Estimation. Med Image Comput Comput Assist Interv Lecture Notes in Computer Science. 2010;6361:189–190. doi: 10.1007/978-3-642-15705-9_23. [DOI] [PubMed] [Google Scholar]
- 17.Wakana H, Jiang LM, Nagae-Poetscher PC, van Zijl PCM, Mori S. Fiber tract-based atlas of human white matter anatomy. Radiology. 2004;230(1):77–87. doi: 10.1148/radiol.2301021640. [DOI] [PubMed] [Google Scholar]
- 18.Concha L, Gross DW, Beaulieu C. Diffusion tensor tractography of the limbic system. AJNR. 2005;26:2267–2274. [PMC free article] [PubMed] [Google Scholar]
- 19.Ding Z, Gore JC, Anderson AW. Classification and quantification of neuronal fiber pathways using diffusion tensor MRI. Magn Reson Med. 2003;49(4):716–721. doi: 10.1002/mrm.10415. [DOI] [PubMed] [Google Scholar]
- 20.Maddah M, Grimson WEL, Warfield SK, Wells WM. A unified framework for clustering and quantitative analysis of white matter fiber tracts. Med Image Anal. 2008;12(2):191–202. doi: 10.1016/j.media.2007.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ziyan U, Sabuncu MR, Grimson WE, Westin CF. Consistency clustering: a robust algorithm for group-wise registration, segmentation and automatic atlas construction in diffusion MRI. Int J Comput Vis. 2009;85(3):279–290. doi: 10.1007/s11263-009-0217-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Park HJ, Kubicki M, Westin CF, Talos IF, Brun A, Peiper S, Kikinis R, Jolesz FA, McCarley RW, Shenton ME. Method for combining information from white matter fiber tracking and gray matter parcellation. AJNR. 2004;25(8):1318–24. [PMC free article] [PubMed] [Google Scholar]
- 23.Xia Y, Turken U, Whitfield-Gabrieli SL, Gabrieli JD. Knowledge-based classification of neuronal fibers in entire brain. Med Image Comput Computer-Assisted Intervention. 2005:205–212. doi: 10.1007/11566465_26. [DOI] [PubMed] [Google Scholar]
- 24.Xu Q, Anderson AW, Gore JC, Ding Z. Unified bundling and registration of brain white matter fibers. IEEE Trans Med Imaging. 2009;28(9):1399–1411. doi: 10.1109/TMI.2009.2016337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Duda RO, Hart PE. Pattern Classification and Scene Analysis. New York: John Wiley & Sons, Inc; 1973. [Google Scholar]
- 26.Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans Pattern Anal Machine Intell. 1984;6(6):721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- 27.Tuch DS. Q-ball imaging. Magn Reson Med. 2004;52(6):1358–72. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- 28.Wedeen VJ, Hagmann P, Tseng WY, Reese TG, Weisskoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med. 2005;54(6):1377–86. doi: 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]
- 29.Tournier JD, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage. 2007;35(4):1459–72. doi: 10.1016/j.neuroimage.2007.02.016. [DOI] [PubMed] [Google Scholar]
- 30.Anderson AW. Measurement of fiber orientation distributions using high angular resolution diffusion imaging. Magn Reson Med. 2005;54(5):1194–206. doi: 10.1002/mrm.20667. [DOI] [PubMed] [Google Scholar]
- 31.Mahajan M, Nimbhorkar P, Varadarajan K. The Planar k-Means Problem is NP-Hard. Lecture Notes in Computer Science. 2009;5431:274–285. [Google Scholar]
- 32.Dubes RC. How many clusters are best?- An experiment. Pattern Recognition. 1987;20(6):645–663. [Google Scholar]
- 33.Smith PJ, Shafi M, Gao H. Quick simulation: A review of importance sampling techniques in communication systems. IEEE J Select Areas Commun. 1997;15:597–613. [Google Scholar]
- 34.Morgan VL, Mishra A, Newton AT, Gore JC, Ding Z. Integrating functional and diffusion magnetic resonance imaging for analysis of structure-function relationship in the human language network. PlosOne. 2009;4(8):e6660. doi: 10.1371/journal.pone.0006660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Frieerici AD. Pathways to language: fiber tracts in the human brain. Trends in Cognitive Sciences. 2009;13(4):175–181. doi: 10.1016/j.tics.2009.01.001. [DOI] [PubMed] [Google Scholar]
- 36.Parker GJ, Luzzi S, Alexander DC, Wheeler-Kingshott CA, Ciccarelli O, Lambon, Ralph MA. Lateralization of ventral and dorsal auditory-language pathways in the human brain. Neuroimage. 2005;24(3):656–66. doi: 10.1016/j.neuroimage.2004.08.047. [DOI] [PubMed] [Google Scholar]
- 37.Lazar M. Mapping brain anatomical connectivity using white matter tractography. NMR in biomedicine. 2010;23:821–835. doi: 10.1002/nbm.1579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Roosendaal SD, Geurts JJ, Vrenken H, Hulst HE, Cover KS, Castelijns JA, Pouwels PJ, Barkhof F. Regional DTI differences in multiple sclerosis patients. NeuroImage. 2009;44(4):1397–1403. doi: 10.1016/j.neuroimage.2008.10.026. [DOI] [PubMed] [Google Scholar]
- 39.Caeyenberghs K, Leemans A, Geurts M, Taymans T, Linden CV, Smits-Engelsman BC, Sunaert S, Swinnen SP. Brain-behavior relationships in young traumatic brain injury patients: DTI metrics are highly correlated with postural control. Human Brain Mapping. 2010;31(7):992–1002. doi: 10.1002/hbm.20911. [DOI] [PMC free article] [PubMed] [Google Scholar]


