Abstract
Conclusions about normal and pathologic shoulder motion are frequently made from studies using skin surface markers, yet accuracy of such sensors representing humeral motion is not well known. Nineteen subjects were investigated with flock of birds electromagnetic sensors attached to transcortical pins placed into the scapula and humerus, and a thermoplastic cuff secured on the arm. Subjects completed two repetitions of raising and lowering the arm in the sagittal, scapular and coronal planes, as well as shoulder internal and external rotation with the elbow at the side and abducted to ninety degrees. Humeral motion was recorded simultaneously from surface and bone fixed sensors. The average magnitude of error was calculated for the surface and bone fixed measurements throughout the range of motion. ANOVA tested for differences across angles of elevation, raising and lowering, and differences in body mass index. For all five motions tested, the plane of elevation rotation average absolute error ranged from 0-2°, while the humeral elevation rotation average error ranged from 0-4°. The axial rotation average absolute error was much greater, ranging from 5° during elevation motions to approaching 30° at maximum excursion of internal/external rotation motions. Average absolute error was greater in subjects with body mass index greater than 25. Surface sensors are an accurate way of measuring humeral elevation rotations and plane of elevation rotations. Conversely, there is a large amount of average error for axial rotations when using a humeral cuff to measure glenohumeral internal/external rotation as the primary motion.
Keywords: shoulder, kinematics, skin motion error, biomechanics
Introduction
Shoulder motion has been studied for many years beginning with Inman, et al. (1944) producing the widely reported ratio of 2:1, describing the amount of motion at the glenohumeral joint compared to the scapulothoracic interface. More recently, shoulder motion has been studied with many different methods (An et al., 1991; Harryman et al., 1991; Freedman and Munro, 1966; Graichen et al., 2000, Ludewig et al., 2009). A commonly used non-invasive method is three dimensional (3D) surface sensors. Electromagnetic sensors on the scapula, humerus, and sternum have been used extensively to study both normal and pathologic motion (Meskers et al., 1998; Johnson and Anderson, 1990; Finley and Lee, 2003). However, the accuracy of these surface sensors is minimally investigated. Skin motion may result in measurement error when compared with the gold standard of direct bone motion measurement. Prior studies evaluating skin motion artifact for other joints quantified this error and found good agreement between skin markers and bone pins for flexion/extension motions, with larger differences for rotational motions (Reinschmidt et al, 1997a; Reinschmidt et al., 1997b; Cappozzo et al., 1996).
In the shoulder, few studies have been done to examine the validity of surface sensors. Karduna et al. (2001) performed a validation study comparing a surface scapula tracker to bone pins placed in the scapular spine. Comparison yielded low root mean square error (<5°) and percent errors <15% for rotational and elevation motions up to 120° of forward elevation. However, this study looked solely at scapular markers and did not address humeral surface sensors.
A single subject study looked specifically at a thermoplastic humeral cuff simultaneously comparing humeral sensor data from an external fixator. (Ludewig et al. 2002) Root mean square (RMS) errors for humeral rotations ranged from 1° (1%) during scapula abduction to 7.5° (9%) for humeral internal/external rotation. These authors concluded that a humeral cuff could be used to accurately measure glenohumeral elevation motion but larger error was encountered with internal and external rotation. Data were limited, however, because of the single subject with less than full range of motion.
Given the lack of data identifying the accuracy of the most commonly used non-invasive method of tracking humeral motion, the purpose of this study was to evaluate the accuracy of a humeral cuff measuring shoulder motion in a broad subject sample. We hypothesized that the humeral cuff would accurately represent motion for humeral elevation rotations (around the initially anterior x axis) and plane of elevation rotations (around the initially lateral z axis) during all motions. However, we also hypothesized that greater measurement error would result with axial rotations (around the initially superior y axis). A secondary purpose was to assess the effects of body mass index (BMI) on the accuracy of shoulder motion measurement.
Materials and Methods
This study was approved by the Institutional Review Board Human Subjects Committee at the University of Minnesota. Subjects provided written informed consent and were part of a larger investigation of shoulder complex motion (Ludewig et al., 2009). Nineteen subjects (9 men, 10 women) were included in this analysis. Nine subjects had no prior history of shoulder problems while 10 subjects had symptomatic shoulder pathology clinically consistent with shoulder impingement. Ages ranged from 21 to 59 years old with an average age of 34.9. Subject BMI ranged from 20.5 to 34.5 with an average 26.3. Height and weight averaged 170.4 (± 8.9) cm and 76.2 (± 12.3) kg, respectively. Twelve right and seven left arms were evaluated. The dominant arm was tested for ten of the subjects.
Motion testing was performed with the Flock of Birds miniBIRD electromagnetic tracking sensors (Ascension Technology, Burlington, Vermont) and Motion Monitor software (Innovative Sports Training, Chicago, IL). Simultaneous tracking of seven sensors occurred at a sampling rate of 100 Hz per sensor. Previously reported RMS accuracy of this system is <1° (Ludewig et al., 2009).
Subjects underwent placement of 2.5 mm transcortical pins into the clavicle, scapula, and humerus by the same orthopaedic surgeon (RFL). Skin incisions around each pin measured between 1 to 2 cms allowing for full mobile skin excursion around the pin. The scapula pin was placed into base of the acromion, and the humeral pin placed just distal to the deltoid insertion (Figure 1). Minifluoroscopy (1 mrem radiation exposure) was used to confirm transcortical fixation. Three dimensional motion sensors were attached to each pin using custom housings (Figure 1). Two surface sensors were also placed, one sensor taped to the thorax over the sternum and one on a flexible thermoplastic cuff located just proximal to the epicondyles at the elbow (Figure 1). This distal placement is in the area with least underlying musculature and subsequently, least potential contribution to skin motion artifact. The cuff was 6 cm in height and encircled ¾ of the subject’s arm diameter, with Velcro straps (Velcro USA, Inc) securely fastening the anterior humerus. Three cuffs were fabricated for small, medium, and large arms to allow best fit across varying subject size. Digitization of landmarks for anatomical reference frames was performed using International Society of Biomechanics (ISB) recommendations, except for the scapula where the previously recommended acromioclavicular joint landmark was used instead of the currently recommended posterolateral acromion (Wu et al., 2005). The humeral long axis was directed from the midpoint of the epicondyles to the center of the humeral head. The humeral head center was estimated using a pivot point method (An et al., 1990)
Figure 1.
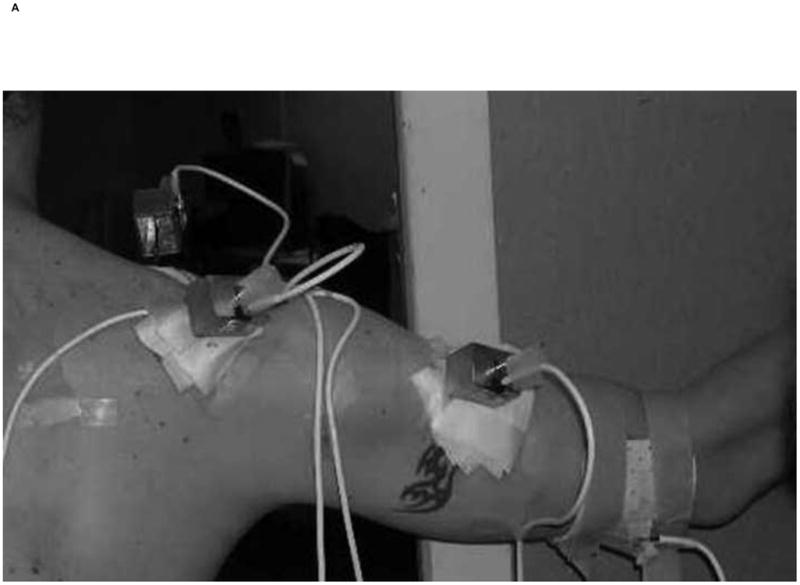
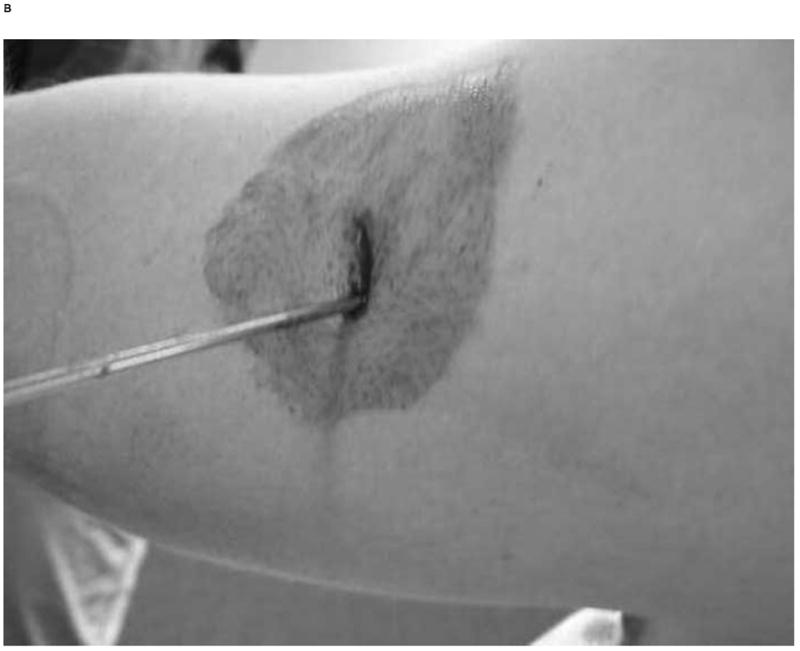
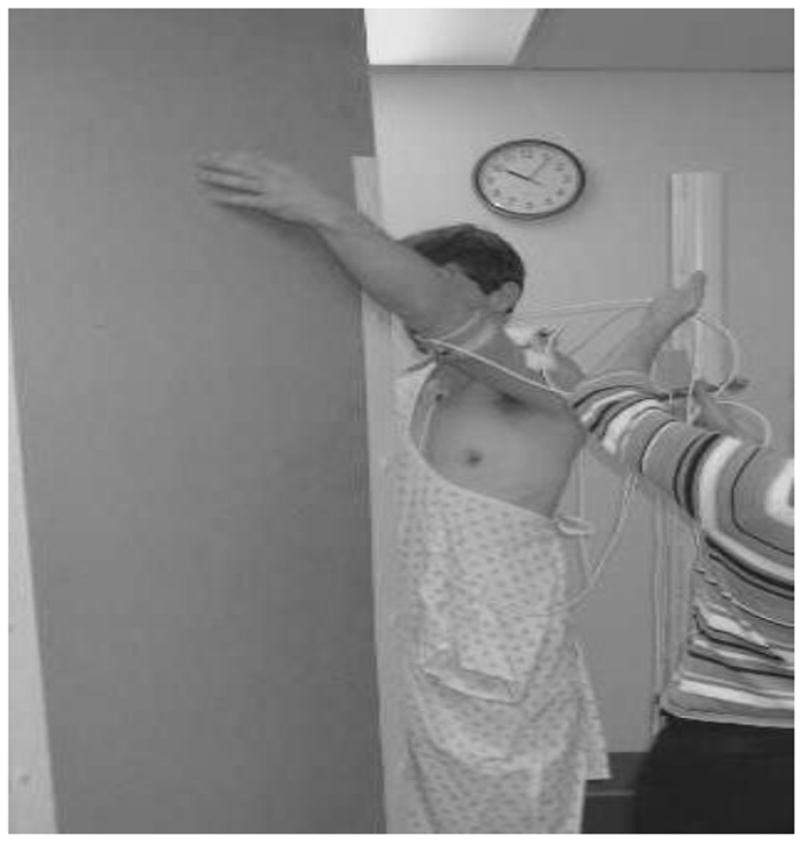
Scapular plane abduction demonstrating the pin placements and sensor housings, the thermoplastic cuff (A), and closeup of the humeral skin incision allowing free movement around the pin (B). The flat planar surface guided the direction of motion testing (C).
Subjects were asked to perform two repetitions each for abduction in the scapular plane, forward flexion in the sagittal plane, abduction in the coronal plane, axial rotation with the elbow at the side and axial rotation with the elbow at 90° of abduction. The subjects were asked to raise and lower their arms over 6 seconds for the complete cycle, while guided by a flat plane surface (Figure 1). They were monitored for any discomfort, as well as any loosening of the motion sensors or pins. Motion data were recorded simultaneously for both pin sensors and surface sensors, allowing for direct comparison between the two methods.
Data were recorded with reference to the scapula pin (glenohumeral joint). Humeral pin to humeral cuff measurement differences with respect to the scapula pin allowed for isolation of the thermoplastic cuff error. Positions in space were described using Cardan angles identifying humeral position as a sequence of rotations about three anatomical axes. In reference to the scapula, rotations were defined using a XZ’Y” sequence as humeral elevation about the initially anterior x axis, perpendicular to the medial to lateral epicondylar line, the plane of elevation about the initially lateral z axis, parallel with the epicondylar line, and internal-external axial rotation about the initially superior y axis directed along the long axis toward the humeral head center (Figure 2).
Figure 2.
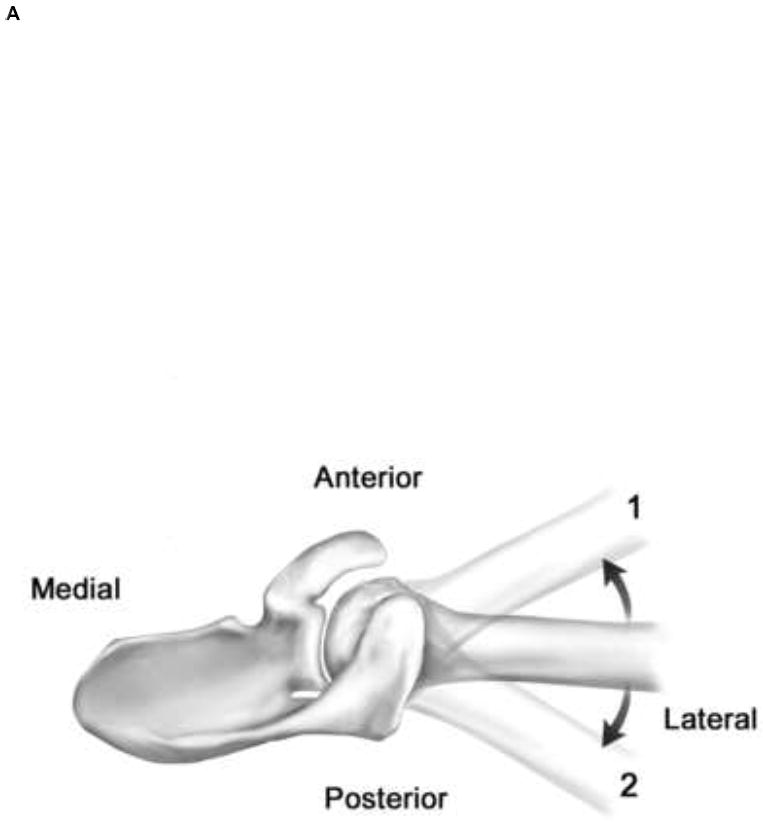
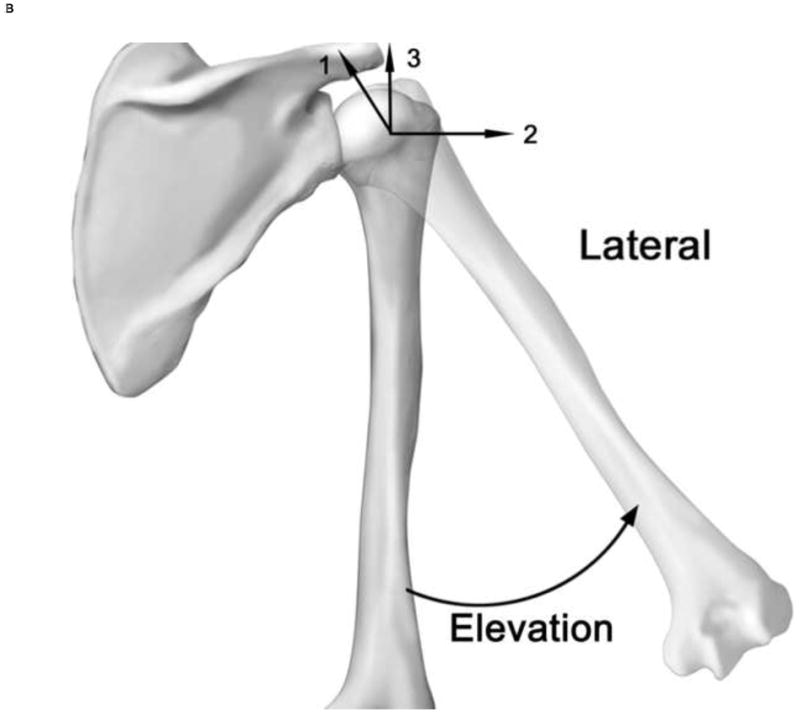
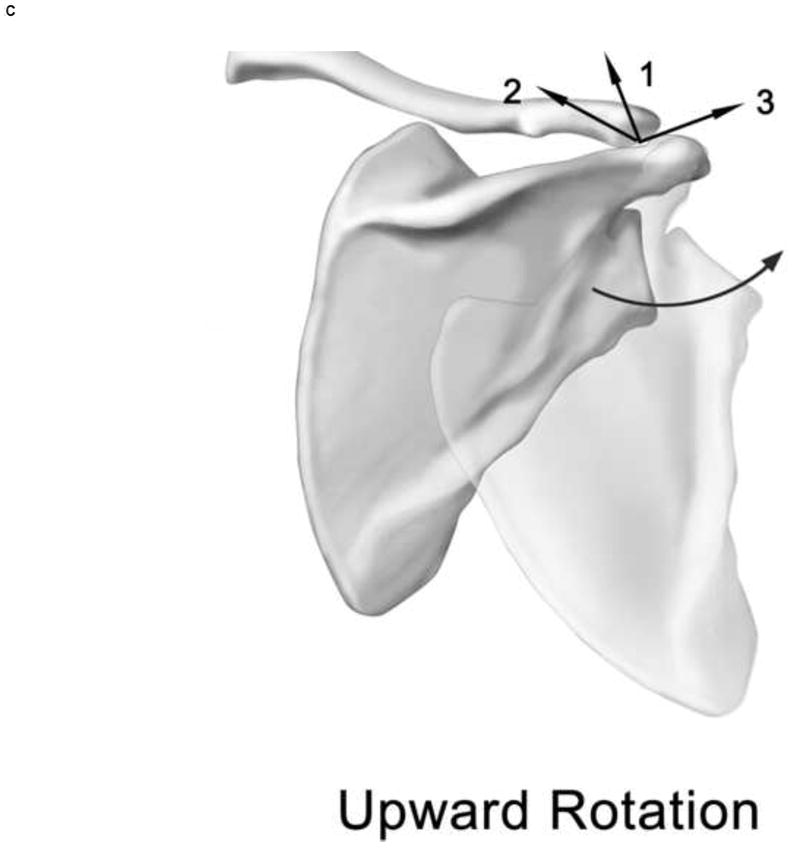
Cardan rotations. Plane of elevation rotation (A, position 1 is anterior to the scapular plane and position 2 is posterior to the scapular plane) and humeral elevation rotation (B). Adapted from Ludewig, et al. (2009). Joint axes for the humerus (B) and scapula (C) are displayed. The first ordered rotation of the humerus is elevation about axis 1 (anteriorly directed x axis), which is aligned perpendicular to the epicondylar line. The second rotation is plane of elevation about axis 2 (initially laterally directed z axis) which is aligned parallel to the epicondyles. The final axial rotation is about axis 3 (initially superiorly directed y axis) which is aligned with the long axis from the midpoint of the epicondyles to the estimated humeral head center. The scapular axes (C) are aligned with 1 (y axis) initially superior, 2 (x axis) perpendicular to the plane of the scapula, and 3 (z axis) aligned approximately parallel to the spine of the scapula).
Data Analysis
Data were processed using Matlab (Mathworks Inc). The anatomical coordinate system for the humeral pin sensor was embedded from the digitized landmarks using the ISB protocol. The same anatomical coordinate system for the humeral cuff sensor was built using the position of the landmarks from the first data point of each new motion to synchronize both coordinate systems. This allowed the analysis of data without potential effects of order of motion testing, but still allowed for errors to be detected if present due to progressive slipping of the cuff over the two repetitions of the same motion. This approach also prevented errors of repeated digitizing from confounding the comparisons of measurement methods.
The differences between the pin and surface sensors were calculated at 30° increments for scapular plane abduction, forward flexion, and coronal plane abduction. Differences were calculated at 10° increments for axial rotation motions. These error calculations were made for all nineteen subjects individually and then aggregated as an average absolute value for each reference angle throughout the tested range of motion. Absolute values were used to avoid under-representing typical errors if some subject’s humeral cuff values were lower and others higher as compared to the pin-based direct bone measures.
Means and standard deviations of humeral cuff to humeral pin absolute errors were calculated for all three Cardan rotations for all five motions of interest. Percentage error for each rotation was also calculated by dividing the average absolute value error by the arc of motion for that rotation.
To assess for any effects of angle of elevation or raising or lowering the arm, two-way repeated measures analysis of variance models were calculated separately for each motion (scapular plane abduction, flexion, coronal plane abduction, axial rotation with the elbow at the side, and axial rotation with the elbow at 90° of abduction) and rotation (angle of elevation, plane of elevation, and axial rotation) across angles of raising and lowering. For all planar elevation motions, results were analyzed at 30°, 60°, 90° and 120° of humerothoracic elevation. For axial rotations with the elbow at the side of the body, results were analyzed at neutral, 10° and 30° each of internally and externally rotated positions of the arm. For axial rotation at 90° abduction, results were analyzed at externally rotated positions of 70°, 50°, 30° and 10°, neutral and 10° of internally rotated positions of the arm. In the case of any significant interactions, Tukey post-hoc analyses allowed for pairwise comparisons without alpha inflation. An overall significance level of p<0.01 was used in all analyses, to adjust for the 5 non-independent motions.
To assess for any effects of subject BMI differences on error values, Pearson correlation analyses were run relating BMI to error values for each motion and rotation. Where there were significant correlations of BMI and rotation errors, ANOVA analyses were re-run dividing subjects into groups—those with a BMI below 25 (minimum value for overweight) and those with a BMI above 25.
Results
Descriptive results
All nineteen subjects completed both repetitions for all motions. For scapular plane abduction, the mean errors (the average of absolute errors between the cuff and the gold standard pins across subjects) for humeral elevation and plane of elevation rotations were remarkably consistent throughout both repetitions (Figure 3). The mean error for the measurement of the plane of elevation rotation averaged 1.3° ± 0.3 (range: 0.18 to 1.6) throughout the range of motion from 30 to 120°. The error associated with the humeral elevation rotation measurements during scapular plane abduction behaved similarly with a mean error of 2.1° ± 0.8 (range: 0.7 to 3.5) throughout the 120° range of motion. Conversely, the mean error for the axial rotation had more variation. The mean error was 4.8° ± 1.1 throughout the range of motion (range: 1.9 to 7.0) (Figure 3).
Figure 3.
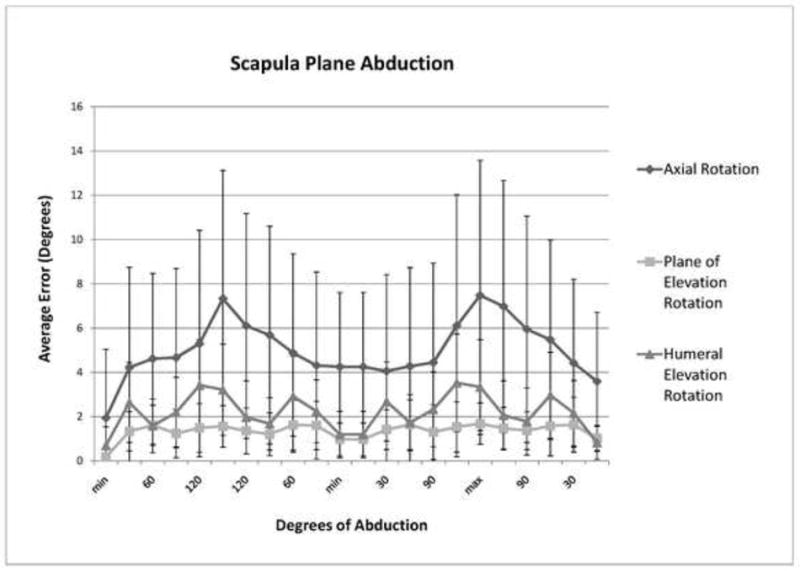
Average errors (degrees) for each 3D rotation component during scapular plane abduction.
Trials for forward flexion and abduction in the coronal plane yielded results very similar to the scapular plane abduction trials. The mean error for the complete trial for the plane of elevation rotation was 1.2° ± 0.4 (range: 0.2 to 1.8 for flexion and 0.1 to 2.1 for abduction) for both forward flexion and coronal plane abduction. The mean error for the humeral elevation rotation was 2.3° ± 1.1 (range: 0.4 to 4) and 1.9° ± 0.9 (range: 0.2 to 3.9) for forward flexion and coronal plane abduction, respectively. Mean error was greatest for axial rotation with averages of 5.5° ± 2.8 (range: 0.6 to 10.9) and 5.3° ± 1.1 (range: 1.0 to 6.3) for forward flexion and coronal plane abduction, respectively (Table 1).
Table 1.
Average error (degrees) for each 3D rotation component during forward flexion in the sagittal plane, and coronal plane abduction.
| Angle | Angle of Elevation | Plane of Elevation | Axial Rotation |
|---|---|---|---|
|
Flexion | |||
| Min | 0.66 ± 0.7 | 0.44 ± 0.3 | 1.53 ± 1.4 |
| 30 | 3.94 ± 1.9 | 0.90 ± 0.9 | 4.44 ± 3.9 |
| 60 | 2.08 ± 2.2 | 1.77 ± 1.0 | 3.36 ± 3.3 |
| 90 | 2.71 ± 1.8 | 1.38 ± 1.1 | 5.78 ± 3.8 |
| 120 | 3.08 ± 1.7 | 1.00 ± 1.0 | 9.63 ± 5.3 |
| Max | 2.75 ± 1.6 | 1.24 ± 1.1 | 11.40 ± 5.5 |
| 120 | 2.02 ± 1.5 | 1.07 ± 1.1 | 10.55 ± 5.4 |
| 90 | 1.96 ± 1.6 | 1.41 ± 1.0 | 6.75 ± 4.4 |
| 60 | 3.71 ± 2.2 | 1.21 ± 0.9 | 4.57 ± 3.3 |
| 30 | 1.83 ± 1.2 | 0.89 ± 0.7 | 3.62 ± 3.6 |
| Min | 0.85 ± 0.6 | 0.84 ± 0.7 | 3.48 ± 3.6 |
|
Abduction | |||
| Min | 0.52 ± 0.4 | 0.49 ± 0.6 | 3.19 ± 2.6 |
| 30 | 1.01 ± 0.7 | 1.48 ± 1.0 | 5.12 ± 3.5 |
| 60 | 1.56 ± 1.1 | 1.04 ± 0.8 | 5.08 ± 4.2 |
| 90 | 2.22 ± 1.5 | 0.84 ± 0.7 | 5.70 ± 4.5 |
| 120 | 3.50 ± 2.2 | 0.89 ± 0.5 | 5.94 ± 4.4 |
| Max | 3.64 ± 1.9 | 1.37 ± 1.0 | 5.50 ± 3.9 |
| 120 | 2.45 ± 1.5 | 1.52 ± 1.0 | 5.48 ± 4.3 |
| 90 | 1.73 ± 1.2 | 1.22 ± 0.8 | 5.49 ± 3.9 |
| 60 | 2.06 ± 1.7 | 1.11 ± 0.9 | 5.31 ± 3.6 |
| 30 | 2.19 ± 1.5 | 1.80 ± 1.1 | 5.18 ± 3.8 |
| Min | 0.74 ± 0.5 | 1.05 ± 1.2 | 4.54 ± 2.8 |
For axial rotation motions, the mean errors were consistent for both the humeral elevation rotation and plane of elevation rotations. The mean error for the plane of elevation rotation was 1.0° ± 0.3 (range: 0.1 to 1.7) and 1.0° ± 0.4 (range: 0.2 to 1.7) for rotation with the elbow at the side and rotation with the elbow at 90° of abduction, respectively. The mean error for the humeral elevation rotation was 1.1° ± 0.4 (range: 0.1 to 1.8) and 1.8° ± 1.1 (range: 0.3 to 1.0) for rotation with the elbow at the side and rotation with the elbow at 90° of abduction, respectively. Axial rotation average error values were much greater for these rotary motions. The mean error for rotation with the elbow at the side was 14.3° ± 10.3 (range: 0.8 to 32.5). The mean error for rotation with the elbow at 90° of abduction was 11.5° ± 9.1 (range: 0.8 to 29.4) (Figures 4 and 5).
Figure 4.
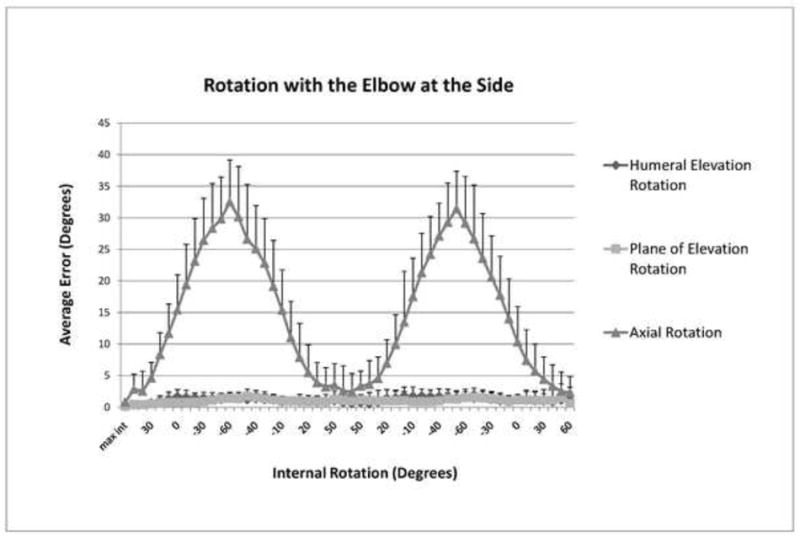
Average errors (degrees) for each 3D rotation component during axial rotation with the elbow at the side.
Figure 5.
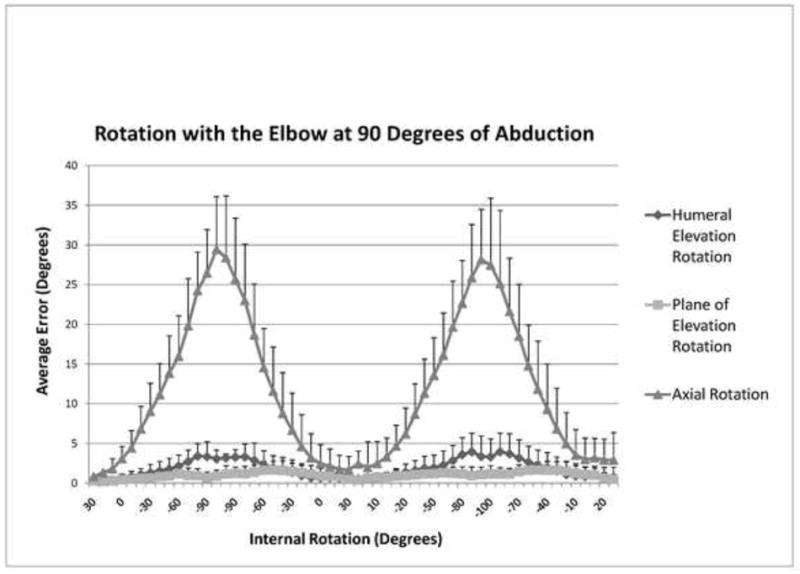
Average errors (degrees) for each 3D rotation component during axial rotation with the elbow at 90° of abduction.
Statistical Results
For statistical comparisons, we only report significant findings where the magnitude of difference exceeded 1°. The possible effects included differences across angles, differences between raising and lowering (phase) or interaction of angle and phase, which are summarized in Table 2 and 3.
Table 2.
Significant differences in error values across angles or raising versus lowering the arm.
| Motion | Rotation | Significant Effect | P value | Interpretation | Magnitude of difference |
|---|---|---|---|---|---|
| Abduction | Angle of Elevation | Interaction of humerothoracic elevation angle and phase | < 0.001 | - Raising arm -30° different from 90°,120°; 60° different from 120° | 1.5° to 2.5° |
| - Raising different from lowering at 30° and 120° | 1° to 1.2° | ||||
| Flexion | Angle of Elevation | Interaction of humerothoracic elevation angle and phase | < 0.001 | - Raising arm - 60° is different from other angles | 1.7° |
| - Raising different from lowering at 30° and 60° | 1.6° to 2° | ||||
| Axial Rotation | Interaction of humerothoracic elevation angle and phase | *0.011 | - Raising arm - all angles different from other angles except 30° with 60° and 90° | 3.8° to 6.6° | |
| - Lowering arm - all angles different from other angles except 30° and 60° | 3.8° to 6.9° | ||||
| - Raising different from lowering at 60° | 1.2° | ||||
| Scapular Plane elevation | Angle of Elevation | Interaction of humerothoracic elevation angle and phase | < 0.001 | - Raising arm - 60° different from 120° | 1.8° |
| - Raising different from lowering at 60° and 120° | 1.3° | ||||
| Axial Rotation | Main effect of elevation angle | < 0.001 | - 30° and 60° are different from 120° | 1.7° to 2.3° | |
Note this alpha level is slightly above our adjusted alpha level, but is included in the table due to its being at the threshold.
Table 3.
Significant difference in error values across angles or internally versus externally rotating the arm.
| Motion | Rotation | Significant Effect | P value | Interpretation | Magnitude of difference |
|---|---|---|---|---|---|
| Axial rotation by side of body | Axial Rotation | Interaction of humerothoracic elevation angle and phase | 0.001 | - All angles different from each other | 4° to 21° |
| - Internal rotation different from external rotation at all angles except at 30° external rotation | 3.5° | ||||
| Axial Rotation | Interaction of humerothoracic elevation angle and phase | < 0.001 | - All angles different from each other except 10° of external rotation with 10° of internal rotation | 4.7° to 18.3° | |
| - Internal rotation different from external rotation at 30° and 50° | 2.1° | ||||
BMI Comparisons
Eleven subjects had a BMI > 25. Significant correlations between the magnitude of error and BMI ranging from 0.21 to 0.60 were found for all elevation motions. Correlations between the magnitude of error and BMI for axial rotation motions did not reach statistical significance (P> 0.05).
The humeral elevation rotation error was significantly but slightly reduced in the BMI < 25 group during abduction in the coronal plane (< 1° reduction, p<0.01), scapular plane abduction (<1° reduction, p<0.002), and forward flexion (1.2° reduction, p<0.01). The plane of elevation rotation error was not significantly different between BMI groups for any of the motions. The axial rotation error was significantly reduced during scapular plane abduction (4.9° reduction, p<0.02) and forward flexion (4.4° reduction, p<0.01). The reduction in axial rotation error during elevation motions for subjects with BMI < 25 approached 10° at maximum excursion.
Discussion
Overall, the thermoplastic humeral cuff proved accurate when measuring glenohumeral motion in the plane of elevation rotation and the humeral elevation rotation, as well as axial rotations during elevation of the arm (typically < 5°). However, significantly larger errors averaging 12-14° and approaching 30° at maximum excursions were encountered when measuring motion in axial rotation.
When looking specifically at the measurements for the plane of elevation and humeral elevation rotations, average cuff error was typically between 1° to 2° for all 5 motions tested. In fact, no average error measured for the plane of elevation rotation exceeded 2.0° and no average error measured for the humeral elevation rotation exceeded 4.0° at any point throughout the range of motion. When the average excursion measured for the humeral elevation rotation was greater than 80°, the average error for this rotation was consistently less than 3% of the total arc of motion. This was the case for all elevation motions. When the average excursion measured for the plane of elevation rotation was greater than 25°, as was the case for the coronal plane abduction and forward flexion repetitions, the average error for this rotation was less than 5% of the total arc of motion.
Not surprisingly, the largest cuff error was encountered with the axial rotation measurements. Average error for the axial rotation was significantly greater than the other two rotations for all 5 motions (Table 4). Scapular plane and coronal plane abduction represented the smallest average arc of motion for axial rotation. The average error in this plane was 11.8% and 14.3% of the total arc, respectively (Table 4). Rotation with the elbow at the side represented the greatest arc of motion for axial rotation. However, the average error was only 15.3% of the total arc (Table 4). In fact, all average errors for the axial rotation were between 9.2% and 15.3% of the total arc. This observation suggests that the average error measured in degrees increases proportionally with the arc of motion (Table 4). However, when looking more closely at each movement, it becomes evident that the percent error increases with larger excursions. This is true for all five motions when considering rotation excursion greater than 20°. Average percent error started at approximately 10% at 15° of rotation excursion and increased to greater than 30% for excursion past 90° (Figure 6). This finding implies that skin motion artifact can underestimate excursion for axial rotation by up to 30% at maximum excursion.
Table 4.
Percentage errors relative to the arc of motion.
| Motion Arcs (Degrees) | Average Error (Degrees) | % Arc of Motion | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Humeral Elevation Rotation | Plane of Elevation Rotation | Axial Rotation | Humeral Elevation Rotation | Plane of Elevation Rotation | Axial Rotation | Humeral Elevation Rotation | Plane of Elevation Rotation | Axial Rotation | |
| Scapular Plane Abduction | 85.6 | 16.1 | 42.4 | 2.2 | 1.3 | 5.0 | 2.7% | 8.9% | 11.8% |
| Coronal Plane Abduction | 81.5 | 29.0 | 41.7 | 2.0 | 1.2 | 5.4 | 2.6% | 4.6% | 14.3% |
| Forward Flexion in the Sagittal Plane | 85.6 | 26.5 | 61.8 | 2.4 | 1.1 | 5.7 | 2.8% | 4.9% | 9.3% |
| Rotation with the Elbow at the Side | 12.4 | 9.8 | 95.8 | 1.2 | 1.1 | 14.6 | 10.2% | 11.8% | 15.3% |
| Rotation with the Eblow at 90° of Abduction | 13.7 | 10.6 | 89.3 | 1.6 | 1.1 | 9.7 | 13.1% | 12.2% | 10.8% |
Figure 6.
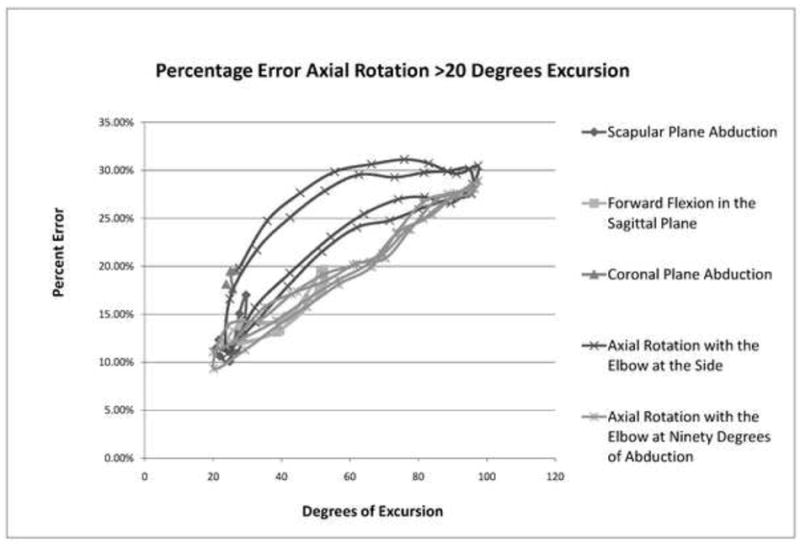
Average percent errors for axial rotation greater than 20 degrees excursion, plotted by movement direction.
Our data compares favorably to the prior surface marker accuracy report. In their trial comparing surface marker recordings to external fixator recordings, Ludewig, et al. (2002) examined glenohumeral elevation, plane of elevation, and axial rotations for flexion, scapular plane abduction, and internal/external rotation at the side in a single subject. As in our study, plane of elevation rotation error was minimal ranging from 1.3° for internal/external rotation to 3.8° for flexion. Similarly, humeral elevation rotation error ranged from 1.3° to 3.1°. The largest error was encountered for axial rotation with an RMS error of 7.5° for internal/external rotation. This axial rotation error was considerably less than the error identified in our study, however, it is consistent with the finding that the largest error was found in axial rotation measurements for internal/external rotation. It may be possible to improve accuracy measures of humeral axial rotation with more distal markers on the forearm, or a cuff extending to the forearm segment. This may be particularly useful in measuring humeral axial rotation with the elbow flexed and arm at the side. However, a distal segment marker approach allows the carrying angle, varus/valgus, and pronation/supination motions at the elbow to influence the axial rotation values differently at differing angles of elbow flexion. Subsequently, such an approach likely requires “locking in” elbow joint and forearm positions, preventing elbow or forearm joint motion during testing. This approach may not be practical when testing functional arm motions, where elbow or forearm motion is a typical component motion. Another approach may be to extend a humeral cuff to the distal forearm and fit it snugly around the humeral medial and lateral epicondyles. This design would likely be most successful for subjects with low body mass index, where the epicondyles are more prominent. Based on the humeral cuff design tested, axial rotation can be successfully measured with acceptable accuracy during arm elevation motions, or short arcs of humeral internal rotation (Figure 4). Maximal excursion humeral external rotation will be substantially underrepresented.
A strength of this study is that our subjects represented a diverse population. We included both dominant and non-dominant extremities, males and females, multiple ethnicities, individuals with shoulder pathology, and individuals with wide-ranging BMIs. This last inclusion allowed us to assess the influence of BMI on the accuracy of humeral motion measures.
When examining a subset of 11 subjects with BMIs less than 25 in comparison to the remaining subjects, overweight subjects consistently had increased average error. This was most evident for the axial rotations, with error reductions in the low BMI group averaging 5° for all three elevation motions analyzed. Differences for the elevation motion were also identified; however, the magnitude (~1°) was less than that encountered for axial rotation, and likely of little practical significance. Those subjects with more soft tissue—the overweight subjects—are susceptible to higher average measurement error. However, when measuring axial rotation as the primary motion, where error values are higher for all subjects, there was not significant reduction in the axial rotation error for those with low BMI. When lower BMI subjects are reasonably representative for an investigation, selective use of these subjects can improve measurement accuracy for elevation motions. However, for many research questions, or where axial rotation is of primary interest, such an inclusion restriction may not reasonably represent the underlying population of interest, or improve the overall accuracy of primary axial rotation measurements.
Conclusions
Where primary interest is in describing the elevation angle or plane of elevation, a thermoplastic humeral cuff is a highly accurate way of measuring these shoulder motions with average error ranging from 1° to 2°. Measurements for axial rotation are subject to increased error, particularly when this is the primary motion (up to 30° and ranging from 15% to 30% of the total motion arc), with the greatest measurement error at maximum excursion. Where axial rotation is of interest in an investigation of elevation motions, excluding subjects with BMIs greater than 25 will result in significantly reduced error. Forearm segment marker methods may also be considered to reduce axial rotation errors when axial rotation is the primary motion.
Acknowledgments
This manuscript was supported in part by NIH grant K01HD042491 from the National Institute of Child Health and Human Development. The content is solely the responsibility of the authors and does not necessarily represent the views of the National Institute of Child Health and Human Development or the National Institutes of Health. Study sponsors had no involvement in the data analysis, interpretation of the data, writing of the manuscript or the decision to submit for publication. The authors would like to thank Cort J. Cieminksi, PhD, PT, ATC, CSCS; Daniel R Hassett, PT; Fred Wentorf, PhD; Ed Gonda; Michael McGinnity, RN; and Kelley Kyle, CST/CFA for their assistance with completing various aspects of data collection and analysis for this project.
Footnotes
Conflict of Interest Statement: None of the authors had any financial or personal relationships with other people or organizations that could inappropriately influence or bias the work.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- An K, Browne A, Korinek S, Tanaka S, Morrey B. Three-dimensional kinematics of glenohumeral elevation. Journal of Orthopaedic Research. 1991;9:143–149. doi: 10.1002/jor.1100090117. [DOI] [PubMed] [Google Scholar]
- An KN, Korinek SL, Kilpela T, Edis S. Kinematic and kinetic analysis of push-up exercise. Biomedical Sciences Instrumentation. 1990;26:53–57. [PubMed] [Google Scholar]
- Cappozzo A, Cantani F, Leardini A, Benedetti MG, Della Croce U. Position and orientation in space of bones during movement: experimental artifacts. Clinical Biomechanics. 1996;11:90–100. doi: 10.1016/0268-0033(95)00046-1. [DOI] [PubMed] [Google Scholar]
- Finley MA, Lee RY. Effect of sitting posture on 3-dimensional scapular kinematics measured by skin-mounted electromagnetic tracking sensors. Archives of Physical Medicine and Rehabilitation. 2003;84(4):563–568. doi: 10.1053/apmr.2003.50087. [DOI] [PubMed] [Google Scholar]
- Freedman L, Munro R. Abduction of the arm in the scapular plane: scapular and glenohumeral movements: A roentgenographic study. Journal of Bone and Joint Surgery. 1996;48A:1503–1510. [PubMed] [Google Scholar]
- Graichen H, Stammberger T, Bonel H, Haubner M, Englmeier K, Reiser M, Eckstein F. Magnetic resonance based motion analysis of the shoulder during elevation. Clinical Orthopaedics and Related Research. 2000;370:154–163. doi: 10.1097/00003086-200001000-00014. [DOI] [PubMed] [Google Scholar]
- Harryman DT, Sidles JA, Harris SL, Matsen FA. The role of the rotator interval capsule in passive motion and stability of the shoulder. Journal of Bone and Joint Surgery. 1992;74A:53–66. [PubMed] [Google Scholar]
- Inman VT, dec M Saunders JB, Abbott LC. Observations of the function of the shoulder joint. Journal of Bone and Joint Surgery. 1944;26A:1–31. [Google Scholar]
- Johnson GR, Anderson JM. Measurement of three-dimensional shoulder movement by an electromagnetic sensor. Clinical Biomechanics. 1990;5:131–136. doi: 10.1016/0268-0033(90)90015-X. [DOI] [PubMed] [Google Scholar]
- Karduna AR, McClure PW, Michener LA, Sennett B. Dynamic measurements of three-dimensional scapular kinematics: a validation study. Journal of Biomechanical Engineering. 2001;123:184–190. doi: 10.1115/1.1351892. [DOI] [PubMed] [Google Scholar]
- Ludewig PM, Cook TM, Shields RK. Comparison of surface sensor and bone-fixed measurement of humeral motion. Journal of Applied Biomechanics. 2002;18:163–170. [Google Scholar]
- Ludewig PM, Phadke V, Braman JP, Hassett DR, Cieminski CJ, LaPrade RF. Motion of the shoulder complex during multiplanar humeral elevation. Journal of Bone and Joint Surgery. 2009;91A:378–89. doi: 10.2106/JBJS.G.01483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meskers CGM, Vermeulen HM, de Groot JH, van der Helm FCT, Rozing PM. 3D shoulder position measurements using a six-degree-of-freedom electromagnetic tracking device. Clinical Biomechanics. 1998;13:280–292. doi: 10.1016/s0268-0033(98)00095-3. [DOI] [PubMed] [Google Scholar]
- Reinschmidt C, van den Bogert AJ, Nigg BM, Lundberg A, Murphy N. Effect of skin movement on the analysis of skeletal knee joint motion during running. Journal of Biomechanics. 1997a;30:729–732. doi: 10.1016/s0021-9290(97)00001-8. [DOI] [PubMed] [Google Scholar]
- Reinschmidt C, van den Bogert AJ, Murphy N, Lundberg A, Nigg BM. Tibiocalcaneal motion during running, measured with external and bone markers. Clinical Biomechanics. 1997b;12:8–16. doi: 10.1016/s0268-0033(96)00046-0. [DOI] [PubMed] [Google Scholar]
- Wu G, van der Helm FC, Veeger HE, Makhsous M, Van Roy P, Anglin C, et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion-Part II: shoulder, elbow, wrist and hand. Journal of Biomechanics. 2005;38(5):981–92. doi: 10.1016/j.jbiomech.2004.05.042. [DOI] [PubMed] [Google Scholar]


