Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Apr 30.
Published in final edited form as: J Biomech. 2012 Feb 28;45(7):1288–1292. doi: 10.1016/j.jbiomech.2012.01.030

Mechanical Property Changes During Neonatal Development and Healing Using a Multiple Regression Model

Heather L Ansorge 1, Sheila Adams 2, Abbas F Jawad 3, David E Birk 2, Louis J Soslowsky 1
PMCID: PMC3327817  NIHMSID: NIHMS356299  PMID: 22381737

Abstract

During neonatal development, tendons undergo a well orchestrated process whereby extensive structural and compositional changes occur in synchrony to produce a normal tissue. Conversely, during the repair response to injury, structural and compositional changes occur, but a mechanically inferior tendon is produced. As a result, developmental processes have been postulated as a potential paradigm for elucidation of mechanistic insight required to develop treatment modalities to improve adult tissue healing. The objective of this study was to compare and contrast normal development with injury during early and late developmental healing. Using backwards multiple linear regression, quantitative and objective information was obtained into the structure function relationships in tendon. Specifically, proteoglycans were shown to be significant predictors of modulus during early developmental healing but not during late developmental healing or normal development. Multiple independent parameters predicted percent relaxation during normal development, however, only biglycan and fibril diameter parameters predicted percent relaxation during early developmental healing. Lastly, multiple differential predictors were observed between early development and early developmental healing; however, no differential predictors were observed between late development and late developmental healing. This study presents a model through which objective analysis of how compositional and structural parameters that affect the development of mechanical parameters can be quantitatively measured. In addition, information from this study can be used to develop new treatment and therapies through which improved adult tendon healing can be obtained.

Keywords: tendon, mechanics, development, neonatal, regression

Introduction

Tendons are complex tissues whose mechanical behavior depends on their structure, composition, and location within the body. It has long been hypothesized that the structure and composition of tendons are a result of the specific function tendons perform (Parry et al., 1978). Tendon is composed mainly of type I collagen organized into aligned fibrils and fibers. It is believed that these aligned fibers bear the tensile loads tendons experience in vivo. Proteoglycans are minor constituents in tendon and it has been hypothesized that they also play a significant role in mechanics (Danielson et al., 1997; Robinson et al., 2005). Specifically, proteoglycans play a role in resisting compression (Arokoski et al., 2000) but they may also bridge the gap between neighboring fibers, providing shear resistance within the tendon. However, the removal of dermatan sulfate did not have any effect on shear or tensile mechanics (Lujan et al., 2007). Based on these facts and assumptions, previous studies have used numerous methods to measure compositional and structural parameters of tendon to correlate them to mechanical behavior.

Previous studies have provided insight into the complex interplay of a tendon’s constituents, which is critical to formalizing structure function relationships (Andarawis-Puri et al., 2010; Derwin et al., 1999; Goh et al., 2008; Robinson et al., 2004). For example, collagen fibril cross-sectional area fraction explained more than half the changes in mechanical properties of mature tendons through linear regression (Goh et al., 2008). Interestingly, the addition of data from younger tendons improved the regression model, thereby supporting the need for further structure-function analyses of developing tendons. While these studies have made significant contributions to understanding the structure-function relationships in tendon, there are still areas that require further investigation. For example, one previous study found significant correlations between compositional and structural parameters with mechanics; however, the models accounted for only 50–70% of the variance (Robinson et al., 2004). Therefore, studies using new experimental techniques or different independent parameters may better predict mechanics.

While many studies have demonstrated that fibril diameter size is correlated with tendon mechanics in normal tendons, similar relationships have not been shown in healing tendons. A study in the healing MCL showed that the mean fibril diameter did not change up to 104 weeks post injury; however, there was an increase in the spread of the fibril diameters (Frank et al., 1997). This finding indicates fibril diameter mean and standard deviation are important parameters to investigate during tendon healing.

Regression models provide a statistical relationship between a dependent (response) variable and independent (predictor) variables. By regressing independent compositional and structural parameters against dependent mechanical parameters, the level of contribution of each of the parameters on mechanical properties can be determined while simultaneously incorporating the effect of the presence of all the independent parameters. Therefore, the objective of this study is to use rigorous statistical models to objectively and quantitatively compare and contrast not only normal development but also healing during early and late development. This study will determine which parameters are beneficial or detrimental to mechanical properties. Regression will be conducted on the independent parameters collagen content, biglycan and decorin mRNA content and fibril diameter average and standard deviation against the dependent mechanical parameters percent relaxation, maximum stress and elastic modulus.

Methods and Materials

Data collection

The experimental methods used for this study have been previously published (Ansorge et al., 2011). Briefly, Achilles tendon in neonatal mice were unilaterally injured at both 7 and 21 days old and allowed to heal for 3 or 10 days post injury. The following parameters were quantified: collagen content by hydroxyproline analysis, biglycan and decorin mRNA content by quantitative real time PCR, fibril diameter average and standard deviation by transmission electron microscopy and mechanical parameters percent relaxation, maximum stress and elastic modulus by tensile testing with local tissue strain measured optically. These measurements were taken for both the injured and contralateral uninjured Achilles tendon for each mouse. Imputation was conducted using the regression method (Zantop et al., 2006) where missing values were observed in a specimens. Lastly, the data was examined for outliers and each group was found to have one specimens as an outlier. Outliers were defined as being at least two standard deviations from the mean and having corroborating experimental evidence of some experimental difficulty (for instance, an observation during experimentation that there may have been a dissection/specimen preparation error). Therefore, each group had a total of 11 specimen.

To determine the sample size for multiple regression analysis, an a priori power analysis was performed based on 5 predictors (total collagen content, biglycan and decorin mRNA content, fibril diameter average and standard deviation), an alpha set at 0.05, an anticipated R-squared of 0.8 and a desired statistical power of 0.8. The R2 was chosen assuming the current study would predict mechanical parameters better than a previous study done in our laboratory with an R2 between 0.5 and 0.7. Calculating the sample size based on these expectations (Soper, 2008), an n of eleven is needed for each group. An n of 12 was used to account for experimental error due to the small size and fragile nature of developmental tendons.

Multiple regression analysis assumes that each dependent and independent parameter is obtained from a single specimen. It was assumed that a litter was a single specimen (Festing, 2006). All litters were weaned to 6 pups to account for experimental error associated with variations in litter size. For each specimen, four distinct and reproducible injuries (along with uninjured contralateral tendons) are needed, one for each of the following assays: biomechanics (percent relaxation, maximum stress, and elastic modulus), transmission electron microscopy (fibril diameter average and standard deviation), biochemistry (collagen content) and QPCR (biglycan and decorin mRNA expression).

General Linear Model (GLM)

Summary statistics of all variables were examined and described by mean, median, standard deviation, minimum and maximum to ensure that assumptions for linear analysis were met. Pearson’s correlations were conducted between all independent parameters to determine correlations. A general linear model (GLM) was run to determine if the dependent variables (percent relaxation, maximum stress and elastic modulus) were significantly related to the independent parameters: collagen content (Col), biglycan (Big) and decorin (Dec) mRNA content, fibril diameter average (Ave) and standard deviation (StDev) and categorical parameters and interactions (age at injury (Age), days post injury (Days), injured or uninjured (Injury)). For all specimens, equations for percent relaxation, stress and modulus were calculated for the injured and uninjured tendon. This resulted in a total of 96 y-values inputted in the GLM for Equation 6.1, where Y1–Y3 were percent relaxation, stress and modulus respectively.

E{Yi}=β0+β1Col+β2Big+β3Dec+β4Ave+β5StDev+β6Age+β7Days+β8Injury+β9(Age*Days)+β10(Age*injury)+β11(Days*Injury)+β12(Age*Days*Injury) Equation 6.1

Upon determining that there are significant effects from the independent parameters, an analysis of how the dependent parameters vary with the independent parameters can be conducted.

Model Refinement

Upon determining which main categorical effects and interactions were significant, a backward regression analysis for the entire model was performed to find the “best” predictors of the dependent parameters (n=96) (Equation 6.2). It was initially assumed the categorical parameters would have statistically significant interactions. Based on this assumption, the initial study design seperated experimental groups for regression analysis. The following analysis was conducted to confirm this assumption; however, the a priori power analysis based on 0.05 for sample size was done for only 5 independent parameters. Since the number of independent parameters in Equation 6.3 is larger than 5, the level of significance was set to 0.1 for this analysis. Therefore, a p-value of 0.10 and a tolerance of 0.001 was used due to the larger number of independent variables being regressed against the dependent variables, which decreases the power. This analysis gives an overall understanding of how the mechanical parameters vary within the framework of the entire study. If there are significant effects of the categorical parameters, then the data can be broken down into experimental groups for further analysis by multiple regression.

E{Yi}=β0+β1Col+β2Big+β3Dec+β4Ave+β5StDev+β6Age+β7Injury+β8(Age*Days)+β9(Days*Injury)+β10(Age*Days*Injury)+β11(Col*Age)+β12(Big*Age)+β13(Dec*Age)+β14(Ave*Age)+β15(StDev*Age)+β16(Col*Injury)+β17(Big*Injury)+β18(Dec*Injury)+β19(Ave*Injury)+β20(StDev*Injury)+β21(Col*Age*Days)+β22(Big*Age*Days)+β23(Dec*Age*Days)+β24(Ave*Age*Days)+β25(StDev*Age*Days)+β26(Col*Injury*Days)+β27(Big*Injury*Days)+β28(Dec*Injury*Days)+β29(Ave*Injury*Days)+β30(StDev*Injury*Days)+β31(Col*Age*Days*Injury)+β32(Big*Age*Days*Injury)+β33(Dec*Age*Days*Injury)+β34(Ave*Age*Days*Injury)+β35(StDev*Age*Days*Injury) Equation 6.2

Final Multiple Regression Models

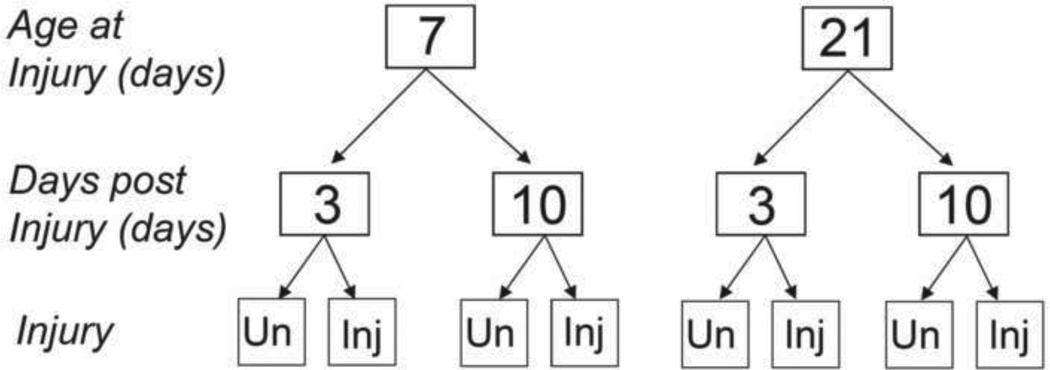
Due to the high number of categorical interaction terms, the data for final analysis was split into experimental groups. Analysis of the equations for the entire model (above) confirmed that this is an appropriate refinement for the data. The final multiple linear regression models quantified the relationship between the dependent variables (percent relaxation, stress and modulus) and the continuous independent variables (collagen content, biglycan and decorin content, fibril diameter average and standard deviation) (Equation 6.3) within each experimental group (Neter, 1996) (Figure 1). The data was delineated into 8 categories based on age at injury (7 and 21 days old), days post injury (3 and 10 days post injury) and injured or uninjured (I, U). This resulted in a total of 11 y-values inputted in the linear regression for equations 6.4, where Y1–Y3 were percent relaxation, stress and modulus respectively. Backward linear regression was then performed as described in Neter, 1996. Specifically, the F to enter was set at 3.3 and F to be removed was set at 3.2. The criteria for choosing the appropriate range of F to enter and F to remove is based on the degrees of freedom in the model. This range for F corresponds to a significance level of 0.1 for a single test. Tolerance is defined as 1-R2k is the coefficient of multiple determination the Xk is regressed over the other included x variables in the model. The tolerance level was set at 0.01 which means that a variable is excluded if its coefficient of multiple determination, when it is regressed over the other x-variables, exceeds 0.99. Typical values for tolerance level range between 0.01 and 0.001. This is one measure to prevent entry of variables that are highly correlated with other x-variables. Significance was again set at p ≤ 0.1, this time due to the small sample size (n=11) per regression model and variances within the data.

Yi=β0+β1Col+β2Big+β3Dec+β4Ave+β5StDev Equations 6.3

Figure 1.

Figure 1

Open in a new tab

Schematic demonstrating the 8 groups investigated in the current study. Un = Uninjured; Inj = Injured

Durbin Watson (DW) statistic was calculated to identify the existence of correlations between independent variables. For each equation 6.4 (n=11/group), based on established guidelines for interpretation of DW statistic, a DW value lower than 1.08 indicated correlation between the independent variables (Neter, 1996).

Results

Correlations between the independent parameters

The Pearson correlation coefficients (r) showed some relationships between the independent variables. Correlations were determined between independent variables within each group. Correlations were considered strong for r < 0.7, moderate for 0.5 < r < 0.7 and weak for r < 0.5 (Devore, 1991). In the 8 experimental groups examined, fibril diameter average was correlated to fibril diameter standard deviation moderately in 2 groups and strongly in 3 groups. Similarly, decorin and biglycan were moderately correlated in 3 groups and strongly correlated in 3 groups. Finally, collagen content and fibril diameter average were moderately correlated in 3 groups.

General Linear Model

A general linear model showed that the interaction terms Days*Age and Days*Age*Injury both had a significant effect on all the mechanical parameters. In addition, injury had a significant effect on stress and modulus. This analysis states that the mechanical parameters are highly dependent on all three categorical parameters (age at injury, days post injury and injury) providing support to analyze this data through regression analysis.

Whole Model Analysis Backward Stepwise Linear Regression Model

To further understand the relationships present in the entire data set, a set of linear regression models was developed (Equation 6.2). Results of this analysis showed not only predictive effects from the main categorical parameters but also from many of the interactions, including interactions with Age, Days and Injury. Due to the complexity of interpreting these equations and the hypotheses developed prior to initiation of the study, the data was separated into experimental groups (age, days, injury). A clearer understanding of how the structural and compositional parameters affect the mechanics, without the confounding effects of the age, days and injury, will therefore be obtained.

Grouped Analysis – Refined Backward Stepwise Linear Regression Analysis

For this analysis, data was grouped according to age at injury (7, 10 days old), days post injury (3, 10 days post injury) and whether the tendon was injured or uninjured. This resulted in 8 groups with 3 regression equations for each (percent relaxation, stress and modulus) for a total of 24 equations (Table 1). 13 equations were found to be significant. Table 2 is broken into the 8 experimental groups and the three dependent mechanical variables; therefore, each box in the table represents an equation. The independent parameters that were found to be significant within each equation are represented in the corresponding box. Briefly, proteoglycans were shown to be significant predictors of modulus during early developmental healing but not during late developmental healing or normal development. Multiple independent parameters predicted percent relaxation during normal development; however, only biglycan and fibril diameter parameters predicted percent relaxation during early developmental healing. Lastly, multiple differential predictors were observed between early development and early developmental healing; however, no differential predictors were observed between late development and late developmental healing. None of the significant models had a Durban Watson score lower than 1.08.

Table 1.

Multiple regression equations for percent relaxation, maximum stress and modulus with statistically significant predictors. Subscript = age at injury (7 or 21), days post injury (3 or 10), Injured/Uninjured (I/U). Col = Collagen content; Ave = Fibril diameter average; StDev = Fibril diameter standard deviation; Big = Biglycan; Dec = Decorin

Linear Regression Equation Model p Model R2
Perc Relax7.3.U = 18.4 − 0.12 * Col + 0.77 * Ave 0.04 0.57
Perc Relax7.3.J = 54.14 − 1.05 * Ave + 2.75 * StDev 0.07 0.30
Modulus7.3.J = 14.65 − 4.62 * Big + 3.00 * Dec 0.01 0.50
Perc Relax7.10.U = 70.80 − 28.14 * Dec 0.01 0.50
Perc Relax7.10.J = 40.54 + 1.25 * StDev 0.08 0.60
Mod7.10.J = 31.7 + 102.2 * Big − 66.35 * Dec 0.05 0.65
Perc Refax21.3.U = 78.00 − 0.06 * Col 0.03 0.59
Stress21.3.U = 47.81 − 0.38 * Ave 0.05 0.50
Modulus21.3.U = 478.26 − 255.52 * Big − 8.76 * Ave + 16.62 * StDev 0.06 0.50
Stress21.3.J = 29.10 − 0.23 * Ave 0.01 0.57
Modulus21.3.J = 370.5 − 3.19 * Ave 0.00 0.77
Perc Relax21.10.U = 136.14 − 0.03 * Col − 60.84 * Big − 0.57 * Ave 0.06 0.34
Modulus21.10.U = −39.94 + 3.66 * Ave − 6.75 * StDeV 0.04 0.39
Open in a new tab

Table 2.

Each box demonstrates one of the equations analyzed in the current study for each of 8 group (Uninjured and Injured, Age at Injury (7 and 21 days old), Days post Injury (3 and 10 days)). Independent parameters that are statistically signifcant in each equation are represented by the following abbreviations: C = Collagen content, B = Biglycan, D = Decorin, A = Fibril diameter average, S = Fibril diameter standard deviation.

Uninjured Injured
Age at Injury 7 (Early) 21 (Late) 7 (Early) 21 (Late)
Days post injury 3 10 3 10 3 10 3 10
Perc Relax CA D C CBA AS S
Stress A A
Modulus BAS AS BD BD A
Open in a new tab

Discussion

This study employed an Achilles tendon neonatal healing model (Ansorge et al, 2011) in a mouse to study the structure-function relationships in tendon development and healing. A unilateral injury was created in developing neonatal Achilles tendons at two ages (7 and 21 days old) and two time points post injury (3 and 10 days post injury). The uninjured and injured Achilles tendons were assayed for mechanical parameters (percent relaxation, maximum stress and elastic modulus), compositional parameters (collagen content, biglycan and decorin expression) and structural parameters (fibril diameter average and standard deviation). The compositional and structural parameters were used as independent variables in multiple regression models to predict the mechanical parameters. Briefly, proteoglycans were shown to be significant predictors of modulus during early developmental healing but not during late developmental healing or normal development. Multiple independent parameters predicted percent relaxation during normal development; however, only biglycan and fibril diameter parameters predicted percent relaxation during early developmental healing. Lastly, multiple differential predictors were observed between early development and early developmental healing; however, no differential predictors were observed between late development and late developmental healing.

Prior to this study, the viscoelastic parameter percent relaxation had not been regressed against compositional and structural parameters in tendon. We demonstrated that collagen content is a predictor of percent relaxation in three of the four uninjured percent relaxation equations. In addition, both proteoglycans are predictors in one uninjured percent relaxation equation while fibril diameter average is a predictor in two. Proteoglycans and water, along with the inherent viscoelasticity of the collagen itself, are thought to be primarily responsible for viscoelastic behavior (Woo et al., 2000; Woo, 1997). Uniform fibrils are thought to contribute to viscoelastic parameters due to possible discontinuity allowing sliding between the fibrils (Zhang et al., 2006). Surprisingly, in the current study, only fibril diameter average and standard deviation are significant predictors of percent relaxation during healing. This may be due to increased discontinuity of fibrils in the injured tendon. Future studies will further investigate the differential mechanisms behind viscoelastic parameters during normal development and developmental healing.

When examining the elastic modulus during early develop and healing, decorin and biglycan were the only significant predictors in healing tendon. It has been previously hypothesized that collagen bears the main load in elastic tensile mechanics; however, the results in this study are not surprising as chondroitin sulfate and dermatan sulfate have previously been demonstrated to significantly predict elastic mechanical parameters (Robinson et al., 2004). In addition, we previously demonstrated that the same experimental group had an accelerated healing response with a return of mechanical function (Ansorge et al., 2011). This could indicate that increased proteoglycan expression is beneficial during healing. Proteoglycans are modulators at multiple stages of fibrillogenesis during development (Zhang et al, 2005). The current study points to a potential role of proteoglycans during fibrillogenesis during healing. Due to size constraints of the neonatal tendons, the actual protein levels of proteoglycans were not measured and this is a limitation of this study. However, previous studies have shown that the mRNA message is similar to the protein level expression in C57BL/6 mice at both 30 and 60 days old (Appendix). Therefore, the message levels measured can be useful to get some estimate of proteoglycans for this analysis and can be useful. Future studies should develop more sensitive techniques to measure proteoglycan levels to further understand their role in development and healing. Further investigation into the role of the proteoglycans could lead to new treatments for improved tendon healing.

Interestingly, no significant predictors were seen in any group for maximum stress. During development, tendon fibroblasts must ensure that the tendon is growing and functionally strong enough to accommodate an increasing body size. However, these tendons probably do not experience stresses that would cause rupture. Based on this study, we hypothesize that functional mechanical parameters are more important during development, than failure mechanics. Therefore, it is possible that in the developmental healing tendon fibroblasts first respond to injury by regulating the functional mechanics via matrix production and remodeling.

We previously demonstrated an accelerated healing response during early development that was not seen in late developmental. Interestingly, 4 out of the 6 possible early developmental healing equations had significant predictors and only 2 out of the 6 had significant predictors during late developmental healing. The predictors in late developmental healing were also present in normal development in comparable groups, indicating that these predictors may be an effect of developmental growth and not healing. One possible explanation is that the healing response during late development is slower and the only significant predictors are those seen during normal development. The information from these comparisons is important because it will help focus new research on possible treatments for improved adult tendon healing. For instance, the addition of proteoglycans to adult healing tendons may help recapitulate mechanical parameters quickly, as seen during early developmental healing.

An analysis of the independent parameters measured in this study revealed some multicollinearity between independent parameters. In particular, the pairs, fibril diameter average and standard deviation, decorin and biglycan, and collagen content and fibril diameter all showed correlations in some of the groups analyzed. These correlations are observationally supported by previous studies that have examined compositional and structural properties of tendon. For instance, as tendons develop, both the fibril diameter average and standard deviation (spread) increase with age (Zhang et al., 2005). In addition, biglycan and decorin are thought to have differential effects on collagen fibrillogenesis and be differentially regulated (Danielson et al., 1997; Robinson et al., 2005; Zhang et al., 2006). Lastly, increased collagen production and increased fibril diameter average occur during similar stages of development (Ansorge et al., 2011; Birk et al., 1997; Bland et al., 1997; Zhang et al., 2005).

The coefficient of determination (R2) for the significant equations ranged from 0.3 to 0.77. A low R2 indicates that a small portion of the variability in the mechanical parameter is attributable to these independent parameters. It is likely that the inclusion of factors not considered in these models would result in an improvement in some of the R2 values. Such additional factors could include compositional parameters such as type XII and XIV collagens, and structural parameters, such as fibril area fraction, or biologic parameters such as the number of inflammatory cells present.

In summary, 8 different experimental groups (based on age at injury, days post injury and injured or uninjured) were analyzed in backward stepwise linear regression to determine how the structural and compositional parameters (collagen, biglycan and decorin content, and fibril diameter average and standard deviation) predicted the mechanical parameters (percent relaxation, maximum stress and elastic modulus). 13 out of the 24 possible equations were demonstrated to have significant predictors. This study provides quantitative, objective information on the development of mechanical strength not only during healing, but also during normal development. This information can be used to focus future research on improving healing in adult tendons. Understanding the exact mechanisms of action behind these predictor variables could provide new therapeutic treatments for the improvement of mechanical properties during adult healing.

Supplementary Material

01. Figure 1.

mRNA and protein expression data for decorin and biglycan demonstrating similar expression patterns at both 30 and 60 days old.

02
03. Table 1.

mRNA expression of decorin (dcn) and biglycan (bgn) relative to beta actin (Actb) is represented by the mean ratio of the proteoglycan genes to Actb (EffCT from quantitative PCR). Protein content of decorin (dcn) and biglycan (bgn) relative to beta actin (Actb) is represented by intensity/mm2 from Western blot quantifications for the proteoglycans and for Actb. *: n=2, all other groups are n=3

Acknowledgements

The authors would like to thank Michael Mienaltowski and the Birk Lab (Department of Pathology and Cell Biology, College of Medicine, University of South Florida) for their work on the Appendix. This work was supported by National Institutes of Health Grant AR050950 from NIAMS, supporting the Penn Center for Musculoskeletal Disorders and by National Institues of Health Grant AR44745.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflicts of Interest

None of the authors of this paper have any conflicts of interest to disclose.

References

  1. Andarawis-Puri N, Kuntz AF, Jawad AF, Soslowsky LJ. Infraspinatus and supraspinatus tendon strain explained using multiple regression models. Annals of Biomedical Engineering. 2010;38:2979–2987. doi: 10.1007/s10439-010-0056-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ansorge HL, Adams S, Birk DE, Soslowsky LJ. Mechanical, Compositional, and Structural Properties of the Post-natal Mouse Achilles Tendon. Annals Biomedical Engineering. 2011 Jul;39(7):1904–1913. doi: 10.1007/s10439-011-0299-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ansorge HL, Hsu JE, Edelstein L, Adams S, Birk DE, Soslowsky LJ. Recapitulation of the Achilles Tendon Mechanical Properties During Neonatal Development: A Study of Differential Healing During Two Stages of Development in a Mouse Model. J Orthop Res. 2011 doi: 10.1002/jor.21542. Accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Arokoski JP, Jurvelin JS, Vaatainen, U, Helminen HJ. Normal and pathological adaptations of articular cartilage to joint loading. Scand J Med Sci Sports. 2000;10:186–198. doi: 10.1034/j.1600-0838.2000.010004186.x. [DOI] [PubMed] [Google Scholar]
  5. Birk DE, Mayne R. Localization of collagen types I, III and V during tendon development. Changes in collagen types I and III are correlated with changes in fibril diameter. Eur J Cell Biol. 1997;72:352–361. [PubMed] [Google Scholar]
  6. Bland YS, Ashhurst DE. Fetal and postnatal development of the patella, patellar tendon and suprapatella in the rabbit; changes in the distribution of the fibrillar collagens. J Anat. 1997;190(Pt 3):327–342. doi: 10.1046/j.1469-7580.1997.19030327.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Danielson KG, Baribault H, Holmes DF, Graham H, Kadler KE, Iozzo RV. Targeted disruption of decorin leads to abnormal collagen fibril morphology and skin fragility. J Cell Biol. 1997;136:729–743. doi: 10.1083/jcb.136.3.729. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Derwin KA, Soslowsky LJ. A quantitative investigation of structure-function relationships in a tendon fascicle model. J Biomech Eng. 1999;121:598–604. doi: 10.1115/1.2800859. [DOI] [PubMed] [Google Scholar]
  9. Devore JL. Probability and statistics for engineering and the sciences. xvi. Pacific Grove, CA: Duxbury; 1991. p. 775. [Google Scholar]
  10. Festing MF. Design and statistical methods in studies using animal models of development. Ilar J. 2006;47:5–14. doi: 10.1093/ilar.47.1.5. [DOI] [PubMed] [Google Scholar]
  11. Frank C, McDonald D, Shrive N. Collagen fibril diameters in the rabbit medial collateral ligament scar: a longer term assessment. Connect Tissue Res. 1997;36:261–269. doi: 10.3109/03008209709160226. [DOI] [PubMed] [Google Scholar]
  12. Goh KL, Holmes DF, Lu HY, Richardson S, Kadler KE, Purslow PP, Wess TJ. Ageing changes in the tensile properties of tendons: influence of collagen fibril volume fraction. J Biomech Eng. 2008;130:021011. doi: 10.1115/1.2898732. [DOI] [PubMed] [Google Scholar]
  13. Lujan TJ, Underwood CJ, Henninger HB, Thompson BM, Weiss JA. Effect of dermatan sulfate glycosaminoglycans on the quasi static material properties of the human medial collateral ligament. J Orthop Res. 2007;25:894–903. doi: 10.1002/jor.20351. [DOI] [PubMed] [Google Scholar]
  14. Neter J. Building the regression model i: Selection of predictor variables Applied linear regression models. Chicago, Ill: Irwin; 1996. pp. 327–355. [Google Scholar]
  15. Neter J. Applied linear regression models. Chicago, Ill: Irwin; 1996. Table B.7 Durbin Watson Test Bounds; p. 1349. [Google Scholar]
  16. Parry DA, Barnes GR, Craig AS. A comparison of the size distribution of collagen fibrils in connective tissues as a function of age and a possible relation between fibril size distribution and mechanical properties. Proc R Soc Lond B Biol Sci. 1978;203:305–321. doi: 10.1098/rspb.1978.0107. [DOI] [PubMed] [Google Scholar]
  17. Robinson PS, Huang TF, Kazam E, Iozzo RV, Birk DE, Soslowsky LJ. Influence of decorin and biglycan on mechanical properties of multiple tendons in knockout mice. J Biomech Eng. 2005;127:181–185. doi: 10.1115/1.1835363. [DOI] [PubMed] [Google Scholar]
  18. Robinson PS, Lin TW, Jawad AF, Iozzo RV, Soslowsky LJ. Investigating tendon fascicle structure-function relationships in a transgenic-age mouse model using multiple regression models. Ann Biomed Eng. 2004;32:924–931. doi: 10.1023/b:abme.0000032455.78459.56. [DOI] [PubMed] [Google Scholar]
  19. Soper DS. The Free Statistics Calculators Website. Online Software. 2008 http://www.danielsoper.com/statcalc/
  20. Woo SL, An K, Frank CB, Livesay GA, Ma CB, Zeminski J, Wayne JS, Myers BS. Anatomy, Biology, and Biomechanics of Tendon and Ligament. Rosemont, IL: American Academy of Orthopaedic Surgeons; 2000. pp. 581–616. [Google Scholar]
  21. Woo SLL, Runco TJ, Young EP. Structure and Function of Tendons and Ligaments. In: Mow VC, Hayes WC, editors. Basic orthopaedic biomechanics. Lippincott Raven, Philadelphia: 1997. p. 518. [Google Scholar]
  22. Zantop T, Gilbert TW, Yoder MC, Badylak SF. Extracellular matrix scaffolds are repopulated by bone marrow-derived cells in a mouse model of achilles tendon reconstruction. J Orthop Res. 2006;24:1299–1309. doi: 10.1002/jor.20071. [DOI] [PubMed] [Google Scholar]
  23. Zhang G, Ezura Y, Chervoneva I, Robinson PS, Beason DP, Carine ET, Soslowsky LJ, Iozzo RV, Birk DE. Decorin regulates assembly of collagen fibrils and acquisition of biomechanical properties during tendon development. J Cell Biochem. 2006;98:1436–1449. doi: 10.1002/jcb.20776. [DOI] [PubMed] [Google Scholar]
  24. Zhang G, Young BB, Ezura Y, Favata M, Soslowsky LJ, Chakravarti S, Birk DE. Development of tendon structure and function: regulation of collagen fibrillogenesis. J Musculoskelet Neuronal Interact. 2005;5:5–21. [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01. Figure 1.

mRNA and protein expression data for decorin and biglycan demonstrating similar expression patterns at both 30 and 60 days old.

NIHMS356299-supplement-01.tif (1.6MB, tif)
02
NIHMS356299-supplement-02.doc (24.5KB, doc)
03. Table 1.

mRNA expression of decorin (dcn) and biglycan (bgn) relative to beta actin (Actb) is represented by the mean ratio of the proteoglycan genes to Actb (EffCT from quantitative PCR). Protein content of decorin (dcn) and biglycan (bgn) relative to beta actin (Actb) is represented by intensity/mm2 from Western blot quantifications for the proteoglycans and for Actb. *: n=2, all other groups are n=3

NIHMS356299-supplement-03.xls (13.5KB, xls)

RESOURCES