Predictive simulation of gait at low gravity reveals skipping as the preferred locomotion strategy

Abstract

The investigation of gait strategies at low gravity environments gained momentum recently as manned missions to the Moon and to Mars are reconsidered. Although reports by astronauts of the Apollo missions indicate alternative gait strategies might be favored on the Moon, computational simulations and experimental investigations have been almost exclusively limited to the study of either walking or running, the locomotion modes preferred under Earth's gravity. In order to investigate the gait strategies likely to be favored at low gravity a series of predictive, computational simulations of gait are performed using a physiological model of the musculoskeletal system, without assuming any particular type of gait. A computationally efficient optimization strategy is utilized allowing for multiple simulations. The results reveal skipping as more efficient and less fatiguing than walking or running and suggest the existence of a walk-skip rather than a walk-run transition at low gravity. The results are expected to serve as a background to the design of experimental investigations of gait under simulated low gravity.

1. Introduction

As the interest on manned missions to the Moon, Mars and beyond is revived and the establishment of settlements outside the Earth is envisioned, the importance of studying locomotion strategies at different gravitational environments becomes evident. Information on the preferred gait features under altered gravitational conditions such as physiological requirements, average locomotion speed and range of motion of the limbs can help on the planning of missions, prediction of load to ensure bones are getting enough exercise while preventing injuries, prediction of metabolic energy expenditure and the design of appropriate spacesuits. Also, the study of gait strategies at altered gravity addresses the more fundamental question concerning the reason for the choice of walking and running as the only two locomotion strategies adopted in a regular basis on the Earth's surface out of several other possible gaits.

On Earth, walking is the favored strategy at locomotion speeds not exceeding approximately 2.0 m/s, speed at which adult humans usually switch to running (Thorstensson and Roberthson, 1987; Hreljac, 1995). There is experimental evidence showing that gait type and features such as speed, step length and cadence are largely dictated by the energy expenditure per unit of distance traveled (Bertram and Ruina, 2001). Other gaits are possible but seem to be uneconomical on Earth. In particular, Minetti (1998) points out skipping as a “third locomotion paradigm”, a gait sometimes adopted by children but over 150% more demanding than walking or running on Earth. He notices that astronauts from the Apollo missions report skipping as the preferred locomotion strategy on the Moon's surface in post-flight debriefings ¹ (refer also to the video “Cernan bounds across the moon” at http://www.hq.nasa.gov/oce/pao/History/40thann/videos.htm). This indicates skipping might be a physiologically favorable gait at low gravity, in detriment to its mere recreational character on the Earth.

In spite of these observations, different gait strategies have been scarcely addressed in experimental and in computational studies. Experimental studies of gait at simulated low gravity have mostly ignored the possibility of a gait strategies different than walking or running (Kram et al., 1997; Griffin et al., 1999). For instance, in Kram et al. (1997) subjects were asked to either walk or run in order to determine the walk-run transition at low gravity. These studies were designed to test the validity of the dynamic similarity hypothesis (DSH) (Alexander, 1976, 1989) under changing gravity acceleration (Minetti, 2001a,b; Raichlen, 2008). Two different gaits are said to be dynamically similar if they feature the same Froude number (Fr), a dimensionless parameter proportional to the ratio between the kinetic and potential energy as

$$Fr=\frac{v^2}{gh},$$ (1)

where v is the gait speed, g is the gravity acceleration, and h is the height of the center of mass, which is usually approximated by the leg length. Empirical data show that bipedal and quadrupedal animals prefer to switch from walking to other gaits at Fr ≈ 0.5 (Alexander, 1989; Kram et al., 1997; Alexander, 1989), but the same might not hold at low gravity acceleration as indicated in experiments by (Kram et al., 1997), although part of the differences observed at simulated low-gravity may be attributed to the fact that the subjects’ legs were exposed to earth's gravity. More importantly, dynamic similarity applies to pendulum-like gaits such as walking and may, therefore, be inadequate as a tool to compare gaits characterized by different mechanical paradigms.

Computational simulation studies, on the other hand, have been limited in their ability to predict new gait strategies either by the simplicity of the models or by the enormous computational cost of simulating locomotion using realistic musculoskeletal models. In spite of the great insights provided by and the elegance of studies such as by Srinivasan and Ruina (2006) and Geyer et al. (2006) they were designed mainly to investigate walking and running and the simplicity of the models employed limits their predictive capability. Fairly realistic models of the musculoskeletal system are available (Delp and Loan, 2000), but the utilization of such complex and high dimensional models in predictive simulations is often inhibited by the enormous computational cost required to solve the associated optimal neuromuscular control problem (Anderson and Pandy, 2001).

The aim of this study was to investigate gait strategies likely to be adopted at low gravity environments such as on the surfaces of the Moon and Mars by means of predictive simulations using a physiological musculoskeletal model. The formulation of the problem does not impose any restriction on the optimal control strategy allowing the model to display a wide variety of different gaits. A computationally efficient method to solve the associated optimal neuromuscular control problem, the direct collocation, was used (Betts, 1998; Kaplan and Heegaard, 2001; Ackermann and van den Bogert, 2008, 2010) allowing the performance of several computational simulations at two different locomotion speeds and three different gravity accelerations in a realistic time frame. All simulations were performed using two different performance criteria, one related to energetic requirements and the other to muscle fatigue. The investigation is expected to widen the understanding of the preferred gaits adopted at different locomotion speeds and gravity conditions and to provide a background for the design of experimental investigations of gait at simulated low gravity that foresee locomotion strategies other than walking or running.

2. Methods

2.1. Musculoskeletal Model

The musculoskeletal model (Gerritsen et al., 1998; Hardin et al., 2004) is contained in the sagittal plane, consists of seven body segments (trunk, thighs, shanks, and feet), and has nine kinematic degrees of freedom. Arm motion influences primarily vertical axis reaction moments (Park, 2008) and would, therefore, have a marginal influence on sagittal plane dynamics and on the selection of locomotion strategies. Eight muscle groups are included in each lower extremity: Iliopsoas, Glutei, Hamstrings, Rectus Femoris, Vasti, Gastrocnemius, Soleus, and Tibialis Anterior. Each muscle is represented by a 3-element Hill-type model, using the equations from McLean et al. (2003) and muscle properties from Gerritsen et al. (1998). This model has 50 state variables in the state vector x:f = 9 generalized coordinates in q,f = 9 generalized velocities in q̇, m = 16 muscle contractile element (CE) lengths in l_ce, and m = 16 muscle activations in a, where x = [q^T q̇^T l^T_ce a^T]^T. The equations of motion were generated by SD/Fast (Parametric Technology Corp., Needham, MA).

2.2. Contact Model

The interaction between feet and ground is modeled by means of 10 spring-damper elements uniformly distributed along each foot sole. The vertical force for each contact element j, was modeled as

$$f_{y,j}=a{\delta }_j^3(1-b{\stackrel{.}{\delta }}_j),$$ (2)

where δ_j is the ground penetration of element j, a is a vertical stiffness parameter set to a = 5.0e7 Nm⁻³, and b is a vertical damping parameter set to b = 1.0 m⁻¹s. These parameter values are consistent with dynamic force-deformation tests from Aerts and de Clercq (1993).

The horizontal force at contact element j was modeled by an approximation of the Coulomb friction (van den Bogert et al., 1989) using a logistic function:

$$f_{x,j}=-\frac{1-\text{exp}(-v_{s,j}∕v_c)}{1+\text{exp}(-v_{s,j}∕v_c)}\mu f_{y,j},$$ (3)

where f_y,j is the vertical force at contact element j, v_s,j is the sliding velocity at element j, and v_c is a scaling factor set to v_c = 0.05 ms⁻¹. The friction coefficient μ was 1.0.

2.3. Optimization Framework

The optimal neuromuscular control problem for gait was formulated as: for a given gait speed v find trajectories of the neural excitations u(t) and states x(t), and stride period T that minimize a cost function J subject to the constraints due to system dynamics

$$\stackrel{.}{\mathit{x}}=\mathit{f}(\mathit{x},\mathit{u}),$$ (4)

bounded neural excitations

$$0\le \mathit{u}\le 1,$$ (5)

and periodicity

$$\mathit{x}\left(T\right)=\mathit{x}\left(0\right)+vT\widehat{\mathit{x}}\text{and}$$ (6)

and

$$\mathit{u}\left(T\right)=\mathit{u}\left(0\right),$$ (7)

where x̂ is the state space unit vector for forward translation.

The optimal control problem was transformed into a Nonlinear Programming Problem (NLP) by means of a temporal discretization of states and controls using direct collocation (Betts, 1998; Kaplan and Heegaard, 2001; Ackermann and van den Bogert, 2010). Unknowns were T and states and controls at each node k. The system dynamics was discretized using the Euler discretization scheme (Betts, 2001) as

$$\frac{{\mathit{x}}_k-{\mathit{x}}_{k-1}}{t_k-t_{k-1}}={\mathit{f}}_k,$$ (8)

resulting in a large set of algebraic constraints. Bilateral symmetry was assumed and half a gait cycle was discretized using 50 nodes, a discretization shown to be sufficiently accurate in previous work (Ackermann and van den Bogert, 2010). The NLP was solved using SNOPT (tomopt.com/tomlab), a sparse sequential quadratic programming solver.

2.4. Simulations

Simulations were performed at two different locomotion speeds, 1.1 m/s and 2.0 m/s, and three different gravity accelerations corresponding to approximate values on the surfaces of the Earth (g_Earth = 9.81 m/s²), Mars (g_Mars = 3.72 m/s²), and Moon (g_Moon = 1.63 m/s²). For each one of these six combinations of speed and gravity acceleration two different cost functions were used (Ackermann and van den Bogert, 2010), one related to energetic requirements, which will be referred to as the “effort” cost function, and the other to muscle fatigue, which will the referred to as the “fatigue” cost function.

The “effort” cost function reads as

$$J_e=\frac{1}{\sum V_i}\sum _{i=1}^m\frac{V_i}{T}{\int }_0^T{a}_i^2\left(t\right)dt,$$ (9)

where m is the number of muscle groups, a is the muscle activation, and V is the muscle volume. This cost function relates to energy expenditure by weighting individual muscle activations by muscle volume and corresponds to cost functions traditionally used to locally solve the muscle force-sharing problem (Glitsch and Baumann, 1997; Thelen and Anderson, 2006).

The “fatigue” cost function reads as

$$J_f={\left(\sum _{i=1}^m{\Phi }_i^{10}\right)}^{1∕10}\approx \underset{i}{\text{max}}{\Phi }_i,$$ (10)

where Φ is a measure of muscle fatigue as

$${\Phi }_i=\frac{1}{T}{\int }_0^T{a}_i^3\left(t\right)dt.$$ (11)

The high power 10 in Eq. (10) serves solely the purpose of approximating the min/max problem of minimizing the maximal muscle fatigue with a continuous function. Note that this could alternatively be implemented by using the standard reformulation of the min/max problem with the appropriate addition of variables and constraints to the optimization problem (Rasmussen et al., 2001). The muscle fatigue expression in Eq. (11) is based on the assumption that the inverse of muscle endurance, i.e. muscle fatigue, is approximately proportional to the cube of the muscle activation (Crowninshield and Brand, 1981).

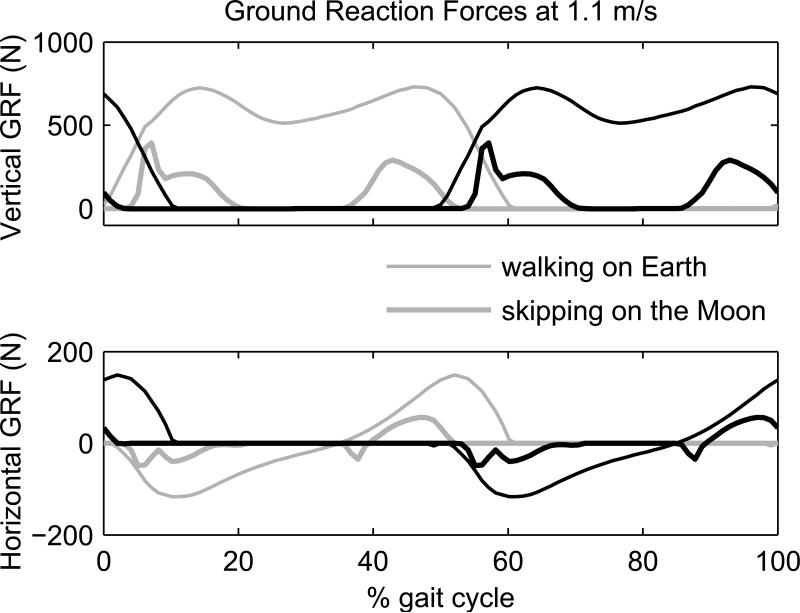
In order to better explore the solution space and increase the likelihood of finding global minima, two different initial guesses were used for each combination of locomotion speed, gravity acceleration and cost function. One initial guess, i1, corresponded to the solution of a tracking problem that approximated target kinematics and ground reaction forces extracted from Winter (1991), refer to Fig. 6 for the corresponding ground reaction forces obtained in this simulation. The other initial guess, i2, was the solution for g_Earth, v = 1.1 m/s and the “effort” cost function.

Figure 6.

Predicted vertical and horizontal ground reaction forces in simulations at a locomotion speed of 1.1 m/s. The walking pattern on Earth was obtained by tracking normative data by Winter (1991). The skipping pattern on the Moon is obtained by minimization of the “effort” cost function.

3. Results

Depending on the speed/gravity conditions, three different gait types were predicted, walking (W), running (R) or skipping (S) (Table 1 and Figs. 1-4). For each combination of speed, gravity acceleration and performance criterion, two different initial guesses were used in the optimization. For completeness, the predicted gait type for both initial guesses are displayed in Table 1. However, in the following discussion only the solution resulting in the lower cost function value (marked bold and enclosed in brackets in Table 1) will be considered. The other solution was deemed a local minimum.

Table 1.

Gait types (W - walking, R - running, or S - skipping) predicted for each combination of locomotion speed, gravity acceleration (on Earth's, Mars’ or Moon's surfaces), cost function (J_e - Eq. 9, or J_f - Eq. 10), and initial guess (i1 or i2). The solution corresponding to the initial guess that led to the lower value of the cost function is marked by a bold letter enclosed by square brackets. Refer to the animations available in the Supplementary Material.

		1.1 m/s			2.0 m/s
		Earth	Mars	Moon	Earth	Mars	Moon
Je	il	[W]	[W]	[S]	[W]	[R]	[S]
	i2	W	W	S	W	S	S
Jf	il	[W]	[W]	[S]	[W]	R	[S]
	i2	W	S	S	W	[S]	S

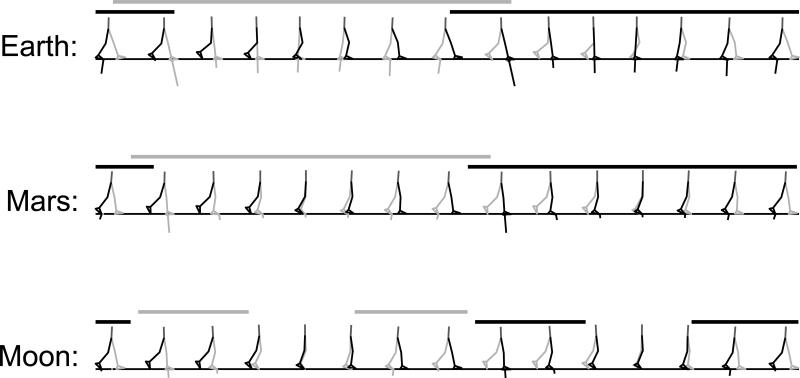
Figure 1.

Stick figures of predicted gait patterns using the effort cost function at a locomotion speed of 1.1 m/s. (Bars indicate ground contact of the color-matching foot.)

Figure 4.

Stick figures of predicted gait patterns using the fatigue cost function at a locomotion speed of 2.0 m/s. (Bars indicate ground contact of the color-matching foot.)

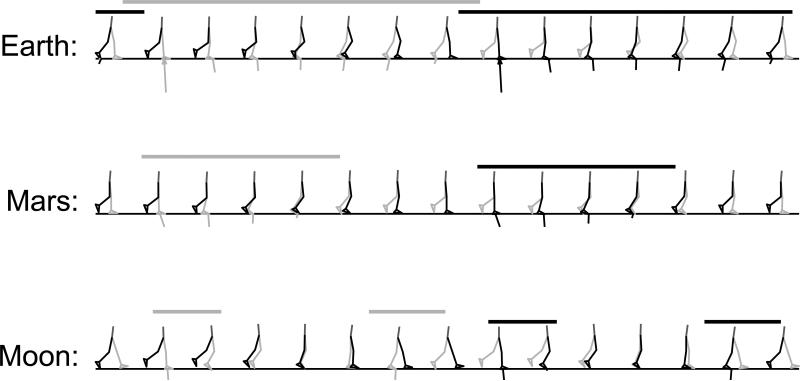
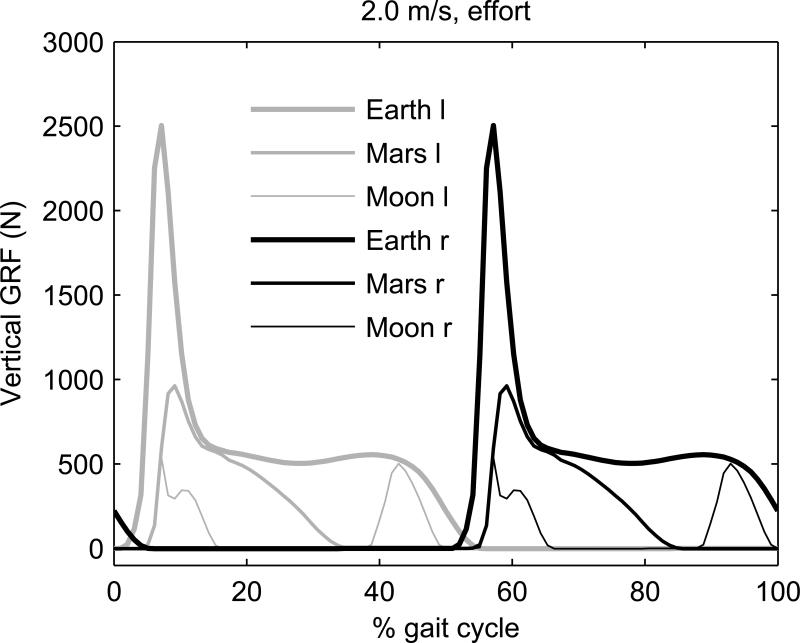
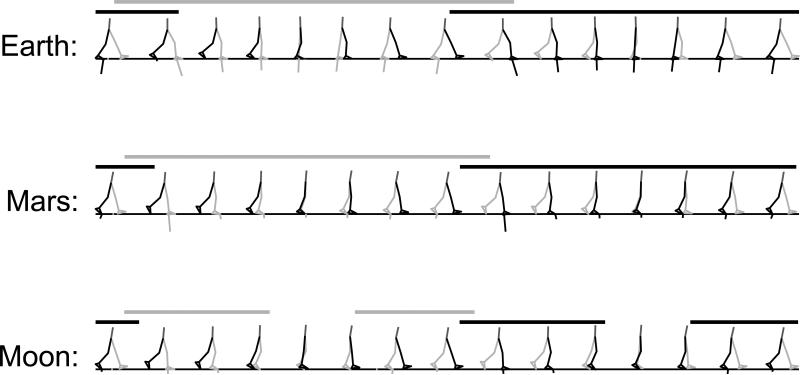
Under Earth's gravity acceleration walking was predicted as the preferred gait mode. Notice, however, that the gait at 2.0 m/s has a short double stance phase, refer to the horizontal bars indicating foot-ground contact on Figs. 3 and 4, and a slight increase in speed would probably lead to running with the appearance of a flight phase. Under the Moon's gravity acceleration, on the contrary, skipping was predicted as the preferred gait strategy at both speeds and performance criteria (Figs. 1-4). Skipping is characterized by an aerial phase during the would-be stance phase (of walking or running) resulting in a gait characterized by two consecutive ipsilateral foot-ground contact events. This phenomenon is absent in walking or running, in which one foot-ground contact event is always preceded by a contralateral foot-ground contact, either while the contralateral foot is still in contact with the ground as in walking, or in the air as in running. The vertical ground reaction forces computed for the simulations at 2.0 m/s with the effort cost function exemplify the typical sequence of contact events in each gait type (Fig. 5). The differences in the patterns of ground reaction forces predicted for skipping and walking at 1.1 m/s are illustrated in Fig. 6. Note that also the horizontal ground reaction forces in skipping differ notably from those observed in walking.

Figure 3.

Stick figures of predicted gait patterns using the effort cost function at a locomotion speed of 2.0 m/s. (Bars indicate ground contact of the color-matching foot.)

Figure 5.

Predicted vertical ground reaction forces in simulations using the effort cost function at a locomotion speed of 2.0 m/s, where “l” indicates the left leg and “r” the right leg . Note that, for this speed and cost function, walking (W), running (R) and skipping (S) were predicted on Earth on Mars and on the Moon, respectively.

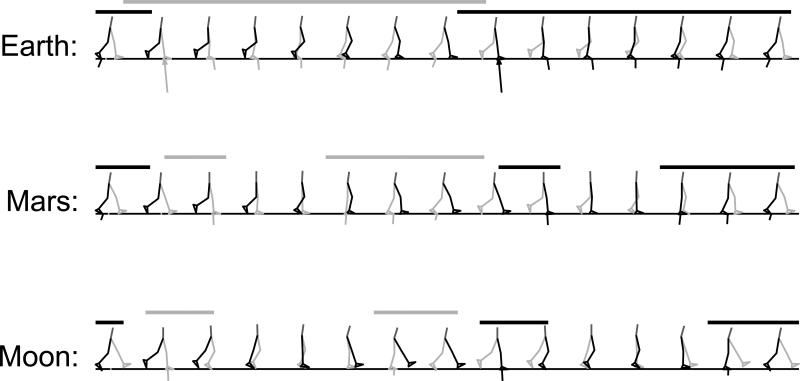
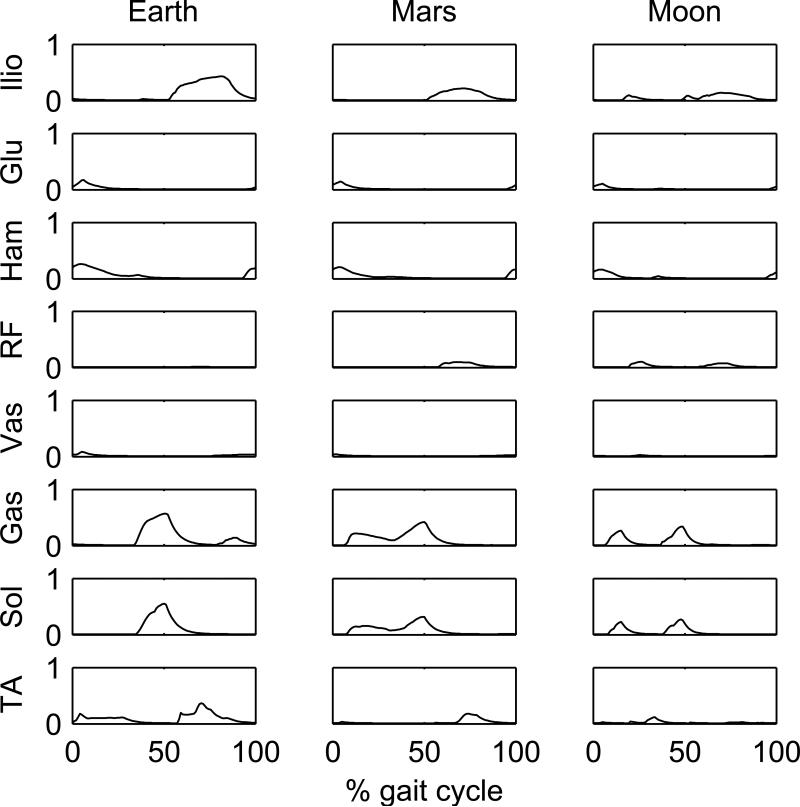
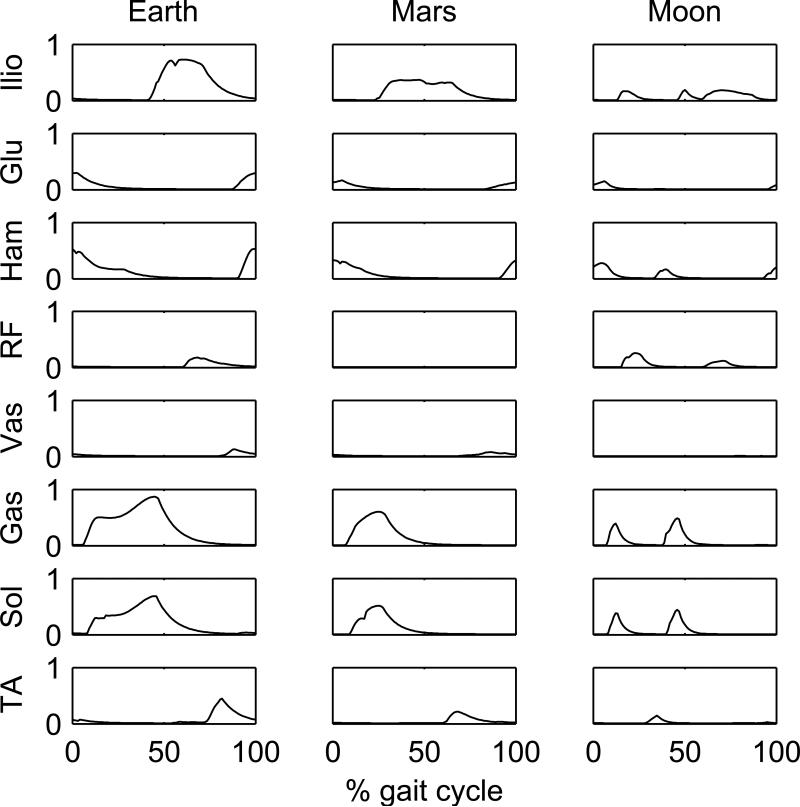
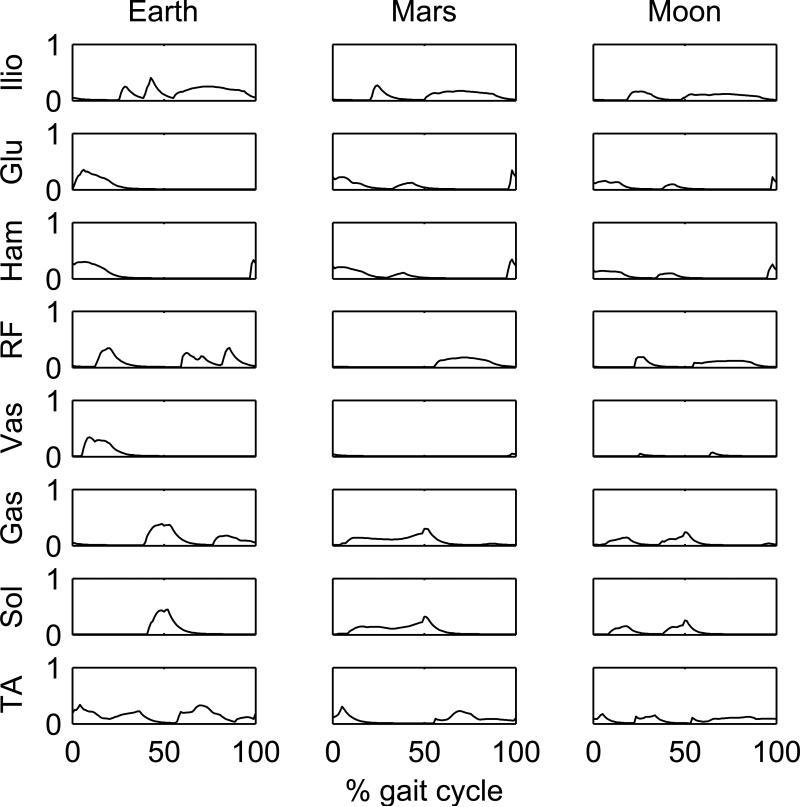
Interestingly, the simulations at Mars’ gravity resulted in all three gait types depending on the speed/gravity conditions and were not independent of the performance criterion. While walking was predicted at 1.1 m/s (Figs. 1 and 2), at 2.0 m/s running was predicted for the effort cost function (Fig. 3) and skipping for the fatigue cost function (Fig. 4). The differences in muscle recruitment pattern reflect the distinct strategies required by different gait types (Figs. 7-10). A good example is the difference in muscle recruitment patterns predicted at 2.0 m/s for the effort cost function (Fig. 9).

Figure 2.

Stick figures of predicted gait patterns using the fatigue cost function at a locomotion speed of 1.1 m/s. (Bars indicate ground contact of the color-matching foot.)

Figure 7.

Predicted left leg muscle activations in simulations using the effort cost function at a locomotion speed of 1.1 m/s.

Figure 10.

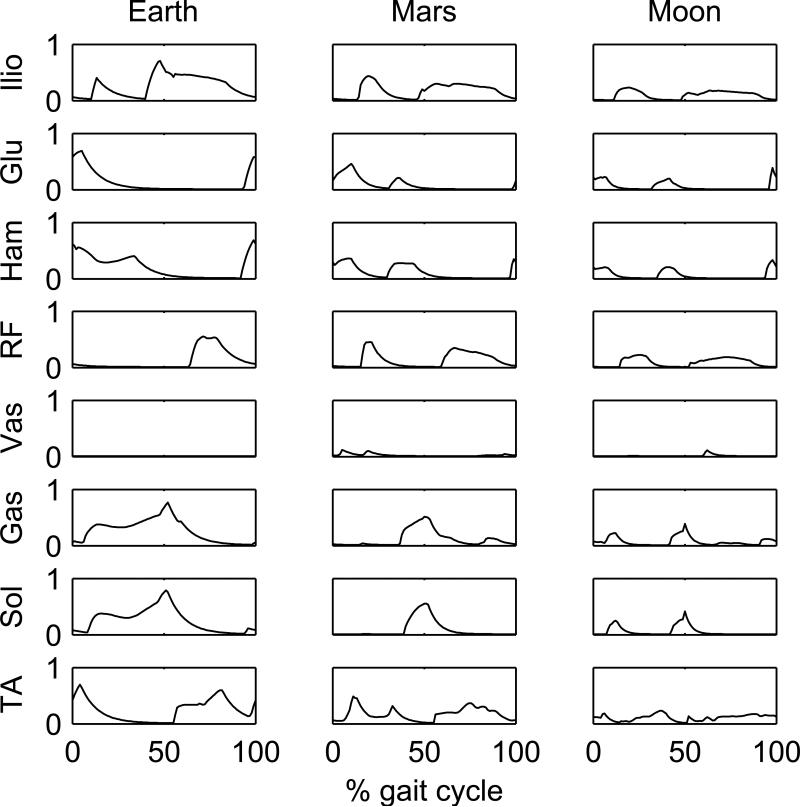
Predicted left leg muscle activations in simulations using the fatigue cost function at a locomotion speed of 2.0 m/s.

Figure 9.

Predicted left leg muscle activations in simulations using the effort cost function at a locomotion speed of 2.0 m/s.

4. Discussion

The gait types predicted (Fig. 11) are generally consistent with available observations and experimental data. The model correctly predicts that the switching from walking to running on the Earth's surface occurs at a speed of about 2.0 m/s, refer e.g. to the very short double stance phase in Fig. 5. The predictions are also consistent with reports by astronauts of the Apollo missions which point to skipping as a favored gait strategy on the Moon's surface.

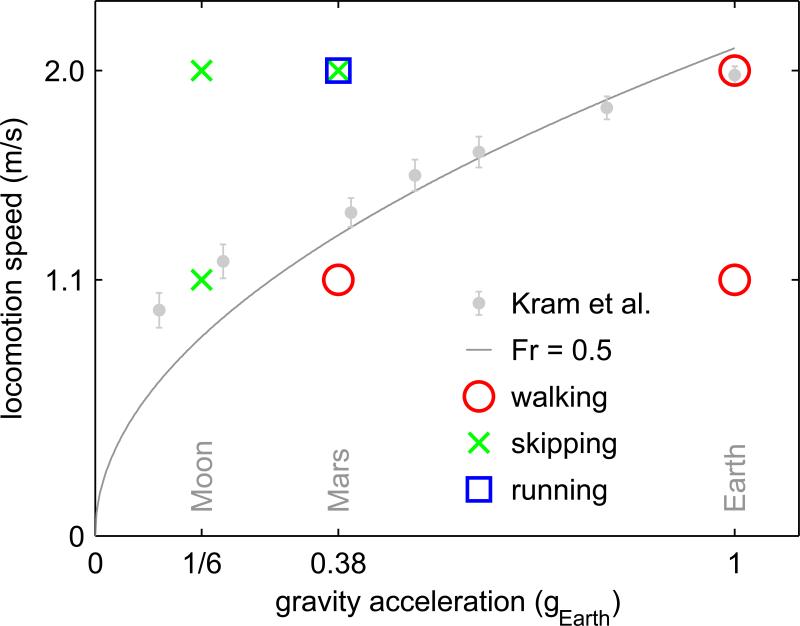
Figure 11.

Gait types predicted at each condition of speed and gravity acceleration. The diagram also shows the walk-run transition speeds during experiments at different simulated low gravity accelerations by Kram et al. (1997), and the walk-run transition speed predicted by dynamic similarity with a Froude number Fr = 0.5 and h = 0.897 m in Eq. 1.

The predictions are compatible with both the walk-run transition speeds at simulated low gravity by Kram et al. (1997), and with the predicted transition speeds by dynamic similarity in sub-gravity with Fr = 0.5 as proposed by Minetti (2001a), refer to Fig. 11. However, the results suggest the existence of a walk-skip rather than a walk-run transition at low gravity (Fig. 11). Skipping was predicted as the preferred gait strategy on the Moon for both performance criteria and speeds investigated and seems to be the gait of choice at the corresponding gravity acceleration. On the contrary, all three locomotion strategies might coexist as physiologically favorable gaits on Mars. While walking was predicted at 1.1 m/s, at 2.0 m/s running minimized “effort”, Eq. 9, while skipping minimized “fatigue”, Eq. 10. This performance criterion dependency might indicate the existence of a transition between running and skipping somewhere in the neighborhood of this speed/gravity condition.

Interestingly, the stance phase of skipping is characterized by a peculiar inversion of the typical deceleration and acceleration phases observed in walking or running, refer to Fig. 6. This observation is consistent with experimental data reported by Minetti (1998) for skipping at Earth's gravity (refer to Fig. 7(a) of this manuscript). The stance phase of walking and running is characterized by a deceleration phase (negative horizontal GRF) followed by a unilateral acceleration phase (positive horizontal GRF). On the contrary, the stance phase of the predicted skipping at 1.1 m/s is characterized by an acceleration phase followed by a contralateral deceleration phase, Fig. 6. The simulation results at Moon's gravity indicate, however, that this contiguous contralateral foot contact sequence characterizing a single stance phase in skipping at low speeds (e.g. at 1.1 m/s) is replaced at larger locomotion speeds (e.g. 2.0 m/s) by two consecutive contralateral foot contact periods which are separated by a flight phase, refer to Figs. 3-5.

The muscle coordination pattern leading to skipping is remarkably consistent across the simulations (Figs. 7-10). Regardless of gravity acceleration, speed or performance criterion, the muscle recruitment in skipping is characterized by a two-spike activation pattern of the plantarflexors (Gastrocnemius and Soleus) and hip extensors (Gluteus and Hamstrings) occurring during the two consecutive foot support phases, interspersed by one activation spike of the hip flexors (Iliopsoas and Rectus Femoris). The hip extensors contract concentrically for forward propulsion of the body during the two consecutive stance phases. The two-spike activation pattern of the plantar flexors during the contact phases evidences the bouncy character of skipping, with contacts occurring predominantly in the anterior portion of the foot and the Achilles tendon working as a spring that stores and releases energy at each bounce. This is the same energy-saving mechanism occurring in running (Kram and Taylor, 1990) with the difference that skipping has two unilateral bounces instead of a single one in each gait cycle. The one-spike activation of the hip flexors in turn repositions the limb during the flight phase between the consecutive unilateral foot contact phases.

The only exception to this general skipping pattern is the simulation result for Mars gravity, at 2.0 m/s and the“fatigue” cost function. In this simulation the first of the two consecutive, unilateral contact phases is characterized by a contact occurring exclusively in the posterior portion of the foot with the first plantar-flexor spike being replaced by a spike of the dorsiflexors (Tibialis Anterior), refer to Fig. 10. This indicates that the Tibialis Anterior tendon works as a spring resisting the plantar flexion caused by the ground reaction force applied to the posterior portion of the foot, refer to the corresponding animation in the Supplementary Material.

It is important to stress that we did not have the aspiration of solving the more intricate problem of accurately predicting transition speeds at different conditions and that the simulations performed here do not consider and did not have as a goal modeling specific conditions potentially present on extraterrestrial missions, other than gravity acceleration. For instance, the significant constraints imposed by current space suits (Carr and Newman, 2008) or specific foot-ground contact properties might affect significantly the selection of gait strategies (Carr and McGee, 2009). Furthermore, in real conditions, other performance criteria such as risk of tripping or stability might outweigh energy consumption or muscle fatigue in importance and possibly lead to different optimal locomotion strategies. Previous work has shown the importance of selecting appropriate cost functions (Ackermann and van den Bogert, 2010) and the simulations shown here in fact predict the existence of cost function-dependent strategies for locomotion on the surface of Mars at 2.0 m/s.

Previous simulation results (Ackermann and van den Bogert, 2010) have also shown that the model utilized in this study is able to reproduce the main features of normal gait in a completely predictive fashion without imposing any particular constraint. However, some predicted patterns did not fully agree with normal measured patterns. For instance, the “effort” cost function led to a straight-leg pattern and, consequently, to a high impact force in the weight acceptance phase of gait as discussed in Ackermann and van den Bogert (2010). Besides the cost function selection, this might be a consequence of model limitations related e.g. to its planar nature or to particularities of the foot-ground contact definition. Further limitations that can compromise the predictive power of the simulations include the assumption of bilateral symmetry excluding unsymmetrical gaits such as unilateral skipping and the solution of the optimal control problem utilizing a gradient-based optimization algorithm which is by nature prone to finding local as opposed to global minima.

Perhaps the most important contribution of this paper is showing that skipping arises at low gravity as both less fatiguing and more economical than walking or running, as opposed to its high cost and mere recreational character on the Earth (Minetti, 1998). To the best of our knowledge, this is the first time skipping was predicted through a computational simulation using a realistic musculoskeletal model. This study provides hints on the speed/gravity conditions at which skipping, running or walking are likely to be selected and is expected to help on the design of experiments involving locomotion under simulated low gravity that anticipate skipping as a physiologically favorable alternative to running or walking.

Figure 8.

Predicted left leg muscle activations in simulations using the fatigue cost function at a locomotion speed of 1.1 m/s.