A Robotics-Based Approach to Modeling of Choice Reaching Experiments on Visual Attention

Abstract

The paper presents a robotics-based model for choice reaching experiments on visual attention. In these experiments participants were asked to make rapid reach movements toward a target in an odd-color search task, i.e., reaching for a green square among red squares and vice versa (e.g., Song and Nakayama, 2008). Interestingly these studies found that in a high number of trials movements were initially directed toward a distractor and only later were adjusted toward the target. These “curved” trajectories occurred particularly frequently when the target in the directly preceding trial had a different color (priming effect). Our model is embedded in a closed-loop control of a LEGO robot arm aiming to mimic these reach movements. The model is based on our earlier work which suggests that target selection in visual search is implemented through parallel interactions between competitive and cooperative processes in the brain (Heinke and Humphreys, 2003; Heinke and Backhaus, 2011). To link this model with the control of the robot arm we implemented a topological representation of movement parameters following the dynamic field theory (Erlhagen and Schoener, 2002). The robot arm is able to mimic the results of the odd-color search task including the priming effect and also generates human-like trajectories with a bell-shaped velocity profile. Theoretical implications and predictions are discussed in the paper.

Introduction

Recent experimental evidence in cognitive psychology suggests that choice reaching tasks can shed new light on cognitive processes, such as visual attention, memory, or language processing (see Song and Nakayama, 2009; for a review). In these experiments participants are asked to make rapid visually guided reach movements toward a target. The trajectories of these movements often reflect important characteristics of the cognitive processes necessary to determine the target. The current paper will present a model for these empirical findings focusing on evidence for visual attention from reach movements in a visual search task (Song and Nakayama, 2006, 2008).

In classical visual search tasks, participants see a number of items on the screen and are asked to indicate whether a pre-defined target item is present or absent by a pressing a designated button on the keyboard. Typically, the speed with which they produce this response (reaction time) is interpreted as a signature for the way selective attention is influenced by visual characteristics of the search displays. For instance, a red square among green squares is faster detected/attended than a red vertical bar among green vertical bars and red horizontal bars (see Wolfe, 1998; Muller and Krummenacher, 2006; for reviews).

Recently Song and Nakayama (2006, 2008, 2009) published a series of experiments in which they asked participants to make rapid reach movements toward the search target instead of button presses. In their experiments the search displays consisted of a green square among red squares and vice versa and the participants’ task was to reach for the odd-color square. Note that the target could be easily reached with straight trajectories. Despite this, Song and Nakayama found that in a high number of trials, movements were initially directed toward a distractor and only later were adjusted toward the target. These “curved” trajectories occurred particularly frequently when the target in the directly preceding trial had a different color (see also Tipper et al., 1998 for similar evidence, albeit for a reaching and grasping task with targets and distractors as wooden blocks placed on a horizontal board). Song and Nakayama’s explanation of these findings can be summarized as follows. They stipulated that the selection process operates in parallel to the execution of the movement and that the selection process is implemented as a dynamic competition between search items. Hence, initially the target color from the preceding trials preactivates or primes distractors directing the competition toward the distractors. Consequently the reach movement is guided toward a distractor. Their interpretation was supported further by the fact that the initial latency (time between search display presentation and start of the movement) was shorter in curved trajectories compared to the initial latency in trials with straight trajectories. Hence because the movements started earlier they are influenced by the erroneous selection due to the priming effect. The model presented in the current paper will follow Song and Nakayama’s interpretation of their findings.

In fact, Song and Nakayama’s view of the selection process as a dynamic competition process is also held by one of the most popular theory on visual attention (e.g., Chelazzi et al., 1993; Desimone and Duncan, 1995; Duncan, 2006). Computational modeling work in our lab has also contributed to the development of this theory of visual attention. There we developed a computational model of visual selective attention termed SAIM (Selective Attention for Identification model; Heinke and Humphreys, 2003; Heinke and Backhaus, 2011). SAIM implements translation-invariant object identification in multiple object scenes. A crucial element of this implementation is the usage of dynamic competition processes to select an object and ignore others. With this model we were able to simulate a broad range of experimental evidence on selective attention, such as visual search tasks, object-based attention, spatial attention, etc. For instance, Heinke and Backhaus (2011) showed that reaction times in visual search tasks (target detection) can be explained by the time it takes the dynamic competition process to complete the target selection. For the purpose of the current paper we simplified SAIM to focus on the odd-one detection. On the other hand, to model Song and Nakayama’s reaching tasks we extended our modeling approach to attention by adding a motor control stage. Moreover, to mimic the visually guided movements, we embedded our extension in a closed-loop control of a robot arm (see Webb, 2009 and Ziemke, 2011 for similar approaches utilizing robotics to advance understanding of human behavior). Finally to link the selection process with the control of the robot arm we integrated the dynamic field theory by Erlhagen and Schoener (2002) into our modeling approach. The dynamic field theory assumes that movement parameters are topologically represented in the brain. Like SAIM, the dynamic field theory also postulates that the dynamic neural processes of competition are crucial for understanding human behavior albeit for the preparation of movements. In fact, for the sake of simplicity, our new model implements the competition processes in both stages, the attention stage and the motor control stage, with the mathematical formalism used in the dynamic field theory.

The dynamic field theory will be introduced in more detail in the next section of this paper. After that we will describe the hardware setup and the model in more detail. Note that this paper gives little details on the mathematics of the model. Instead we will focus on a qualitative explanation of the inner working. We decided that this emphasis is justified as the mathematical details are not relevant for the theoretical implications of the model reported here. Nevertheless, the mathematical details and the code of the model can be downloaded from www.comp-psych.bham.ac.uk/Supplementaryinfo/Frontiers2012. After the description of the model we will present results from three experiments. In the first experiment we demonstrate that the new model successfully guides the robot arm to a target in a single target setup. This also shows that the motor control stage produces human-like trajectories, i.e., the trajectories have bell-shaped velocity profile (e.g., Jeannerod, 1984). The second experiment shows that the new model can mimic Song and Nakayama’s findings. The third experiment will contrast two possible mechanisms of how distractors influence the reaching movements. Finally, in the general discussion we will discuss the theoretical implications of our results.

Dynamic Field Theory

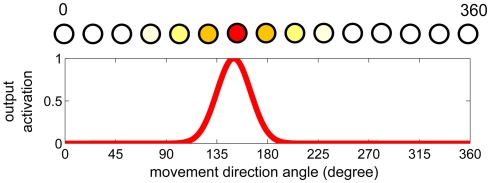
The motor control stage of our model is based on the dynamic field theory (Erlhagen and Schoener, 2002; Erlhagen and Bicho, 2006). The theory stipulates that the brain topographically represents movement parameters in a neural layer (field). In such a representation, similar parameter values are encoded in a spatial neighborhood whereas very different values are represented at locations that are far apart in the neural field. The output activation of the neural field indicates how likely it is that a particular parameter value influences the movement. Figure 1 illustrates this theory for encoding the direction of movements. There is biological evidence that some parameters are encoded in a similar way. For instance there exist motor cortex cells representing the movement direction in monkeys (Bastian et al., 2003) or the head-direction cells in rats (Taube and Bassett, 2003). Also for the purpose of this paper, it is important to note that the dynamic field theory implicitly assumes a linear relationship between the spatial representation of a parameter value and the value itself. For instance for the difference of a movement direction of 10° the two corresponding peaks should be 10 neurons apart (if we assume a spatial discretization of a neuron per degree) at all locations in the dynamic field. In the first experiment we will demonstrate that the arm movements improve if we use a non-linear encoding schema for the encoding of velocity.

Figure 1.

Example of a dynamic neural field. The top graph shows the topological encoding of a movement direction in degrees of heading (0–360). The bottom graph illustrates a possible output activation (see also neuron colors in top graph) that could be the result of the neural field dynamics. In this particular case the output activation represents a movement heading of approximately 150° as the neuron corresponding to this direction has the highest output activation.

In addition, Erlhagen and Schoener (2002) assumes that the neural dynamics in the neural fields are governed by a simple mathematical model proposed by Amari (1977):

$$\tau \stackrel{.}{u}\left(x,t\right)=-u\left(x,t\right)+s\left(x,t\right)+h+\int w\left(x-x^{\prime }\right)f\left[u\left(x^{\prime },t\right)\right]d{x}^{\prime }$$

Hereby τ > 0 defines the time scale, f a sigmoidal output function, u the internal field activity, s an external stimulus, h < 0 the resting level of the field, x represents the positions of neurons in the neural field and time respectively, and w(x) the field’s interaction kernel, defining the interaction between neurons within the field:

$$w\left(x\right)=w_{\text{excite}}\cdot exp\frac{-{\left(x\right)}^2}{2{\sigma }_w^2}-w_{\text{ inhibit}}$$

Hereby w_excite defines the strength of excitatory connections and σ_w their spread. w_inhibit parameterizes the strength of the inhibition between neurons. Hence the dynamic neural field (DNF) follows the biologically plausible principles of local excitation and global inhibition (competition). Erlhagen and Schoener (2002) showed that with the DNF it is possible to model a broad range of empirical findings on movement initiation, e.g., stimulus uncertainty effect, Simon effect, etc.

For the purpose of our model there are three points to note. First, the model employs DNFs not only for the motor control stage but also for the target selection stage. Second, a DNF can also encode two-dimensional parameters, e.g., speed in x- and y-direction in planar space, by using a two-dimensional layer. Such two-dimensional DNFs play an important role in our model. More technical details on the implementation of the DNF can be found in the supplementary info (www.comp-psych.bham.ac.uk/Supplementaryinfo/Frontiers2012). Third, the exact behavior of the DNF depends on the parameters of the kernel w(x) (see Amari, 1977 for a mathematical analysis). For instance, the kernel can be chosen so that with little or no external input, the DNF drifts toward the resting level h. With a large enough input activation at a certain location, the field can establish a single activation peak at this location which can be maintained even after the input is removed. Moreover, if there are many regions with input activations, a DNF with the appropriate parameter setting chooses the largest region. Finally and most important for our model, Amari (1977) showed that DNFs can exhibit a “moving blob” behavior. In this type of behavior an already-established activation peak can move around in a layer in a continuous fashion. The movements of the peak are guided by the gradient of the input activation. The direction of the peak’s movement at a specific location is given by the direction of the steepest gradient in the input activation at this location. The speed of the movement is proportional to the steepness of the gradient. The moving blob behavior will be used in the motor control stage to ensure jerk-free arm movements.

Setup

Figure 2 shows the experimental setup. As the main effects of the targeted experiments occurred in a horizontal plane we used a planar robot arm with two joints. The robot arm was built with the LEGO Mindstorms NXT kit and the LEGO Education set. The sensors, motors, and the programmable brick of these kits offer a flexible and inexpensive way to design programmable robots. We tested several robot designs inspired by Bagnall (2007) and we eventually settled for the construction shown in the two photos in Figure 2B). The configuration is mechanically very stable and the joints have only a little slack. The total length of the arm is approximately 36 cm (forearm 19 cm, upper arm 17 cm). We use the Java leJoS API (Bagnall, 2007) to interface with the programmable brick.

Figure 2.

(A) Lego Mindstorms robot arm with the environment consisting of camera and lamps. (B) Details of robot arm.

The robot arm and its environment is filmed with the Bumblebee XB3 stereo camera (using only one camera) from a birds-eye view (see top right corner in Figure 2A). The distance between camera and table is 90 cm. The photo also shows that we used a normal desk light (gray object next to the camera) to keep the lighting roughly constant. For an easier detection of the robot arm blue markers are attached to the arm base and to the end effector. For the search items red and green colored markers are used (see bottom of the photo in Figure 2A).

The Control Architecture

Overview

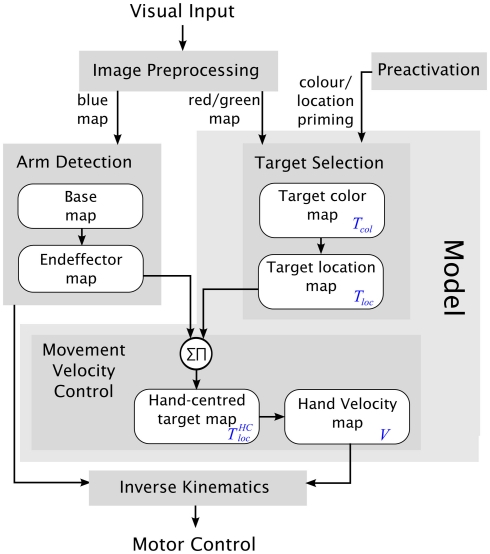
Figure 3 gives an overview of the control architecture. The input to the control architecture is the images from the Bumblebee camera. The outputs set the speed values of the robot arm joints. The control architecture continually updates the speed values based on the input images so that the robot arm is controlled in a closed-loop fashion. The control architecture is made up of five modules. The module Image Preprocessing detects the blue, red, and green markers in the camera images. The ArmDetection determines the location of the arm’s end effector by using the blue markers. The Target Selection finds the odd-color marker. The Movement Velocity Control combines the location of the end effector with the target location and determines the speed and direction of the movement for the arm in Cartesian coordinates. These movement parameters are then converted into the speed of the robot arm joints in the Inverse Kinematics.

Figure 3.

Overview of the control architecture. The light gray box contains the model. Dark gray boxes are the modules of the model. White boxes symbolize DNFs. In the text the blue abbreviations are used for the respective DNFs.

It is important to note that the modules fall into into two categories. The first type of modules (Image Preprocessing, Arm Detection, and Inverse Kinematics) implements technical solutions which were necessary for successfully controlling the robot’s behavior. However we do not claim that the implementations of these modules model human behavior. Moreover, these modules are not crucial for the implementation of the theory we fleshed out in the introduction nor for modeling the experimental data of choice reaching tasks. The second type of modules (Target Selection and Movement Velocity Control) constitutes “the model” implementing the theoretical assumptions explained in the introduction. These assumptions are: The processes in the target selection stage and the motor control stage use competitive and excitatory interactions between neurons. These are implemented with dynamic neural fields (DNFs). Both stages, the motor stage and the selection stage, operate in parallel. (Indeed all modules operate in parallel but this is not of theoretical significance.)

Image Preprocessing

The Image Preprocessing detects the three markers, blue, red, and green in the camera images and encodes their location in the respective color maps, the blue map, the red map, and the green map. This is achieved by first transforming the camera image from the RGB color space to the HSV color space. In the next step the Hue (H-dimension) is used to detect the markers’ color. Note that the usage of Hue improves the robustness of the control architecture against changing lighting conditions. The detection is implemented by testing each pixel if it falls into an interval around a pre-set H value. If this is true, the color map is set to one at the corresponding location. The pre-set H value takes on a different value, a “blue-,” “green-,” or “red”-value, for the different color maps. But if the pixels have an extreme saturation (S) or brightness (V) the activation is set to zero in order to avoid the detection of white or black areas. Finally, an erosion filter is applied to the maps to decrease the likelihood of isolated pixels in order to remove artifacts, e.g., isolated pixels, undesired reflections etc. (Jähne, 2008).

Arm detection

The detection of the robot arm encodes the locations of the arm’s base and the end effector in two separate DNFs. It exploits the fact that the marker on the base is slightly larger than the one on the end effector. So the first DNF (base map) receives the blue color map as input and selects the larger marker, as the DNF’s parameters ensure that an activation peak is only formed at the larger region. The output of the base map is topologically subtracted from the blue color map. The subtraction leaves activation at the location of the end effector but removes activation at the arm’s base. Subsequently a second DNF (end effector map) detects the location of the end effector. The parameters of the end effector map are set so that the output peak follows the movements of the end effector with only a slight delay.

Note that the arm detection implements a technical solution for the simple fact that humans need to keep track of the arm position. Alternatively or in addition we could have used proprioceptive information (joint angles). However, how humans determine the arm position is not relevant to the current research question. Therefore we simply used the camera images as they were necessary for the central research question anyway.

Target selection

This module is designed to detect the odd-color object. Two characteristics are important to determine the target: color and location. Therefore, the module consists of two DNFs, encoding target color (T_col map) and target location (T_loc map). The T_col map uses two neurons representing the two colors, red and green. As input, the T_col map receives the total activations of the red color map and the green color map. The parameters of the T_col map ensure that the neuron with the higher input is activated while the other neuron is deactivated. Consequently the T_col map establishes a high activation in the neuron which represents the more frequent color.

The input to the T_loc map is the topologically summed activation from the green color map and the red color map. The summation is weighted by the output of the T_col map whereby the colors are swapped to implement the odd-one detection.

Preactivation

In order to simulate the color priming effects, the T_col map in the target selection module receives an external input that activates the maps before the robot arm starts moving. After starting the movement of the robot arm this input is switched off. Nevertheless, the external input preactivates the T_col map thereby influencing the early phase of the reaching process. Hence the preactivation can potentially decrease the initial latency as found in Song and Nakayama (2008). In addition we also implemented a preactivation for the T_col map as there is also evidence for spatial priming from standard visual search tasks (e.g., Maljkovic and Nakayama, 1996).

Movement Velocity Control

The aim of this module is to generate arm movements toward the selected target item. This aim is achieved with two DNFs. The first DNF ($T_{loc}^{HC}$ map) represents the target in end effector-centered (hand-centered) coordinates. This representation is generated through a spatial correlation between the end effector map and the target selection map. The spatial correlation is performed in a way that the origin of the effector-centered coordinates are in the center of the $T_{loc}^{HC}$ map. Note that a biologically plausible implementation of the spatial correlation can be achieved with sigma-pi units. Sigma-pi units were first proposed by Rumelhart and McClelland (1986) (see Heinke and Humphreys, 2003 for another example of an application). Now with the effector-centered coordinates the $T_{loc}^{HC}$ map can encode how far the arm is from the target and what the direction of the movement should take. Therefore the $T_{loc}^{HC}$ map could successfully direct the robot arm to the target.

However if the $T_{loc}^{HC}$ map was directly used to encode the arm’s velocity the movement would be jerky, as the selection of the target would result in a sudden encoding of a high speed (proportional to the distance from the target). Therefore we introduced a second DNF (V map) that converts the representation of the movement direction in the $T_{loc}^{HC}$ map to an encoding of movement velocity. The representations of the $T_{loc}^{HC}$ map and the V map are aligned accordingly, meaning that the center of the $T_{loc}^{HC}$ map encodes zero distance from the target and the center of the V map encodes zero speed while activation peaks far away from the center of the $T_{loc}^{HC}$ map correspond to a large speeds in the V map (see Figure 4 for an illustration). In order to achieve more smooth, human-like movements, the V map realizes a “moving blob” behavior in the following way. At the beginning of a reach movement the V map has a peak at its center, thereby encoding zero speed. Then the peak moves toward the direction of the target (as encoded in the $T_{loc}^{HC}$ map), ramping up the arm’s speed in the direction of the target. While the arm is getting closer to the target the activation peak in the $T_{loc}^{HC}$map is moving closer to the center of the map, eventually aligning its location with the output peak of the V map and moving in parallel. Once this situation is achieved the V map guides the arm in the target by way of the closed-loop control. To be more specific, the arm moves closer to the target and subsequently the peaks in the $T_{loc}^{HC}$ map and the V map move closer to the center, thereby lowering the speed of the arm. This process continues until the arm reaches the target and stops.

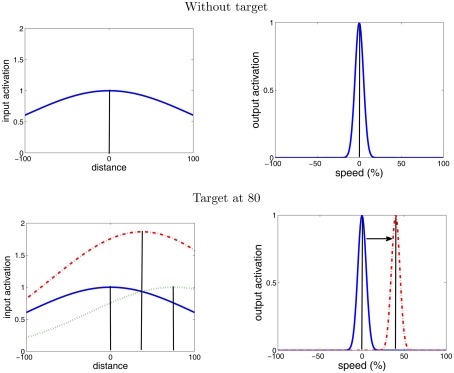
Figure 4.

“Moving blob” behavior in the V map. The top graphs show the behavior of the V map without a target being selected. The input activation for the V map is the Gaussian activation with its maximum in the center of the field causing the output activation of the V map to establish a peak at the center. With a target present (bottom graphs) its activation (dashed green line) is added to the activation around the center (blue line) resulting in a combined activation (red dashed line). This new input activation causes the output activation to move toward the new input maximum leading to an increase of the end effector’s speed (“Moving blob” behavior).

To realize this behavior the gradient in the input activation had to be designed appropriately as the gradient determines the “moving blob” behavior. We created an input activation that is made up of two parts (see Figure 4 for an illustration). One part is the output of the $T_{loc}^{HC}$ map but convolved with Gaussian function with a large sigma. Note that this convolution is a biologically plausible operation as it models how spatial activation diverges when traveling from one neural layer to the next neural layer. The purpose of the large sigma is explained at the end of this section. The second part is added to this activation and constitutes a Gaussian-distributed activation at the center of the V map. Without a target selection (before the start of the reach movement) this second part induces a peak at the center of the V map (see top of Figure 4). Once the target selection begins the first part of the input activation forms a gradient directing the peak toward the target location (see bottom of Figure 4). Hence the peak moves and subsequently the arm smoothly increases its movement velocity toward the target.

A final important point of the “moving blob” behavior is that the speed of the peak’s movement is proportional to the steepness of the gradient, as mentioned in the section on the dynamic field theory. Now since the input activation of V map is based on a Gaussian distribution with a large sigma, the gradient is steeper when the arm is far away from the target compared to when the arm is closer to the target (see red line in the bottom left graph of Figure 4). Hence, when the arm is far away from the target the acceleration of the arm is high while when the arm is getting closer to the target the acceleration is getting lower. In general this implements a good control strategy, since on the one hand it is efficient to move the arm as fast as possible when the arm is far away so that it reaches the target as fast as possible, while on the other hand if the target is close the arm should slowly maneuver toward the target so that it does not overshoot it. Moreover and interestingly this qualitative description is also reminiscent of the left part of the bell-shaped velocity profile. Hence it is conceivable that the arm exhibits this bell-shaped velocity profile. However as the Movement Velocity Control is embedded in a control-loop, ultimately this needs to be tested in experiments, e.g., is it successful in a noisy environment; what happens when the arm gets close to the target, will it reach the target, etc.

Inverse kinematics

The output of the Movement Velocity Control (V map) encodes the speed of the end effector in Cartesian coordinates. However in order to generate the actual movements of the robot arm, the Cartesian speed needs to be transformed into the speed of the robot arm joints. Here we follow the standard approach of using an approximation of the inverse of the Jacobian matrix (e.g., Siciliano and Khatib, 2008; see www.comp-psych.bham.ac.uk/Supplementaryinfo/Frontiers2012 for detail). Future versions will consider a more biologically motivated approach.

Single Target Experiment

The single target experiment aimed to demonstrate that the control architecture is able to reach successfully for objects in a noisy real world environment. We also wanted to show that the model generates human-like reach trajectories, i.e., the arm moves in a straight trajectory to the target and the velocity profile of the trajectory is bell-shaped (e.g., Jeannerod, 1984). These experiments also provided a baseline for second set of experiments, the choice reaching task.

Since this experiment used only single targets, the control architecture was simplified. As the target color did not play a role the T_col map was removed and the input for T_loc consisted of the combined red and green map.

Methods

The target objects were square colored markers (red or green) with a size of 3.5 cm × 3.5 cm. Targets were located on a virtual circle with the radius of 22 cm at 0°, 45°, 90°, 135°, and 180° (from left to right). The center of this circle was the starting position of the robot arm’s end effector. The starting position was located 9 cm in front of the arm’s base (shoulder). Before the experiment began the parameters of the image preprocessing were adapted to the current lighting conditions. After starting a trial the position of the end effector was recorded until the target was reached. The arm was considered to have reached the target when it was in a 6 cm × 6 cm area around the center of the target (see shaded area in Figure 6) and when its speed was less than 0.7 cm/s. For each possible target location five trajectories were recorded.

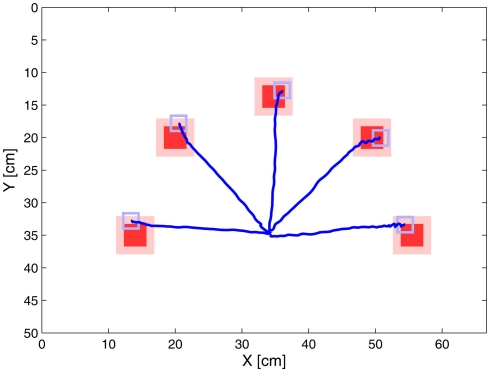
Figure 6.

Trajectories of the single target experiment. Targets of the reach movements are shown in red. When the arm reached at least the shaded area around the targets it was deemed to have reached the target. The gray square illustrates the size of the tip of the end effector. The base of the robot arm (shoulder) was positioned approximately 9 cm under the starting point of the end effector. The end effector itself was located in the origin of the trajectories (35 cm, 35 cm). The robot arm was able to follow a quasi straight path to the target. All trajectories are mean trajectories of 5 trials.

Since the sampling rate varied during each trial the data points for each trajectory (50–80 data points) were not recorded at the same points in time. In order to obtain an averaged trajectory we pre-processed each trajectory with the following steps. A spline function was fitted to each trajectory, then the resulting function was sampled with 100 equal time steps. Since the trajectories were fairly noisy, we smoothed the result with a moving average over 10 time steps. Finally, the averaged trajectory was obtained by averaging across the same time slice.

Results and discussion

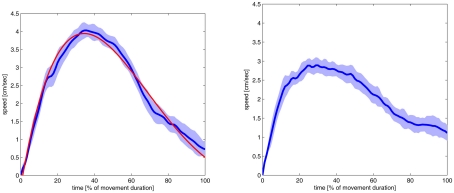
Our first experiments with the robot arm showed that, in principle, the arm exhibited the desired straight trajectories and the bell-shaped velocity profiles. This was expected from the design of the Movement Velocity Control. However the behavior turned out to be fairly unstable and noisy. For instance, even though the arm was able to move close to the target it had problems fully reaching the target. We therefore chose to modify the V map. Originally the V map followed the linear encoding schema commonly used in DNFs (see Figure 1 for an illustration). In the new version the neural layer is mapped onto the parameter space in a non-linear fashion in which many neurons map onto low speeds whereas only a few neurons map into high speeds. We expected that this encoding should lead to a better behavior of the arm as it represents a good compromise between two objectives. On the one hand it leads to more precise movements when the end effector is close to the target, while on the other hand it allows the arm move more coarsely while it is still far away from the target. Indeed, this encoding schema led to better behavior of the arm (see Figure 5 for a comparison). Overall, the movement was less noisy and more bell-shaped. The peak velocity was higher but in the vicinity of the target the velocity was lower which resulted in a better target reaching behavior. It is also interesting to note that the maximum speed was reached later in the movement (at around 40%) which fits better to the experimental findings with humans (e.g., Jeannerod, 1984).

Figure 5.

Velocity profiles of the simulated movements to the top center position of Figure 6. The profiles are shown with their standard deviation (light blue area) and the point where the initial latency end and the movement starts (black line). Negative time values represent the initial latency. The movement ended at 100%, the time scale goes slightly higher than this value, because the dark blue line represents the moving average of 10 time slices of the movement. The result on the right side was produced with a standard topological encoding in the V map of the Movement Velocity Control module. On the left a non-linear encoding was used. This encoding schema let to better reaching movements. The red line documents the outcome of the VITE-model fitted to the robot arm behavior (see main text for detailed discussion). Both velocity profiles are the average of 25 trials.

Figure 6 shows the mean trajectories toward the five target markers. The trajectories were almost straight with only a little curvature. These results are comparable with experimental findings on humans. For example Haggard and Richardson (1996) found that humans reach with similar (almost straight) paths in different regions of the workspace. Also Desmurget et al. (1999) support the model’s approach that compliant movements in the horizontal plane are planned in the extrinsic space, which results in straight hand trajectories. Taking together the results of this experiment gave support for the implementation of the Movement Velocity Control module.

For an additional verification of our model we compared the arm’s behavior with a mathematical model for velocity profiles. In fact, there are several mathematical models for velocity profiles such as the Minimum Hand Jerk model, the Minimum Commanded Torque Change model, etc. A recent review by Petreska and Billard (2009) suggested that a modified vector integration to endpoint (VITE) model (Bullock and Grossberg, 1988) yields the best fit to human movement trajectories. In the current paper we used the VITE-model as the reference model for our model. The VITE-model is described with the following equations:

$$\begin{array}{llll}\stackrel{.}{\mathbf{\text{y}}}\left(t\right)& =\alpha \left(-\mathbf{\text{y}}\left(t\right)+{\mathbf{\text{x}}}_{target}\left(t\right)-\mathbf{\text{x}}\left(t\right)\right)& & \text{(1)}\\ \stackrel{.}{\mathbf{\text{x}}}\left(t\right)& =\beta t^v\mathbf{\text{y}}\left(t\right)& & \text{(2)}\end{array}$$

The parameters α, β, and v are real positive constants and control the changing rate of the acceleration. x_target and x are the position of the target and the end effector respectively. y is a secondary variable and related to the speed of the end effector.

To compare the VITE-model with the robot arm’s velocity profile we used the average velocity profile shown in Figure 5. For each time step in this profile we determined whether the VITE-model produced a velocity value that fell within the one standard deviation interval. Then we calculated that percentage of time steps which fulfilled this criterion. For the following parameters 98% of time steps fulfilled this criterion: x_target = 10, α = 0.058, β = 0.01, and v = 0.0286 (see Figure 5 for the resulting velocity profile). In other words for these parameters the VITE-model and the robot arm’s velocity profile were very close in 98% time steps providing further support for our model.

Odd-Color Experiment

After having shown that the model is able to reproduce human reaching trajectories, the next aim was to replicate the odd-color experiment by (Song and Nakayama, 2008). Here the aim was two fold: The model should be able to direct the robot arm to the odd-color and second, the model should reproduce the effects of color priming, i.e., the curved trajectories with longer movement times and the reduction of the initial latency.

As pointed out in the introduction of the preactivation module there is also evidence for spatial priming from standard search tasks (e.g., Maljkovic and Nakayama, 1996). Even though there is no evidence from choice reaching tasks it seems plausible to expect spatial priming effects similar to the color priming effects. Since the model also allows us to implement spatial priming we will also present these experiments here and compare them to color priming.

Methods

The setting of this experiment is similar to the single target experiment except that similar to the setup in Song and Nakayama’s (2008) experiment we used an odd-color display. There were three markers placed in the workspace: either two red and one green or two green and one red marker (see Figure 2 for an example). Both colors can be easily distinguished by the Image Preprocessing. The possible locations for the marker were at 45°, 90°, and 135°, the three central locations in the single target experiment. All modules of the model were used including the non-linear encoding of the velocity DNF developed in Experiment 1, so the target selection should be able to perform the odd-color search task. Moreover, and importantly, the preactivation module should be able to induce the priming effects in the model.

The data analysis followed the same steps as in Experiment 1 using spline function and moving average to obtain smoothed trajectories. In addition the following durations were extracted from the smooth trajectories: the initial latency (IL) and the movement duration (MD). The beginning of the movement (and the end of the IL) was determined at the point in time when the velocity was higher than 0.3 cm/s for the first time. These times allowed us to relate our results to Song and Nakayama’s (2008) findings.

Results and discussion

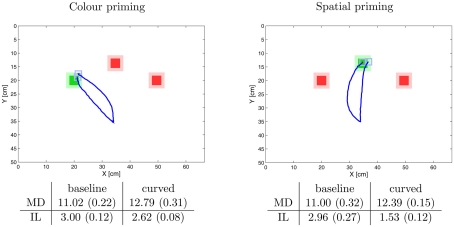
Figure 7 shows the trajectories of the robot arm in the odd-color experiment. To begin with the results demonstrate that the model is able to detect the odd-color marker and successfully directs the arm to the target marker. Moreover, with the help of the preactivation module (priming) we were able to generate the curved trajectories found by Song and Nakayama (2008). The results also mimic Song and Nakayama’s (2008) finding that the initial latency was shorter in the priming condition compared to the baseline and that the movement duration of the curved trajectory was longer. Interestingly the size of the effect depended on the type of priming, either color priming or spatial priming. For spatial priming the effect of the initial latency was larger than for the color priming. In contrast, the movement time was longer for the color priming than for the spatial priming.

Figure 7.

Example trajectories with measured time intervals of the simulation of the odd-color experiment. The trajectories are mean trajectories of five trials. The time intervals are also the average times from five trials in seconds. The figures in brackets indicate the standard deviation. The abbreviations stand for initial latency (IL) and movement duration (MD). The results demonstrate that the model can successfully direct to the robot arm to the odd-color target. The “curved” trajectories result from the preactivation of the spatial map (spatial priming, on the right) and the color map (color priming, on the left). In both conditions, compared to the straight trajectories the initial latency decreases and the movement times increases matching the experimental data by (Song and Nakayama, 2008). Interestingly the effect on the initial latency is stronger in spatial priming than in color priming. This effect is discussed in the main text.

Taken together the results demonstrate that the model can successfully mimic the findings by Song and Nakayama (2008). In particular the preactivation initially directs the competition in the target selection module toward distractors. In turn, this guides the moving blob in the V map and the robot arm toward the distractors. However after some time the preactivation is overwritten and the moving blob and the robot arm are directed toward the target. In some way the priming effect in our model can be conceptualized as the distractors first “pulling” the arm toward their direction. We will return to this point in the next experiment. However, it is also worth noting that a model by Tipper et al. (1998) proposes a similar pulling effect based on a similar mechanism. Their model suggests that the directions of movements toward the target and the distractors are encoded with distributed representations similar to the one postulated in the DNFs. Moreover the model determines that resulting movement direction by calculating the center of gravity of the combined representation of target and distractors. Consequently the resulting movement veers toward the distractors. However, Tipper et al.’s (1998) model does not include a mechanism of how such distorted movement directions are translated into actual movements and how humans eventually reach the target.

Furthermore our model predicts that additional experiments with humans should find a difference between spatial priming and color priming. Even though the difference found with the robot arm can be due to different parameter settings, e.g., the preactivation is higher in spatial priming than in color priming, the difference originates from an architectural difference of how the two dimensions influence the selection process. The spatial priming directly influences the selection map whereas the color priming affects selection via the weighting of the two color maps. In addition the difference between color priming and spatial priming also plays out differently for the initial latency and for the curved trajectory. For the initial latency, the structural difference is responsible for the difference. In contrast, for the movement duration the difference nature of the features is important. In the color priming two distractors attract movements whereas for the spatial priming only one location distorts movements.

“Continuous” vs. “Threshold” Experiment

In the previous experiment we pointed out that the curved trajectories in the model are the result of the distractors pulling the arm toward their location. In other words, the activation in the competitive selection does not necessarily need to pass a threshold for it to affect the reaching process (“continuous” hypothesis). This contrasts with a suggestion by Song and Nakayama (2008). They proposed that the competitive selection first has to reach a threshold before it can direct movements toward an item, e.g., a distractor (“threshold” hypothesis). In fact, this hypothesis can be also simulated with our model by adding a threshold at the output of the selection stage. The current experiment will illustrate the different reaching movements the two hypotheses would predict.

Methods

The settings of this experiment were similar to the ones of Experiment 2. However, the color priming activation was increased to make the illustration clearer. To implement the “threshold” hypothesis a threshold between the T_loc map and the $T_{loc}^{HC}$ map was introduced so that only high activations in the T_loc map can influence the behavior of the $T_{loc}^{HC}$ map.

Results and discussion

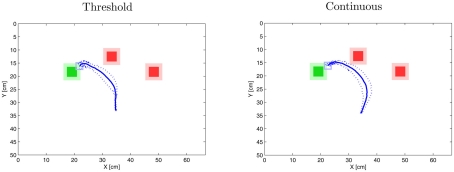
Figure 8 depicts the results based on five trials in for each hypotheses and highlights the differences. As expected, trajectories in the “threshold” setup pointed toward one of the distractors in an early stage of the movement, while trajectories in the “continuous” condition fell somewhere between the two distractors. Hence in order to distinguish between the two hypotheses it makes sense to determine the orientation of the movements at their early phase. Now for these movement orientations the “threshold” hypothesis predicts are bimodal distribution with the two modes roughly pointing toward the distractors. In contrast, the “continuous” hypothesis predicts an unimodal distribution with a peak roughly between the two distractors. Moreover Figure 8 illustrates that the variation of the movement orientation is smaller for the “threshold” hypothesis than for the “continuous” hypothesis. The large variation in the “continuous” hypothesis is due to the fact that the two distractors induce noise onto the movements whereas in the threshold hypothesis only one distractor influences the movements. Note that the latter point implies that we expect a variation around each mode in the order of magnitude of the single target displays. Future experiments with human participants will need to test this prediction.

Figure 8.

Comparison of “ continuous” vs. “ threshold” hypothesis (Experiment 3). The result on the left shows the outcome of the threshold hypothesis. Note that in this setting the trajectory veers toward the middle or the right distractor randomly depending on the noise in the DNFs. For the above figure only the trajectories toward the middle distractor were chosen. The trajectory on the right is the effect of the “continuous” hypothesis (see main text for detail). Each mean trajectory shows the results from 5 trials. The broken lines documents the standard deviation.

General Discussion

Recently Song and Nakayama (2008) published evidence that the process of attentional selection can influence reach movements toward a target. In this study, the reaching target was given by an object with the odd-color, e.g., a red square among green squares. In this current paper we presented a robotics-based approach to modeling the results of this choice reaching experiment. To take into account that these experiments use human movements the output of model is a robot arm built with LEGO Mindstorms NXT. The first stage of the model, the attention stage, is based on our earlier work in modeling visual attention (e.g., Heinke and Humphreys, 2003; Heinke and Backhaus, 2011) and implements a competitive selection process of the odd-color target. In order to link the output of this stage with the robot arm we based the motor control stage on the dynamic field theory by Erlhagen and Schoener (2002). Crucially, the motor control stage uses a “moving blob”-dynamics in a neural field to ensure jerk-free (human-like) movements. Overall the model is consistent with Song and Nakayama’s (2009) suggestions that there is a direct link between target selection and movement planning, that both processes work in parallel and that the target selection process is implemented in a dynamic competition.

Three experiments were performed to test the model’s abilities. The first experiment used a single target setup and demonstrated that the model can guide the robot arm to the target in quasi straight trajectories. Moreover, the trajectories exhibited a bell-shaped velocity profile often found in experiments with humans. Crucial for the produce of the bell-shaped velocity is the “moving blob”-behavior in the Movement Velocity Control. This implements the ramping up and down of the velocity. This behavior was theoretically examined by Amari (1977). However, to the best of our knowledge it has never been used to describe human behavior in a functional model before. It also remains an open question whether the brain employs this behavior. The second interesting outcome of the first experiment is that we had to introduce an inhomogeneous spatial encoding of the velocity parameter. The inhomogeneity is such that at small velocities the encoding has a high spatial resolution, whereas at high velocities the encoding is coarse. This divergence from the normal linear encoding schema in DNFs was necessary to achieve a better control of the arm in terms of robustness and higher peak speed, but also made the speed profile similar to human velocity profiles. Importantly the encoding schema is reminiscent of the way the visual cortex represents stimuli, i.e., the “cortical magnifying factor” (e.g., Rovamo and Virsu, 1979). In this representation visual stimuli are represented with a fine grain resolution in the foveal region, while in the parafoveal region stimuli are represented with a coarse resolution. Hence it is not inconceivable that the brain has reused this mechanism in the motor cortex as suggested by our model. However, as with the “moving blob” behavior, this prediction remains to be tested in physiological experiments.

The second experiment demonstrated that the model performs the odd-color search task by Song and Nakayama (2008), i.e., the robot arm successfully reached the object with the odd-color. This success also included the reproduction of the curved trajectories. Moreover, the curved trajectories showed a lower initialization time of the movement while the movement time increased due the longer length of the trajectories, again mimicking Song and Nakayama’s (2008) findings. The model also predicts that these priming effects not only occur for color but also for space (see Maljkovic and Nakayama, 1996 for spatial priming effects in a standard visual search task). Moreover the model suggests that the priming effects are stronger for space than for color. This prediction is in part due to the different way the two dimensions are processed in the model and in part due to how the two dimensions are differently reflected in the visual search display. The latter point refers to the fact that spatial priming may a effect a single distractor whereas color may affect a group of distractors. This prediction remains to be tested.

In Experiment three we illustrated a subtle but important difference in the way Song and Nakayama (2008) explain the priming effect and in the way the model realizes the priming effect. In both explanations it is assumed that the priming effect is the effect of residual activation from the target in the preceding trial misdirecting the reach movement. However, while Song and Nakayama (2008) suggest that the competitive selection reaches a threshold in order for it to cause reaching toward a distractor (“threshold”-hypothesis), our model suggests a different mechanism. It suggests that the competitive selection does not necessarily need to pass a threshold for it to affect the reaching process. Instead, items during the competition process pull the reaching movements toward their position and the strength of the attraction is related to how much they are selected (“continuous”-hypothesis). The experiment makes predictions for the directions of “curved” movements at their early stage. The “threshold”-hypothesis predicts that the distribution of the directions should be bimodal with the two modes at the directions of the distractors. In contrast the “continuous” hypothesis suggests a unimodal distribution with a peak roughly falling between two distractors. Future experiments with humans will have to test these predictions.

Finally, it is also worth pointing out that the robotics-based modeling approach taken here can be employed to other choice reaching tasks concerning processing of numbers or phonology.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.